圆的面积奥数
六年级奥数专题圆的面积
平面图形面积————圆的面积【1】在正方形里的最大圆的面积占所在正方形的面积的3.144,而在圆内的最大正方形占所在圆的面积的23.14例题1。
求图中阴影部分的面积（单位：厘米）。
练习11.求下面各个图形中阴影部分的面积（单位：厘米）。
2.求下面各个图形中阴影部分的面积（单位：厘米）。
答练习21、计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。
答2、计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。
答1 2练习41、 如图所示，三角形ABC 是直角三角形，AC 长4厘米，BC 长2厘米。
以AC 、BC 为直径画半圆，两个半圆的交点在AB 边上。
求图中阴影部分的面积。
答例题5。
在图中，正方形的边长是10厘米，求图中阴影部分的面积。
练习51、求下面各图形中阴影部分的面积（单位：厘米）。
答2、求右面各图形中阴影部分的面积（单位：厘米）。
答3、求右面各图形中阴影部分的面积（单位：厘米）。
答例题6。
在图的扇形中，正方形的面积是30平方厘米。
求阴影部分的面积。
练习61、 如图所示，平行四边形的面积是100平方厘米，求阴影部分的面积。
答圆的面积与组合圆积专题训练一、填空题1.算出下面圆内正方形的面积为.2.右下图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角,以扇形的半径为边长画一个正方形,这个正方形的面积是1206厘米 2E D C B A 平方厘米.这个扇形面积是.4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米.(保留两位小数)5.左下图三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长厘米6.如右下图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为.7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是.度。
8.图中扇形的半径OA=OB=6厘米.,AC 垂直OB 于C,那么图中阴影部分的面积是平方厘米. 9.在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.10.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大平方厘米.11.左下图在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是平方厘米.(取3.14,结果精确到1平方厘米) 12.右上图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).13.如左下图所示,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.14.如右下图,的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是.15. 如左下图已知:ABCD 是正方形, ED=DA=AF=2厘米,阴影部分的面积是.6C B A O 4512 15 20 C ②① AB16.右下图中,扇形BAC 的面积是半圆ADB 的面积的倍,那么,是度. E D C BA GF O D C A B。
奥数专题平面图形之圆的面积(有例题讲解和相应的练习)
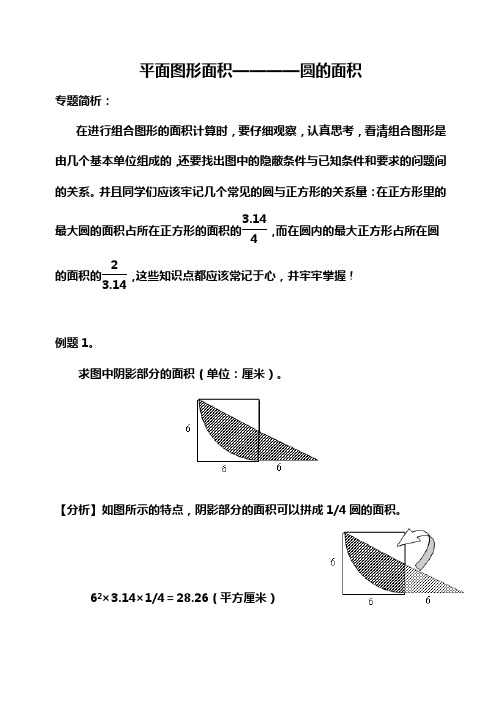
平面图形面积————圆的面积专题简析：在进行组合图形的面积计算时，要仔细观察，认真思考，看清组合图形是由几个基本单位组成的，还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。
并且同学们应该牢记几个常见的圆与正方形的关系量：在正方形里的最大圆的面积占所在正方形的面积的3.144,而在圆内的最大正方形占所在圆的面积的23.14,这些知识点都应该常记于心，并牢牢掌握！例题1。
求图中阴影部分的面积（单位：厘米）。
【分析】如图所示的特点，阴影部分的面积可以拼成1/4圆的面积。
62×3.14×1/4＝28.26（平方厘米）练习11.求下面各个图形中阴影部分的面积（单位：厘米）。
2.求下面各个图形中阴影部分的面积（单位：厘米）。
答例题2。
求图中阴影部分的面积（单位：厘米）。
【分析】阴影部分通过翻折移动位置后，构成了一个新的图形（如图所示）。
从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。
3.14×42×1/4－4×4÷2÷2＝8.56（平方厘米）练习21、计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。
答2、计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。
答1 2例题3。
如图19－10所示，两圆半径都是1厘米，且图中两个阴影部分的面积相O的面积。
等。
求长方形ABO1【分析】因为两圆的半径相等，所以两个扇形中的空白部分相等。
又因为图中两个阴影部分的面积相等，所以扇形的面积等于长方形面积的一半（如图19－10右图所示）。
所以3.14×12×1/4×2＝1.57（平方厘米）练习31、如图所示，圆的周长为12.56厘米，AC两点把圆分成相等的两段弧，阴影部分（1）的面积与阴影部分（2）的面积相等，求平行四边形ABCD的面积。
答2、如图所示，AB＝BC＝8厘米，求阴影部分的面积。
六年级上册数学圆计算 奥数
多少厘米？O2.将半径分别是3厘米和2厘米的两个半圆如下图形状放置，求阴影部分的周长。
2cm 3cm 3.下图中，正方形ABCD的边长4厘米，求长方形EFGD的面积。
4.李大伯用长48米的篱笆在院子墙边（一面靠墙）围出了一个长方形花坛，怎样围，面积最大?5.已知正方形的边长是4厘米，求阴影部分的周长44CDCD多少厘米？36×54＝45（厘米）2.将半径分别是3厘米和2厘米的两个半圆如下图形状放置，求阴影部分的周长。
2π＋3π＝5π＝15.7（厘米） 2×2－3＋3＝4（厘米） 15.7＋4＝19.7（厘米）3.下图中，正方形ABCD 的边长4厘米，求长方形EFGD 的面积。
做辅助线AG,△AGD 既是正方形的一半，又是长方形EFGD 也就是说，正方形的面积等于长方形的面积。
4×4＝16平方厘米4.李大伯用长48米的篱笆在院子墙边（一面靠墙）围出了一个长方形花坛，怎样围，面积最大?方法一：长：46、44、42、40、38、36、34 32、30、28 26、 24、 22、 20、 18、 16 宽：1、 2、 3、 4、 5、 6、 7、 8、 9、 10、 11、 12、 13、 14、 15、 16 长：24米 宽：12 面积：24×12＝288（平方米）方法二：假设用96米围成一个正方形，再取正方形面积的一半。
48×2＝96（米） 96÷4＝24（米） 24÷2＝12（米） 面积：24×12＝288（平方米）5.已知正方形的边长是4厘米，求阴影部分的周长3.14×4＝12.56（厘米）。
奥数专题圆的面积
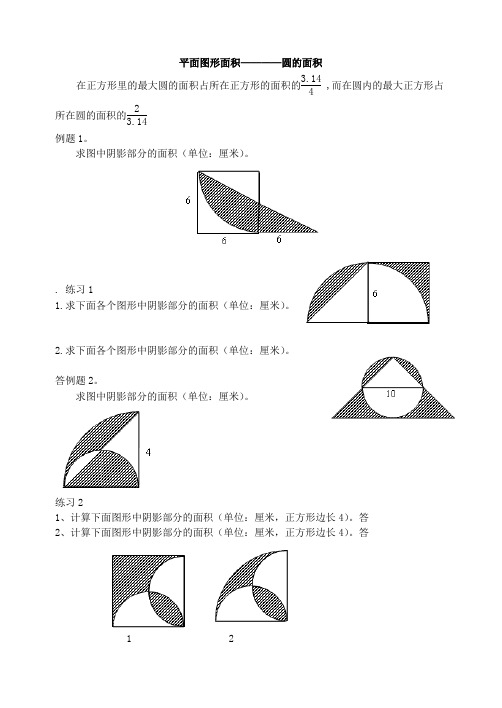
平面图形面积————圆的面积在正方形里的最大圆的面积占所在正方形的面积的3.144 ,而在圆内的最大正方形占所在圆的面积的23.14例题1。
求图中阴影部分的面积（单位：厘米）。
. 练习11.求下面各个图形中阴影部分的面积（单位：厘米）。
2.求下面各个图形中阴影部分的面积（单位：厘米）。
答例题2。
求图中阴影部分的面积（单位：厘米）。
练习21、计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。
答2、计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。
答1 2例题3。
如图所示，图中圆的直径AB是4厘米，平行四边形ABCD的面积是7平方厘米，∠ABC ＝30度，求阴影部分的面积（得数保留两位小数）。
例题4。
如图所示，求图中阴影部分的面积。
. 练习41、如图所示，三角形ABC是直角三角形，AC长4厘米，BC长2厘米。
以AC、BC为直径画半圆，两个半圆的交点在AB边上。
求图中阴影部分的面积。
答例题5。
在图中，正方形的边长是10厘米，求图中阴影部分的面积。
.练习51、求下面各图形中阴影部分的面积（单位：厘米）。
答2、求右面各图形中阴影部分的面积（单位：厘米）。
答3、求右面各图形中阴影部分的面积（单位：厘米）。
答.例题6。
在图的扇形中，正方形的面积是30平方厘米。
求阴影部分的面积。
练习61、 如图所示，平行四边形的面积是100平方厘米，求阴影部分的面积。
答圆的面积与组合圆积专题训练一、填空题1.算出下面圆内正方形的面积为 .2.,直角边长2厘米,图中阴影部分面积是 平方厘米3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.左下图三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长 厘米6.如右下图,阴影部分的面积为2平方厘米,7.157平方厘米,这个扇形的圆心角是 .度。
六年级上册数学培优奥数讲义-第12讲 圆的面积
第12讲 圆的面积知识装备1、圆的面积公式：S ＝πr 2； 扇形的面积公式：S ＝360nπr 2。
2、在与圆有关的面积计算中，经常需要添加辅助线，根据圆的特征进行面积转化，使之变成有利于计算的图形，再计算。
初级挑战1求下面图形中阴影部分的面积。
（单位：厘米）思维点拨 ：阴影部分面积＝（ ）的面积－（ ）的面积，半圆直径是8厘米，正方形边长是（ ）厘米。
答案：正方形的面积：8×8=64（cm ²） 圆的面积：3.14×（8÷2）²=50.24（cm ²） 阴影部分的面积：64-50.24=13.76（cm ²）能力探索11、求下面图形中阴影部分的面积。
（单位：厘米） （1） （2）答案：（1）大半圆的面积：3.14×[（30+50）÷2]²÷2=2512（cm ²） 小半圆的面积：3.14×（30÷2）²÷2=353.25（cm ²） 中半圆的面积：3.14×（50÷2）²÷2=981.25（cm ²） 阴影部分的面积：2512-353.25-981.25=1177.5（cm ²） （2）大半圆的面积：3.14×（8÷2+2）²÷2=56.52（cm ²） 小半圆的面积：3.14×（8÷2）²÷2=25.12（cm ²） 阴影部分的面积：56.52-25.12=31.4（cm ²）2、下图是半径为24厘米的扇形，求图中阴影部分的面积。
答案：两个相同的图形拼成一个四分之一扇形。
3.14×24²÷4-24×24÷2=616.32（平方厘米） 616.32÷2=308.16（平方厘米）初级挑战2如图，等腰直角三角形直角边长为14厘米，两个半圆的直径是三角形的直角边，求图中阴影部分的面积。
(六年级奥数讲义)第七讲--圆的面积
第六讲 圆的面积
一、学习目标
1、熟悉圆的面积公式。
2、学会利用圆的面积公式求阴影部分面积。
二、重难点突破
1、圆的面积公式：22d r 2s ⎛⎫== ⎪⎝⎭ππ；半圆的面积公式：2
2211d 1r d 2224s ⎛⎫=== ⎪⎝⎭πππ；2
2c c 24s ⎛⎫=== ⎪⎝⎭
πππ（其中r 为半径，d 为直径，c 为周长）。
2、1°扇形的面积：2r 360s =π，n °扇形的面积：2
n r 360
s =π。
三、例题精讲
【例题1】下图中阴影部分的面积是50cm 2,求环形的面积。
思路点拨：
【例题2】每个扇形的半径均为6厘米，求阴影部分的面积。
思路点拨：
【例题3】如下图，已知圆的面积是628平方厘米，求正方形的面积。
思路点拨：
【例题4】如果圆的半径增加1
4
，那么它的面积就增加72平方分米，求原来圆的面积。
思路点拨：
【例题5】下图三角形ABC是直角三角形，阴影Ⅰ比阴影Ⅱ的面积小23m2,问：BC长多少米？
思路点拨：
四、巩固精练
【精练1】求下面图形阴影部分的面积。
（单位：dm）
（1）（2）
【精练2】如
下图，三个圆的周长都是25.12厘米，求阴影部分的面积。
【精练3】已知正方形的边长为8cm，以两条边长为直径作两个半圆（如下图），求出阴影部分的面积。
精练4】如下左图，图中圆的周长是62.8厘米，圆的面积与长方形的面积正好相等，图中阴影部分的周长是多少厘米？。
圆的面积奥数
圆的面积圆是一种平面图形，再日常生活中到处可见．如圆桌，圆盘，车辆的轱辘，以及游戏用的棋子，飞盘，呼啦圈等，由于圆有着本身独特的性质，在某些地方是其它形状所不能代替的，车轱辘就是一个很好的例子．这一讲我们着重研究圆以及和圆有关的组合图形的求面积方法．圆的面积计算公式，扇形面积计算公式，同学们在课本上已经都有初步的理解和掌握，我们主要讨论组合图形的面积的计算方法与技巧．请注意常用的扇形：四分之一圆对应圆心角是90度，八分之一圆对应的圆心角是45度．经典题再现如下图所示，O是圆心，圆的周长等于75.36分米，点A、B、C都在圆周上，OABC是梯形，梯形的面积是98.28平方分米．AB=20.76分米，那么阴影部分的面积是多少平方分米?（π取3.14）解：由圆的周长可求圆的半径：75.36 = 2 × 3.14 × r ，r = 12．即OC = 12．由梯形的面积及它的上底，下底已知，可求梯形的高．98.28 = (12 + 20.76) × 高 ÷ 2，高 = 6．阴影的面积 = 12 × 6 ÷ 2 = 12 × 3 = 36（平方分米）．典型例题【例1】 长方形长6分米，宽4分米，分别以长、宽为半径画弧，如图．那么阴影部分的面积是多少平方分米？解：226 3.144 3.1464⎛⎫⨯⨯-⨯- ⎪⎝⎭= 16.82（平方厘米） 答：影阴部分的面积是16.82平方厘米．【例2】 如图，半圆S 1的面积是14.13平方厘米，圆S 2的面积是19.625平方厘米，那么阴影部分的面积是多少平方厘米?解：因为s 1的面积为14.13平方厘米，所以半径的平方为14.13⨯2÷3.14 = 9，故半径为3厘米，直径为6厘米．又因为s 2的面积为19.625平方厘米，所以S 2的半径的平方为19.625÷3.14 = 6.25（平方厘米），所以它的半径为2.5厘米，直径为5厘米，所以阴影部分面积为（6 - 5）⨯5 = 5（平方厘米）．答：阴影部分的面积是5平方厘米．【例3】 如图，A 与B 是两个圆（只有1）的圆心，那么，两个阴影部分的面积相差多少平方厘米?解：观察上图可以发现大14圆的面积减去长方形的面积（包括小阴影和大空白两部分）再减去小14圆的面积．就是两个影阴部分的面积差． 即22113.14424 3.142⨯⨯-⨯-⨯⨯= 1.42（平方厘米） 答：两个阴影部分的面积相差1.42平方厘米．【例4】 如图，圆的直径AB 是4cm 的面积是7cm 2，∠ABC等于30°，求阴影部分面积．解：这个题许多同学将ABC 看成是圆心角为30°的扇形．这是错误的，因为AB 是直径，BC 不是，AB ，BC 不一样长，所以，ABC 不是扇形．如下图，找到圆心O，连CO，AOC才是扇形．先要求这个扇形的圆心角，就可以求出它的面积．然后再求三角形COB的面积，用ABCD阴影面积等于平行四边形面积减去扇形AOC的面积，再减去△BOC 的面积．扇形的圆心角=180°-（180°-30°×2）=60°．扇形的面积=2×2×3.14×60÷360=2.09（平方厘米）．△BOC的面积=7÷2÷2=1.75（平方厘米）．阴影部分的面积=7–2.09 1.75=3.16．答：阴影部分的面积是3.16平方厘米．【例5】下图中阴影部分的面积是多少平方厘米？解：两个空白部分拼起来正好是一个4×4的正方形．所以阴影部分面积等于2×4的长方形面积．2×4=8（平方厘米）答：影阴部分的面积是8平方厘米．【例6】如图所示，这是一个正六边形，它的面积为1040平方厘米．空白部分是半径为10cm的6个小扇形．求阴影部分的面积．解：图中阴影部分的面积显然是正六边形的面积减去六个小扇形的面积．正六边形的面积已知，所以关键是求六个小扇形面积．我们观察每3个小扇形可以拼成一个半径为10厘米的圆，6个小扇形可以拼成2个小圆形．阴影部分的面积就是正六边形的面积减去2个半径为10厘米的小圆的面积．6个扇形的面积为3.14×102×2=628（平方厘米），阴影部分的面积：1040-628=412（平方厘米）．答：阴影部分的面积为412平方厘米．难题详解如下图所示，在4×7的方格纸板上画出如阴影所示的“9”字，阴影边缘是线段或圆弧．问阴影面积占纸板面积的几分之几?圆周．非阴影部分共6解：矩形纸板共28个小正方形．其中弧线是14个，也共6个．可拼成6个小正方格．因此阴影部分共28-6-3=19个小方格．所以，阴影面积占纸板面积的19．28．答：阴影面积占纸板面积的1928同步练习1．如下图，ABCD为正方形，且F A=AD=DE=2厘米，求阴影部分的面积？2．有三个形状相同的圆形纸片，面积都是90平方厘米，重叠在一起（如图），盖住桌面的总面积是150平方厘米，三张纸片重叠的面积是28平方厘米，那么图中三个阴影部分面积和是多少平方厘米？3．已知图中各圆相切，小圆半径为1，求阴影部分面积．4．已知每个圆的直径为6厘米，求阴影部分的面积．5．图中正方形ABCD的边长是20厘米，求阴影部分面积．6．如图，已知每个小正方形的面积为1平方厘米，求阴影部分面积．（注：所用分点均理解为所在边中点）．7．如图，大圆直径上的黑点是五等分点，求A，B，C三部分面积之比．8．如图，O为圆心，C为扇形ACB的圆心，CO垂直于AB，三角形ABC的面积为45平方厘米，求阴影部分面积．同步练习解答1．图形DGC 为图形DBC 面积的一半，于是，阴影部分的面积为()()2211133.1422222 3.1424242⨯⨯-⨯⨯+⨯-⨯⨯⨯=2.43（平方厘米） 2．解：90 × 3 - 150 - 28 × 2 = 64（平方厘米）3．如图I ，II ，III 部分面积是相等的，剩余3块小阴影面积也相等．那么所求阴影部分面积是一个小半圆面积加上大半圆减去2个小圆和3个小半圆剩余部分的13． 阴影面积为：2π1π3πππ52π3π2322236⎛⎫⨯+⨯--⨯=+= ⎪⎝⎭4．如图，长方形外的阴影部分一共3311442+=个圆，移至长方形内正好填满长方形，阴影部分的面积就是长方形面积．阴影部分面积 = 6 × 2 × 6 = 72（平方厘米）．5．充分利用圆的对称性，如图，大扇形ABC 的半径是20，它的面积减去三角形ABC 的面积就是I 的面积．正方形ABCD 减去圆O 的面积就是4个II 的面积．阴影部分就是ABCD 面积减去2个I ，4个II 的面积．20()2211202π2020204(2020π10)42⨯-⨯⨯⨯-⨯⨯-⨯⨯-⨯ = 129（平方厘米）6．阴影分成两部分，一部分是字母“A ”，一部分是字母“r ”． 字母“A ”的面积，我们只需算一半，再2倍就可以了．平行四边形ABCD 面积=13322⨯= 梯形EFHG 面积=()131********+⨯⨯= 字母“A ”的面积()3529123 3.62521688+⨯===． 字母“r ”的面积2π3662212.26⨯-⨯÷+=．最后，阴影面积为3.625 + 12.26 = 15.885（平方厘米）．7．显然，A 与C 面积相等，B 与C 面积比为（1.52 - 12）：[（2.52 - 1.52 + 12）÷ 2] = 1∶2．所以，A ，B ，C 面积比为：2∶1∶2．8．设CA = CB = a ，OC = OB = OA = r ．则由三角形ABC 面积为45知，1452a a ⨯⨯=，a 2 = 90． 再以AB 为底计算三角形ABC 面积：AB ⨯OC ⨯12=2⨯OA ⨯OC ⨯12=b 2知，b 2 = 45．阴影部分面积 = 半圆面积 + 三角形ABC 面积 - 扇形ACB 面积．即 45 + b 2⨯3.14⨯12- a 2 ⨯3.14⨯14= 45 + 45⨯3.14⨯12- 90⨯3.14⨯14= 45。
奥数专题平面图形之圆的面积
平面图形面积————圆的面积之勘阻及广创作专题简析：在进行组合图形的面积计算时，要仔细观察，认真思考，看清组合图形是由几个基本单位组成的，还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。
而且同学们应该牢记几个罕见的圆与正方形的关系量：在正方形里的最大圆的面积占所在正方形的面积的3.144,而在圆内的最大正方形占所在圆的面积的23.14,这些知识点都应该常记于心，并牢牢掌握！例题1。
求图中阴影部分的面积（单位：厘米）。
【分析】如图所示的特点，阴影部分的面积可以拼成1/4圆的面积。
62×3.14×1/4＝28.26（平方厘米）练习11.求下面各个图形中阴影部分的面积（单位：厘米）。
2.求下面各个图形中阴影部分的面积（单位：厘米）。
答例题2。
求图中阴影部分的面积（单位：厘米）。
【分析】阴影部分通过翻折移动位置后，构成了一个新的图形（如图所示）。
从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。
3.14×42×1/4－4×4÷2÷2＝8.56（平方厘米）练习21、计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。
答2、计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。
答1 2例题3。
如图19－10所示，两圆半径都是1厘米，且图中两个阴影部分的面积相等。
求长方形ABO1O的面积。
【分析】因为两圆的半径相等，所以两个扇形中的空白部分相等。
又因为图中两个阴影部分的面积相等，所以扇形的面积等于长方形面积的一半（如图19－10右图所示）。
所以3.14×12×1/4×2＝1.57（平方厘米）练习31、如图所示，圆的周长为12.56厘米，AC两点把圆分成相等的两段弧，阴影部分（1）的面积与阴影部分（2）的面积相等，求平行四边形ABCD的面积。
答2、如图所示，AB＝BC＝8厘米，求阴影部分的面积。
六年级上册奥数题圆的面积
小学六年级奥数教材课程圆的周长和面积一条线段绕着它固定的一端在平面内旋转一周，它的另一端在平面内画出一条封闭的曲线，这条封闭的曲线就是圆。
画圆时，固定的一点叫做圆心，从圆心到圆上任意一点的线段叫做圆的半径，在同一个圆中，所有的半径都相等。
通过圆心，并且两端在圆上的线段叫做直径。
在同一个圆中，所有的直径都相等，且等于半径的2倍。
圆心决定圆的位置，半径决定圆的大小。
任意一个圆，它的周长除以直径的商总是一个固定的数，这个数叫圆周率。
如果用C 表示圆周的长度，d 表示这个圆的直径，r 表示它的半径，π表示圆周率，就有C dπ=或2C r。
π是一个无限不循环小数，π=3.14159265358979323846…。
圆的周长：C=2πr 或C=πd，圆的面积：S=πr 2。
圆的周长和面积计算的基本方法是仔细观察，发现特点，找出内在的联系，常常通过对图形的割补、旋转、平移、等积变形等方法加以解决。
需要精巧的构思和恰当的设计，把形象思维和抽象思维结合起来。
(本讲π均取 3.14)例1、上海外滩海关大钟钟面的直径是5.8米，钟面的面积是多少平方米？时针长2.7米，时针绕一圈时针尖端走过途径的长度是多少米？(得数保留一位小数)分析与解法：钟面的直径是5.8米这个条件是直接的，时针长指的是半径。
解：钟面的面积是：3.14×(5.8×2)2≈26.4(平方米)。
时针绕一圈时针尖端走过途径的长度是：2×3.14×2.7≈17.0(米)。
例2、如图所示，试比较大圆的面积与阴影部分的面积、大圆的周长与阴影部分的周长。
图图(1)分析与解法：本题有两问，一是比较阴影部分面积与大圆的面积；二是比较阴影部分周长与大圆的周长。
为了考虑问题方便，我们把图经过割补成图(1)，在图(1)中更容易看出大圆与小圆阴影部分的关系。
学习目标总结重点AOB解：先比较大圆面积与阴影部分的面积。
设大圆半径为r，则小圆半径为r，大圆面积为S 1=πr 2。
小学圆的面积奥数题100道及答案(完整版)
小学圆的面积奥数题100道及答案(完整版)题目1一个圆的半径是3 厘米，它的面积是多少平方厘米？答案：圆的面积= π×半径×半径，即3.14×3×3 = 28.26（平方厘米）题目2圆的直径是8 分米，求面积。
答案：半径= 8÷2 = 4 分米，面积= 3.14×4×4 = 50.24（平方分米）题目3一个圆的周长是18.84 米，求其面积。
答案：周长= 2×π×半径，所以半径= 18.84÷（2×3.14）= 3 米，面积= 3.14×3×3 = 28.26（平方米）题目4圆的面积是12.56 平方厘米，求半径。
答案：3.14×半径×半径= 12.56，半径×半径= 4，半径= 2 厘米题目5直径为10 厘米的圆，面积比半径为6 厘米的圆的面积小多少？答案：直径10 厘米的圆半径为5 厘米，面积为 3.14×5×5 = 78.5 平方厘米；半径6 厘米的圆面积为3.14×6×6 = 113.04 平方厘米，小113.04 - 78.5 = 34.54 平方厘米题目6一个圆的半径扩大3 倍，面积扩大多少倍？答案：原来面积= π×半径×半径，半径扩大3 倍后，面积= π×（3×半径）×（3×半径）= 9×π×半径×半径，面积扩大9 倍题目7两个圆的半径分别是2 厘米和3 厘米，它们面积的和是多少？答案：面积分别为3.14×2×2 = 12.56 平方厘米，3.14×3×3 = 28.26 平方厘米，和为12.56 + 28.26 = 40.82 平方厘米题目8一个圆的面积是50.24 平方分米，在里面画一个最大的正方形，正方形的面积是多少？答案：圆的半径= √（50.24÷3.14）= 4 分米，正方形的对角线是圆的直径为8 分米，正方形面积= 对角线×对角线÷2 = 8×8÷2 = 32 平方分米题目9圆的半径由4 厘米增加到6 厘米，面积增加了多少平方厘米？答案：原来面积= 3.14×4×4 = 50.24 平方厘米，新面积= 3.14×6×6 = 113.04 平方厘米，增加了113.04 - 50.24 = 62.8 平方厘米题目10在一个边长为8 厘米的正方形中画一个最大的圆，圆的面积是多少？答案：圆的直径= 8 厘米，半径= 4 厘米，面积= 3.14×4×4 = 50.24 平方厘米题目11已知圆的面积是28.26 平方米，求周长。
重点小学奥数圆面积的典型题和解法
精心整理页脚内容 圆面积的典型题和解法一、半径r 2替代法题的特点：一般将正方形，三角形和圆放到一起，一般已知条件是正方形或三角形面积，求圆的面积。
解法：一般设法求出r ，或者求出r 2，★注意：园内直角三角形一般为等腰直角三角形，两腰等长，斜边是斜边上高的2倍。
例1：已知下图阴影部分面积为8平方米，求圆的面积：解：由已知条件可得r 2=8，因此，圆的面积为：814.32⨯=r π例2：ABCD 为正方形，已知AC 长6m ，求阴影部分面积：解：△ACD 为等腰直角三角形，则S △ACD=6*3/2=9㎡AD=DC=rAD*DC/2=9因此，r 2=18,扇形DAC 的面积为：4/1814.34/2⨯=rπ 因此，阴影部分面积为：18-4/1814.34/2⨯=r π例3：求圆与圆内最大正方形的面积比值。
解：△ABC 为等腰直角三角形，则S △ABC=22/2r r r =⨯正方形的面积是两个三角形面积和，为：22r圆的面积为：2r π，则圆与圆内最大正方形的比为：2/π练习题：1、已知下图阴影部分面积为5平方米，求圆的面积：2:、在右图扇形中，正方形面积为30平方米，求阴影部分面积：3：求正方形与正方形内最大圆的面积比值。
二、图像平移填补法题的特点：一般圆内由多个阴影部分面积构成，阴影由弧线和弧线构成，或者由弧线和直线构成。
解法：注意观察面积相同的部分，将相同的部分移动替换，若遇到轴对称图形可尝试旋转图形，记住常见的面积平移图例。
，例1：求阴影部分的面积：解：正方形外三角形底为6，和正方形内三角形底相同，由于顶角相同，所以两个三角形可以互换。
阴影部分面积则为：正方形面积-1/4圆的面积例2：求阴影部分的面积：解：平移得到下图：则阴影部分面积为扇形面积-三角形面积例3：求阴影部分的面积：精心整理页脚内容 解：注意观察，：阴影部分面积为：1*1-1*1/2=1/2练习题：求阴影部分面积：三、图像关联扩张法题的特点：图有好几个部分组合而成，各部分之间存在着一定的关系。
圆的面积计算奥数题
圆的面积计算奥数题一、知识、规律、方法本单元主要讲解与圆面积有关的组合图形面积的问题。
在进行组合图形的面积计算时，必顺掌握有关的概念、公式，要仔细观察，认真思考，看清组合图形是由哪几个基本图形组成的，要注意找出图中的隐蔽条件与已知条件和问题的联系。
计算组合图形的面积，必须将组合图形进行分解，看清组合图形是由哪几个基本图形合并起来的，或是从哪一个基本图形里去掉哪一个或几个基本图形得到的。
有时需要把其中的部分图形进行平移、翻转、添上辅助线，化难为易，从而找出解答的方法。
1. 圆面积的计算公式： 2S r π= 2. 扇形面积的计算：2360nS r π=⨯（n 为扇形圆心角的度数）。
二、范例、解析、拓展例1． 求图中阴影部分的面积。
（单位：厘米）拓展一 计算下图阴影部分的面积。
（单位：厘米）拓展二 求图中阴影部分的面积。
（单位：厘米）拓展三 如图，已知扇形的面积是3.14平方厘米，求图中阴影部分的面积。
例2． 一个直径为3厘米的半圆，让A 点不动，把整个半圆顺时针旋转60°，此时点B 移到点1B 处（如图）。
求图中阴影部分的面积。
拓展一 图中三角形ABC 是直角三角形，阴影Ⅰ的面积比阴影Ⅱ的面积小23平方米。
问BC 的长度是多少米？（π 取3）O ABC410468拓展二 求下图中的阴影部分的面积。
（单位：厘米）拓展三 计算图中阴影部分的面积。
（单位：厘米）拓展四 计算图中阴影部分的面积。
（单位：厘米）拓展五 如左下图,∠1=15°的圆周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是多少平方厘米?检测、反馈、应用1. 求左下图中阴影部分面积。
（单位：厘米）2. 右上图中三角形的面积是12平方厘米，求阴影部分的面积是多少。
3. 已知图中两个正方形的边长分别为1厘米和2厘米，求阴影部分的面积。
4. 正方形面积是12平方厘米，求图中阴影部分的面积。
5. 计算阴影部分的面积。
六年级举一反三奥数
第十二讲圆的面积点击例题1求下图中阴影部分的面积。
(单位：厘米)举一反三1.已知阴影部分的面积是40cm2,求圆环的面积。
2.已知扇形的面积是3.14cm2,求阴影部分的面积。
2.有四块半径为2cm的扇形(阴影部分)，它们的面积和是多少?点击例题2求下图中阴影部分的面积。
(单位：厘米)1.如右下图所示，半圆内有一个直角三角形ABC,AB长3厘米，AC长4厘米，求阴影部分的面积。
2.如图，圆的直径AB是6厘米，平行四边形ABCD的面积是7平方厘米，∠ABC=30°，求阴影部分的面积。
3. 右下图中，半圆的面积为6.28平方厘米，让A点不动，把整个半圆顺时针旋转90°，求半圆经过的面积。
点击例题3在图中，正方形的边长是10cm,求图中阴影部分的面积。
1.如右下图所示，△ABC是等腰直角三角形，求阴影部分面积。
(单位：cm)2.求下面图形中阴影部分的面积。
(单位：cm)3.如图所示，图中平行四边形的一个角为60°，两条边的长分别为6cm和8cm,高为5.2cm。
求图中阴影部分的面积。
点击例题4求阴影部分①比阴影部分②的面积少多少？1.草场上有一个木屋，木屋是边长为4米的正方形(如下图)A是木屋的一角，在A处有一根木桩，用8米长的绳子拴头牛在木桩上，这头牛的活动范围有多大？2.将一个圆分成若干等份，再改拼成一个近似的长方形，已知这个长方形的周长是8.28分米，求这个圆的面积是多少？3.如图所示，O是小圆的圆心，CO垂直于AB,三角形ABC的面积是45cm2。
求阴影部分的面积.点击例题5在扇形图中，正方形的面积是30cm2。
求阴影部分的面积.1.如图，O为半圆的圆心，ABCD是平行四边形，BC长16cm,求阴影部分的面积。
2.如图所示，半圆的面积是62.8cm2。
求阴影部分的面积3.求下图阴影部分的面积(单位：cm)。
第十七讲表面积和体积点击例题1如图，边长5的正方体，如果它的左上方截去一个边长分别是5、3、2的长方体，那么，它的表面积减少了百分之几？举一反三1.下图是一个校长为25毫米的正方体，在正方体上表面的正中，向下钻穿一个半径为5毫米的圆洞，那么得到的立体图形的表面积是多少平方毫米？2.如下图，在棱长为4厘米的正方体的上、下、前、后、左、右的正中位置各挖去一个棱长为1厘米的正方体，问：此图形的表面积是多少？3.在一个底面积为324平方厘米的正方体铸铁中，以相对的两面为底，挖出一个最大的圆柱体，然后在剩下的铸铁表面涂上油漆，求涂漆的面积是多少？点击例题2如图是由18个边长为1cm的小正方体拼成的，求它的表面积。
圆的面积奥数
在奥数中，圆的面积是一个重要的话题，可以涉及很多方面。
下面是一些重要的概念：
1. 圆的周长：圆的周长定义为环绕圆一周的距离，计算公式为C=2πr，其中r 为半径。
2. 圆的面积：圆的面积定义为圆内所有点的集合的面积，计算公式为A=πr²，其中r 为半径。
3. 相切线：直线与圆相切时，相切线与圆只有唯一交点，并且相切线距离等于半径。
4. 半径、直径、弦长和弧长：圆的半径是从圆心到圆周上任意一点的距离，直径是过圆心的最长直线，弦长是在圆上连接两点的线段长度，弧长是围绕圆的一部分的长度。
5. 圆的内外关系：如果一个圆被另一个更大的圆包围，则称前者为内圆，后者为外圆。
小学奥数 圆的周长和面积
第七章圆的周长和面积
一、典型例题
1、一个半径10米的圆形花坛，它的占地面积是多少？在它的一周围一圈篱笆，篱笆长多少米？
思路点拨：圆的面积公式：S=πr2,圆的周长公式：C=2πr,根据公式可以做出来。
解答：
S=π102C=2πr
=3.14×100 =2×3.14×10
=314（平方米） =62.8（米）
答：它的占地面积是314平方米，篱笆长62.8米。
二、知识运用
1、一根长5米的绳子系着一只羊，栓在草地中央的树桩上，羊吃草的面积最多是多少平方米？
2、一种麦田的自动旋转喷灌器的射程是10米，它能喷灌的面积多少平方米？
3、求右图阴影部分面积：（单位：厘米）
4、一元硬币的半径是1.2厘米，求它的周长和面积。
5、用一块边长6分米的正方形纸剪一个最大的圆，圆的面积是多少？
6、用26米长的篱笆围成一个圆形苗圃，篱笆接头处用去0.88米。
苗圃的面积多少？
7、在长6分米，宽4分米的长方形中画一个最大的圆，圆的周长和面积各是多少？
8、求各图的周长和面积：（单位：米）。
奥数专题平面图形之圆的面积
平面图形面积————圆的面积之欧侯瑞魂创作 创作时间：二零二一年六月三十日专题简析：在进行组合图形的面积计算时, 要仔细观察, 认真思考, 看清组合图形是由几个基本单元组成的, 还要找出图中的隐蔽条件与已知条件和要求的问题间的关系.而且同学们应该牢记几个罕见的圆与正方形的关系量：在正方形里的最年夜圆的面积占所在正方形的面积的3.144,而在圆内的最年夜正方形占所在圆的面积的23.14,这些知识点都应该常记于心, 并牢牢掌握！ 例题1.求图中阴影部份的面积（单元：厘米）.【分析】如图所示的特点, 阴影部份的面积可以拼成1/4圆的面积.62×3.14×1/4＝28.26（平方厘米）练习11.求下面各个图形中阴影部份的面积（单元：厘米）.2.求下面各个图形中阴影部份的面积（单元：厘米）.答例题2.求图中阴影部份的面积（单元：厘米）.【分析】阴影部份通过翻折移动位置后, 构成了一个新的图形（如图所示）.从图中可以看出阴影部份的面积即是年夜扇形的面积减去年夜三角形面积的一半.3.14×42×1/4－4×4÷2÷2＝8.56（平方厘米）练习21、计算下面图形中阴影部份的面积（单元：厘米, 正方形边长4）.答2、计算下面图形中阴影部份的面积（单元：厘米, 正方形边长4）.答1 2例题3.如图19－10所示, 两圆半径都是1厘米, 且图中两个阴影部份的面积相等.求长方形ABO1O的面积.【分析】因为两圆的半径相等, 所以两个扇形中的空白部份相等.又因为图中两个阴影部份的面积相等, 所以扇形的面积即是长方形面积的一半（如图19－10右图所示）.所以3.14×12×1/4×2＝1.57（平方厘米）练习31、如图所示, 圆的周长为12.56厘米, AC两点把圆分成相等的两段弧, 阴影部份（1）的面积与阴影部份（2）的面积相等, 求平行四边形ABCD的面积.答2、如图所示, AB＝BC＝8厘米, 求阴影部份的面积.答例题4.如图所示, 图中圆的直径AB是4厘米, 平行四边形ABCD的面积是7平方厘米, ∠ABC＝30度, 求阴影部份的面积（得数保管两位小数）.【分析】阴影部份的面积即是平行四边形的面积减去扇形AOC的面积, 再减去三角形BOC的面积.半径：4÷2＝2（厘米）扇形的圆心角：180－（180－30×2）＝60（度）扇形的面积：2×2×3.14×60/360≈2.09（平方厘米）三角形BOC的面积：7÷2÷2＝1.75（平方厘米）7－（2.09+1.75）＝3.16（平方厘米）练习41、如图, 三角形ABC的面积是31.2平方厘米, 圆的直径AC＝6厘米, BD：DC＝3：1.求阴影部份的面积.答2、如图所示, 求阴影部份的面积（单元：厘米.得数保管两位小数）.答3、如图所示, 求阴影部份的面积（单元：厘米.得数保管两位小数）.答1 2 3例题5.如图所示, 求图中阴影部份的面积.【分析】解法一：阴影部份的一半, 可以看做是扇形中减去一个等腰直角三角形（如图）, 等腰直角三角形的斜边即是圆的半径, 斜边上的高即是斜边的一半, 圆的半径为20÷2＝10厘米【3.14×102×1/4－10×（10÷2）】×2＝107（平方厘米）解法二：以等腰三角形底的中点为中心点.把图的右半部份向下旋转90度后, 阴影部份的面积就酿成从半径为10厘米的半圆面积中, 减去两直角边为10厘米的等腰直角三角形的面积所得的差.（20÷2）2×1/2－（20÷2）2×1/2＝107（平方厘米）练习51、如图所示, 求阴影部份的面积（单元：厘米）答2、如图所示, 用一张斜边为29厘米的红色直角三角形纸片, 一张斜边为49厘米的蓝色直角三角形纸片, 一张黄色的正方形纸片, 拼成一个直角三角形.求红蓝两张三角形纸片面积之和是几多？答例题6如图所示, 求图中阴影部份的面积（单元：厘米）.【分析】解法一：先用长方形的面积减去小扇形的面积, 无暇白部份（a）的面积, 再用年夜扇形的面积减去空白部份（a）的面积.如图所示.3.14×62×1/4－（6×4－3.14×42×1/4）＝16.82（平方厘米）解法二：把阴影部份看作（1）和（2）两部份如图20－8所示.把年夜、小两个扇形面积相加, 刚好多计算了空白部份和阴影（1）的面积, 即长方形的面积.3.14×42×1/4+3.14×62×1/4－4×6＝16.28（平方厘米）练习61、如图所示, 三角形ABC是直角三角形, AC长4厘米, BC长2厘米.以AC、BC为直径画半圆, 两个半圆的交点在AB边上.求图中阴影部份的面积.答2、如图所示, 图中平行四边形的一个角为600, 两条边的长分别为6厘米和8厘米, 高为5.2厘米.求图中阴影部份的面积.答例题7.在图中, 正方形的边长是10厘米, 求图中阴影部份的面积.【分析】先用正方形的面积减去一个整圆的面积, 无暇部份的一半（如图所示）, 再用正方形的面积减去全部空白部份.空白部份的一半：10×10－（10÷2）2×3.14＝21.5（平方厘米）阴影部份的面积：10×10－21.5×2＝57（平方厘米）练习71、求下面各图形中阴影部份的面积（单元：厘米）.答2、求右面各图形中阴影部份的面积（单元：厘米）.答3、求右面各图形中阴影部份的面积（单元：厘米）.答例题8.在正方形ABCD中, AC＝6厘米.求阴影部份的面积.【分析】这道题的难点在于正方形的边长未知, 这样扇形的半径也就不知道.但我们可以看出, AC是等腰直角三角形ACD的斜边.根据等腰直角三角形的对称性可知, 斜边上的高即是斜边的一半（如图所示）, 我们可以求出等腰直角三角形ACD的面积, 进而求出正方形ABCD的面积, 即扇形半径的平方.这样虽然半径未求出, 但可以求出半径的平方, 也可以把半径的平方直接代入圆面积公式计算.既是正方形的面积, 又是半径的平方为：6×（6÷2）×2＝18（平方厘米）阴影部份的面积为：18－18×3.14÷4＝3.87（平方厘米）答：阴影部份的面积是3.87平方厘米.练习81、如图所示, 图形中正方形的面积是50平方厘米, 分别求出每个图形中阴影部份的面积.答2、如图所示, 正方形中对角线长10厘米, 过正方形两个相对的极点以其边长为半径分别做弧.求图形中阴影部份的面积（试一试, 你能想出几种法子）.答例题9.在图的扇形中, 正方形的面积是30平方厘米.求阴影部份的面积.【分析】阴影部份的面积即是扇形的面积减去正方形的面积.可是扇形的半径未知, 又无法求出, 所以我们寻求正方形的面积与扇形面积的半径之间的关系.我们以扇形的半径为边长做一个新的正方形（如图所示）, 从图中可以看出, 新正方形的面积是30×2＝60平方厘米, 即扇形半径的平方即是60.这样虽然半径未求出, 但能求出半径的平方, 再把半径的平等直接代入公式计算.3.14×（30×2）×1/4－30＝17.1（平方厘米）答：阴影部份的面积是17.1平方厘米.练习91、如图所示, 平行四边形的面积是100平方厘米, 求阴影部份的面积.答2、如图所示, O是小圆的圆心, CO垂直于AB,三角形ABC的面积是45平方厘米, 求阴影部份的面积.答上面所举的例子只是罕见的圆的组合图形面积解法, 在以后的练习中, 还希望同学们能举一反三, 总结自己的学习方法与心得与体会, 到达举一反三的效果！圆的面积与组合圆积专题训练一、填空题 1.算出圆内正方形的面积为.2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部份面积是120,120.4.如图所示,以B 、C 2厘米,则阴影部份的周长是厘米.(保管两位小数)ABC 是直角三角形,阴影部份①的面积比阴影部份②的面积小28平方厘米. AB 长40厘米, BC 长厘米.2平方厘米,平方.8.图中扇形的半径OA=OB=6厘米.45=∠AOB ,AC 垂直OB 于C,那么图中阴影部份的面积是平方厘米.)14.3(=π 9.右图中正方形周长是20厘米.图形的总面积是平方厘米.10.在右图中(单元:厘米),两个阴影部份面积的和是平方厘米.11.如图,阴影部份的面积是.12.年夜圆的半径比小圆的半径长6厘米,且年夜圆半径是小圆半径的4倍.年夜圆的面积比小圆的面积年夜平方厘米.13.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是平方厘米.(π取3.14,结果精确到1平方厘米)14.右图中三角形是等腰直角三角形,阴影部份的面积是.15.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部份的周长是厘米.)14.3(=π16.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部份的面积是.17.已知:ABCD 是正方形,ED=DA=AF=2厘米,阴影部份的面积是.6C BAO 45 1215 20 2 1 2E D C B AG F18.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是度.20.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部份的面积差(年夜减小)是平方厘米.(π取3.14)2创作时间：二零二一年六月三十日创作时间：二零二一年六月三十日 二、解答题11.ABC 是等腰直角三角形. D 是半圆周的中点,BC 是半圆的直径,已知:AB=BC=10,那么阴影部份的面积是几多?(圆周率14.3=π)12.如图,平方厘米,圆S2的面积是19.625)是几多平方厘米?13.如图,厘米,1521=∠=∠,那么阴影部份。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆的面积奥数
圆的面积
严1 1
圆是一种平面图形，再日常生活中到处可见•如圆桌，圆盘，车辆的轱辘，以及游戏用的棋子，飞盘，呼啦圈等，由于圆有着本身独特的性质，在某些地方是其它形状所不能代替的，车牯辘就是一个很好的例子•这一讲我们着重研究圆以及和圆有关的组合图形的求面积方法.圆的面积计算公式，扇形面积计算公式，同学们在课本上已经都有初步的理解和掌握，我们主要讨论组合图形的面积的计算方法与技巧.
请注意常用的扇形：四分之一圆对应圆心角是90度，八分之一圆对应的圆心角是45度.
4F经典题再现
如下图所示，0是圆心，圆的周长等于75.36分米，点A、B、C都在圆周上，OABC 是梯形，梯形的面积是98.28平方分米.AB= 20.76分米，那么阴影部分的面积是
多少平方分米？（ n取3.14）
解：由圆的周长可求圆的半径：
75.36=2 X3.14Xr, r = 12.
即0C=12.
由梯形的面积及它的上底，下底已知，可求梯形的高.
98.28=(12 + 20.76) X高* 高=6.
阴影的面积=12 X6十2= 12 X3 = 36 (平方分米).
匕了典型例题
【例1】长方形长6分米，宽4分米, 分别以长、宽为半径画弧，如图.那么阴影部
分的面积是多少平方分米？
解：丁亠-叮4=16.82（平方厘米）答：影阴部分的面积是16.82平方厘米.
【例2】如图，半圆S i的面积是14.13 平方厘米，圆S2的面积是19.625平方厘米，那么阴影部分的面积是多少平方厘米？
解：因为S1的面积为14.13平方厘米，
所以半径的平方为14.13 2 3.14=9,故半径为3厘米，直径为6厘米.
又因为s的面积为19.625平方厘米，所以S2的半径的平方为19.625 3.14=6.25（平方厘米），所以它的
半径为2.5厘米，直径为5厘米，所以阴影部分面积为（6 5）5=5（平方厘米）.
答：阴影部分的面积是5平方厘米.
【例3】如图，A与B是两个圆（只有
4）的圆心，那么，两个阴影部分的面积相差多少平方厘米？
答：两个阴影部分的面积相差 1.42平方厘米.
【例4】如图，圆的直径AB是4cm, ABCD的面积是7cm2, / ABC等于30° , 求阴影部分面积.
解：这个题许多同学将ABC看成是圆心角为30°的扇形•这是错误的，因为AB是直径，BC不是，AB, BC不一样长，所以，ABC 不是扇形.
如下图，找到圆心0,连CO, AOC才是扇形.先要求这个扇形的圆心角，就可以求出它的面积•然后再求三角形
COB的面积，用ABCD的面积减去，
就是阴影面积.
阴影面积等于平行四边形面积减去扇
形AOC的面积，再减去厶BOC的面积.
扇形的圆心角=180° - （180 ° - 30°
X2）=60° .
扇形的面积=2 X2 X3.14 X60 -360= 2.09 （平方厘米）.
△ BOC的面积=7汽-2=1.75（平方厘米）.
阴影部分的面
积=7 -2.09 1.75=3.16.
答：阴影部分的面积是3.16平方厘米.
【例5】下图中阴影部分的面积是多少平方厘米？
解：两个空白部分拼起来正好是一个
4 >4的正方形.
所以阴影部分面积等于2M的长方形面积.
2 >4 = 8 （平方厘米）
答：影阴部分的面积是8平方厘米.
【例6】如图所示，这是一个正六边
形，它的面积为1040平方厘米•空白部分是半径为10cm的6个小扇形.求阴影部分的面积.
H C
解：图中阴影部分的面积显然是正六边形
的面积减去六个小扇形的面积.正六边形的面积已知，所以关键是求六个小扇形面积.
我们观察每3个小扇形可以拼成一个半径为10厘米的圆，6个小扇形可以拼成2个小圆形.阴影部分的面积就是正六边形的面积减去2个半径为10厘米的小圆的面积.
6个扇形的面积为3.14 X102 X2 = 628（平方厘米），
阴影部分的面积：1040- 628=412 （平方厘米）.
答：阴影部分的面积为412平方厘米.
g------ 1
难题详解
如下图所示，在4 X7的方格纸板上画出如阴影所示的“ 9”字，阴影边缘是线段或
圆弧.问阴影面积占纸板面积的几分之几？
解：矩形纸板共28个小正方形.其中弧线是4圆周.非阴影部分共6个，也共6个.可拼成6个小正方格.因此阴影部分共28-6-3=佃个小方格.所以，阴影面积占纸板面积的28.
答：阴影面积占纸板面积的霧.
同步练习
1 .如下图，ABCD为正方形，且
FA=AD = DE=2厘米，求阴影部分的面积？
2.有三个形状相同的圆形纸片，面积都是90平方厘米，重叠在一起（如图），盖住桌面的总面积是150平方厘米，三张纸片重叠的面积是28平方厘米，那么图
中三个阴影部分面积和是多少平方厘米？
3 •已知图中各圆相切，小圆半径为1, 求阴影部分面积.
4•已知每个圆的直径为6厘米，求阴影部分的面积.
5•图中正方形ABCD的边长是20厘米，求阴影部分面积.
6•如图，已知每个小正方形的面积为
1平方厘米，求阴影部分面积.（注：所用分点均理解为所在边中点）.
7.如图，大圆直径上的黑点是五等分
点，求A, B, C三部分面积之比.
8 .如图，O为圆心，C为扇形ACB的
圆心，CO垂直于AB,三角形ABC的面积为45平方厘米，求阴影部分面积.
石尸同步练习解答
1 •图形DGC为图形DBC面积的一半，于是，阴影部分的面积为
4 3.14 22—扌 2 2］亠［2 2—富 3.14 22| = 2.43 （平方厘
米）
2.解：90 X3-150- 28 X2 = 64 （平方厘米）
3.如图1,11 , III部分面积是相等的，剩余3块小阴影面积也相等.那么所求阴影部分面积是一个小半圆面积加上大半
圆减去2个小圆和3个小半圆剩余部分的 1
3・
阴影面积为： 4 •如图，长方形外的阴影部分一共 4 3=ii 个圆，移至长方形内正好填满长方 形，阴影部分的面积就是长方形面积.
阴影部分面积 =6 X 2 X6 = 72 （平方厘 米）.
5.充分利用圆的对称性，如图，大扇 形ABC 的半径是20，它的面积减去三角 形
ABC n n 5
n
的面积就是I的面积.正方形
ABCD减去圆O的面积就是4个II的面积.
阴影部分就是ABCD面积减去2个I,
4个II的面积.
20 20 —2 4 n 202— * 20 20 -4 (20 20 — n 102)
= 129 (平方厘米)
6 •阴影分成两部分，一部分是字母
“ A ”，一部分是字母“ r ”.
字母“A”的面积，我们只需算一半, 再2倍就可以了.
a
平行四边形ABCD面积=1
梯形EFHG面积=畀1舞
字母“ A "的面积号16 2=29=31 =3.625 .
字母“ r”的面积
2
n 3 -6 ^'2 2 =12.26
最后，阴影面积为3.625+12.26=15.885 (平方厘米).
7 .显然，A与C面积相等，B与C面积比为
(1.52 12): [(2.52 1.52 + 12) 一2] = 1 ：所以，A, B, C面积比为：2 ： 1 ：2. 8•设CA=CB = a, OC = OB=OA = r.
则由三角形ABC面积为45知,a 1=45, a2 =
90.
再以AB为底计算三角形ABC面积：AB OC 舟=2 OA OC 土=b2知，b2 = 45.
阴影部分面积=半圆面积+三角形ABC面积-扇形ACB面积.即
45+b2 3.14厂a2 3144 = 45 + 453.141
90 3.14 J = 45
2 理2 疔
解：观察上图可以发现大4圆的面积减去长方形的面积（包括小阴影和大空白两部分）再减去小4圆的面积•就是两个影阴部分的面积差.
即
1 X3.14 甘一
2 江4 —* 汇3.14 汇22= 1.42
（平方厘米）。