主成分分析学习笔记
简单易懂！一文理清主成分分析思路
简单易懂！⼀⽂理清主成分分析思路主成分分析是⼀种浓缩数据信息的⽅法，可将很多个指标浓缩成综合指标（主成分），并保证这些综合指标彼此之间互不相关。
可⽤于简化数据信息浓缩、计算权重、竞争⼒评价等。
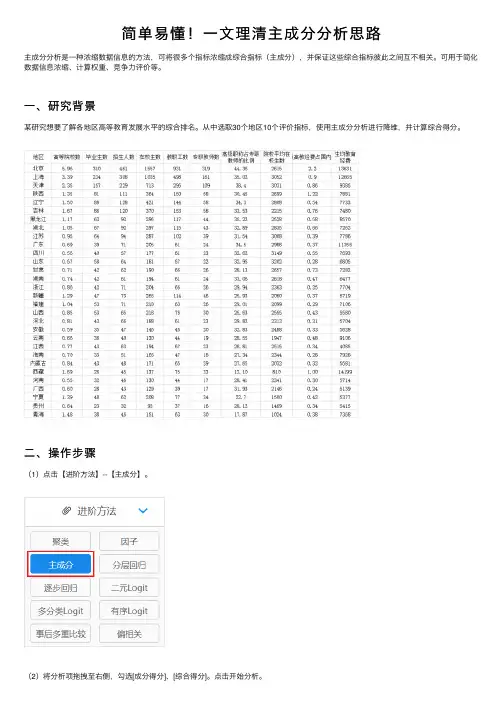
⼀、研究背景某研究想要了解各地区⾼等教育发展⽔平的综合排名。
从中选取30个地区10个评价指标，使⽤主成分分析进⾏降维，并计算综合得分。
⼆、操作步骤（1）点击【进阶⽅法】--【主成分】。
（2）将分析项拖拽⾄右侧，勾选[成分得分]、[综合得分]。
点击开始分析。
也可以根据⾃⼰的分析需要，主动设置主成分个数。
三、分析思路Step1：判断是否适合进⾏主成分分析上表展⽰KMO检验和Bartlett 的检验结果，⽤来看此数据适不适合进⾏主成分分析。
通常KMO值的判断标准为0.6。
⼤于0.6说明适合进⾏分析，反之，说明不适合进⾏分析。
同时Bartlett检验对应P值⼩于0.05也说明适合分析。
SPSSAU输出的结果中会给出智能解读结果，直接查看智能分析：Step2：确定主成分个数，及判断主成分与分析项对应关系确定可以使⽤主成分分析后，下⼀步重点确定主成分个数。
⽅差解释率表格主要⽤于判断提取多少个主成分合适。
以及每个主成分的⽅差解释率和累计⽅差解释率情况。
⽅差解释率越⼤说明主成分包含原数据信息的越多。
从上表可知：本次共提取了2个主成分。
这2个主成分的⽅差解释率分别是75.024%，15.767%，累积⽅差解释率为,90.791%。
说明两个主成分能够表达10个分析项90.791%的信息量，主成分分析效果很好。
碎⽯图同时可结合碎⽯图辅助判断主成分提取个数。
当折线由陡峭突然变得平稳时，陡峭到平稳对应的主成分个数即为参考提取主成分个数。
实际研究中更多以专业知识，结合主成分与研究项对应关系情况，综合权衡判断得出主成分个数。
载荷系数表格，主要展⽰主成分对于研究项的信息提取情况，以及主成分和研究项对应关系。
蓝⾊数值代表载荷系数绝对值⼤于0.4，如⾼等院校数对应的载荷系数（0.958，-0.247）说明这个分析项更适合归于主成分1下。
SAS学习系列33.-主成分分析
SAS学习系列33.-主成分分析33. 主成分分析（一）原理一、基本思想主成份分析，是数学上对数据降维的一种方法，是将多个变量转化为少数综合变量（集中了原始变量的大部分信息）的一种多元统计方法。
其主要目的是将变量减少，并使其改变为少数几个相互独立的线性组合形成的新变量（主成份，其方差最大），使得原始资料在这些成份上显示最大的个别差异来。
在所有的线性组合中所选取的F1应该是方差最大的，称为第一主成分。
如果第一主成分不足以代表原来所有指标的信息，再考虑选取第二个线性组合F2, 称为第二主成分。
为了有效地反映原有信息，F1已有的信息就不需要再出现在F2中，用数学语言表达就是要求Cov(F1，F2)＝0. 依此类推可以构造出第三、第四、…、第p个主成分。
主成份分析，可以用来综合变量之间的关系，也可用来减少回归分析或聚类分析中的变量数目。
二、基本原理设有n个样品（多元观测值），每个样品观测p项指标（变量）：X1，…，X p，得到原始数据资料阵：其中，X i = (x1i，x2i，…，x ni)T，i = 1, …, p.用数据矩阵X的p个列向量（即p个指标向量）X1，…，X p作线性组合，得到综合指标向量：简写成：F i = a1i X1 + a2i X2+…+a pi X p i = 1, …, p限制系数a i = (a1i，a2i，…，a pi)T为单位向量，即且由下列原则决定：（1）F i与F j互不相关，即COV(F i, F j)=a i T∑a i=0，其中∑为X 的协方差矩阵；（2）F1是X1，X2，…，X p的所有满足上述要求的线性组合中方差最大的，即F2是与F1不相关的X1，…，X p所有线性组合中方差最大的，…，F p是与F1，…，F p-1都不相关的X1，…，X p所有线性组合中方差最方向对应。
F1，F2，…，F p可以理解为p维空间中互相垂直的p 个坐标轴。
三、基本步骤1. 计算样品数据协方差矩阵Σ = (s ij)p p，其中2. 求出Σ的特征值及相应的特征向量λ1>λ2>…>λp>0, 及相应的正交化单位特征向量：则X的第i个主成分为F i= a i T X，i=1, …, p.3. 选择主成分在已确定的全部p个主成分中合理选择m个来实现最终的评价分析。
spss学习笔记之主成分分析
spss学习笔记：因子分析因子分析（主成分分析法）Analyse—>data reduction—>Factor除了variables对话框外，还有五个对话框。
descriptive对话框：提供描述性统计量与相关矩阵有关的统计量。
这个对话框关键是以下一些选项：1）statistics选项Initial solution：输出有comunalities（公因子方差）,Total variance explained（提供特征值、各因子解释的方差比例和累计比例等信息）。
2）Correlation matrix选项：Coefficients输出观察变量的相关系数矩阵；Reproduced输出重构的相关系数矩阵(我用的spss版本显示的residual和produced correlation是分开的)；KMO and Bartlett’s test ofsphericity：KMO测度和巴特里特球体检验。
KMO 值的可接受区间0.5~1。
球体检验则看显著性水平。
其他一般不必用。
Extraction对话框：Method选Principal components主成分分析法（系统默认）Analyse 选correlation matrix即可。
Display下的两个选项都选中。
分别输出未经旋转的因子矩阵和碎石图。
Extract决定提取因子的个数，有两种情况。
Eigenvalue over指定要提取因子的最小特征值；Number of factors直接指定要提取的因子数。
Rotation 对话框：Method下选择旋转方法：最常用的是varimax方差最大法；Direct Oblimin斜交旋转，在变量之间的相关性比较大时使用。
Display下：Rotated solution 输出旋转后的因子矩阵。
Loading Plots输出因子负载图（觉得这个东东没什么用，因子大于二时估计就已经看不清了）。
主成分分析的概念及基本思想主成分分析PrincipleComponent
1、主成分分析的概念及基本思想主成分分析(Principle Component Analysis, PCA)是最为常用的特征提取方法，被广泛应用到各领域，如图像处理、综合评价、语音识别、故障诊断等。
它通过对原始数据的加工处理，简化问题处理的难度并提高数据信息的信噪比，以改善抗干扰能力。
主成分概念首先由Karl parson在1901年引进，不过当时只是对非随机变量进行讨论，1933年Hotelling将这个概念推广到随机向量。
在实际问题中，研究多指标(变量)问题是经常遇到的，然而在多数情况下，不同指标之间是有一定相关性。
由于指标较多并且指标之间有一定的相关性，势必增加了分析问题的复杂性。
主成分分析就是设法将原来众多具有一定相关性的指标(比如p个指标)，重新组合成一组新的相互无关的综合指标来代替原来指标。
通常数学上的处理就是将原来p个指标作线性组合，作为新的综合指标，但是这种线性组合，如果不加限制，则可以有很多，我们应该如何去选取呢？如果将选取的第一个线性组合即第一个综合指标记为F1，自然希望F1尽可能多的反映原来指标的信息，这里的“信息”用什么来表达？最经典的方法就是用F1的方差来表达，即Var(F1)越大，表示F1包含的信息越多。
因此在所有的线性组合中所选取的F1应该是方差最大的，故称F1为第一主成分。
如果第一主成分不足以代表原来P个指标的信息，再考虑选取F2即选第二个线性组合，为了有效地反映原来信息，F1已有的信息就不需要再出现在F2中，用数学语言表达就是要求Cov(F1，F2)=0 ，称F2为第二主成分，依此类推可以构造出第三，四，…，第p个主成分。
不难想象这些主成分之间不仅不相关，而且它们的方差依次递减。
因此在实际工作中，就挑选前几个最大主成分，虽然这样做会损失一部分信息，但是由于它使我们抓住了主要矛盾，并从原始数据中进一步提取了某些新的信息。
因而在某些实际问题的研究中得益比损失大，这种既减少了变量的数目又抓住了主要矛盾的做法有利于问题的分析和处理。
【笔记】主成分分析法PCA的原理及计算
【笔记】主成分分析法PCA的原理及计算主成分分析法PCA的原理及计算主成分分析法主成分分析法（Principal Component Analysis），简称PCA，其是⼀种统计⽅法，是数据降维，简化数据集的⼀种常⽤的⽅法它本⾝是⼀个⾮监督学习的算法，作⽤主要是⽤于数据的降维，降维的意义是挺重要的，除了显⽽易见的通过降维，可以提⾼算法的效率之外，通过降维我们还可以更加⽅便的进⾏可视化，以便于我们去更好的理解数据，可以发现更便于⼈类理解，主成分分析其⼀个很重要的作⽤就是去噪，有的时候，经过去噪以后再进⾏机器学习，效果会更好我们可以基于主成分分析法的降维来理解其原理原理及计算我们设⼀个⼆维的坐标系，横轴为特征⼀，纵轴为特征⼆，相应的存在⼀些样本，其对应相应的点，既然是⼆维的，那么我们就可进⾏降维那么降维到⼀维的具体操作是什么呢？⼀个很明显的⽅案就是对这两个特征选⼀个特征，将另⼀个特征去除掉，如果说我们将特征⼆扔掉保留特征⼀的话，那么全部的点就会相应的全部映射到横轴上，相反，我们选择特征⼆的话，所有的点就会映射到纵轴上这就是对应的两种降维的⽅案，这两个⽅案哪⼀个是更好的呢，我们将所有的点映射到了横轴以后，点和点之间距离是相对⽐较⼤的的⽅案就是更好的⽅案，为什么呢，点和点之间的距离⼤，即点和点之间有着更⾼的可区分度，这样也更好的保持了原来的点和点之间的距离，虽然也不同，但是也相应的更⼩的还有⼀种更好的⽅案，我们可以选取⼀条直线，将所有的点都映射到这根直线上，使⽤这种⽅式，所有的点更趋近于原来的分布情况，区分度也⽐映射到横纵轴上更加明显那么如何找到这个让样本间间距最⼤的轴？为了找到这个轴，我们先使⽤⽅差来定义⼀下这个样本间间距这样这个问题就变成了，我们需要找到⼀个轴（直线），使得样本空间中的所有点在映射到这个轴以后，⽅差是最⼤的那么怎么操作呢？⾸先，我们将样本的均值归0，即所有的样本都减去这批样本的均值，这样就相当于让坐标轴进⾏了移动，使得样本在每个维度上均值都为0，这样我们就可以将⽅差的式⼦变成（xi是已经映射到新的轴上的新的样本）然后我们要求这个轴的⽅向w=(w1,w2)（此处⽤⼆维来表⽰），使得我们所有的样本，在映射到w以后，有使映射以后的样本Xproject的⽅差值最⼤，式⼦展开如下需要注意的是：对于这个X来说，可能有多个维度，因此每⼀个X都是⼀个有多个元素的向量，因此更准确的式⼦应该是其均值等依然是含有多个内容的向量，为什么呢，因为虽然映射到了这个轴上，但是本⾝这个轴还是处在这个n维的坐标系中，那么这实际上就是这两个向量相减之后的模的平⽅，⼜因为我们之前对样本进⾏了demean处理（均值取0），因此，这个式⼦化简以后为，即为映射完的点的模的平⽅和再除以m最⼤那么这个Xprojecti到底是要怎么表⽰呢？我们设这个轴为w，样本点为Xi，其也是⼀个向量，那么现在这个Xi要映射到w轴上的话，可以向w轴做⼀个垂直的直线，那么其与w轴的交点就是我们对应的Xproject这⼀点，那么说⽩了我们要求的模的平⽅就是指向交点的这个直线，相当于我们要求将⼀个向量映射到另⼀个向量上对应的映射的长度是多少实际上这种映射就是点乘的定义我们知道现在这个w轴是⼀个⽅向向量，所以其模为1，那么式⼦就化简成运⽤数学定理，很明显可以得出那么我们带⼊之前的式⼦就可以得到我们真正要求的式⼦，即Xi与w点乘完以后的平⽅和再除以m以后的结果最⼤这样我们的主成分分析法就是要求⼀个w轴，使得映射上去的点与w点乘完以后的平⽅和再除以m以后的结果最⼤，这样主成分分析法就变成了⼀个⽬标函数的最优化问题，求⼀个函数的最⼤值，我们就可以使⽤梯度上升法来解决线性回归和这个是不⼀样的，最直观的不同在于线性回归的样本是关于这个新的垂直的⽅向是关于特征的⽅向，并不是垂直于这根直线的⽤梯度上升法来求解PCA问题我们说可以使⽤梯度上升法来解决主成分分析问题，那么怎么⽤梯度上升法来求解此类问题呢？那么我们知道，求⼀个函数的最⼤值，关键是我们要求这个函数的梯度，对于上⾯最终的式⼦来说，除了w以外就没有未知数了，那么对应的梯度就是函数对w求偏导，整理合并以后可以写成对这个式⼦进⾏向量化的处理，我们观察这个式⼦，我们可以发现其中的式⼦就是点乘的形式，其实际上每⼀项就是Xw这个向量和X中的第n列中的每⼀个元素相乘再相加，Xw可以写成这种⾏向量的形式⽽上⾯的计算过程计算下来就是Xw和⼀个矩阵相乘，这个矩阵可以写成（其就是X这个矩阵，有m个样本，n个特征）其最后将梯度的计算的向量化的结果就可以写成（经过转置之后符合要求的）介就是最后的计算公式啦我们可以在直接使⽤这个公式来进⾏计算，最后得到需要的结果。
(完整版)主成分分析法的步骤和原理.doc
（一）主成分分析法的基本思想主成分分析（ Principal Component Analysis ）是利用降 的思想，将多个 量 化 少数几个 合 量（即主成分） ，其中每个主成分都是原始 量的 性 合，各主成分之 互不相关， 从而 些主成分能 反映始 量的 大部分信息，且所含的信息互不重叠。
[2]采用 种方法可以克服 一的 指 不能真 反映公司的 情况的缺点，引 多方面的 指 ， 但又将复 因素 几个主成分， 使得复 得以 化，同 得到更 科学、准确的 信息。
（二）主成分分析法代数模型假 用 p 个 量来描述研究 象，分 用 X 1， X 2⋯X p 来表示， p 个 量构成的 p 随机向量 X=(X 1，X 2⋯X p )t 。
随机向量 X 的均 μ， 方差矩 Σ。
X 行 性 化，考 原始 量的 性 合：Z 1=μ11 X 1+μ12 X 2+⋯μ 1p X p Z 2=μ21 X 1+μ22 X 2+⋯μ 2p X p ⋯⋯ ⋯⋯ ⋯⋯Z p =μp1 X 1+μp2 X 2+⋯μ pp X p主成分是不相关的 性 合 Z 1，Z 2⋯⋯ Z p ，并且 Z 1 是 X 1，X 2 ⋯X p 的 性 合中方差最大者， Z 2 是与 Z 1 不相关的 性 合中方差最大者，⋯， Z p 是与 Z 1， Z 2 ⋯⋯ Z p-1 都不相关的 性 合中方差最大者。
（三）主成分分析法基本步第一步： 估 本数 n ， 取的 指 数 p ， 由估 本的原始数据可得矩 X=(x ij ) m ×p ，其中 x ij 表示第 i 家上市公司的第 j 指 数据。
第二步： 了消除各 指 之 在量 化和数量 上的差 ， 指 数据 行 准化，得到 准化矩 （系 自 生成） 。
第三步：根据 准化数据矩 建立 方差矩 R ，是反映 准化后的数据之 相关关系密切程度的 指 ， 越大， 明有必要 数据 行主成分分析。
主成分分析法总结
主成分分析法总结在实际问题研究中，多变量问题是经常会遇到的。
变量太多，无疑会增加分析问题的难度与复杂性，而且在许多实际问题中，多个变量之间是具有一定的相关关系的。
因此，人们会很自然地想到，能否在相关分析的基础上，用较少的新变量代替原来较多的旧变量，而且使这些较少的新变量尽可能多地保留原来变量所反映的信息？一、概述在处理信息时，当两个变量之间有一定相关关系时，可以解释为这两个变量反映此课题的信息有一定的重叠，例如，高校科研状况评价中的立项课题数与项目经费、经费支出等之间会存在较高的相关性；学生综合评价研究中的专业基础课成绩与专业课成绩、获奖学金次数等之间也会存在较高的相关性。
而变量之间信息的高度重叠和高度相关会给统计方法的应用带来许多障碍。
为了解决这些问题，最简单和最直接的解决方案是削减变量的个数，但这必然又会导致信息丢失和信息不完整等问题的产生。
为此，人们希望探索一种更为有效的解决方法，它既能大大减少参与数据建模的变量个数，同时也不会造成信息的大量丢失。
主成分分析正式这样一种能够有效降低变量维数，并已得到广泛应用的分析方法。
主成分分析以最少的信息丢失为前提，将众多的原有变量综合成较少几个综合指标，通常综合指标（主成分）有以下几个特点：↓主成分个数远远少于原有变量的个数 原有变量综合成少数几个因子之后，因子将可以替代原有变量参与数据建模，这将大大减少分析过程中的计算工作量。
↓主成分能够反映原有变量的绝大部分信息因子并不是原有变量的简单取舍，而是原有变量重组后的结果，因此不会造成原有变量信息的大量丢失，并能够代表原有变量的绝大部分信息。
↓主成分之间应该互不相关通过主成分分析得出的新的综合指标（主成分）之间互不相关，因子参与数据建模能够有效地解决变量信息重叠、多重共线性等给分析应用带来的诸多问题。
↓主成分具有命名解释性总之，主成分分析法是研究如何以最少的信息丢失将众多原有变量浓缩成少数几个因子，如何使因子具有一定的命名解释性的多元统计分析方法。
什么是主成分分析精选全文
可编辑修改精选全文完整版主成分分析（principal component analysis, PCA）如果一组数据含有N个观测样本，每个样本需要检测的变量指标有K个, 如何综合比较各个观测样本的性质优劣或特点？这种情况下，任何选择其中单个变量指标对本进行分析的方法都会失之偏颇，无法反映样本综合特征和特点。
这就需要多变量数据统计分析。
多变量数据统计分析中一个重要方法是主成份分析。
主成分分析就是将上述含有N个观测样本、K个变量指标的数据矩阵转看成一个含有K维空间的数学模型，N个观测样本分布在这个模型中。
从数据分析的本质目的看，数据分析目标总是了解样本之间的差异性或者相似性，为最终的决策提供参考。
因此，对一个矩阵数据来说，在K维空间中，总存在某一个维度的方向，能够最大程度地描述样品的差异性或相似性(图1)。
基于偏最小二乘法原理，可以计算得到这个轴线。
在此基础上，在垂直于第一条轴线的位置找出第二个最重要的轴线方向，独立描述样品第二显著的差异性或相似性；依此类推到n个轴线。
如果有三条轴线，就是三维立体坐标轴。
形象地说，上述每个轴线方向代表的数据含义，就是一个主成份。
X、Y、Z轴就是第1、2、3主成份。
由于人类很难想像超过三维的空间，因此，为了便于直观观测，通常取2个或者3个主成份对应图进行观察。
图（1）PCA得到的是一个在最小二乘意义上拟合数据集的数学模型。
即，主成分上所有观测值的坐标投影方差最大。
从理论上看，主成分分析是一种通过正交变换，将一组包含可能互相相关变量的观测值组成的数据，转换为一组数值上线性不相关变量的数据处理过程。
这些转换后的变量，称为主成分（principal component, PC）。
主成分的数目因此低于或等于原有数据集中观测值的变量数目。
PCA最早的发明人为Karl Pearson，他于1901年发表的论文中以主轴定理（principal axis theorem）衍生结论的形式提出了PCA的雏形，但其独立发展与命名是由Harold Hotelling于1930年前后完成。
系统工程第5讲 系统模型化之主成份分析
设X的协方差阵为
12 12 1 p 2 2 2p 21 Σx 2 p1 p 2 p
由于Σ x为非负定的对称阵，则有利用线性代数的 知识可得，必存在正交阵U，使得
0 1 UΣ X U p 0
这种由讨论多个指标降为少数几个综合指 标的过程在数学上就叫做降维。主成分分析通 常的做法是，寻求原指标的线性组合Fi。
F1 u11 X 1 u21 X 2 u p1 X p F2 u12 X 1 u22 X 2 u p 2 X p Fp u1 p X 1 u2 p X 2 u pp X p
（ 2 ） 选择几个主成分。主成分分析的目的 是简化变量，一般情况下主成分的个数应该 小于原始变量的个数。关于保留几个主成分 ，应该权衡主成分个数和保留的信息。 （3）如何解释主成分所包含的经济意义。
§2
数学模型与几何解释
假设我们所讨论的实际问题中，有p个指 标，我们把这p个指标看作p个随机变量，记为X1， X2，…，Xp，主成分分析就是要把这p个指标的问 题，转变为讨论p个指标的线性组合的问题，而 这些新的指标F1，F2，…，Fk(k≤p），按照保留 主要信息量的原则充分反映原指标的信息，并且 相互独立。
平移、旋转坐标轴
x2
F1
主 成 分 分 析 的 几 何 解 释
F2
•• • • • • • • • • • • •• •• • • •• • • • •• • • • • •• • • • • • •
x1
平移、旋转坐标轴
x2
F1
主 成 分 分 析 的 几 何 解 释
F2
பைடு நூலகம்
stata学习笔记（四）：主成份分析与因子分析
stata学习笔记（四）：主成份分析与因⼦分析1.判断是否适合做主成份分析，变量标准化Kaiser-Meyer-Olkin抽样充分性测度也是⽤于测量变量之间相关关系的强弱的重要指标，是通过⽐较两个变量的相关系数与偏相关系数得到的。
KMO介于0于1之间。
KMO越⾼，表明变量的共性越强。
如果偏相关系数相对于相关系数⽐较⾼，则KMO⽐较低，主成分分析不能起到很好的数据约化效果。
根据Kaiser（1974），⼀般的判断标准如下：0.00-0.49,不能接受（unacceptable）;0.50-0.59,⾮常差（miserable）；0.60-0.69，勉强接受（mediocre）；0.70-0.79,可以接受（middling）；0.80-0.89，⽐较好（meritorious）；0.90-1.00,⾮常好（marvelous）。
SMC即⼀个变量与其他所有变量的复相关系数的平⽅，也就是复回归⽅程的可决系数。
SMC⽐较⾼表明变量的线性关系越强，共性越强，主成分分析就越合适。
. estat smc. estat kmo. estat anti//暂时不知道这个有什么⽤得到结果，说明变量之间有较强的相关性，适合做主成份分析。
Squared multiple correlations of variables with all other variables-----------------------Variable | smc-------------+---------x1 | 0.8923x2 | 0.9862y1 | 0.9657y2 | 0.9897y3 | 0.9910y4 | 0.9898y5 | 0.9769y6 | 0.9859y7 | 0.9735-----------------------变量标准化. egen z1=std(x1)2.对变量进⾏主成份分析. pca x1 x2 y1 y2 y3 y4 y5 y6 y7. pca x1 x2 y1 y2 y3 y4 y5 y6 y7, comp(1)得到下⾯两个表格,第⼀个表格中的各项分别为特征根、difference这个不知道是啥、⽅差贡献率、累积⽅差贡献率。
主成分分析(principalcomponentsanalysis,PCA)又称：主分量分析,主成分回归分析法
主成分分析（principal components analysis，PCA）又称：主分量分析，主成分回归分析法什么是主成分分析法主成分分析也称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标。
在统计学中，主成分分析（principal components analysis,PCA）是一种简化数据集的技术。
它是一个线性变换。
这个变换把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上，依次类推。
主成分分析经常用减少数据集的维数，同时保持数据集的对方差贡献最大的特征。
这是通过保留低阶主成分，忽略高阶主成分做到的。
这样低阶成分往往能够保留住数据的最重要方面。
但是，这也不是一定的，要视具体应用而定。
[编辑]主成分分析的基本思想在实证问题研究中，为了全面、系统地分析问题，我们必须考虑众多影响因素。
这些涉及的因素一般称为指标，在多元统计分析中也称为变量。
因为每个变量都在不同程度上反映了所研究问题的某些信息，并且指标之间彼此有一定的相关性，因而所得的统计数据反映的信息在一定程度上有重叠。
在用统计方法研究多变量问题时，变量太多会增加计算量和增加分析问题的复杂性，人们希望在进行定量分析的过程中，涉及的变量较少，得到的信息量较多。
主成分分析正是适应这一要求产生的，是解决这类题的理想工具。
同样，在科普效果评估的过程中也存在着这样的问题。
科普效果是很难具体量化的。
在实际评估工作中，我们常常会选用几个有代表性的综合指标，采用打分的方法来进行评估，故综合指标的选取是个重点和难点。
如上所述，主成分分析法正是解决这一问题的理想工具。
因为评估所涉及的众多变量之间既然有一定的相关性，就必然存在着起支配作用的因素。
根据这一点，通过对原始变量相关矩阵内部结构的关系研究，找出影响科普效果某一要素的几个综合指标，使综合指标为原来变量的线性拟合。
主成分分析原理及详解
第14章主成分分析1 概述1.1 基本概念1.1.1 定义主成分分析是根据原始变量之间的相互关系，寻找一组由原变量组成、而彼此不相关的综合变量，从而浓缩原始数据信息、简化数据结构、压缩数据规模的一种统计方法。
1.1.2 举例为什么叫主成分，下面通过一个例子来说明。
假定有N 个儿童的两个指标x1与x2，如身高和体重。
x1与x2有显著的相关性。
当N较大时，N观测量在平面上形成椭圆形的散点分布图，每一个坐标点即为个体x1与x2的取值，如果把通过该椭圆形的长轴取作新坐标轴的横轴Z1，在此轴的原点取一条垂直于Z1的直线定为新坐标轴的Z2，于是这N个点在新坐标轴上的坐标位置发生了改变；同时这N个点的性质也发生了改变，他们之间的关系不再是相关的。
很明显，在新坐标上Z1与N个点分布的长轴一致，反映了N个观测量个体间离差的大部分信息，若Z1反映了原始数据信息的80%，则Z2只反映总信息的20%。
这样新指标Z1称为原指标的第一主成分，Z2称为原指标的第二主成分。
所以如果要研究N个对象的变异，可以只考虑Z1这一个指标代替原来的两个指标（x1与x2），这种做法符合PCA提出的基本要求，即减少指标的个数，又不损失或少损失原来指标提供的信息。
1.1.3 函数公式通过数学的方法可以求出Z1和Z2与x1与x2之间的关系。
Z1=l11x1+ l12x2Z2=l21x1+ l22x2即新指标Z1和Z2是原指标x1与x2的线性函数。
在统计学上称为第一主成分和第二主成分。
若原变量有3个，且彼此相关，则N个对象在3维空间成椭圆球分布，见图14-1。
通过旋转和改变原点（坐标0点），就可以得到第一主成分、第二主成分和第三主成分。
如果第二主成分和第三主成分与第一主成高度相关，或者说第二主成分和第三主成分相对于第一主成分来说变异很小，即N个对象在新坐标的三维空间分布成一长杆状时，则只需用一个综合指标便能反映原始数据中3个变量的基本特征。
1.2 PCA满足条件1.2.1 一般条件一般来说，N个对象观察p个指标，可以得到N*p个数据（矩阵）。
第六章-主成分分析法精选全文
可编辑修改精选全文完整版第六章 主成分分析法主成分分析法是将高维空间变量指标转化为低维空间变量指标的一种统计方法。
由于评价对象往往具有多个属性指标，较多的变量对分析问题会带来一定的难度和复杂性。
然而，这些指标变量彼此之间常常又存在一定程度的相关性，这就使含在观测数据中的信息具有一定的重叠性。
正是这种指标间的相互影响和重叠，才使得变量的降维成为可能。
即在研究对象的多个变量指标中，用少数几个综合变量代替原高维变量以达到分析评价问题的目的。
当然，这少数指标应该综合原研究对象尽可能多的信息以减少信息的失真和损失，而且指标之间彼此相互独立。
第一节 引言主成分分析，也称主分量分析，由皮尔逊（Pearson ）于1901年提出，后由霍特林（Hotelling ）于1933年发展了，这也正是现在多元统计分析中的一种经典统计学观点。
经典统计学家认为主成分分析是确定一个多元正态分布等密度椭球面的主轴，这些主轴由样本来估计。
然而，现代越来越多的人从数据分析的角度出发，用一种不同的观点来考察主成分分析。
这时，不需要任何关于概率分布和基本统计模型的假定。
这种观点实际上是采用某种信息的概念，以某种代数或几何准则最优化技术对一个数据阵的结构进行描述和简化。
主成分分析方法的主要目的就是通过降维技术把多个变量化为少数几个主要成分进行分析的统计方法。
这些主要成分能够反映原始变量的绝大部分信息，它们通常表示为原始变量的某种线性组合。
为了使这些主要成分所含的信息互不重迭，应要求它们互不相关。
当分析结束后，最后要对主成分做出解释。
当主成分用于回归或聚类时，就不需要对主成分做出解释。
另外，主成分还有简化变量系统的统计数字特征的作用。
对于任意p 个变量，描述它们自身及其相互关系的数字特征包括均值、方差、协方差等，共有)1(21-+p p p 个参数。
经过主成分分析后，每个新变量的均值和协方差都为零，所以，变量系统的数字特征减少了)1(21-+p p p 个。
主成分分析实例和含义讲解
主成分分析实例和含义讲解1.数据标准化：对原始数据进行标准化处理，使得每个变量的均值为0，方差为1、这一步是为了将不同量级的变量进行比较。
2.计算协方差矩阵：根据标准化后的数据，计算协方差矩阵。
协方差矩阵反映了各个变量之间的线性关系。
3.特征值分解：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。
特征值表示了各个特征向量的重要程度。
4.选择主成分：根据特征值的大小，选择前k个特征向量作为主成分，k通常是根据主成分所解释的方差比例进行确定。
5.数据投影：将原始数据投影到选取的主成分上，得到降维后的数据。
主成分分析的含义可以从两个方面来解释。
一方面，主成分分析表示了原始数据在新坐标系下的投影，可以帮助我们理解数据的结构和变化。
通过选择前几个主成分，我们可以找到最能够代表原始数据的几个因素，从而实现数据的降维。
例如，在一个包含多个变量的数据集中，如果我们选择了前两个主成分，那么我们可以通过绘制数据在这两个主成分上的投影，来理解数据的分布和变化规律。
同时，主成分的累计方差贡献率可以帮助我们评估所选择的主成分对原始数据方差的解释程度，从而确定降维的精度。
另一方面，主成分分析还可以用于数据的预处理和异常值检测。
通过计算每个变量在主成分上的权重，我们可以判断每个变量对主成分的贡献大小。
如果一些变量的权重很小，那么可以考虑将其从数据集中剔除，从而减少数据的维度和复杂度。
此外，主成分分析还可以检测数据集中的异常值。
在降维的过程中，异常值对主成分的计算结果会产生较大的影响，因此可以通过比较各个主成分的方差贡献率，来识别可能存在的异常值。
总之，主成分分析是一种常用的数据降维方法，它能够帮助我们理解数据集的结构，并鉴别对数据变化影响最大的因素。
通过选择适当的主成分，我们可以实现数据的降维和可视化，并对异常值进行检测。
在实际应用中，主成分分析常常与其他数据挖掘和机器学习方法结合使用，从而发现数据的隐藏模式和关联规则，提高数据分析的效果和准确性。
PCA（主成分分析）详解（写给初学者）
PCA（主成分分析）详解（写给初学者）学习图像处理，无疑会涉及到降维的操作，而PCA是常用的降维算法，既然经常用到，所以需要抠明白才行啊~~PCA（PrincipalComponents Analysis）即主成分分析，是图像处理中经常用到的降维方法，大家知道，我们在处理有关数字图像处理方面的问题时，比如经常用的图像的查询问题，在一个几万或者几百万甚至更大的数据库中查询一幅相近的图像。
这时，我们通常的方法是对图像库中的图片提取响应的特征，如颜色，纹理，sift，surf，vlad等特征，然后将其保存，建立响应的数据索引，然后对要查询的图像提取相应的特征，与数据库中的图像特征对比，找出与之最近的图片。
这里，如果我们为了提高查询的准确率，通常会提取一些较为复杂的特征，如sift，surf等，一幅图像有很多个这种特征点，每个特征点又有一个相应的描述该特征点的128维的向量，设想如果一幅图像有300个这种特征点，那么该幅图像就有300*vector（128维）个，如果我们数据库中有一百万张图片，这个存储量是相当大的，建立索引也很耗时，如果我们对每个向量进行PCA处理，将其降维为64维，是不是很节约存储空间啊？一、简介PCA（Principal Components Analysis）即主成分分析，是图像处理中经常用到的降维方法，大家知道，我们在处理有关数字图像处理方面的问题时，比如经常用的图像的查询问题，在一个几万或者几百万甚至更大的数据库中查询一幅相近的图像。
这时，我们通常的方法是对图像库中的图片提取响应的特征，如颜色，纹理，sift，surf，vlad等等特征，然后将其保存，建立响应的数据索引，然后对要查询的图像提取相应的特征，与数据库中的图像特征对比，找出与之最近的图片。
这里，如果我们为了提高查询的准确率，通常会提取一些较为复杂的特征，如sift，surf等，一幅图像有很多个这种特征点，每个特征点又有一个相应的描述该特征点的128维的向量，设想如果一幅图像有300个这种特征点，那么该幅图像就有300*vector（128维）个，如果我们数据库中有一百万张图片，这个存储量是相当大的，建立索引也很耗时，如果我们对每个向量进行PCA处理，将其降维为64维，是不是很节约存储空间啊？对于学习图像处理的人来说，都知道PCA是降维的，但是，很多人不知道具体的原理，为此，我写这篇文章，来详细阐述一下PCA及其具体计算过程：二、PCA详解1、原始数据：为了方便，我们假定数据是二维的，借助网络上的一组数据，如下：x=[2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1]Ty=[2.4, 0.7, 2.9, 2.2, 3.0, 2.7, 1.6, 1.1, 1.6, 0.9]T2、计算协方差矩阵什么是协方差矩阵？相信看这篇文章的人都学过数理统计，一些基本的常识都知道，但是，也许你很长时间不看了，都忘差不多了，为了方便大家更好的理解，这里先简单的回顾一下数理统计的相关知识，当然如果你知道协方差矩阵的求法你可以跳过这里。
张敏强《教育与心理统计学》修订本笔记和课后习题(含考研真题)详解(主成分分析)【圣才出品】
张敏强《教育与心理统计学》修订本笔记和课后习题（含考研真题）详解第11章主成分分析【本章重点】☆主成分分析的基本原理☆主成分分析的步骤11.1复习笔记一、主成分分析的基本原理主成分分析主要是用来寻找判断某种事物或现象的主要综合指标，它是在不损失或很小损失原有信息的前提下，将原来多个彼此相关的指标转换为新的少数几个彼此独立的综合指标的一种多元统计分析方法。
实际上，主成分分析是一个数据降维的过程，即将反映复杂现象的相关变量用综合变量来代表。
主成分的分析原理是：设有n个观测点（x il，x i2），i=1，2，…，n。
这n个观测点的分布如图11-2。
主成分分析的原理是先对n个观测点（x il，x i2）求出第一条“最佳”拟合直线，使得这n个观测点到该直线的垂直距离的平方和最小，这时称此直线为第一主成分，然后再求与第一主成分相互独立（在此表现为相互垂直）的且与n个观测点（x i1，x i2）的垂直距离平方和最小的第二主成分。
如图11-2所示。
图11-2主成分分析示意图假如有P个变量，共得到n个点（x i1，x i2，x ip），此时，若要求第k个主成分，就必须使它与前k-1个主成分不相关，且使它与n个观测点的垂直距离平方和为最小。
如此继续，直至求出P个主成分。
注意：只有变量间存在一定相关才可以降维，原有的变量数和主成分数相等，并且具体选取几个主成分，应视具体情况而定。
二、主分量的导出主分量的导出是对主成分分析数学模型的讨论。
由主成分分析的基本原理可知，主成分分析，实际上就是分解相关矩阵，从而使P个相关的变量分解成P个独立的分量。
（一）主成分的定义及满足条件设X=（x1，x2，…，x P）'是一个p维随机向量。
并假设X的数学期望E（X）=0，记X的协方差矩阵为E（XX'）=∑，令U=（u1，u2，…，u P）'是-P维向量，且满足W'=U'U=I，则X的第i主成分定义为：（11.1）且满足条件：1．第一主成分F1是一切形如中使F的方差达到最大者。
主成分分析法(PCA)
可知 β = 0 ，并且可得
∑ w2 = α w2
，
这表明w2应该是 ∑ 的特征向量，具有第二大特征 值 λ2 = α , 类似的，我们可以证明其它维被具有递减的特征值 的特征向量给出
z = W T x,W是矩阵 我们来看另一种推导：
如果我们建立一个矩阵C，其第i列是 ∑ 的规范化 的特征向量，则 C T C = I ，并且 ∑ = ∑ CC T = ∑(c1 , c2 ,L cn )C T
前 k 个主成分的贡献率之和
∑λ
i =1
k
i
∑λ
j =1
n
j
称为主成分 λ1 , λ2 L λk 的累计贡献率，它表明 z1 , z2 ,L zk 解释 x1 , x2 L xn 的能力。 通常取较小的 k ，使得累计贡献达到一个较高的百分比(如 80％～90％)。此时，z1 , z2 ,L zk 可用来代替 x1, x2 L xn ，从而 达到降维的目的，而信息的损失却不多。
同时我们还得到
T T w1 ∑ w1 = αw1 w1 = α
为了使方差最大，选择具有最大特征值的特征向量 ， 因此，第一个主成分 w1 是输入样本的协方差阵的 具有最大特征值对应的特征向量
第二个主成分 w2 也应该最大化方差，具有单位长度， 并且与 w1 正交 对于第二个主成分，我们有
T T T max w2 ∑ w2 − α ( w2 w2 − 1) − β ( w2 w1 − 0) w2
( 2)
关于w2求导并令其为0，我们有
2 ∑ w2 − 2αw2 − βw1 = 0
上式两边乘以
T w1
T T 2 w1 ∑ w2 − 2α ， 1 w2 − βw1 w1 = 0 wT
主成分总结
主成分分析（Principal Component Analysis）总结引言主成分分析（Principal Component Analysis，PCA）是一种常用的降维技术，用于发现数据集中的最重要的特征。
在数据分析和机器学习领域广泛应用的PCA 算法，通过线性变换将原始数据转换为一组新的变量，这些新变量是原始数据的无关主成分。
本文将介绍PCA的基本思想、原理和应用，并总结其优点和缺点。
PCA的基本思想PCA的基本思想是通过线性变换将原始数据转换为一组新的变量，这组新变量被称为主成分。
主成分是原始数据在正交方向上的线性组合，其中第一个主成分（PC1）方差最大，第二个主成分（PC2）方差次之，依此类推。
主成分之间是相互无关的。
PCA的数学原理PCA的数学原理基于对协方差矩阵的特征值分解。
具体步骤如下： 1. 数据标准化：对原始数据进行均值中心化和标准差缩放，确保每个特征具有相同的重要性。
2. 构建协方差矩阵：计算标准化后的数据的协方差矩阵。
3. 特征值分解：对协方差矩阵进行特征值分解，得到特征值和特征向量。
4. 选择主成分：按特征值从大到小的顺序，选择最大的k个特征值对应的特征向量作为主成分。
5. 构造新的特征空间：使用选择的主成分构造新的特征空间，实现数据的降维。
PCA的应用1.数据降维：PCA可以将高维数据降低到低维空间，减少特征数量，便于可视化和处理。
例如，在图像识别中，可以使用PCA将图像特征从像素级降低到更高级的特征，提高分类准确性。
2.噪声过滤：通过保留较大的主成分，PCA可以过滤掉原始数据中的噪声，提高数据质量和模型性能。
3.数据可视化：PCA可以将高维数据映射到二维或三维空间，使得数据可以可视化展示，帮助我们观察数据之间的关系和结构。
4.特征提取：PCA可以将原始数据转换为一组主成分，这些主成分可以用于构建更简单、更高效的模型，提取数据的最重要特征。
PCA的优点1.简化数据：PCA可以帮助我们减少特征数量，降低数据的维度，简化分析过程。
主成分分析(PCA)原理详解_精品
主成分分析（PCA）原理详解_精品
PCA的基本思想是将原始数据通过线性变换，转化为一组新的互相独
立的变量，这些新变量是原始数据中的线性组合，且保留了原始数据的最
大方差。
这意味着通过选择保留方差较大的线性组合，可以有效减少数据
的维度，同时尽量保留数据的有用信息。
具体来说，PCA的实现过程如下：
1.数据标准化：首先，要对原始数据进行标准化处理，保证每个特征
的均值为0，方差为1、这是因为PCA是基于方差最大化的，如果特征的
尺度差异较大，会导致方差较大的特征主导整个PCA过程，而忽略了方差
较小但是有用的特征。
2.计算协方差矩阵：计算标准化后的数据的协方差矩阵，其中协方差
矩阵的第i行第j列表示第i个和第j个特征之间的协方差。
3.计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征
值和特征向量。
特征向量是协方差矩阵的特征值对应的单位长度向量。
4.选择主成分：根据特征值的大小，选择前k个特征向量作为主成分，这些主成分对应的特征值表示了数据中的主要信息。
5.数据转换：将原始数据乘以选取的特征向量构成的变换矩阵，实现
数据的降维。
转换后的数据保留了原始数据的主要信息。
需要注意的是，PCA只能对线性关系进行降维，对非线性关系的数据
效果不好。
此时可以使用核主成分分析（Kernel PCA）来处理非线性关系
的数据。
总结起来，PCA通过将原始数据进行线性变换，得到一组新的互相独立的变量，以降低数据的维度和特征之间的相关性。
它能够在保留数据主要信息的同时，减少数据的冗余和噪音，提高数据分析和建模的效果。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Y1
Y2
x1
图三：主成分与方差之间的关系
3) 坐标变换和基变换：
表 1：基变换与坐标变换的对比
基变换 (������↓1 ������↓2 ������↓3) = (������↓1 ������↓2 ������↓3)������
������11 ������12 ������13 ������ = (������21 ������22 ������23)
原始数据
降维数据
相互相关
相互独立
PCA
无用
有用
图一：PCA 的作用
1. 数据构成
已知 m 个数据样本，每个数据样本都是 n 维的向量，这些数据可以组成数
据矩阵������������������：（根据 m 和 n 的大小可以分为两种情况，后续详述）
������11 ������12 … ������1������
a) 变换的基必须是标准正交基
由表一可知： ������−1 = ������������ 。
b) 变换后信号具有非相关性，即协方差项均为零：
〈������1→, ������1→〉
0
…
0
������������������(������������������)������ = (
0 ⋮
〈������2→, ������2→〉
3
2) 主成分的衡量指标： 协方差能够体现不同维度数据之间的相关性，而方差则能够作为衡量某一 维度数据是否有效的指标。如图三所示，样本分布的主方向 Y1 方向的方差较 大，而 Y2 方向方差较小，可以省去 Y2，以 Y1 作为主成分。 体现在协方差矩阵中，为对角线上的元素越大，对应的维度数据越重要。
图二左侧所显示的从 X1X2 坐标到 Y1Y2 坐标的转换方法即为坐标变换。即 寻找一个变换矩阵������������������,使得：
������������������ = (������������������)������������������������ 并且要求该变换具有如下性质：
(������↓1 ������↓2 ������↓3)均为单位向量 则→ 任意〈������↓������ ������↓������〉 = ������
实际特征值求解时的情况 证明：实对称矩阵不同特征值对应特征向量正交 设 AX＝λX, AY＝μY. A,X,Y,λ,μ皆实，λ≠
μ，A'＝A.
（λX）'＝λX'＝（AX）'＝X'A'＝X'A, λX'＝X'A,此式右乘 Y:
3. PCA 的计算流程
因为从������������������ 到��������������� ��� 的变换过程为标准正交变换，变换矩阵������������������ 为正交矩阵。根 据正交矩阵的性质：
(������������������)−1 = (������������������)������
⋮
⋱
0 ⋮
)
0
0
… 〈���������→��� , ���������→��� 〉
——（6） ——（7）
（6）带入（7）：
������������������(������������������)������ = (������������������)������������������������(������������������)������������������������
������������������
=
(������21 ⋮
������22 ⋮
⋱
������2������) ⋮
���������1��� ���������2��� … ������������������
——（1）
������1������
该矩阵中每一列������↓������ =
������2������ ⋮
������3
������3
������1 ������1 (������2)，(������2)同一向量为分别在(������↓1 ������↓2 ������↓3)和
������3 ������3 (������↓1 ������↓2 ������↓3)的假设条件 (������↓1 ������↓2 ������↓3)任意两个向量互相垂直 则→ 任意两个〈������↓������ ������↓������〉 = ������, ������ ≠ ������
������ =
������������221 ⋮
������������222 ⋮
⋱
������������22������ ⋮
=
������
1 −
1
(〈������2→,⋮������1→〉
〈������2→, ������2→〉 ⋮
⋱
〈������2→,⋮���������→��� 〉)
(���������������2���1 ���������������2���2 … ���������������2���������)
������31 ������32 ������33
������↓1向量在(������↓1 ������↓2 ������↓3)坐标系中的坐 ������11
标为������↓1 = (������21)。 ������31
坐标变换
������1
������1
(������2) = ������−1 (������2)
−
��������������� ���������������������)
������=1
1
������1→ − ������1������������������������⁄������1
������������������ = ������2→ − ������2������������������������⁄������2
↓ ������−������ = ������������
λX'Y＝X'AY＝X'（μY）＝μX'Y, （λ-μ）X'Y＝0.
∵λ≠μ，λ-μ≠0， ∵ X'Y＝X·Y＝0. X⊥Y. 但如果要求所有特征向量正交，需要使用施密特正
交化方法，以保证：
〈������↓������ ������↓������〉 = 0（λ = μ）
〈���������→��� , ������1→〉 〈���������→��� , ������2→〉 … 〈���������→��� , ���������→��� 〉
=
1 ������−1
������������������
(������������������)������
——（5）
协方差矩阵ΔX2 对角线上的元素均大于零（没有常数信号的情况下）。理 想情况下该矩阵对角线外的元素应当全为零，表示任何两组不同的信号之间都 互不相关。如何将信号的协方差矩阵������������������ 转变为除对角线外元素全为零的矩 阵。（体现正交性）
��������������� ���������������������
=
1 ������
������
∑
������������������
������=1
������������
=
2
√������
1 −
������
1 ∑(������������������
−
��������������� ���������������������)(������������������
一、
主成分分析 学习笔记
—— Principal Component Analysis
摘要
主成分分析原理和用法 wanglei 2013-05-16
Email:towanglei@
一、 主成分分析介绍
主成分分析(Principal component analysis)是一种数据分析方法，用于 从大量互相混杂的数据中提取出相互独立的少量有用信息，即数据降维。
——（8）
由（8）式可以看出，信号之间的去相关可以用矩阵的对角化方法求出，而 ������������������则体现了是对角化过程中的线性变换。
5
c) 变换后对角线上的方差自大而小排列，以突出主成分。 4) 总结：
PCA 的思路是寻找一个标准正交变换矩阵������������������，使变换后的协方差矩阵 ������������������(������������������)������满足：对角线外的元素为零，对角线上的元素自大到小排列。在矩阵 论中成为矩阵的正交对角分解。
（图二左）X1 与 X2 维度之间具有线性相关相性关（数由据X1 的│值可无以关大数致据确定 X2 的值）。则能够找到一种维度坐标 Y1 和 Y2，Y1图和二Y：2 之不间同互维不度相之关间，数且据分Y1布方情况 向与样本散布方向相一致。则仅以 Y1 维度的数据值即可反应样本之间的差异。 这种 X1、X2 到 Y1 的过程即为降维。
⋮
���������→��� (
−
������������������������������������⁄������3
)
——（2）
2. PCA 的计算思路 PCA 解决的是取消数据不同维度之间的相关性，并找出能够最大反映样本
之间差别的维度。以二维为例如图二所示：
x2
x2
Y1
Y2
x1
x1
x2
图二：不同维度之间数据分布情况（左：相关数据，右：无关数据）
标准化后的信号���������→��� 与信号���������→��� 的协方差为：