平面曲线弧长
曲线的弧长与曲率的计算与性质

曲线的弧长与曲率的计算与性质曲线是我们经常在数学、物理等领域中遇到的概念。
当我们研究曲线的性质时,曲线的弧长和曲率是两个重要的参数。
本文将介绍曲线的弧长和曲率的计算方法,并探讨它们的性质。
一、曲线的弧长计算方法在几何学中,曲线的弧长是指曲线上两点之间的距离。
对于一条平面曲线来说,我们可以通过积分来计算其弧长。
具体计算方法如下:假设有一条曲线C,其方程为y = f(x),其中a ≤ x ≤ b。
我们可以将曲线分割成无穷多个小线段,然后对每个小线段求长度,并将这些长度累加起来,即可得到曲线C的弧长L。
设曲线上某一点P(x, y),其切线与x轴的夹角为θ,则小线段的长度可以通过勾股定理计算得到:ds = √(dx² + dy²) = √(1 + (dy/dx)²)dx将dx用x表示,即可得到弧长的积分表达式:L = ∫√(1 + (dy/dx)²)dx (a ≤ x ≤ b)通过求解上述积分,我们可以计算曲线的弧长。
二、曲线的曲率计算方法曲率是描述曲线弯曲程度的一个参数,它与曲线上某一点处的切线有关。
曲线的曲率可以通过以下公式计算:K = |dθ/ds| = |(d²y/dx²)/(1 + (dy/dx)²)^(3/2)|其中,dθ表示角度的变化量,ds表示弧长的微元。
我们可以根据上述公式,对曲线进行求导,然后带入相应的数值,即可得到曲线上某点的曲率K。
三、曲线弧长与曲率的性质1. 弧长与曲线的形状有关:对于相同起点和终点的两条曲线,其弧长不同,取决于曲线的形状。
比如,一条圆形的曲线与一条直线的曲线相比,弧长要更长。
2. 曲率描述曲线的弯曲程度:曲率大的地方,曲线的弯曲程度越大;曲率小的地方,曲线的弯曲程度越小。
通过计算曲率,我们可以描述曲线的局部形态。
3. 曲率与切线垂直:曲线上任意一点处的切线与曲线的法线(垂直于切线的直线)平行。
曲线弧度计算公式详解

曲线弧度计算公式详解在数学中,曲线弧度是描述曲线弯曲程度的一个重要概念。
在实际问题中,我们经常需要计算曲线的弧度,以便更好地理解和分析曲线的特性。
本文将详细介绍曲线弧度的计算公式及其应用。
一、什么是曲线弧度?曲线弧度是描述曲线弯曲程度的一个量,通常用弧长与半径的比值来表示。
在平面几何中,曲线的弧度可以用弧长s除以半径r来表示,即弧度θ=s/r。
在三维空间中,曲线的弧度可以用弧长s除以半径r来表示,即弧度θ=s/r。
二、曲线弧度的计算公式。
1. 平面曲线的弧度计算公式。
对于平面曲线,其弧度计算公式为θ=s/r,其中s为弧长,r为半径。
在直角坐标系中,如果曲线的参数方程为x=f(t),y=g(t),则弧长可以表示为积分形式:s=∫[a,b]√(f'(t)^2+g'(t)^2)dt。
其中f'(t)和g'(t)分别为x=f(t)和y=g(t)的导数。
因此,曲线的弧度可以表示为:θ=∫[a,b]√(f'(t)^2+g'(t)^2)dt/r。
这就是平面曲线的弧度计算公式。
2. 空间曲线的弧度计算公式。
对于空间曲线,其弧度计算公式同样为θ=s/r,其中s为弧长,r为半径。
在直角坐标系中,如果曲线的参数方程为x=f(t),y=g(t),z=h(t),则弧长可以表示为积分形式:s=∫[a,b]√(f'(t)^2+g'(t)^2+h'(t)^2)dt。
其中f'(t),g'(t)和h'(t)分别为x=f(t),y=g(t)和z=h(t)的导数。
因此,曲线的弧度可以表示为:θ=∫[a,b]√(f'(t)^2+g'(t)^2+h'(t)^2)dt/r。
这就是空间曲线的弧度计算公式。
三、曲线弧度的应用。
1. 几何分析。
曲线弧度可以用来描述曲线的弯曲程度,从而帮助我们更好地理解和分析曲线的特性。
通过计算曲线的弧度,我们可以比较不同曲线的弯曲程度,从而找到最合适的曲线来描述实际问题。
6.4平面曲线的弧长

折线的长 Mi1Mi 的极限存在,则称此极限为曲线
i 1
弧AB的弧长.
二、平面曲线弧长的计算
1.直角坐标情形
设曲线弧为y f ( x) y
(a x b),其中f ( x)在[a,b]
上有一阶连续导数.
dy
取积分变量为x , 在[a , b]上
任取小区间[ x, x dx],
o a x x dx b x
以对应小切线段的长代替小弧段的长,
小切线段的长 (dx)2 (dy)2 1 y2dx,
弧长元素ds 1 y2dx, 弧长s b 1 y2dx. a
例 1 计算曲线 y 2 x3 2 上相应于x从点 a 到 b 的 3
一段弧的长度.
解
因为
y
1
x2,
所以ds
1
(
x
1 2
)2
dx
1 xdx,
2.参数方程情形
设曲线弧为
x y
(t) (t)
( t ).
其中 (t), (t)在[ , ]上具有连续导数.
ds (dx)2 (dy)2 [ 2 (t ) 2 (t )](dt )2
2 (t ) 2 (t )dt,
所以弧长 s 2 (t) 2 (t)dt.
例4 求星形线 x2 3 y2 3 a2 3 (a 0) 的全长.
解 星形线的参数方程为
x a cos3 t
y
a
sin3
t
(0 t 2π),
设s1为第一象限部分的弧长,则根据对称性,
π
s
4s1
4
2 0
x2 y2dt
π
4 2 3a sin t cos tdt 6a. 0
平面曲线的弧长与曲率

O
ax
π
因此 s 4 2 x2(t ) y2(t )dt 0
π
4 2
3a cos2 t sin t
2
3a sin2 t cos t
2
dt
0
12a
π 2
sin
t
cos
tdt
12a
sin2
t
π 2
6a.
0
20
数学分析 第十章 定积分的应用
高等教育出版社
§3 平面曲线的弧长曲率
平面曲线的弧长
n
故 lim T 0 i1
x2(i ) y2(i )Δti
数学分析 第十章 定积分的应用
高等教育出版社
x2(t) y2(t) dt.
§3 平面曲线的弧长曲率
平面曲线的弧长
由第一章§1习题 6 可知
*平面曲线的曲率
x2(i ) y2(i ) x2(i ) y2(i ) y(i ) y(i ) . 又y(t)在[ , ]上连续,从而在[ , ]上一致连续,
b2
ab sin2 t
b2
32.
当 a b 0 时, 在 t 0, π 处曲率最大, 在 t π ,
3π 2
处曲率最小,
Kmax
a b2
, Kmin
b a2
.
2
数学分析 第十章 定积分的应用
高等教育出版社
§3 平面曲线的弧长曲率
平面曲线的弧长
*平面曲线的曲率
由例1可得,若
a
b
R,
则各点处曲率相等,
数学分析 第十章 定积分的应用
高等教育出版社
§3 平面曲线的弧长曲率
平面曲线的弧长
*平面曲线的曲率
数学分析-平面曲线的弧长与曲率

解: 利用对称性
绕 x 轴旋转
星形线
星形线是内摆线的一种.
点击图片任意处 播放开始或暂停
大圆半径 R=a
小圆半径
参数的几何意义
(当小圆在圆内沿圆周滚动
时, 小圆上的定点的轨迹为是内摆线)
内容小结
3. 平面曲线的弧长
曲线方程
参数方程方程
上
半圆为
下
它也反映了环面微元的另一种取法.
第三节、平面曲线的弧长与曲率
定义: 若在弧 AB 上任意作内接折线 ,
当折线段的最大
边长 →0 时,
折线的长度趋向于一个确定的极限 ,
此极限为曲线弧 AB 的弧长 ,
即
并称此曲线弧为可求长的.
定理: 任意光滑曲线弧都是可求长的.
则称
(1) 曲线弧由直角坐标方程给出:
弧长元素(弧微分) :
因此所求弧长
的弧长 .
解:
例12. 求阿基米德螺线
相应于 0≤≤2
一段的弧长 .
解:
第四节、旋转体的侧面积
设平面光滑曲线
求
积分后得旋转体的侧面积
它绕 x 轴旋转一周所得到的旋转曲面的侧面积 .
取侧面积元素:
例19. 计算圆
x 轴旋转一周所得的球台的侧面积 S .
解: 对曲线弧
应用公式得
当球台高 h=2R 时, 得球的表面积公式
极坐标方程
弧微分:
直角坐标方程
注意: 求弧长时积分上下限必须上大下小
4. 旋转体的侧面积
侧面积元素为
(注意在不同坐标系下 ds 的表达式)
思考与练习
1.用定积分表示图中阴影部分的边界长 s .
平面曲线的弧长

由弧长公式得
s
2 0
x '2 ( t ) y '2 ( t )dt
2
0
2a (1 cos t )dt
2
2 0
2a
t sin dt 8a . 2
例 1 求摆线 x a( t sin t ), y a(1 cos t )(a 0) 一拱 的弧长.
求长的, 且弧长为
s
x '2 ( t ) y '2 ( t )dt .
证明
如前所述, 对C 作任意分割T { P0 , P1 ,
Pn },
并设 P0 与 Pn 分别对应 t 与 t ,且
Pi ( xi , yi ) ( x( t i ), y( t i )), i 1,2..., n 1 .
i 1
t
i 1 i
n
i
i t i .
i 1
n
从而公式成立.
例 1 求摆线 x a( t sin t ), y a(1 cos t )(a 0) 一拱 的弧长.
解
x (t ) a(1 cos t ), y (t ) a sin t ,
x'2 ( i ) y'2 ( i )
i
,
x'2 ( i ) y'2 (i )
则有
sT [ x '2 ( i ) y '2 ( i ) i ]t i .
i 1 n
利用三角不等式容易证明
i y' (i ) y' ( i ) y ' (i ) y ' ( i ) ,
7-2平面曲线的弧长及旋转体的侧面积

2 2
2
π
1
1
周所得的旋转面的面积为
2 0
1 5 S 2= ∫ 2π ⋅ x ⋅ dx = 5π . 2 2
因此, 因此,所求旋转体的表面积为
练习题答案
a 2 1 3 5 3 2、 3、 一、1、1 + ln ; 2、 π ; 3、 + ln . 2 2 12 2 2 3 8 5 二、 [( ) 2 − 1]. 9 2 三、6a . 四、8a .
2 3 3 )a, a ) . 六、(( π − 3 2 2
2 2
= n∫
0
sin t + cos t + 2 sin t cos t dt 2 2 2 2
sin t + cos t dt = n∫ = 4n. 0 2 2
π
三、参数方程情形
曲线弧为
x = ϕ (t ) , y = ψ (t )
= r (θ ) + r ′ (θ )dθ ,
2 2
故弧长 s = ∫α r (θ ) + r ′ (θ )dθ .
β
2 2
例 4 求阿基米德螺线 r = aθ (a > 0)上相应
的弧长. 于 θ 从 0 到 2π 的弧长. 解Q
r′ = a,
β α
2π
∴ s=∫
′ 2 (θ )dθ r (θ ) + r
第二节 平面曲线的弧长与 旋转体的侧面积
一、 平面曲线弧长的概念 二、 直角坐标系情况 三、 参数方程情况 四、 极坐标情况 五、旋转体的侧面积 六、 小结
《微积分》第八节 平面曲线的弧长
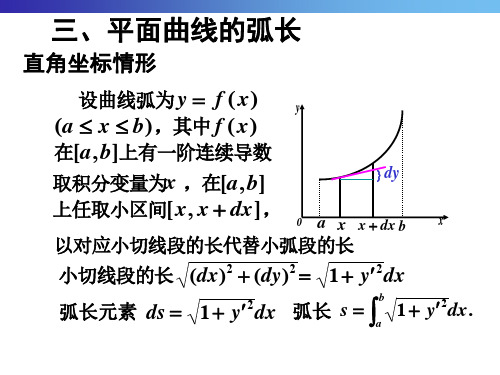
小结
平面曲线弧长的概念
弧微分的概念
直角坐标系下
求弧长的公式
参数方程情形下
极坐标系下
思考题
闭区间[a, b]上的连续曲线 y f ( x)
是否一定可求长?
思考题解答
不一定.仅仅有曲线连续还不够,必须保证 曲线光滑才可求长.
作业
P236习题3_8 1(单),2(2),3,4(2), 5,7(1、4),8,10(单)
三、平面曲线的弧长
直角坐标情形
设曲线弧为 y f ( x) y (a x b),其中 f ( x)
在[a, b]上有一阶连续导数
取积分变量为x ,在[a, b]
dy
上任取小区间[ x, x dx],
o a x x dx b x
以对应小切线段的长代替小弧段的长
小切线段的长 (dx)2 (dy)2 1 y2dx
曲线弧为 ( ) ( )
其中 ( ) 在[ , ]上具有连续导数.
x y
( (
)cos )sin
( )
dx [()cos ()sin]d,
dy [()sin ()cos]d,
ds (dx)2 (dy)2 2( ) 2( )d,
弧长
s
2( ) 2( )d .
例5
求极坐标系下曲线r
a
sin
3
3
的长.
(a 0) (0 3)
解
r
3a
sin
3
2
cos
3
1 3
a sin
2
cos
,
3 3
s
r 2( ) r2( )d
3 0
a2
sin
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
低体内血糖水平,然后通过给病人注射大量的糖,假
设测得病人血液中胰岛素的浓度C(t)(单位/ml)符合
分段函数
ln 2 其中 k ,时间t的单位为分钟,试求血液中胰岛 10 素在一小时内的浓度变化的平均值.
t (10 t ) C (t ) k ( t 5) 25 e
0t 5 t5
三、平面曲线弧长
设y=f(x)在[a,b]上有连续导数f’(x), x)
o
a
b
x
用微元法,在[a,b]上取小区间[x,x+dx],相应地截取一
小段弧AD,过A作切线AC,则BC=dy,若dx很小,则
AC≈AD,而
AC (dx) 2 (dy ) 2
1
课堂思考
x2 y2 椭圆 2 2 1 绕x轴与绕y轴旋转所 a b
成的体积是否相同,为什么?
y
o
x
水的重力为1000 gπ·32dx, 把这层水抽出池外需做功近 似为dW=9000gπdx
3m 5m
o x
x dx
于是所求的功为
2 x W 9000 gxdx 9000 9.8 [ ]5 3463604.2 0 0 2
5
五、定积分在医药学中的应用
例7 在测定病人胰岛素时,先让病人禁食以达到降
解:由函数的平均值公式,有
60 60 1 1 5 C (t )dt [ 0 C (t )dt 5 C (t )dt ] C (t ) 60 60 0 0
60 1 5 2 [ (10t t )dt 25e k ( t 5) dt ] 11.62 (单位/ml) 5 60 0
dl AD (dx) 2 (dy ) 2
y
y f ( x)
A
D
dy 2 1 ( ) dx dx
C
B
x
o
a
x x dx b
l
b
a
dy 2 1 ( ) dx dx
例5 证明:半径为a的圆的周长为2aπ。
解:设半径a的圆的方程为x2+y2=a2,则
y a x
2
a
2
课堂练习
1
1 x 2
sin x
2
1 x
dx ?
1 sin x x2 dx dx 2 2 1 1 x 1 1 x 1
2 x 1 1 dx 0 2 dx 2 0 1 x 2 1 x
x
2
1
1 1 2 (1 ) dx 2( x arctan x) |0 2 2 0 1 x 2
y
x a2 x2
l 4
0
a a x2 dx 1 2 2 dx 40 2 2 a x a x
x a 4[arcsin ]0 2a a
四、变力做功
知道一个常力F(力的方向,大小都不变)将物体沿 力的方向从点a 推到点b,所做的功 W=F(b-a)。如 何求变力F(x)(方向不变)将物体沿力的方向从点a移 到点b 所做的功W ?
在[a,b]内任取一点x,小区间[x,x+dx]上功的微元
dW=F(x)dx
W F ( x)dx
a
b
F ( x)
a
x
x dx
b
例6 设一圆柱形的贮水池高为5米,底面半径为3米,
池内装满了水,试问把池内的水全部抽出需做功多 少?
o x
5m
x dx
3m
解:小区间[x,x+dx],这层
