多元函数的极值
多元微积分-多元函数的极值

( x0, y0 ) 处 有 极 值 , 则 它 在 该 点 的 偏 导 数 必 然 为 零 :
fx(x0,y0) 0 , fy(x0,y 0) 0 .
(称驻点)
注意:极值点
驻点
例如, 点(0,0)是函数z xy的驻点,但不是极值点.
定理2 (充分条件)
设函数z f ( x, y)在点( x0 , y0 ) 的某邻域内连续,
小值.
使函数取得极值的点称为极值点. 极大值、极小值统称为极值.
例1 函数 z 3x2 4 y2
在 (0,0) 处有极小值.
(1)
例2 函数 z x2 y2
(2)
在 (0,0) 处有极大值.
例3 函数 z xy
(3)
在 (0,0) 处无极值.
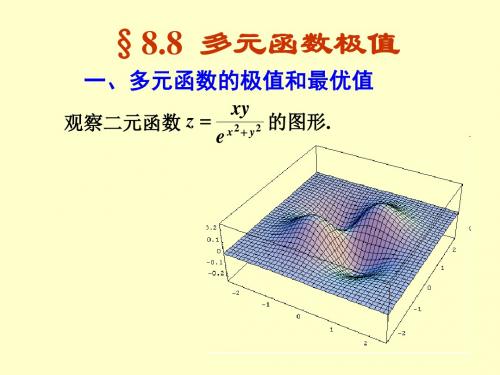
观察二元函数 z
xy ex2 y2
的图形
回忆一元函数的极值及其求法
100 5x2 48x 10 y2 24 y ,
令
Lx 10x 48 0 Ly 20y 24 0
解得惟一驻点
x 4.8, y 1.2,
A f xx 10 , B f xy 0 , C f yy 20 ,
B2 AC 0 , A 0 , 惟一驻点为极大值点,
即为最大值点,
解 fx (x, y) 3x2 3y fy (x, y) 3y2 3x
fxx (x, y) 6x fxy (x, y) 3 f yy (x, y) 6 y
解方程组
f f
x y
(x, (x,
y) y)
3x2 3y2
3y 3x
0 0
在 0, 0点处
得驻点 0, 0,1,1
A fxx (0, 0) 0 B fxy (0, 0) 3 C f yy (0, 0) 0
多元函数极值

提示: 当(x, y)=(0, 0)时, z=0, 而当(x, y)≠(0, 0) 时, z>0. 因此z=0是函数的极小值.
首页 上页 返回 下页 结束 铃
一,多元函数的极值及最大值,最小值
极值的定义 设函数z=f(x, y)在点(x0, y0)的某个邻域内有定义, 如果对 于该邻域内任何异于(x0, y0)的点(x, y), 都有 f(x, y)<f(x0, y0)(或f(x, y)>f(x0, y0)), 则称函数在点(x0, y0)有极大值(或极小值)f(x0, y0). 例2 函数z = x2 + y2 在 (0, 0)处有极大值 点 .
首页
上页
返回
下页
结束
铃
二,条件极值 拉格朗日乘数法
条件极值 对自变量有附加条件的极值称为条件极值. 求条件极值的方法 (1)将条件极值化为无条件极值 有时可以把条件极值问题化为无条件极值问题. 例如, 求V=xyz在条件2(xy+yz+xz)=a2下的最大值.
a2 2xy 由条件2(xy+ yz + xz)=a2 , 解得z = 得 , 于是 2(x+ y) xy a2 2xy V= ( ). 2 (x+ y) 这就把求条件极值问题转化成了求无条件极值问题.
首页 上页 返回 下页 结束 铃
二,条件极值 拉格朗日乘数法
条件极值 对自变量有附加条件的极值称为条件极值. 求条件极值的方法 (1)将条件极值化为无条件极值 (2)用拉格朗日乘数法 在多数情况下较难把条件极值转化为无条件极值, 需要 用一种求条件极值的专用方法, 这就是拉格朗日乘数法. 下面导出函数z=f(x, y)在条件(x, y)=0下取得的极值的必 要条件. 假定f(x, y)及(x, y)有各种所需要的条件.
多元函数的极值及最大值

例5 求表面积为 a 而体积为最大的长方体 的体积 .
2
三、最小二乘法
作业:P70 1 5 8
要找函数z f ( x, y)在附加条件 ( x, y) 0 下的可能极值点,可以 先构成辅助函数 F ( x, y) f ( x, y) ( x, y) f x ( x, y ) x ( x, y ) 0 由: f y ( x, y ) y ( x, y ) 0 ( x, y ) 0
例3:某厂要用铁板做成一 个体积为2m 的有盖 长方形水箱 .问长、宽、高各取怎样 的尺 寸时,才能使用料最省 ?
例4:有一宽为 24cm的长方形铁板,把它两 边 折起来做成一个断面为 等腰梯形的水槽 . 问怎样折法才能使断面 的面积最大?
3
二、条件极值 拉格郎日乘数法
无条件极值 条件极值 拉格郎日乘数法
(1) AC B 2 0时具有极值,且当 A 0时有极大 值,当A 0时有极小值;
(2) AC B2 0时没有极值;
(3) AC B 2 0时可能有极值,也可能 没有极值, 还需另作讨论 . 3 3 2 2 例2:求函数f ( x, y) x y 3x 3 y 9x的极值 .
驻点:能使 f x ( x, y) 0, f y ( x, y) 0同时成立的点 .
可导:极值点 驻点. 驻点 ?极值点.
定理2(充分条件):设函数z f ( x, y )在点( x0 , y0 )的 某邻域内连续且有一阶 及二阶连续偏导数,又 f x ( x0 , y0 ) 0, f y ( x0 , y0 ) 0.令 f xx ( x0 , y0 ) A, f xy ( x0 , y0 ) B, f yy ( x0 , y0 ) C , 则f ( x, y )在( x0 , y0 )处是否取得极值的条件 如下:
多元函数的极值

x yz xy z x y z定理1 (必要条件)函数偏导数,证:据一元函数极值的必要条件可知定理结论成立.0),(,0),(0000=′=′y x f y x f yx 取得极值,取得极值取得极值且在该点取得极值,则有),(),(00y x y x f z 在点=存在),(),(00y x y x f z 在点因=在),(0y x f z =0x x =故在),(0y x f z =0y y =zox y对于三元函数,若M 0是f (x , y , z )的驻点,f (x , y , z )在M 0处所有的二阶偏导数连续,则当矩阵在M 0处为正定阵时( ),M 0为极小值点,为负定阵时( ),M 0为极大值点.类似的,可以将以上结论推广到三元以上的函数.H=xx xy xz xyyy yz xz yz zz f f f f f f f f f ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦112233H 0,H 0,H 0>>>112233H 0,H 0,H 0<><αcos 24x αcos 22x −)sin (cos 222−+ααx =x A αsin 24αsin 4x −0cos sin 2=+ααx =αA 解得:由题意知,最大值在定义域D 内达到,而在域D 内只有一个驻点,故此点即为所求.,0sin ≠α0≠x ααααsin cos sin 2sin 2422x x x A +−=)0,120:(2πα<<<<x D 0cos 212=+−αx x 0)sin (cos cos 2cos 2422=−+−ααααx x (cm)8,603===x D πα作业P121 4, 6, 7, 13。
高等数学中的多元函数极值

高等数学中的多元函数极值引言:在高等数学中,多元函数极值是一个重要的概念。
在实际问题中,我们经常需要求解多元函数的最大值或最小值,以便优化问题的解或者找到问题的最优解。
本教案将介绍多元函数的极值问题,包括极值的定义、求解极值的方法以及一些实际问题的应用。
一、极值的定义多元函数的极值是指函数在一定范围内取得的最大值或最小值。
与一元函数的极值类似,多元函数的极值点也是函数的驻点,即导数为零的点或者导数不存在的点。
然而,多元函数的极值问题相对复杂,因为多元函数的自变量有多个,需要考虑各个自变量的变化对函数值的影响。
二、求解极值的方法1. 雅可比矩阵法雅可比矩阵法是求解多元函数极值的一种常用方法。
通过计算多元函数的雅可比矩阵,可以得到极值点的一些性质。
具体步骤包括计算雅可比矩阵、求解雅可比矩阵的特征值和特征向量,以及判断特征值的正负来确定极值点的性质。
2. 拉格朗日乘数法拉格朗日乘数法是求解多元函数在约束条件下的极值的一种方法。
通过引入拉格朗日乘子,将约束条件转化为等式,然后利用极值点的一阶条件和约束条件求解未知数,最终得到极值点的坐标。
3. 边界条件法边界条件法是一种适用于有界区域的多元函数极值问题的求解方法。
通过将多元函数在边界上的取值与内部取值进行比较,可以确定函数的最大值或最小值。
这种方法在实际问题中应用广泛,特别是在优化领域。
三、实际问题的应用多元函数极值在实际问题中有广泛的应用。
例如,在经济学中,我们可以利用多元函数极值来求解最大化利润或最小化成本的问题;在物理学中,可以利用多元函数极值来求解最小作用量原理等问题;在工程学中,可以利用多元函数极值来优化设计参数等。
这些实际问题的求解都离不开多元函数极值的理论和方法。
结论:多元函数极值是高等数学中的重要概念,对于解决实际问题具有重要意义。
通过本教案的学习,我们了解了多元函数极值的定义、求解方法以及实际问题的应用。
希望同学们能够掌握多元函数极值的基本理论和方法,能够灵活运用于解决实际问题。
88多元函数极值
在点(1, 2)处, AC–B2=12(–6)<0, 在点(–3, 0)处,
AC–B2=(–12)6<0, 所以f(–3, 0)和f(1, 2)不是极值;
在点(–3, 2)处, AC–B2= –12(–6)>0, 且A= –12<0,
所以函数在点(–3, 2)处有极大值f(–3, 2)=31.
推广: 如果三元函数 u=f(x, y, z) 在点P(x0, y0, z0)处 具有偏导数, 则它在点P(x0, y0, z0)处有极值的必要条件 为: fx(x0, y0, z0)=0, fy(x0, y0, z0)=0, fz(x0, y0, z0)=0.
仿照一元函数, 凡能使一阶偏导数同时为零的点, 称为此函数的驻点.
的存在性可知: 这时长方体在第一卦限顶点的坐标为:
(a , b , c )
333
最大长方体的长宽高分别为: 2a , 2b , 2c .
最大体积为:
8abc . 3
3
3
解二:
作变量替换:
33 X
x,
Y y,
Z z.
a
b
c
问题变成在单位球面X2+Y2+Z2=1内求内接长方体
的最大体积问题.
例2: 求由方程 x2+y2+z2–2x+2y–4z–10=0 确定的隐
函数z=f(x, y)的极值.
解: 在方程两边分别对x, y求偏导, 得
2 x 2 y
2z 2z
zx zy
2 2
4zx 4zy
0 0
由函数取极值的必要条件知, 求驻点. 令
zx 0, zy 0, 得驻点P(1, –1). 在上述方程组两边再分别对x, y求偏导数, 得
第八章第六节多元函数的极值

H h 2 3 3V , 才能使制作材料最省。
50
总结求实际问题的最值步骤如下:
第一步:建立函数关系式,确定定义域;
第二步:求出所有驻点;
第三步:结合实际意义,判定最大或最小值。
三 条件极值
先看如下的例子:
在 x y 1 的条件下,求函数 z xy 的极值。
解:从 x y 1 中解出 y 1 x, 并代入 z xy
若固定 y y0, 则 z f (x, y0 ) 是 一个一元函数,则该
函数在 x x0处取得极值,又因为 z f (x, y0 ) 对
x x0处可导,故 z
df (x, y0 )
0
x x x0 y y0
dx
x x0
同理可证
z 0 y x x0
y y0
将二元函数的两个偏导数为零的点称为驻点, 则必要条件可叙述为:
是否为极值点。 总结:求极值的步骤:
第一步:确定定义域(若未给出);
第二步:解方程组 f x( x, y) 0, f y( x, y) 0 求得一切实数解,可得一切驻点。
第三步:对每个驻点,求出二阶偏导数的值A, B,C。
第四步:定出 B2 AC 的符号,按充分条件的 结论做出结论。
例1 求函数 z x2 ( y 1)2 的极值。 解:此函数的定义域为{(x, y) | x R, y R}
(1) 当 B2 AC 0, 点 P0 ( x0, y0 ) 是极值点, 且 A 0 时,点 P0 ( x0, y0 ) 是极大值点,且 A 0 时, 点 P0 ( x0 , y0 ) 是极小值点。
(2) 当 B2 AC 0时,点 P0 ( x0, y0 ) 不是极 值点。
(3)当 B2 AC 0 时,不能确定点 P0 ( x0, y0 )
多元函数的极值

定理 2. 若函数z = f (x, y)在某 U ( P0 ) 内存在连续的二阶 偏导数, 且 f x ( P0 ) = f y ( P0 ) = 0, 记 A = f xx ( P0 ), B = f xy ( P0 ), C = f yy ( P0 ), 则当 AC B 2 0 时, 若 A 0 , P0 为极小值点; 若 A 0 , P0 为极大值点。 AC B 2 0 时, P0 非为极值点。
AC B 2 = 0 时, P0 是否极值点需进一步讨论。
f ( x , y ) = (1 e y ) cos x y e y 的极值。 例 1. 求
f x = (1 e y ) sin x = 0 解: 由 解得驻点 (2n , 0) , y f y = e (cos x 1 y ) = 0 (( 2n 1) , 2) , 其中 n Z . 那么 A = f xx = (1 e y ) cos x ,
2 2 2
在点 P1 (1, 1, 2) 的某邻域内方程可确定一个隐函数,此时, 1 1 A = z xx | P1 = = 0 . B = z xy | P1 = 0, 2 z z = 2 4 1 1 1 2 0. C = z yy | P1 = = . AC B = 16 2 z z = 2 4 因此 (1, 1) 为隐函数的极小值点, 极小值为 z = 2 . 在点 P2 (1, 1, 6) 的某邻域内方程也可确定一个隐函数。 对应地, A = z xx | P2 = 1 4 0, B = z xy | P2 = 0, C = z yy | P2 = 1 4 . AC B 2 = 1 16 0 . 因此 (1, 1) 为隐函数的极大值点, 极大值为 z = 6 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xy
( x , y ) = − 3,
f yy ( x , y ) = 6 y 。
( 1)在驻点( 0, 0)处,
A= f
xx
( 0, 0) = 0, B = f
xy
( 0, 0) = −3, C = f
yy
( 0, 0) = 0 ,
∵ AC − B 2 = −9 < 0 , ∴函数 f ( x , y ) 在点( 0, 0)无极值。
F ( x , y , z , λ ) = f ( x , y , z ) + λϕ ( x , y , z ) ,
⎧ Fx = 0 ⎪ ⎪Fy = 0 (2)解方程组 ⎨ , ⎪ Fz = 0 ⎪ϕ ( x , y , z ) = 0 ⎩
得可能极值点 ( x0 , y0 , z0 ) 。
⎧ f x + λϕ x = 0 ⎪ ⎪ f y + λϕ x = 0 即⎨ , ⎪ f z + λϕ z = 0 ⎪ϕ ( x , y , z ) = 0 ⎩
9
例 2.求函数 z = ( x 2 + y 2 − 2 x ) 2 在圆域 D = {( x , y ) x 2 + y 2 ≤ 2 x } 的最大值和最小值。
∂z = 2( x 2 + y 2 − 2 x ) ⋅ ( 2 x − 2) = 0 , 解: ∂x ∂z = 2( x 2 + y 2 − 2 x ) ⋅ 2 y = 0 , ∂y
5
4.求函数 z = f ( x , y ) 的极值的步骤
(1)求偏导数 f x , f y , f xx , f xy , f yy ;
⎧ ⎪ f x ( x, y) = 0 (2)解方程组 ⎨ ,求出一切驻点; ⎪ ⎩ f y ( x, y) = 0
(3)对于每一驻点 ( x0 , y0 ) ,求出 A = f xx ( x0 , y0 ) ,
例如,点 (0 , 0) 为 函数 z = xy 的驻点,但不是极值点。4
3.定理 2(极值存在的充分条件)
设函数 z = f ( x , y ) 在点 M 0 ( x0 , y0 ) 的某邻域内具有一阶 及二阶连续偏导数,又 f x ( x0 , y0 ) = 0 , f x ( x0 , y0 ) = 0 , 记 f xx ( x0 , y0 ) = A , f xy ( x0 , y0 ) = B , f yy ( x0 , y0 ) = C ,则
7
( 2)在驻点( 1, 1)处,
A = f xx (1, 1) = 6, B = f xy (1, 1) = −3, C = f
yy
(1, 1) = 6 ,
∵ AC − B 2 = −9 + 36 = 27 > 0 , 且 A > 0 , ∴函数 f ( x , y ) 在点( 1, 1)有极小值 f (1, 1) = −1 。
7.2
多元函数的极值
一、极值
1.二元函数的极值的定义
定义 设函数 z = f ( x , y ) 在点 ( x 0 , y 0 ) 的某邻域内有定义, 对于该邻域内异于点 ( x 0 , y 0 ) 的点 ( x , y ) ,如果都适合不 等式 f ( x , y ) < f ( x 0 , y 0 ) ,则称函数在点 ( x 0 , y 0 ) 有极大值
f ( x 0 , y 0 ) ;如果都适合不等式 f ( x , y ) > f ( x 0 , y 0 ) ,则称
函数在点 ( x 0 , y 0 ) 有极小值 f ( x 0 , y 0 ) 。极大值和极小值统 称为极值,使函数取得极值的点 ( x 0 , y 0 ) 称为极值点。
2
z
函数 f ( x , y ) = x 2 + y 2 在 点 (0, 0) 处有极小值 f (0, 0) = 0 。
解之,得 x = y = 3 2 ,
11
∵函数 A 在定义域 D = {( x , y ) x > 0, y > 0} 内只有唯一的 驻点 ( 3 2 , 3 2 ) ,又由问题的实际意义可知,函数 A 在定 义域 D 内一定有最小值,
2 ∴当水箱的长和宽均为 2m ,高为 3 3 = 3 2m 时, 2⋅ 2
ϕy ϕx ∂z ∂z =− =− , , ϕz ∂y ∂x ϕz
13
将 z = z ( x , y ) 代入 u = f ( x , y , z ) 得 u = f ( x , y , z ( x , y )) , fz ∂u ∂z = f x + fz ⋅ = f x − ⋅ϕ x , ∂x ∂x ϕz fz ∂z ∂u = f y + fz ⋅ = f y − ⋅ϕ y , ∂y ∂y ϕz
⎧max V = xyz ( x > 0, y > 0, z > 0) ⎨ 2 + + = 2 xy 2 yz 2 xz a ⎩
构造 Lagrange 函数 F ( x , y , z , λ ) = xyz + λ ( 2 xy + 2 yz + 2 xz − a 2 ) ,
⎧ Fx = yz + 2λ ( y + z ) = 0 ⎪ ⎪ F y = xz + 2λ ( x + z ) = 0 令 ⎨ ⎪ Fz = xy + 2λ ( x + y ) = 0 ⎪ F = 2 xy + 2 yz + 2 xz − a 2 = 0 ⎩ λ
14
⎧ f x + λϕ x = 0 ⎪ fz ⎪ f y + λϕ x = 0 = λ ,方程组可改写为 ⎨ 令− ϕz ⎪ f z + λϕ z = 0 ⎪ϕ ( x , y , z ) = 0 ⎩
从这个方程组解出 x0 , y0 , z 0 , λ ,其中 ( x0 , y0 , z0 ) 即为可能极值点。这种方法叫做拉格朗日乘数法。
上面方程组表示了函数
F ( x , y , z , λ ) = f ( x , y , z ) + λϕ ( x , y , z )
函数 F ( x , y , z , λ ) 称为拉格朗 的四个一阶偏导数等于 0: 日函数, 数 λ 称为拉格朗日乘数。
15
3.用拉格朗日乘数法求条件极值的步骤
(1) 构造 Lagrange 函数:
a ∴函数 V 在驻点处取得最大值,即当长、宽、高均为 时, 6
长方体有最大体积:Vmax
6 3 = a 。 36
19
例 5.在旋转椭球面 2 x 2 + y 2 + z 2 = 1 上,求距离平面
2 x + y − z = 6 的最近点和最远点。
例 6.在椭球面 4 x 2 + y 2 + z 2 = 4 的位于第一卦限部分上 求一点,使得在此点的切平面与三个坐标面所围成的 三棱锥的体积最小。
x
函数 f ( x , y ) = a 2 − x 2 − y 2 在 点 (0, 0) 处有极大值 f ( 0, 0) = a 。
o
z
y
o x
二元函数极值的概念可推广到 n 元函数 。
3
y
2.定理 1(极值存在的必要条件) 设函数 z = f ( x , y ) 在点 ( x0 , y0 ) 具有偏导数,且在点
16
注: (1)若由问题的实际意义知必存在条件极值,且只有 唯一的驻点,则该驻点即为所求的极值点。 (2)拉格朗日乘数法可推广到自变量多于三个而约束 条件多于一个的情形。
例如:求函数 u = f ( x , y, z , t ) 在约束条件 ϕ ( x , y, z , t ) = 0 ,
ψ ( x , y, z , t ) = 0 下的极值,可构造辅助函数
8
二、最大值及最小值
有界闭区域 D 上连续的函数一定有最大值和最小值。若使 函数取得最大值或最小值的点在区域 D 的内部,则这个点必然 是函数驻点,或者是一阶偏导数中至少有一个不存在的点,然 而最大值和最小值也可能在该区域的边界上取得。
因此,求有界闭区域 D 上二元函数的最大值和最小值 时,首先要求出函数在 D 内的驻点、一阶偏导数不存在的点 处的函数值及该函数在 D 的边界上的最大值和最小值,比较 这些值,其中最大者就是该函数在 D 上的最大值,最小者就是 该函数在 D 上的最小值。
B = f xy ( x0 , y0 ) , C = f yy ( x0 , y0 ) 的值;
(4)定出 AC − B 2 的符号,按定理 2 的结论判定 出 f ( x0 , y0 ) 是否是极值、是极大值还是极小值。
6
例 1.求函数 f ( x , y ) = x 3 + y 3 − 3 xy 的极值。
f ( x , y ) 在点 M 0 ( x0 , y0 ) 处是否取得极值的条件如下:
(1)当 AC − B 2 > 0 时有极值, 且 A < 0 时有极大值 ,当 A > 0 时有极小值 ; (2)当 AC − B 2 < 0 时没有极值; (3)当 AC − B 2 = 0 时可能有极值,也可能没有极值。
( x0 , y0 ) 处有极值,则必有 f x ( x 0 , y0 ) = 0 , f y ( x 0 , y0 ) = 0 。
定理 1 可推广到 n 元函数 。
同时满足 f x ( x0 , y0 ) = 0 , f y ( x0 , y0 ) = 0 的点 ( x0 , y0 ) 称为函数 z = f ( x , y ) 的驻点。 ⎯ ⎯→ 注意: 可导函数的极值点 驻点 ← ⎯⎯
2 ⎧ = − 3y = 0 ⎧x = 0 ( , ) 3 f x y x ⎧x = 1 ⎪ x ⇒⎨ 解: ⎨ 和 ⎨ , 2 ⎪ ⎩y =1 ⎩ f y ( x, y) = 3 y − 3 x = 0 ⎩ y = 0
