上海十年中考相似及锐角三角比试题集锦

合集下载

2020年上海中考数学相似三角形专题(含答案)

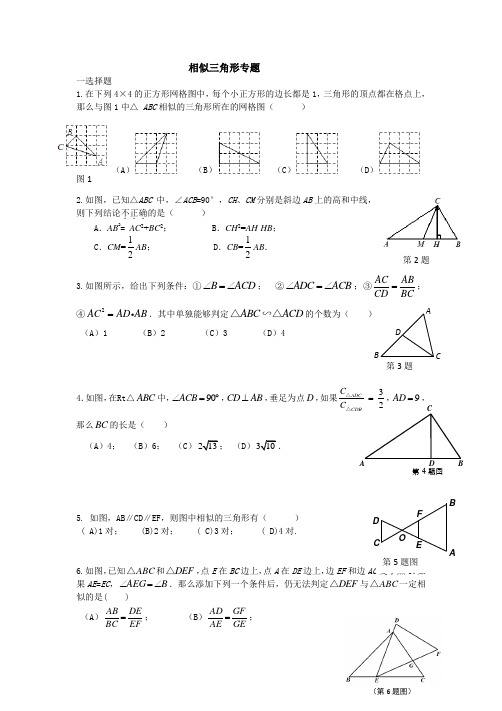
相似三角形专题一选择题1.在下列4×4的正方形网格图中，每个小正方形的边长都是1，三角形的顶点都在格点上，那么与图1中△ ABC 相似的三角形所在的网格图（）（A ）（B ）（C ）（D ）2.如图，已知△ABC 中，∠ACB =90°，CH 、CM 分别是斜边AB 上的高和中线，则下列结论不正确．．．的是（） A ．AB 2= AC 2+BC 2； B ．CH 2=AH ·HB ； C ．CM =12AB ； D ．CB =12AB ．3.如图所示，给出下列条件：①B ACD ∠=∠； ②ADC ACB ∠=∠；③AC ABCD BC=；④2AC AD AB =．其中单独能够判定ABC ACD △∽△的个数为（）（A ）1 （B ）2（C ）3（D ）44．如图，在Rt △ABC 中，90ACB ∠=︒，CD AB ⊥，垂足为点D ，如果32ADC CDB C C =△△，9AD =，那么BC 的长是（）（A ）4；（B ）6；（C ）213；（D ）310．5. 如图，AB ∥CD ∥EF ，则图中相似的三角形有（） ( A)1对； (B)2对； ( C)3对； ( D)4对.6.如图，已知ABC △和DEF △，点E 在BC 边上，点A 在DE 边上，边EF 和边AC 交于点G ．如果AE =EC ，B AEG ∠=∠．那么添加下列一个条件后，仍无法判定DEF △与ABC △一定相似的是( )（A ）EF DE BC AB =；（B ）GEGFAE AD =；图1 第4题图A D CB ACD B 第3题第2题（第6题图）AB C DEF O 第5题图第18题E D C BA （C ）EF EG AC AG =；（D ）EAEGEF ED =．二填空题7．如果两个三角形相似，其中一个三角形的两个内角分别为50°和60°，那么另一个三角形的最大角为度．8．如果两个相似三角形的相似比是1:2，那么这两个三角形的周长的比是9.在△ABC 中，点D 、E 分别在边BC 、AC 的延长线上，∠E=∠B ，AC=2，BC=3，CE=6，那么CD= ．10 .如果两个相似三角形的对应角平分线比为2︰3，两个三角形的周长的和是100cm ，那么较小的三角形的周长为 cm ．11.如图，已知⊿ABC 中，P 是AB 上的一点，∠ACP =∠B ，AB=9，AC=6，那么AP= . 12.如图，在△ABC 中，点D 、E 分别在AB 、AC 上， ADE C ∠=∠，如果=2AE ，△ADE 的面积是4，四边形BCED 的面积是5，那么AB 的长是．13.如图,R t ΔA B C 中,∠A C B =900,C D ⊥A B ,A C =8,B C =6,则AD=__ _ 14.如图，在△ABC 中，D 、E 分别是边AB 、AC 上的点，如果21==EC AE DB AD ，那么△ADE 与△ABC 面积的比是．15.已知等腰梯形的上、下两底长分别为4cm 和6cm ，将它的两腰分别延长交于一点，这个交点到上、下两底的距离之比为．16.△ABC 中，AB ＝8，AC ＝6，点D 在AC 上，AD ＝2，在AB 上找一点E ，使 △ADE 与△ABC 相似，则AE 的长为． 17.如图，在ABC ∆中，AD 平分BAC ∠交边BC 于点D ，AD BD =，3=AB ，2=AC ，那么AD 的长是 _． 18.如图，点E 是矩形ABCD 的边AD 上一点，且AE=4ED ，且BE ⊥CE ，则AB:BC=______________.三解答题19．如图，已知AB ⊥AD ，BD ⊥DC ，且BC AB BD ⋅=2，求证：∠ABD=∠DBC.E D C BA第12题BACD第14题A 第11题 B CP 第13题第17题20. 已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：（1）DA DE DB ⋅=2；（2）DAC DCE ∠=∠．21如图，在梯形ABCD 中，AD //BC ，点E 在边AD 上， CE 与BD 相交于点F ， AD =4，AB =5，BC =BD =6，DE =3．（1）求证：△DFE ∽△DAB ；（2）求线段CF 的长．22.如图，在AH ABC 中，∆是BC 边上的高，矩形DEFG 内接于ABC ∆（即点G F E D 、、、都在ABC ∆的边上），6,18==AH BC ，矩形DEFG 的周长是20． ACDEBBCD AEF求：DEFG S 矩形的值．23．如图，已知△ABC 中，AB=AC=10,BC=16，点P 、D 分别在边BC 、AC 上， BP=12，∠APD=∠B ，求CD 的长.24.如图：在Rt ⊿ABC 中，∠ACB=90°，CD ⊥AB ，E 是斜边AB 延长线上一点，且∠ECB=∠BCD （1）求证：⊿ECB ∽⊿EAC ；（2）若AC=，AB=5cm ，求BE 的长.EDBCA相似三角形专题参考答案一、1、B ，2、D ，3、C ，4、C ，5、C ，6、C二、7、70， 8、1:2 9、4 10、40 11、4，12、3 13、6.4 14、1:9 15 、2：3 16、23或38 17、5103 18、2:5．三、19、证明Rt△DBC ∽△ABD Rt20、(1)证明∽△ADB △BDE ；(2)由DB=DC 可得DC 2=DE*DA ，可证∽△ADC △CDE 21、(1)由AD//BC 可得21==BF DF BC DE ，∴31=BD DF ,得DF=2, ∴BD DEAD DF =再由BDA EDF ∠=∠可证 (2)由1的结论可求EF=2.5,再可得CF=2EF=522、设AH 与DG 相交于M ，由∽△ABC △ADG 可得AHAMBC DG =可算出DE=4,DG=6 S=2423、证∽△PBA △DCP 可得ABCPBP CD =可得CD=4.8 24、1、证A BCD ECB ∠=∠=∠2、由勾股定理可求BC=5 ,由1的结论可得21===AE EC EC BE AC BC ,可得41=AE BE ，得BE=35。

上海数学学科九年级相似三角形测试题及答案

相似三角形测试题及答案图形的放缩与比例线段（1）、填空题（每小题4分，共40分）X_ = yχ + y1、如果㊁那么x-y = _______________ tX _ I y _ z X + 4y ÷z2、已知： 2 ? 4 ,贝U 2x= __________ F3、2口与3"的比例中项是_________ 。

4、对一段长为20cm的线段进行黄金分割，那么分得的较长线段长为____________ Cm （不取近似值）DE5、如图，DE// BC AD= 1, DB= 2,贝UEC 的值为___________ 。

6、如图，DE// BC AB= 12, AC= 16, AE= 10,贝U AD= _______ 。

AC 3 AD 37、如图，线段AB= 10Cm CB2 , ED 2 ,贝U CD= ______________ CmAE 29、如图，AD// EF// BC EB 3, DF= 4cm,贝U DC= ____________ CmAE _ m10、如图，AB// EF// DC AB^^ , DC= , ED K,则EF= ________________ 。

（用EAb式子表示）、选择题（每小题4分,共16 分）"y _Ii = 1 _6y =58已知：线段AB= 10Cm点C是AB的黄金分割点，且AO CB 贝U BC= _______ Cm （不取近似值）一岭题图一E题團一了题图一9蠱图—10® 图1若1 ^ ,则下列等式中不正确的是（）(A) •' ;(B)I 'l ;(C)- ; (D)^ 。

2、如图，△ ABC中，DE// BC,则下列等式中不成立的是()。

AD =AE AD = AE AD _ DE AD _ DE(A)栄_丘；(B)丄］；(C)忑一詰；(D)^ 03、如图，△ ABC中，DEll BC AD= 1, EC= 3,则下列等式中成立的是()。

沪教版(上海)初中数学专题锐角的三角比中考模拟题(解析版)

专题锐角的三角比中考模拟题一、单选题1．（2018·上海奉贤中考模拟）如图，电线杆CD 的高度为h ，两根拉线AC 与BC 互相垂直（A 、D 、B 在同一条直线上），设∠CAB＝α，那么拉线BC 的长度为（）A ．sin h αB ．cos h αC ．tan h αD ．cot h α【答案】B【解析】根据垂直的定义和同角的余角相等，可由∠CAD+∠ACD=90°，∠ACD+∠BCD=90°，可求得∠CAD=∠BCD，然后在Rt△BCD 中 cos∠BCD=CD BC ，可得BC=cos cos CD h BCD α=∠. 故选B ．点睛：本题主要考查解直角三角形的应用，熟练掌握同角的余角相等和三角函数的定义是解题的关键．2．（2020·上海大学附属学校初三三模）在Rt △ABC 中，∠C=90°，AB=10，AC=8.下列四个选项，不正确是( )A ．sinA=45B ．cosA=45C ．tanA=34D ．cotA=43【答案】A【解析】【分析】根据锐角三角函数逐一判断即可.【详解】A 、3sin 5BC A AB ==,故该选项错误； B 、4cos 5AC A AB ==,故该选项正确；C、3tan4BCAAC==,故该选项正确；D、4cot3ACABC==，故该选项正确故选A.【点睛】本题主要考查直角三角形中的锐角三角函数，掌握锐角三角函数是解题的关键. 3．（2020·浙江萧山初三其他）如图，一块矩形木板ABCD斜靠在墙边(OC⊥OB，点A、B、C、D、O在同一平面内)，已知AB=a，AD=b，∠BCO=x，则点A到OC的距离等于()A．sin sina xb x B．cos cosa xb x C．sin cosa xb x D．cos sina xb x 【答案】D【解析】【分析】根据题意，作出合适的辅助线，然后利用锐角三角函数即可表示出点A到OC的距离，本题得以解决．【详解】解：作AE⊥OC于点E，作AF⊥OB于点F，∵四边形ABCD是矩形，∴∠ABC=90°，∵∠ABC=∠AEC，∠BCO=x，∴∠EAB=x ，∴∠FBA=x ，∵AB=a ，AD=b ，∴FO=FB+BO=a •cosx+b •sinx ，故选：D ．【点睛】本题考查解直角三角形的应用、矩形的性质，解答本题的关键是明确题意，利用数形结合的思想解答．4．（2020·上海崇明�初三一模）在Rt ABC ∆中，90C ∠=︒，如果 8AC =， 6BC =，那么B 的余切值为（）A ．34B ．43C ．35D ．45【答案】A【解析】【分析】根据余切函数的定义解答即可．【详解】如图，在Rt △ABC 中，∵∠C ＝90°，AC ＝8，BC ＝6，∴cotB ＝6384BC AC ==，故选：A ．【点睛】本题考查解直角三角形，解题的关键是熟练掌握基本知识，属于中考常考题型． 5．（2020·上海松江�初三一模）如图，两条宽度都为1的纸条，交叉重叠放在一起，它们的夹角为锐角α，它们重叠部分（阴影部分）的面积是1.5，那么sin α的值为（）A ．34B ．12C ．23D ．32 【答案】C【解析】【分析】重叠部分为菱形，运用三角函数定义先求边长AE ，再根据面积求出sin α．【详解】解：如图示：作BC CD ⊥交CD 于C 点，AD CD ⊥交CD 于D 点，由阴影部分是两条宽度都为1的纸条，交叉重叠放在一起可知，阴影部分是一个菱形，则有AB AE =，1AD =，∴1sin AB AE α==∴1=1 1.5sin S AB AD α=⨯=阴影解之得：2sin 3α=，故选：C【点睛】本题考查了菱形的判定与性质，三角函数的应用，判断出阴影部分是一个菱形是解题的关键．6．（2020·上海杨浦�初三二模）如果正十边形的边长为a ，那么它的半径是（） A ．sin 36a ︒ B ．cos36a ︒ C ．2sin18a ︒ D ．2cos18a ︒【答案】C【解析】【分析】如图，画出图形，在直角三角形OAM 中，直接利用三角函数即可得到OA.【详解】如图，正十边形的中心角∠AOB=360°÷10=36°，AB=a∴∠AOM=∠BOM=18°，AM=MB=12a ； ∴OA=AM sin OAM ∠=218a sin ︒故选C.【点睛】本题考查三角函数，能够画出图形，找到正确的三角函数关系是解题关键.7．（2020·安徽谯城�初三月考）如图，一架飞机在点A 处测得水平地面上一个标志物P 的俯角为α，水平飞行m 千米后到达点B 处，又测得标志物P 的俯角为β，那么此时飞机离地面的高度为( )A ．cot cot m αβ-千米 B ．cot cot m βα-千米 C ．tan tan m αβ-千米D ．tan tan m βα-千米【答案】A【解析】【分析】根据锐角三角函数的概念进行作答.【详解】在P 点做一条直线垂直于直线AB 且交于点O ，由锐角三角函数知，AO=PO cot α，BO=PO cot β，又AB=m=AO-BO= PO cot α- PO cot β=cot cot m αβ-. 所以答案选A. 【点睛】本题考查了锐角三角函数的概念，熟练掌握锐角三角函数是本题解题关键.8．（2020·安徽谯城�初三一模）在Rt △ABC 中，∠C = 90°，∠A 、∠B 、∠C 所对的边分别为a 、b 、c ，下列等式中不成立的是（）A ．tan bB a =B ．cos a B c =C ．sin a A c =D ．cot a A b = 【答案】D【解析】【分析】根据三角函数的定义进行判断，就可以解决问题．【详解】解：∵Rt △ABC 中，∠C ＝90°，∠A 、∠B 、∠C 所对的边分别为a 、b 、c ， ∴tan b B a=，故A 选项成立； cos a B c=，故B 选项成立； sin a A c=，故C 选项成立； cot b A a =，故D 选项不成立；故选D ．【点睛】本题主要考查了锐角三角函数的定义，我们把锐角A 的对边a 与斜边c 的比叫做∠A 的正弦，记作sin A ．锐角A 的邻边b 与斜边c 的比叫做∠A 的余弦，记作cos A ．锐角A 的对边a 与邻边b 的比叫做∠A 的正切，记作tan A ．9．（2020·安徽瑶海�初三期末）如图，反比例函数k y x=(0)k ≠第一象限内的图象经过ABC ∆的顶点A ，C ，AB AC =，且BC y ⊥轴，点A ，C ，的横坐标分别为1，3，若120BAC ∠=︒，则k 的值为（）A ．1B ．2C ．3D ．2【答案】C【解析】【分析】先表示出CD ，AD 的长，然后在Rt △ACD 中利用∠ACD 的正切列方程求解即可．【详解】过点A 作AD BC ⊥，∵点A 、点C 的横坐标分别为1，3，且A ，C 均在反比例函数k y x=第一象限内的图象上， ∴(1,)A k ，3,3k C ⎛⎫ ⎪⎝⎭， ∴CD=2，AD=k-3k ， ∵AB AC =，120BAC ∠=︒，AD BC ⊥，∴30ACD ∠=︒，90ADC ∠=︒，∵tan ∠ACD=AD DC， ∴3DC AD =，即233k k ⎛⎫=- ⎪⎝⎭，∴3k =．故选：C ．【点睛】本题考查了等腰三角形的性质，解直角三角形，以及反比例函数图像上点的坐标特征，熟练掌握各知识点是解答本题的关键．10．（2020·广西初三一模）如图，某数学兴趣小组想测量斜坡CD旁一棵树AB的高度，他们先在点C处测得树顶B的仰角为60︒，然后在坡顶D测得树顶B的仰角为30，已知斜坡CD的长度为10m，DE的长为5m，则树AB的高度是（）A．10m B．15m C．153m D．53m【答案】B【解析】【分析】先根据已知条件结合三角函数得∠DCE=30°，进而得到∠DCB=90°，再由∠BDF=30°，可知∠DBE=60°，由DF//AE可得出∠BGF =60°，进一步可得∠ABC=30°，∠DCB=90°.故∠DBF=30°，所以∠DBC=30°，再由锐角三角函数的定义即可解答．【详解】解：在Rt△CDE中，CD=10m，DE=5m，∴sin∠DCE=51102 DE mCD m==∴.∠DCE=30°∵∠ACB=60°，DF//AE.∴∠BGF=60°∴∠ABC=30°，∠DCB=90°∵∠BDF=30°，∴∠DBF=60°，∴∠DBC=30°，∴103tan303CDBC︒===（m）∴3sin60103152AB BC︒=⋅==（m）．故选答案为B ．【点睛】本题考查的是解直角三角形的应用，正确作出辅助线、构造直角三角形并灵活运用锐角三角函数的知识是解答本题的关键．第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题11．（2020·上海宝山�初三二模）如图，在△ABC 中，AB=AC=5，3tan =4B ，将△ABC 绕点B 逆时针旋转，得到11A BC ∆，当点1C 在线段CA 延长线上时1ABC ∆的面积为_________．【答案】46825【解析】【分析】过B 作BD ⊥AC 1，过A 作AF ⊥BC 于F ，解直角三角形求出BC 和BD ，进而得出CD ，然后根据等腰三角形的性质和三角形面积公式即可解答．【详解】解：如图，过B 作BD ⊥AC 1，过A 作AF ⊥BC 于F ，∴BC=BC 1，∴∠BC 1C=∠C ，∵3tan =4ABC ∠， ∴3tan =4AF ABC BF ∠=，设AF=3x ，BF=4x ，则AB=5x ，∵AB ＝5，∴x=1，即AF=3，BF=4，∴BC=8，∴sin ∠C=35BD BC =， ∴BD=245，在Rt △ABD 中，tan ∠C=BD DC =34， ∴24354DC， ∴DC=325， ∵BC=BC 1 ，BD ⊥AC 1，∴CC 1=2DC=645， ∴A 1C= CC 1－AC=645－5=395， ∴1ABC ∆的面积为：1243946825525⨯⨯=．【点睛】本题考查了旋转变换和解直角三角形，通过做辅助线构造直角三角形是解答本题的关键．12．（2019·上海徐汇�中考模拟）在梯形ABCD 中，AB ∥DC ，∠B ＝90°，BC ＝6，CD ＝2，tan A ＝34．点E 为BC 上一点，过点E 作EF ∥AD 交边AB 于点F ．将△BEF 沿直线EF 翻折得到△GEF ，当EG 过点D 时，BE 的长为_____．【答案】65 12.【解析】【分析】根据平行线的性质得到∠A＝∠EFB，∠GFE＝∠AMF，根据轴对称的性质得到∠GFE ＝∠BFE，求得∠A＝∠AMF，得到AF＝FM，作DQ⊥AB于点Q，求得∠AQD＝∠DQB ＝90°．根据矩形的性质得到CD＝QB＝2，QD＝CB＝6，求得AQ＝10﹣2＝8，根据勾股定理得到AD＝64+36＝10，设EB＝3x，求得FB＝4x，CE＝6﹣3x，求得AF＝MF＝10﹣4x，GM＝8x﹣10，根据相似三角形的性质得到GD＝6x﹣152，求得DE＝152﹣3x，根据勾股定理列方程即可得到结论．【详解】如图，∵EF∥AD，∴∠A＝∠EFB，∠GFE＝∠AMF，∵△GFE与△BFE关于EF对称，∴△GFE≌△BFE，∴∠GFE＝∠BFE，∴∠A＝∠AMF，∴△AMF是等腰三角形，∴AF＝FM，作DQ⊥AB于点Q，∴∠AQD＝∠DQB＝90°．∵AB∥DC，∴∠CDQ＝90°．∵∠B＝90°，∴四边形CDQB是矩形，∴CD＝QB＝2，QD＝CB＝6，∴AQ＝10﹣2＝8，在Rt△ADQ中，由勾股定理得AD10，∵tan A＝34，∴tan∠EFB＝BEBF＝34，设EB＝3x，∴FB＝4x，CE＝6﹣3x，∴AF＝MF＝10﹣4x，∴GM＝8x﹣10，∵∠G＝∠B＝∠DQA＝90°，∠GMD＝∠A，∴△DGM∽△DQA，∴DG GM DQ AQ，∴GD＝6x﹣152，∴DE＝152﹣3x，在Rt△CED中，由勾股定理得（152﹣3x）2﹣（6﹣3x）2＝4，解得：3x＝65 12，∴当EG过点D时BE＝65 12．故答案为：65 12．【点睛】本题考查了相似三角形的判定和性质，等腰三角形的判定及性质的运用，矩形的性质的运用，勾股定理的性质的运用，轴对称的性质的运用，正确的作出辅助线是解题的关键．13．（2020·上海杨浦�初三二模）如图，已知在平行四边形ABCD中，AB＝10，BC＝15，tan∠A＝43，点P是边AD上一点，联结PB，将线段PB绕着点P逆时针旋转90°得到线段PQ，如果点Q恰好落在平行四边形ABCD的边上，那么AP的值是_____．【答案】6或10【解析】【分析】分情况解答：当点Q落在CD上时，作BE⊥AD于E，QF⊥AD交AD的延长线于F．设PE＝x，通过证明△PBE≌△QPF，得出PE＝QF＝x，DF＝x﹣1，由tan∠FDQ＝tan A＝43＝FQDF，即可得出AP的值；当点Q落在AD上时，得出∠APB＝∠BPQ＝90°，由tan A＝43，即可得出AP的值；当点Q落在直线BC上时，作BE⊥AD于E，PF⊥BC于F．则四边形BEPF是矩形．由tan A＝BEAE＝43，可得出△BPQ是等腰直角三角形，此时求出BQ不满足题意，舍去.【详解】解：如图1中，当点Q落在CD上时，作BE⊥AD于E，QF⊥AD交AD的延长线于F．设PE＝x．在Rt△AEB中，∵tan A＝BEAE＝43，AB＝10，∴BE＝8，AE＝6，∵将线段PB绕着点P逆时针旋转90°得到线段PQ，∴∠BPQ＝90°，∴∠EBP+∠BPE＝∠BPE+∠FPQ＝90°，∴∠EBP＝∠FPQ，∵PB＝PQ，∠PEB＝∠PFQ＝90°，∴△PBE≌△QPF（AAS），∴PE＝QF＝x，EB＝PF＝8，∴DF ＝AE +PE +PF ﹣AD ＝x ﹣1，∵CD ∥AB ，∴∠FDQ ＝∠A ，∴tan ∠FDQ ＝tan A ＝43＝FQ DF ， ∴1x x ＝43， ∴x ＝4，∴PE ＝4，∴AP ＝6+4＝10；如图2，当点Q 落在AD 上时，∵将线段PB 绕着点P 逆时针旋转90°得到线段PQ ，∴∠BPQ ＝90°，∴∠APB ＝∠BPQ ＝90°，在Rt △APB 中，∵tan A ＝AP BP ＝43，AB ＝10， ∴AP ＝6；如图3中，当点Q 落在直线BC 上时，作BE ⊥AD 于E ，PF ⊥BC 于F ．则四边形BEPF 是矩形．在Rt △AEB 中，∵tan A ＝BE AE ＝43，AB ＝10， ∴BE ＝8，AE ＝6，∴PF ＝BE ＝8， ∵△BPQ 是等腰直角三角形，PF ⊥BQ ，∴PF ＝BF ＝FQ ＝8，∴PB ＝PQ ＝2，BQ 2PB ＝16＞15（不合题意舍去），综上所述，AP 的值是6或10，故答案为：6或10．【点睛】本题主要考查旋转的性质，由正切求边长，正确画出图形，分情况解答是解题的关键. 14．（2020·上海初三月考）如图：正方形ABCD 的边长为1，点E ，F 分别为BC ，CD 边的中点，连接AE ，BF 交于点P ，连接PD ，则tan APD ∠=______．【答案】2【解析】【分析】连接AF ，先证明Rt ΔABE ≌Rt ΔBCF ，可得BAE CBF ∠∠=，继而证明A 、P 、F 、D 四点共圆，由圆周角定理可得AFD APD ∠∠=，进而根据正切的定义即可求得答案.【详解】连接AF ，E ，F 分别是正方形ABCD 边BC ，CD 的中点，CF BE ∴=，AD 2DF=，在ΔABE 和ΔBCF 中，AB BC ABE C BE CF =⎧⎪∠=∠⎨⎪=⎩，∴Rt ΔABE ≌Rt ΔBCF(SAS)，BAE CBF ∠∠∴=，又BAE BEA 90∠∠︒+=，CBF BEA 90∠∠︒∴+=，BPE APF 90∠∠︒∴==，ADF 90∠︒=，ADF APF 180∠∠︒∴+=，∴A 、P 、F 、D 四点共圆，AFD APD ∠∠∴=， AD tan APD tan AFD 2DF ∠∠∴===，故答案为：2．【点睛】本题考查了正方形的性质，全等三角形的判定与性质，四点共圆，正切等知识，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.15．（2019·上海市上外民办劲松中学初三二模）如图，矩形ABCD 中，2BC =，将矩形ABCD 绕点D 顺时针旋转90°，点A 、C 分别落在点A '、C '处，如果点A '、C '、B 在同一条直线上，那么tan ABA ∠'的值为__________．【答案】512-．【解析】试题分析：如下图，设矩形的边长CD ＝x ，由'''A D A C C D BC =，得222x x +=，整理，得：，解得：15x =-±，所以，CD ＝51-，所以，tan ∠BA'C=''C D A D =512-．故答案为512-．考点：三角形相似的性质，一元二次方程，三角函数．16．（2018·上海静安�初三二模）等腰△ABC中，AB=AC，它的外接圆⊙O半径为1，如果线段OB绕点O旋转90°后可与线段OC重合，那么∠ABC的余切值是_____．【答案】21±．【解析】分两种情况，（1）当△ABC为锐角三角形，∵AB=AC，OB=OC，∴AD垂直平分BC，∵OB=OC，∠BOC=90°，∴∠OBD=45°，∵OB=1,∴BD=OD=22，在Rt△ABD中，tan∠ABC=2122122ADBD+==+;（2）当△ABC为钝角三角形，∵AB=AC，OB=OC，∴AD垂直平分BC，∵OB=OC，∠BOC=90°，∴∠OBD=45°，∵OB=1，∴BD=OD=22，在Rt△ABD中，tan∠ABC=2122122ADBD-==-.故答案为21±．点睛：本题是圆的综合题，主要考查的知识点有垂径定理、等腰直角三角形的性质、锐角三角函数的定义，解决本题要注意分△ABC为锐角三角形和△ABC为钝角三角形两种情况求解，不要漏解.17．（2018·全国初三单元测试）如图是利用四边形的不稳定性制作的菱形凉衣架．已知其中每个菱形的边长为13cm，5cos13ABC∠=，那么凉衣架两顶点A、E之间的距离为________cm．【答案】【解析】【详解】连接AC、BD交于点O，作AM⊥BC于点M，∵AB=BC=13cm，cos∠ABC=513，∴BM=BC•cos∠ABC=13×513=5，∴由勾股定理得：AM=12∴MC=8，由勾股定理得：AC=13∴在直角三角形ABO中，22313AB AO-=∴BD=2BO=613 ∴凉衣架两顶点A 、E 之间的距离为61318．（2020·上海宝山�初三一模）如图，△ABC 中，DE 是BC 的垂直平分线，DE 交AC 于点E ，连接BE ，若BE=9，BC=12，则cosC=_____．【答案】23 【解析】试题分析：线段中垂线上的点到线段的两个端点的距离相等.根据DE 是BC 的中垂线可得CE=BE=9，CD=12BC=6，∠EDC=90°，则cosC=6293CD CE ==. 考点：中垂线的性质、三角形函数.19．（2019·上海市民办新竹园中学初三月考）如图，由10个完全相同的正三角形构成的网格图中，αβ∠∠、如图所示，则()cos αβ+=______.【答案】217. 【解析】【分析】给图中各点标上字母，连接DE ，利用等腰三角形的性质及三角形内角和定理可得出∠α=30°，同理，可得出：∠CDE=∠CED=30°=∠α，由∠AEC=60°结合∠AED=∠AEC+∠CED 可得出∠AED=90°，设等边三角形的边长为a ，则AE=2a ，3，利用勾股定理可得出AD 的长，再结合余弦的定义即可求出cos （α+β）的值．【详解】给图中各点标上字母，连接DE ，如图所示．在△ABC 中，∠ABC=120°，BA=BC ，∴∠α=30°．同理，可得出：∠CDE=∠CED=30°=∠α．又∵∠AEC=60°，∴∠AED=∠AEC+∠CED=90°．设等边三角形的边长为a ，则AE=2a ，DE=2×sin60°•a=3a ， ∴227AD AE DE a =+=，∴cos （α+β）=217DE AD =．故答案为：217．【点睛】本题考查了解直角三角形、等边三角形的性质以及规律型：图形的变化类，构造出含一个锐角等于∠α+∠β的直角三角形是解题的关键．三、解答题20．（2020·上海大学附属学校初三三模）如图，在梯形ABCD 中，AD ∥BC ，∠BCD =90°，5AB BC ==，2,AD =⑴求CD 的长；⑵若∠ABC 的平分线交CD 于点E ，连结AE ，求∠AEB 的正切值．【答案】（1）4；（2）2【解析】【分析】(1) 过点A 作AF ⊥BC 垂足为F ，得到BF 的长度，在Rt △AFB 中运用勾股定理即可得到AF 的长度，利用AF=DC 进而得到答案；(2)先证明ABE ∆≌CBE ∆（SAS ），根据全等三角形的性质得到∠AEB=∠CEB ，运用勾股定理求解CE 的长度即可得到答案；【详解】解：（1）过点A 作AF ⊥BC 垂足为F ，由题意得FC =AD =2，AF =CD ，.∵BC =5，∴BF =5-2=3，在Rt △AFB 中：222AB AF BF =+ （勾股定理），即：22253AF =+解得AF =4，∴CD =4；（2）由AB =BC ，∠ABE =∠CBE ，BE =BE ，得到ABE ∆≌CBE ∆（SAS ），∴∠AEB=∠CEB （全等三角形对应边相等），∴AE=EC （全等三角形对应边相等），设AE=EC =x ，则DE=4x -，在Rt △ADE 中，222AE AD DE =+222(4)2x x =-+，解得52x =，5tan tan 252BC AEB CEB CE ∠=∠=== 【点睛】本题主要考查了勾股定理的运用、三角函数得运用、全等三角形的判定与性质，证明∠AEB=∠CEB 是解题的关键．21．（2019·上海长宁�初三二模）如图，在Rt ABC ∆中，9043ACB AC BC ∠===，，，点D 是边AC 的中点，CF BD ⊥，垂足为点F ，延长CF 与边AB 交于点E ．求：（1）ACE ∠的正切值；（2）线段AE 的长．【答案】（1）2tan 3ACE ∠=；（2）4017AE =．【解析】【分析】（1）由Rt △ABC ，且CF 垂直于BD ，利用同角的余角相等得到∠ACE=∠CBD ，根据AC 的长确定出CD 的长，利用锐角三角函数定义求出所求即可；（2）过点E 作EH ⊥AC ，垂足为点H ，在Rt △EHA 中，利用锐角三角函数定义表示出tanA ，进而表示出AE ，在Rt △CEH 中，利用锐角三角函数定义表示出CH ，由CH+AH 表示出AC ，根据已知AC 的长求出k 的值，即可确定出所求．【详解】（1）∵∠ACB=90°，∴∠ACE+∠BCE=90°，又∵CF ⊥BD ，∴∠CFB=90°，∴∠BCE+∠CBD=90°，∴∠ACE=∠CBD ，∵AC=4且D 是AC 的中点，∴CD=2，又∵BC=3，在Rt △BCD 中，∠BCD=90°．∴tan ∠CBD=23CD BC =， ∴tan ∠ACE=tan ∠CBD 23=；（2）过点E 作EH ⊥AC ，垂足为点H ，在Rt △EHA 中，∠EHA=90°，∴tanA=EH HA， ∵BC=3，AC=4，在Rt △ABC 中，∠ACB=90°，∴tanA=34BC AC =， ∴34EH HA =，设EH=3k ，AH=4k ，∵222AE EH AH =+，即()()2223k 4k AE =+，∴AE=5k ，在Rt △CEH 中，∠CHE=90°，∴tan ∠ECA=23EH CH =， ∴CH=92k ， ∴AC=AH+CH=9174422k k k +==，解得：817k =， ∴AE=5k=4017．【点睛】本题考查了解直角三角形，涉及的知识有：勾股定理，锐角三角函数定义，正确作出辅助线、利用参数列方程求解是解决本题的关键．22．（2020·上海金山�初三二模）如图，已知在四边形ABCD 中∠A=∠ABC=90°，点E是CD 的中点，△ABD 与 △EBD 关于直线BD 对称，1AD =，3AB =．（1）求点A 和点E 之间的距离；（2）联结AC 交BE 于点F ，求AF AC 的值．【答案】（1） AE 3；（2）35AF AC = 【解析】【分析】（1）连接AE 交BD 于H ，根据△ABD 与 △EBD 关于直线BD 对称，得AE ⊥BD ，AH=HE ，利用勾股定理求出BD=2，利用1122ABD SAB AD BD AH =⋅=⋅求出23AH =得到答案；（2）根据∠A=90°，1AD =， BD=2求出∠ABD=30°，由△ABD 与 △EBD 关于直线BD 对称，得到∠BED=∠A=90°，DE=AD=1，∠DBE=∠ABD=30°，由点E 是CD 的中点，求出BC=BD=2，∠CBE=∠DBE=30°，求出∠M =30°，AM=3，利用AM ∥BC ，32AF AM CF BC ==，即可求出35AF AC =. 【详解】（1）连接AE 交BD 于H ，∵△ABD 与 △EBD 关于直线BD 对称，∴AE ⊥BD ，AH=HE ，∵∠A=90°，1AD =，3AB =∴BD=2，∵1122ABD S AB AD BD AH =⋅=⋅, ∴AB AD BD AH ⋅=⋅， ∴23AH =∴AE=23AH =（2）延长AD 、BE 交于点M ，∵∠A=90°，1AD =， BD=2，∴sin ∠ABD=12AD BD =， ∴∠ABD=30°，∵△ABD 与 △EBD 关于直线BD 对称，∴∠BED=∠A=90°，DE=AD=1，∠DBE=∠ABD=30°，∵点E 是CD 的中点，∴BE 垂直平分CD ，∴BC=BD=2，∴∠CBE=∠DBE=30°，∵∠A=∠ABC=90°，∴AD ∥BC ，∴∠M=∠CBE=30°，∴AM=3tan 30AB =， ∵AM ∥BC ，∴32AF AM CF BC ==， ∴35AF AC =.【点睛】此题考查轴对称的性质，锐角三角函数，勾股定理，平行线的性质，线段垂直平分线的判定及性质.23．（2020·上海浦东新�初三二模）已知：如图，在Rt ABC △中，90ACB ∠=︒，8AC =，16BC =，点O 为斜边AB 的中点，以O 为圆心，5为半径的圆与BC 相交于E 、F 两点，连结OE 、OC ．（1）求EF的长；（2）求COE∠的正弦值．【答案】（1）6；（2）55．【解析】【分析】（1）过点O作OG⊥EF于点G，根据垂径定理得出EG=FG，然后由O为AB的中点，OG∥AC可推出OG为△ABC的中位线，从而可求出OG的长，在Rt△OEG中，由勾股定理可求出EG的长，从而可得出EF的长；（2）首先由直角三角形斜边中线的性质可得出CO=BO，然后根据等腰三角形的性质可得出CG=BG，由（1）中EG=3可得，CE=5=OE，所以∠COE=∠OCE，在Rt△OCG 中，求出sin∠OCG的值即可得出结果．【详解】解：（1）过点O作OG⊥EF于点G，∴EG=FG，OG∥AC，又O为AB的中点，∴G为BC的中点，即OG为△ABC的中位线，∴OG=12AC=4，在Rt△OEG中，由勾股定理得，223OE OG-=，∴EF=2EG=6；（2）在Rt△ABC中，由勾股定理得，2285AC BC+=又O为AB的中点，∴5OG⊥BC，∴CG=BG=12BC=8，∴CE=CG-EG=8-3=5，∴CE=EO，∴∠COE=∠OCE，∴sin∠OCE=45545OGCO==．∴∠COE的正弦值为55．【点睛】本题是圆的综合题，考查了垂径定理，中位线的性质，直角三角形斜边中线的性质，三角函数，等腰三角形的性质以及勾股定理等知识，作出辅助线，综合运算基本性质进行推理是解题的关键．24．（2020·上海闵行�初三二模）已知：如图，在△ABC中，AB=AC=6，BC=4，AB的垂直平分线交AB于点E，交BC的延长线于点D．（1）求CD的长；（2）求点C到ED的距离．【答案】（1）CD=5；（2）5 3【解析】【分析】（1）过A点作AF⊥BC于点F，通过等腰三角形三线合一求出BF的长度，进而求出cos B∠的值，再通过垂直平分线求出BE的长度，在Rt△DEB中利用cos B∠即可求出BD的长度，进而CD的长度可求；（2）过C点作CH⊥ED于点H，通过平行线的判定得出CH∥AB，则有CH CD BE BD=，进而可求出CH的长度，则点C到ED的距离可求．【详解】解：（1）过A点作AF⊥BC于点F．∵AB=AC=6，BC=4，AF⊥BC，∴BF=FC=2，∠BF A=90°．∴在Rt△ABF中，1 cos3BFBAB∠==．∵DE垂直平分AB，AB=6，∴AE=BE=3，∠DEB=90°．在Rt△DEB中，1 cos3BEBBD∠==，∴BD=9，∴CD=BD-BC=5．（2）过C点作CH⊥ED于点H．∵CH⊥ED，AB⊥ED，∴∠DEB=∠DHC=90°，∴CH∥AB，∴CH CD BE BD=． ∵BE=3，BD=9，CD=5，∴53CH =， ∴点C 到ED 的距离CH 为53．【点睛】本题主要考查等腰三角形的性质，锐角三角函数，平行线的判定和平行线分线段成比例，掌握等腰三角形的性质，锐角三角函数，平行线的判定和平行线分线段成比例是解题的关键．25．（2020·上海市民办新复兴初级中学初三月考）如图，已知抛物线y ＝ax 2﹣2x+c 经过△ABC 的三个顶点，其中点A(0，1)，点B(9，10)，AC ∥x 轴．(1)求这条抛物线的解析式.(2)求tan ∠ABC 的值.(3)若点D 为抛物线的顶点，点E 是直线AC 上一点，当△CDE 与△ABC 相似时，求点E 的坐标．【答案】(1)21213y x x =-+；(2)1tan 2ABC ∠=；(3)E(4，1)或E(﹣3，1)．【解析】【分析】 (1)将点A 和点B 的坐标代入抛物线的解析式求得a 、c 的值即可；(2)过点B 作BH ⊥AC 交AC 延长线于点H ，过点C 作CG ⊥AB 于点G ，先证明△ABH 和△ACG 均为等腰直角三角形，再求出CG 和BG 的长，然后依据锐角三角函数的定义求解即可；(3)过点D 作DK ⊥AC ，垂足为K ，先证明△DCK 为等腰直角三角形，则∠DCK ＝∠BAC ，当AC EC AB CD =或AC DC AB EC=时，△CDE 与△ABC 相似，然后可求得CE 的长．【详解】解：(1)∵抛物线y ＝ax 2﹣2x +c 经过点A (0，1)和点B (9，10)，∴1811810c a c =⎧⎨-+=⎩，解得131a c ⎧=⎪⎨⎪=⎩． ∴这条抛物线的解析式为21213y x x =-+． (2)过点B 作BH ⊥AC 交AC 延长线于点H ，∵AC ∥x 轴，A (0，1)，B (9，10)，∴H (9，1)，∴BH ＝AH ＝9．又∵∠BHA ＝90°，∴△HAB 是等腰直角三角形，∴∠HAB ＝45°． ∵AC ∥x 轴，A (0，1)，对称轴为直线3x =，∴C (6，1). 过点C 作CG ⊥AB ，垂足为点G ，∵∠GAC ＝45°，∠AGC ＝90°，∴sin 4532CG AC =︒=，∴32AG =．又∵在Rt △ABH 中，92sin 45BH AB ==︒，∴923262BG =-=． ∴在Rt △BCG 中，1tan 2CG ABC BG ∠==． (3)如图2所示：过点D 作DK ⊥AC ，垂足为K ，∵点D 是抛物线21213y x x =-+的顶点，∴D (3，﹣2)． ∴K (3，1)，∴CK ＝DK ＝3．又∵∠CKD ＝90°，∴△CDK 是等腰直角三角形，∴∠DCK ＝45°又∵∠BAC ＝45°，∴∠DCK ＝∠BAC ．∴要使△CDE 与△ABC 相似，则点E 在点C 的左侧．当AC EC AB CD =时，则69232EC =，∴EC ＝2，∴E (4，1)；当AC DC AB EC =时，则63292EC=，∴EC ＝9，∴E (﹣3，1)．综上所述，当△CDE 与△ABC 相似时，点E 的坐标为(4，1)或(﹣3，1)．【点睛】本题是二次函数综合题，重点考查了待定系数法求二次函数的解析式、等腰直角三角形的判定和性质、锐角三角函数的定义和相似三角形的判定和性质，熟练掌握待定系数法是解（1）题的关键；添加适当辅助线、熟练求解相关点的坐标和线段的长是解（2）题的关键；正确分类、熟练运用相似三角形的判定和性质是解（3）题的关键. 26．（2019·上海长宁�初三二模）如图1，在Rt ABC ∆中，90,3,4,ACB AC BC ∠===点P 在边AC 上（点P 与点A 不重合），以点P 为圆心，PA 为半径作⊙P 交边AB 于另一点D ，ED DP ⊥，交边BC 于点E ．（1）求证：BE DE =；（2）若,BE x AD y ==，求y 关于x 的函数关系式并写出定义域；（3）延长ED 交CA 的延长线于点F ，联结BP ，若BDP ∆与DAF ∆相似，求线段AD 的长．【答案】（1）证明见解析；（2）258725()588x y x -=≤≤；（3）185或7039．【解析】【分析】（1）首先得出∠BDE +∠PDA =90°，进而得出∠B +∠A =90°，利用PD =P A 得出∠PDA =∠A 进而得出答案；（2）由AD =y 得到：BD =BA -AD =5-y ．过点E 作EH ⊥BD 垂足为点H ，构造Rt △EHB ，所以52cosyBHBBE x-==，通过解Rt△ABC 知：4cos5BCBAB==，易得答案；（3）需要分类讨论：①当∠DBP=∠ADF时AD AFBD PD=即61857655aaaa=-；②当∠DBP=∠F时，AD AFPD BD=即61857655aaa a=-，借助于方程求得AD的长度即可．【详解】解：（1）证明：∵ED⊥DP，∴∠EDP=90°，∴∠BDE+∠PDA=90°，又∵∠ACB=90°，∴∠B+∠P AD=90°，∵PD=P A，∴∠PDA=∠P AD，∴∠BDE=∠B，∴BE=DE；（2）过点E作EH⊥BD垂足为点H，由（1）知BE=DE，∵AD=y，BD=BA-AD=5-y，∴1522y BH BD-==，在Rt△EHB中，∠EHB=90°，∴52 cosyBHBBE x-==，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，∴AB=5，∴4 cos5BCBAB==，5425yx-=∴，∴258725()588xy x-=≤<．（3）如图，设PD=a，则65AD a=，655BD BA AD a=-=-，在等腰△PDA中，3 cos5PAD∠=，易得：7 cos25DPA∠=，则在Rt△PDF中，∠PDF=90°，7 cos25PDDPAPF∠==，∴257aPF=，187aAF=，①当∠DBP=∠ADF时，AD AFBD PD=即61857655aaaa=-；解得a=3，此时61855 AD a==，②当∠DBP=∠F时，AD AFPD BD=即61857655aaa a=-，解得175117a=，此时670539AD a==，综上所述，若△BDP与△DAF相似，线段AD的长为185或7039．【点睛】此题主要考查了圆的综合应用以及切线的性质与判定以及勾股定理等知识，利用数形结合以及分类讨论的思想得出是解题关键．。

2023年上海市16区数学中考二模专题汇编6 相似、锐角三角比与平面向量含详解

专题06相似、锐角三角比与平面向量（36题）一、单选题A ．4B ．83．（2023·上海松江·统考二模）如图，点A ．124．（2023·上海嘉定·统考二模）如图，已知点么:DEC DBC S S △△等于（A ．1:2B 二、填空题5．（2023·上海徐汇·统考二模）如图，已知在ABC 中，点D 是边AC 上一点，且2CD AD =．设BA a = ，BC b =，那么向量BD =______．（用xa yb + 的形式表示，其中x 、y 为实数）6．（2023·上海松江·统考二模）如图，已知在矩形ABCD 中，点E 在边AD 上，且2AE ED =，设,AB a BC b ==，那么BE ＝________（用a 、b的式子表示）．7．（2023·上海嘉定·统考二模）如图，在ABC 中，点D 是AC 边上一点，且21AD DC =：：．设BA a = ，BC b=，那么BD =____．(用a 、b 表示)8．（2023·上海崇明·统考二模）已知梯形ABCD 中，AD BC ∥，2BC AD =，设AB a=，AD b = ，那么DC 可用a 、b表示为________．9．（2023·上海浦东新·统考二模）我们规定：两个正多边形的中心之间的距离叫做中心距，在同一个平面内有边长都为6的正三角形和正方形，当它们的一边重合时，中心距为_____．10．（2023·上海静安·统考二模）如图，已知四边形ABCD 中，点P 、Q 、R 分别是对角线AC 、BD 和边CD 的中点．如果设AD a = ，BC b =，那么向量PQ =uu u r ______（用向量a 、b表示）．11．（2023·上海崇明·统考二模）在六张卡片上分别写有一张，卡片上的数为无理数的概率是12．（2023·上海金山·统考二模）如图，已知果AC a = ，BC b =，当AB 13．（2023·上海闵行·统考二模）如图，在菱形旋转后，点A 恰好落在菱形14．（2023·上海闵行·统考二模）阅读理解：如果一个三角形中有两个内角15．（2023·上海浦东新交于点F．如果2AD=16．（2023·上海嘉定·统考二模）如图，在径作圆，使A、B两点一点在圆内，一点在圆外，那么17．（2023·上海金山·统考二模）已知在线段AC上，如果点E关于直线AD对称的点21．（2023·上海闵行·统考二模）如图，在平面直角坐标系是x 轴正半轴上一点，点k 的值是__________．22．（2023·上海崇明·统考二模）如图，23．（2023·上海金山·统考二模）如图，已知那么ACAD的值等于________24．（2023·上海浦东新果用a 、b表示）三、解答题(1)如果3BC =，求cot B 的值；(2)如果AB BC =，求四边形ABCD(1)求证：四边形ABCD 是菱形；(2)当:3:2AB BE =，5CE =时，求(1)求OAE ∠的度数；(2)如果6BC =，cos B=；(1)求证：AM MN(2)连接BE，求MBE∠正弦值．32．（2023·上海嘉定·统考二模）如图，上，点C在圆O内，且(1)求圆O的半径长；(2)求BC的长．的半径长；(1)求O∠．(2)联结DC，求sin BCD 35．（2023·上海徐汇·统考二模）如图，(1)求AD的长；∠的值．(2)求sin BAE(1)求线段CD的长；(2)求CDDE的值．专题06相似、锐角三角比与平面向量（36题）一、单选题【点睛】本题主要考查了相似三角形的性质与判定，向量的计算，证明的关键．2．（2023·上海浦东新·统考二模）的面积是上，如果，ABCA．4B．8【答案】A∵ABC 的面积是32，BC ∴2132BC AH ⋅=，∴8AH =，设正方形DEFG 的边长为x ∵GF BC ∥，A ．12【答案】B【分析】连接DE ，根据三角形中位线定理以及中线的性质可得∵点G 是ABC 的重心，∴点D ，E 分别为,AC ∴1,2DE BC DE BC =∥∴ADE ACB △△∽，A ．1:2B ．1:3C ．2:3D ．1:4【答案】D【分析】根据题意得ADE ABC ，DEC S 与DBC S △是同高，故底之比等于1:3，从而得出面积之比．【详解】解：∵DE BC ∥，∴ADE ABC ，∴::DE BC AD AB =，∵:1:3AD DB =，∴:1:4AD AB =，∴:1:4DE BC =，∵DEC S 和DBC S △的高相同，∴:1:4DEC DBC S S =△△，故选：D ．【点睛】本题考查了相似三角形的判定和性质，高相等的两个三角形的面积之比等于底之比是解题的关键．二、填空题【答案】23a b-+ 【分析】根据矩形的性质得出【详解】解：∵四边形【答案】1233a b+【分析】根据BD BA =+ 【详解】解：由题意知BD【答案】ˆˆb a +/ˆˆa b+【分析】连接BD ，利用三角形法则，进行求解即可．【详解】解：连接BD 则：BD AD AB b =-= ∵AD BC ∥，2BC AD =∴22BC AD b == ，在正方形ABCD 和正三角形∴点O ，E 均在BC 的垂直平分线上，∴点E ，O ，P ，G 四三点共线，∵正方形ABCD 和正三角形∴6BC BE ==．116OG BG BC ===⨯=在正方形ABCD 和正三角形∴点O ，E 均在BC 的垂直平分线上，∴点E ，O ，P ，G 四三点共线，∵正方形ABCD 和正三角形∴6BC BE ==．∴11622OG BG BC ===⨯【答案】1122a b- 【分析】先证明QR PQ ，【详解】解：∵点P 、∴QR PQ ，分别是BCD △AB【答案】13 b a -【分析】利用平行线分线段成比例定理，向量的计算解答即可．【详解】∵DE BC∥，∴23 AE ADAC AB==，【答案】3【分析】如图，旋转、菱形的性质可知，180ADE DEA ∠=︒-∠-∠由旋转、菱形的性质可知，∴80DEA A ∠=∠=︒，ABD ∠∴180ADE DEA ∠=︒-∠-∠【答案】253【分析】由题意可分：,A B βα∠=∠=，过点∴A ADC ∠=∠，∵4tan 3A =，∴4tan 3ADC ∠=，∵ABC 是特征三角形，即∴2ABE ABC ∠=∠，∴BC 平分ABE ∠，【答案】35【分析】通过证明AEF △得出边之间的关系，即可求解．【详解】解：∵2=AD AB ∴设,2AB a AD a ==，∵AEC △由ABC 沿AC ∴AE AB CD a ===，在AEF △和CDF 中，【点睛】本题主要考查了矩形的折叠问题，以及解直角三角形的方法和步骤．16．（2023·上海嘉定·统考二模）如图，在径作圆，使A 、B 两点一点在圆内，一点在圆外，那么【答案】512R <</125R >>【分析】求出线段AC 、BC ，再根据点与圆得位置关系判断即可．【点睛】本题考查解直角三角形，轴对称的性质，掌握垂线段最短是解题的关键．18．（2023·上海宝山·统考二模）角互余三角形”．已知在Rt△角形”，那么BD的长等于__________【答案】9或41441-则tan tan DAC ∠=∠∴t n a CD DAC AC ∠==∴165CD =∴1695BD =-=；作DE AB ⊥于E ，则∵AD AD =，∴Rt △∵，90ACB ∠=︒，设BD x =，则CD DE =【点睛】本题考查三角形的重心，向量的计算等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．20．（2023·上海崇明·统考二模）30CAB CDE ∠=∠=︒，3BC =，【答案】3372-【分析】利用含30度角的直角三角形的性质，分别求出出90DBE ∠=︒，在Rt【答案】8-【分析】当1x =，22y x ==，即D 是AB 中点，在Rt AOC 中，由勾股定理求∴2AC =，1OC =，【答案】1 3【分析】如图，延长AD ADE ABC△△∽，可得∵点D是ABC的重心，∴23AD AF=，【答案】233/23【分析】过点D 作【详解】过点D 作∴CD CF BD FE =，AG AD =∵,BD CD AE CE ==∴CF EF =，AG AD =2【答案】2133a b - 【分析】由BC b = ，AB a = 质，即可求出结果．【详解】解：∵AD 过ABC 三、解答题(1)如果3BC =，求cot B 的值；(2)如果AB BC =，求四边形ABCD 【答案】(1)1∵,AD BC AD CD ⊥∥，∴90AEC D BCD ∠=∠=∠=︒∵,AD BC AD CD ⊥∥，∴90AEC D BCD ∠=∠=∠=︒，∴四边形ADCE 是矩形，(1)求证：四边形ABCD 是菱形；(2)当:3:2AB BE =，5CE =时，求【答案】(1)证明见解析(2)5(1)求OAE ∠的度数；(2)如果6BC =，cos B 【答案】(1)90OAE ∠=∵OA 平分BAC ∠，∴AF BC ⊥，BF CF =∵3cos 5BF ABC AB ∠==∴5AB =，(1)求证：AM MN =；(2)连接BE ，求MBE ∠正弦值．【答案】(1)见解析(2)35【分析】（1）证明ABF （2）根据NDE DAN ∠=∠55BE EC a ==，进而根据正弦的定义即可求解．【详解】（1）证明：∵四边形∴,AB CD DA BAF ==∠∵E 、F 分别为边CD 、∴AF DE =，∴(SAS ABF DAE △≌△∴DAE ABF ∠=∠，∵1 tan2DEDAEAD∠==又∵AM MN=，∴12DN AN MN==，∵NDE ADN ADE ∠+∠=∠因为AC AB =，所以3425AB r AD r +==，解得=5r ，经检验，=5r 是方程的解；由（1）得5AB AC ==(1)求B ∠的正弦值；(2)求线段AD 的长．【答案】(1)223(2)17∵6AB AC ==，BC =∴122BM CM BC ===∴3BE EN EB BN ==-，∴22EC EN CN =+=∵CD AB ∥，∴AF EF FC FD=，(1)求O 的半径长；(2)联结DC ，求sin BCD ∠．【答案】(1)72(2)714【分析】（1）连接,,,OA OC OD CD 解即可；（2）过点D 作DF BC ⊥，勾股定理求出进行求解即可．【详解】（1）解：连接,,OA OC OD ∵点C 是 AD 的中点，∴AC CD =，AOC DOC ∠=∠，∴OE AD ⊥，∴1232AE DE AD ===，∴223CE AC AE =-=，设圆的半径为r ，则：OA OC OD ==∴3OE OC CE r =-=-，则1122BDC S BD CE BC DF =⋅=⋅ ，即：∴32DF =，由（1）知：21CD AC ==，∴372sin 1421DF BCD CD ∠===．(1)求AD 的长；(2)求sin BAE ∠的值．【答案】(1)2(2)55∵AE分别是ABC边BC上的中线，∴142CE BE BC===，∵1 tan3B=，(1)求线段CD的长；(2)求CDDE的值．。

沪教版(上海)九年级上册数学-第二十五章-锐角的三角比-单元测试卷(含答案)

第二十五章锐角的三角比单元测试卷一、选择题：1、等腰三角形底边长为10cm ，周长为36cm ，则底角的正弦值为（）。

A 、185 B 、165 C 、1513 D 、1312&2、在直角三角形中，各边的长度都扩大3倍，则锐角A 的三角函数值（）A 也扩大3倍B 缩小为原来的31C 都不变D 有的扩大，有的缩小 3、以直角坐标系的原点O 为圆心，以1为半径作圆。

若点P 是该圆上第一象限内的一点，且OP 与x 轴正方向组成的角为α，则点P 的坐标为（） A (cosα,1) B (1,sinα) C (sinα,cosα) D (cosα,sinα)4．如图所示，小明要测量河内小岛B 到河边公路l 的距离，在A 点测得∠BAD ＝30°，在C 点测 .得∠BCD ＝60°，又测得AC ＝50米，那么小岛B 到公路l 的距离为( )．A ．25米B ．253米C ．1003米 D ．25253 5、已知a 为锐角，sina=cos500则a 等于（） A 20° B 30° C 40° D 50° 6、)7、若tan(a+10°)=3，则锐角a 的度数是( )A 、20°B 、30°C 、35°D 、50°7、在△ABC 中，∠C=90°，则下列关系成立的是（）A. AC=ABsinAB. BC=ACsinBC. AC=ABsinBD. AC=BCtanA 8、已知sin α=23，且α为锐角，则α=（）。

|A 、75°B 、60°C 、45°D 、30°9、如图，△ABC 中AB=AC=4，∠C=72°，D 是AB 中点，点E 在AC 上，DE ⊥AB ，则cosA 的值为（）A ．B ．C ．D ．)10、如果∠A 是等边三角形的一个内角，那么cosA 的值等于（）。

上海数学中考二模复习锐角三角比专题

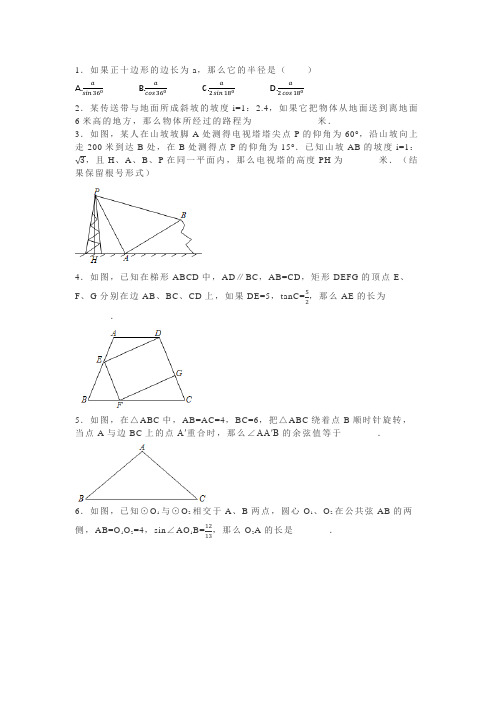
1．如果正十边形的边长为a，那么它的半径是（）A.asin360B.acos360C.a2sin180D.a2cos1802．某传送带与地面所成斜坡的坡度i=1：2.4，如果它把物体从地面送到离地面6米高的地方，那么物体所经过的路程为_____________米．3．如图，某人在山坡坡脚A处测得电视塔塔尖点P的仰角为60°，沿山坡向上走200米到达B处，在B处测得点P的仰角为15°．已知山坡AB的坡度i=1：√3，且H、A、B、P在同一平面内，那么电视塔的高度PH为_______米．（结果保留根号形式）4．如图，已知在梯形ABCD中，AD∥BC，AB=CD，矩形DEFG的顶点E、F、G分别在边AB、BC、CD上，如果DE=5，tanC=52，那么AE的长为_______．5．如图，在△ABC中，AB=AC=4，BC=6，把△ABC绕着点B顺时针旋转，当点A与边BC上的点A′重合时，那么∠AA′B的余弦值等于_______．6．如图，已知⊙O1与⊙O2相交于A、B两点，圆心O1、O2在公共弦AB的两侧，AB=O1O2=4，sin∠AO1B=1213，那么O2A的长是_______．7．如图，已知在正方形网格中，点A、B、C、D在小正方形的顶点上，线段AB与线段CD相交于点O，那么tan∠AOC=___________．8．如图，某水库水坝的坝高为24米，如果迎水坡AB的坡度为1：0.75，那么该水库迎水坡AB的长度为___________米．9．已知传送带和水平面所成斜坡的坡度i=1：3，如果物体在传送带上经过的路程是30米，那么该物体上升的高度是_________米（结果保留根号）．10．七宝琉璃玲珑塔（简称七宝塔），位于上海市七宝古镇的七宝教寺内，塔高47米，共7层．学校老师组织学生利用无人机实地勘测，如果无人机在飞行的某一高度时传回数据，测得塔顶的仰角为60°，塔底的俯角为45°，那么此时无人机距离地面的高度为___________米．（结果保留根号）11．如图1，一扇窗户打开后可以用窗钩AB将其固定，窗钩的一个端点A固定在窗户底边OE上，且与转轴底端O之间的距离为20cm，窗钩的另一个端点B可在窗框边上的滑槽OF上移动，滑槽OF的长度为17cm，AB、BO、AO构成一个三角形．当窗钩端点B与点O之间的距离是7cm的位置时（如图2），窗户打开的角∠AOB的度数为37°．（1）求钩AB的长度（精确到1cm）；（2）现需要将窗户打开的角∠AOB的度数调整到45°时，求此时窗钩端点B与点O之间的距离（精确到1cm）．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，√2≈1.4）．D是AB边的中点，12．如图，在Rt△ABC中，∠ACB=90°，AC=6，cosA=35过点D作直线CD的垂线，与边BC相交于点E．（1）求线段CE的长；（2）求sin∠BDE的值．13．已知：四边形ABCD是正方形，点E是BC边的中点，点F在边AB上，联结DE、EF．，求证：EF⊥DE；（1）如图1，如果tan∠BEF=12（2）如图2，如果tan∠BEF=3，求证：∠DEF=3∠CDE．414．如图，在Rt△ABC中，∠ACB=90°，AC=3，sin∠ABC=1，D是边AB上一点，且3CD=CA，BE⊥CD，垂足为点E．（1）求AD的长；（2）求∠EBC的正切值．15．如图，在梯形ABCD中，AD∥BC，AB=CD=5，对角线BD平分∠ABC，．cosC=45（1）求边BC的长；（2）过点A作AE⊥BD，垂足为点E，求cot∠DAE的值．16．如图，四边形ABCD是平行四边形，联结AC，AB=5，BC=7，cosB=3．5（1）求∠ACB的度数；（2）求sin∠ACD的值．17．如图，已知梯形ABCD中，AD∥BC，∠B=90°，CD=15，BC=16，AB=12，点E是边BC上的一点，联结DE，且DE=CE．（1）求梯形ABCD的面积；（2）求∠DEC的正切值．18．如图1是一种手机平板支架，由底座、支撑板和托板构成，手机放置在托板上，如图2是其侧面示意图，量得底座长AB=11cm，支撑板长BC=8cm，托板长CD=6cm，托板CD固定在支撑板顶端点C处，托板CD可绕点C旋转，支撑板BC可绕点B转动．（1）如果∠ABC=60°，∠BCD=70°，求点D到直线AB的距离（精确到0.1cm）；（2）在第（1）小题的条件下，如果把线段CD绕点C顺时针旋转20°后，再将线段BC绕点B逆时针旋转，使点D落在直线AB上，求线段BC旋转的角度．（参考数据：sin40°≈0.64，co s40°≈0.77，tan40°≈0.84，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，√3≈1.73），BC=10．19．如图，在△ABC中，∠ACB=45°，cotB=32（1）求AB的长；（2）如果CD为边AB上的中线，求∠DCB的正切值．20．图1是某地摩天轮的图片，图2是示意图．已知线段BC经过圆心D且垂直于地面，垂足为点C，当座舱在点A时，测得摩天轮顶端点B的仰角为15°，同时测得点C的俯角为76°，又知摩天轮的半径为10米，求摩天轮顶端B与地面的距离．（精确到1米）参考数据：sin15°≈0.26，cos15°≈0.96，tan15°≈0.27，sin76°≈0.97，cos76°≈0.24，tan76°≈4.01．21．如图，已知，在Rt△ABC中，∠C=90°，AB=4，BC=2，点D是AC的中点，联结BD并延长至点E，使∠E=∠BAC．（1）求sin∠ABE的值；（2）求点E到直线BC的距离．22．如图，有一拱桥的桥拱是圆弧形，已知桥拱的水面跨度AB（弧所对的弦的长）为8米，拱高CD（弧的中点到弦的距离）为2米．（1）求桥拱所在圆的半径长；（2）如果水面AB上升到EF时，从点E测得桥顶D的仰角为α，且cotα=3，求水面上升的高度．23．已知：如图，在△ABC中，AB=AC=6，BC=4，AB的垂直平分线交AB于点E，交BC的延长线于点D．（1）求CD的长；（2）求点C到ED的距离．。

上海初三数学相似三角形经典题型

上海初三数学相似三角形经典题型集团文件发布号：（9816-UATWW-MWUB-WUNN-INNUL-DQQTY-相似三角形的判定练习例题分析：例1：已知如图，在△ABC 中，D 是AB 上的一点，连结CD ，∠ACD=∠B,求证：2 AE AD AC =例2：如图，在Rt ΔABC 中，∠ACB=90°，CD ⊥AB ，垂足为D ，(1)求证：△ACD ∽△ABC ∽△CBD(2)求证：222(1) (2) (3)AC AD AB CD AD DB BC BD AB ===例3：已知如图，点D 是AB 上的一点，CA ⊥AB,EB ⊥AB,CD ⊥DE,求证：△ACD ∽△BDE 例4：在△ABC 中，AB=6，AC=9，D 为AC 上的一点，AD=3，在AB 上找一点E ，使得△ADE 与△ABC 相似并求出AE 的长。

两个三角形相似的六种图形：1. 如图在△ABC 中，D 是BC 边的中点，且AD ＝AC ，DE ⊥BC ，交AB 于点E ，EC 交AD 于点F ．求证：△ABC ∽△FCD ；2、已知：如图，△ABC 中，∠ACB=900，AB 的垂直平分线交AB 于D ，交BC 延长线于F 。

求证：CD 2=DE ·DF3. 如图3，△ABC 中，AD 平分∠BAC ， AD 的垂直平分线FE 交BC 的延长线于E ．求证：DE 2＝BE·CE．4.如图，已知△ABC 中，AB=AC ，AD 是BC 边上的中线，CF ∥BA ，BF 交AD 于P 点，交AC 于E 点。

求证：BP 2=PE ·PF 。

A EB D CF5.如图，CD是Rt△ABC的斜边AB上的高，∠BAC的平分线分别交BC、CD于点E、F，AC·AE=AF·AB6.如图4，在△ABC中，∠BAC=90°，AD⊥BC，E是AC的中点，ED交AB的延长线于点F．求证：AB DF AC AF．7.已知如图，在平行四边形ABCD中，AC=2AB,求证：△AOB∽△ABC8. 已知:如图,ΔABC中,CE⊥AB,BF⊥AC.求证:(1)△AEC∽△AFB (2) △AEF∽△ACB 6.如图5，在△ABC中，∠ACB=90°，CD是斜边AB上的高，G是DC延长线上一点，过B作BE⊥AG，垂足为E，交CD于点F．求证：CD2＝DF·DG．7.如图，△ABC中，点DE在边BC上，且△ADE是等边三角形，∠BAC=120°求证：（1）△ADB∽△CEA;（2）DE2=BD·CE;(3)AB·AC=AD·BC.8．如图，平行四边形ABCD中，E为BA延长线上一点，∠D=∠ECA.求证：AD·EC=AC·EB9.如图，E是平行四边形的边DA延长线上一点，EC交AB于点G,交BD于点F,求证：FC2=FG·EF.10.如图，ABCD为直角梯形，AB∥CD,AB⊥BC,AC⊥BD。

上海市初三数学相似三角形经典题型

例题分析:例1:已知如图，在△ ABC中，D是AB上的一点，连结CD / ACD2 B,求证：AE2=ADJAC例 2 :如图，在Rt△ ABC中，/ ACB=90 , CDL AB,垂足为D,(1)求证：△ AC3A AB3A CBD⑵求证：⑴AC2二AD AB (2)CD2二AD_DB (3)BC2二BD _AB例3 :已知如图，点D是AB上的一点，CA丄AB,EB丄AB,CD丄DE,求证：△ ACS A BDE例4 :在△ ABC中，AB=6, AC=9 D为AC上的一点，AD=3,在AB上找一点E,使得△ADE与△ ABC相似?相似三角形的判定练习BC,交A卄E,D厶—X型图A并求出AE的长。

AA两个三角形相似的六种图形:BC边的中点△ABCC BB中,1.如求证：A ABCB Dc DAD = AC , DE 点F.EC2 3.如图3, △ABC中，AD平分/ BAC , AD的垂直平分线FE交BC的延长线于E.求证：DE = BE-CE.A4•如图，已知△ ABC 中，AB=AC ，AD 是BC 边上的中线， CF // BA , BF 交AD 于P 点，交 AC 于E 点。

BP 2=pE . PF 。

ACB=90° ,CD 是斜边AB 上的高，G 是DC 延长线上一点，过 B 作BE 丄AG , 求证：CD 7•如求证：二图，△ ABC 中，点DE 在边BC 上，且△ ADE 是等边三角形，/ BAC=120 (1 )△ ADB^A CEA;(2) DE2=BD- CE;(3)AB - AC=AD BC.AEF^A ACBF-DG .6•如图5，在△ABC 中，/垂足为E ,交CD 于点F .10.如图，ABCD为直角梯形，AB// CD,ABL BC,AC丄BD。

AD=BD 过E作EF// AB交AD于F. 是说明：(1) AF=BE;(2)AF 2=AE - EC.&如图，平行四边形ABCD中，E为BA延长线上一点, D=Z ECA.1112 13.如图，已知：在△ ABC 中，/ BAC=900 , AD 丄BC , E 是AC 的中点，ED 交AB 的延长线于 F 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

上海十年中考相似及锐角三角比试题集锦朱合强
1已知：如图3，在ABC △中，AD 是边BC 上的高，E 为边AC 的中点，14BC =，12AD =，4
sin 5B =．求（1）线段DC 的长；（2）tg EDC ∠的值．
2．在ABC △中，AD 是BC 边上的中线，G 是重心．如果6AG =，那么线段DG 的长为（）
3．某飞机在离地面1200米的上空测得地面控制点的俯角为60°，此时飞机与该地面控制点之间的距离是米． 4．如图4，在△ABC 中，∠C ＝90°，点D 在BC 上，BD ＝4，AD ＝BC ，cos ∠ADC ＝5
3
．求：（1）DC 的长；（2）sin B 的值．
图4
5．在△ABC 中，点D 、E 分别在边AB 、AC 上，DE ∥BC ，如果AD ＝8，DB ＝6，EC ＝9，那么AE ＝__________． 6．在离旗杆20米处的地方用测角仪测得旗杆顶的仰角为a ，如果测角仪高为1.5米，那么旗杆的高为__________米， 7．在△ABC 中，如果AB ＝AC ＝5cm ，BC ＝8cm ，那么这个三角形的重心G 到BC 的距离是__________cm ． 8．如图1，已知四边形ABCD 中，BC ＝CD ＝DB ，∠ADB ＝90°，cos ∠ABD ＝
5
4
，求S △ABD ︰S △BCD ．
A
E C
D
B 图
3
9．如图4，直线y ＝
2
1
x ＋2分别交x 、y 轴于点A 、C ，P 是该直线上在第一象限内的一点，PB ⊥x 轴，B 为垂足，S △ABP
＝9．（1）求点P 的坐标；
（2）设点R 与点P 的同一个反比例函数的图象上，且点R 在直线PB 的右侧，作RT ⊥x 轴，T 为垂足，当△BRT 与△AOC 相似时，求点R 的坐标.
10.在△ABC 中，点D 、E 分别在边AB 、AC 上，CD 平分∠ACB ，DE ∥BC ，如果AC ＝10，AE ＝4，那么BC ＝。

11.正方形ABCD 的边长为1。

如果将线段BD 绕着点B 旋转后，点D 落在BC 延长线上的点D’处，那么tg ∠BAD ’＝。

12.将两块三角板如图放置，其中∠C ＝∠EDB ＝90º，∠A ＝45º，∠E ＝30º，AB ＝DE ＝6。

求重叠部分四边形DBCF 的面积。

13.在△ABC 中,点D 、E 分别在边AB 、AC 上,DE ∥BC,AD=1,BD=2,则S △A D E :S △A B C =
.
14.在△ABC 中,∠A=90°,设∠B=θ,AC=b,则AB= (用b 和θ的三角比表示).
15.某山路的路面坡度I=1:399 ,沿此山路向上前进200米,升高了米. 16.在△ABC 中,点G 为重心,若BC 边上的高为6,则点G 到BC 边的距离为 .
17.如图2,在△ABC 中,AB=AC, ∠A=36°,BD 平分∠ABC,DE ∥BC,那么在下列三角形中,与△ABC 相似的三角形是………………………( ) A 、△DBE B 、△ADE C 、△ABD D 、△BDC
18.如图3,等腰梯形ABCD 中,AD ∥BC,∠DBC=45°.翻折梯形ABCD,使点B 重合于点D,折痕分别交边AB 、BC 于点F 、E.若AD=2,BC=8,求: (1)BE 的长; (2) ∠CDE 的正切值.
19如图6，在直角坐标平面内，O 为原点，点A 的坐标为(100)，，点B 在第一象限内，
，3
．
求：（1）点B 的坐标；（2）cos BAO ∠的值．
B C E 图6
20如图8，在梯形ABCD 中，AD BC ∥，CA 平分BCD ∠，DE AC ∥，交BC 的延长线于点E ，2B E =∠∠．（1）求证：AB DC =；（2）若tg 2B =
，AB =BC 的长．
21如图9，在直角坐标平面内，函数m
y x
=
（0x >，m 是常数）的图象经过(14)A ，，()B a b ，，其中1a >．过点A 作x 轴垂线，垂足为C ，过点B 作y 轴垂线，垂足为D ，连结AD ，DC ，CB ．
（1）若ABD △的面积为4，求点B 的坐标；（2）求证：DC AB ∥；（3）当AD BC =时，求直线AB 的函数解析式．
图
8
图9。