第二章 复变函数
第二章复变函数的积分

f (z)dz lim f (k )(zk zk1)
l
积分n函 数k1
积分路径 一般来说,复变函数的积分值与积分路径有关.
2、复变函数积分计算方法
n
f (z)dz lim f (k )(zk zk1) n k 1
l
1)将复变函数的路积分化为两个实变函数的线积分
2)参数积分法
若积分曲线的参数方程z=z(t) ( ),dz z'(t)dt
则
f (z)dz f [z(t)]z'(t)dt
l
(极坐标法,通常用来计算积分路径为圆弧时的情况)
通常思路:
积分路径l为圆弧: 宗量用指数形式表示:
z z0
z z0 ei
n
n
f (z)dz f (z)dz;l lk
l
k 1 lk
k 1
f (z)dz f (z)dz
lAB
lBA
f (z)dz
l
f (z) dz ; dz
dx2 dy2 ds
l
Ms; M f (z) , s l的长度
用来求积分的估计值
r
1
z3 z
2
dz
z3 z r 1 z2
dz
(1)
z3
z r 1 z2
dz M
dz M
z r
ds Ms
z r
(2)
由(1)(2)式,得:
z3 dz Ms
z r 1 z2
M
1
r
3
r
2
s ds 2 r z r
数学物理方法第二章复变函数的积分
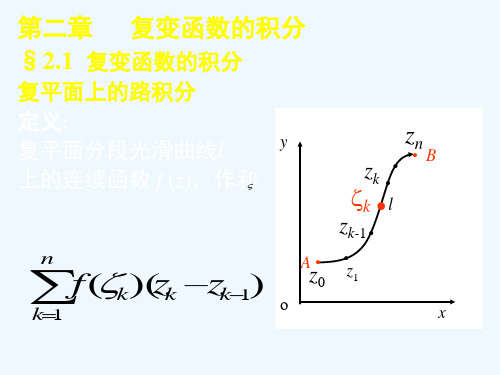
一般而言,复变函数的积分不仅与起点和终点有 关, 同时还与路径有关。
§2.2 柯西(Cauchy)定理
——研究积分与路径之间的关系 (一)单连通域情形 单连通域: 在其中作任何简单闭合围线,围 线内的点都是属于该区域内的点。 单连通区域的Cauchy 定理 :如果函数 f (z) 在闭 单连通区域 B 中单值且解析, 则沿 B 中任 何一个分段光滑的闭合曲线 l (也可以是 B 的 边界 l0 ), 函数的积分为零。
lim f( z z ) k)( k k 1
n
存在且与 k 的选取无关, 则这个和的极限称为 函数 f (z) 沿曲线 l 从 A 到 B 的路积分,记为
即
l
f (z) dz
n k k k 1
z ) d z lim f ( )( z z f(
l n k 1 max | z | 0 k
l 1 l 2
f (z)=Re (z)不是解析函数!
y i l2 o l1 1 l2
I1 Rez d z xd( x iy) 1 xd x i d y i 0 0 2 ( y = 0) (x=1)
1 1
1+i
l1 x
1 I 0 id y x d x 2 0 0 (x=0) ( y=i ) 2
l l l
v u u v d x d y i d x d y s s x y y x
又u、v 满足C-R条件 u v u v , x y y x
y
f ( z ) d z 0
l
B
l
o
复变函数第2章

By 宋朝红2.1 复变函数的极限2.2 复变函数的连续性2.3 导数2.4 解析函数2.5 调和函数Math HZAU第二章导数zz f z z f z Δ)()Δ(lim 000Δ−+→1 导数与微分定义:设函数w=f(z)在包含z 0的某邻域D 内有定义,点z 0+⊿z ∈D. 如果极限存在, 则称f (z )在z 0可导, 此极限值就称为f (z )在z 0的导数, 记作0000Δ0(Δ)()d ()lim .d Δ|z z z f z z f z w f z z z=→+−′==如果f (z )在区域D 内处处可导, 则称f(z)在D内可导.例1求f (z )=z 2的导数例3讨论函数f (z )=|z|2的可导性函数可导一定连续,但连续却不一定可导例2问:函数f (z )=x +2yi 是否可导?求导公式与法则①常数的导数c ′=(a+ib )′=0.②(z n )′=nz n-1(n 是自然数).③设函数f (z ),g (z ) 均可导,则[f (z )±g (z )]′=f ′(z )±g ′(z ),[f (z )g (z )]′= f ′(z )g (z )+ f (z )g ′(z )----实函数中求导法则的推广)0)((,)()(')()()('')()(2≠−=⎥⎦⎤⎢⎣⎡z g z g z g z f z g z f z g z f④复合函数的导数( f [g (z )])′=f ′(w )g ′(z ),其中w=g (z )。
.0)()()()(10处可导点外)处在复平面上(除分母为导;在整个复平面上处处可由以上讨论z Q z P z R z a z a a z P nn =+++=⇒"⑤反函数的导数,其中: w=f (z )与z=ϕ(w )互为单值的反函数,且ϕ′(w )≠0。
)('1)('w z f ϕ=例3求f (z )=Arcsinz=-iLn (iz+ )的导数。
复变函数第二章

该定理将求复变函数 f ( z ) = u( x , y ) + iv ( x , y ) 的极限问题 , 转化为求 两个二元实变函数 u( x , y ) 和 v ( x , y ) 的极限问题 .
x → x0 y → y0
x → x0 y → y0
定理 : 设 lim f ( z ) = A, lim g ( z ) = B , 那末
4
例2 : 求极限 lim cos z
解:因为 cos z = cos( x + yi ) = cos xchy − i sin xshy
z → z0
若取 u(x,y) = cos xchy , v(x,y) = sin xshy , z 0 = x 0 + iy 0 , 则有
( x , y )→ ( x0 , y0 )
0
→ 那末称 A 为 f ( z ) 当 z 趋向于 z0 时的极限 . 记作 lim f ( z ) = A. (或 f ( z ) zz → A) z→ z →
0
注意: 注意: 定义中 z → z0 的方式是任意的 . 几何意义: 几何意义 当变点z一旦进 当变点 一旦进 入z0 的充分小去 心邻域时,它的象 心邻域时 它的象 就落入A的 点f(z)就落入 的 就落入 一个预先给定的 ε邻域中 邻域中
z → z0 z → z0
(1) lim[ f ( z ) ± g ( z )] = A ± B;
z → z0 z → z0
(2) lim[ f ( z ) g ( z )] = AB; f (z) A (3) lim ( B ≠ 0). = z → z0 g ( z ) B
与实变函数的极限运算法则类似. 与实变函数的极限运算法则类似
复变函数 第二章

解 (1) 设z=x+iy w=x-iy u=x, v= -y 则
u 1 x v 0 x
u 0
y v
1
u x
v y
y
故 w z在全平面不可导,不解 析。
2020/12/16
张晓斌编辑(47页)
z0
x iy
x 2yi 1
lim z0
x yi
2
当y 当x
0, x 0, y
0时 0时
不存在!
故函数f (z) x 2 yi处处不可导,但处处连续.
2020/12/16
张晓斌编辑(47页)
5
(2)求导公式与法则
----实函数中求导法则的推广
① 常数的导数 c=(a+ib)=0.
z0
小, f (z0 ) z 是函数 w f (z)的改变量 w 的 线性部分. f (z0 ) z 称为函数 w f (z)在点 z0 的微分, 记作 dw f (z0 ) z.
2020/12/16
张晓斌编辑(47页)
14
如果函数在 z0 的微分存在, 则称函数 f (z) 在 z0 可微.
f (z0 ), 所以f (z)在z0连续
2020/12/16
张晓斌编辑(47页)
13
4.微分的概念:
复变函数微分的概念在形式上与一元实变 函数的微分概念完全一致. 定义 设函数 w f (z)在 z0 可导, 则 w f (z0 z) f (z0 ) f (z0 ) z (z)z, 式中 lim (z) 0, (z)z 是 z 的高阶无穷
u v v u x y x y
第1篇 复变函数论-第2章 复变函数积分

Anhui University 在上一章学习了复变函数,重点介绍了解析函数的许多性质,这些性质都是在可导和可微的基础上得出的。
第2章复变函数积分()(,)(,) 若函数在区域内解析则有:f z u x y iv x y D =+1. 解析函数的调和性:解析函数的实部与虚部均满足二维拉普拉斯方程:(由C-R 条件可证明)。
220,0.xx yy xx yy u u u u v v v v ∆≡∇=+=∆≡∇=+=2. 解析函数的共轭性:解析函数的实部与虚部由C-R 方程联系,称为解析函数的共轭性。
具体说只要知道解析函数的实部或者虚部就可求得解析函数。
3. 解析函数的实部与虚部是彼此相互正交的曲线。
0),(),(=∇⋅∇y x v y x u为了深入理解复变函数,本章用积分理论来分析复变函数积分。
基本内容:1、掌握复积分的概念、性质和计算方法;2、掌握解析函数的基本定理-Cauchy定理及其应用;3、掌握解析函数的基本公式-Cauchy公式及其应用2.1 复数函数积分一. 复积分的定义1max 0()lim ()k n k k n C k z f z dz f z ζ→∞=∆→=∆∑∫记作:()w f z l =为被积函数,为积分路径。
二. 复积分存在的条件1max 0()lim ()k n k kn l k z f z dz f z ζ→∞=∆→=∆∑∫由上式可知:一个复积分的实质是两个实积分的和。
实积分存在的条件:(,)(,)分段光滑,,在上连续l u x y v x y l因此复积分存在的条件:分段光滑,在上连续。
()l f z l注1:所说的曲线总是指光滑或逐段光滑曲线。
注2:边界的正方向:规定当观察者沿曲线边界前进时,所围的区域始终在观察者的左手边,则前进的方向为正方向。
rzz<−单连通区域Rzzr<−<复连通区域正方向正方向三. 复积分的性质(1)()d ()d l lf z z f z z −=−∫∫反转积分路径:(2)()d ()d ;() l l kf z z k f z z k =∫∫为复常数(3)[()()]d ()d ()d ;l l l f z g z z f z z g z z ±=±∫∫∫121()(),,k n n k L l f z dz f z dz n l l l ==∑∫∫"(4),若曲线L由段线段组成被积函数的线性可叠加性积分路径的可叠加性(5)|()||()|||L L f z dz f z dz ≤⋅∫∫(6) , () () ()d ()d .设曲线的长度为函数在上满足那么l l l L f z l f z M f z z f z s ML ≤≤≤∫∫积分估值定理四. 计算方法1. 用定义计算2. 通过计算实积分结果表明:被积函数与积分路径有关。
第二章复变函数

v( x, y) = xy
∂u =0 ∂y ∂v =x ∂y
Q 都是初等函数,在复平面内处处连续;
∂u ∂v ∂x = ∂y 针对柯西 − 黎曼方程 仅在 z = 0处成立 ∂u = − ∂v ∂y ∂x
∂u ∂v 导数: f ' ( z = 0 ) = [ + i ] | z = 0 = ( 2 x + iy ) | x = 0, y = 0 = 0 ∂x ∂x
∂u ∂v |( x, y ) +i |( x, y ) ∂x ∂x
()∆z 0 2 →
沿虚轴
∆ z = i∆ y
{u ( x, y + ∆y ) + iv ( x, y + ∆y )} − {u ( x, y ) + iv ( x, y )} lim i∆ y ∆y → 0 1 u ( x, y + ∆y ) − u ( x, y ) v ( x , y + ∆y ) − v ( x , y ) + lim lim ∆y i ∆y →0 ∆y ∆y → 0
f 例: f ( z ) = u + iv为解析函数, ' ( z ) ≠ 0, 则曲线u ( x, y) = c1
v( x, y ) = c2必互相正交。
证: ux 曲线 u ( x , y ) = c1 斜率为 k1 = − uy vx 曲线 v ( x , y ) = c 2 斜率为 k 2 = − vy
w = f ( z) = z
2
的可导性。
2 2 ∆ w f ( z + ∆z ) − f ( z ) z + ∆z − z = = ∆z ∆z ∆z
第二章 复变函数的积分

一.复变函数的积分
(复平面的路径积分) 复平面的路径积分)
∫ f (z )dz ≡ lim ∑ f (ξ )(z
l n →∞ k =1 k
l l
n
k
− z k −1 ) ≡ lim ∑ f (ξ k )dz k n→∞
k =1
n
∫ f (z )dz = ∫ u (x, y )dx − v(x. y )dy + i ∫ v(x, y )dx + u (x. y )dy
ez I =∫ 2 dz c ( z + 1) 2
z 2
2π i (n−1) f (ξ ) ∫ (ξ − z)n dξ = (n −1)! f (z) l
例:计算
z = a (> 1)
解:
I=∫
c1
e z /( z − i ) 2 e /( z + i) dz dz + ∫ 2 2 c2 ( z + i) ( z − i)
1
I 2 = ∫ xdz + ∫ xdz =
0
1
1+i
i
1 ∫ 0idy + ∫ xdx = 2 0 0
直线参数方程 : z = (1 + i)t或( y = x)
1
I 3 = ∫ t (1 + i )dt = 1 + i 2 0
(可见积分与路径有关)
例2
1+i
z 2 dz = ? 1)沿折线 0—1---1+i ∫
= 2π i [e z /( z + i) 2 ]′z =i + 2π i [e z /( z − i ) 2 ]′z = −i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 复变函数第一节 解析函数的概念及C.-R.方程1、导数、解析函数定义2.1:设()w f z =是在区域D 内确定的单值函数,并且0z D ∈。
如果极限00,0()()lim z z z D f z f z z z →∈-- 存在,为复数a ,则称)(z f 在0z 处可导或可微,极限a 称为)(z f 在0z 处的导数,记作0'()f z ,或0z z dw dz =。
定义2.2:如果()f z 在0z 及0z 的某个邻域内处处可导,则称()f z 在0z 处解析;如果()f z 在区域D 内处处解析,则我们称()f z 在D 内解析,也称()f z 是D 的解析函数。
解析函数的导(函)数一般记为'()f z 或d ()d f z z。
注解1、εδ-语言,如果任给0ε>,可以找到一个与ε有关的正数()0δδε=>,使得当z E ∈,并且0||z z δ-<时,00()()||f z f z a z z ε--<-,则称)(z f 在0z 处可导。
注解2、解析性与连续性:在一个点的可导的函数必然是这个点的连续函数;反之不一定成立;注解3、解析性与可导性:在一个点的可导性是一个局部概念,而解析性是一个整体概念;注解4、函数在一个点解析,是指在这个点的某个邻域内解析,因此在此点可导;反之,在一个点的可导性不能得到在这个点解析。
解析函数的四则运算:()f z 和()g z 在区域D 内解析,那么()()f z g z ±,()()f z g z ,()/()f z g z (分母不为零)也在区域D 内解析,并且有下面的导数的四则运算法则:(()())''()'()[()()]''()()()'()f zg z f z g z f z g z f z g z f z g z ±=±=+ 2()'()()()'()()[()]'f z f z g z f z g z g z g z -⎡⎤=⎣⎦。
复合求导法则:设()f z ζ=在z 平面上的区域D 内解析,()w F ζ=在ζ平面上的区域1D 内解析,而且当z D ∈时,1()f z D ζ=∈,那么复合函数[()]w F f z =在D 内解析,并且有d [()]d ()d ()d d d F f z F f z z zζζ=求导的例子:(1)、如果()f z a ≡(常数),那么d ()0d f z z=; (2)、d 1d z z=,1d d n n z nz z -=; (3)、z 的任何多项式01()...n n P z a a z a z =+++在整个复平面解析,并且有112'()2...n n P z a a z na z -=+++(4)、在复平面上,任何有理函数,除去使分母为零的点外是解析的,它的导数的求法与z 是实变量时相同。
2、柯西-黎曼条件可微复变函数的实部与虚部满足下面的定理:定理 2.1 设函数(,)(,)(,)f x y u x y iv x y =+在区域D 内确定,那么(,)f x y 在点z x iy D =+∈可微的充要条件是:1、 实部(,)u x y 和虚部(,)v x y 在(,)x y 处可微;2、 (,)u x y 和(,)v x y 满足柯西-黎曼条件(简称C R -方程)u v u v x y y x ∂∂∂∂∂∂∂∂==-证明:(必要性)设()f z 在z x iy D =+∈有导数a ib α=+,根据导数的定义,当z z D +∆∈时(0)z ≠()()(||)f z z f z z o z α+∆-=∆+∆()()(||)a ib x i y o z =+∆+∆+∆ 其中,z x i y ∆=∆+∆。
比较上式的实部与虚部,得(,)(,)(||)u x x y y u x y a x b y o z +∆+∆-=∆-∆+∆(,)(,)(||)v x x y y v x y b x a y o z +∆+∆-=∆+∆+∆因此,由实变二元函数的可微性定义知,(,)u x y ,(,)v x y 在点(,)x y 可微,并且有, ,, uu v v x y x y a b b a ∂∂∂∂∂∂∂∂==-==因此,柯西-黎曼方程成立。
(充分性)设(,)u x y ,(,)v x y 在点(,)x y 可微,并且有柯西-黎曼方程成立:u v u v x y y x∂∂∂∂∂∂∂∂==- 设, ,u v x xa b ∂∂∂∂==则由可微性的定义,有: (,)(,)(||)u x x y y u x y a x b y o z +∆+∆-=∆-∆+∆(,)(,)(||)v x x y y v x y b x a y o z +∆+∆-=∆+∆+∆令z x i y ∆=∆+∆,当z z D +∆∈(0z ∆≠)时,有()()(||)f z z f z z o z α+∆-=∆+∆()()(||)a ib x i y o z =+∆+∆+∆令a ib α=+,则有00()()(||)lim lim()z z f z z f z o z z zαα∆→∆→+∆-∆=+=∆∆ 所以,(,)f x y 在点z x iy D =+∈可微的。
定理 2.2 设函数(,)(,)(,)f x y u x y iv x y =+在D 区域D 内确定,那么(,)f x y 在区域D 内解析的充要条件是:1、 实部(,)u x y 和虚部(,)v x y 在D 内可微;2、 (,)u x y )和(,)v x y 在D 内满足柯西-黎曼条件(简称C R -方程)uv u v x y y x∂∂∂∂∂∂∂∂==-关于柯西-黎曼条件,有下面的注解:注解1、解析函数的实部与虚部不是完全独立的,它们是C R -方程的一组解,它们是在研究流体力学时得到的;注解2、解析函数的导数形式更简洁:公式可避免利用定义计算带来的困难。
注解3、利用两个定理,可以判断一个复变函数是否在一点可微或在一个区域内解析。
3、例题例1 证明()f z z x iy ==-在任何点都不可微。
解 (,),1,0,x y u x y x u u === (,),0,1x y v x y y v v =-==-, 四个偏导数在复平面内连续,但任何点都不满足C R -方程, 故()f z z x iy ==-在任何点都不可微。
例2 试讨论定义于复平面内的函数222()()2f z z x y ixy ==-+的可导性。
解:22(,),2,2,x y u x y x y u x u y =-==- (,)2,2,2,x y v x y xy v y v x ===四个偏导数在复平面内连续,且()f z 在复平面内满足C R -方程, 故222()()2f z z x y ixy ==-+在复平面内处处可导。
例3 设函数3232()()f z my nx y i x lxy =+++在复平面可导,试确定常数,,m n l 之值。
解 3222(,),2,3,x y u x y my nx y u nxy u my nx =+==+3222(,),3,2,x y v x y x lxy v x ly v lxy =+=+=由C R -方程 ,x y y x u v u v ==- 得 ()0,xy n l -= (1)222233my nx x ly +=-- (2)由(1) 得 ,n l = (3)由(2) 得 30,n += (4)30,m l += (5)解(3),(4),(5)得 3,1n l m ==-=。
第二节 初等解析函数1、幂函数利用对数函数,可以定义幂函数:设a 是任何复数,则定义z 的a 次幂函数为Ln (0)a a z w z e z ==≠当a 为正实数,且0z =时,还规定0a z=。
由于 ln 2(ln10,arg )a a z a k i w z e e z πππ===-<≤因此,对同一个0,a z w z ≠=的不同数值的个数等于不同数值的因子2(),a k i e k Z π⋅∈个数。
2、幂函数的基本性质:1、由于对数函数的多值性,幂函数一般是一个多值函数;2、当a 是正整数时,幂函数是一个单值函数;3、当1a n =(当n 是正整数)时,幂函数是一个n 值函数; 4、当m a n=是有理数时,幂函数是一个n 值函数; 5、当a 是无理数或虚数时,幂函数是一个无穷值多值函数。
设在区域G 内,我们可以把Lnz 分成无穷个解析分支。
对于Lnz 的一个解析分支,相应地a z 有一个单值连续分支。
根据复合函数求导法则,a w z =的这个单值连续分支在G 内解析,并且 ln d 1d aa z w z a e a z z z=⋅=⋅, 其中a z 应当理解为对它求导数的那个分支,ln z 应当理解为对数函数相应的分支。
对应于Lnz 在G 内任一解析分支:当a 是整数时,a z 在G 内是同一解析函数;当(1)m a n n=>既约分数,时,a z 在G 内有n 个解析分支;当a 是无理数或虚数时,幂函数a z 在G 内有无穷多个解析分支,是一个无穷值多值函数。
例如当n 是大于1的整数时,1nw z ==n z w =的反函数。
当0z ≠时,有1111ln 2(ln||arg )21(arg 2) (arg ,)z k i z i z k i n n n n i z k n w e e e ez k Z πππππ++====-<≤∈ 这是一个n 值函数。
在复平面上以负实轴(包括0)为割线而得得区域D 内,它有n 个不同的解析分支:1(arg 2)(arg ;0,1,...,1)i z k n w z k n πππ+=-<<=-它们也可以记作12)i k n w e π==,这些分支在负实轴的上沿与下沿所取的值,与相应的连续分支在该处所取的值一致。
当a 不是整数时,原点及无穷远点是a w z =的支点。
但按照a 是有理数或者a 不是有理数,这两个支点具有完全不同的性质。
为了理解这些结论,我们在0或无穷远点的充分小的邻域内,任作一条简单闭曲线C 围绕0或无穷远点。
在C 上任取一点1z ,确定Argz 在1z 的一个值11arg z θ=;相应地确定(ln ) a a z iArgz w z e +==,在1z 的一个值111(ln arg )ln a z i z a z e e +=。
现在考虑下列两种情况: (1) a 是有理数(1)m n n>既约分数,,当一点z 从1z 出发按反时针或顺时针方向连续变动n 周时,arg z 从1θ连续变动到12n θπ±,而mn w z =则从111ln (ln||) m m z z i n n e e θ+=相应地连续变动到11(ln 2)ln m m z n z n n e e π+=,也即第一次回到了它从1z 出发时的值。
