相似图形
相似图形

在综 合题 中要 对 相似 形灵 活运 用 , 尤
其是 应用 相 等线 段代 换 、 比代 换解 等 决相 似问题 是这里 的重点 和难 点.
1 2 1 四川 宜 宾 ) 图 1 示 , .(0 0 如 所
在 R △AB t C中 , AC = 0 , B 9 。 /A= 0 , 3。
A
AD
—
AB
一 ‘
( 相似 比与叙 述的顺 序有 关 ) ・ .
3 相 似三角 形 的判定定 理 : . () 1 如果 两个 三 角形 的 两个 角分
)
别对应相等( 或三个角分别对应相等) ,
则 这两个 三角形 相似 ( 简叙 为两 角对 应相 等两 三角形 相似 ) .
列结 论 :
C的中点 , 则下
三个对 应 角相 等 、 三条 对应 边 成
比例 的两 个 三角 形 叫 做相 似 三 角形 .
相 似 三 角 形 对 应 边 的 比 叫 做 相 似 比
@B =D ② AA E-AA C C 2 E; D ' " B;
相 似 知 识 是 中 考 中 的重 点 考 查 内容 , 求 能够 运用 相 似 的相关 知识 要 解决 一些 实 际 问题 . 这就 进 一步 要求 注 意培 养 解决 数 学 问题 的建 模思 想 . 其 中正 确 的有 (
B
D
() B 4A = 、 2 若A = ,D 3 /3,E 3 A =,
求 A瑚 长 .
A
() 证: 1求 △AD AC AE;
() 2 当AD 8 DC 6 点E、 别是 = , =, 盼 B C 中点 时 .求直 角 梯 形ABC C 的 D
图形相似ppt

27.1 图形的相似
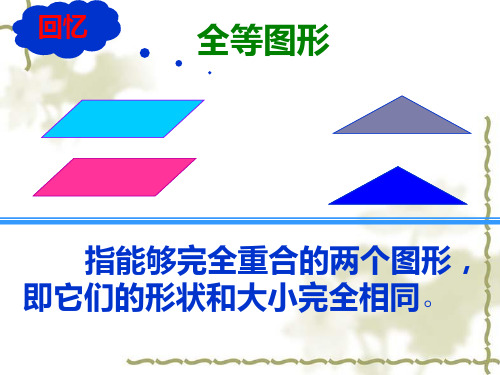
1.相似图形 (1)定义:把___形__状__相__同___的图形叫做相似图形. (2)特点:①形状相同;②图形的大小,位置没有要求. 注意:“全等”是“相似”的一种特殊情况.全等的两个 图形一定相似,而相似的图形则未必全等.
2.成比例线段(比例线段) 对于四条线段 a,b,c,d,如果其中两条线段的__比____与 另外两条线段的___比__相__等___,如___ab_=__dc__(ad=bc),我们就说这 四条线段是成比例线段. 注意:线段的比值是一个正数,与度量关系无关,但要注 意度量单位的统一.
图 27-1-3
4 . 等 腰 梯 形 ABCD 与 等 腰 梯 形 A′B′C′D′ 相 似 , AD=BC,∠A=65°,AB=8 cm,A′B′=6 cm,AD=5 cm, 求出 A′D′的长度及梯形 A′B′C′D′各角的度数.
解:∵A′ABB′=A′ADD′,即86=A′5D′.∴A′D′=145 cm. 在等腰梯形 ABCD 中,AD=BC,∠A=65°, ∴∠B=∠A=65°,∠D=∠C=180°-∠A=115°. ∴∠A′=∠B′=65°,∠C′=∠D′=115°.
Hale Waihona Puke 解:∵四边形 ABCD 相似于四边形 A′B′C′D′, ∴A′ABB′=B′BCC′=C′CDD′=D′DAA′, 即A′7B′=59=C′6D′=D′8A′.
∴A′B′=12.6,C′D′=10.8,D′A′=14.4. ∴四边形A′B′C′D的周长为 12.6+9+10.8+14.4=46.8.
知识点 1 相似图形 【例 1】 下列各组图形:①两个平行四边形;②两个圆; ③两个矩形;④有一个内角是 80°的两个等腰三角形;⑤两个正 五边形;⑥有一个内角是 100°的两个等腰三角形,其中一定是 相似图形的是________(填序号). 思路点拨:判断两个图形是不是相似图形的关键:这两个 图形的形状是不是相同,与其大小、位置无关.
23.2相似图形

2 B ' C ' ___, 2 A ' D ' _____. 1 C ' D ' ____, A ' B '=____, 5
AB BC CD AD A ' B ' B 'C ' C ' D ' A' D ' A A ', B B ', 通过度量,可得: C C ', D D '
0.9m
2.2cm 1.8cm
x
5.一个矩形宽为1(宽<长),剪去一个以宽为边长的正方形后 ,所剩下的矩形与原矩形相似,求原矩形的长.
解:设原矩形的长为x,则剩下矩形的 宽(x﹣1), ∵剩下的矩形与原矩形相似, ∴ =
整理得,x2﹣x﹣1=0, 解得x1= ,x =
2
(舍去),
所以,原矩形的长是
否相似的 定义
两个边数相同的多边形,如果各边 对应成比例,各角对应相等,就称这两 个多边形相似。
相似多边形的判定:
AB BC CD AD ∵ A ' B ' B 'C ' C ' D ' A' D '
A A ', B B ', C C ', D D '
∴四边形ABCD与四边形A′B′C′D′相似
想一想: 下列各组图形相似吗?
(1)
(2)
(3)
ቤተ መጻሕፍቲ ባይዱ
(4)
(5)
(6)
你知道吗
放大镜下的图形和 原来的图形相似吗?
放大镜下的角与原图 形中角是什么关系?
相似图形的概念ppt课件
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
(B)
(1)所有的圆都是形状相同的图形; (2)所有的正方形都是形状相同的图形; (3)所有的等腰三角形都是形状相同的图形; (4)所有的矩形都是形状相同的图形;
A、1个 B、2个 C、3个 D、4个
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
4、下列说法中正确的是 (D ) A、所有平行四边形都是相似图形 B、所有菱形都是相似图形 C、所有等腰梯形都是相似图形 D、所有全等三角形都是相似图形
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
想一想:我们刚才所见到的图形有什么相同 和不同的地方?
相似图形的性质和应用

相似图形的性质和应用一、相似图形的定义知识点:相似图形的定义相似图形是指形状相同但大小不一定相同的两个图形。
在数学中,如果两个图形的对应角度相等,对应边成比例,则这两个图形是相似的。
二、相似图形的性质知识点:相似图形的性质1.对应角度相等:相似图形的对应角度相等。
2.对应边成比例:相似图形的对应边成比例。
3.对应边上的高、中线、角平分线成比例:相似图形的对应边上的高、中线、角平分线成比例。
4.面积比等于相似比的平方:相似图形的面积比等于相似比的平方。
5.周长比等于相似比:相似图形的周长比等于相似比。
三、相似图形的应用知识点:相似图形的应用1.图形放大与缩小:通过相似变换,可以将一个图形放大或缩小到所需的大小。
2.测量未知长度或角度:在实际问题中,可以通过相似图形的性质来测量未知的长度或角度。
3.计算面积和体积:在已知相似图形比例的情况下,可以通过相似图形的性质来计算未知图形的面积或体积。
4.解决实际问题:在实际生活中,相似图形可以用来解决诸如建筑设计、机械制造、生物学研究等领域的问题。
四、相似图形的判定知识点:相似图形的判定1.AA相似定理:如果两个三角形的两个角分别相等,则这两个三角形相似。
2.SAS相似定理:如果两个三角形的两边及其夹角分别相等,则这两个三角形相似。
3.RHS相似定理:如果两个直角三角形的斜边及一个锐角分别相等,则这两个直角三角形相似。
五、相似图形在几何学习中的应用知识点:相似图形在几何学习中的应用1.证明:在几何证明中,相似图形可以用来证明图形的性质或定理。
2.计算:在几何计算中,相似图形可以简化计算过程,降低解题难度。
3.转换:在解决几何问题时,可以通过相似图形将复杂问题转换为简单问题,便于解答。
4.拓展:相似图形的学习可以拓展到其他学科领域,如物理学、工程学等。
知识点:总结相似图形是数学中的重要概念,掌握相似图形的性质和应用对于中小学生的数学学习具有重要意义。
通过学习相似图形,学生可以更好地理解图形的变换、解决实际问题,并为后续学习更高级的数学知识打下基础。
相似图形

放大镜下的图形和 原来的图形相似吗?
放大镜下的角与原图 形中角是什么关系?
想一想: 放大镜下的图形和原来的图形相似吗?
(1)
(2)
(3)
你看到过哈哈镜吗?哈哈镜中的形 象与你本人相似吗?
(A)
(B)
(C)
试一试
“行家”看门道!
观察下列图形,哪些是相似形?
?
⑴ ⑵ ⑶ ⑷ ⑸ ⑹ (7) (8) (9)
对应边成比例,但对应角不相等,两个图 形不是相似图形
基础训练
口答: (2)如图,正方形的边长a=10,矩形的 宽b=5,长a=10,它们相似吗?请说明 理由.
对应角相等,但对应边不成比例,两个图 形不是相似图形
如何判断两个多边形是否为相似多边形
• 1,两个多边形的边数必须相同 • 2,各对应边必须成比例 • 3,各对应角必须相等 • 三个条件同时满足时,两个多边形 为相似多边形
做一做
图23.2.1是某个城市的大小不同的两张地图,当然,它 们是相似的图形.设在大地图中有A、B、C三地,在小地 图中的相应三地记为A′、B′、C′,试用刻度尺量一量两张 地图中A(A′)与B(B′)两地之间的图上距离、B(B′) 与C(C′)两地之间的图上距离.
2 5 •AB=_____cm , BC=______cm ; 1 .4 3 .5 •A′B′=______cm , B′C′=______cm . •显然两张地图中AB和A′B′、BC和B′C′的长度都是不相 等的,那么它们之间有什么关系呢?小地图是由大地图 缩小得来的,我们能感到线段A′B′、B′C′与AB、BC的 长度相比都“同样程度”地缩小了.
§23.2 相似图形
• 通过具体实例认识相似图形. • 理解掌握相似图形的性质和判定,并会应 用其解决问题.
相似图形的定义-完整版PPT课件

O O
图中每幅图中的两个多边形不仅相似,而且对应顶点 的连线相交于一点,对应边互相平行,像这样的两个 图形叫做位似图形, 这个点叫做位似中心.
相似图形的定义
利用位似,可以将一个图形放大或缩小. 例如,要把四边形ABCD缩小到原来的1/2, 1. 在四边形外任选一点O(如图),
2. 分别在线段OA、OB、OC、OD上取点A'、B'、C'、D', 使得 OA' OB' OC' OD' 1
分别画出这时得到的图形.
C' B'
O
D'
A'
A B
C
D
A
A
D
B
B
ODCFra bibliotekCOA OB OC OD 2
3. 顺次连接点A'、B'、C'、D',所得四边形A'B'C'D'就是所要求的图形.
A
B
D
A'
B'
D' C
C' O
相似图形的定义
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在 OA、OB、OC、OD的反向延长线上取A' ,B' 、C' 、D' ,使得
OA' OB' OC' OD'呢 ?1 如果点O取在四边形ABCD内部呢? OA OB OC OD 2
相似图形知识点典型例题

相似图形知识点典型例题TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】第四章 相似图形 一、知识要点 1、成比例线段:若线段a ,b ,c ,d 满足d c b a =,则a ,b ,c ,d 称为成比例线段. 2、比例的性质:(1) dc b a = ab cd =(互逆的时候是否需要条件?) (2)d c b a = dd c b b a ±=± (3)n m d c b a === ba n db mc a =++++++ (0≠+++nd b ) 3、黄金分割:点C 把线段AB 分成两条线段AC 和BC ,如果ACBC AB AC =,那么线段AB 被点C 黄金分割,点C 叫线段AB 的黄金分割点,AC 与AB 的比叫做黄金比.AC :AB =1:618.01:215≈- 4、相似多边形:如果两个多边形的角对应相等,边对应成比例,那么这个多边形叫做相似多边形.对应边的比叫做相似比.5、相似三角形的判定:(1)两个角对应相等的两个三角形相似;(2)两边对应成比例且夹角相等的两个三角形相似;(3)三边对应成比例的两个三角形相似.6、相似三角形的性质:(1)相似三角形的对应角相等,对应边成比例;(2)相似三角形的对应高的比、对应角平分线的比、对应中线的比都等于相似比;(3)相似三角形的周长比等于相似比,面积的比等于相似比的平方.7、位似图形:如果两个图形不仅是相似图形,而且每组对应点所在直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.8、位似图形的性质:位似图形上任意一对对应点到位似中心的距离之比等于位似比.二、典型例题: 例1 如果31==d c b a ,求b b a +,b b a -,d b c a ++,d b c a 22--.例2 以长为2cm 的定线段AB 为边,作正方形ABCD ,取AB 的中点P .在BA 的延长线上取点F ,使PF =PD .以AF 为边长作正方形AFEM .点M 落在AD 上.(如图)(1)试求AM ,DM 的长;(2)点M 是线段AD 的黄金分割点吗?请说明理由.例3 一位同学想利用树影测出树高,他在某时刻测得直立的标杆高1米,影长是0.9米,但他去测树影时,发现树影的上半部分落在墙CD 上,(如图所示)他测得BC =2.7米,CD =1.2米.你能帮他求出树高为多少米吗?例4 如图,矩形ABCD 中,E ,F 分别在BC ,AD 上,矩形ABCD ∽矩形EC DF ,且AB =2,ABCD EC 3DF S S =矩形矩形,试求ABCD S 矩形.E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009---2010八年级下第四单元相似图形整章测试题一、 填空题(每小题3分,共30分)1、(2006年宁波市)如图1,在△ABC 中,AB :DB=1:2,DE ∥BC ,若△ABC 的 面积为9,则四边形DBCE 的面积为. 2、由三角形三边中位线所围成的三角形的面积是原三角 形面积的 . 3、图2中,2224、在△ABC 中,AB >BC >AC ,D 是AC 的中点,过D 作直线l ,使截得的三角形与原三角形相似,这样的直线l 有 条.5、已知M 是线段AB 延长线上的一点,且AM :BM=7:3,那么AM :AB= .6、雨后天晴,一学生在运动场上玩耍,从他前面2m 远处的一块小积水里,他看到了旗杆顶端的倒影,如果旗杆底端到积水处的距离为40m ,该学生的眼部高度为1.5m ,那么旗杆的高为 .7、已知两个相似多边形的周长比为1:2,它们的面积和为25,则这两个多边形的面积分别是 和 .8、如图3,已知在等腰直角三角形ABC 中,∠A=90°,四边形EFDH 为内接正方形,则AE :AB= .9、如果点C 是线段AB 靠近B 的黄金分割点,且AC=2,那么AB= .10、如图4,将矩形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上F 点处,已知CE=3cm , AB=8cm ,则图中阴影部分面积为 cm 2. 二、 选择题(每小题4分,共40分)11、(2006年,大连市)如图5,点A 、B 、C 、D 、E 、F 、G 、H 、K 都是7×8方格纸上的格点,为使△DEM ∽△ABC ,则点M 应是F 、G 、H 、K 四点中的( ) A 、F B 、G C 、H D 、K12、已知△ABC ∽△DEF ,AB :DE=1:2,则△ABC 与△DEF 的周长比等于( ) A 、1:2 B 、1:4 C 、2:1 D 、4:113、(2006年天津)如图6,AB ∥CD ,AE ∥FD ,AE 、FD 分别交BC 于点G 、H ,则图中共有相似三角形ABCDE 图x30°) (105图2AB CDFEH图3A BCFED 图4DEA BCDEGHF 图6( )A 、4对 B 、5对 C 、6对 D 、7对14、已知4a =5b =6c ,且a-b+c=10,则a+b-c 的值为( )A 、6 B 、5 C 、4 D 、315、两个相似五边形,一组对应边的长分别为3cm 和4.5cm ,如果它们的面积之和是78cm 2,则较大的五边形面积是( )cm 2.A 、44.8 B 、52 C 、54 D 、4216、如图7所示,它是小孔成像的原理,根据图中尺寸(AB ∥CD),如果已知物体AB=30,则CD 的长应是( )A 、15 B 、30 C 、20 D 、1017、有同一三角形地块的甲、乙两地图,比例尺分别为1:100和1:500,那么甲地图与乙地图表示这一地块的三角形的面积之比是( )A 、25:1 B 、5:1 C 、1:25 D 、1:518、如图8,在等边△ABC 中,P 为BC 上一点,D 为AC 上一点,且∠APD=60°,BP=1,CD=32,则△ABC 的边长是( )A 、3 B 、4 C 、5 D 、619、一个钢筋三角架三边长分别为20cm 、50cm 、60cm ,现要再做一个与其相似的钢筋三角架,而只有长为30cm 和50cm 的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( )种A 、一 B 、二 C 、三 D 、四20、如图9,在正方形ABCD 中,点E 、F 分别在边BC 、CD 上,如果AE=4,EF=3,AF=5,那么正方形ABCD 的面积等于( ) A 、16225 B 、15256 C 、17256 D 、16289三、 解答题(每小题7分,共35分) 21、(1)若b a =dc ,判断代数式cd ab c a ++22-22d b cd ab +++1值的符号(2)若c b a +=a c b +=b a c +,求abc a c c b b a ))()((+++的值.22、已知四边形ABCD 与四边形A ′B ′C ′D ′相似,且AB :BC :CD :DA=20:15:9:8,四边形A ′B ′C ′D ′的周长为26,求四边形A ′B ′C ′D ′各边的长.ABCDO图7ABCD P) 60° 图8ECF D图123623、如图10,为了测量一棵树AB的高度,测量者在D点立一高CD等于2m的标杆,现测量者从E处可以看到标杆顶点C与树顶A在同一条直线上,如果测得BD=20m,FD=4m,EF=1.8m,求树高.24、如11图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且∠BFE=∠C(1)求证:△ABF∽△EAD (2)若AB=4,ABCD=3316,求AE的长(3)在(1)、(2)条件下,若AD=3,求BF的长(计算结果可含根号)25、如图12,△ABC中,∠BAC=90°,AB=AC=1,点D是BC上一个动点(不与B、C重合),在AC 上取E点,使∠ADE=45°(1)求证:△ABD∽△DCE(2)设BD=x,AE=y,求y与x的函数关系式四、拓广探索题(共15分)26、(7分)已知,如图13,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC交于点E,EF⊥BD,垂足为F,我们可以证明AB1+CD1=EF1成立,若将图13中的垂直改为斜交,如图14,AB∥CD,AB与BC交ABCDEF图△△CE图AB CDE图于点E ,过点E 作EF ∥AB 交BD 于F ,则(1)AB 1+CD 1=EF1还成立吗?如果成立,给出证明;如果不成立,请说明理由. (2) 请找出S △ABC ,S △BED 和S △BDC 间的关系,并给出证明.27、(8分)若矩形的一个短边与长边的比值为215-,(黄金分割数),我们把这样的矩形叫做黄金矩形(1) 操作:请你在如图15所示的黄金矩形ABCD (AB >AD )中,以短边AD 为一边作正方形AEFD . (2) 探究:在(1)中的四边形EBCF 是不是黄金矩形?若是,请予以证明;若不是,请说明理由. (3) 归纳:通过上述操作及探究,请概括出具体有一般性的结论(不需证明)28、如图1,四边形ABCD 是正方形,G 是CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边在正方形ABCD 外作正方形CEFG ,连结BG ,DE .我们探究下列图中线段BG 、线段DE 的长度关系及所在直线的位置关系: (1)①猜想如图1中线段BG 、线段DE 的长度关系及所在直线的位置关系;②将图1中的正方形CEFG 绕着点C 按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.ABCDEF图13ABC DE F图14ABC图15(2)将原题中正方形改为矩形(如图4—6),且AB=a ,BC=b ,CE=ka , CG=kb (a ≠b ,k >0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.(3)在第(2)题图5中,连结DG 、BE ,且a =3,b =2,k =12,求22BE DG +的值.29、如图Ⅰ,△ABC 是边长为4的等边三角形,点D 在BC 上,沿直线AD 将△ABC 剪开,将△ABD 的边AB 与AC 重合,拼在△ACE 位置得四边形ADCE (如图Ⅱ),连结DE 交AC 于F .⑴你还能拼出哪些与图Ⅱ所示的不一样的四边形?试画出示意图进行说明.⑵在图Ⅱ中,当BD 长为1时,求AD 的长. ⑶在图Ⅱ中,设BD=x ,CF=y ,求y 与x 的关系.图Ⅰ 图Ⅱ相似图形整章测试题参考答案一、填空题 1~10 841 2 4 7:4 30 5,20 311+5 30 提示:4、如图1,过D 分别作BC 、AB 的平分线有两条,另外,作∠ADE=∠ABC 又一条,作∠CDF=∠ABC 又一条,共4条8、AB AE =BC EH =DC FD BF EH ++=EH EH 3=319、∵AB AC =AC BC =2BC ,又∵AB AC =215- ∴2BC =215- ∴BC=5-1 ∴AB=2+5-1=1+5 10、如题图:EF=DE=8-3=5 ∵EC=3,∴FC=4,易证△ABF ∽△EFC ∴BF :3=8:4 BF=6 ∴S 阴影=21·6·8+21·4·3=30 二、选择题11~20 CACAC DAABC提示:18、∵△ABC 为等边三角形 ∴∠B=∠C=60°,又∠APD=60°∴∠BAP+∠APB=∠APB+∠CPD=120°,∴∠BAP=∠DPC ,∴△APB ∽△PCD ∴32:1=(AB-1):AB ∴AB=3 20、∵AE 2+EF 2=42+32=52=AF 2∴∠AEF=90°,∴易证△ABE ∽△EFC ∴AB :EC=4:3 设AB=x x :(=4:3 ∴x 2=17256三、解答题 21、解:(1)设b a =dc =k ,则a=bk ,c=dk ,代入,得,求值式=kd k b k d k b 222222++-2222d b kd k b +++1=k-k+1=1>0,故所求式的符号为正 A B C DE F 图1(2)当a+b+c ≠0时,因为abc ≠0,所以由等比性质得:c b a c b a ++++)(2=c b a +=ac b +=b ac +所以a+b=2c ,b+c=2a ,c+a=2b ,代入得,求式=abcba c 222⨯⨯=8当a+b+c=0,a+b=--c ,b+c=-a ,c+a=-b ,代入所求式=abcb ac ))((---=-122、解:∵四边形ABCD 与四边形A ′B ′C ′D ′相似,且AB :BC :CD :DA=20:15:9:8,∴A ′B ′:B ′C ′:C ′D ′:D ′A ′=20:15:9:8设A ′B ′=20x ,B ′C ′=15x ,C ′D ′=9x ,D ′A ′=8x ,由四边形A ′B ′C ′D ′的周长为26,得20x+15x+9x+8x=26,解得x=21 ∴A ′B ′=10,B ′C ′=7.5,C ′D ′=4.5,D ′A ′=423、解:如图2,过E 作EN ⊥AB ,交AB 于N 点交CD 于M 点,由题意知,MN=BD=20,EM=FD=4,MB=MD=EF=1.8,则CM=0.2 由CM ∥AN ,得△ECM ∽△EAN ∴CM :AN=EM :EN∴AN=CM EN EM ⨯=1.2∴AB=AN+NB=1.2+1.8=3 所以树高为3m 24、证明:(1)∵四边形ABCD 为平行四边形,∴∠BAF=∠AED∠C+∠D=180°,∴∠C=∠BFE ,∠BFE+∠BFA=180°,∴∠D=∠BFA ∴△ABF ∽△EAD (2)解:∵=3316,∴AB ·BE=3316,∵AB=4 ∴BE=334 ∴AE 2=AB 2+BE 2=42+(334)2 AE=338 (3)解:由(1)有EA AB =AD BF ,又AD=3,∴BF=EA AD AB ⨯=4×3×383=233 25、(1)证明:∵∠BAC=90°,AB=AC ,∴∠B=∠C=45°∴∠ADB+∠DAB=135°,∵∠ADE=45°,∴∠ADB+∠EDC=135° ∴∠DAB=∠EDC ,∴△ABD ∽△DCE (2)解:∵△ABD ∽△DCE ,∴CD AB =CEBD∴AB=AC=1,∠BAC=90°, ∴BC=2,CD=2-x , ∴x -21=CEx∴CE=2x-x 2ABCD E F 图2△ △MN∴AE=AC-CE=1-(2x-x 2)=x 2-2x+1 即y=x 2-2x+1(0<x <2) 四、拓广探索题 26、(1)解:成立,证明如下由AB ∥EF ∥CD 得,AB EF =DB DF ,CD EF =DBBF两式相加,得AB EF +CD EF =DB DF +DB BF =DB BF DF +=DBDB=1∴EF ·CD+EF ·AB=AB ·CD ,两边同除以AB ·CD ·EF 得AB 1+CD 1=EF1(2)解:BDAS ∆1+BDCS ∆1=BDES ∆1证明如下:作AG ⊥BD 于G ,EH ⊥BD 于H ,CK ⊥BD 交BD 延长线于k ,由平行线性质得:AG EH =DA DE =DB DF ,CK EH =BC BE =BDBF所以AG EH +CKEH =1,∴AG BD ⨯211+CK BD ⨯211=EH BD ⨯211∴ABDS ∆1+BDCS ∆1=BDES ∆127、解(1)以AD 为边可作出两个正方形AEFD 与AE ′F ′D ′(AB >AD ),如图4所示(2)矩形EBCF 不是黄金矩形,理由如下:设AB=a ,AD=b (a >b ),则BE=BA+AE=a+b ,BE ′=BA-E ′A=a-b , 由ABCD 为黄金矩形,得a b =215- ∴BE BC =b a b +=a b ÷(1+a b )=215-÷(1+215-)=253-≠215- ∴矩形EBCF 不是黄金矩形 矩形E ′BCF ′是黄金矩形ABGEF H DCK图3A B CD E E ’ 图4证明:如图4,∵BC B E '=b b a -=(1-a b )÷a b =(1-215-)÷215-=215- ∴E ′BCF ′是黄金矩形(3)由(1)、(2)可发现结论:若以黄金矩形的短边为边在矩形内作(截割)正方形,则剩余矩形必为黄金矩形.。
