8 3 毕奥 萨伐尔定律概述
合集下载
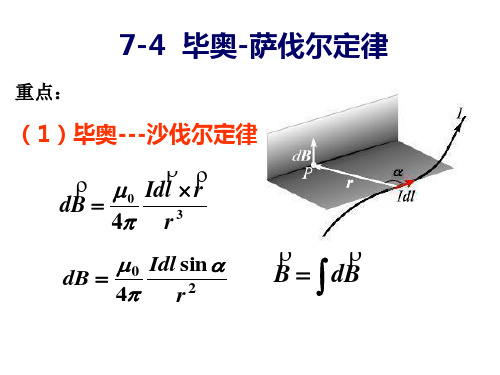
毕奥---萨伐尔定律

毕奥---萨伐尔定律 毕奥 萨伐尔定律
两电流元之间的安培定律也可表示成 两电流元之间的安培定律也可表示成
u r r uur u r ˆ I1 I 2 dl2 × (dl1 × r12 ) d F12 = k = I 2 dl2 × dB1 2 r 12
电流元 I1d l1产生的磁场
ˆ ˆ Idl × r µ0 Idl × r dB = k = 2 2 r 4π r
• 求二阶导数
d 2B 在O 令x = 0处的 2 = 0 ⇒ 在O点附近磁场最均匀的条件 dx µ0 d 2B 2a 2 − 2 R 2 = 6π R 2 I = 0 ⇒ a2 = R2 7 2 dx 2 x =0 4π 2 a 2 2 R + 4
a=R
例1、无限长载流直导线弯成如图形状
大小
µ0 Idl dB = 4π r2
r r 方向 Idl × r0
分析对称性、 分析对称性、写出分量式
r r B⊥ = ∫ dB = 0
⊥
µ0 Idl sinα Bx = ∫ dBx = ∫ 4π r2
统一积分变量
µ0 Idl sinα Bx = ∫ dBx = ∫ 4π r2 µ0IR µ0IR dl = π = ⋅2 R 3 ∫ 3 4 r 4 r π π
a
•
•
P T
µ0I 3 BL′A = (cos π − cosπ ) 4πa 4
µ0I π BLA = (cos0 − cos ) 方向 ⊗ 4 a 4 π
方向 ⊗
T点
Bp = BLA + BL′A = 2.94×10−5T 方向 ⊗
r 电流元 Idl
——右手定则 右手定则 r r r µ0 Idl ×r 毕奥-萨伐尔定律 毕奥 萨伐尔定律 dB = 4 π r3 r r r r µ0 Idl ×r 对一段载流导线 B = ∫ dB = ∫ 4π L r3
两电流元之间的安培定律也可表示成 两电流元之间的安培定律也可表示成
u r r uur u r ˆ I1 I 2 dl2 × (dl1 × r12 ) d F12 = k = I 2 dl2 × dB1 2 r 12
电流元 I1d l1产生的磁场
ˆ ˆ Idl × r µ0 Idl × r dB = k = 2 2 r 4π r
• 求二阶导数
d 2B 在O 令x = 0处的 2 = 0 ⇒ 在O点附近磁场最均匀的条件 dx µ0 d 2B 2a 2 − 2 R 2 = 6π R 2 I = 0 ⇒ a2 = R2 7 2 dx 2 x =0 4π 2 a 2 2 R + 4
a=R
例1、无限长载流直导线弯成如图形状
大小
µ0 Idl dB = 4π r2
r r 方向 Idl × r0
分析对称性、 分析对称性、写出分量式
r r B⊥ = ∫ dB = 0
⊥
µ0 Idl sinα Bx = ∫ dBx = ∫ 4π r2
统一积分变量
µ0 Idl sinα Bx = ∫ dBx = ∫ 4π r2 µ0IR µ0IR dl = π = ⋅2 R 3 ∫ 3 4 r 4 r π π
a
•
•
P T
µ0I 3 BL′A = (cos π − cosπ ) 4πa 4
µ0I π BLA = (cos0 − cos ) 方向 ⊗ 4 a 4 π
方向 ⊗
T点
Bp = BLA + BL′A = 2.94×10−5T 方向 ⊗
r 电流元 Idl
——右手定则 右手定则 r r r µ0 Idl ×r 毕奥-萨伐尔定律 毕奥 萨伐尔定律 dB = 4 π r3 r r r r µ0 Idl ×r 对一段载流导线 B = ∫ dB = ∫ 4π L r3
毕奥萨伐尔定律介绍课件

定律的物理意义
物理意义
毕奥-萨伐尔定律揭示了电流在空间 中产生磁场的基本规律,对于电磁场 理论的发展和应用具有重要意义。
应用举例
在电磁学、电机学、变压器、电磁铁 等领域中,毕奥-萨伐尔定律被广泛应 用于分析和计算磁场分布。
Part
02
毕奥萨伐尔定律的推导
毕奥萨伐尔的生平与贡献
毕奥出生于1774年,是 法国物理学家和数学家。
在物理学中的应用
01
02
03
描述磁场分布
毕奥-萨伐尔定律可以用来 描述磁场在空间中的分布 ,特别是在电流和磁铁附 近产生的磁场。
计算磁场力
根据毕奥-萨伐尔定律,可 以计算磁场对电流和磁铁 的作用力,即洛伦兹力和 安培力。
解决电磁问题
在解决电磁学问题时,毕 奥-萨伐尔定律常与其他电 磁学定律一起使用,以完 整地描述电磁场的行为。
毕奥萨伐尔定律介绍 课件
• 毕奥萨伐尔定律概述 • 毕奥萨伐尔定律的推导 • 毕奥萨伐尔定律的应用 • 毕奥萨伐尔定律的实验验证 • 毕奥萨伐尔定律的扩展与展望
目录
Part
01
毕奥萨伐尔定律概述
定义与公式
定义
毕奥-萨伐尔定律描述了电流在空间中产生的磁场分布,特别是电流元在空间中产生的磁 场。
公式
毕奥和萨伐尔通过实验观 测到电流在空间中产生磁 场的现象。
毕奥萨伐尔定律的数学表达形式
毕奥萨伐尔定律可以用数学公式 表示,描述了电流产生的磁场的
大小和方向。
这个定律在电磁学中非常重要, 是研究电磁场和电磁力的基础。
通过应用毕奥萨伐尔定律,可以 解决许多与电流和磁场相关的问
题。
Part
03
毕奥萨伐尔定律的应用
毕奥-萨伐尔定律

结果对比
将实验结果与毕奥-萨伐尔定律的理论值进行对比,评估定律的准确性。
结果分析
分析实验误差来源,如设备精度、环境干扰等,提高实验的可靠性和准确性。
05
毕奥-萨伐尔定律的扩展与 推广
对三维空间的推广
总结词
毕奥-萨伐尔定律最初是在二维空间中 推导出来的,但通过引入矢量运算, 该定律可以扩展到三维空间中。
Idl
电流元,表示电流的一 部分。
r
观察点到电流元的径矢 ,表示观察点与电流元
之间的距离。
03
毕奥-萨伐尔定律的应用场 景
电场与磁场的关系
磁场是由电流产生的,而电场是由电 荷产生的。毕奥-萨伐尔定律描述了 电流和磁偶极子产生的磁场,以及变 化的电场产生的磁场。
毕奥-萨伐尔定律揭示了电场和磁场之 间的相互关系,表明它们是电磁场的 两个方面,而不是独立存在的。
THANKS
对微观尺度的适用性问题
毕奥-萨伐尔定律在描述微观尺度的电磁场时,其精确度受 到限制。在量子尺度下,电磁场的涨落和量子效应可能导 致定律的不适用。
未来研究需要进一步探索毕奥-萨伐尔定律在微观尺度下 的适用性和修正,以更好地描述量子电磁场的行为。
对超导态物质的适用性问题
毕奥-萨伐尔定律在描述超导态物质的 电磁场时,可能存在局限性。超导态 物质的电磁行为与常规物质有所不同, 需要更复杂的理论模型来描述。
电流与磁场的相互作用
根据毕奥-萨伐尔定律,电流产生磁场,而磁场对电流有作用 力。这种作用力被称为洛伦兹力,它描述了电流在磁场中所 受到的力。
毕奥-萨伐尔定律是电动机和发电机等电气设备工作的基础, 它解释了电流如何在磁场中受到作用力,从而产生旋转或线 性运动。
磁力线的描绘
将实验结果与毕奥-萨伐尔定律的理论值进行对比,评估定律的准确性。
结果分析
分析实验误差来源,如设备精度、环境干扰等,提高实验的可靠性和准确性。
05
毕奥-萨伐尔定律的扩展与 推广
对三维空间的推广
总结词
毕奥-萨伐尔定律最初是在二维空间中 推导出来的,但通过引入矢量运算, 该定律可以扩展到三维空间中。
Idl
电流元,表示电流的一 部分。
r
观察点到电流元的径矢 ,表示观察点与电流元
之间的距离。
03
毕奥-萨伐尔定律的应用场 景
电场与磁场的关系
磁场是由电流产生的,而电场是由电 荷产生的。毕奥-萨伐尔定律描述了 电流和磁偶极子产生的磁场,以及变 化的电场产生的磁场。
毕奥-萨伐尔定律揭示了电场和磁场之 间的相互关系,表明它们是电磁场的 两个方面,而不是独立存在的。
THANKS
对微观尺度的适用性问题
毕奥-萨伐尔定律在描述微观尺度的电磁场时,其精确度受 到限制。在量子尺度下,电磁场的涨落和量子效应可能导 致定律的不适用。
未来研究需要进一步探索毕奥-萨伐尔定律在微观尺度下 的适用性和修正,以更好地描述量子电磁场的行为。
对超导态物质的适用性问题
毕奥-萨伐尔定律在描述超导态物质的 电磁场时,可能存在局限性。超导态 物质的电磁行为与常规物质有所不同, 需要更复杂的理论模型来描述。
电流与磁场的相互作用
根据毕奥-萨伐尔定律,电流产生磁场,而磁场对电流有作用 力。这种作用力被称为洛伦兹力,它描述了电流在磁场中所 受到的力。
毕奥-萨伐尔定律是电动机和发电机等电气设备工作的基础, 它解释了电流如何在磁场中受到作用力,从而产生旋转或线 性运动。
磁力线的描绘
毕奥-萨伐尔定律 磁通量 磁场的高斯定理
0 Idz sin B dB 4 r2
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
毕奥-萨伐尔定律

例1 载流长直导线的磁场.
dB 方向均沿
z
D
2
dz
r
r0
Iz1源自 dB* y Pr2 0 Idz sin B dB CD r 2 4π
解 dB
x 轴的负方向 0 Idz sin
4π
x
C
o
z r0 cot , r r0 / sin 2 dz r0d / sin 0 I 2 B 1 sin d 4π r0
4π r
2
dq 2π rdr
v r
dr
dB B
0
2
R
dr
0
2
0
dr
0 R
2
小 • 磁场
电 流 运动电荷 磁 铁
结
磁 场
电
流
运动电荷 磁 铁
0 Idl r • 毕奥-萨伐尔定律 dB 4 r 3 o I o qv r B (cos 1 cos 2 ) B 4ro 3
Pm
en
I S
说明:只有当圆形电流的面积S很小,或场点距 圆电流很远时,才能把圆电流叫做磁偶极子.
例3 载流直螺线管的磁场 如图所示,有一长为l , 半径为R的载流密绕直螺 线管,螺线管的总匝数为N,通有电流I. 设把螺线管 放在真空中,求管内轴线上一点处的磁感强度.
R
o * p
dx
x
x
++ ++++ ++ +++ ++ +
解 由圆形电流磁场公式
B
0 IR
毕奥萨伐尔定律

电磁炉具有加热速度快、热效率高、安全可靠等优点,广泛 应用于家庭和餐饮行业。
磁力发电机
磁力发电机是一种利用磁场产生电能的装置。根据毕奥萨 伐尔定律,当导体在磁场中运动时,会在导体中产生感应 电流。磁力发电机通过转子产生的旋转磁场与定子绕组相 对运动,使定子绕组中产生感应电流,实现发电的目的。
磁力发电机广泛应用于风力发电、水力发电、汽车发动机 等领域,为可再生能源的开发和节能减排做出了重要贡献 。
06
毕奥萨伐尔定律的未来研 究与展望
磁场产生的原因与机制
磁场产生的原因
毕奥-萨伐尔定律指出,运动电荷或电流会产生磁场,这是磁场产生的根本原因。
磁场产生的机制
磁场的产生与电荷或电流的运动有关,当电荷或电流运动时,会激发周围的磁场 ,磁场的大小和方向与电荷或电流的运动状态有关。
磁场对物质的作用与影响
核磁共振成像等磁现象在医疗领域具有广泛的应用前景,同时磁 约束核聚变等前沿技术也在积极探索中。
磁现象在太阳能领域的应用
太阳能电池板在吸收太阳能时,利用磁性原理可以提高太阳能利 用率。
感谢您的观看
THANKS
磁场强度的方向与单位
磁场强度的方向
在右手螺旋定则中,拇指指向电流的方向 ,四指环绕的方向就是磁场的方向。
VS
磁场强度的单位
安培/米(A/m),国际单位制中,磁场强度 的单位是安培/米。
03
毕奥萨伐尔定律的实验验 证
实验设计思路
确定实验目标
验证毕奥萨伐尔定律在特定情况下 的适用性,即通过实验手段测量物 理量以验证理论的准确性。
总结词
描述电磁场基本规律的方程组。
详细描述
麦克斯韦方程组是描述电磁场基本规律的方程组,其 中包括了电场、磁场和电荷密度等物理量的关系。毕 奥萨伐尔定律是麦克斯韦方程组的一个推论,它描述 了磁场与电流之间的关系。此外,麦克斯韦方程组还 预言了电磁波的存在,即光、无线电波等。
磁力发电机
磁力发电机是一种利用磁场产生电能的装置。根据毕奥萨 伐尔定律,当导体在磁场中运动时,会在导体中产生感应 电流。磁力发电机通过转子产生的旋转磁场与定子绕组相 对运动,使定子绕组中产生感应电流,实现发电的目的。
磁力发电机广泛应用于风力发电、水力发电、汽车发动机 等领域,为可再生能源的开发和节能减排做出了重要贡献 。
06
毕奥萨伐尔定律的未来研 究与展望
磁场产生的原因与机制
磁场产生的原因
毕奥-萨伐尔定律指出,运动电荷或电流会产生磁场,这是磁场产生的根本原因。
磁场产生的机制
磁场的产生与电荷或电流的运动有关,当电荷或电流运动时,会激发周围的磁场 ,磁场的大小和方向与电荷或电流的运动状态有关。
磁场对物质的作用与影响
核磁共振成像等磁现象在医疗领域具有广泛的应用前景,同时磁 约束核聚变等前沿技术也在积极探索中。
磁现象在太阳能领域的应用
太阳能电池板在吸收太阳能时,利用磁性原理可以提高太阳能利 用率。
感谢您的观看
THANKS
磁场强度的方向与单位
磁场强度的方向
在右手螺旋定则中,拇指指向电流的方向 ,四指环绕的方向就是磁场的方向。
VS
磁场强度的单位
安培/米(A/m),国际单位制中,磁场强度 的单位是安培/米。
03
毕奥萨伐尔定律的实验验 证
实验设计思路
确定实验目标
验证毕奥萨伐尔定律在特定情况下 的适用性,即通过实验手段测量物 理量以验证理论的准确性。
总结词
描述电磁场基本规律的方程组。
详细描述
麦克斯韦方程组是描述电磁场基本规律的方程组,其 中包括了电场、磁场和电荷密度等物理量的关系。毕 奥萨伐尔定律是麦克斯韦方程组的一个推论,它描述 了磁场与电流之间的关系。此外,麦克斯韦方程组还 预言了电磁波的存在,即光、无线电波等。
毕奥-萨伐尔定律介绍

cos2
cos1
(1)P点位于管内轴线中点 1 π 2
cos 1 cos 2
cos 2
l/2
l / 22 R2
R
1
* P
2
x
×× ××× × ×× ××× ×× ×
18
B
0nI
cos2
0nI
2
l l 2 / 4 R2 1/2
若 l R
B 0nI
R
1
* P
2
x
×× ××× × ×× ××× ×× ×
选择进入下一节:
7-3 磁场 磁感强度 7-4 毕奥-萨伐尔定律 7-5 磁通量 磁场的高斯定理 7-6 安培环路定理 7-7 带电粒子在电场和磁场中的运动 7-8 载流导线在磁场中所受的力
28
2 π x3
B
0m
2 π x3
en
说明:m的方向与圆电流
的单位正法矢 en的方向相同.
I S
enm
m
en
I S
13
例3 载流直螺线管内部的磁场. 如图所示,有一长为l ,半径为R的载
流密绕直螺线管,螺线管的总匝数为N, 通有电流I. 设把螺线管放在真空中,求管 内轴线上一点处的磁感强度.
R
P
*
×× ××× × ×× ××× ×× ×
R
0 IR
2x3
2
,
I
B 0IS
2 π x3
10
(1)
R
B0
x
Io
推 (2)
I
R
广
o×
(3) I
R ×o
11
B0
0I
2R
B0
毕奥-萨伐尔定律

x
l 2
17
B
I0 I0
从以上分析可以看出长直载流螺线管的磁场 分布情况:在螺线管中心区域为均匀磁场,在 管端口处,磁场等于中心处的一半,在螺线管 外部距管轴中心约七个管半径处,磁场就几乎 等于零了。
18
例4. 在半径R=2cm的无限长的半圆形金属薄片中, 有电流I=6A自下而上的通过,如图求 圆柱轴线上任一点的磁感应强度。
位矢量,指向与电流的方向满足右螺旋关系。
多匝平面线圈电流I 应以线圈的总匝数与每匝
线圈的电流的乘积代替。
0 m m 0 圆电流 B n 3 3 2π x 2x
10
三 磁矩
m ISen
2
I
例2 中圆电流磁感强度 公式也可写成
S
en
m
B
0 IR
2x
3
0 IR 2
0 IR 2
a
4π a
25
例7 在玻尔的氢原子模型中,电子绕原子核运动相 当于一个圆电流,具有相应的磁矩(称为轨道磁 矩)。求轨道磁矩 与轨道角动量之间的关系。 解: 设电子的轨道半径为r,每秒转速为ν。 电流:
I e 2 磁矩: IS e πr
圆电流面积: S π r 2
4π d
R
o ( 3) I R
B0
0 I
4R
R2
*o
B0
o
0 I
8R
B0
0 I
4 R2
0 I
4 R1
0 I
4π R1
13
例3 载流直螺线管的磁场 如图所示,有一长为 l , 半径为R的载流密绕直螺 线管,螺线管的总匝数为N,通有电流 I. 设把螺线管 放在真空中,求管内轴线上一点处的磁感强度.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2?
? 0m?
(R2 ? x2 )32
m? e?n
S I
? B?
? 0IR2
2(R2 ? x2 )32
? i?
2?
? 0m?
(R2 ? x2 )32
(2)圆心处磁场 x ? 0
B0
?
?0I
2R
;
N匝:
B0
?
N? 0I
2R
(3)在远离线圈处 x ?? R, x ? r
B
?
?0 2?
IS x3
?
?0 2?
? B?0
2.载流圆线圈轴线上的磁场( I,R)
?
Idl
?
?
R
r dB
Io
?
P
x
?
解:在圆电流上取电流元 Idl
dB
?
? 0 I d lsin 90 ? 4? r 2
?
? 0Idl 4? r 2
方向如图
各电流元在
P点
? dB
大小相等,方向不同,由对称性:
? Idl
R
Io
? Idl ?
?? r dB
1820年10月:
法国物理学家毕奥和沙伐尔发表《运动的电传递给金属 的磁化力》,提出直线电流对磁针作用的实验规律。
法国数学、物理学家拉普拉斯由实验规律推出载流线段 元(电流元)磁场公式。毕奥和沙伐尔用实验验证了该 公式。
一 毕奥—萨伐尔定律 (电流元在空间产生的磁场 )
? Idl
? dB
? 电流元:Idl
? B?
? dB ?
? 0I
4π
? dl ?
r?
r3
试比较点电荷电场公式与电流元毕奥 —萨伐尔定律
? dE
?
1
4 π?0
dq ? r3
r?
? dB ?
?
4
0
π
?
I
? dl ? r3
r?
毕—萨定律:电流元产生磁场的规律 , 与点电荷电场公式作用地位等价。
二 毕奥—萨伐尔定律的应用 求解电流磁场分布基本思路:
?P
x
? dB'
z ?
dB
P
y
? B? ? dB? ? 0
? Idl
R
Io
? Idl '
? r
? dB
?P
x
? dB'
? ? B ? B// ?
dB sin?
?
2?R 0
? 0Idl 4?r 2
R r
? ?
? 0IR 4? r 3
2? R
dl ?
0
? 0 IR2
2(R2 ? x2 ) 32
方向: ? x (右螺旋法则)
B0
?
?0I
8R
(4)
(5) I
BA
?
? 0I
4π d
d *A
R1
R2
*o
B0
?
? 0I
4 R2
?
? 0I
4 R1
?
? 0I
4π R1
亥姆霍兹圈:两个完全相同的 N匝共轴密绕短线圈,其 中心间距与线圈半径 R相等,通同向平行等大电流 I。
求轴线上 o1 . o2之间任一点 P的磁场。
R
N匝
N匝
RR
同 学 们 好
§8-3 毕奥-萨伐尔定律
历史之旅:
1820 年4月: 丹麦物理学家奥斯特(1777~1851) 发现电流的磁效应。
“猛然打开了科学中一个黑暗领域的大门。” ——法拉第
历史之旅:
1820 年8月: 法国物理学家阿拉果在瑞士得到消息,并于 9月向 法国科学院介绍了奥斯特实验,引起极大反响。
讨论:
B?
? 0 nI
2
(cos
? 2 ? cos ? 1 )
将电流视为 电流元的集合
电流元磁场公式 磁场叠加原理
1.载流长直导线的磁场
已知: I , a , ?1 , ?2
求:
? B
分布
电流磁场分布
? 解:取电流元 Id l
dB ?
? 0 Id l sin ? 4? r 2
; 方向 ?
? 各电流元在 P 点 dB同向
? ? B ?
dB
?
B A
? 0Idl sin? 4?r 2
I o1 o?P? I o2 x
B1
B2
x
o o1
o2
BP ? 2 [(
? 0 NIR 2?Biblioteka R2 ?(R?
x
)2
3
]2
2
? 0 NIR 2
2 [(
R2
?
(R
?
x
)2
3
]2
2
B0
?
0.72 ?
0 NI R
实验室用近似
B01
?
B02
?
0.68 ?
0NI R
均匀磁场
3.载流直螺线管内部的磁场
设螺线管的半径为 R,电流为 I ,每单位长度有 线圈 n 匝。
?1 r ?
R
? d l ? ? R csc2 ? d ? A1
?2
p?
dB
A2
又? R2 ? l 2 ? R2 csc2 ?
B
?
?L
? 0R2nI d l
2(R 2 ? l 2 )3 / 2
l dl
? ? ? 0 nI ? 2 ?? sin ? ?d ?
2
?1
?
?0
2
nI (cos ? 2
?
cos ?1)
轴线上
? B
?
? 0 IR2
2( R2 ? x 2 ) 32
? i
讨论: (1) 定义电流的磁矩
m? ? IS e?n
S : 电流所包围的面积
规定正法线方向: n?与 I指向成右旋关系 圆电流磁矩: m? ? I? R 2 e?n
圆电流轴线上磁场:
? B?
? 0IR2
2(R2 ? x2 )32
? i?
统一变量:
l ? ? actg?
dl
?
ad? sin 2?
r? a
sin?
lI
B ?2
?
dB
oa ?
P
? ? r?
I dl
?1
A
? B ? ? 0 I ? 2 sin ? d?
4? a ? 1
?
? 0I 4? a
(cos
?
1
?
cos ? 2 )
方向
?
B?
? 0I 4? a
(cos ?
1
?
cos ?
? r?
I
dB
dB ?
k
I
d
l sin r2
?
dB
?
?0
4π
Idl sin?
r2
P *r?
??
Idl
真空磁导率 ?0 ? 4π?10?7 N?A?2
方向
? dB ?
?0
4π
? Idl ?
r?
r3
? Idl
? dB
? r?
I
dB
P * r?
??
Idl
? ? 任意载流导线在点
磁感强度叠加原理
P
处的磁感应强度
?1 r ?
A1
?2
p
?
dB
R
A2
l dl
由于每匝可作平面线圈处理, ndl匝线圈可作
In dl的一个圆电流,在 P点产生的磁感应强度:
dB
?
? 0R2nI d l
2(R2 ? l 2 )3 / 2
B
?
?L dB
?
?L
? 0R2nI d l
2(R2 ? l 2 )3 /
2
? l ? R cot ?
2
)
方向
?
讨论:
B
?
?0I 4? a
(cos
?
1
?
cos ? 2 )
(1)无限长直电流: ? 1 ? 0 , ? 2 ? ?
I
I
B ? ? 0I
? B
2? a
内密外疏
(2)导线半无限长,场点与一端的连线垂
直于导线
B ? ? 0I 4? a
(3)直导线及其延长线上点
? ? ? 0 或 ? , dB ? 0
IS r3
? B?
?0 2?
m? r3
(4)画 B? x曲线
? B?
? IR2 0
2( R 2
?
x )2
3 2
? i
练习: Bo ? ?
I
R
o
B0
?
?0I
8R
?
B
o
x
R
I
o
B0
?
3? 0I
8R
?
? 0I 4? R
?
(1) I
R o
? B0
x
B0
?
? 0I
2R
(2 ) I R
o
B0
?
? 0I
4R
(3) I R o
