2011年揭阳市高中毕业班高考第一次模拟考数学 (理科)
广东省揭阳一中2011-2012学年高二下学期第一次段考题数学理
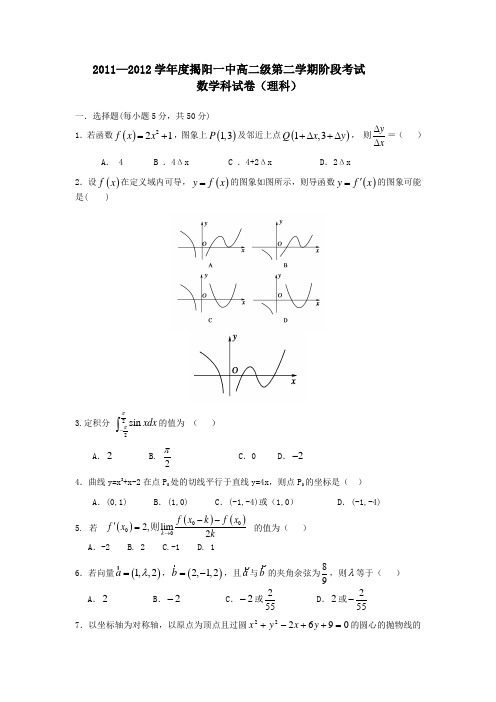
2011—2012学年度揭阳一中高二级第二学期阶段考试数学科试卷(理科)一.选择题(每小题5分,共50分)1.若函数()221f x x =+,图象上()1,3P 及邻近上点()1,3Q x y +∆+∆,则yx∆∆=( ) A . 4 B .4Δx C .4+2Δx D .2Δx2.设()f x 在定义域内可导,()y f x =的图象如图所示,则导函数()y f x '=的图象可能是( )3.定积分22sin xdx ππ-⎰的值为 ( )A .2 B.2πC .0D .2- 4.曲线y=x 3+x-2在点P 0处的切线平行于直线y=4x ,则点P 0的坐标是( ) A .(0,1) B .(1,0) C .(-1,-4)或(1,0) D .(-1,-4)5.若 的值为( ) A .-2 B. 2 C.-1 D. 16.若向量()1,,2a λ=,()2,1,2b =-,且a 与b 的夹角余弦为98,则λ等于( )A .2B .2-C .2-或552D .2或552-7.以坐标轴为对称轴,以原点为顶点且过圆096222=++-+y x y x 的圆心的抛物线的()()()0002,lim 2k f x k f x f x k→--'=则方程是( )A .23x y =或23x y -= B .23x y =C .x y 92-=或23x y = D .23x y -=或x y 92=8.已知函数()f x 的定义域为(),-∞+∞,()f x '为()f x 的导函数,函数()y f x '=的图象如图所示,且(2)1f -=,(3)1f =,则不等式2(6)1f x >-的解集为( )A .()2,3(32)-,-B.(C .()2,3D.((),2,-∞+∞二.填空题(每小题5分,共20分)9.函数sin ()xf x x=的导函数为_________. 10.设若0lg ,0,()8,0,ax x f x x tdt x >⎧⎪=⎨+≤⎪⎩⎰((1))1f f =,则a =_________. 11.函数xe x xf )3()(-=的单调递增区间是_________.12.从如图所示的长方形区域内任取一个点(),M x y ,则点M 取自图中非阴影部分的概率为_________.13.设双曲线22221x y a b-=(0a <,0b >)的渐近线与抛物线21y x =+相切,则该双曲线的离心率等于_________. 14.已知函数()sin cos 4f x f x x π⎛⎫'=+⎪⎝⎭,则()4f π=_________. 三.解答题:(本大题共6小题,共80分)15.(本小题满分12分)已知函数x x x f 3)(3-=,过点)6,2(-P 作曲线)(x f y =的切线的方程,求切线方程.16.(本小题满分12分)已知函数()()211ln 2f x x ax a x =-+-,其中1a >,讨论函数()f x 的单调性.17. (本小题满分14分)某公司决定采用增加广告投入和技术改造投入两项措施来获得更大的收益.通过对市场的预测,当对两项投入都不大于3(百万元)时,每投入x (百万元)广告费,增加的销售额可近似的用函数21214y x x =-+(百万元)来计算;每投入x (百万元)技术改造费用,增加的销售额可近似的用函数3221253y x x x =-++(百万元)来计算.现该公司准备共投入3(百万元),分别用于广告投入和技术改造投入,请设计一种资金分配方案,使得该公司的销售额最大. (参考数据:2≈1.41,3≈1.73)18.(本小题满分14分)已知函数bx ax x x f ++=23)(在1x =处有极值2-. (1)求常数a 、b ;(2)求曲线()y f x =与x 轴所包围的面积。
广东省揭阳市高三数学第一次模拟考试试题 理

揭阳市2017年高中毕业班高考第一次模拟考试数学(理科)本试卷共4页,满分150分.考试用时120分钟.注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮搽干净后,再选涂其他答案标号,写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卡上,答在本试题上无效.4.考试结束,将本试题和答题卡一并交回.第Ⅰ卷一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.(1)已知集合}2,1,0,1{-=A ,集合={|23,}B y y x x A =-∈,则AB =(A ){1,0,1}- (B ){1,1}-(C ){1,1,2}-(D ){0,1,2}(2)已知复数1234,z i z t i =+=-,且21z z ⋅是实数,则实数t =(A )43 (B )34 (C )43- (D )34- (3)若(cos 20,sin 20)a =,(cos10,sin190)b =, 则a b ⋅=(A )12 (B (C )cos10 (D )2(4)已知命题:p 存在向量,,a b 使得||||a b a b ⋅=⋅,命题:q 的向量a 、b 、c ,若a b a c ⋅=⋅则b c =. (A )命题p q ∨是假命题 (B )命题p q ∧是真命题(C )命题()p q ∨⌝是假命题 (D )命题()p q ∧⌝是真命题(5)秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法. 如图1所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n ,x 的值分别为4,2,则输出v 的值为 (A )66 (B )33 (C )16 (D )8图2(6)如果实数x y 、满足条件⎪⎩⎪⎨⎧≤++≥+≥+-010101y x y y x , 那么2x y -的最大值为(A )2 (B )1 (C )2- (D )3-(7)在同一坐标系中,曲线xy )31(=与抛物线2y x =的交点横坐标所在区间为(A ))31,0((B ))21,31( (C ))32,21( (D ))1,32( (8)在421)(1)x ⋅-的展开式中,x 项的系数为(A )-4 (B )-2 (C )2(D )4(9)某工件的三视图如图2所示,现将该工件通过切割, 加工成一个体积尽可能大的正方体新工件,并使新工件的 一个面落在原工件的一个面内,则新工件的体积为 (A )18 (B )1 (C ) 2 (D )43π (10)已知正数,a b 满足4a b +=,则曲线()ln xf x x b=+在点(,())a f a 处的切线的倾斜角的 取值范围为 (A ),4π⎡⎫+∞⎪⎢⎣⎭ (B )5,412ππ⎡⎫⎪⎢⎣⎭(C ),42ππ⎡⎫⎪⎢⎣⎭ (D ),43ππ⎡⎫⎪⎢⎣⎭ (11)已知双曲线22142x y -=右焦点为F ,P为双曲线左支上一点,点A ,则△APF 周长的最小值为(A)4(1+ (B)4(C) (D(12)已知函数()=|s i n|([,]f x x x ππ∈-,()g x x x sin 2-=(],[ππ-∈x ),设方程(())0f f x =,(())0f g x =,(())0g g x =的实根的个数为分别为m 、n 、t ,则m n t ++=(A )9 (B)13 (C)17 (D) 21第Ⅱ卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须做答.第(22)题~第(23)题为选考题,考生根据要求做答.俯视图ACBA 1C 1B 1DE图31105x1210频率图4二、填空题:本大题共4小题,每小题5分,共20分,请把正确的答案填写在答题卡相应的横线上.(13)已知函数3()1f x ax bx =++,若()8f a =,则()f a -=_________.(14)连续掷两次骰子,以先后得到的点数m , n 作为点P 的坐标(,)m n ,那么点P 在圆2217x y +=内部(不包括边界)的概率是 .(15)已知△ABC 的顶点都在球O 的球面上,AB=6,BC=8,AC=10,三棱锥O-ABC的体积为则该球的表面积等于 . (16)在△ABC 中,6B π∠=,1AC =,点D 在边AB 上,且DA=DC ,BD=1,则DCA ∠= .三、解答题:解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分)设等差数列{}n a 的前n 项和为n S ,且244S S =,2123n n a a +=-. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)设数列{}n b 满足11222332n n nn a b a b a b ++++=-,求{}n b 的前n 项和n T . (18)(本小题满分12分)如图3,在直三棱柱ABC —A 1B 1C 1中,AB=BC=BB 1,11AB A B E =,D 为AC 上的点,B 1C ∥平面A 1BD ;(Ⅰ)求证:BD ⊥平面11ACC A ;(Ⅱ)若1AB =,且1AC AD =⋅,求二面角11B D A B -- 的余弦值.(19)(本小题满分12分)某地政府拟在该地一水库上建造一座水电站,用泄流水 量发电.图4是根据该水库历年的日泄流量的水文资料画成 的日泄流量X (单位:万立方米)的频率分布直方图(不完 整),已知)120,0[∈X ,历年中日泄流量在区间[30,60) 的年平均天数为156,一年按364天计. (Ⅰ)请把频率分布直方图补充完整;(Ⅱ)该水电站希望安装的发电机尽可能运行,但每30万立方米的日泄流量才够运行一台发电机,如60≤X <90时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机? (20)(本小题满分12分)如图5,已知椭圆)0(12222>>=+b a by a x 顶点为B 、C ,右焦点为F ,|AF |=3,且ABC ∆的周长为(I )求椭圆的离心率;(II )过点M (4, 0)的直线l 与椭圆相交于不同两点P 点N 在线段PQ 上.设||||||||QN MQ PN MP ==λ,试判断点N 是否在一条定直线上,并求实数λ的取值范围. (21)(本小题满分12分)已知函数()(2)=-+xf x x e ax .(a R ∈)(I )试确定函数()f x 的零点个数;(II )设12,x x 是函数()f x 的两个零点,当122+≤x x 时,求a 的取值范围. 请考生在第(22)、(23)题中任选一题作答,如果多做,则按所做的第一个题目计分. (22)(本小题满分10分)选修4-4:坐标系与参数方程已知曲线C 的参数方程为12cos 12sin x y θθ=-+⎧⎨=+⎩(θ为参数).以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系.(Ⅰ)求曲线C 的极坐标方程;(Ⅱ)若直线l :αθ=)),,0[(R ∈∈ρπα与曲线C 相交于A 、B 两点,设线段AB 的中点为M ,求||OM 的最大值.(23)(本小题满分10分)选修4-5:不等式选讲设函数)1()(-=x a x f .(Ⅰ)当1a =时,解不等式|()||()|3f x f x x +-≥; (Ⅱ)设1||≤a ,当1||≤x 时,求证:45|)(|2≤+x x f .揭阳市2017年高中毕业班高考第一次模拟考试数学(理科)参考答案及评分说明一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数. 一、选择题:(9,高为2,要使加工成的正方体新工件体积最大,则该正方体为圆锥的内接正方体,设棱长为2x 222x-=,解得12x =,故2x =1,故新工件的体积为1.(10)设曲线在点(,())a f a 处的切线的倾斜角为α,则122211)('tan =+≥≥+==b a abb a a f α,故42ππα≤<. (11)易得点F ,△APF 的周长l =||||||AF AP PF ++||2|'|||AF a PF AP =+++,要△APF 的周长最小,只需|||'|AP PF +最小,如图,当A 、P 、F 三点共线时取到,故l 2||24(1AF a =+=+.(12)由条件可在函数()f x 的值域为[0,1],方程()0f x =的根为0,π-,π,所以方程(())0f f x =的根为方程()0f x =或π-=)(x f 或()f x π=的根,显然方程()0f x =有3个实根,π-=)(x f 与()f x π=均无实根,所以方程(())0f f x =的实根个数为3,即3m =;因x x xg sin 2)(-=是奇函数,先考虑],0[π∈x 的图象,因x x g cos 21)('-=,由0)('>x g 得],3(ππ∈x ,可知)(x g 在],3(ππ上递增,在]3,0(π上递减,又0)0(=g ,ππ=)(g ,由图象关于原点对称得)(x g 的示意图如右,极小值为7.033)3(-≈-=ππg ,DCBA极大值为7.0)3(≈-πg . 方程(())0f g x =的实根为方程()0g x =或π-=)(x g 或π=)(x g 的根,显然方程()0g x =有3个根, 方程π-=)(x g 与π=)(x g 各有1个根,从而方程(())0f g x = 实根的个数为5,即n =5;记方程()0g x =除0外的另外两个实根分别为00,x x -,可知10>x ,方程(())0g g x =的实根为方程()0g x =或0)(x x g =或0)(x x g -=的根,显然方程()0g x =有3个根,方程0)(x x g =与0)(x x g -=各有1个根,从而方程(())0g g x =根的个数为5,即t =5,故m n t ++=13. 二、填空题:(15)依题意知△ABC 为直角三角形,其所在圆面的半径为152AC =,设三棱锥O-ABC 的高为h ,则由116832h ⨯⨯⨯=得h =,设球O 的半径为R ,则由2225h R +=得10R =,故该球的表面积为400π.(16)解法1:设A A C D θ∠=∠=,02πθ<<,则2A D C πθ∠=-,又1AC =,由正弦定理得:1.sin 2sin 2cos AC CD CD θθθ=⇒=在△BDC 中由正弦定理得:112cos 5sin sin sin sin(2)66CD BD B BCD θππθ=⇒=∠∠-55cos sin(2)sin()sin(2)626πππθθθθ⇒=-⇒-=-,由02πθ<< 550,222666πππππθθ⇒<-<-<-<,得5226ππθθ-=-或5226ππθθπ-+-=3πθ⇒=或9π. [注:该题若考生漏掉一解扣2分] 【或5cos sin(2)cos cos(2)63ππθθθθ=-⇒=-23πθθ⇒-=±3πθ⇒=或9π】解法2:过点C 作CE AB ⊥于E ,A ACD θ∠=∠=,则2CDB θ∠=,在Rt △AEC 中,sin CE θ=,则在Rt △CED 中,θθθ2tan sin 2tan -=-=CE DE ,在Rt△CEB 中,tan 6CEBE θπ==,由BD=1得sin 1tan 2θθθ=sin cos 2sin 2sin 2θθθθθ⇒+=cos 222cos θθθ⇒+=cos cos(2)3πθθ⇒=-23πθθ⇒-=±3πθ⇒=或9π.】三、解答题:(17)解:(Ⅰ)设{}n a 的公差为d ,则有1111464(2)(21)2()3a d a d a n d a nd +=+⎧⎨+-=⋅+-⎩,解得11,a d ==--------------------------------------------------------------------------------------4分1(1)21n a a n d n ∴=+-=-------------------------------------------------------------------------6分 (Ⅱ)由11222332n n nn a b a b a b ++++=-①当1n =时,1112a b =,所以112b =-----------------------------------------------------------------7分 当2n ≥时,112212132n n n n a b a b a b ---++++=-②-----------------------------8分 ①式减去②式得212n n nn a b -=, 求得12n nb =,易知1n =也成立, 所以数列{}n b 为等比数列,-------------------------------------------------------------------------10分其前n项和1211[1()]1221()1212n n n n T b b b -=+++==--------------------------------------12分E DB 1C 1A 1BCA(18)解:(Ⅰ)连结ED ,-------------------------------------------1分∵平面AB 1C ∩平面A 1BD=ED ,B 1C ∥平面A 1BD ,∴B 1C ∥ED ,-------------------------------------------------------2分 ∵E 为AB 1中点,∴D 为AC 中点,∵AB=BC , ∴BD ⊥AC ①,--------------------------------3分法一:由A 1A ⊥平面ABC ,⊂BD 平面ABC ,得A 1A ⊥BD ②, 由①②及A 1A 、AC 是平面11ACC A 内的两条相交直线,得BD ⊥平面11ACC A .-------------------------------------------5分 【法二:由A 1A ⊥平面ABC ,A 1A ⊂平面11ACC A ∴平面11ACC A ⊥平面ABC ,又平面11ACCA 平面ABC=AC ,得BD ⊥平面11ACC A .】(Ⅱ)由1AB =得BC=BB 1=1,由(Ⅰ)知AC DA 21=,又1=⋅DA AC 得22AC =,----------------------------------------6分∵2222BC AB AC +==,∴BC AB ⊥,如图以B 为原点,建立空间直角坐标系xyz B -如图示, 则)1,0,1(1A ,)1,0,0(1B ,)0,21,21(D , 得)0,0,1(11=A B ,111(,,1)22B D =-, 设),,(z y x m =是平面A 1B 1D 的一个法向量,则⎪⎩⎪⎨⎧⊥⊥B m A B m 111 ,得⎪⎩⎪⎨⎧=-+=⋅==⋅021210111z y x B m x A B m ,令z =1,得)1,2,0(=m ,----------9分 设(,,)n a b c =为平面A 1BD 的一个法向量,则⎪⎩⎪⎨⎧⊥⊥1BA n BDn ,得⎪⎩⎪⎨⎧=+=⋅=+=⋅00221c a BA n b a n , 令1c =得(1,1,1)n =-,---------------------------------------------------------------------------10分依题意知二面角11B D A B --为锐二面角,设其大小为θ,则 |||||||,cos |cos m n m n m n⋅⋅=><=θ515353=⋅=, 即二面角11B D A B --的余弦值为1701105x1210频率515.----------------------------------------------------12分 其它解法请参照给分. (19)解:(Ⅰ)在区间[30,60)的频率为73364156=分31==73070⨯频率组距,----------------2分 设在区间[0,30)上,a =频率组距,则130)21011051701(=⨯+++a , 解得2101=a ,-------------------------------------------------3分 补充频率分布直方图如右;-----------------------------------------------------------------------6分 (Ⅱ)记水电站日利润为Y 元.由(Ⅰ)知:不能运行发电机的概率为71,恰好运行一台发电机的概率为73,恰好运行二台发电机的概率为72,恰好运行三台发电机的概率为71, ①若安装1台发电机,则Y 的值为-500,4000,其分布列为E (Y )=72350076400071500=⨯+⨯-;----------------------------------8分 ②若安装2台发电机,则Y 的值为-1000,3500,8000,其分布列为E (Y )=3335001000350080007777-⨯+⨯+⨯=;-----------------------------10分 ③若安装3台发电机,则Y 的值为-1500,3000,7500,12000,其分布列为E (Y )=7345007112000775007300071500=⨯+⨯+⨯+⨯-; ∵345003350023500777>> ∴要使水电站日利润的期望值最大,该水电站应安装3台发电机.--------------12分 (20)解:(I )由2222||a c b AF =+=,得3=a ,--------------------------1分ABC ∆的周长为14)(2=+a AC ,即722=++a a b ,得72=b ,所以2=c ,椭圆的离心率为32=e ;---------------------------------------------4分 (II )显然直线l 的斜率存在,设l 的方程为)4(-=x k y ,设P (x 1,y 1),Q (x 2,y 2),N (x 0,y 0), 由||||||||QN MQ PN MP =,得022101y y y y y y -=-,化简得)(221021y y y y y +=①,-----6分由22(4),1.97=-⎧⎪⎨+=⎪⎩y k x x y 消去x ,得04956)79(222=+++k ky y k ,得7956221+-=+k ky y ,79492221+=k k y y ,----------------------------------------------------8分代入①式得k y 470-=,由)4(00-=x k y 得490=x , 49471414||||1010011-+-=--+-=--==x x x x x x x PN MP λ,---------------------------------------10分因为3491≤<x ,得434901≤-<x ,所以34371=+-≥λ, 因此,N 在一条直线49=x 上,实数),34[∞+∈λ.------------------------------------------12分【法二:显然直线l 的斜率存在,设l 的方程为)4(-=x k y ,不妨设0>k ,设P (x 1,y 1),Q (x 2,y 2),N (x 0,y 0),12y y <, 由||||||||QN MQ PN MP ==λ,得022101y y y y y y -=-=λ,化简得)(221021y y y y y +=①,6分 由)(101y y y -=λ,)(022y y y -=λ,得)(1221y y y y -=+λ②, 由22(4),1.97=-⎧⎪⎨+=⎪⎩y k x x y 消去x ,得04956)79(222=+++k ky y k , 可知=∆=⋅+-22249)79(4)56(k k k 0)1(364922>-⋅k k , 得7956221+-=+k k y y ,79492221+=k k y y ,)79(25622,1+∆±-=k k y ,----------------------8分代入①式得k y 470-=,由)4(00-=x k y 得490=x ,---------------------------------------9分 由②式得79562+-k k 792+∆-⋅=k λ,得341341425622≥-=-=k k k k λ, 因此,N 在一条直线49=x 上,实数),34[∞+∈λ.--------------------------------------12分】 【法三:设P (x 1,y 1),Q (x 2,y 2),N (x 0,y 0),21x x <,由||||||||QN MQ PN MP ==λ, 得,,MP PN MQ QN λλ==------------------------------------------------------------------------5分 所以01010202411411x x y y x x y y λλλλλλλλ+⎧=⎪+⎪⎪=⎪+⎨-⎪=⎪-⎪-⎪=-⎩将()11,A x y ,()22,B x y 代入椭圆方程得------------------7分2200222002222002004()()(4)()111(1)97974(4)()()()(1)1197197x y x y x y x y λλλλλλλλλλλλλλ+⎧⎪⎧++++=+=+⎪⎪⎪⎪⇒⎨⎨----⎪⎪+=-⎪⎪--⎩+=⎪⎩-----------------9分 上面两式相减化简得490=x 0110101744||4119||4x x MP PN x x x x x λ--∴===-+=-+---, 因为3491≤<x ,得434901≤-<x ,所以34371=+-≥λ, 因此,N 在一条直线49=x 上,实数),34[∞+∈λ.----------------------------------12分】(21)解法1:(I )函数()f x 的零点即方程()0=f x 的根,由(2)0-+=xx e ax 得(2)=-x ax x e ,令()(2)=-x g x x e , 则'()(2)(1)=-+-=-x x x g x e x e x e ,--------------------2分由'()0g x >得1x <,∴函数()g x 在(,1)-∞单调递增,由'()0g x <得1x >,∴函数()g x 在(1,)+∞上单调递减,----3分∴当1=x 时,函数()g x 有最大值,max ()(1)==g x g e ,又当1x <时,()g x >0,当→-∞x 时()0→g x ;当2<x 时()g x >0,(2)0=g ,当2>x 时()0<g x ,----------------------------------------4分∴当0≥a 时,ax y =与()g x 只有一个公共点,从而函数()f x 有一个零点;---------- 5分 当0<a 时,ax y =与()g x 有两个公共点,从而函数()f x 有两个零点.-----------------6分(II )设12<x x 由(I )知0<a 且120,2<>x x ,由1111()(2)0=-+=x f x x e ax ,得111(2)-=-x x e a x (10<x ) 由2222()(2)0=-+=x f x x e ax ,得222(2)-=-x x e a x (22>x )-----------------------8分∴2a 111)2(x e x x -=222)2(x e x x -⋅21212121]4)(2[x x e x x x x x x +++-=, -------------------------9分∵221≤+x x ∴0)(2421≥+-x x ,2210e e x x ≤<+,(两者仅当221=+x x 时取等号) ∴212121)(24x x x x x x ≥++-,又021<x x , ∴1]4)(2[212121≤++-x x x x x x ,----------------------------------------------------------------------11分∴22211e e a x x ≤⋅≤+,由0<a 得0<≤-a e .--------------------------------------------------------------------------------12分【解法2:(I )∵02)0(≠-=f ,0=∴x 不是函数的零点;当0≠x 时,由0)2()(=+-=ax e x x f x 得x e x a x)2(--=,------------------------------1分 设x e x x g x)2()(--=,则0)22()('22<+--=x e x x x g x,----------------------------------2分所以)(x g 在)0,(-∞和),0(∞+上单调递减,-----------------------------------------------------3分当0>x 且0→x 时,+∞→)(x g ;当+∞→x 时,-∞→)(x g ;当0<x 且0→x 时,-∞→)(x g ;当-∞→x 时,0)(→x g ;当0<x 时,由0)(<x g ,有)0,()(-∞∈x g ,当0>x 时,有0)2(=g ,),()(∞+-∞∈x g ,所以当0≥a 时,曲线a y =与)(x g 只一个公共点,函数)(x f 有一个零点; -----------5分 当0<a 时,曲线a y =与()g x 有两个公共点,函数)(x f 有两个零点; -----------------6分(II )不妨设21x x <,由(I )得0<a ,且01<x ,22>x ,由0)(1=x f ,0)(2=x f ,得)(1x g a =,)(2x g a =,∴)()(212x g x g a ⋅=111)2(x e x x -=222)2(x e x x -⋅21212121]4)(2[x x e x x x x x x +++-=,-----8分 ∵221≤+x x ∴0)(2421≥+-x x ,2210e e x x ≤<+,(两者仅当221=+x x 时取等号) ∴212121)(24x x x x x x ≥++-,又021<x x ,----------------------------------------------------10分 ∴1]4)(2[212121≤++-x x x x x x ,------------------------------------------------------------------------11分 ∴22211e e a x x ≤⋅≤+,由0<a 得0<≤-a e .------------------------------------------------12分】选做题:(22)解:(I )曲线C 的普通方程为222(1)(1)2x y ++-=,-------------------------------------2分由⎩⎨⎧==θρθρsin cos y x ,得22c o s 2s ρρθρθ+--=;---------------------------------------5分 (II )解法1:联立αθ=和22cos 2sin 20ρρθρθ+--=,得22(cos sin )20ρραα+--=,-----------------------------------------------------------------6分设),(1αρA 、),(2αρB ,则)4sin(22)cos (sin 221παααρρ-=-=+,---------8分 由|2|||21ρρ+=OM , 得2|)4sin(|2||≤-=παOM ,--------------------------------9分 当34πα=时,|OM |取最大值2.----------------------------------------------------------------10分【解法2:由(I )知曲线C 是以点P (1,1)-为圆心,以2为半径的圆,在直角坐标系中,直线l 的方程为x y ⋅=αtan ,则ta n||PM =,-----------------------------------------------------6分 ∵2222||||||2OM OP PM =-=-22tan 11tan αα=-+,---------------------------------8分 当(,)2παπ∈时,t an 0α<,21tan 2|tan |αα+≥,222|tan |||121tan OM αα=+≤+,当且仅当t an 1α=-,即34πα=时取等号,∴||OM ≤,即||OM 的最大值为2.------------------------------------------------------------10分】(23)解:(I )当1a =时,不等式|()||()|3f x f x x +-≥即|1||1|3x x x -++≥当1x ≤-时,得113x x x ---≥0x ⇒≤,∴1x ≤------------------------------------------1分当11x -<<时,得113x x x -++≥23x ⇒≤,∴213x -<≤------------------------------2分 当1x ≥时,得11x x x -++≥0x ⇒≤,与1x ≥矛盾,--------------------------------------3分 综上得原不等式的解集为2{|1}{|1}3xx x x ≤--<≤=2{|}3x x ≤-------------------------5分 (II )|)1(||)(|22x x a x x f +-=+|||)1(|2x x a +-≤-----------------------------------------------6分∵1||≤a ,1||≤x∴2|()|f x x +||)1(||2x x a +-≤||12x x +-≤--------------------------------------------------7分4545)21|(|1||||22≤+--=++-=x x x ,------------------------------------------------------9分 当21||=x 时取“=”,得证. ------------------------------------------------------------------------10分。
广东省揭阳一中2011届高三入学摸底考试(理综)

揭阳一中2011届高三摸底考试理科综合能力测试试卷考生请注意:1、本卷为物理、化学、生物三科合卷,考试用时150分钟,共300分,请把选择题答案用2B铅笔涂在答题卡上,非选择题答案用对应填在各科答题卷上,不按规定作答以零分计。
2、可能用到的相对原子质量:H-1 C-12 N-14 O-16 Na-23 Mg-24 Al-27 Cl-35.5 K-39 Fe-56第Ⅰ卷(选择题,共118分)一、选择题:(本题共16小题,每题4分,共64分。
每小题只有一个选项是最符合题意)1.下列关于生物膜的叙述,不.正确的是A.功能越复杂的生物膜,蛋白质种类和数量越多B.生物膜的功能特性是选择透过性C.叶绿体类囊体薄膜也属于生物膜系统D.溶酶体、液泡、核糖体均具有单层膜结构2.在玉米的营养液中加入某种阴离子,结果发现玉米根细胞在吸收该种阴离子的同时,对氯离子的吸收减少了,但对钾离子的吸收没有受影响,最可能的原因是该种离子A.妨碍了A TP的形成B.抑制了主动运输C.与氯离子的载体相同D.抑制了细胞的呼吸作用3.下列关于细胞结构和功能的叙述,不.正确的是A.蓝藻和酵母菌细胞都含有核糖体B.能进行有氧呼吸的细胞不一定含线粒体C.细胞核是细胞代谢和遗传的控制中心D.细胞分化后,mRNA种类和数量有所不同,遗传物质改变4.下图所示生物体部分代谢过程。
有关分析正确的是A.过程②需要的酶均存在于线粒体内 B.能进行过程③的生物无核膜,属于生产者C.过程②和④只能发生于不同的细胞中 D.过程①只能在植物细胞的叶绿体中进行5.下列对有关实验的叙述,正确的是A.在观察洋葱细胞有丝分裂实验中,将已经解离、漂洗、染色的根尖置于载玻片上,轻轻盖上盖玻片后即可镜检B.对酵母菌计数时,用吸管吸取培养液滴满血球计数板的计数室及其四周边缘,轻轻盖上盖玻片后即可镜检C.在叶绿体色素提取实验中,研磨绿叶时应加一些有机溶剂,如无水乙醇等D.检测试管中的梨汁是否有葡萄糖,可加入适量斐林试剂后,摇匀并观察颜色变化6.下列各项组合中,能体现生命系统由简单到复杂的正确层次的是①核酸②肌纤维③呼吸道的上皮④病毒⑤皮肤⑥野猪⑦同一片森林中的所有野猪⑧亚热带常绿阔叶林⑨一个池塘中的所有鱼类⑩一个池塘中的所有生物A.①④②③⑤⑥⑦⑨⑩⑧B.②③⑤⑥⑦⑩⑧C.①④③⑤⑥⑦⑧⑨⑩D.①②③④⑤⑥⑦⑧⑨⑩7.分类方法在化学学科的发展中起到了非常重要的作用。
2011年广东一模理科数学试题

试卷类型:A2011年普通高等学校招生全国统一考试密卷数 学 (理 科)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1. 已知集合}{220A x x x =-≤,}{11B x x =-<<, 则A B =A .}{01x x ≤<B .}{10x x -<≤ C .}{11x x -<< D .}{12x x -<≤ 2. 若复数(1-i )(a +i )是实数(i 是虚数单位),则实数a 的值为A .2-B .1-C .1D .23. 已知向量p ()2,3=-,q (),6x =,且//p q ,则+p q 的值为A B C .5 D .13 4. 函数ln xy x=在区间()1,+∞上 A .是减函数 B .是增函数 C .有极小值 D .有极大值 5. 阅读图1的程序框图. 若输入5n =, 则输出k 的值为. A .2 B .3 C .4 D .56. “a b >” 是“22a b ab +⎛⎫> ⎪⎝⎭”成立的A .充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件7. 将18个参加青少年科技创新大赛的名额分配给3所学校, 至少有一个名额且各校分配的名额互不相等, A .96 B .114C .128D .136DNMD 1C 1B 1A 1DCBA图3(度)150140110100 图1 8. 如图2所示,已知正方体1111ABCD A BC D -的棱长为2, 长 为2的线段MN 的一个端点M 在棱1DD 上运动, 另一端点N 在正方形ABCD 内运动, 则MN 的中点的轨迹的面积为 A .4π B .2π C .π D .2π图2 二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9.为了了解某地居民月均用电的基本情况, 抽 取出该地区若干户居民的用电数据, 得到频 率分布直方图如图3所示, 若月均用电量在 区间[)110,120上共有150户, 则月均用电量在区间[)120,150上的居民共有 户.10. 以抛物线2:8C y x =上的一点A 为圆心作圆,若该圆经过抛物线C 的顶点和焦点, 那么该圆的方程为 .11. 已知数列{}n a 是等差数列, 若468212a a a ++=, 则该数列前11项的和为 . 12. △ABC 的三个内角A 、B 、C 所对边的长分别为a 、b 、c ,已知3,,3c C π== 2a b =,则b 的值为 .13. 某所学校计划招聘男教师x 名,女教师y 名, x 和y 须满足约束条件25,2,6.x y x y x -≥⎧⎪-≤⎨⎪<⎩则该校招聘的教师最多是 名.(二)选做题(14~15题,考生只能从中选做一题) 14. (几何证明选讲选做题) 如图4, CD 是圆O 的切线, 切点为C ,点A 、B 在圆O 上,1,30BC BCD ︒=∠=,则圆O 的面积为 . 15. (坐标系与参数方程选讲选做题) 在极坐标系中,若过点()1,0且与 极轴垂直的直线交曲线4cos ρθ=于A 、B 两点,则AB = .图4 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知函数()2sin cos cos2f x x x x =+(x ∈R ). (1) 当x 取什么值时,函数()f x 取得最大值,并求其最大值; (2) 若θ为锐角,且8f πθ⎛⎫+= ⎪⎝⎭,求tan θ的值.17.(本小题满分12分)某企业生产的一批产品中有一、二、三等品及次品共四个等级,1件不同等级产品的利润 (单位:元)如表1,从这批产品中随机抽取出1件产品,该件产品为不同等级的概率如表2. 若从这批产品中随机抽取出的1件产品的平均利润(即数学期望)为4.9元.表1 表2 (1) 求,a b 的值;(2) 从这批产品中随机取出3件产品,求这3件产品的总利润不低于17元的概率.18.(本小题满分14分)DC 1A 1B 1CBA如图5,在三棱柱111-ABC A B C 中,侧棱1AA ⊥底面ABC ,,⊥AB BC D 为AC 的中点, 12A A AB ==.(1) 求证:1//AB 平面1BC D ;(2) 若四棱锥11-B AAC D 的体积为3, 求二面角1--C BC D 的正切值.图519.(本小题满分14分)已知直线2y =-上有一个动点Q ,过点Q 作直线1l 垂直于x 轴,动点P 在1l 上,且满足 OP OQ ⊥(O 为坐标原点),记点P 的轨迹为C . (1) 求曲线C 的方程;(2) 若直线2l 是曲线C 的一条切线, 当点()0,2到直线2l 的距离最短时,求直线2l 的方程.20.(本小题满分14分)已知函数()2f x ax bx c =++()0a ≠满足()00f =,对于任意x ∈R 都有()f x x ≥,且1122f x f x ⎛⎫⎛⎫-+=-- ⎪ ⎪⎝⎭⎝⎭,令()()()10g x f x x λλ=-->. (1) 求函数()f x 的表达式;(2) 求函数()g x 的单调区间;(3) 研究函数()g x 在区间()0,1上的零点个数.21.(本小题满分14分)已知函数y =()f x 的定义域为R , 且对于任意12,x x ∈R ,存在正实数L ,使得 ()()1212f x f x L x x -≤-都成立. (1) 若()f x =求L 的取值范围;(2) 当01L <<时,数列{}n a 满足()1n n a f a +=,1,2,n = .① 证明:112111nk k k a a a a L+=-≤--∑; ② 令()121,2,3,k k a a a A k k ++== ,证明:112111nk k k A A a a L +=-≤--∑.2011年普通高等学校招生全国统一考试密卷数学(理科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分. 一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,考生作答6小题,每小题5分,满分30分.其中14~15题是选做题,考生只能选做一题. 说明:第10小题写对一个答案给3分.9. 325 10. ()(2219x y -+±= 11. 33 12. 13. 1014.π 15. 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)(本小题主要考查三角函数性质, 同角三角函数的基本关系、两倍角公式等知识, 考查化归与转化的数学思想方法和运算求解能力) (1) 解: ()2sin cos cos2f x x x x =+sin 2cos 2x x =+ …… 1分2222x x ⎫=+⎪⎪⎭…… 2分24x π⎛⎫=+ ⎪⎝⎭. …… 3分∴当2242x k πππ+=+,即(8x k k ππ=+∈Z )时,函数()f x 取得最大值, …… 5分(2)解法1:∵83f πθ⎛⎫+= ⎪⎝⎭, 223πθ⎛⎫+= ⎪⎝⎭. …… 6分 ∴1cos 23θ=. …… 7分 ∵θ为锐角,即02πθ<<, ∴02θπ<<.∴sin 23θ==…… 8分∴sin 2tan 2cos 2θθθ==…… 9分∴22tan 1tan θθ=-. …… 10分2tan 0θθ+=.∴)(1tan 0θθ-=.∴tan θ=或tan θ=不合题意,舍去) …… 11分∴tan 2θ=. …… 12分解法2: ∵83f πθ⎛⎫+= ⎪⎝⎭, 223πθ⎛⎫+= ⎪⎝⎭. ∴1cos 23θ=. …… 7分 ∴212cos 13θ-=. …… 8分∵θ为锐角,即02πθ<<,∴cos θ=. …… 9分∴sin 3θ==. …… 10分∴sin tan cos 2θθθ==. …… 12分解法3:∵83f πθ⎛⎫+= ⎪⎝⎭, 223πθ⎛⎫+= ⎪⎝⎭. ∴1cos 23θ=. …… 7分 ∵θ为锐角,即02πθ<<, ∴02θπ<<.∴sin 23θ==…… 8分 ∴sin tan cos θθθ=…… 9分 22sin cos 2cos θθθ= …… 10分sin 21cos 2θθ=+=…… 12分 17.(本小题满分12分)(本小题主要考查数学期望、概率等知识, 考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识)(1)解:设1件产品的利润为随机变量ξ,依题意得ξ的分布列为:GFEODC 1A 1B 1CBA…… 2分 ∴ 60.6540.1 4.9E a b ξ=⨯++⨯-=,即50.9a b -=. …… 3分 ∵ 0.60.20.11a b ++++=, 即0.3a b +=, …… 4分 解得0.2,0.1a b ==.∴0.2,0.1a b == . …… 6分 (2)解:为了使所取出的3件产品的总利润不低于17元,则这3件产品可以有两种取法:3件都 是一等品或2件一等品,1件二等品. …… 8分故所求的概率P =30.6+C 2230.60.2⨯⨯0.432=. …… 12分18. (本小题满分14分)(本小题主要考查空间线面关系、二面角的平面角、锥体的体积等知识, 考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力) (1)证明: 连接1B C ,设1B C 与1BC 相交于点O ,连接OD , ∵ 四边形11BCC B 是平行四边形,∴点O 为1B C 的中点. ∵D 为AC 的中点, ∴OD 为△1ABC 的中位线,∴ 1//OD AB . …… 2分 ∵OD ⊂平面1BC D ,1⊄AB 平面1BC D , ∴1//AB 平面1BC D . …… 4分 (2)解: 依题意知,12AB BB ==,∵1⊥AA 平面ABC ,1AA ⊂平面11AAC C ,∴ 平面ABC ⊥平面11AAC C ,且平面ABC 平面11AAC C AC =.作BE AC ⊥,垂足为E ,则BE ⊥平面11AAC C , ……6分 设BC a =,在Rt △ABC中,AC =AB BC BE AC ==∴四棱锥11-B AAC D 的体积()1111132V AC AD AA BE =⨯+126=a =. …… 8分依题意得,3a =,即3BC =. …… 9分 (以下求二面角1--C BC D 的正切值提供两种解法)解法1:∵11,,AB BC AB BB BC BB B ⊥⊥= ,BC ⊂平面11BB C C ,1BB ⊂平面11BB C C , ∴AB ⊥平面11BB C C .取BC 的中点F ,连接DF ,则DF //AB ,且112DF AB ==. ∴DF ⊥平面11BB C C .作1FG BC ⊥,垂足为G ,连接DG , 由于1DF BC ⊥,且DF FG F = , ∴1BC ⊥平面DFG . ∵DG ⊂平面DFG , ∴1BC ⊥DG .∴DGF ∠为二面角1--C BC D 的平面角. …… 12分 由Rt △BGF ~Rt △1BCC ,得11GF BFCC BC =,得113213BF CC GF BC ⨯=== ,在Rt △DFG 中, tan DF DGF GF ∠=3=.∴二面角1--C BC D的正切值为3. …… 14分 解法2: ∵11,,AB BC AB BB BC BB B ⊥⊥= ,BC ⊂平面11BB C C ,1BB ⊂平面11BB C C ,∴AB ⊥平面11BB C C .以点1B 为坐标原点,分别以11B C ,1B B ,11B A y 轴和z 轴,建立空间直角坐标系1B xyz -. 则()0,2,0B ,()13,0,0C ,()0,2,2A ,3,2,12D ⎛⎫⎪⎝⎭. ∴()13,2,0BC =- ,3,0,12BD ⎛⎫= ⎪⎝⎭设平面1BC D 的法向量为n (),,x y z =,由n 10BC = 及n 0BD = ,得320,30.2x y x z -=⎧⎪⎨+=⎪⎩令2x =,得3,3y z ==-.故平面1BC D 的一个法向量为n ()2,3,3=-, …… 11分又平面1BC C 的一个法向量为()0,0,2AB =-,∴cos 〈n ,AB 〉= ⋅n AB n AB200323⨯+⨯+-⨯-==. …… 12分 ∴sin 〈n ,AB 〉==. …… 13分 ∴tan 〈n ,AB 〉= 3.∴二面角1--C BC D 的正切值为3. …… 14分 19.(本小题满分14分)(本小题主要考查求曲线的轨迹方程、点到直线的距离、曲线的切线等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识)(1) 解:设点P 的坐标为(),x y ,则点Q 的坐标为(),2x -. ∵OP OQ ⊥,∴1OP OQ k k =- .当0x ≠时,得21y x x-=-,化简得22x y =. …… 2分 当0x =时, P 、O 、Q 三点共线,不符合题意,故0x ≠.∴曲线C 的方程为22x y =()0x ≠. …… 4分 (2) 解法1:∵ 直线2l 与曲线C 相切,∴直线2l 的斜率存在.设直线2l 的方程为y kx b =+, …… 5分 由2,2,y kx b x y =+⎧⎨=⎩ 得2220x kx b --=. ∵ 直线2l 与曲线C 相切,∴2480k b ∆=+=,即22k b =-. …… 6分点()0,2到直线2l的距离d =212=…… 7分12⎫= …… 8分12≥⨯…… 9分=…… 10分=,即k =.此时1b =-. ……12分∴直线2l10y --=10y ++=. …… 14分 解法2:由22x y =,得'y x =, …… 5分 ∵直线2l 与曲线C 相切, 设切点M 的坐标为()11,x y ,其中21112y x =,则直线2l 的方程为:()111y y x x x -=-,化简得211102x x y x --=. …… 6分 点()0,2到直线2l的距离d =212=…… 7分12⎫= …… 8分12≥⨯ …… 9分=…… 10分=,即1x =. ……12分∴直线2l10y --=10y ++=. …… 14分 解法3:由22x y =,得'y x =, …… 5分 ∵直线2l 与曲线C 相切, 设切点M 的坐标为()11,x y ,其中211102y x =>, 则直线2l 的方程为:()111y y x x x -=-,化简得110x x y y --=. …… 6分 点()0,2到直线2l的距离d ==…… 7分12⎫=+…… 8分12≥⨯…… 9分=…… 10分=11y =时,等号成立,此时1x =. ……12分∴直线2l10y --=10y ++=. …… 14分 20.(本小题满分14分)(本小题主要考查二次函数、函数的性质、函数的零点、分段函数等知识, 考查函数与方程、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和应用意识)(1) 解:∵()00f =,∴0c =. …… 1分 ∵对于任意x ∈R 都有1122f x f x ⎛⎫⎛⎫-+=-- ⎪ ⎪⎝⎭⎝⎭, ∴函数()f x 的对称轴为12x =-,即122b a -=-,得a b =. …… 2分 又()f x x ≥,即()210ax b x +-≥对于任意x ∈R 都成立, ∴0a >,且∆()210b =-≤. ∵()210b -≥, ∴1,1b a ==.∴()2f x x x =+. …… 4分(2) 解:()()1g x f x x λ=--()()22111,,111,.x x x x x x λλλλ⎧+-+≥⎪⎪=⎨⎪++-<⎪⎩…… 5分① 当1x λ≥时,函数()()211g x x x λ=+-+的对称轴为12x λ-=,若112λλ-≤,即02λ<≤,函数()g x 在1,λ⎛⎫+∞⎪⎝⎭上单调递增; …… 6分 若112λλ->,即2λ>,函数()g x 在1,2λ-⎛⎫+∞⎪⎝⎭上单调递增,在11,2λλ-⎛⎫ ⎪⎝⎭上单调递减.…… 7分 ② 当1x λ<时,函数()()211g x x x λ=++-的对称轴为112x λλ+=-<, 则函数()g x 在11,2λλ+⎛⎫-⎪⎝⎭上单调递增,在1,2λ+⎛⎫-∞- ⎪⎝⎭上单调递减. …… 8分 综上所述,当02λ<≤时,函数()g x 单调递增区间为1,2λ+⎛⎫-+∞ ⎪⎝⎭,单调递减区间为 1,2λ+⎛⎫-∞- ⎪⎝⎭; …… 9分当2λ>时,函数()g x 单调递增区间为11,2λλ+⎛⎫-⎪⎝⎭和1,2λ-⎛⎫+∞ ⎪⎝⎭,单调递减区间为1,2λ+⎛⎫-∞- ⎪⎝⎭和11,2λλ-⎛⎫ ⎪⎝⎭. …… 10分(3)解:① 当02λ<≤时,由(2)知函数()g x 在区间()0,1上单调递增, 又()()010,1210g g λ=-<=-->,故函数()g x 在区间()0,1上只有一个零点. …… 11分 ② 当2λ>时,则1112λ<<,而()010,g =-<21110g λλλ⎛⎫=+> ⎪⎝⎭, ()121g λ=--,(ⅰ)若23λ<≤,由于1112λλ-<≤,且()211111222g λλλλ---⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭()21104λ-=-+≥, 此时,函数()g x 在区间()0,1上只有一个零点; …… 12分 (ⅱ)若3λ>,由于112λ->且()121g λ=--0<,此时,函数()g x 在区间()0,1上有两个不同的零点. …… 13分 综上所述,当03λ<≤时,函数()g x 在区间()0,1上只有一个零点;当3λ>时,函数()g x 在区间()0,1上有两个不同的零点. …… 14分 21.(本小题满分14分)(本小题主要考查函数、数列求和、绝对值不等式等知识, 考查化归与转化的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识) (1) 证明:对任意12,x x ∈R ,有 ()()12f x f x -=-==. …… 2分由()()1212f x f x L x x -≤-,12L x x ≤-.当12x x ≠时,得L ≥.12,x x >>且1212x x x x +≥+,12121x x x x +<≤+. …… 4分∴要使()()1212f x f x L x x -≤-对任意12,x x ∈R 都成立,只要1L ≥. 当12x x =时, ()()1212f x f x L x x -≤-恒成立.∴L 的取值范围是[)1,+∞. …… 5分 (2) 证明:①∵()1n n a f a +=,1,2,n = ,故当2n ≥时,()()111n n n n n n a a f a f a L a a +---=-≤-()()21212112n n n n n L f a f a L a a L a a -----=-≤-≤≤- . …… 6分∴112233411nkk n n k aa a a a a a a a a ++=-=-+-+-++-∑()21121n L L La a -≤++++- …… 7分 1211nL a a L-=--. …… 8分 ∵01L <<, ∴112111nk k k a a a a L+=-≤--∑(当1n =时,不等式也成立). …… 9分 ②∵12kk a a a A k++=,∴1212111k k k k a a a a a a A A k k ++++++++-=-+ ()()12111k k a a a ka k k +=+++-+()()()()()12233411231k k a a a a a a k a a k k +=-+-+-++-+()()12233411231k k a a a a a a k a a k k +≤-+-+-++-+ . …… 11分 ∴1122311nkk n n k AA A A A A A A ++=-=-+-++-∑ ()()122311111121223123341a a a a n n n n ⎛⎫⎛⎫≤-++++-+++ ⎪ ⎪ ⎪ ⎪⨯⨯+⨯⨯+⎝⎭⎝⎭()()34111113344511n n a a n a a n n n n +⎛⎫+-+++++-⨯ ⎪ ⎪⨯⨯++⎝⎭ 1223112111111n n n a a a a a a n n n +⎛⎫⎛⎫⎛⎫=--+--++-- ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭≤12231n n a a a a a a +-+-++- 1211a a L≤--. ……14分。
揭阳一中2011届高三下学期第一次测试理综试题及答案

广东揭阳一中2010-2011学年度第二学期高三第一次测试理科综合能力试题第Ⅰ卷(选择题,共118分)可能用到的相对原子质量:H 1;C 12; N 14; O 16; Fe 56; Cl 35.5一、选择题:(本题共16小题,每题4分,共64分。
每小题只有一个选项是最符合题意)1.下列关于细胞结构和功能的叙述,不正确的是 ( )A .生物膜相互转化的基础是膜的成分和结构的相似性B .唾液腺细胞和胰腺细胞中高尔基体的数量较多C .细菌和酵母菌都有细胞膜、核糖体和DNAD .生物体的性状都是由细胞核内的遗传物质控制的2.免疫接种包括两种方法:①注射抗体,②注射抗原。
下列相关说法正确的是 ( )A .用治愈者的血清进行的治疗属于方法②B .方法①在接种对象体内引起B 细胞的增殖、分化C .方法②是通过使人体患病然后获得免疫力D .医学上一般采用方法②预防一些传染病3.猪笼草是一种食虫植物,为了验证猪笼草分泌液中有蛋白酶,某学生设计了两组实验,如右下图所示。
在35℃水浴中保温一段时间后,甲、乙试管中加入适量的双缩脲试剂,丙、丁试管中不加任何试剂,下列实验能达到目的的是 ( )A .只有实验①能B .只有实验②能C .实验①、实验②都能D .实验①、实验②都不能4.下图表示基因型为AaBb (两对等位基因分别位于两对同源染色体上)的某哺乳动物产生生殖细胞的过程,错误的说法是( )A .Ⅰ过程表示细胞进行有丝分裂B .细胞中染色体数目减少一半是通过Ⅱ过程实现C .一个A 细胞经过减数分裂形成的C 细胞有4种基因型D .该哺乳动物为雄性个体5.下图是某陆地生态系统食物网的结构模式图。
下列叙述错误的是 ( )A .此生态系统中的生产者是甲和戊B .辛从食物链甲→丙→乙→丁→辛获得的能量最多C .若甲种群数量下降,丙种群数量也会下降D .丁和辛之间既存在竞争关系又存在捕食关系 6( )乙 甲丙丁辛 戊 己 庚 ① ② ③ ④ ⑤A.五种结构广泛存在于各种细胞内B.①③④⑤上进行的反应都需要②提供能量C.观察活细胞中的④需要进行染色D.①与③间的转化能体现生物膜的流动性7.下列生产工艺不能体现“绿色化学”思想的是()A.海水提镁:用电解氯化镁产生的氯气制取盐酸B.工业制硫酸:提高尾气排放的烟囱高度C.工业制胆矾:使用稀硫酸、双氧水溶解铜D.火力发电:在燃煤中加入适量生石灰8.下列有关物质分类或归类正确的一组是()①液氨、液氯、干冰、碘化银均为化合②氢氟酸、盐酸、水玻璃、氨水均为混合物③明矾、小苏打、醋酸、次氯酸均为电解质④碘酒、牛奶、豆浆、漂粉精均为胶体⑤Na2O2、Na2CO3、NaHCO3、Na2SiO3均为钠盐A.①和②B.②和③C.③和④D.②③⑤9.由短周期的两种元素组成的化合物XY3,下列说法错误的是()A.X和Y可能位于同一周期,也可能位于不同周期B.X可能是金属,也可能是非金属C.化合物XY3溶于水,溶液可能显碱性,也可能显酸性D.X和Y一定位于不同主族10.若NA表示阿伏加德罗常数的值,下列说法正确的是()A.0.1molNa2O2中含有的离子数为0.4NAB.利用氧化还原反应原理制取1mol氧气,转移的电子数一定为4NAC.7.1g氯气与足量NaOH溶液反应电子转移数为0.2NAD.0.1mol氯气与金属铁完全反应时,转移电子数为0.2NA11.下列制备和收集气体的实验装置合理的是()图一图二图三图四A.图一用氯化铵和氢氧化钙制NH3 B.图二用铜片和稀硝酸制NOC.图三用锌粒和稀硫酸制H2 D.图四用双氧水和二氧化锰制O212.已知通过乙醇制取氢气有如下两条路线:a.CH3CH2OH(g)+H2O(g)==4H2(g)+2CO(g)△H= +255.6kJ·mol-1 b.CH3CH2OH(g)+1/2O2(g)==3H2(g)+2CO(g)△H= +13.8kJ·mol-1则下列说法不正确的是()A .降低温度,可提高b 路线中乙醇的转化率B .从能量消耗的角度来看,b 路线制氢更加有利C .乙醇可通过淀粉等生物原料发酵制得,属于可再生资源D .由a 、b 知:2H2(g )+O2(g )=2H2O (g ) △H=-483.6kJ·mol -113.在同一水平直线上的两位置分别沿同方向抛出两小球A 和B ,其运动轨迹如图所示,不计空气阻力.要使两球在空中相遇,则必须( )A .先抛出A 球B .先抛出B 球C .同时抛出两球D .使两球质量相等14.科学家发现在月球上含有丰富的He 32,它是一种高效、清洁、安全的核聚变燃料,其参与的一种核聚变反应的方程式为He He He He 421132322+→+,关于He 32聚变下列表述正确的是 ( )A .聚变反应不会释放能量B .聚变反应产生了新的原子核C .聚应反应没有质量亏损D .目前核电站都采用He 32聚变反应发电15.在如图所示的装置中,木块B 与水平桌面的接触是光滑的,子弹A 沿水平方向射入木块后留在木块内。
【数学】广东省揭阳市高三第一次模拟考试试卷(理)

广东省揭阳市高三第一次模拟考试数学试卷一、选择题:本题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|60}A x x x =+-<,(2,2)B =-,则A C B = ( ) A .(3,2)--B .(3,2]--C .(2,3)D .[2,3)2.已知向量(1,2),(2,1),(1,)a b c λ==-=,若()a b c +⊥,则λ的值为( ) A .3-B .13-C .13D .33.已知z 是复数z 的共轭复数,(1)(1)z z +-是纯虚数,则||z =( ) A .2B .32C .1D .124.若3sin(2)25πα-= ,则44sin cos αα-的值为( ) A .45 B .35 C .45-D .35-5.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产 方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人, 第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务 的工作时间(单位:min )绘制了如右茎叶图:则下列结论中表述不正确...的是( ) A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟 B. 第二种生产方式比第一种生产方式效率更高 C. 这40名工人完成任务所需时间的中位数为80D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.6. 函数()f x 在[0,)+∞单调递减,且为偶函数.若(12)f =-,则满足3()1x f -≥-的x 的 取值范围是( ) A .[1,5]B .[1,3]C .[3,5]D .[2,2]-7. 如图,网格纸上虚线小正方形的边长为1,实线画出的是某几何体的三视图,则该几何体的体积为 ( )A .643B .52C .1533D .56 8.某班星期一上午安排5节课,若数学2节,语文、物理、化学各1节,且物理、化学不 相邻,2节数学相邻,则星期一上午不同课程安排种数为( ) A .6 B .12 C .24 D .489. 过双曲线22221(0,0)x y a b a b-=>>两焦点且与x 轴垂直的直线与双曲线的四个交点组成一个正方形,则该双曲线的离心率为( ) A1 BC .32D .210. 选图为中国古代刘徽的《九章算术注》中研究“勾股容方”问题的图形,图中△ABC 为直角三角形,四边形DEFC 为它的内接正方形,记正方形为区域Ⅰ,图中阴影部分为区域Ⅱ,在△ABC 上任取一点,此点取自区域Ⅰ、Ⅱ的概率分别记为1p 、2p ,则( )A .12p p =B .12p p <C .12p p ≤D .12p p ≥11.已知△ABC 中,AB =AC =3,sin 2sin ABC A ∠= ,延长AB 到D 使得BD =AB ,连结 CD ,则CD 的长为( ) A .BCD.12.已知函数()cos f x x π=,1()(0)2ax g x e a a =-+≠,若12[0,1]x x ∃∈、,使得 12()()f x g x =,则实数a 的取值范围是( )BA .1[,0)2-B .1[,)2+∞C .1[,0)[,)2-∞+∞D .11[,0)(0,]22- 二、填空题:本题共4小题,每小题5分,共20分. 13.命题“对2[1,1],310x x x ∀∈-+->”的否定是 _______; 14.在曲线()sin cos f x x x =-,(,)22x ππ∈-的所有切线中,斜率为1的切线方程为 .15.已知圆锥的顶点为S ,底面圆周上的两点A 、B 满足SAB ∆为等边三角形,且面积为8,则圆锥的表面积为 .16. 已知点P 在直线210x y +-=上,点Q 在直线230x y ++=上,M 00(,)x y 为PQ 的 中点,且0021y x >+,则y x 的取值范围是 . 三、解答题:共70分,解答应写出文字说明,证明过程或演算步骤.第17题~第21题为必考题,每个试题考生都必须做答.第22题~第23题为选考题,考生根据要求做答. (一)必考题:共60分 17.(12分)已知数列{}n a 的前n 项和为n S ,且23nn S p m =⋅+,(其中p m 、为常数),又123a a ==.(1)求数列{}n a 的通项公式;(2)设3log n n b a =,求数列{}n n a b ⋅的前n 项和n T .18.(12分)如图,在四边形ABED中,AB//DE,AB⊥BE,点C在AB上,且AB⊥CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE与平面PBC所成的角为45°.(1)求证:平面PBC⊥平面DEBC;(2)求二面角D-PE-B的余弦值.19.(12分)某地种植常规稻A 和杂交稻B ,常规稻A 的亩产稳定为500公斤,今年单价为3.50元/公斤,估计明年单价不变的可能性为10%,变为3.60元/公斤的可能性为60%,变为3.70元/公斤的可能性为30%.统计杂交稻B 的亩产数据,得到亩产的频率分布直方图如下;统计近10年来杂交稻B 的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为(,)(1,2,10)i i x y i =,并得到散点图如下,参考数据见下.(1)估计明年常规稻A 的单价平均值;(2)在频率分布直方图中,各组的取值按中间值来计算,求杂交稻B 的亩产平均值;以频率作为概率,预计将来三年中至少有二年,杂交稻B 的亩产超过765公斤的概率; (3)判断杂交稻B 的单价y (单位:元/公斤)与种植亩数x (单位:万亩)是否线性相关?若相关,试根据以下的参考数据求出y 关于x 的线性回归方程;调查得知明年此地杂交稻B 的种植亩数预计为2万亩.若在常规稻A 和杂交稻B 中选择,明年种植哪种水稻收入更高? 统计参考数据: 1.60x =, 2.82y =,101()()0.52iii x x y y =--=-∑,1021()0.65ii x x =-=∑,附:线性回归方程ˆybx a =+,121()()()niii nii x x y y b x x ==--=-∑∑.20.(12分)已知点2P 在椭圆C :22221(0)x y a b a b+=>>上,椭圆C 的焦距为2. (1)求椭圆C 的方程;(2)斜率为定值k 的直线l 与椭圆C 交于A 、B 两点,且满足22||||OA OB +的值为常数,(其中O 为坐标原点) (i )求k 的值以及这个常数;(ii )写出一般性结论(不用证明):斜率为定值k 的直线l 与椭圆22221(0)x y a b a b+=>>交于A 、B 两点,且满足22||||OA OB +的值为常数,则k 的值以及这个常数是多少?21.(12分)设函数1()ln f x ax x b x=-++()∈a b R 、, (1)讨论()f x 的单调性;(2)若函数()f x 有两个零点1x 、2x ,求证:121222x x ax x ++>.(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22. [选修4-4:坐标系与参数方程] (10分)以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为22cos 2a ρθ=(∈a R ,a 为常数),过点(2,1)P 、倾斜角为30︒的直线l的参数方程满足22x =+,(t 为参数). (1)求曲线C 的普通方程和直线l 的参数方程;(2)若直线l 与曲线C 相交于A 、B 两点(点P 在A 、B 之间),且||||2PA PB ⋅=,求a 和||||||PA PB -的值.23. [选修4-5:不等式选讲] (10分) 已知函数()|1||1|f x x x =+--, (1)求函数()f x 的值域;(2)若[2,1]x ∈-时,()3f x x a ≤+,求实数a 的取值范围.【参考答案】一、选择题递增,由()(22)1f f =-=-,则23215x x -≤-≤⇒≤≤.故选D . 法二:由3()1x f -≥-得()2)3(f x f ≥-或3()(2)x f f ≥--,即303532x x x-≥⎧⇒≤≤⎨-≤⎩或301332x x x -<⎧⇒≤<⎨-≥-⎩,综合得15x ≤≤.7. 由三视图知该几何体为一长方体与一直三棱柱的组合体,其体积为2143414562⨯+⨯⨯⨯=.8. 第一步:将两节数学捆在一起与语文先进行排列有22A 种排法,第二步:将物理、化学在 第一步排后的3个空隙中选两个插进去有23A 种方法,根据乘法原理得不同课程安排种数为222312=A A .9. 将x c =代入双曲线的方程得4222b b y y a a =⇒=±,则222b c ac c a a=⇒=- 11e e⇒-=,解得e =. 10. 法一:设△ABC 两直角边的长分别为,a b ,其内接正方形的边长为x ,由x b xa b -=abx a b=+,则122()ab p a b =+,222122211()()ab a b p p a b a b +=-=-=++22()ab a b ≥+(当且仅当 a b =时取等号). 法二(特殊法):设1,2,BC AC ==CD x =,则23x =,故12445,1999p p ==-=,从而 排除A 、D ,当△ABC 为等腰直角三角形时12p p =,排除B ,故选C . 11. 由sin 2sin ABC A ∠=结合正弦定理得1322BC AC ==,在等腰三角形ABC 中311cos 434ABC ∠=⨯=,从而1cos 4DBC ∠=-,由余弦定理得:2222cos CD BD BC BD BC DBC =+-⋅⋅∠272=,故CD =.12. 设F 、G 分别为函数()f x 与()g x 定义在区间上[0,1]上的值域,则[1,1]F =-,当a >0时1a e >,1()()2a x g x e a =-+单调递增,当a <0时,()g x 单调递减, 31[,],(0);2213[,],(0).22a a a e a a G e a a a ⎧-+-+>⎪⎪=⎨⎪-+-+<⎪⎩12[0,1]x x ∃∈、使得12()()f x g x =FG φ⇔≠()()003111122131122a a a a a e a e a a ⎧⎧⎪⎪><⎪⎪⎪⎪⇔-+≤-+≤⎨⎨⎪⎪⎪⎪-+≥--+≥-⎪⎪⎩⎩或2,因为1()2a h a e a =-+在(0,)+∞上递增,在(,0)-∞上递减,所以3()(0)2h a h >=, 所以解得()1式12a ⇔≥,()2式⇔∅. 二、填空题【解析】14.设切点为00(,)x y ,则由000'()cos sin 1f x x x =+=且0(,)22x ππ∈-,得00x =, 01y =-,故所求的切线方程为10x y --=(或1y x =-).15. 设圆锥母线长为l ,由SAB ∆为等边三角形,且面积为24l =⇒=,又 设圆锥底面半径为r ,高为h ,则由轴截面的面积为8得8rh =,又2216r h +=,解得r =(或设轴截面顶角为S ,则由21sin 82l S =得90S =︒,可得圆锥底面直径2r =,)故2=1)S rl r πππ+=表.16. 因直线210x y +-=与230x y ++=平行,故点M 的轨迹为与两直线距离相等且平行 于两直线的直线,其方程为210x y ++=,即点M 00(,)x y 满足00210x y ++=,而满足 不等式0021y x >+的点在直线21y x =+的上方,易得直线210x y ++=与21y x =+的交点为31(,)55--,故问题转化为求射线(不含端点)00210x y ++=(035x <-)上的点 M 00(,)x y 与坐标原点(0,0)连线斜率、即00y x 的取值范围, 故0011(,)23OM y k x =∈-.三、解答题17.解:(1)由123a a ==得36p m +=,122()912a a p m +=+=,解得1,3p m ==,-------------------------------------------------------------------------------2分即233nn S =+,-------------①当2n ≥时,11233n n S --=+-------------②①-②得1233n n n a -=-,即13(2)n n a n -=≥,--------------------------------------------4分∵ 13a =不满足上式, ∴13,1;3, 2.n n n a n -=⎧=⎨≥⎩----------------------------------------------------------------------------------6分(2)依题意得31,1;log 1, 2.n n n b a n n =⎧==⎨-≥⎩-------------------------------------------------------7分当1n =时,1113T a b ==, 当2n ≥时,112233n n n T a b a b a b a b =++++213131323(1)n n -=⨯+⨯+⨯++⨯-223133131323(2)3(1)n n n T n n -=⨯+⨯+⨯++⨯-+⨯-两式相减得:231233333(1)n n n T n --=-++++-⨯----------------------------------9分13(31)63(1)31n n n -⨯-=-+-⨯--3(32)152n n --=3(23)154n n n T -+=.-------------------------------------------------------------------------------11分 显然当1n =时,13T =符合上式 ∴3(23)154n n n T -+=-------------------------------------------------------------------------------12分 18.(1)证明:∵AB ⊥CD ,AB ⊥BE ,∴CD //EB ,--------------------------1分∵AC ⊥CD ,∴PC ⊥CD ,∴EB ⊥PC ,--------------------------------------------------------3分 且PC ∩BC =C ,∴EB ⊥平面PBC ,----------------------------------------------------------------------------------4分 又∵EB ⊂平面DEBC ,∴平面PBC ⊥平面DEBC ; ---------------------------------------5分(2)解:由(1)知EB ⊥平面PBC ,∴EB ⊥PB ,由PE 与平面PBC 所成的角为45°得∠EPB =45°,--------------------------------6分∴△PBE 为等腰直角三角形,∴PB =EB ,∵AB //DE ,结合CD //EB 得BE =CD =2,∴PB =2,故△PBC 为等边三角形,--------------------7分取BC 的中点O ,连结PO ,∵ PO ⊥BC ,∴PO ⊥平面EBCD ,--------------------8分以O 为坐标原点,过点O 与BE 平行的直线为x 轴,CB 所在的直线为y 轴,OP 所在的直线为z 轴建立空间直角坐标系如图,则(010),(2,1,0),(2,1,0)B E D -,,,P ,从而(0,2,0)DE =,(2,0,0)BE =, (2,1,PE = ,设平面PDE 的一个法向量为(,,)m x y z =,平面PEB 的一个法向量为(,,)n a b c =,则由00m DE m PE ⎧⋅=⎪⎨⋅=⎪⎩得2020y x y =⎧⎪⎨+-=⎪⎩,令2z =-得(3,0,2)m =--,----------------9分由00n BE n PE ⎧⋅=⎪⎨⋅=⎪⎩得2020a a b =⎧⎪⎨+=⎪⎩ ,令1c =得(0,3,1)n =,------------------------10分 设二面角D -PE -B 的大小为θ,则cos ||||7m n m n θ⋅===⋅⨯, 即二面角D -PE -B 的余弦值为-.----------------------------------------------------------------12分 (其它解法请参照给分!) 19.解:(1)设明年常规稻A 的单价为ξ,则ξ的分布列为3.62,估计明年常规稻A 的单价平均值为3.62(元/公斤);----------------------------------------3分(2)杂交稻B 的亩产平均值为:[(730790800)0.005(740780)0.01(750770)0.027600.025]10++⨯++⨯++⨯+⨯⨯ 116152304190762=+++=.--------------------------------------------------------------------5分 依题意知杂交稻B 的亩产超过765公斤的概率为:0.2+0.1+0.52=0.4p =⨯,则将来三年中至少有二年,杂交稻B 的亩产超过765公斤的概率为: 22330.4(10.4)0.40.352C ⨯⨯-+=.--------------------------------------------------------------7分(3)因为散点图中各点大致分布在一条直线附近,所以可以判断杂交稻B 的单价y 与种植亩数x 线性相关, ----------------------------------------------------8分由题中提供的数据得:0.520.80.65b -==-,由y bx a =+ 2.820.8 1.60 4.10a y bx =-=+⨯=,所以线性回归方程为ˆ0.8 4.10yx =-+,------------------------------------10分 估计明年杂交稻B 的单价ˆ0.82 4.10 2.50y=-⨯+=元/公斤; 估计明年杂交稻B 的每亩平均收入为762 2.501905⨯=元/亩,估计明年常规稻A 的每亩平均收入为500()500 3.621810E ξ⨯=⨯=元/亩,因1905>1875,所以明年选择种植杂交稻B 收入更高. -----------------------------12分20.解:(1)由点P 在椭圆上得223112a b +=,2c =2, -------------------------------1分 2222322b a a b ∴+=,c =1,又222a b c =+,222232(1)2(1)b b b b ∴++=+,422320b b ∴--=,解得22b =,得23a =,∴椭圆C 的方程为22132x y +=;----------------------------------------4分 (2)(i )设直线l 的方程为y kx t =+,联立22132x y +=,得222(32)6360k x ktx t +++-=, ∴2121222636(1)(2)3232kt t x x x x k k -+=-=++------------------------------------------5分 又22112(1)3x y =-,22222(1)3x y =-, 2222221122||||()()OA OB x y x y +=+++ 22121()43x x =++212121[()2]43x x x x =+-+ 22221636[()2]433232kt t k k -=-⨯+++ 222221(1812)362443(32)k t k k -++=⨯++----------------------------------------------------------------8分 要使22||||OA OB +为常数,只需218120k -=,得223k =,------------------------------9分 ∴22||||OA OB+212424453(22)+=⨯+=+, ∴k ==,这个常数为5; ----------------------------------------------------------10分 (ii )b k a =±,这个常数为22a b +.------------------------------------------------------------12分 21.解:(1)222111'()(0)ax x f x a x x x x--=--=>,--------------------------------1分 设2()1(0)g x ax x x =-->,①当0a ≤时,()0g x <,'()0f x <;------------------------------------------------------------2分 ②当0a >时,由()0gx =得x =0x =<, 记x =0x =则201()1()(),(0)2g x ax x a x x x x a =--=-->,∵102x a-> ∴当0(0,)x x ∈时,()0g x <,'()0f x <,当0(,)x x ∈+∞时,()0g x >,'()0f x >,--------------------------------------4分∴当0a ≤时,()f x 在(0,)+∞上单调递减;当0a >时,()f x在(0,上单调递减,在)+∞上单调递增.---5分 (2)不妨设12x x <,由已知得1()0f x =,2()0f x =, 即1111ln ax x b x =--,2221ln ax x b x =--,---------------------------------------------------6分 两式相减得21212111()ln ln ()a x x x x x x -=---, ∴212121ln ln 1x x a x x x x -=+-,---------------------------------------------------------------------------7分 要证121222x x ax x ++>, 即要证2112122121ln ln 122()x x x x x x x x x x -++>+-, 只需证21121221ln ln 2x x x x x x x x -+>⋅⋅-, 只需证222121212ln x x x x x x ->,即要证2121212ln x x x x x x ->,---------------------------------------9分 设21x t x =,则1t >,只需证12ln t t t->,------------------------------------------------------10分 设1()2ln (1)h t t t t t=-->,只需证()0h t >, 222221221(1)'()10t t t h t t t t t -+-=+-==>, ()h t ∴在(1,)+∞上单调递增,()(1)0h t h ∴>=,得证.---------------------------------------------------------------------------12分22.解:(1)由22cos 2a ρθ=得2222(cos sin )a ρθθ-=, -------------------------1分 又cos x ρθ=,sin y ρθ=,得222x y a -=,∴C 的普通方程为222x y a -=,-------------------------------------------------------------------2分 ∵过点(2,1)P 、倾斜角为30︒的直线l的普通方程为2)13y x =-+,--------------3分由22x t =+得112y t =+ ∴直线l的参数方程为212x ty ⎧=⎪⎪⎨⎪=+⎪⎩ (t 为参数);-------------------------------------------5分(2)将212x ty ⎧=⎪⎪⎨⎪=+⎪⎩代入222x y a -=,得221)2(3)0t t a ++-=,----------------------------------------------------------------6分依题意知221)]8(3)0a ∆=-->则上方程的根1t 、2t 就是交点A 、B 对应的参数,∵2122(3)t t a ⋅=-,由参数t 的几何意义知1212||||||||||PA PB t t t t ⋅=⋅=⋅,得12||2t t ⋅=,∵点P 在A 、B 之间,∴120t t ⋅<,∴122t t ⋅=-,即22(3)2a -=-,解得24a =(满足0∆>),∴2a =±,-------------8分 ∵1212||||||||||||||PA PB t t t t -=-=+,又121)t t +=-,∴||||||2PA PB -=.-------------------------------------------------------------------------10分 23.解:(1)法一:|()|||1||1|||(1)(1)|2f x x x x x =+--≤+--=,∴ 2()2f x -≤≤, ()f x 的值域为[-2, 2];----------------------------------------------------4分 法二:2,1()2,112,1x f x x x x -<-⎧⎪=-≤<⎨⎪≥⎩,得2()2f x -≤≤,∴()f x 的值域为[-2, 2];----------------------------------------------------------------------------4分 (2)由()3f x x a ≤+得|1||1|3a x x x ≥+---,由[2,1]x ∈-得10x -≤,∴ |1|13|1|21a x x x x x ≥++--=+--,----------------------------------------------------5分 设()|1|21g x x x =+-- (21)x -≤≤,①当21x -≤≤-时,10x +≤,()(1)2132g x x x x =-+--=--,∴ max ()(2)4g x g =-=;--------------------------------------------------------------------------7分 ②当11x -<≤时,10x +>,()121g x x x x =+--=-,∴ ()(1)1g x g <-=;-------------------------------------------------------------------------------9分 综上知,max ()4g x =,由()a g x ≥恒成立,得4a ≥,即a 的取值范围是[4,)+∞.---------------------------------10分。
揭阳一中2011届高三下学期第一次测试数学(理)试题及答案

广东揭阳一中2010-2011学年度第二学期高三第一次测试数学(理)试题第一部分(选择题,40分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合2{|0},{||2},M x x x N x x =-<=<则( ) A .M N φ= B .M N M = C .M N M = D .M N R =2.为了调查某厂2000名工人生产某种产品的能力,随机抽查了m 位工人某天生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35],频率分布直方图如右图所示,已知生产的产品数量在[20,25]之间的工人有6位,则m的值为 ( )A .600B .30C .20D .363.一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了ξ次球,则(12)P ξ=等于( ) A .101021235()()88C B .99211353()()888C ⋅ C .9921153()()88C D .9921135()()88C4.如果(,),2παπ∈且4sin ,sin()cos()542πααπα=+--那么= ( )A B . C D 5.若复数20101,1i z z i +==-则( ) A .—1 B .0 C .1D .(1)i +1005 6.下列说法错误的是( ) A .如果命题""p ⌝与命题“p q ∨”都是真命题,那么命题q 一定是真命题;B .命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0”;C .若命题:22:,10,:,10p x R x x p x R x x ∃∈-+<⌝∀∈-+≥则;D .1"sin ""30"2θθ==︒是的充分不必要条件 7.执行如图的程序框图,若p=8,则输出的S=( ) A .910 B .718C .89D .25 8.无论m 为任何数,直线:l y x m =+与双曲线222:12x y C b -=(b>0)恒有公共点,则双曲线C 的离心率e 的取值范围是( )A .(1,)+∞ B.)+∞ C.)+∞ D .(2,)+∞第二部分(非选择题 110分)二、填空题(本大题共6小题,每小题5分,共30分)(一)必做题(9—13题)9.一几何体的三视图(单位:cm )如右图所示,则此几何体的体积是 cm 3。
2011揭阳一模理综试题答案

2011年揭阳市高考“一模”理科综合试题参考答案及评分标准 第 1 页 共 5 页2011年揭阳市高考“一模”试题 理科综合参考答案及评分意见一、单项选择题(本题包括16小题,每小题4分,共64分。
每小题给出的四个选项中,只有一个选项符合题目要求)二、双项选择题(本题包括9小题,每小题6分,共54分。
每小题给出的四个选项中,有两个选项符合题目要求,全选对得6分,只选1个且正确得3分,错选、不选得0分)三、非选择题(本题包括11小题,共182分)(生物部分,4小题,共64分)26.(16分)(1)用高倍显微镜观察叶绿体 氧气 光能转变为储存在ATP 中的化学能(2)单位时间产生气泡多少(或单位时间收集到的气体体积量) 增加水中的二氧化碳的含量;或者是适当提高水温。
(3)BC (或B 点以后) 温度(或温度和氧气浓度,缺少“温度”不正确) (4)a+b 27.(16分)(1)次级卵母细胞 1 4 (2)② 联会、分离(3)100 DNA 分子的复制方式为半保留复制 (4)1/32 28.(16分)(1)抗体 T 促进B 细胞的增殖与分化(2)受体 兴奋或抑制 进行细胞间信息交流 (3)促甲状腺激素释放激素 、甲状腺激素(写出两种才得分)。
(4)神经-体液-免疫 29.(16分)2011年揭阳市高考“一模”理科综合试题参考答案及评分标准 第 2 页 共 5 页(1)①生长 两重②空白琼脂块 有无生长素③丙组落叶明显早于甲、乙组 三组的叶片几乎同时脱落(2)氯化钠溶液:不同浓度的NaCl 溶液,能使DNA 溶解或析出,从而起到提取DNA 的作用;95%乙醇:DNA 不溶于酒精,可以用于提取出含杂质较少的DNA ; 二苯胺:作为鉴定DNA 的试剂;洗涤剂:能溶解细胞膜,有利于细胞内DNA 的释放(答出每种试剂的名称和用途得2分)。
(化学部分,4小题,共64分)30.(16分)假设3:白色物质是Na 2O 和Na 2CO 3的混合物 (2分) (1)Na 2CO 2溶液显碱性,也会使酚酞变红(2分) (2)假设2(2分);方案2①中出现的白色沉淀是CaCO 3,所以燃烧后的白色产物中有Na 2CO 3存在;方案2②中滴加无色酚酞试液无明显现象,说明燃烧后的白色产物中没有Na 2O 存在(4分)(3)4Na+3CO 2====2Na 2CO 3+C (3分)(4)不同意,因为反应物中无氢元素(或违背质量守恒定律)(3分)(其他合理解释也给分) 31.(16分)(1)① 不能(3分) ② b 、 d (2分)(2)① 0.13mol/(L•min) (3分) ② 放(2分) 0.17 (3分)③ a=2b 且b>1(或a=2b 且 a>2) (3分)32.(16分)(1)MgCl 2(或氯化镁)(2分) 过滤(2分) 洗涤(2分)Mg 2+ + Ca (OH )2 = Mg (OH )2 + Ca 2+ (3分) (2)制备干燥的HCl 气体,抑制MgCl 2的水解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
oyxoy xoy xoxy侧视图正视图D C B A 揭阳市2011年高中毕业班高考第一次模拟考数学 (理科)本试卷共4页,21小题,满分150分.考试用时120分钟.参考公式:如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率k n kk n n P P C k P --=)1()(.锥体的体积公式:13V Sh =,其中S 表示底面积,h 表示高. 一.选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一 项是符合题目要求的. 1.函数2()lg(1)2x f x x x=---的定义域是A. (0, 2)B. (1,2)C. (2,)+∞D. (,1)-∞2.已知复数(tan 3)1i z iθ--=,则“3πθ=”是“z 是纯虚数”的A .充要条件B .必要不充分条件C .充分不必要条件D .既不充分也不必要条件3.已知(2,1,3)a =- ,(1,2,1)b =- ,若()a a b λ⊥-,则实数λ的值为A. -2B.143-C.145D. 2 4.已知函数(),0(),0.f x x y g x x >⎧=⎨<⎩是偶函数,()log a f x x =的图象过点(2,1),则()y g x =对应的图象大致是A B C D5. 一个正方体截去两个角后所得几何体的正视图(又称主视图)、 侧视图(又称左视图)如右图所示,则其俯视图为6. 已知函数()sin 3cos (0)f x x x ωωω=->的图象与x 轴的两个相邻交点的距离等于2π,则为得到函数()y f x =的图象可以把函数sin y x ω=的图象上所有的点A. 向右平移6π,再将所得图象上所有的点的纵坐标变为原来的2倍; B. 向右平移3π,再将所得图象上所有的点的纵坐标变为原来的2倍;C. 向左平移12π,再将所得图象上所有的点的纵坐标变为原来的12倍;D. 向左平移12π,再将所得图象上所有的点的纵坐标变为原来的2倍.7. 某市汽车牌照号码可以上网自编,但规定从左到右第二个号码只能从字母B 、C 、D 中选择,其他四个号码可以从09 这十个数字中选择(数字可以重复),某车主第一个号码(从左到右)只想在数字3、5、6、8、9中选择,其他号码只想在1、3、6、9中选择,则他的车牌号码可选的所有可能情况有. A .180种 B .360种 C .720种 D .960种 8. 已知直线:60l x y +-=和M :222220x y x y +---=,点A 在直线l 上,若直线AC 与M 至少有一个公共点C,且30MAC ∠=,则点A 的横坐标的取值范围是.A.(0,5)B.[1,5]C.[1,3]D.(0,3]二.填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~13题)9. 已知1{1,,1,2}2α∈-,则使函数y x α=在[0,)+∞上单调递增的所有α值为 .10.已知双曲线22221x y a b-=(a >0, b >0)的离心率为2,一个焦点与抛物线216y x =的焦点相同,则双曲线的焦点坐标为 ;渐近线方程为 . 11.已知α为锐角,且4cos(),45πα+=则cos α= . 12.记函数2()2f x x x =-+的图象与x 轴围成的区域为M ,满足0,,2.y y x y x ≥⎧⎪≤⎨⎪≤-⎩的区域为N ,若向区域M 上随机投一点P ,则点P 落入区域N 的概率为 .S=S/10i=i+1S=S+(a i -a)2输入a i 开始否结束输出S i≥10?i =1S =0是D EACB13. 某市新年第一个月前10天监测到空气污染指数如下表(主要污染物为可吸入颗粒物):(第i 天监测得到的数据记为i a )在对上述数据的分析中,一部分计算见右图所示的算法流程图 (其中a 是这10个数据的平均数),则输出的S 值是 ,S 表示的样本的数字特征是 .(二)选做题(14、15题,考生只能从中选做一题)14.(几何证明选做题)如图所示,圆的内接三角形ABC 的角平分线BD 与AC 交于点D ,与圆交于点E,连结AE ,已知ED=3, BD=6 ,则线段AE 的长= . 15.(坐标系与参数方程选做题) 已知直线112,:()2.x t l t y kt =-⎧⎨=+⎩为参数,2,:12.x s l y s =⎧⎨=-⎩(s 为参数),若1l //2l ,则k = ;若12l l ⊥,则k = . 三.解答题:本大题共6小题,满分80分.解答须写出文字说明、 证明过程和演算步骤. 16.(本小题满分12分)已知数列{}n a 是首项为2,公比为12的等比数列,n S 为{}n a 的前n 项和. (1)求数列{}n a 的通项n a 及n S ;(2)设数列{}n n b a +是首项为-2,第三项为2的等差数列,求数列{}n b 的通项公式及其前n 项和n T .i 1 2 3 4 5 6 7 8 9 10i a 61 59 60 57 60 63 60 6257 61第13题图 第14题图0.080.09(重量/克)0.050.045155105055004954900.020.030.06频率/组距0.0100.07产品重量(克)频数(490,495](495,500](500,505](505,510](510,515]481486某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图) (1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;(2)若以频率作为概率,试估计从乙流水线上任取5件产品,恰有3件产品为合格品的概率; (3)由以上统计数据完成下面22⨯列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关” .甲流水线乙流水线合计 合格品 a = b = 不合格品 c =d =合 计n =附:下面的临界值表供参考:(参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++)2()p K k ≥0.15 0.10 0.05 0.025 0.010 0.005 0.001 k2.0722.7063.8415.0246.6357.87910.828HGDE FABC已知如图:平行四边形ABCD 中,2BC =, BD ⊥CD ,正方形ADEF 所在平面与平面ABCD 垂直,G ,H 分别是DF ,BE 的中点.(1)求证:GH ∥平面CDE ; (2)记CD x =,()V x 表示四棱锥F-ABCD 体积,求()V x 的表达式;(3)当()V x 取得最大值时,求平面ECF 与平面ABCD所成的二面角的正弦值.如图,某人在塔的正东方向上的C处在与塔垂直的水平面内沿南偏西60°的方向以每小时6千米的速度步行了1分钟以后,在点D处∠=α,α的望见塔的底端B在东北方向上,已知沿途塔的仰角AEB最大值为60 .(1)求该人沿南偏西60°的方向走到仰角α最大时,走了几分钟;(2)求塔的高AB.在直角坐标系xoy 上取两个定点12(2,0),(2,0)A A -,再取两个动点1(0,),N m 2(0,)N n ,且3mn =.(1)求直线11A N 与22A N 交点的轨迹M 的方程;(2)已知点(1,)A t (0t >)是轨迹M 上的定点,E,F 是轨迹M 上的两个动点,如果直线AE 的斜率AE k 与直线AF 的斜率AF k 满足0AE AF k k +=,试探究直线EF 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.已知函数()||,()f x x x a a R =-∈(1)若2a =,解关于x 的不等式()f x x <;(2)若对(0,1]x ∀∈都有()(,f x m m R m <∈是常数),求a 的取值范围.66y=6-xy xOCBAM 揭阳市2011年高中毕业班高考第一次模拟考答案数学 (理科)一.选择题:B C D B C A D B 解析: 2. ∵(tan 3)1(tan 3)i z i iθθ--==-+,当3πθ=时,z i =是纯虚数,反之当z 是纯虚数时,θ未必为3π,故选C. 3. (2,12,3)a b λλλλ-=--- ,由()a a b λ⊥-得2(2)12930λλλ--+-+-=2λ⇒=,选D.4. 依题意易得2()log f x x =(0x >)因函数的图象关于y 轴对 称,可得2()log ()g x x =-(0x <),选B.5. 依题意可知该几何体的直观图如右,其俯视图应选C. 资料来源:数学驿站 6. 依题意知2ω=,故()2sin(2)3f x x π=-2sin 2()6x π=-,故选A. 7. 共有1111153444960A A A A A ⋅⋅⋅⋅=种,选D.8. 如右图,设点A 的坐标为00(,6)x x -,圆心M 到直线AC 的距离为d,则||sin30d AM = ,因直线AC 与M 有交点,所以||sin302d AM =≤2200(1)(5)16x x ⇒-+-≤015x ⇒≤≤,故选B.二.填空题:9. 1,1,22;10.(-4,0),(4,0)、3y x =±; 11.7210; 12.34; 13. 3.4、样本的方差;14. 33;15. 4、-1. 解析:10. 依题意得双曲线的焦点坐标为(-4,0),(4,0),由22ce a a==⇒= ∴2223b c a =-=,∵双曲线的焦点在x 轴,∴双曲线的渐近线方程为3y x =±. 11. cos cos 44ππαα⎡⎤⎛⎫=+-== ⎪⎢⎥⎝⎭⎣⎦1027(1,1)2y=2-xy=x oyxD EACB12. 如图由定积分的几何意可得区域M 的面积,22(2)M S x x dx =-+=⎰1(3-32204)|3x x +=,区域N 的面积12112N S =⨯⨯=,由几何概型的概 率计算公式可得所求的概率34N M S P S ==. 14. ∵,E E EAD EBA ∠=∠∠=∠∴EDA ∆∽EAB ∆AE EDBE AE⇒= 2AE ED BE ⇒=⋅39=⨯33AE ⇒=.15. 将1l 、2l 的方程化为直角坐标方程得:1:240l kx y k +--=,2:210l x y +-=,由1l //2l 得24211k k+=≠⇒4k =,由12l l ⊥得220k +=1k ⇒=- 三、解答题:16. 解:(1)∵数列{}n a 是首项12a =,公比12q =的等比数列 ∴1212()22n n n a --=⋅=,--------------------------------3分 12(1)124(1)1212n n n S -==--.------------------------------6分 (2)依题意得数列{}n n b a +的公差2(2)22d --==----------------- -7分 ∴22(1)24n n b a n n +=-+-=-∴2242n n b n -=----------------------------------------------9分 设数列{}n n b a +的前n项和为n P则(224)(3)2n n n P n n -+-==---------------------------------10分∴221(3)4(1)3422nn n n n T P S n n n n -=-=---=--+.--------- -12分(其他解法请参照给分) 17. 解:(1)甲流水线样本的频率分布直方图如下:-----------------------------------------------4分(2)由图1知,乙样本中合格品数为(0.060.090.03)54036++⨯⨯=,H G DEFABC 故合格品的频率为360.940=,据此可估计从乙流水线上任取一件产品该产品为合 格品的概率0.9P =,----------------------------------------------------6分设ξ为从乙流水线上任取5件产品中的合格品数,则(5,0.9)ξ∴3325(3)(0.9)(0.1)0.0729P C ξ===.即从乙流水线上任取5件产品,恰有3件产品为合格品的概率为0.0729.------8分 (3)22⨯列联表如下:-------10分 ∵22()()()()()n ad bc K a b c d a c b d -=++++=280(120360) 3.11766144040⨯-≈⨯⨯⨯ 2.706> ∴有90%的把握认为产品的包装质量与两条自动包装流水线的选择有关.----------12分18、(1)证法1:∵//EF AD ,//AD BC ∴//EF BC 且EF AD BC == ∴四边形EFBC 是平行四边形 ∴H 为FC 的中点-------------2分 又∵G 是FD 的中点 ∴//HG CD ---------------------------------------3分 ∵HG ⊄平面CDE ,CD ⊂平面CDE∴GH ∥平面CDE ---------------------------------4分 证法2:连结EA ,∵ADEF 是正方形 ∴G 是AE 的中点 -------1分∴在⊿EAB 中,//GH AB -------------------------------------------2分 又∵AB ∥CD ,∴GH ∥CD ,----------------------------------------3分 ∵HG ⊄平面CDE ,CD ⊂平面CDE∴GH ∥平面CDE ---------------------------------------------------4分 (2)∵平面ADEF ⊥平面ABCD ,交线为AD且FA ⊥AD , ∴FA ⊥平面ABCD .-------------------------------6分∵BD ⊥CD, 2BC =,CD x = ∴FA =2,24BD x =-(02x <<) ∴ ABCD S CD BD =⋅ =24x x - ∴212()433ABCD V x S FA x x =⋅=- (02x <<)---------------------8分 (3)要使()V x 取得最大值,只须24x x -=22(4)x x -(02x <<)取得最大值,∵222224(4)()42x x x x +--≤=,当且仅当224,x x =-即2x =时 ()V x 取得最大值--------------------------------------------------10分甲流水线 乙流水线 合计 合格品 a =30 b =36 66 不合格品 c =10d =414合 计4040n =80HGDEFABCMz yxHGDEFABC解法1:在平面DBC 内过点D 作DM BC ⊥于M ,连结EM ∵BC ED ⊥ ∴BC ⊥平面EMD ∴BC EM ⊥∴EMD ∠是平面ECF 与平面ABCD 所成的二面角的平面角-------12分 ∵当()V x 取得最大值时,2CD =,2DB =∴112DM BC ==,225EM ED DM =+=∴25sin 5ED EMD EM ∠==即平面ECF 与平面ABCD 所成的二面角的正弦值为255.-------------------------14分 解法2:以点D 为坐标原定,DC 所在的直线为x轴建立空间直角 坐标系如图示,则(0,0,0)D ,(2,0,0),(0,2,0),(0,0,2)C B E∴(0,0,2)DE = ,(2,0,2)EC =- ,(0,2,2)EB =--------12分设平面ECF 与平面ABCD 所成的二面角为θ,平面ECF 的法向量(,,)n a b c =由,,n EC n EB ⊥⊥得220,220a c b c -=-=令1c =得(2,2,1)n =又∵平面ABCD 的法向量为DE∴25cos 5||||25DE n DE n θ⋅===⋅⋅∴25sin 5θ=.------------------14分 19、解:(1)依题意知在△DBC 中30BCD ∠= ,18045135DBC ∠=-=CD=6000×160=100(m),1801353015D ∠=--=,------3分由正弦定理得sin sin CD BCDBC D=∠∠∴sin 100sin15sin sin135CD D BC DBC ⋅∠⨯==∠=6210050(62)450(31)222-⨯-==-(m)-----6分 在Rt △ABE 中,tan ABBEα= 资料来源:数学驿站 ∵AB 为定长 ∴当BE 的长最小时,α取最大值60°,这时BE CD ⊥------------------8分 当BE CD ⊥时,在Rt △BEC 中cos EC BC BCE =⋅∠350(31)25(33)2=-⋅=-(m),--------------------9分 设该人沿南偏西60°的方向走到仰角α最大时,走了t 分钟, 则25(33)606060006000EC t -=⨯=⨯334-=(分钟)--------------------------------10分(2)由(1)知当α取得最大值60°时, BE CD ⊥,在Rt △BEC 中,sin BE BC BCD =⋅∠--------------------- -----------12分∴tan 60sin tan 60AB BE BC BCD =⋅=⋅∠⋅=150(31)325(33)2-⋅⋅=-(m ) 即所求塔高为25(33)-m.----------------------------------------- -----14分 20、解:(1)依题意知直线11A N 的方程为:(2)2my x =+------------------------①-----1分 直线22A N 的方程为:(2)2ny x =-----------------------------------②----------2分 设(,)Q x y 是直线11A N 与22A N 交点,①×②得22(4)4mn y x =-- 由3mn = 整理得22143x y +=----------------------------------------5分 ∵12,N N 不与原点重合 ∴点12(2,0),(2,0)A A -不在轨迹M 上-----------------6分∴轨迹M 的方程为22143x y +=(2x ≠±)-----------------------------------7分 (2)∵点(1,)A t (0t >)在轨迹M 上 ∴21143t +=解得32t =,即点A 的坐标为3(1,)2-----8分设AEk k =,则直线AE 方程为:3(1)2y k x =-+,代入22143x y +=并整理得 2223(34)4(32)4()1202k x k k x k ++-+--=-------------------------10分设(x ,y )E E E ,(x ,y )F F F , ∵点3(1,)2A 在轨迹M 上,∴2234()122x 34E k k--=+ ------③, 32E E y kx k =+------④---------------------11分 又0AE AF k k +=得AF k k =-,将③、④式中的k 代换成k -,可得2234()122x 34F k k +-=+,32F Fy kx k =-++------------12分∴直线EF 的斜率()2F E F E EFF E F Ey y k x x kK x x x x --++==--∵2228624,4343E F F Ek k x x x x k k -+=-=++ ∴22222862(86)2(43)1432424243EF k k kk k k k k K k k k --⋅+--+++===+即直线EF 的斜率为定值,其值为12-----------------------------------14分21、解:(1)当2a =时,不等式()f x x <即|2|x x x -<显然0x ≠,当0x >时,原不等式可化为:|2|1121x x -<⇒-<-<13x ⇒<<-------2分当0x <时,原不等式可化为:|2|121x x ->⇒->或21x -<-3x ⇒>或1x <∴0x <-----4分综上得:当2a =时,原不等式的解集为{|130}x x x <<<或-----------------5分 (2)∵对(0,1]x ∀∈都有()f x m <,显然0m >即()m x x a m -<-<⇒对(0,1]x ∀∈,m mx a x x-<-<恒成立 ⇒对(0,1]x ∀∈,m mx a x x x-<<+-------------------------------------6分 设(),(0,1]m g x x x x =-∈,()mp x x x =+,(0,1]x ∈则对(0,1]x ∀∈,m mx a x x x-<<+恒成立⇔max min ()()g x a p x <<,(0,1]x ∈----8分∵2'()1,mg x x=+当(0,1]x ∈时'()0g x >∴函数()g x 在(0,1]上单调递增,∴max ()1g x m =------9分又∵2'()1m p x x =-=2()()x m x m x-+,当1m ≥即1m ≥时,对于(0,1]x ∈,'()0p x < ∴函数()p x 在(0,1]上为减函数∴min ()(1)1p x p m ==+----------------11分 当1m <,即01m <<时,当(0,]x m ∈,'()0p x ≤当(,1]x m ∈,'()0p x > ∴在(0,1]上,min ()()2p x p m m ==-------12分 (或当01m <<时,在(0,1]上,()m p x x x =+22mx m x≥⋅=,当x m =时取等号) 又∵当01m <<时,要max min ()()g x a p x <<即12m a m -<<还需满足21m m >-解得3221m -<<∴当3221m -<<时,12m a m -<<; ---------13分当1m ≥时,11m a m -<<+.------------------------------------14分。
