配位化学价键理论
合集下载
配位化学第三章
实例：
[Ti(H2O)6]3+ K3[Mn(CN)6] K3[Fe(CN)6]
Ti3+： 3d1 Mn3+： 3d4 Fe3+： 3d5
µ=1.73 n =1 µ=3.18 n =2 µ=2.40 n =1
配位化学第三章
配合物的空间构型与中心离子的 杂化类型、配位数的关系
配位数 2
4
6
杂化
类型 sp
CN-的成键π2pz 轨道肩并肩重叠形成离域π键。
CN
NC
CN
Ni2+
配位化学第三章
NC
3.1.2 价键理论的应用
（1）解释了配合物的空间构型 （2）说明配合物的磁性 （3）比较同类配合物的稳定性
配位化学第三章
举例说明：
1. 已知[Ag(NH3)2]+的μm=0，用VB法说明其空
间结构。
4d
5s
5p
Ag+ [Kr]
4d
5p
[Ag(NH3)2]+
NH3 NH3 sp杂化 所以[Ag(NH3)2]+的空间构型为直线型。
配位化学第三章
2. [BeX4]2-的空间构型为四面体。为什么？
Be2+
1s
2s
2p
[BeX4]2-
1s
X- X- X- X-
sp3杂化
在[BeX4]2- 中，由于Be2+采取sp3杂化，所以 [BeX4]2-的 空间构型是正四面体。
dsp2
sp3 sp3d2或d2sp3
型空 间 构
直线形 平面正方形
四面体
八面体
举例：Ag(NH3)2 Ni(C)N24 NiCl24
配位化合物的化学键理论
八面体场中的中心原子d轨道
X X
X MX X X
八面体场中d轨道的分裂
球形场
成键作用和电子结构 八面体场中的d轨道能级分裂
Eeg-Et2g=Δo 2Eeg+3Et2g=0
成键作用和电子结构 四面体场中的中心原子d轨道
成键作用和电子结构
八面体和四面体晶体场能级分裂图
Δt＝ 49Δo
平面四方形 线形
16
对于Fe3+而言，它的内轨型配合物与外轨型配 合物的未成对电子数分别为1和5，差距甚大。这使 得它们的磁性不同。因而用磁性可以判断Fe3+的6配 位络合物属于哪种杂化类型。例如：
配离子 计算磁矩 实测磁矩 杂化类型
Fe(CN)63- 1.73 Fe(H2O)63+ 5.92
2.3 内轨型(低自旋) 5.88 外轨型(高自旋)
10
1. ns np nd 杂化 （外轨型配合物）
例 讨论Fe(H2O)63＋ 配离子中的成键情况Leabharlann 解:3d4s
4p
4d
Fe [Ar]
Fe3+ [Ar]
Fe3+ [Ar]
sp3d2（ 外 轨 型 ）
Fe3+ [Ar]
d2sp3（ 内 轨 型 ） 铁(III)离子的内轨型和外轨型电子构型
11
3d
Ni [Ar]
配合物的化学键理论
配位化合物的价键理论 配位化合物的晶体场理论
1
1 配位化合物的基本概念
1） 配位化合物定义 由中心原子（或离子）和几个配体分子（或离子）
以配位键相结合而形成的复杂分子或离子，通常称为配位 单元，含有配位单元的化合物称为配位化合物。
配位阳离子： [Co ( NH3 )6 ]3＋ 和 [Cu ( NH3 )4]2＋ 配位阴离子： [Cr(CN)6]3－ 和 [Co(SCN)4]2－ 中性配合物分子：Ni(CO)4 和Cu(NH2CH2COO)2
X X
X MX X X
八面体场中d轨道的分裂
球形场
成键作用和电子结构 八面体场中的d轨道能级分裂
Eeg-Et2g=Δo 2Eeg+3Et2g=0
成键作用和电子结构 四面体场中的中心原子d轨道
成键作用和电子结构
八面体和四面体晶体场能级分裂图
Δt＝ 49Δo
平面四方形 线形
16
对于Fe3+而言，它的内轨型配合物与外轨型配 合物的未成对电子数分别为1和5，差距甚大。这使 得它们的磁性不同。因而用磁性可以判断Fe3+的6配 位络合物属于哪种杂化类型。例如：
配离子 计算磁矩 实测磁矩 杂化类型
Fe(CN)63- 1.73 Fe(H2O)63+ 5.92
2.3 内轨型(低自旋) 5.88 外轨型(高自旋)
10
1. ns np nd 杂化 （外轨型配合物）
例 讨论Fe(H2O)63＋ 配离子中的成键情况Leabharlann 解:3d4s
4p
4d
Fe [Ar]
Fe3+ [Ar]
Fe3+ [Ar]
sp3d2（ 外 轨 型 ）
Fe3+ [Ar]
d2sp3（ 内 轨 型 ） 铁(III)离子的内轨型和外轨型电子构型
11
3d
Ni [Ar]
配合物的化学键理论
配位化合物的价键理论 配位化合物的晶体场理论
1
1 配位化合物的基本概念
1） 配位化合物定义 由中心原子（或离子）和几个配体分子（或离子）
以配位键相结合而形成的复杂分子或离子，通常称为配位 单元，含有配位单元的化合物称为配位化合物。
配位阳离子： [Co ( NH3 )6 ]3＋ 和 [Cu ( NH3 )4]2＋ 配位阴离子： [Cr(CN)6]3－ 和 [Co(SCN)4]2－ 中性配合物分子：Ni(CO)4 和Cu(NH2CH2COO)2
13-2配位化合物
1
(二)配合物的形成和空间构型
1、 sp杂化（配位数为2，直线型）
[Ag(NH3)2]+：Ag+的外围电子构型 4d105s05p0
2
中心离子Ag+的结构
4d
5s
5p
[Ag(NH3)2]+的结构
4d
sp杂化
5p
结果： [Ag(NH3)2]+形成之前和之后, 中心原子的d电子排
布没有变化 。配合物是直线型，μ = 0
H2O以前------弱场 H2O ~ NH3之间------中间场 NH3以后------强场
37
(三) d 轨道能级分裂后，d 电子在轨道上排布 遵循的原则 (重点掌握)
概念：电子成对能( p ) 分裂能()
1、能量最低原理 2、 p > ，弱场 3、 p < ，强场
电子尽可能以自旋相同方式分占不同的轨道 弱场—高自旋排布方式 如：[FeF6]3-
CN
中心原子的d电子
CN
CN CN
Question
Solution
1s
试画出[BeF4]2–或[Be(H2O) 4]2+ 的结构。
2s 2s
2p 2p
Be 2
[BeX4 ]
2
1s
F（H 2 O）
F-
F-
F-
（ （ （H 2 O） H 2 O） H 2 O）
sp3杂化
4， sp3d2杂化（配位数为6， 八面体构型） [FeF6]3–
d
z
2
能 量
= 4.45 Dq d E = -2.67 Dq
d xy
s = 17.42Dq
四面体场
八面体场
(二)配合物的形成和空间构型
1、 sp杂化（配位数为2，直线型）
[Ag(NH3)2]+：Ag+的外围电子构型 4d105s05p0
2
中心离子Ag+的结构
4d
5s
5p
[Ag(NH3)2]+的结构
4d
sp杂化
5p
结果： [Ag(NH3)2]+形成之前和之后, 中心原子的d电子排
布没有变化 。配合物是直线型，μ = 0
H2O以前------弱场 H2O ~ NH3之间------中间场 NH3以后------强场
37
(三) d 轨道能级分裂后，d 电子在轨道上排布 遵循的原则 (重点掌握)
概念：电子成对能( p ) 分裂能()
1、能量最低原理 2、 p > ，弱场 3、 p < ，强场
电子尽可能以自旋相同方式分占不同的轨道 弱场—高自旋排布方式 如：[FeF6]3-
CN
中心原子的d电子
CN
CN CN
Question
Solution
1s
试画出[BeF4]2–或[Be(H2O) 4]2+ 的结构。
2s 2s
2p 2p
Be 2
[BeX4 ]
2
1s
F（H 2 O）
F-
F-
F-
（ （ （H 2 O） H 2 O） H 2 O）
sp3杂化
4， sp3d2杂化（配位数为6， 八面体构型） [FeF6]3–
d
z
2
能 量
= 4.45 Dq d E = -2.67 Dq
d xy
s = 17.42Dq
四面体场
八面体场
配位化学2
为什么？ ★物质的磁矩于物质中原子或离子的未成对 电子数n有关
m B n(n 2)
[FeF6]3-
(4)sp3(4)d2
3d
4s
4p
4d
[Fe(CN)6
]3-
(3)d2(4)sp3
[Co(CN)6]3-
Co3+ d6电子构型
(3)d2(4)sp3
μ= 4.9B· M μ=0 B· M
3、解释配合物的稳定性
配位原子的电负性很大，对中心原子的结构影 响很小。 Fe3+, d1d1d1d1d1(sp3d2+6F-)12 外轨型配合物
配位原子的电负性很小，对中心原子的结构 影响很大。 Fe3+, d2d2d1(d2sp3+6CN-)12 内轨型配合物
4、电中性原理和反馈π键 ★电中性原理：中心原子的净电荷量越接近于 零，配合物才能越稳定存在。 [Co(NH3)6]3+
五、姜－泰勒效应
在对称的非线性分子中，体系不可能在轨道简并状 态下保持稳定，而必然要发生畸变并使得一个轨道 的能级降低，消除简并性。
对于d9组态的Cu2+
(t2 g ) 6 ( d z 2 ) 2 ( d x2 y 2 )1 (t2 g ) 6 ( d x2 y 2 ) 2 ( d z 2 )1
◆
平面正方形配合物 主要是d8电子构型的过渡金属。
低自旋
d轨道在其他构型配合物中的能级分裂 E = 12.28 Dq
d
x y2
2
能 量
E = 1.78 Dq d
= 4.45 Dq d E = -2.67 Dq
d E = 6 Dq E = 0 Dq = 10 Dq E = 2.28 Dq d xy
9.3 配位化合物的化学键理论
1s22s2p
Be2+
sp3杂化
[BeCl4]2-:四面体
例3：[NiCl4]2-和[Ni(CN)4]2-
Ni2+,3d8构型,性质与杂化方式和几何构型？
[NiCl4]2-:3d84s4p
Ni2+
sp3杂化
[NiCl4]2-四面体
2单电子，顺磁性
[Ni(CN)4]2-3d84s4p
Ni2+
dsp2杂化
这种键具有部分双键特征，它比通常的σ配键的键能大，键长短，其配合物的稳定性强。
注意：反馈π键必须与σ配键同时存在。
形成反馈π键的条件：
M有成对ｄ电子，L有匹配的空轨道。
显然，Be2+,Al3+没有d电子，不形成反馈π键；而Sn2+, Sb3+, Pb2+等d电子被外层的s电子屏蔽，也不能形成反馈π键。
高←d8→低
(3)稳定性
同一金属离子配合物稳定性：内轨型>比外轨型。
内轨型总键能-成对能>外轨型总键能
(4)判断外轨型(高自旋)和内轨型(低自旋)配合物的方法：
*测量配合物的磁矩
外轨型配合物单电子数较多，磁矩大；
内轨型配合物单电子数目较少，磁矩小。
单电子数n与物质的磁矩μ的近似关系式为：
B.M
例如：[FeF6]3-中有5个单电子，理论磁矩值为：
[Ni(CN)4]2-
无单电子，抗磁性几何构型：正方形
注意：
Zn2+、Cd2+、Hg2+:d10，只能用外层轨道，它们形成的4配位配合物:sp3杂化，四面体
(n-1)d10nsnp
Pd2+、Pt2+、Au3+:d8，能用1个内层d轨道，它们形成的4配位配合物:dsp2杂化，正方形
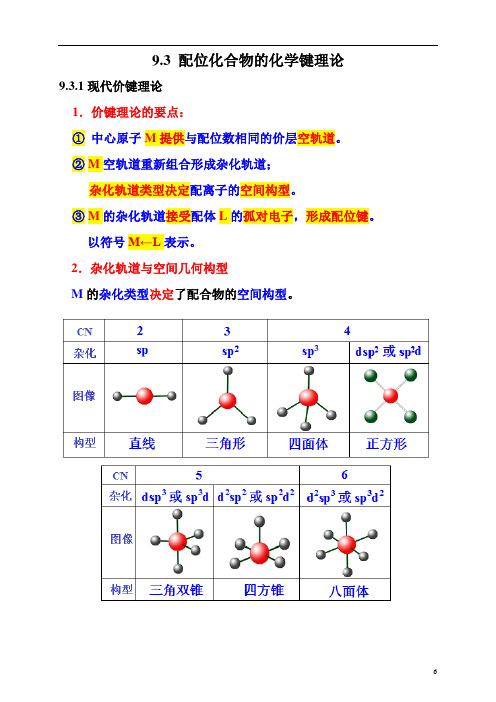
Be2+
sp3杂化
[BeCl4]2-:四面体
例3：[NiCl4]2-和[Ni(CN)4]2-
Ni2+,3d8构型,性质与杂化方式和几何构型？
[NiCl4]2-:3d84s4p
Ni2+
sp3杂化
[NiCl4]2-四面体
2单电子，顺磁性
[Ni(CN)4]2-3d84s4p
Ni2+
dsp2杂化
这种键具有部分双键特征，它比通常的σ配键的键能大，键长短，其配合物的稳定性强。
注意：反馈π键必须与σ配键同时存在。
形成反馈π键的条件：
M有成对ｄ电子，L有匹配的空轨道。
显然，Be2+,Al3+没有d电子，不形成反馈π键；而Sn2+, Sb3+, Pb2+等d电子被外层的s电子屏蔽，也不能形成反馈π键。
高←d8→低
(3)稳定性
同一金属离子配合物稳定性：内轨型>比外轨型。
内轨型总键能-成对能>外轨型总键能
(4)判断外轨型(高自旋)和内轨型(低自旋)配合物的方法：
*测量配合物的磁矩
外轨型配合物单电子数较多，磁矩大；
内轨型配合物单电子数目较少，磁矩小。
单电子数n与物质的磁矩μ的近似关系式为：
B.M
例如：[FeF6]3-中有5个单电子，理论磁矩值为：
[Ni(CN)4]2-
无单电子，抗磁性几何构型：正方形
注意：
Zn2+、Cd2+、Hg2+:d10，只能用外层轨道，它们形成的4配位配合物:sp3杂化，四面体
(n-1)d10nsnp
Pd2+、Pt2+、Au3+:d8，能用1个内层d轨道，它们形成的4配位配合物:dsp2杂化，正方形
配位化合物的化学键理论
2 晶体场稳定化能 ( C F S E )
d 电子在晶体场中分裂后的d轨道中排布，其能量
用E晶 表示，在球形场中的能量用E球 表示。因晶体场
的存在，体系总能量的降低值称为晶体场稳定化能 ( Crystal Field Stabilization Energy )。 由E球＝0，则 CFSE ＝ E球－E晶 ＝ 0 － E晶
d
dz2 dx2-y2
d
dxy dxz dyz
Jahn－Teller 效应
解释 Cu(NH3)42＋ 离子的正方形结构，
[Cu(NH3)4(H2O)2]2＋ 离子为拉长的八面体结构？
按晶体场理论，Cu2＋ 为d9 电子构型。在八面体场
中，最后一个电子有两种排布方式：一种是最后一个电子
应用： 用晶体场稳定化能解释水合热的双峰 曲线 M2+(g) + 6H2O(l) = M(H2O)62+(aq)
d 电子数 |H|
第一过渡元素M2+的水合热绝对值 对其d电子数作图 热力学对水合热的计算，随d电子数的增加，水合热 应是平缓上升的直线，如图中虚线所示，但是实验数 据作图为双峰曲线，为什么？
原子轨道；
Pauli原理：同一原子轨道只能容纳自旋方
式不同的两个电子；
Hund规则：电子分布到能量简并的原子轨
道上时，优先以自旋相同的方式分占不同
轨道。
例 讨论过渡金属 d 4 组态在八面体场中电子排布。
低自旋方式 △ > P
高自旋方式 △ < P
分裂能△ ：简并的d轨道分裂后最高能量d
轨道和最低能量d轨道之差；
配位阴离子： [Cr(CN)6]3－ 和 [Co(SCN)4]2－
配位化学讲义 第四章(1) 价键理论、晶体场理论
配位化学讲义第四章（1）价键理论、晶体场理论第三章配合物的化学键理论目标：解释性质，如配位数、几何结构、磁学性质、光谱、热力学稳定性、动力学反应性等。
三种理论：①价键理论、②晶体场理论、③分子轨道理论第一节价键理论（Valencebond theory）由L.Pauling提出要点：①配体的孤对电子可以进入中心原子的空轨道；②中心原子用于成键的轨道是杂化轨道（用于说明构型）。
一、轨道杂化及对配合物构型的解释能量相差不大的原子轨道可通过线性组合构成相同数目的杂化轨道。
对构型的解释（依据电子云最大重叠原理：杂化轨道极大值应指向配体）指向实例sp3、sd3杂化四面体顶点Ni(CO)4sp2、sd2、dp2、d3杂化三角形顶点[AgCl3]2-dsp2、d2p2 杂化正方形顶点[PtCl4]2-d2sp3杂化八面体顶点[Fe(CN)6]4-sp杂化直线型[AgCl2]-二、AB n型分子的杂化轨道1、原子轨道的变换性质考虑原子轨道波函数，在AB n分子所属点群的各种对称操作下的变换性质。
类型轨道多项式sp x xp p y yp z zd xy xyd xz xzd d yz yzd x2-y2x2-y2d z22z2-x2-y2（简记为z2）*s轨道总是按全对称表示变换的。
例：[HgI3]- (D3h群)平面三角形A1′：d z2、sE′：(p x、p y )、(d x2-y2、d xy)A 2″：p zE″：(d xz、d yz)2、σ轨道杂化方案1）四面体分子AB4（Td）[CoCl4]2-以四个杂化轨道的集合作为分子点群(Td)表示的基，确定该表示的特征标：r1r4r2r3恒等操作，χ(E)=4 C3操作，χ(C3)=1对C2、S4和σd用同样方法处理，得T d E 8C3 3C2 6S46σdΓ 4 1 00 2约化：T d E 8C3 3C2 6S4 6σdA1 1 1 1 11A2 1 1 1 -1 - 1E 2 -1 2 00 (z2, x2-y2)T1 3 0 -1 1 -1T2 3 0 -1 -11 (xy,xz,yz) (x,y,z)a(A1)=1/24(1×4+8×1×1+3×1×0+6×1×0+6×1×2)=1a(A2)=1/24 [1×4+8×1×1+3×1×0+6×(-1)×0+6×(-1)×2]=0a(E)=1/24 [2×4+8×(-1)×1+3×2×0+6×0×0+6×0×2]=0a(T1)=1/24 [3×4+8×0×1+3×(-1)×0+6×1×0+6×(-1)×2]=0a(T2)=1/24 [3×4+8×0×1+3×(-1)×0+6×(-1)×0+6×1×2]=1约化结果Γ=A1+T2由特征标表：A1T2s(p x、p y、p z)(d xy、d xz、d yz)可有两种组合：sp3（s、p x、p y、p z）、sd3（s、d xy、d xz、d yz)* 以一组杂化轨道为基的表示的特征标的简化计算规则：①不变（1）②改变符号（-1）③与其他函数变换（0）2）再以[CdCI5]3-三角双锥(D3h)为例：41325D3h E 2C33C2σh2S3 3σvΓ 5 2 13 0 3约化结果：Γ= 2A1′+A2〞+E′A1′A2〞E′s p z (p x、p y)d z2(d xy、d x2-y2)两种可能的组合：（s、d z2、p z 、p x、p y）( s、d z2、p z、d xy、d x2-y2)3）[HgI3]- ( D3h)123D3h E 2C3 3C2σh2S33σvΓ 3 0 13 0 1约化得：Γ=A1′+E′A1′E′s (p x、p y)d z2(d xy、d x2-y2)可能的组合有：（s、p x、p y）、(s、d xy、d x2-y2)、(d z2、p x、p y)、(d z2、d xy、d x2-y2)4）平面AB4型分子（D4h）例：[PtCl4]2-C2′C2″D4h E 2C4(C41,C43) C2(C42) 2C2′2C2″i 2S4σh 2σv2σdΓ 4 0 0 20 0 0 4 2 0约化得：Γ=A1g+B1g+E uA1g B1g E us d x2-y2(p x、p y)d z2两种类型：dsp2（d x2-y2、s、p x、p y）、d2p2（d z2、d x2-y2、p x、p y）5）八面体AB6(O h) 例：[Fe(H2O)6]3+O h E 8C3 6C26C4 3C2i 6S4′8S6 3σh 6σdΓ 6 0 0 2 2 0 0 0 4 2约化得：Γ=A1g+E g+T1u A1g E gT1us (d z2、d x2-y2) (p x、p y、p z)只有唯一的d2sp3杂化（d z2、d x2-y2、s、p x、p y、p z)3、π成键杂化方案在AB n分子中，原子A上要有2n个π型杂化轨道和在B原子上的2n个π原子轨道成键。
配合物化学键理论
强场：o > P 弱场：o < P
d5 型
强场o > P
弱场o < P
（4） 影响CFSE的因素 ① d电子数目； ② 配位体的强弱； ③ 晶体场的类型
表1 过渡金属络离子的稳定化能(CFSE)
弱场CFSE/Dq
dn d0 离子 Ca2+，Sc3+ 正方型 0 正八面体 0 正四面 体 0 正方型 0
中心离子用外层(n-1)d，ns，np杂化轨道与电负性 较小的配位原子，如CN-、NO2-等形成内轨型配合 物。例如[Fe(CN)6]3-配离子，Fe采用d2sp3内轨型 杂化轨道，配合物的键能大，稳定，在水中不易 离解。
(3)内、外轨型配合物的测定---磁矩
由磁矩可判断内轨或外轨型配合物
s n—分子中未成对电子数
z
y
x
x
dz2
y z
dx2-y2
z
x
x
y
dxy
dxz
dyz
1.分裂能 （1）分裂能与配合物几何构型的关系
八面体型的配合物
在八面体型的配合物中，6个配位体分别占据八 面体的6个顶点，由此产生的静电场叫做八面体场。
(1)八面体场
八面体场中d轨道能级分裂
dz2 dx2-y2 eg 3 5 Δo =6Dq Δ o =10Dq 2 5 Δ o = 4Dq t2g dxy dxz dyz
[CrCl6]313600
[MoCl6]319200
分裂能与配位体的关系：光谱化学序列
[CoF6]3- [Co(H2O)6]3+ [Co(NH3)6]3+ o/cm-1 13000 18600 22900 [Co(CN)6]334000
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
杂化轨道理论(HOT)
原子在化合过程中为了使形成的化学键 强度更大，更利于体系能量的降低，趋向于 将原有的原子轨道进一步组合成新的相同数 目的原子轨道。这种线性组合称为杂化，杂 化后的原子轨道称为杂化轨道。 原有的原子轨道要组合成新的原子轨 道，必须具备能量近似的条件。
电价配合物和共价配合物
在配合物的价键理论中，Pauling曾把配合物分 为电价配合物和共价配合物两大类。在电价配合物 中，把作为中心原子的阳离子与配体之间的键合归 结为静电吸引，该金属离子在配合物中的电子分布 情况与相应的自由金属离子的相同。 在共价配合物中，中心原子以适当的空轨道接 受配体提供的孤对电子而形成配位键。
5.重键（双键和叁键）电子对对单键电子对的斥力 大于单键之间的斥力。例如乙烯和甲醛分子的C原 子的SN均为3，因此其理想的键角为120º，而实 验测得的结构为：
116.6°
121.7° H H C C H H 121.7°
115.8°
122.1° H C O H 122.1°
VSEPR法对SN为2至6的分子所预测出的分子构型
SN 2 3 3 4 4 4 5 孤对电 子数 0 0 1 0 1 2 0 分子构 型 直线型 平面三 角形 V型 四面体 例子 BeH2, CO2 SO3, BF3 SO2, O3 CH4, CF4, SO42NH3, PF3, AsCl3 H2O, H2S, SF2 PF5, PCl5, AsF5 SN 5 5 5 6 6 6 孤对电 子数 1 2 3 0 1 2 分子构 型 “跷跷板” T型 直线型 八面体 例子 SF4 ClF3 XeF2, I3-, IF2SF6, PF6-, SiF62IF5, BrF5 XeF4, IF4-
第二章 配合物的化学键理论
• 配合物的化学键理论处理中心原子与配体 之间键合的本质问题，用以阐明中心原子 的配位数，配合物的立体结构，以及配合 物的热力学性质，动力学性质，吸收光谱， 磁性等。 • 几十年来提出的配合物的化学键理论主要 有静电理论，价键理论，晶体场－配位场 理论和分子轨道理论。
1. 配合物的静电理论（EST： Electrostatic Theory）
5. 各种配体与金属离子配位时, 配位的原子按下列 次序: I<Br<Cl<S<F<O<N<C, 这个序列近似对应于 原子半径减少的次序, 而从F以后又正比于它们的电 负性减少的次序. 6. 对于同样的配体, 按△值从小到大的次序，可把 中心离子排列为： Mn2+<Co2+∼Ni2+<V2+<Fe3+<Cr3+<Co3+<Mo3+<Rh3+ <Ir3+<Pt4+ 7. 混合配合物MAnB6-n的Dq值可以近似地由内插公 式求得. 8. △值的大小既决定于配体又决定于中心离子。由 实验归纳得出△的公式为:△= f.g, 其中f决定于配 体, g决定于中心离子.
1916年，W. Kossel提出离子键理论，随即 将其应用于处理作为中心原子的阳离子与作 为配体的阴离子间结合成配合物的问题。后 来，A. Magnus开始用类似的办法处理作为中 心原子的阳离子与作为配体的分子间结合成 配合物的问题。随后又有多人用EST对配合物 做更细致的研究。
该理论假定中心原子和配体都是点电荷或 偶极子，利用经典的静电公式对配合物进行定 量计算，所需的参数是中心原子的电荷和半 径、配体的大小、电荷、偶极矩和极化率。 静电理论只能简单地说明配位数和立体构 型等问题，而不能处理化合物的吸收光谱和磁 学性质等等问题，该理论有较严重的缺陷。
eg ○○ 球形场中的○○○○○ 离子 6Dq 4Dq ○○○
ℇ0
10Dg
t2g
自○○○○○ 由离子
d轨道 在正八面体场中的 能级分裂 轨
分裂能△
从上图可以看到自由离子的五个d轨道的能量是 相同的(简并的).当离子被引进球形对称的负静电 场中(即假定六个配体的负电荷均匀地分布在配体 球面上),d轨道的能量都升高ℇ0,但并不发生分裂. 在以后的讨论中将不考虑这种影响.当六个配体处 在正八面体的六个顶点时,eg和t2g两组轨道的能量 差称为分裂能,以符号△或10Dq来表示,其中Dq称 为场强参数. E(eg) - E(t2g) = △ ≡ 10Dq
Cr2+ —— —— Mn3+ —— ——
13900 —— 21000 ——
3d5 Mn2+ Fe3+ 3d6 Fe2+ Co3+ 4d6 Rh3+
—— —— —— —— 18900
—— —— —— —— 20300
7800 21000 10400 18600 27000
—— —— —— 23000 33900
例，在八面体型的共价配离子[Fe(CN)6]3-中， Fe(III)腾出的2个3d轨道，与1个4s、3个4p轨 道组成的d2sp3杂化轨道接受了6个CN-离子的6 个配位原子C提供的6对孤对电子，形成6个配 4p 4s 3d 位键： [Fe(CN)6]3Pauling依据磁矩的测定来确定一种配离 子是电价还是共价的.µ＝[n(n + 2)]0.5 n为金 属离子中未成对的电子数， μ的单位为 B.M.(波尔磁子)
12600 15100 ——
光谱化学序
分裂能△的数值可以根据配位场理论计算出来,然 而从理论上计算的△值和实验值常有较大的偏差, 这是因为受到推广离子模型的限制.为此,人们常 采用由光谱数据得到的实验值,某些正八面体配合 物的△≡10Dq的数值见上页表: 1. 属于同一过渡金属系列并有相同电荷的中心 离子,和同样配体生成的配合物,有很相似的 △值. 2. 对于具有相同配体的配合物, △值随中心离 子的电荷的增加而增大.
• 这个规则反映了部分配合物的实质，特别 是大多数羰基配合物和一些有机金属化合 物符合的很好。对了解配合物的化学性质 和空间几何构型有一定的指导意义。 • 我国唐敖庆教授提出了(1)适用于非正三角 面多面骨架及其衍生物过渡金属原子簇化 合物的9n－L结构规则(n为骨架中过渡金属 原子数，L为骨架多面体及其衍生物的边数) 和(2)适用于具有正三角面多面体及其衍生 物过渡金属原子簇化合物的9n－F规则( n 为骨架中过渡金属原子数，F = f ＋ 3(s ＋1) ，f为基础多面体的面数，s为顶点 数) 。
某些正八面体配合物的△值（单位cm-1）
D电 中心 Br子层 离子 3d1 3d2 3d3 4d3 3d4 Ti3+ V3+ V2+ Cr3+ Mo3+ ClH2O NH3 CN—— —— —— 26300 —— —— ——
—— —— —— —— —— —— 13600 —— 19200
20300 —— 17700 12600 17400 —— —— —— 21600 ——
3. 对于同样配体而中心离子属于不同过渡金属系列 的配合物,那么当中心离子从第一过渡系列转换 到第二过渡系列或从第二过渡系列转换到第三过 渡系列时,△值增加30-40%. 4. 对于给定的中心离子,不同配体的△值可由小到 大排列成下列顺序,称为“光谱化学序列”: I-<Br-<Cl- ∼ SCN-<F-<(NH2)2CO<OH- ∼ 3CO2∼CH ∼<HCO2-<(CO2)22-<H2O<NCS-<edta4∼ <Py<NH3<NO2-<CN上面在化学符号下划线的原子是配位原子.在这个序 列中,配体的次序与配合物的中心离子无关.
外轨型配离子
而在[FeF6]3-中，Taube认为，中心原子Fe(III)以一 个4s，三个4p和两个4d轨道组成的sp3d2杂化轨道 接受了六个F-离子提供的六对孤对电子，形成六 个配位键： [FeF6]3sp 3d2杂化轨 道 4s 3d 4p 4d
在这个例子中，中心原子提供的空轨道都是最外 层的轨道，这样形成的配离子称为外轨(型)配离 子。
—— —— 33000 34000 ——
5d6 Ir3+ 23100 24900 —— Pt4+ 24000 29000 —— 3d7 Co2+ —— —— 9300 3d8 Ni2+ 7000 3d9 Cu2+ —— 7300 —— 8500
—— —— —— —— 10100 —— 10800 ——
价电子对互斥理论（VSEPR: Valence 价电子对互斥理论（ Shell Electron Paris Repulsion ）
价电子对互斥理论是由西奇维克 （Sidgewick）和鲍威尔（Powell）于1940 年提出的，吉莱斯皮（Gillespie）和尼霍姆 （Nyholm）发展了这一理论。它是说明和 预言非过渡元素以及含d0 ，d5 ，d10 过渡金 属配合物的几何构型的一种有用方法。其 要点如下:
d轨道的角度分布图
Z
z
+ _ + _
+
Y
_ +
_
y
X
d z2
x
d x2-y2
z
z
y
+
+
d xz
x
+
+
d yz
y
+
+
d xy
x
d 轨道分裂和分裂能△
首先来探讨过渡金属离子M的正八面体型配离子 ML6离子(L代表配体,可以是阴离子,也可以是偶极分 子;略去L和ML6可能有的电荷)的情况.
在自由原子或自由离子中,同一电子层中五个d 轨道是简并的,即它们的能级是相同的(能级相同的 五个轨道称为简并轨道).五个d轨道的角度分布情况 如图5-1所示.
3. 不同类型的电子对之间的斥力大小不同。由于孤对电子 (Lp)没有键联原子而只受中心原子的吸引，因而显得比键 对电子(Bp)“肥大”些，或者说对相邻电子对的排斥作用要 大一些。不同类型电子对排斥力大小有如下次序： Lp-Lp > Lp-Bp > Bp-Bp 利用这一规则，可以解释AB3E(E代表孤对电子)的键角小 于正四面体角，AB2E2的键角更小。例如CH4的∠HCH、 NH3的∠HNH和H2O的∠HOH分别为109.5º、107.3º和 104.5º。 4. 成键电子对之间的斥力随配位原子的电负性增加而减小。 因为配位原子电负性越大，吸引键电子能力越强，键电子 将向配体方向移动，键电子对之间的斥力将减少，从而可 解释下述键角的变化规律： PF3(98º) < PCl3(100º ) < PBr3(～120º ) ≈ PI3(～122º)； F3PO(102.5 º) < Cl3PO(103.6º) < Br3PO(106º)。