铁路缓和曲线的设计
铁路三次抛物线缓和曲线的计算

次抛 物线 形 、 次 抛 物 线 余 弦 改 善 型 、 次 四项 式 三 七 型 、 波 正弦 型等 , 于三 次 抛 物 线 线 形 简 单 、 计 半 鉴 设 方便 、 立面有 效 长度 长 、 平 现场 轨道 铺设 和养 护 容易 的特 点 , 目前在 国内 外 铁路 和 高 速铁 路 中大 部 分 采
Te h o o y & Ec n m y i e s o Co c n lg o o n Ar a f mmun c to s i ain
交 通 科 技 与 经 济
2 1 年第 1 总第 6 01 期( 3期)
铁 路 三 次 抛 物 线 缓 和 曲线 的计 算
王 国栋 马 俊Байду номын сангаас海 ,
中桩 坐标计算 , 以一算例说 明 。 并
关 键 词 : 和 曲线 ; 次 抛 物 线 ; 缓 三 曲线 要 素 ; 标 坐 中 图分 类 号 : 8 . U2 4 2 文献标识码 : A 文 章 编 号 :0 85 9 (0 1 0—0 30 1 0—6 6 2 1 ) 10 1 —4
特点 , 据研究 成 果 , 和 曲线 也 有 多 种 形 式 , 根 缓 如三
…
Y一 — ・ 6 C —
L l J
式 中 : 三 次 抛 物 线 参 数 , 回旋 曲线 中 的 A 相 C为 和
似, 与抛 物 线 的长度 L 及 圆曲线 的半 径 R 有关 。 。 设 P 为抛 物线 线上 任 意一 点 , P 点处 的 转 向 则 角 或切 线偏 角 ( P点 处 的切 线 与 ZH 点 的切 线 的 夹
它 的半 径 等 于圆 曲线 的半径 R。这样 随着 半径 的减
小 , 相应 的超 高 逐 渐 增 大 , 到 了过 渡 的 作用 , 使 起 这 种 曲线 称 缓和 曲线 。 缓 和 曲线 的线 型可 以有 很多 种 , 目前 , 国公 路 我 上 广泛采 用 的缓 和 曲 线 是 回旋 曲线 , 曲线 的方 程 为 A一 ̄R ・ 。而在铁 路 路 线 设 计 中 , 虑 到 铁 路 的 / 考
铁路曲线超高计算例题

铁路曲线超高计算例题铁路曲线通常由圆曲线和缓和曲线两部分组成,其中圆曲线主要用于转弯处,而缓和曲线则用于连接直线段与圆曲线。
超高是指列车在曲线中行驶时车身与轨道之间的垂直距离差,计算超高是铁路设计中的一项重要工作。
下面举一个例题进行计算:一条铁路线路,限速120公里/小时,列车长度200米,弯曲半径800米。
计算该曲线的超高值。
解题思路:根据铁路设计规定,车辆在曲线上行驶时需要满足一定的超高限制,以确保列车安全稳定。
为了计算出该曲线的超高值,首先需要确定列车在曲线的最大超高值。
1. 确定最大超高限制首先,根据铁路行车规定,列车在曲线上的最大超高值应为铁路限速值除以25,再加上1.5米。
因此,在本题中最大超高值为:MaxH = 120 / 25 + 1.5 = 6.5米2. 确定最大列车超高其次,需要根据列车长度和弯曲半径计算出列车在曲线上可能出现的最大超高值,以便确定超高是否符合安全要求。
根据铁路设计公式,列车在圆曲线上行驶时的最大超高可以用以下公式计算:Maxh = (L^2 / 24R) + (R/2)其中,L是列车长度,R是弯曲半径。
带入数据可得:Maxh = (200^2 / (24×800)) + (800/2) = 3.47米因此,该曲线上可能出现的最大超高值是3.47米。
3. 确定实际超高值最后,根据弯曲半径和曲线长度的关系,可以利用铁路设计公式计算出该曲线的实际超高值:H = (L/2) × (L/(24×R))带入数据可得:H = (200/2) × (200/(24×800)) = 0.65米因此,该曲线的超高值为0.65米,低于最大允许超高值6.5米,符合安全要求。
结论:通过计算,我们得出该曲线的超高值为0.65米,符合安全要求。
因此,该曲线可以使用,列车可以在曲线上正常通行。
加加速度_加速度的时间变化率_冲击_乘座舒适性_缓和曲线

人体受力有一定限度 , 因而对加速度的 承受也有一定范围 . 一般地说 ,当加速度 a 比 重力加速度 g 小几倍时 , 人尚能忍受 . 根据实 测结果 [ 6 ] , 对于汽车内的普通乘客 , 法向加速 度 an ≤ 118m ・ s - 2 时 , 人感觉不显著 , a n 达到
316m・ s - 2 时 , 人 能 感 觉 到 , 但 可 忍 受 , an ≥ 510m・ s - 2 时 , 难以忍受 . 不仅如此 , 如果加速
9
3 匀速率曲线运动中的加加速度
1/ 8 41063 1/ 4 21125 1/ 2 11250 3/ 4 110417 1 1
缓和曲线 [ 1 ] 质点做匀速率曲线运动时 , 其加速度沿 着法线方向 , 当法向加速度 a n 方向改变的影 响可忽略不计时 ,它的加加速度 j = d a n/ dt 也 是沿着法线方向的 ,其数值即等于 d a n/ d t . 这 里我们以铁路曲线轨道的铺设为例 , 引入缓 和曲线设计的问题 , 此时应考虑到法向加速 度的变化率 ( 即法向加加速度 ) ( 可参考 [ 11 ] 所引参考文献) . 在铺设铁路时 , 需要把平直轨道和圆弧 形弯曲轨道用适当方法连接起来 , 这种起连 接作用的曲线轨道称为缓和曲线 . 缓和曲线 的设计需要考虑多种因素 , 以下介绍简化了 的理论分析 . 如果把直轨道和圆弧形轨道直接连接 , 那么 , 在连接点处车辆的法向加速度 a n 就会 由零突然增加到 v 2 / R ( R 为圆弧轨道的半 径) , 惯性离心力将会使外侧轨道突然受到压 力 m v 2 / R , 因而在连接点处引起冲击载荷 , 从而产生剧烈振动 、 冲击钢轨等不良作用 . 如 果在中间接上一段曲率由零逐渐均匀地增加 到 1/ R 的缓和曲线 , 就可以使法向加速度由 零均匀地增加到 v 2 / R , 从而避免出现冲击载 荷 . 显然 , 如果不考虑设计和维护的困难等技 术问题 , 缓和曲线越长越有利 , 在实际设计 时 , 要按照技术条件及要求 , 选定最大容许缓 和曲线长度 . 常用的缓和曲线是三次方曲线 ( 参见图 2) , 设直线段在负 x 轴上并与缓和曲线在坐 标原点处相连接 , 则缓和曲线方程可以写成 1 3 ( 2) y = kx 6 上式中 k 代表缓和曲线的曲率变化率 ( 即在 单位距离内曲率 1/ ρ 的增量 ) . 这种缓和曲线 可以使法向加速度 a n 值均匀地从零渐增到 圆弧轨道上行驶时的数值 v 2 / R , 见图 2 . 显 然 , 在这种情况下 , 加速度的变化率沿法线方 向的分量为常数 , 因而加加速度沿法线方向
常用缓和曲线.
K
K0
l l0
ห้องสมุดไป่ตู้
①
l Rl0 C ②
由式①可见,缓和曲线长度l与其曲率K成正比。符合 这一条件的曲线称为放射螺旋线。
d dl Kdl
d
K0
l l0
dl
1 Rl0
ldl
l 0时, 0,C 0 l 2
2Rl0
d l2 D
2Rl0
l 0 时, 0 , D 0
为缓和曲线上任一点的偏角,
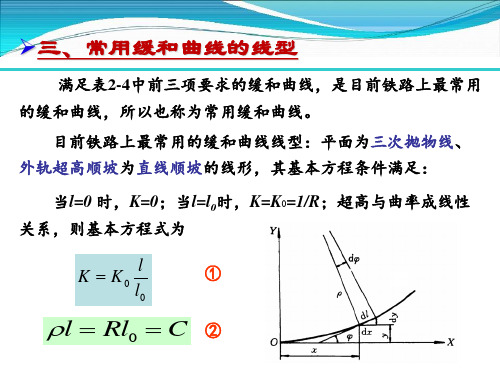
➢三、常用缓和曲线的线型
满足表2-4中前三项要求的缓和曲线,是目前铁路上最常用 的缓和曲线,所以也称为常用缓和曲线。
目前铁路上最常用的缓和曲线线型:平面为三次抛物线、 外轨超高顺坡为直线顺坡的线形,其基本方程条件满足:
当l=0 时,K=0;当l=l0时,K=K0=1/R;超高与曲率成线性 关系,则基本方程式为
在HY点,l
l0
,
0
l0 2R
l2 2Rl0
直角坐标表示的缓和曲线方程
dx dl cos, dy dl sin
0,sin
c os
cos2 2 cos 2 dx
1
2 2
dl
1
l4 8R2l02
2dl
sin 2
2
1 2sin2
1 2
2
2
1
2
2
2
dx
1
2
2
dl
1
l4 8R 2l02
dl
积分上两式,得:
dx
(1
2
)dl
(1
l4 8R 2l02
)dl
dy dl l 2 dl
2Rl0
对上两式进行积分,得
缓和曲线的长度概要

保证外轮的升高(或降低)速度不超过限值,以满足旅 客舒适要求。车轮在外轨上的升高速度为:
hVmax f 3.6l0
由此可得保证旅客舒适要求的缓和曲线长度为:
hVmax l0 3.6 f
算例2:高速铁路,曲线半径8000m,超高为90mm,动车组 速度350km/h,设置常用缓和曲线,超高顺坡率不大于 1/(9vmax),超高时变率不大于25mm/s,欠超高时变率不大于 23mm/s,问该缓和曲线长度应为多少? 解:超高顺坡率:i0= 1/(9vmax) =3.6/(9×350)=1.1 ‰
2 2 V 350 欠超高为: hq 11.8 max h 11.8 90 90.7mm R 8000 按安全条件确定:l h 90 10-3 81.8m 01 i0 1.1‰
按超高时变率舒适条件确定:
l02
h 90 Vmax 350 350m 3.6 f 3.6 25
i0 外轨超高顺坡坡度;
Lmax - 最大固定轴距;
f min - 轮缘最小高度。
1、按安全条件确定缓和曲线长度
• 曲线型超高顺坡:找坡度最大的点。 • 坡度 i dh E dK ,
dl dl 求i的最大值,必须使 E 11.8V p2
di d 2K 0, 即 2 0, dl dl 曲线型缓和曲线,坡度 最大在l l0 / 2处, imax dh 2 dK 11.8V p dl l l0 / 2 dl l l0 / 2
高速铁路缓和曲线长度
h l0 Vmax 3.6 f
单位: 超高时变率:mm/s 欠超高时变率:mm/s 超高:mm 速度:km/h 缓和曲线长度:m
铁路缓和曲线超高设置的分析

铁路缓和曲线超高设置的分析【摘要】针对目前铁路缓和曲线直缓(或缓直)、缓圆(或圆缓)点超高设置不合理的做法,按照铁路相关设计规范要求,在直线型超高顺坡的基础上,通过对缓和曲线外轨断面的设置,改善轮轨接触状态,提高动力响应。
【关键词】超高顺坡;竖曲线;缓和曲线超高设置【 Abstract 】 In view of the present railway easement curve straight slow (or slow straight), slow (slow) or circle point ultra-high set unreasonable, in accordance with the relevant railway design specification requirements, on the basis of linear high slope, through to the easement curve rail profile Settings, improving the wheel/rail contact state, improving the dynamic response。
【 Key words 】 Ultra high slope; Vertical curve; Detente curve ultra high setting1 概述行驶在曲线轨道的机车车辆,出现一些与直线运行显著不同的受力特征,如转向力、离心力等。
为了上述力不至于突然产生和消失,需要在直线与圆曲线轨道之间设置一段曲率半径和外轨超高逐渐变化的曲线,我们称这段曲线为缓和曲线。
曲线超高是确定缓和曲线长度及曲线线间距加宽值等平面标准的主要参数,曲线超高的取值将对平面标准产生重要影响;影响列车行车速度、旅客舒适度和钢轨磨耗,甚至影响行车安全。
2 曲线超高与超高顺坡2.1 确定超高在线路曲线地段,应根据曲线半径和实测行车速度,在外股钢轨合理设置超高(允许速度大于120 km/h的线路宜按旅客的舒适条件进行检算和调整超高值)。
圆曲线、缓和曲线的作用

圆曲线、缓和曲线的作用
圆曲线和缓和曲线在工程和建筑领域中起着重要的作用。
首先,让我们来看一下圆曲线的作用。
圆曲线是道路、铁路或管道等线性
基础设施中常用的曲线形式。
它的作用之一是在道路设计中用于平
滑地连接两段直线道路,从而减少车辆在转弯时的惯性力,提高行
车的舒适性和安全性。
此外,圆曲线还可以用于铁路轨道的设计,
使列车能够平稳地通过弯道,减少对轨道和列车的磨损,延长使用
寿命。
在水利工程中,圆曲线也被用于设计水渠和管道,以确保流
体能够平稳地通过弯道,减少能量损失和管道磨损。
接下来是缓和曲线的作用。
缓和曲线是一种用于连接两条直线
或两条曲线的平滑过渡曲线。
在道路设计中,缓和曲线被用于减少
车辆在转弯或变道时的急剧转向,从而减少车辆的横向加速度,提
高行车的舒适性和安全性。
此外,缓和曲线还可以减少车辆驶入或
驶出匝道时的冲击和振动,有助于减少交通事故的发生。
在铁路设
计中,缓和曲线也被用于平稳地连接不同半径的铁路轨道,使列车
能够平稳地通过过渡曲线,减少对轨道和列车的影响。
总的来说,圆曲线和缓和曲线在工程和建筑领域中的作用是为
了平滑地连接不同的线性结构,减少急剧转向和横向加速度,提高
行车的舒适性和安全性,减少对基础设施和车辆的磨损,从而延长其使用寿命。
这些曲线的设计和应用对于交通运输和基础设施工程具有重要意义。
竖曲线、缓和曲线计算公式
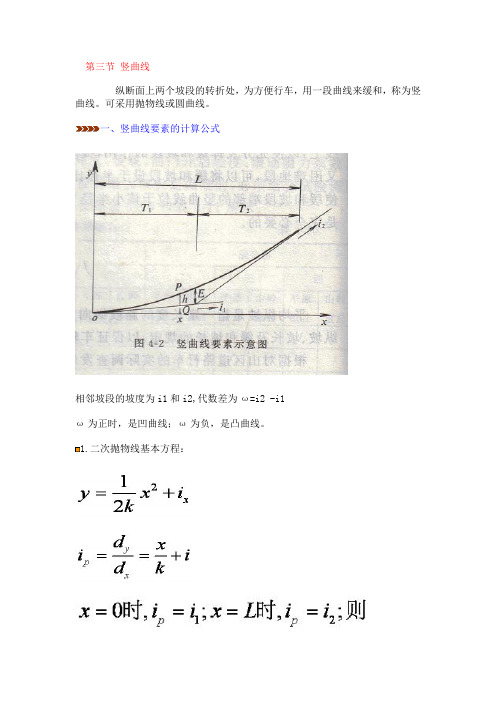
第三节竖曲线纵断面上两个坡段的转折处,为方便行车,用一段曲线来缓和,称为竖曲线。
可采用抛物线或圆曲线。
一、竖曲线要素的计算公式相邻坡段的坡度为i1和i2,代数差为ω=i2 -i1ω为正时,是凹曲线;ω为负,是凸曲线。
1.二次抛物线基本方程:或ω:坡度差(%);L:竖曲线长度;R:竖曲线半径2.竖曲线诸要素计算公式竖曲线长度或竖曲线半径R: (前提:ω很小)L=Rω竖曲线切线长:T=L/2=Rω/2竖曲线上任一点竖距h:竖曲线外距:二、竖曲线最小半径(三个因素)1.缓和冲击对离心加速度加以控制。
ν(m/s)根据经验,a=0.5~0.7m/s2比较合适。
我国取a=0.278,则Rmin=V2/3.6 或Lmin=V2ω/3.62.行驶时间不过短 3s的行程Lmin=V.t/3.6=V/1.23.满足视距的要求分别对凸凹曲线计算。
(一)凸形竖曲线最小半径和最小长度按视距满足要求计算1.当L<ST时,Lmin = 2ST - 4/ω2.当L≥ST时,ST为停车视距。
以上两个公式,第二个公式计算值大,作为有效控制。
按缓和冲击、时间行程和视距要求(视距为最不利情况)计算各行车速度时的最小半径和最小长度,见表4-13。
表中:(1)一般最小半径为极限最小半径的1.5~2倍;(2)竖曲线最小长度为3s行程的长度。
(二)凹曲线最小半径和长度1.夜间行车前灯照射距离要求:1)L<ST2) L≥STL<ST Lmin = 2ST - 26.92/ω (4-14)L≥STω /26.92 (4-15)3s时间行程为有效控制。
例:设ω=2%=0.02;则L=ωR竖曲线最小长度L=V/1.2速度V=120km/h V=40km/h 一般最小半径R凸17000 700一般最小半径R凹6000 700 L凸340 14L凹120 14 例题4-3ω=-0.09 凸形;L=Rω=2000*0.09=180mT=L/2=90mE=T2/2R=2.03m起点桩号=k5+030 - T =K4+940起始高程=427.68 - 5%*90=423.18m桩号k5+000处:x1=k5+000-k4+940=60m切线高程=423.18+60*0.05=426.18m h1=x21/2R=602/2*2000=0.90m设计高程=426.18 - 0.90=425.28m 桩号k5+100处:x2=k5+100-k4+940=160m切线高程=423.18+160*0.05=431.18m h2=x22/2R=1602/2*2000=6.40m设计高程=431.18 - 6.40=424.78m第一节平面线形概述一、路线路线指路的中心线;路线在水平面上的投影叫路线的平面;路线设计:确定路线空间位置和各部分几何尺寸的工作;可分为平面设计、纵断面设计、横断面设计。
