大学 管理运筹学 课程设计 实验报告详解 第四版 薛声家 左小德编著
《管理运筹学》第4版课后习题解析(韩伯棠)
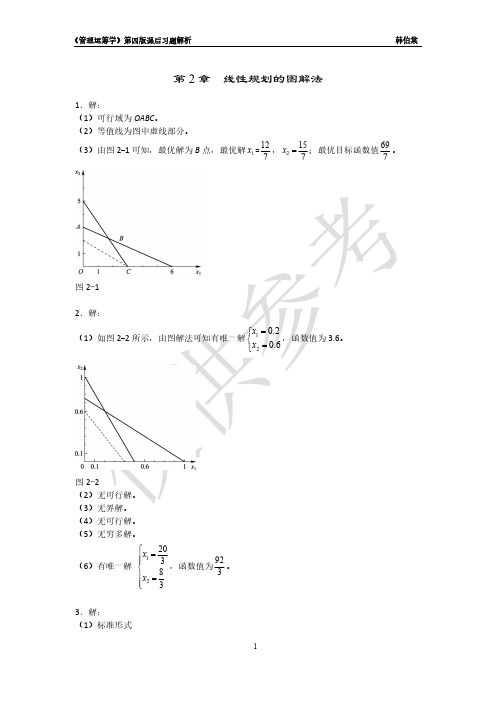
10 x1 2 x2 s1 20 3x1 3x2 s2 18 4 x1 9 x2 s3 36 x1 , x2 , s1 , s2 , s3 ≥ 0
2
《管理运筹学》第四版课后习题解析
韩伯棠
剩余变量(0, 0, 13) 最优解为 x1=1,x2=5。 6.解: (1)最优解为 x1=3,x2=7。 (2) 1 c1 3 。 (3) 2 c2 6 。 (4)
x1 6。 x2 4。
(5)最优解为 x1=8,x2=0。 (6)不变化。因为当斜率 1 ≤
c1 1 ≤ ,最优解不变,变化后斜率为 1,所以最优解不变。 c2 3
7.解: 设 x,y 分别为甲、乙两种柜的日产量, 目标函数 z=200x+240y, 线性约束条件: 6 x 12 y 120 8 x 4 y 64 x 0 y 0 x 2 y 20 2 x y 16 x 0 y 0
作直线 960x+360y=0. 即 8x+3y=0,向上平移至过点 B(10,8)时,z=960x +360y 取到最小值. z 最小=960×10+360×8=12480 答:大卡车租 10 辆,农用车租 8 辆时运费最低,最低运费为 12480 元. 11.解: 设圆桌和衣柜的生产件数分别为 x、y,所获利润为 z,则 z=6x+10y. 0.18 x 0.09 y 72 2 x y 800 0.08 x 0.28 y 56 2 x 7 y 1400 即 x 0 x 0 y 0 y 0
. 但 E 不是可行域内的整点,在可行域的整点中,点 ( 4,8) 使 z 取得最小值。 答:应截第一种钢板 4 张,第二种钢板 8 张,能得所需三种规格的钢板,且使所 用钢板的面积最小. 9.解: 设用甲种规格原料 x 张,乙种规格原料 y 张,所用原料的总面积是 zm2,目标函 x 2 y 2 2 x y 3 数 z=3x+2y,线性约束条件 作出可行域.作一组平等直线 3x+ x 0 y 0 x 2 y 2 2y=t. 解 得 C ( 4 / 3,1 / 3) 2 x y 3
管理运筹学课程实验报告

背景资料
1、某同学暑假到某精品加工厂实习,生产甲、乙两种精品原件,每生产一件的提成分别为2元、1元,完成一件所需时间分别为30min、40min。而生产机器每天只能运行180min。按照领导下达的生产计划,甲产品的月需求量最多为100件,乙产品最多为75件,而该同学该月的工作时间只有25天。则应如何生产才能满足下述目标:
(1)每天提成不少于9元;
(2)甲、乙量产品的产量尽量满足两者需求量之间的比例;
(3)充分利用生产机器的运行能力但还要尽量避免加班。
数学模型
设:甲、乙的日产量分别为X1、X2件
Min z=P1 +P2( )+P3( )
X1<=4
X2<=3
S.t 2X1+X2+ =9
30X1-40X2+ =0
30X1+40X2+ =180
X1,X2,
求解结果
结果分析
甲产品每日产量为3.2727件,满足目标规划;乙产品每日产量为2.4545件,
满足目标规划。而且,每天需要加班16.3636min。
教师评分:签名:日期:
管理运筹学课程
实验报告
实验名称Байду номын сангаас目标规划
实验者:
实验日期:
专业年级:12级工程管理
指导教师:
目的与要求
实验目的:
通过实验掌握以及实际问题建立线性规划模型的方法,并熟练运用运筹学软件求解线性规划问题,以及根据求解结果进行灵敏度分析。
实验要求:
(1)根据所给出的实际问题,建立其相应的数学模型,并利用软件进行求解。
管理运筹学实训报告案例

一、实训背景随着市场竞争的日益激烈,企业对于管理运筹学的需求日益增长。
为了提高企业内部管理效率,培养具备运筹学知识的应用型人才,我校组织了一次管理运筹学实训活动。
本次实训旨在通过实际案例,让学生深入了解运筹学在实际工作中的运用,提高学生的实践能力。
二、实训目标1. 理解运筹学的基本概念和原理,掌握运筹学的基本方法。
2. 通过案例分析,了解运筹学在企业管理中的应用。
3. 培养学生运用运筹学解决实际问题的能力。
4. 增强学生的团队协作精神和沟通能力。
三、实训内容本次实训以某企业为例,该企业面临以下问题:1. 生产部门生产计划不合理,导致产能过剩或不足。
2. 仓库管理混乱,物资储备过多,增加库存成本。
3. 销售部门业绩不佳,客户满意度低。
针对以上问题,我们将运用运筹学中的线性规划、库存管理、销售预测等方法进行分析和解决。
四、实训过程1. 案例分析(1)生产计划问题根据企业历史数据,建立线性规划模型,确定生产计划,实现产能均衡。
(2)库存管理问题运用库存管理方法,建立最优库存模型,降低库存成本。
(3)销售预测问题运用时间序列分析法,预测未来一段时间内销售情况,为销售部门提供决策依据。
2. 模型求解(1)生产计划问题利用Excel求解线性规划模型,得出最优生产计划。
(2)库存管理问题利用库存管理软件,进行库存优化,降低库存成本。
(3)销售预测问题利用Excel中的时间序列分析工具,预测销售情况。
3. 案例实施(1)生产计划实施根据最优生产计划,调整生产部门的生产计划,实现产能均衡。
(2)库存管理实施根据最优库存模型,调整库存管理策略,降低库存成本。
(3)销售预测实施根据销售预测结果,调整销售部门的市场营销策略,提高客户满意度。
五、实训结果1. 生产部门的生产计划得到优化,产能得到均衡。
2. 库存成本得到有效降低,物资储备合理。
3. 销售部门业绩得到提升,客户满意度提高。
4. 学生在实训过程中,掌握了运筹学的基本方法,提高了实践能力。
《管理运筹学》第4版课后习题解析(韩伯棠)

《管理运筹学》第四版课后习题解析
韩伯棠
C 不是整点,C 不是最优解.在可行域内的整点中,点 B(1,1)使 z 取得最小 值. z 最小=3×1+2×1=5, 答:用甲种规格的原料 1 张,乙种原料的原料 1 张,可使所用原料的总面积最 小为 5m2. 10.解: 设租用大卡车 x 辆, 农用车 y 辆, 最低运费为 z 元. 目标函数为 z=960x+360y.
即
作
出
可
行
域. x 2 y 20 解 得 Q ( 4,8) 2 x y 16
z最大 200 4 240 8 2720
3
《管理运筹学》第四版课后习题解析
韩伯棠
答:该公司安排甲、乙两种柜的日产量分别为 4 台和 8 台,可获最大利润 2720 元.
8.解:
设需截第一种钢板 x 张,第二种钢板 y 张,所用钢板面积 zm2. 目标函数 z=x+2y, 线性约束条件: x y 12 2 x y 15 x 3 y 27 x 0 y 0 x 3 y 27 作出可行域,并做一组一组平行直线 x+2y=t.解 得 E ( 9 / 2,15 / 2) x y 12
. 但 E 不是可行域内的整点,在可行域的整点中,点 ( 4,8) 使 z 取得最小值。 答:应截第一种钢板 4 张,第二种钢板 8 张,能得所需三种规格的钢板,且使所 用钢板的面积最小. 9.解: 设用甲种规格原料 x 张,乙种规格原料 y 张,所用原料的总面积是 zm2,目标函 x 2 y 2 2 x y 3 数 z=3x+2y,线性约束条件 作出可行域.作一组平等直线 3x+ x 0 y 0 x 2 y 2 2y=t. 解 得 C ( 4 / 3,1 / 3) 2 x y 3
管理运筹学毕业实习报告

一、实习目的随着我国经济的快速发展和市场竞争的日益激烈,企业对管理运筹学的需求日益增长。
为了将所学的理论知识与实际工作相结合,提高自身的实践能力和综合素质,我选择了管理运筹学作为毕业实习的方向。
本次实习旨在通过实际工作,深入了解管理运筹学的应用,掌握相关软件的使用方法,提高解决问题的能力,为今后从事相关工作打下坚实基础。
二、实习时间及地点实习时间:2023年6月1日至2023年8月31日实习地点:XX科技有限公司三、实习单位及岗位介绍XX科技有限公司是一家集研发、生产、销售为一体的高新技术企业,主要从事XX产品的研发和生产。
在实习期间,我担任了公司生产部管理运筹学助理的岗位,主要负责以下工作:1. 参与生产计划的制定和优化,运用运筹学方法提高生产效率;2. 分析生产过程中的瓶颈,提出改进措施,降低生产成本;3. 协助进行库存管理,优化库存结构,减少库存积压;4. 参与公司项目管理,运用运筹学方法进行项目风险评估和资源分配。
四、实习内容及过程1. 生产计划制定与优化在实习期间,我参与了公司生产计划的制定和优化工作。
首先,我收集了生产数据,包括产品需求、生产设备能力、原材料供应等信息。
然后,运用线性规划、整数规划等运筹学方法,对生产计划进行优化。
通过优化,提高了生产效率,降低了生产成本。
2. 生产瓶颈分析及改进在生产过程中,我发现存在一些瓶颈问题,如设备故障、原材料供应不及时等。
针对这些问题,我运用运筹学方法进行分析,找出原因,并提出改进措施。
例如,针对设备故障问题,我建议加强设备维护保养,提高设备可靠性;针对原材料供应不及时问题,我建议与供应商建立长期合作关系,确保原材料供应稳定。
3. 库存管理优化库存管理是企业生产过程中非常重要的一环。
在实习期间,我协助进行库存管理,运用运筹学方法优化库存结构,减少库存积压。
具体做法如下:(1)建立库存模型,确定最优订货量;(2)分析库存变化趋势,提前预警,避免缺货或积压;(3)优化库存盘点流程,提高盘点效率。
《运筹学》实验报告

《运筹学》实验报告专业:工商管理专业班级:11-2班:胡坤学号:8指导老师:雷莹前言第十一周、十二周,我们在雷莹老师的指导下,用计算机进行了有关运筹学的一系列实验。
本实验报告即是对这次试验的反馈。
本这次试验是为了帮助我们顺利完成有关《运筹学》课程容的学习。
在先期,雷老师带领我们进行了《运筹学》理论课程的学习,不仅使我们了解和掌握了运筹学的相关知识,而且让我们认识到运筹学的现实意义,认识到现代社会数学与人们生产、生活之间的紧密联系和对人们生产、生活的巨大促进作用。
然而,与此同时,现代社会同时是一个计算机时代,我们只拥有理论知识还不够,必须把理论知识和计算技术结合起来,这样才能进一步提高生产力。
我相信这也是老师要求我们做这次试验的目的和初衷。
在实验中,我们主要是利用WinQSB软件进行相关试验,根据实验指导书中详细给出的各个实验的基本步骤和容,独立完成各项实验。
本次实验中共包含4个实验,分别是线性规划实验、运输问题实验、整数规划实验,以及网络优化实验。
每个实验均与理论课中讲解的容相对应。
部分实验容用于使我们了解WinQSB软件的基本操作,而其它实验容要求我们能够根据给出的问题,进行分析、建模和求解。
通过完成各项实验任务,使我们得以巩固已有的理论课程学习容,为将来进一步的学习和实际应用打下基础。
线性规划实验通过对以下问题的分析,建立线性规划模型,并求解:某工厂要用三种原材料C、P、H混合调配出三种不同规格的产品A、B、D。
已知产品的规格要求,产品单价,每天能供应的原材料数量及原材料单价分别见下表1和2。
该厂应如何安排生产,使利润收入为最大?表2实验报告要求(1)写出自己独立完成的实验容,对需要建模的问题,给出问题的具体模型;(2)给出利用WinQSB软件得出的实验结果;(3)提交对实验结果的初步分析,给出自己的见解;实验过程:一、建立模型设Ac是A产品中用c材料,同理得出Ap、Ah、Bc、Bp、Bh、Dc、Dp、Dh⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎧≤++≤++≤++≤++≥++≤++≥++++++++++++++++=60Dh Bh Ah 100Dp Bp Ap 100Dc Bc Ac 5.0Bh Bp Bc Bp 25.0Bh Bp Bc Bc 25.0Ah Ap Ac Ap 5.0Ah Ap Ac Ac Dh Bh Ah 35-Dp Bp Ap 25-Dc Bc Ac 65-Dh Dp Dc 25Bh Bp Bc 35)(50 max )()()()()(H P C A A A z二、求解过程三、实验分析实验结果表明,在题目的要求下,该工厂只能生产A产品才能盈利,并且在使用c材料100个单位、p材料50个单位、h材料50个单位时,即生产200个单位的A产品时,才能获得最大利润,最大利润为500。
运筹学课程设计报告
关于生产计划的线性规划模型摘 要本文利用问题中的数据信息,建立了线性规划模型,并运用LINGO 软件求解,得出了让工厂赢利最大的生产计划,并讨论了增加设备、投产新产品、改进产品工艺等各种情况对生产计划的影响。
对于问题(1):按照题目给出的数据,可以得到一个每月生产赢利最大为目标的线性规划模型。
然后利用LINGO 软件求解出模型的全局最优解,最优值为134.5,最优解为52424321===x x x ,,。
即每月安排生产24件产品Ⅰ,24件产品Ⅱ,5件产品Ⅲ,能使工厂获得最大赢利为134.5千元。
对于问题(2):因为设备B 每台时的租金为0.3千元,高于它的对偶价格,所以得出结论:借用设备B 是不合算的。
我们又建立了线性规划模型来验证结论。
模型计算结果显示借用设备B ,工厂最大赢利为127千元,比原生产计划下的赢利134.5千元少,证明了借用设备B 确实是不合算的。
对于问题(3):为了更好的讨论新产品Ⅳ、Ⅴ投产是否合算,我们分三种情况建立模型:同时投产Ⅳ和Ⅴ、只投产Ⅳ、只投产Ⅴ。
结合三个模型的结果可知:若单独投产Ⅳ或Ⅴ,工厂赢利的增量分别是0.1千元和1.36千元。
只投产Ⅳ则利润增长是很小的,同时投产Ⅳ和Ⅴ的收益增量是最大的,为1.46千元。
所以在计划新产品的投产时,不能单独投产新产品Ⅳ,最好是同时投产新产品Ⅳ和Ⅴ。
对于问题(4):根据新数据,可以得到线性规划模型,模型的最优解为22422321===x x x ,,。
改进工艺结构后最大赢利为152.8千元,给工厂增加了18.3千元的赢利。
关键词:工厂赢利,生产计划,线性规划,LINGO 软件,对偶价格一、问题重述已知某工厂计划生产Ⅰ,Ⅱ,Ⅲ三种产品,各产品需要在C B A ,,设备上加工,有关数据见下表。
试回答:(1)如何充分发挥设备能力,使生产赢利最大?(2)若为了增加产量,可借用其他工厂的设备B ,每月可借用60台时,租金为8.1万元,问借用B 设备是否合算?(3)若另有两种新产品Ⅳ,Ⅴ,其中Ⅳ需用设备A 为12台时,B 为5台时;C 为10台时,单位产品赢利1.2千元;新产品Ⅴ需用设备A 为4台时,B 为4台设备代号 ⅠⅡ Ⅲ 设备有效台时/月 A 82 10 300 B 105 8 400 C 213 10 420 单位产品利润/千元3 2 2.9时;C 为12台时,单位产品赢利87.1千元。
管理运筹学实验报告(三次实验)
湖北科技学院管理运筹学实验报告年级 10级专业工商管理学生姓名学号指导教师吴睿经济与管理学院工商管理系2012年3月《管理运筹学》实验报告(一)实验时间:实验地点:经管院实验室专业班级:10工管姓名:学号:成绩:【实验内容】线性规划问题的计算机求解【实验目的】1、掌握线性规划问题的计算机求解方法;2、通过“管理运筹学”软件(2.5版)等教学软件的应用,深化和拓展学生对线性规划理论知识的认识,提高学生的科学素养,培养学生利用计算机技术解决实际问题的能力。
【实验要求】1、记录实验结果、填写实验结论、保存实验输出结果,课后打印上交;2、填写实验报告按时保质保量上交。
【实验过程】(一)安装并了解“管理运筹学”2.0版软件(参阅教材P434的附录说明);(二)实验分组及内容安排A组(学号为单号者用):1、第二章例1中(P10、28)若单位产品Ⅰ可获利80元,单位产品Ⅱ可获利20元,其他条件不变,则用计算机软件求得目标函数最优值为,最优解为X1= ,X2= 。
2、第二章例2中(P16、32)若A,B两种原料至少为450吨,而公司共有650个加工工时,其他条件不变,则用计算机软件求得目标函数最优值为,最优解为X1= ,X2= ;约束条件1、2、3的对偶价格分别为、、。
3、第二章习题第8题(1)中(参见P26、35)若某公司准备把160万元投资到基金A和B,而其他条件不变,则用计算机软件求得此时总的投资风险指数为,购买基金A和B的数量分别为和。
4、请用计算机软件求解第四章习题6(P59)中的问题。
可求得应该每天安排生产雏鸡饲料、蛋鸡饲料、肉鸡饲料各吨、吨、吨,所获最大利润为百元。
B组(学号为双号者用):1、第二章例1中(P10、28)若原料A的资源限制为500kg,原料B的资源限制为200kg,其他条件不变,则用计算机软件求得目标函数最优值为,最优解为X1= ,X2= 。
2、第二章例2中(P16、32)若每吨原料A的价格为1万元,每吨原料B的价格为4万元,其他条件不变,则用计算机软件求得目标函数最优值为,最优解为X1= ,X2= ;约束条件1、2、3的对偶价格分别为、、。
《管理运筹学》第四版 第4章 线性规划在工商管理中的应用 课后习题解析
《管理运筹学》第四版课后习题解析第4章线性规划在工商管理中的应用1.解:为了用最少的原材料得到10台锅炉,需要混合使用14种下料方案。
设14种方案下料时得到的原材料根数分别为x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,如表4-1所示。
表4-1 各种下料方式1234567891011121314s.t. 2x1+x2+x3+x4≥80x2+3x5+2x6+2x7+x8+x9+x10≥350x3+x6+2x8+x9+3x11+2x12+x13≥420x4+x7+x9+2x10+x12+2x13+3x14≥10x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14≥0通过管理运筹学软件,我们可以求得此问题的解为:x1=40,x2=0,x3=0,x4=0,x5=116.667,x6=0,x7=0,x8=0,x9=0,x10=0,x11=140,x12=0,x13=0,x14=3.333最优值为300。
2.解:(1)将上午11时至下午10时分成11个班次,设x i表示第i班次新上岗的临时工人数,建立如下模型。
min f=16(x1+x 2+x3+x4+x5+x6+x7+x8+x9+x10+x11)s.t.x1+1≥9x1+x2+1≥9x1+x2+x3+2≥9x1+x2+x3+x4+2≥3x2+x3+x4+x5+1≥3x3+x4+x5+x6+2≥3x4+x5+x6+x7+1≥6x5+x6+x7+x8+2≥12x6+x7+x8+x9+2≥12x7+x8+x9+x10+1≥7x8+x9+x10+x11+1≥7x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11≥0通过管理运筹学软件,我们可以求得此问题的解如下:x1=8,x2=0,x3=1,x4=1,x5=0,x6=4,x7=0,x8=6,x9=0,x10=0,x11=0,最优值为320。
运筹学课设报告
运筹学课设报告⽬录Ⅰ研究报告 (1)课程设计题⽬(⼀):值班安排问题 (1)摘要 (1)1.问题提出 (1)2.问题分析 (1)3.基本假设与符号说明 (1)4.模型建⽴于求解 (2)5.结果分析 (3)6.模型评价 (3)课程设计题⽬(⼆):⽣产任务分配问题研究 (4)摘要 (4)1.问题提出 (4)2.问题分析 (5)3.基本假设与符号说明 (5)4.模型的建⽴及求解结果 (6)5.结果分析 (7)6.模型评价 (7)课程设计题⽬(三):数学建模⼩组成员的系统综合评价 (8)摘要 (8)1.问题提出 (8)2.问题分析 (8)3.系统评价 (10)4.系统决策 (13)5.模型评价 (13)参考⽂献 (15)Ⅱ⼯作报告 (16)1.本组成员分⼯情况 (16)2.⼼得与体会 (16)附件⼀:值班安排问题lingo程序及结果 (18)附件⼆:⽣产任务分配问题lingo程序及结果 (22)Ⅰ研究报告课程设计题⽬(⼀):值班安排问题摘要本题主要是有关⼤学计算机机房值班的问题,其中受到⼤学⽣和研究⽣⼈数以及各⾃值班时间的限制,还要求总报酬费⽤最低。
从实际出发,建⽴简单可⾏的基本模型,得出符合要求的最优可⾏⽅案,进⽽为⼤学计算机机房值班问题提供参考和指导。
1.问题提出某⼤学计算机机房聘⽤三名⼤学⽣(代号1,2,3)和三名研究⽣(代号4,5,6)值班。
已知每⼈从周⼀⾄周五每天最多可安排的值班时间及每⼈每⼩时的报酬见表下表。
该实验室开放时间为上午9:00⾄晚上10:00,开放时间内须有且仅须⼀名学⽣值班,规定⼤学⽣每周值班不少于8⼩时,研究⽣每周不少于9⼩时,每名学⽣每周值班不超过5次,每次值班不少于2⼩时,每天安排值班的学⽣不超过4⼈,且其中必须有⼀名研究⽣。
试为该实验室安排⼀张⼈员的值班表,使总⽀付的报酬为最少。
2.问题分析此问题考虑如何合理的安排学⽣值班,并且花费的费⽤最少。
1:每位学⽣⼀周的值班天数对安排值班的约束;2:每天每位学⽣的值班时间对安排值班的约束;3:每位学⽣每周的值班时间不能低于8⼩时对安排值班的约束;3.基本假设与符号说明3.1基本假设x (i ,j ):表⽰学⽣i 周j 值班的时间; 3.2 符号说明pay (i ):学⽣i 每⼩时值班的报酬; t (i ,j ):学⽣i 周j 最多值班时间; c (i ,j ):学⽣i 周j 是否值班; 4.模型建⽴于求解 4.1模型的建⽴⽬标函数minZ=约束条件s.t ①学⽣每天值班时间约束: x(i,j)≤t(i,j)②值班的次数约束: c(i,j)=1(x>0)(i,j)=0(x=0)③值班⼈数的约束:1),(64≥∑=i j i c④学⽣每周值班时间的约束:8),(51≥∑=j j i x (i =1,2,3)9),(51≥∑=j j i x (i=4,5,6)⑤开放时间为上午9:00⾄晚上10:00,且开放时间内须有且仅须⼀名学⽣值班:13),(61=∑=i j i xx 为整数;4.2模型求解的结果Global optimal solution found.Objective value: 739.0000 Infeasibilities: 0.000000 Total solver iterations: 478∑∑==5161),(*)(j i j i x i pay 4),(61≤∑=i j i c 5),(6151≤∑∑j i c5.结果分析通过对求解结果的观察与分析,按求解结果表中进⾏⼤学⽣和研究⽣的值班安排为全局最优结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(一)解:设决定决策变量为四种家具的日产量,即:x1,x2,x3,x4。
目标要求日利润最大,约束条件为三种资源的供应量限制和产品销售量限制。
根据题意建模得:(其中X1,X2,X3,X4分别为四种家具的日产量) 接下来用Excel|中的“规划求解”功能求解有: 一:在Excel 描述问题、建立模型,如下图所示:二:在“工具”→“规划求解”(已导入)⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≥≤≤≤≤≤+++≤+++≤++++++=(非负约束)需求量约束)(家具需求量约束)(家具需求量约束)(家具需求量约束)(家具(劳动时间约束)(玻璃约束)(木材约束)0,,,41003502200110040023121000226600224..30402060432143214321432143214321x x x x x x x x x x x x x x x x x x x x t s x x x x MaxZ三: 在“规划求解参数”对话框进行选择——点击确定同理再“添加”第二个条件,得如下结果:再点“选项”进行选择,设计完毕后求解即可,得到结果如下图所示:其灵敏度报告截图如下所示:四:根据模型运行结果写出分析结果得:(1)由模型运行结果可知:这四种家具的最优日产量为:100、80、40、0.当取用这些值时能得到最大利润9200.(2)由模型运行结果可知:劳动时间的影子价格为12,当劳动时间增量不超过25小时的情况下,每多工作一小时,则能多获利12元,而支付一工人的工资仅为10元,还可获利2元,所以是值得的。
(3)由模型运行结果可知,当可提供劳动时间由400减少到398时,减少量低于允许范围内的减量,故劳动时间的影子价格没变,仍为12元。
(4)由模型运行结果可知:劳动时间与木材使用量和供应量是相同的,故他们约束时间为“紧”的;而玻璃的使用量为800,可供量为1000,故玻璃的约束条件是“非紧”的,是有余的。
所以,应优先考虑购买劳动时间和木材。
(5)由模型运行结果可知:家具一的单位利润允许减少量为20,只要家具一的单位利润减少量不超过20元,最优解不变。
而当单位一的利润从60降到55元(60-55=5元)减少量未超过20,所以最优解不改变。
仍为:100、80、40、0(6)最优解为:9200+(55-60)X100=8700(二)解:一:在Excel上建立模型如下:并按照题目要求填入数据二:“工具”→“规划求解”进行参数设定和约束条件设定如下图所示:约束条件设定三:执行“求解”处理,并选择“运算结果报告”得到如下图所示:最后得到运算报告为(部分截图):故由结果报告可知:其最短路径为:1→3→5→8→10;最短路长为:19。
(二)解:设Xij表示第i年年初给项目j提供的投资额(单位:万元),i=1,2,3,4,5;j=A,B,C,D,E;故由题意知一共有11个变量:X1A,X1D,X2A,X2C,X2D,X3A,X3B,X3D,X4A,X4D和X5D最后得到如下的线性规划模型(该模型假定项目A、C都要选择)Max z=1.06X4A+1.15X3B+1.2X2C+1.02X5Ds.t.:X1A+X1D=100-1.02X1D+X2A+X2C+X2D=0-1.06X1D-1.02X2D+X3A+X3C+X3D=0-1.06X2A-1.02X3D+X4A+X4D=0-1.06X3A-1.02X4D+X5D=0Xij≥0,X2C≤30,X3B≤40用LINDO表求解结构如下图所示:点工具栏中的“Solve”中的“Solve”得到如下图所示点击“是”后得到如下图所示:上机求解可的结果:第一年年初:X1A=70.588234(万元),X1D=29.411764(万元)第二年年初:X2A=0,X2C=30(万元),X2D=0第三年年初:X3A=0,X3B=40(万元),X3D=34.823528(万元)第四年年初:X4A=35.52(万元),X4D=0第五年年初:X5D=0所以到第五年年末该公司回收资金的本利总额为119.6512万元。
即盈利2:(一)建模型可设xij表示i厂为用户生产和运输的设备数量(单位:台),则一共有12个变量:X11,X21,X31,X41,X21,X22,X23,X24,X31,X32,X33,X34。
min z= 70X1l+40X12+80X13+60X14+70X32+100X22+110X23+50X24+80X21+70X32+130X33+40X34s.tX11+X21+X31=20X12+X22+X32=15X13+X23+X33=23X14+X24+X34=32X11+X12+X13+X14=20X21+X22+X23+X24=30X31+X32+X33+X34=40X11,X22,X33,X21,X22,X23,X24,X31,X32,X33,X34,X41= >0 (二)用LINDO上机求解有:点工具栏中的“Solve”中的“Solve”得到如下图所示点击“是”后得到如下图所示:上机求解得:A为用户生产和运输设备分别为0,7,13,0B为用户生产和运输设备分别为20,0,10,0C为用户生产和运输设备分别为0,8,0,3,2故最小费用Min Z=5860(元)3解:(一)建模型设:Xij表示第i个人完成第j项工作所创造的效益(i,j=1,2,3,4,5,6)MaxZ=20X11+15X12+16X13+5X14+4X15+7X16+17X21+15X22+33X23+12X24+8X25+6X26+9X31+12 X32+18X33+16X34+30X35+13X36+12X41+8X42+11X43+27X44+19X45+14X46+7X52+10X53+21X54 +10X55+32X56+6X64+11X65+13X66s.t.X11+X12+X13+X14+X15+X16=1X21+X22+X23+X24+X25+X26=1X31+X32+X33+X34+X35+X36=1X41+X42+X43+X44+X45+X46=1X52+X53+X54+X55+X56=1X64+X65+X66=1X11+X21+X31+X41=1X12+X22+X32+X42+X52=1X13+X23+X33+X43+X53=1X14+X24+X34+X44+X54+X64=1X15+X25+X35+X45+X55+X65=1X16+X26+X36+X46+X56+X66=1xij =>0(二)用LINDO上机求解有:点工具栏中的“Solve”中的“Solve”得到如下图所示点击“是”后得到如下图所示:由图可知:当第1人→A,第3人→C,第3人→B,第4人→D,第5人→F,第6人→E可使总效益最大为135元。
②(一)建模型同理有:MINZ=20X11+15X12+16X13+5X14+4X15+7X16+17X21+15X22+33X23+12X24+8X25+6X26+9X31+12 X32+18X33+16X34+30X35+13X36+12X41+8X42+11X43+27X44+19X45+14X46+7X52+10X53+21X54 +10X55+32X56+6X64+11X65+13X66s.t.X11+X12+X13+X14+X15+X16=1X21+X22+X23+X24+X25+X26=1X31+X32+X33+X34+X35+X36=1X41+X42+X43+X44+X45+X46=1X52+X53+X54+X55+X56=1X64+X65+X66=1X11+X21+X31+X41=1X12+X22+X32+X42+X52=1X13+X23+X33+X43+X53=1X14+X24+X34+X44+X54+X64=1X15+X25+X35+X45+X55+X65=1X16+X26+X36+X46+X56+X66=1xij =>0(二)用LINDO上机求解有:点工具栏中的“Solve”中的“Solve”得到如下图所示点击“是”后得到如下图所示:由图可知:第1→E,第2人→F,第3人→A,第4人→B第5人→C,第6人→D,才能使总耗费时间最短,即为43小时。
4:解:设Xj表示一周内产品Pj的产量。
下面计算各种资源的限额。
因工厂有九台磨床,每台一周作业96小时,故共有864磨床工时。
同理,每周的钻床工时为576.而装配工作总共使用24名工人,每人每周工作48小时,可给出的工作时间为1152小时。
(一)建模型得:Max z=550x1+600x2+350x3+400x4+200x5s.t 12x1+20x2+25x4+15x5≤86410x1+ 8x2+16x3 ≤57620x1+20x2+20x3+20x4+20x5≤1152x2 ≥10x2 ≤100x4 ≥20x4 ≤150X1,…,x5≥0(二)用LINDO上机求解有:点工具栏中的“Solve”中的“Solve”得到如下图所示点“是”后可得如下图所示:由图可知:最优生产方案为一周内生产产品P113.6667单位,产品P210单位,产品P3 13.9333单位,产品P4 20单位,不生产产品P5,可获得最大利润26393.33元。
(1)由个约束条件的松弛变量值可知工厂有136.4钻床工时的剩余。
(2)增加1台磨床意味每周增加96磨床工时。
由第一行DUAL PRICES列可知磨床工时的影子价格为16.66666,由图RIGHTHAND SIDE RANGES可知,磨床影子价格的有效范围为【700,1031.2】,864+96没有超出这个范围,因此,增加一台磨床将增加利润16.66666*96=1599.99936元(3)由图可知钻孔工时的影子价格为0,故总利润没有变化。
(4)每周增加劳动工时90人时,由OBJ COEFICIENT RANGES中的EDUAL PRICES列可知劳动工时的影子价格为17.5,扣除成本后利润的净增量为90*(17.5-8.5)=810元。
而磨床工时的影子价格为16.66666,租借100磨床工时所带来的利润净增量为100*(16.66666-9.5)=716.666元。
所以,正确的选择应为增加劳动工时。
(5)由目标函数系统的可变范围可见最优生产计划不变,单总利润增加:50X10=500(元) (6)目标函数P1系数的可变范围在[500,0+ INFINITY],所以最优基不变,故总利润随着P1单位利润的变化而变化。
(7)把原题的“20”改为“25”然后再进行求解如下图所示:当最低需求变为5时,有:由图可知:当P4最低需求为25时,总利润为:24560.00元P2的最低需求变为5时,总利润为:26810.00元。
