2014高考数学必考知识点:立体几何
2014年全国各地高考数学试题及解答分类汇编大全(13立体几何)
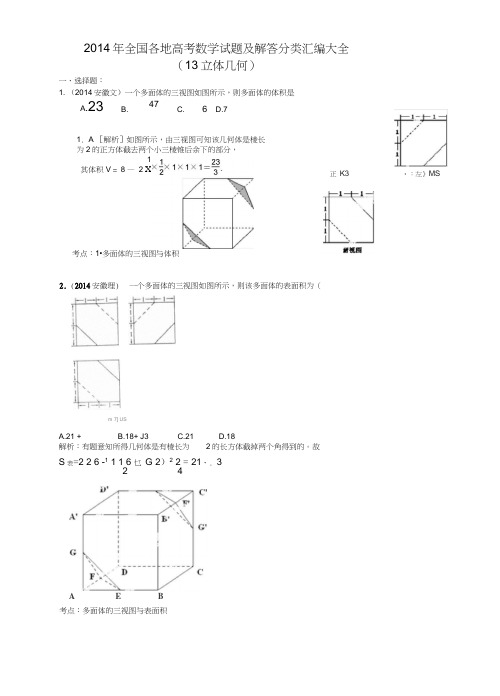
2014年全国各地高考数学试题及解答分类汇编大全(13立体几何)一、选择题:1. (2014安徽文)一个多面体的三视图如图所示,则多面体的体积是m 7] USA.21 +B.18+ J3C.21D.18解析:有题意知所得几何体是有棱长为 2的长方体截掉两个角得到的。
故S 表=2 2 6 -1 1 1 6 乜 G 2)2 2 = 21、. 32 4A E B考点:多面体的三视图与表面积A .23B.47C.6 D.71. A [解析]如图所示,由三视图可知该几何体是棱长 为2的正方体截去两个小三棱锥后余下的部分,考点:1•多面体的三视图与体积2. (2014安徽理) 一个多面体的三视图如图所示,则该多面体的表面积为(1其体积V = 8 — 2 X3正 K3 ・:左》MS3. (2014安徽理)从正方体六个面的对角线中任取两条作为一对, 其中所成的角为60的共有()A.24 对B.30 对C.48 对D.60 对 【答案】C 【解析】试题分析:在正方体ABCD - A'B'C'D'中,与上平面 A'B'C'D'中一条对角线 A'C' 成 60的直 线有BC'f B'C, A'D,AD', D'C,写上平而 ABCD ,中另F 对角线鼠F 的直线也有N 对直绻 所以一牛平面中尸说对直线,一:乂本&个面共有対X&对直线,去掉重复,则考点:1•直线的位置关系;2•异面直线所成的角4. (2014 北京理)在空间直角坐标系 Oxyz 中,已知 A(2,0,0) B(2,2,0), C(0,2,0), D(1,1, J2) •若 S,S 2,S 3分别是三棱锥 A . S = S 2 = S 3 C. S3 = Si 且 R £ 【答案】Dyoz 、zox 的正投影分为D 1、D 2、D 3,则「r4AD 1 =BD 1 = 2 , AB =2 , A S^2 2 2 =2 ,2S 2=S"=1x :2x:<v'2=J 2 , S 3 = S "=丄沢2沢丿2=灯2.2OCD 22 3OAD325.(2014福建文)以边长为1的正方形的一边所在所在直线为旋转轴,将该正方形旋转一周所得圆柱 的侧面积等于 ()A.2 二B.二C.2D.1【答案】/【解析】由已知得,所得團柱的底面辛径和高均—】 所以圆柱的侧面积为2揮,选4D - ABC 在xOy, yOz, zOx 坐标平面上的正投影图形的面积,则(B.S 2 = S 且 S 2 — S3 ・ S 3 = S 2 且 S 3 -j S i【解析】设顶点D 在三个坐标面 xoy 、 AB6. (2014福建理)某空间几何体的正视图是三角形,则该几何体不可能是()A.圆柱B.圆锥C.四面体D.三棱柱【答案】A 【解析】试题分析,由于圆柱旳三视图不-十匕丘三朗册所以选L 考点=三观图.8. (2014湖北文、理)在如图1-1所示的空间直角坐标系 O- xyz 中,一个四面体的顶点坐标分 别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为 ,②,③,④的四个图,则该四面体的正视图和俯视图分别为 图1-1& D [解析]由三视图及空间直角坐标系可知,该几何体的正视图显然是一个直角三角形且内 有一条虚线(一锐角顶点与其所对直角边中点的连线 ),故正视图是④;俯视图是一个钝角三角形,故俯视图是②•故选D.则8 -r 6-^ .82 62 r = 2,故选 B.11.(2014江西理)一几何体的直观图如右图,下列给出的四个俯视图中正确的是理)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我 的术“置如其周,令相乘也•又以高乘之, L 与高h ,计算其体积V 的近似公式V ^^L%.363.那么,近似公式V~€L 2h 相当于将圆锥体积公 759. (2014湖北文、 国现存最早的有系统的数学典籍,其中记载有求“囷盖” 卜六成一.”该术相当于给出了由圆锥的底面周长 它实际上是将圆锥体积公式中的圆周率 n 近似取为式中的n 近似取为()157 C. 50 355 D.1139. B [解析]设圆锥的底面圆半径为1 2 1r ,底面积为S,贝U L = 2 n r.由题意得h ~§Sh ,代入Sn『化简得"3.类比推理,若V -务即时,"鲁.故选B.10 (2014湖南文、理)一块石材表示的几何体的 三视图如图2 所示,将该石材切削、 打磨、加工成球,则能得到的最大球的半径等于(A.1B.2C.3答案】BD.4 来源:]【解析】最大球的半径为正视图直角三角形内切圆的半径K*— h —H IK (左tC B DB垂直AF形是13 4EE 3不确定,故选n【解析】A(0,0,0),E(4,3,12) 【解析】如下图所示,在正吗妨C ;AE ,将线段 【答案】C申,取均L £妫为右・H AL> -qZp EWE 2E 313.(2014江西理)如右图,在长方体 ABC^A 1B 1C 1D 1中,AB =11 , AD =7, AA ,=12, —质点从 顶点A 射向点E 4,3,12,遇长方体的面反射 (反射服从光的反射原理),将i -1次到第i 次反射点之 A【答案】B【解析】俯视图为在底面上的投影,易知选间的线段记为L j i =2,3,4 )1242L 2,L 3,L 4竖直放置在同一水平线上,则大致的图11、I ?、I 3、I 4,满足 h_I 2 , I 2//I 3, I 3 — I4于-5,E 1E 2“儿;取M 為厶,皿为「则石丄d 应血为I 吗2*叩贝%与占异瓯 因此从心的位直关系 2 2312 -13日(8,6,0), E 2(28,7,4), E 3(11,25,9), AE3412. (2014广东文、理)若空间中四条两两不同的直线 则下列结论一定正确的是( )A. 11 I 14B. h //I 4C. 11、14 既不平行也不 【答案】DD.h 、I 4的位置关系不确定52=65E 1E 212工。
【志鸿优化设计】(安徽专用)2014届高考数学一轮复习第八章立体几何8.1空间几何体的结构及其三视图
四棱柱的底面内接于半球的底面,由三视图中的数据可知,正四棱柱的底面边长为
2,高为
3,故半球的底面半径为
2. 所以该几何体的表面积为
1 S= 2×4π ×(
2) 2+ π×(
2) 2 +
4×2×3= 24+ 6π .
2 10. 2+ 2 解析: 原图形中
2 AB= 2, AD= 1,BC= 2 + 1,
2.
6
腰梯形,那么原平面 图形的面积是 (
).
2 A. 2 2 B . 2 C . 2- 1 D . 2+ 2 二、填空题 8.如图,点 O为正方体 ABCD-A′ B′ C′ D′的中心,点 E 为面 B′ BCC′的中心,点 F 为 B′ C′的中点,则空间四边形 D′ OEF在该正方体的各个面上的投影可能是 __________( 填 出所有可能的序号 ) .
(2) ∵ PD⊥平面 ABCD, PD? 平面 PDC,E
∴平面 PDCE⊥平面 ABCD.
∵ BC⊥CD,∴ BC⊥平面 PDCE.
1
1
∵
S
梯形
= PDCE ( 2
PD+
EC)
·
DC=
×3×2= 2
3,
1
1
∴四棱锥
B- CEPD的体积
V S = 3 B- CEPD
梯形
· PDCE BC= 3×3×2=
课时作业 36 空间几何体的结构及其三视图与直观图
一、选择题 1.已知一个几何体的三视图如图所示,分析此几何体的组成为
(
).
A.上面为棱台,下面为棱柱 B.上面 为圆台,下面为棱柱 C.上面为圆台,下面为圆柱 D.上面为棱台,下面为圆柱 2.已知某一几何体的正视图与侧视图如图所示,则在下列图形中,可以是该几何体的 俯视图的图形为 ( ) .
2014年全国高考数学理科分类汇编: 立体几何

数学立体几何空间几何体的结构20.、、[2014·安徽卷] 如图1-5,四棱柱ABCD -A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.图1-5(1)证明:Q为BB1的中点;(2)求此四棱柱被平面α所分成上下两部分的体积之比;(3)若AA1=4,CD=2,梯形ABCD的面积为6,求平面α与底面ABCD所成二面角的大小.G2 空间几何体的三视图和直观图7.[2014·安徽卷] 一个多面体的三视图如图1-2所示,则该多面体的表面积为() A.21+ 3 B.8+ 2C.21 D.185.[2014·湖北卷] 在如图1-1所示的空间直角坐标系Oxyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为()A.①和②B.①和③7.、[2014·湖南卷] 一块石材表示的几何体的三视图如图1-2所示,将该石材切削、打()图1-2A.1 B.2 C.3 D.45.[2014·江西卷] 一几何体的直观图如图1-1所示,下列给出的四个俯视图中正确的是()图1-1A B C D图1-27.、[2014·辽宁卷] 某几何体三视图如图1-1所示,则该几何体的体积为( )A .8-2πB .8-πC .8-πD .8-π4图1-13.[2014·浙江卷] 几何体的三视图(单位:cm)如图1-1所示,则此几何体的表面积是( )1-1A .90 cm 2B .129 cm 2C .132 cm 2D .138 cm 2 12.[2014·新课标全国卷Ⅰ] 如图1-3,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )图1-3A .6 2B .6C .4 2D .46.[2014·新课标全国卷Ⅱ] 如图1-1,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()图1-1A.1727B.59C.1027D.1318.[2014·四川卷] 三棱锥A -BCD及其侧视图、俯视图如图1-4所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.(1)证明:P是线段BC的中点;(2)求二面角A -NP -M的余弦值.18.[2014·广东卷] 如图1-4,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.(1)证明:CF⊥平面ADF;(2)求二面角D -AF -E的余弦值.图1-419.、、[2014·江西卷] 如图1-6,四棱锥P -ABCD中,ABCD为矩形,平面P AD⊥平面ABCD.图1-6(1)求证:AB⊥PD.(2)若∠BPC=90°,PB=2,PC=2,问AB为何值时,四棱锥P -ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.19.、[2014·辽宁卷] 如图1-5所示,△ABC和△BCD所在平面互相垂直,且AB=BC =BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.(1)求证:EF⊥BC;(2)求二面角E-BF-C17.、[2014·天津卷] 如图1-4所示,在四棱锥P -ABCD中,P A⊥底面ABCD, AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.(1)证明:BE⊥DC;(2)求直线BE与平面PBD所成角的正弦值;(3)若F为棱PC上一点,满足BF⊥AC,求二面角F -AB -P的余弦值.图1-419.、[2014·全国卷] 如图1-1所示,三棱柱ABC -A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.(1)证明:AC1⊥A1B;(2)设直线AA1与平面BCC1B1的距离为3,求二面角A1ABC的大小.13.[2014·山东卷] 三棱锥P - ABC 中,D ,E 分别为PB ,PC 的中点,记三棱锥D - ABE 的体积为V 1,P - ABC 的体积为V 2,则V 1V 2=________.8.、[2014·全国卷] 正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )A.81π4 B .16π C .9π D.27π411.[2014·全国卷] 已知二面角α-l -β为60°,AB ⊂α,AB ⊥l ,A 为垂足,CD ⊂β,C ∈l ,∠ACD =135°,则异面直线AB 与CD 所成角的余弦值为( )A.14B.24C.34D.1217.,[2014·山东卷] 如图1-3所示,在四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 是等腰梯形,∠DAB =60°,AB =2CD =2,M 是线段AB 的中点.图1-3(1)求证:C 1M ∥平面A 1ADD 1;(2)若CD 1垂直于平面ABCD 且CD 1=3,求平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值.17.[2014·浙江卷] 如图1-4,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15 m,AC=25 m,∠BCM =30°,则tan θ的最大值是________.(仰角θ为直线AP与平面ABC所成角)20.[2014·浙江卷] 如图1-5,在四棱锥A -BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED =90°,AB=CD=2,DE=BE=1,AC= 2.(1)证明:DE⊥平面ACD;(2)求二面角B -AD -E的大小.10.[2014·江西卷] 如图1-4所示,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为L i(i=2,3,4),L1=AE,将线段L1,L2,L3,L4竖直放置在同一水平线上,则大致的图形是()A BC D图1-57.[2014·北京卷] 在空间直角坐标系Oxyz中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,2).若S1,S2,S3分别是三棱锥D -ABC在xOy,yOz,zOx坐标平面上的正投影图形的面积,则()A.S1=S2=S3B.S2=S1且S2≠S3C.S3=S1且S3≠S2D.S3=S2且S3≠S119.[2014·湖北卷] 如图1-4,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).(1)当λ=1时,证明:直线BC1∥平面EFPQ.(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.。
2014高考理科数学新课标·通用第5专题立体几何

(2)由(1)知 OC⊥AB,OA1⊥AB.
热点重点难点专题透析·数学(理科)
专题5
又平面 ABC⊥平面 AA1B1B,交线为 AB,所以 OC⊥平面 AA1B1B,故 OA,OA1,OC 两两相互垂直.
以 O 为坐标原点,O→A的方向为 x 轴的正方向,|O→A|为单 位长,建立如图所示的空间直角坐标系 O-xyz.
专题5
【解析】(1)∵在图 1 的等腰梯形 PDCB 中,DA⊥PB, ∴在四棱锥 P—ABCD 中,DA⊥AB.又 PA⊥AB, ∴AB⊥平面 PAD, 又 DC∥AB,∴DC⊥平面 PAD.∵DC⊂平面 PCD, ∴平面 PAD⊥平面 PCD. (2)∵DA⊥PA,且 PA⊥AB, ∴PA⊥平面 ABCD, 又 PA⊂平面 PAB,
热点重点难点专题透析·数学(理科)
热点重点难点专题透析·数学(理科)
专题5
二面角的大小.各类角都可以转化为向量的夹角来运算, 但要注意结合实际图形,能够正确判断出两向量所成的角与 线线角、线面角、二面角间的关系,注意角的取值范围,这 是同学们的易混淆点,此外,运算错误也是常见的易错点.
7.探索型(或开放性)试题是近年高考试题命制的“新 宠”,此类问题的命制非常灵活,角度新颖,能够很好地考 查学生对知识的灵活运用及知识的迁移能力.解答开放性问 题的基本策略是先猜结论,后证明,因此大胆假设,严格证 明是解决开放性问题的基本策略.此类问题不知如何作答是 同学们常见的困惑. 8.翻折问题体现了平面问题和空间问题间的相互转化,能 够很好地考查学生的空间想象能力、图形变换能力及识图能 力.在解题过程中,若不能分清翻折前后基本量间的位置
热点重点难点专题透析·数学(理科)
专题5
【考情报告】
江苏省2014年高考数学(文)二轮复习专题提升训练:16 立体几何中的向量方法

常考问题16 立体几何中的向量方法(建议用时:80分钟)1.(2013·新课标全国Ⅱ卷)如图,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点,AA 1=AC =CB =22AB .(1)证明:BC 1∥平面A 1CD ; (2)求二面角D -A 1C -E 的正弦值.(1)证明 连接AC 1交A 1C 于点F ,则F 为AC 1的中点.又D 是AB 的中点,连接DF ,则BC 1∥DF .因为DF ⊂平面A 1CD ,BC 1⊄平面A 1CD ,所以BC 1∥平面A 1CD .(2)解 由AC =CB =22AB 得,AC ⊥BC .以C 为坐标原点,CA→的方向为x 轴正方向,CB →的方向为y轴正方向,CC 1→的方向为z 轴正方向,建立如图所示的空间直角坐标系C -xyz .设CA =2,则D (1,1,0),E (0,2,1),A 1(2,0,2),CD →=(1,1,0),CE →=(0,2,1),CA 1→=(2,0,2). 设n =(x 1,y 1,z 1)是平面A 1CD 的法向量,则⎩⎪⎨⎪⎧n ·CD →=0,n ·CA 1→=0,即⎩⎨⎧x 1+y 1=0,2x 1+2z 1=0.可取n =(1,-1,-1).同理,设m =(x 2,y 2,z 2)是平面A 1CE 的法向量, 则⎩⎪⎨⎪⎧m ·CE →=0,m ·CA 1→=0.即⎩⎨⎧2y 2+z 2=0,2x 2+2z 2=0,可取m =(2,1,-2).从而cos 〈n ,m 〉=n ·m |n ||m |=33,故sin 〈n ,m 〉=63.即二面角D -A 1C -E 的正弦值为63.2.(2013·陕西卷)如图,四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形,O 为底面中心,A 1O ⊥平面ABCD ,AB =AA 1= 2. (1)证明:A 1C ⊥平面BB 1D 1D ;(2)求平面OCB 1与平面BB 1D 1D 的夹角θ的大小.(1)证明 由题设易知OA ,OB ,OA 1两两垂直,以O 为原点建立直角坐标系,如图.∵AB =AA 1=2, ∴OA =OB =OA 1=1,∴A (1,0,0),B (0,1,0),C (-1,0,0),D (0,-1,0), A 1(0,0,1).由A 1B 1→=AB →,易得B 1(-1,1,1). ∵A 1C →=(-1,0,-1),BD →=(0,-2,0), BB 1→=(-1,0,1). ∴A 1C →·BD →=0,A 1C →·BB 1→=0, ∴A 1C ⊥BD ,A 1C ⊥BB 1, 又BD ∩BB 1=B , ∴A 1C ⊥平面BB 1D 1D .(2)解 设平面OCB 1的法向量n =(x ,y ,z ). ∵OC →=(-1,0,0),OB 1→=(-1,1,1), ∴⎩⎪⎨⎪⎧n ·OC →=-x =0,n ·OB 1→=-x +y +z =0,∴⎩⎨⎧x =0,y =-z ,取n =(0,1,-1), 由(1)知,A 1C →=(-1,0,-1)是平面BB 1D 1D 的法向量, ∴cos θ=|cos 〈n ,A 1C →〉|=12×2=12. 又∵0≤θ≤π2,∴θ=π3.3.如图,在四棱锥P -ABCD 中,PC ⊥底面ABCD ,底面ABCD 是直角梯形,AB ⊥AD ,AB ∥CD ,AB =2AD =2CD =2,E 是PB 的中点.(1)求证:平面EAC ⊥平面PBC ;(2)若二面角P -AC -E 的余弦值为63,求直线P A 与平面EAC 所成角的正弦值.(1)证明 ∵PC ⊥平面ABCD ,AC ⊂平面ABCD ,∴AC ⊥PC .∵AB =2,AD =CD =1,∴AC =BC = 2. ∴AC 2+BC 2=AB 2.∴AC ⊥BC . 又BC ∩PC =C ,∴AC ⊥平面PBC . ∵AC ⊂平面EAC , ∴平面EAC ⊥平面PBC .(2)解 如图,以点C 为原点,DA→,CD →,CP →分别为x 轴、y 轴、z 轴正方向,建立空间直角坐标系,则C (0,0,0),A (1,1,0),B (1,-1,0),设P (0,0,a )(a >0),则E ⎝ ⎛⎭⎪⎫12,-12,a 2,CA →=(1,1,0),CP →=(0,0,a ),CE→=⎝ ⎛⎭⎪⎫12,-12,a 2.取m =(1,-1,0),则m ·CA →=m ·CP →=0,m 为面P AC 的法向量.设n =(x ,y ,z )为面EAC 的法向量,则n ·CA →=n ·CE →=0,即⎩⎨⎧x +y =0,x -y +az =0,取x =a ,y =-a ,z =-2,则n =(a ,-a ,-2),依题意,|cos 〈m ,n 〉|=|m ·n ||m ||n |=a a 2+2=63,则a =2.于是n =(2,-2,-2),P A →=(1,1,-2).设直线P A 与平面EAC 所成角为θ,则sin θ=|cos 〈P A →,n 〉|=P A →·n |P A ||n |=23,即直线P A 与平面EAC 所成角的正弦值为23.4.(2013·辽宁卷)如图,AB 是圆的直径,P A 垂直圆所在的平面,C 是圆上的点.(1)求证:平面P AC ⊥平面PBC ;(2)若AB =2,AC =1,P A =1,求二面角C -PB -A 的余弦值.(1)证明 由AB 是圆的直径,得AC ⊥BC , 由P A ⊥平面ABC ,BC ⊂平面ABC ,得P A ⊥BC . 又P A ∩AC =A ,P A ⊂平面P AC ,AC ⊂平面P AC , 所以BC ⊥平面P AC .又BC ⊂平面PBC , 所以平面PBC ⊥平面P AC .(2)解 过C 作CM ∥AP ,则CM ⊥平面ABC .如图,以点C 为坐标原点,分别以直线CB ,CA ,CM 为x 轴、y 轴、z 轴建立空间直角坐标系.在Rt △ABC 中,因为AB =2,AC =1,所以BC = 3. 因为P A =1,所以A (0,1,0),B (3,0,0),P (0,1,1). 故C B →=(3,0,0),C P →=(0,1,1). 设平面BCP 的法向量为n 1=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧C B →·n 1=0,C P →·n 1=0,所以⎩⎨⎧3x 1=0,y 1+z 1=0,不妨令y 1=1,则n 1=(0,1,-1). 因为A P →=(0,0,1),A B →=(3,-1,0), 设平面ABP 的法向量为n 2=(x 2,y 2,z 2),则⎩⎪⎨⎪⎧A P →·n 2=0,A B →·n 2=0,所以⎩⎨⎧z 2=0,3x 2-y 2=0,不妨令x 2=1,则n 2=(1,3,0). 于是cos 〈n 1,n 2〉=322=64.所以由题意可知二面角C -PB -A 的余弦值为64. 5.(2013·合肥第二次质检)在四棱锥P -ABCD 中,底面ABCD 是边长为1的正方形,且P A ⊥平面ABCD . (1)求证:PC ⊥BD ;(2)过直线BD 且垂直于直线PC 的平面交PC 于点E ,且三棱锥E -BCD 的体积取到最大值. ①求此时四棱锥E -ABCD 的高; ②求二面角A -DE -B 的正弦值的大小.(1)证明 连接AC ,因为四边形ABCD 是正方形,所以BD ⊥AC .因为P A ⊥平面ABCD ,所以P A ⊥BD .又AC ∩P A =A ,所以BD ⊥平面P AC . 又PC ⊂平面P AC ,所以PC ⊥BD .(2)解 ①设P A =x ,三棱锥E -BCD 的底面积为定值,在△PBC 中,易知PB =x 2+1,PC =x 2+2,又BC =1,故△PBC 直角三角形.又BE ⊥PC ,得EC =1x 2+2,可求得该三棱锥的高h =x x 2+2=1x +2x.当且仅当x =2x ,即x =2时,三棱锥E -BCD 的体积取到最大值,所以h =24.此时四棱锥E -ABCD 的高为24.②以点A 为原点,AB ,AD ,AP 所在直线为坐标轴建立空间直角坐标系,则A (0,0,0),C (1,1,0),D (0,1,0),P (0,0,2),易求得CE =14CP . 所以AE →=AC →+14CP →=⎝ ⎛⎭⎪⎫34,34,24,AD →=(0,1,0).设平面ADE 的法向量n 1=(x ,y ,z ),则⎩⎪⎨⎪⎧AE →·n =0,AD →·n =0,即⎩⎨⎧34x +34y +24z =0,y =0,令x =2,则n 1=(2,0,-3),同理可得平面BDE 的法向量n 2=CP →=(-1,-1,2),所以cos 〈n 1,n 2〉=n 1·n 2|n 1||n 2|=-22211.所以sin 〈n 1,n 2〉=3311.所以二面角A -DE -B 的正弦值的大小为3311.6.(2013·天津卷)如图,四棱柱ABCD -A 1B 1C 1D 1中,侧棱A 1A ⊥底面ABCD ,AB ∥DC ,AB ⊥AD ,AD =CD =1,AA 1=AB =2,E 为棱AA 1的中点.(1)证明B 1C 1⊥CE ;(2)求二面角B 1-CE -C 1的正弦值;(3)设点M 在线段C 1E 上,且直线AM 与平面ADD 1A 1所成角的正弦值为26,求线段AM 的长.解 如图,以点A 为原点建立空间直角坐标系,依题意得A (0,0,0),B (0,0,2),C (1,0,1),B 1(0,2,2),C 1(1,2,1),E (0,1,0).(1)证明:易得B 1C 1→=(1,0,-1),CE →=(-1,1,-1),于是B 1C 1→·CE →=0,所以B 1C 1⊥CE .(2)B 1C →=(1,-2,-1).设平面B 1CE 的法向量m =(x ,y ,z ),则⎩⎪⎨⎪⎧m ·B 1C →=0,m ·CE →=0,即⎩⎨⎧x -2y -z =0,-x +y -z =0.消去x ,得y +2z =0,不妨令z =1,可得一个法向量为m =(-3,-2,1).由(1),B 1C 1⊥CE ,又CC 1⊥B 1C 1,可得B 1C 1⊥平面CEC 1,故B 1C 1→=(1,0,-1)为平面CEC 1的一个法向量.于是cos 〈m ,B 1C 1→〉=m ·B 1C 1→|m ||B 1C 1→|=-414×2=-277,从而sin 〈m ,B 1C 1→〉=217,所以二面角B 1-CE -C 1的正弦值为217.(3)AE →=(0,1,0),EC 1→=(1,1,1),设EM →=λEC 1→=(λ,λ,λ),0≤λ≤1,有AM →=AE →+EM →=(λ,λ+1,λ).可取AB →=(0,0,2)为平面ADD 1A 1的一个法向量. 设θ为直线AM 与平面ADD 1A 1所成的角,则 sin θ=|cos 〈AM →,AB →〉|=|AM →·AB →||AM →||AB →|=2λλ2+(λ+1)2+λ2×2=λ3λ2+2λ+1, 于是λ3λ2+2λ+1=26,解得λ=13,所以AM = 2.。
2014届高考专题立体几何——正方体(三讲)

A1A正方体三讲1.如图,正方体1111ABCD A B C D -的棱长为1,连结1DB ,交平面11A BC 于点P , 则以下结论中错误的是( ) (A )1DB ⊥平面11A BC (B )点P 是11A BC ∆的重心(C )1PB(D )直线1PB 与1AA 所成角为45︒2.如图,在正方体1111ABCD A B C D -中,P 为对角线1BD 的三等分点,P 到各顶点的距离的不同取值有( )(A )3个 (B )4个 (C )5个 (D )6个3.如图,正方体1111ABCD A B C D -的棱长为2.动点E 、F 在棱11A B 上,点Q 是 棱CD 的中点,动点P 在棱AD 上.若1EF =,DP x =,1A E y =(,x y 大于零), 则三棱锥P EFQ -的体积( ) (A )与x ,y 都有关 (B )与x ,y 都无关 (C )与x 有关,与y 无关 (D )与y 有关,与x 无关A1A1A CA 1AA 1A4.如图,正方体1111ABCD A B C D -的棱长为2.动点E 、F 在棱11A B 上,动点P 、Q 分别在AD 、CD 上.若1EF =,1A E x =,DQ y =,DP z =(,,x y z 大于零), 则四面体PEFQ 的体积( ) (A )与x ,y ,z 都有关 (B )与x 有关,与y ,z 无关 (C )与y 有关,与x ,z 无关 (D )与z 有关,与x ,y 无关5.如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点,E F , 且12EF =,则下列结论中错误的是( ) (A )AC BE ⊥ (B )EF ∥平面ABCD(C )三棱锥A BEF -的体积为定值 (D )AEF ∆的面积与BEF ∆的面积相等6.如图,M 是正方体1111ABCD A B C D -的棱1DD 的中点,给出下列结论:① 过点M 有且只有一条直线与直线AB 、11B C 都相交;② 过点M 有且只有一条直线与直线AB 、11B C 都垂直;③ 过点M 有且只有一条平面与直线AB 、11B C 相交; ④ 过点M 有且只有一条平面与直线AB 、11B C 平行. 其中,正确的结论是( )(A )②③④ (B )①③④ (C )①②④ (D )①②③1A CP 2P 1A 1D 1B 1C 1D BC AA BC D M NP A 1 B 1 C 1D 17.如图,在棱长为1的正方体1111ABCD A B C D -中,点,E F 分别是棱1,BC CC的中点,P 是侧面11BCC B内一点,若1A P ∥平面AEF ,则线段1A P 的长度的取值范围是( ) (A) (B) (C ) (D )8.棱长为1的正方体1111ABCD A B C D -中,点1P 、2P 分别是线段AB 、1BD (不包括端点) 上的动点,且线段12P P 平行于平面11A ADD ,则四面体121PP AB 的体积的最大值是 (A )124 (B )112(C )16 (D )129.如图,动点P 在正方体1111ABCD A B C D -的对角线1BD 上,过点P 作垂直于平面11BB D D 的直线,与正方体表面相交于两点,M N .设BP x =,MN y =,则函数 ()y f x =的图象大致是( )FE C 1B 1D 1A 1DC BA10.如图,正方体1111ABCD A B C D -中,E 是棱11B C 的中点,动点P 在底面ABCD 内,且11PA A E =,则点P 运动形成的图形是( ) (A )线段 (B )圆弧 (C )椭圆的一部分 (D )抛物线的一部分11.如图,正方体1111ABCD A B C D -中,P 为底面ABCD 上的动点,1PE AC ⊥于E , 且PA PE =,则点P 的轨迹是( ) (A )线段 (B )圆弧 (C )椭圆的一部分 (D )抛物线的一部分12.已知正方体的棱长为1,其俯视图是一个面积为1的矩形,则该正方体的正视图的面积等于( ) (A(B )1 (C(D13.已知正方体的棱长为1,其俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于( ) (A )1(B(C)12(D)214.有一个棱长为1的正方体,按任意方向正投影,其投影面积的最大值是( ) (A )1(B)2(C(D注:本题较难,有多种方法.A 1B BA 1D 1C 1B 1A 1D CABA 1AA 1A15.在正方体1111ABCD A B C D -中,异面直线1A B 与1B C 所成角的大小为_______.注:教师应让学生思考,正方体的内接特殊多边形或体. (如:正三角形,正四面体,正四棱锥,正六边形等)16.如图,在正方体1111ABCD A B C D -中,,,,E F G H 分别为1111,,,CC C D D D DC 的中点,N 是BC 的中点,点M 在正方形EFGH 及其内部运动,则当M 满足条件 时, 有MN ∥平面11B BDD17.如图,棱长为2的正方体1111ABCD A B C D -中,E 为BC的中点,点P 在线段1D E 上.点P 到直线1CC 的距离的 最小值为 .18.在正方体1111ABCD A B C D -中,点Q 是线段1DD 上的动点,过点,,A B Q 的平面与正方体1111ABCD A B C D -相截,则截面图形是 .19.已知正方体1111ABCD A B C D -的棱长为1,P 是截面BD A 1内 (包括边界)的动点,则11C P C B ⋅的取值范围是 .A1AA 1AP N MA 1D 1B 1C 1DBCA20.如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点,,A P Q 的平面截该正方体所得的截面记为S .则下列命题正确的是__________.(写出所有正确命题的编号)①②③⑤ ① 当102CQ <<时,S 为四边形; ② 当12CQ =时,S 为等腰梯形;③ 当34CQ =时,S 与11C D 的交点R 满足113C R =;④ 当314CQ <<时,S 为六边形;⑤ 当1CQ =时,S21.如图,在棱长为2的正方体1111ABCD A B C D -中,点P 在ACD ∆内运动,且在线段,AC AD 上的射影分别为M 、N .若||2PA =,则三棱锥1P D MN -体积的最大值为__________.22.已知正方体1111ABCD A B C D -的棱长为1,动点P 在正方体1111ABCDA B C D -表面上运动,且PA r =(0r <<,记点P 的轨迹的长度为()f r ,则1()2f =________; 关于r 的方程()f r k =的解的个数可以为________.(填上所有可能的值)。
2014年高考数学分类汇编(高考真题+模拟新题)立体几何 理
G 单元 立体几何G1 空间几何体的结构 20.、、[2014·安徽卷] 如图15,四棱柱ABCD A 1B 1C 1D 1中,A 1A ⊥底面ABCD ,四边形ABCD 为梯形,AD ∥BC ,且AD =2BC .过A 1,C ,D 三点的平面记为α,BB 1与α的交点为Q .图15(1)证明:Q 为BB 1的中点;(2)求此四棱柱被平面α所分成上下两部分的体积之比;(3)若AA 1=4,CD =2,梯形ABCD 的面积为6,求平面α与底面ABCD 所成二面角的大小. 20.解: (1)证明:因为BQ ∥AA 1,BC ∥AD , BC ∩BQ =B ,AD ∩AA 1=A , 所以平面QBC ∥平面A 1AD ,从而平面A 1CD 与这两个平面的交线相互平行, 即QC ∥A 1D .故△QBC 与△A 1AD 的对应边相互平行, 于是△QBC ∽△A 1AD , 所以BQ BB 1=BQ AA 1=BC AD =12,即Q 为BB 1的中点. (2)如图1所示,连接QA ,QD .设AA 1=h ,梯形ABCD 的高为d ,四棱柱被平面α所分成上下两部分的体积分别为V 上和V 下,BC =a ,则AD =2a .图1V 三棱锥Q A 1AD =13×12·2a ·h ·d =13ahd ,V 四棱锥Q ABCD =13·a +2a 2·d ·⎝ ⎛⎭⎪⎫12h =14ahd ,所以V 下=V 三棱锥Q A 1AD +V 四棱锥Q ABCD =712ahd .又V 四棱柱A 1B 1C 1D 1 ABCD =32ahd ,所以V 上=V 四棱柱A 1B 1C 1D 1 ABCD -V 下=32ahd -712ahd =1112ahd ,故V 上V 下=117.(3)方法一:如图1所示,在△ADC 中,作AE ⊥DC ,垂足为E ,连接A 1E .又DE ⊥AA 1,且AA 1∩AE =A ,所以DE ⊥平面AEA 1,所以DE ⊥A 1E .所以∠AEA 1为平面α与底面ABCD 所成二面角的平面角. 因为BC ∥AD ,AD =2BC ,所以S △ADC =2S △BCA . 又因为梯形ABCD 的面积为6,DC =2, 所以S △ADC =4,AE =4. 于是tan ∠AEA 1=AA 1AE =1,∠AEA 1=π4. 故平面α与底面ABCD 所成二面角的大小为π4.方法二:如图2所示,以D 为原点,DA ,DD 1→分别为x 轴和z 轴正方向建立空间直角坐标系. 设∠CDA =θ,BC =a ,则AD =2a . 因为S 四边形ABCD =a +2a2·2sin θ=6,所以a =2sin θ.图2从而可得C (2cos θ,2sin θ,0),A 1⎝⎛⎭⎪⎫4sin θ,0,4,所以DC =(2cos θ,2sin θ,0),DA 1→=⎝ ⎛⎭⎪⎫4sin θ,0,4.设平面A 1DC 的法向量n =(x ,y ,1),由⎩⎨⎧DA 1→·n =4sin θx +4=0,DC →·n =2x cos θ+2y sin θ=0,得⎩⎪⎨⎪⎧x =-sin θ,y =cos θ,所以n =(-sin θ,cos θ,1).又因为平面ABCD 的法向量m =(0,0,1), 所以cos 〈n ,m 〉=n·m |n||m|=22,故平面α与底面ABCD 所成二面角的大小为π4.8.[2014·湖北卷] 《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:“置如其周,令相乘也.又以高乘之,三十六成一.”该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式V ≈136L 2h .它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V ≈275L 2h 相当于将圆锥体积公式中的π近似取为( )A.227B.258C.15750D.3551138.B [解析] 设圆锥的底面圆半径为r ,底面积为S ,则L =2πr ,由题意得136L 2h ≈13Sh ,代入S =πr 2化简得π≈3;类比推理,若V =275L 2h ,则π≈258.故选B.7.、[2014·辽宁卷] 某几何体三视图如图11所示,则该几何体的体积为( )A .8-2πB .8-πC .8-π2D .8-π4图117.B [解析] 根据三视图可知,该几何体是正方体减去两个体积相等的圆柱的一部分⎝⎛⎭⎪⎫占圆柱的14后余下的部分,故该几何体体积为2×2×2-2×14×π×2=8-π.G2 空间几何体的三视图和直观图7.[2014·安徽卷] 一个多面体的三视图如图12所示,则该多面体的表面积为( )A .21+ 3B .8+ 2C .21D .18图127.A [解析] 如图,由三视图可知该几何体是棱长为2的正方体截去两个小三棱锥后余下的部分,其表面积S =6×4-12×6+2×12×2×62=21+ 3.2.[2014·福建卷] 某空间几何体的正视图是三角形,则该几何体不可能是( ) A .圆柱 B .圆锥 C .四面体 D .三棱柱2.A [解析] 由空间几何体的三视图可知,圆柱的正视图、侧视图、俯视图都不可能是三角形. 5.[2014·湖北卷] 在如图11所示的空间直角坐标系O xyz 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为( )A .①和②B .①和③C 5.D [解析] 由三视图及空间直角坐标系可知,该几何体的正视图显然是一个直角三角形且内有一条虚线(一锐角顶点与其所对直角边中点的连线),故正视图是④;俯视图是一个钝角三角形,故俯视图是②. 故选D.7.、[2014·湖南卷] 一块石材表示的几何体的三视图如图12所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于( )图12A .1B .2C .3D .47.B [解析] 由三视图可知,石材为一个三棱柱(相对应的长方体的一半),故可知能得到的最大球为三棱柱的内切球.由题意可知正视图三角形的内切圆的半径即为球的半径,可得r =6+8-102=2.5.[2014·江西卷] 一几何体的直观图如图11所示,下列给出的四个俯视图中正确的是( )图11A B C D图125.B [解析] 易知该几何体的俯视图为选项B 中的图形. 7.、[2014·辽宁卷] 某几何体三视图如图11所示,则该几何体的体积为( )A .8-2πB .8-πC .8-π2D .8-π4图117.B [解析] 根据三视图可知,该几何体是正方体减去两个体积相等的圆柱的一部分⎝⎛⎭⎪⎫占圆柱的14后余下的部分,故该几何体体积为2×2×2-2×14×π×2=8-π.3.[2014·浙江卷] 几何体的三视图(11所示,则此几何体的表面积是( )11 A .90 cm 2B .129 cm 2C .132 cm 2D .138 cm 23.D [解析] 此几何体是由长方体与三棱柱组合而成的,其直观图如图,所以该几何体的表面积为2(4×3+6×3+6×4)+2×12×3×4+4×3+3×5-3×3=138(cm2),故选D.12.[2014·新课标全国卷Ⅰ] 如图13,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )图13A.6 2 B.6 C.4 2 D.412.B [解析] 该几何体是如图所示的棱长为4的正方体内的三棱锥ECC1D1(其中E为BB1的中点),其中最长的棱为D1E=(4 2)2+22=6.6.[2014·新课标全国卷Ⅱ] 如图11,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )图11A.1727B.59C.1027D.136.C [解析] 该零件是一个由两个圆柱组成的组合体,其体积为π×32×2+π×22×4=34π(cm3),原毛坯的体积为π×32×6=54π(cm3),切削掉部分的体积为54π-34π=20π(cm3),故所求的比值为20π54π=1027.17.[2014·陕西卷] 四面体ABCD及其三视图如图14所示,过棱AB的中点E作平行于AD,BC的平面分别交四面体的棱BD,DC,CA于点F,G,H.(1)证明:四边形EFGH是矩形;(2)求直线AB与平面EFGH夹角θ的正弦值.图1417.解:(1)证明:由该四面体的三视图可知, BD ⊥DC ,BD ⊥AD ,AD ⊥DC , BD =DC =2,AD =1.由题设,BC ∥平面EFGH , 平面EFGH ∩平面BDC =FG , 平面EFGH ∩平面ABC =EH , ∴BC ∥FG ,BC ∥EH ,∴FG ∥EH . 同理EF ∥AD ,HG ∥AD ,∴EF ∥HG . ∴四边形EFGH 是平行四边形.又∵AD ⊥DC ,AD ⊥BD ,∴AD ⊥平面BDC , ∴AD ⊥BC ,∴EF ⊥FG , ∴四边形EFGH 是矩形.(2)方法一:如图,以D 为坐标原点建立空间直角坐标系,则D (0,0,0),A (0,0,1),B (2,0,0),C (0,2,0),DA =(0,0,1),BC =(-2,2,0), BA =(-2,0,1).设平面EFGH 的法向量n =(x ,y ,z ), ∵EF ∥AD ,FG ∥BC , ∴n ·DA =0,n ·BC =0,得⎩⎪⎨⎪⎧z =0,-2x +2y =0,取n =(1,1,0), ∴sin θ=|cos 〈BA →,n 〉|=⎪⎪⎪⎪⎪⎪BA ·n |BA ||n |=25×2=105. 方法二:如图,以D 为坐标原点建立空间直角坐标系, 则D (0,0,0),A (0,0,1),B (2,0,0),C (0,2,0),∵E 是AB 的中点,∴F ,G 分别为BD ,DC 的中点,得E ⎝ ⎛⎭⎪⎫1,0,12,F (1,0,0),G (0,1,0). ∴FE →=⎝⎛⎭⎪⎫0,0,12,FG =(-1,1,0),BA =(-2,0,1).设平面EFGH 的法向量n =(x ,y ,z ), 则n ·FE =0,n ·FG =0,得⎩⎪⎨⎪⎧12z =0,-x +y =0,取n =(1,1,0), ∴sin θ=|cos 〈BA →,n 〉|=⎪⎪⎪⎪⎪⎪BA ·n |BA →||n |=25×2=105. 10.[2014·天津卷] 一个儿何体的三视图如图13所示(单位:m),则该几何体的体积为________m 3.图1310.20π3 [解析] 由三视图可得,该几何体为圆柱与圆锥的组合体,其体积V =π×12×4+13π×22×2=20π3.7.[2014·重庆卷] 某几何体的三视图如图12( )12A .54B .60C .66D .727.B [解析] 由三视图可知该几何体是由一个直三棱柱去掉一个三棱锥所得,三棱柱的底面是一个两直角边长分别为3和4的直角三角形,高为5,截去的锥体的底面是两直角边的边长分别为3和4的直角三角形,高为3,所以表面积为S =12×3×4+3×52+2+52×4+2+52×5+3×5=60.G3 平面的基本性质、空间两条直线4.[2014·辽宁卷] 已知m ,n 表示两条不同直线,α表示平面.下列说法正确的是( ) A .若m ∥α,n ∥α,则m ∥n B .若m ⊥α,n ⊂α,则m ⊥n C .若m ⊥α,m ⊥n ,则n ∥α D .若m ∥α,m ⊥n ,则n ⊥α4.B [解析] B [解析] 由题可知,若m ∥α,n ∥α,则m 与n 平行、相交或异面,所以A 错误;若m ⊥α,n ⊂α,则m ⊥n ,故B 正确;若m ⊥α,m ⊥n ,则n ∥α或n ⊂α,故C 错误.若m ∥α,m ⊥n ,则n ∥α或n ⊥α或n 与a 相交,故D 错误.17.、、[2014·福建卷] 在平面四边形ABCD 中,AB =BD =CD =1,AB ⊥BD ,CD ⊥BD .将△ABD 沿BD 折起,使得平面ABD ⊥平面BCD ,如图15所示.(1)求证:AB ⊥CD ;(2)若M 为AD 中点,求直线AD 与平面MBC 所成角的正弦值.图1517.解:(1)证明:∵平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,AB ⊂平面ABD ,AB ⊥BD ,∴AB ⊥平面BCD .又CD ⊂平面BCD ,∴AB ⊥CD .(2)过点B 在平面BCD 内作BE ⊥BD .由(1)知AB ⊥平面BCD ,BE ⊂平面BCD ,BD ⊂平面BCD ,∴AB ⊥BE ,AB ⊥BD .以B 为坐标原点,分别以BE →,BD →,BA →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图所示).依题意,得B (0,0,0),C (1,1,0),D (0,1,0),A (0,0,1),M ⎝ ⎛⎭⎪⎫0,12,12. 则BC →=(1,1,0),BM →=⎝ ⎛⎭⎪⎫0,12,12,AD →=(0,1,-1).设平面MBC 的法向量n =(x 0,y 0,z 0),则⎩⎪⎨⎪⎧n ·BC →=0,n ·BM →=0,即⎩⎪⎨⎪⎧x 0+y 0=0,12y 0+12z 0=0, 取z 0=1,得平面MBC 的一个法向量n =(1,-1,1).设直线AD 与平面MBC 所成角为θ,则sin θ=||cos 〈n ,AD →〉=|n ·AD →||n |·|AD →|=63.即直线AD 与平面MBC 所成角的正弦值为63. 11.[2014·新课标全国卷Ⅱ] 直三棱柱ABC A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( )11.C [解析] 如图,E 为BC 的中点.由于M ,N 分别是A 1B 1,A 1C 1的中点,故MN ∥B 1C 1且MN =12B 1C 1,故MN 綊BE ,所以四边形MNEB 为平行四边形,所以EN 綊BM ,所以直线AN ,NE 所成的角即为直线BM ,AN所成的角.设BC =1,则B 1M =12B 1A 1=22,所以MB =1+12=62=NE ,AN =AE =52,在△ANE 中,根据余弦定理得cos ∠ANE =64+54-542×62×52=3010.18.,,,[2014·四川卷] 三棱锥A BCD 14所示.设M ,N 分别为线段AD ,AB 的中点,P 为线段BC 上的点,且MN ⊥NP .(1)证明:P 是线段BC 的中点;(2)求二面角A NP M 的余弦值.图1418.解:(1)如图所示,取BD 的中点O ,连接AO ,CO . 由侧视图及俯视图知,△ABD ,△BCD 为正三角形,所以AO ⊥BD ,OC ⊥BD .因为AO ,OC ⊂平面AOC ,且AO ∩OC =O , 所以BD ⊥平面AOC .又因为AC ⊂平面AOC ,所以BD ⊥AC . 取BO 的中点H ,连接NH ,PH .又M ,N ,H 分别为线段AD ,AB ,BO 的中点,所以MN ∥BD ,NH ∥AO , 因为AO ⊥BD ,所以NH ⊥BD . 因为MN ⊥NP ,所以NP ⊥BD .因为NH ,NP ⊂平面NHP ,且NH ∩NP =N ,所以BD ⊥平面NHP . 又因为HP ⊂平面NHP ,所以BD ⊥HP .又OC ⊥BD ,HP ⊂平面BCD ,OC ⊂平面BCD ,所以HP ∥OC .因为H 为BO 的中点,所以P 为BC 的中点.(2)方法一:如图所示,作NQ ⊥AC 于Q ,连接MQ.由(1)知,NP ∥AC ,所以NQ ⊥NP .因为MN ⊥NP ,所以∠MNQ 为二面角A NP M 的一个平面角. 由(1)知,△ABD ,△BCD 为边长为2的正三角形,所以AO =OC = 3. 由俯视图可知,AO ⊥平面BCD .因为OC ⊂平面BCD ,所以AO ⊥OC ,因此在等腰直角△AOC 中,AC = 6. 作BR ⊥AC 于R因为在△ABC 中,AB =BC ,所以R 为AC 的中点, 所以BR =AB 2-⎝ ⎛⎭⎪⎫AC 22=102. 因为在平面ABC 内,NQ ⊥AC ,BR ⊥AC ,所以NQ ∥BR .又因为N 为AB 的中点,所以Q 为AR 的中点,所以NQ =BR 2=104.同理,可得MQ =104. 故△MNQ 为等腰三角形, 所以在等腰△MNQ 中, cos ∠MNQ =MN 2NQ =BD4NQ =105.故二面角A NP M 的余弦值是105. 方法二:由俯视图及(1)可知,AO ⊥平面BCD . 因为OC ,OB ⊂平面BCD ,所以AO ⊥OC ,AO ⊥OB . 又OC ⊥OB ,所以直线OA ,OB ,OC 两两垂直.如图所示,以O 为坐标原点,以OB ,OC ,OA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O xyz .则A (0,0,3),B (1,0,0),C (0,3,0),D (-1,0,0). 因为M ,N 分别为线段AD ,AB 的中点, 又由(1)知,P 为线段BC 的中点,所以M ⎝ ⎛⎭⎪⎫-12,0,32,N ⎝ ⎛⎭⎪⎫12,0,32,P ⎝ ⎛⎭⎪⎫12,32,0,于是AB =(1,0,-3),BC =(-1,3,0),MN =(1,0,0),NP =⎝⎛⎭⎪⎫0,32,-32. 设平面ABC 的一个法向量n 1=(x 1,y 1,z 1), 由⎩⎪⎨⎪⎧n 1⊥AB ,n 1⊥BC ,得⎩⎪⎨⎪⎧n 1·AB =0,n 1·BC =0,即⎩⎨⎧(x 1,y 1,z 1)·(1,0,-3)=0,(x 1,y 1,z 1)·(-1,3,0)=0, 从而⎩⎨⎧x 1-3z 1=0,-x 1+3y 1=0.取z 1=1,则x 1=3,y 1=1,所以n 1=(3,1,1). 设平面MNP 的一个法向量n 2=(x 2,y 2,z 2),由,⎩⎪⎨⎪⎧n 2⊥MN ,n 2⊥NP ,得⎩⎪⎨⎪⎧n 2·MN =0,n 2·NP =0, 即⎩⎪⎨⎪⎧(x 2,y 2,z 2)·(1,0,0)=0,(x 2,y 2,z 2)·⎝⎛⎭⎪⎫0,32,-32=0, 从而⎩⎪⎨⎪⎧x 2=0,32y 2-32z 2=0. 取z 2=1,则y 2=1,x 2=0,所以n 2=(0,1,1). 设二面角A NP M 的大小为θ,则cos θ=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=⎪⎪⎪⎪⎪⎪(3,1,1)·(0,1,1)5×2=105.故二面角A NP M 的余弦值是105.G4 空间中的平行关系 20.、、[2014·安徽卷] 如图15,四棱柱ABCD A 1B 1C 1D 1中,A 1A ⊥底面ABCD ,四边形ABCD 为梯形,AD ∥BC ,且AD =2BC .过A 1,C ,D 三点的平面记为α,BB 1与α的交点为Q .图15(1)证明:Q 为BB 1的中点;(2)求此四棱柱被平面α所分成上下两部分的体积之比;(3)若AA 1=4,CD =2,梯形ABCD 的面积为6,求平面α与底面ABCD 所成二面角的大小. 20.解: (1)证明:因为BQ ∥AA 1,BC ∥AD , BC ∩BQ =B ,AD ∩AA 1=A , 所以平面QBC ∥平面A 1AD ,从而平面A 1CD 与这两个平面的交线相互平行, 即QC ∥A 1D .故△QBC 与△A 1AD 的对应边相互平行, 于是△QBC ∽△A 1AD , 所以BQ BB 1=BQ AA 1=BC AD =12,即Q 为BB 1的中点. (2)如图1所示,连接QA ,QD .设AA 1=h ,梯形ABCD 的高为d ,四棱柱被平面α所分成上下两部分的体积分别为V 上和V 下,BC =a ,则AD =2a .图1V 三棱锥Q A 1AD =13×12·2a ·h ·d =13ahd ,V 四棱锥Q ABCD =13·a +2a 2·d ·⎝ ⎛⎭⎪⎫12h =14ahd ,所以V 下=V 三棱锥Q A 1AD +V 四棱锥Q ABCD =712ahd .又V 四棱柱A 1B 1C 1D 1 ABCD =32ahd ,所以V 上=V 四棱柱A 1B 1C 1D 1 ABCD -V 下=32ahd -712ahd =1112ahd ,故V 上V 下=117.(3)方法一:如图1所示,在△ADC 中,作AE ⊥DC ,垂足为E ,连接A 1E .又DE ⊥AA 1,且AA 1∩AE =A ,所以DE ⊥平面AEA 1,所以DE ⊥A 1E .所以∠AEA 1为平面α与底面ABCD 所成二面角的平面角. 因为BC ∥AD ,AD =2BC ,所以S △ADC =2S △BCA . 又因为梯形ABCD 的面积为6,DC =2, 所以S △ADC =4,AE =4. 于是tan ∠AEA 1=AA 1AE =1,∠AEA 1=π4. 故平面α与底面ABCD 所成二面角的大小为π4.方法二:如图2所示,以D 为原点,DA ,DD 1→分别为x 轴和z 轴正方向建立空间直角坐标系.设∠CDA =θ,BC =a ,则AD =2a . 因为S 四边形ABCD =a +2a2·2sin θ=6,所以a =2sin θ.图2从而可得C (2cos θ,2sin θ,0),A 1⎝⎛⎭⎪⎫4sin θ,0,4,所以DC =(2cos θ,2sin θ,0),DA 1→=⎝ ⎛⎭⎪⎫4sin θ,0,4.设平面A 1DC 的法向量n =(x ,y ,1), 由⎩⎨⎧DA 1→·n =4sin θx +4=0,DC →·n =2x cos θ+2y sin θ=0,得⎩⎪⎨⎪⎧x =-sin θ,y =cos θ, 所以n =(-sin θ,cos θ,1).又因为平面ABCD 的法向量m =(0,0,1), 所以cos 〈n ,m 〉=n·m |n||m|=22,故平面α与底面ABCD 所成二面角的大小为π4.17.、[2014·北京卷] 如图13,正方形AMDE 的边长为2,B ,C 分别为AM ,MD 的中点.在五棱锥P ABCDE 中,F 为棱PE 的中点,平面ABF 与棱PD ,PC 分别交于点G ,H .(1)求证:AB ∥FG ;(2)若PA ⊥底面ABCDE ,且PA =AE ,求直线BC 与平面ABF 所成角的大小,并求线段PH 的长.图1317.解:(1)证明:在正方形AMDE 中,因为B 是AM 的中点,所以AB ∥DE .又因为AB ⊄平面PDE , 所以AB ∥平面PDE .因为AB ⊂平面ABF ,且平面ABF ∩平面PDE =FG , 所以AB ∥FG .(2)因为PA ⊥底面ABCDE , 所以PA ⊥AB ,PA ⊥AE .建立空间直角坐标系Axyz ,如图所示,则A (0,0,0),B (1,0,0),C (2,1,0),P (0,0,2),F (0,1,1),BC →=(1,1,0).设平面ABF 的法向量为n =(x ,y ,z ),则 ⎩⎪⎨⎪⎧n ·AB →=0,n ·AF →=0,即⎩⎪⎨⎪⎧x =0,y +z =0. 令z =1,则y =-1.所以n =(0,-1,1).设直线BC 与平面ABF 所成角为α,则 sin α=|cos 〈n ,BC →〉|=⎪⎪⎪⎪⎪⎪⎪⎪n ·BC→|n ||BC →|=12. 因此直线BC 与平面ABF 所成角的大小为π6.设点H 的坐标为(u ,v ,w ).因为点H 在棱PC 上,所以可设PH →=λPC →(0<λ<1).即(u ,v ,w -2)=λ(2,1,-2),所以u =2λ,v =λ,w =2-2λ. 因为n 是平面ABF 的一个法向量, 所以n ·AH →=0,即(0,-1,1)·(2λ,λ,2-2λ)=0, 解得λ=23,所以点H 的坐标为⎝ ⎛⎭⎪⎫43,23,23. 所以PH =⎝ ⎛⎭⎪⎫432+⎝ ⎛⎭⎪⎫232+⎝ ⎛⎭⎪⎫-432=2.19.、、、[2014·湖北卷] 如图14,在棱长为2的正方体ABCD A 1B 1C 1D 1中,E ,F ,M ,N 分别是棱AB ,AD ,A 1B 1,A 1D 1的中点,点P ,Q 分别在棱DD 1,BB 1上移动,且DP =BQ =λ(0<λ<2).(1)当λ=1时,证明:直线BC 1∥平面EFPQ .(2)是否存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.19.解:方法一(几何方法):(1)证明:如图①,连接AD 1,由ABCD A 1B 1C 1D 1是正方体,知BC 1∥AD 1.当λ=1时,P 是DD 1的中点,又F 是AD 的中点,所以FP ∥AD 1,所以BC 1∥FP . 而FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ ,故直线BC 1∥平面EFPQ .(2)如图②,连接BD .因为E ,F 分别是AB ,AD 的中点,所以EF ∥BD ,且EF =12BD .又DP =BQ ,DP ∥BQ ,所以四边形PQBD 是平行四边形,故PQ ∥BD ,且PQ =BD ,从而EF ∥PQ ,且EF =12PQ .在Rt △EBQ 和Rt △FDP 中,因为BQ =DP =λ,BE =DF =1,于是EQ =FP =1+λ2,所以四边形EFPQ 也是等腰梯形. 同理可证四边形PQMN 也是等腰梯形.分别取EF ,PQ ,MN 的中点为H ,O ,G ,连接OH ,OG , 则GO ⊥PQ ,HO ⊥PQ ,而GO ∩HO =O ,故∠GOH 是面EFPQ 与面PQMN 所成的二面角的平面角.若存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角,则∠GOH =90°. 连接EM ,FN ,则由EF ∥MN ,且EF =MN 知四边形EFNM 是平行四边形. 连接GH ,因为H ,G 是EF ,MN 的中点, 所以GH =ME =2.在△GOH 中,GH 2=4,OH 2=1+λ2-⎝ ⎛⎭⎪⎫222=λ2+12,OG 2=1+(2-λ)2-⎝ ⎛⎭⎪⎫222=(2-λ)2+12,由OG 2+OH 2=GH 2,得(2-λ)2+12+λ2+12=4,解得λ=1±22,故存在λ=1±22,使面EFPQ 与面PQMN 所成的二面角为直二面角. 方法二(向量方法):以D 为原点,射线DA ,DC ,DD 1分别为x ,y ,z 轴的正半轴建立如图③所示的空间直角坐标系.由已知得B (2,2,0),C 1(0,2,2),E (2,1,0),F (1,0,0),P (0,0,λ).BC 1→=(-2,0,2),FP =(-1,0,λ),FE =(1,1,0). (1)证明:当λ=1时,FP =(-1,0,1),因为BC 1→=(-2,0,2),所以BC 1→=2FP →,即BC 1∥FP .而FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ ,故直线BC 1∥平面EFPQ .(2)设平面EFPQ 的一个法向量为n =(x ,y ,z ),则由⎩⎪⎨⎪⎧FE →·n =0,FP →·n =0可得⎩⎪⎨⎪⎧x +y =0,-x +λz =0.于是可取n =(λ,-λ,1).同理可得平面MNPQ 的一个法向量为m =(λ-2,2-λ,1). 若存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角, 则m ·n =(λ-2,2-λ,1)·(λ,-λ,1)=0,即λ(λ-2)-λ(2-λ)+1=0,解得λ=1±22.故存在λ=1±22,使面EFPQ 与面PQMN 所成的二面角为直二面角. 18.、[2014·新课标全国卷Ⅱ] 如图13,四棱锥P ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(1)证明:PB ∥平面AEC ;(2)设二面角D AE C 为60°,AP18.解:(1)证明:连接BD 交AC 于点O ,连接EO . 因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点,所以EO ∥PB . 因为EO ⊂平面AEC ,PB ⊄平面AEC , 所以PB ∥平面AEC .(2)因为PA ⊥平面ABCD ,ABCD 为矩形, 所以AB ,AD ,AP 两两垂直.如图,以A 为坐标原点,AB →,AD ,AP 的方向为x 轴、y 轴、z 轴的正方向,|AP →|为单位长,建立空间直角坐标系A xyz ,则D ()0,3,0,E ⎝ ⎛⎭⎪⎫0,32,12,AE →=⎝⎛⎭⎪⎫0,32,12.设B (m ,0,0)(m >0),则C (m ,3,0),AC =(m ,3,0). 设n 1=(x ,y ,z )为平面ACE 的法向量,则⎩⎪⎨⎪⎧n 1·AC →=0,n 1·AE →=0,即⎩⎪⎨⎪⎧mx +3y =0,32y +12z =0,可取n 1=⎝⎛⎭⎪⎫3m ,-1,3. 又n 2=(1,0,0)为平面DAE 的法向量,由题设易知|cos 〈n 1,n 2〉|=12,即33+4m 2=12,解得m =32. 因为E 为PD 的中点,所以三棱锥E ACD 的高为12.三棱锥E ACD 的体积V =13×12×3×32×12=38.17.,[2014·山东卷] 如图13所示,在四棱柱ABCD A 1B 1C 1D 1中,底面ABCD 是等腰梯形,∠DAB =60°,AB =2CD =2,M 是线段AB 的中点.图13(1)求证:C 1M ∥平面A 1ADD 1;(2)若CD 1垂直于平面ABCD 且CD 1=3,求平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值. 17.解:(1)证明:因为四边形ABCD 是等腰梯形, 且AB =2CD ,所以AB ∥DC , 又M 是AB 的中点, 所以CD ∥MA 且CD =MA .连接AD 1.因为在四棱柱ABCD A 1B 1C 1D 1中,CD ∥C 1D 1,CD =C 1D 1,所以C 1D 1∥MA ,C 1D 1=MA ,所以四边形AMC 1D 1为平行四边形, 因此,C 1M ∥D 1A .又C 1M ⊄平面A 1ADD 1,D 1A ⊂平面A 1ADD 1, 所以C 1M ∥平面A 1ADD 1. (2)方法一:连接AC ,MC . 由(1)知,CD ∥AM 且CD =AM , 所以四边形AMCD 为平行四边形, 所以BC =AD =MC .由题意∠ABC =∠DAB =60°, 所以△MBC 为正三角形, 因此AB =2BC =2,CA =3, 因此CA ⊥CB .设C 为坐标原点,建立如图所示的空间直角坐标系C xyz .所以A (3,0,0),B (0,1,0),D 1因此M ⎝⎛⎭⎪⎫32,12,0, 所以MD 1→=⎝ ⎛⎭⎪⎫-32,-12,3,D 1C 1→=MB →=⎝ ⎛⎭⎪⎫-32,12,0.设平面C 1D 1M 的一个法向量n =(x ,y ,z ), 由⎩⎪⎨⎪⎧n ·D 1C 1→=0,n ·MD 1→=0,得⎩⎨⎧3x -y =0,3x +y -2 3z =0,可得平面C 1D 1M 的一个法向量n =(1,3,1). 又CD 1→=(0,0,3)为平面ABCD 的一个法向量. 因此cos 〈CD 1→,n 〉=CD 1→·n|CD 1→||n |=55,所以平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值为55. 方法二:由(1)知,平面D 1C 1M ∩平面ABCD =AB ,点过C 向AB 引垂线交AB 于点N ,连接D 1N .由CD1⊥平面ABCD,可得D1N⊥AB,因此∠D1NC为二面角C1ABC的平面角.在Rt△BNC中,BC=1,∠NBC=60°,可得CN=32,所以ND1=CD21+CN2=15 2.在Rt△D1CN中,cos∠D1NC=CND1N=32152=55,所以平面C1D1M和平面ABCD所成的角(锐角)的余弦值为55.18.,,,[2014·四川卷] 三棱锥A BCD及其侧视图、俯视图如图14所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN⊥NP.(1)证明:P是线段BC的中点;(2)求二面角A NP M的余弦值.图1418.解:(1)如图所示,取BD的中点O,连接AO,CO.由侧视图及俯视图知,△ABD,△BCD为正三角形,所以AO⊥BD,OC⊥BD.因为AO,OC⊂平面AOC,且AO∩OC=O,所以BD⊥平面AOC.又因为AC⊂平面AOC,所以BD⊥AC.取BO的中点H,连接NH,PH.又M,N,H分别为线段AD,AB,BO的中点,所以MN∥BD,NH∥AO,因为AO⊥BD,所以NH⊥BD.因为MN ⊥NP ,所以NP ⊥BD .因为NH ,NP ⊂平面NHP ,且NH ∩NP =N ,所以BD ⊥平面NHP . 又因为HP ⊂平面NHP ,所以BD ⊥HP .又OC ⊥BD ,HP ⊂平面BCD ,OC ⊂平面BCD ,所以HP ∥OC . 因为H 为BO 的中点,所以P 为BC 的中点.(2)方法一:如图所示,作NQ ⊥AC 于Q ,连接MQ.由(1)知,NP ∥AC ,所以NQ ⊥NP .因为MN ⊥NP ,所以∠MNQ 为二面角A NP M 的一个平面角. 由(1)知,△ABD ,△BCD 为边长为2的正三角形,所以AO =OC = 3. 由俯视图可知,AO ⊥平面BCD .因为OC ⊂平面BCD ,所以AO ⊥OC ,因此在等腰直角△AOC 中,AC = 6. 作BR ⊥AC 于R因为在△ABC 中,AB =BC ,所以R 为AC 的中点, 所以BR =AB 2-⎝ ⎛⎭⎪⎫AC 22=102. 因为在平面ABC 内,NQ ⊥AC ,BR ⊥AC ,所以NQ ∥BR .又因为N 为AB 的中点,所以Q 为AR 的中点,所以NQ =BR 2=104.同理,可得MQ =104. 故△MNQ 为等腰三角形, 所以在等腰△MNQ 中, cos ∠MNQ =MN 2NQ =BD4NQ =105.故二面角A NP M 的余弦值是105. 方法二:由俯视图及(1)可知,AO ⊥平面BCD . 因为OC ,OB ⊂平面BCD ,所以AO ⊥OC ,AO ⊥OB . 又OC ⊥OB ,所以直线OA ,OB ,OC 两两垂直.如图所示,以O 为坐标原点,以OB ,OC ,OA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O xyz .则A (0,0,3),B (1,0,0),C (0,3,0),D (-1,0,0). 因为M ,N 分别为线段AD ,AB 的中点, 又由(1)知,P 为线段BC 的中点,所以M ⎝ ⎛⎭⎪⎫-12,0,32,N ⎝ ⎛⎭⎪⎫12,0,32,P ⎝ ⎛⎭⎪⎫12,32,0,于是AB =(1,0,-3),BC =(-1,3,0),MN =(1,0,0),NP =⎝⎛⎭⎪⎫0,32,-32. 设平面ABC 的一个法向量n 1=(x 1,y 1,z 1), 由⎩⎪⎨⎪⎧n 1⊥AB ,n 1⊥BC ,得⎩⎪⎨⎪⎧n 1·AB =0,n 1·BC =0,即⎩⎨⎧(x 1,y 1,z 1)·(1,0,-3)=0,(x 1,y 1,z 1)·(-1,3,0)=0, 从而⎩⎨⎧x 1-3z 1=0,-x 1+3y 1=0.取z 1=1,则x 1=3,y 1=1,所以n 1=(3,1,1). 设平面MNP 的一个法向量n 2=(x 2,y 2,z 2),由,⎩⎪⎨⎪⎧n 2⊥MN ,n 2⊥NP ,得⎩⎪⎨⎪⎧n 2·MN =0,n 2·NP =0, 即⎩⎪⎨⎪⎧(x 2,y 2,z 2)·(1,0,0)=0,(x 2,y 2,z 2)·⎝⎛⎭⎪⎫0,32,-32=0, 从而⎩⎪⎨⎪⎧x 2=0,32y 2-32z 2=0. 取z 2=1,则y 2=1,x 2=0,所以n 2=(0,1,1). 设二面角A NP M 的大小为θ,则cos θ=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=⎪⎪⎪⎪⎪⎪(3,1,1)·(0,1,1)5×2=105.故二面角A NP M 的余弦值是105.G5 空间中的垂直关系 17.、、[2014·福建卷] 在平面四边形ABCD 中,AB =BD =CD =1,AB ⊥BD ,CD ⊥BD .将△ABD 沿BD 折起,使得平面ABD ⊥平面BCD ,如图15所示.(1)求证:AB ⊥CD ;(2)若M 为AD 中点,求直线AD 与平面MBC 所成角的正弦值.图1517.解:(1)证明:∵平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,AB ⊂平面ABD ,AB ⊥BD ,∴AB ⊥平面BCD .又CD ⊂平面BCD ,∴AB ⊥CD .(2)过点B 在平面BCD 内作BE ⊥BD .由(1)知AB ⊥平面BCD ,BE ⊂平面BCD ,BD ⊂平面BCD ,∴AB ⊥BE ,AB ⊥BD .以B 为坐标原点,分别以BE →,BD →,BA →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图所示).依题意,得B (0,0,0),C (1,1,0),D (0,1,0),A (0,0,1),M ⎝ ⎛⎭⎪⎫0,12,12. 则BC →=(1,1,0),BM →=⎝ ⎛⎭⎪⎫0,12,12,AD →=(0,1,-1).设平面MBC 的法向量n =(x 0,y 0,z 0),则⎩⎪⎨⎪⎧n ·BC →=0,n ·BM →=0,即⎩⎪⎨⎪⎧x 0+y 0=0,12y 0+12z 0=0, 取z 0=1,得平面MBC 的一个法向量n =(1,-1,1).设直线AD 与平面MBC 所成角为θ,则sin θ=||cos 〈n ,AD →〉=|n ·AD →||n |·|AD →|=63. 即直线AD 与平面MBC 所成角的正弦值为63. 18.、[2014·广东卷] 如图14,四边形ABCD 为正方形,PD ⊥平面ABCD ,∠DPC =30°,AF ⊥PC 于点F ,FE ∥CD ,交PD 于点E .(1)证明:CF ⊥平面ADF ;(2)求二面角D AF E 的余弦值.图1419.、[2014·湖南卷] 如图16所示,四棱柱ABCD A 1B 1C 1D 1的所有棱长都相等,AC ∩BD =O ,A 1C 1∩B 1D 1=O 1,四边形ACC 1A 1和四边形BDD 1B 1均为矩形.(1)证明:O 1O ⊥底面ABCD ;(2)若∠CBA =60°,求二面角C 1OB 1D 的余弦值.19.解:(1)如图(a),因为四边形ACC 1A 1为矩形,所以CC 1⊥AC .同理DD 1⊥BD . 因为CC 1∥DD 1,所以CC 1⊥BD .而AC ∩BD =O ,因此CC 1⊥底面ABCD . 由题设知,O 1O ∥C 1C .故O 1O ⊥底面ABCD .(2)方法一: 如图(a),过O 1作O 1H ⊥OB 1于H ,连接HC 1.由(1)知,O 1O ⊥底面ABCD ,所以O 1O ⊥底面A 1B 1C 1D 1,于是O 1O ⊥A 1C 1.又因为四棱柱ABCD A 1B 1C 1D 1的所有棱长都相等,所以四边形A 1B 1C 1D 1是菱形, 因此A 1C 1⊥B 1D 1,从而A 1C 1⊥平面BDD 1B 1,所以A 1C 1⊥OB 1,于是OB 1⊥平面O 1HC 1. 进而OB 1⊥C 1H .故∠C 1HO 1是二面角C 1OB 1D 的平面角.不妨设AB =2.因为∠CBA =60°,所以OB =3,OC =1,OB 1=7.在Rt △OO 1B 1中,易知O 1H =OO 1·O 1B 1OB 1=237.而O 1C 1=1,于是C 1H =O 1C 21+O 1H 2=1+127=197. 故cos ∠C 1HO 1=O 1HC 1H=237197=25719. 即二面角C 1OB 1D 的余弦值为25719.方法二:因为四棱柱ABCD A 1B 1C 1D 1的所有棱长都相等,所以四边形ABCD 是菱形,因此AC ⊥BD .又O 1O ⊥底面ABCD ,从而OB ,OC ,OO 1两两垂直.如图(b),以O 为坐标原点,OB ,OC ,OO 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系O xyz ,不妨设AB =2.因为∠CBA =60°,所以OB =3,OC =1,于是相关各点的坐标为O (0,0,0),B 1(3,0,2),C 1(0,1,2).易知,n 1=(0,1,0)是平面BDD 1B 1的一个法向量.设n 2=(x ,y ,z )是平面OB 1C 1的一个法向量,则⎩⎪⎨⎪⎧n 2·OB →1=0,n 2·OC →1=0,即⎩⎨⎧3x +2z =0,y +2z =0.取z =-3,则x =2,y =23,所以n 2=(2,23,-3). 设二面角C 1OB 1D 的大小为θ,易知θ是锐角,于是cos θ=|cos 〈,〉|=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=2319=25719.故二面角C 1OB 1D 的余弦值为25719.19.、、[2014·江西卷] 如图16,四棱锥P ABCD 中,ABCD 为矩形,平面PAD ⊥平面ABCD .图16(1)求证:AB ⊥PD .(2)若∠BPC =90°,PB =2,PC =2,问AB 为何值时,四棱锥P ABCD 的体积最大?并求此时平面BPC 与平面DPC 夹角的余弦值.19.解:(1)证明:因为ABCD 为矩形,所以AB ⊥AD . 又平面PAD ⊥平面ABCD , 平面PAD ∩平面ABCD =AD , 所以AB ⊥平面PAD ,故AB ⊥PD .(2)过P 作AD 的垂线,垂足为O ,过O 作BC 的垂线,垂足为G ,连接PG . 故PO ⊥平面ABCD ,BC ⊥平面POG ,BC ⊥PG .在Rt △BPC 中,PG =2 33,GC =2 63,BG =63.设AB =m ,则OP =PG 2-OG 2=43-m 2,故四棱锥P ABCD 的体积为 V =13×6·m ·43-m 2=m 38-6m 2. 因为m 8-6m 2=8m 2-6m 4=-6⎝⎛⎭⎪⎫m 2-232+83,所以当m =63,即AB =63时,四棱锥P ABCD 的体积最大.此时,建立如图所示的空间直角坐标系,各点的坐标分别为O (0,0,0),B ⎝⎛⎭⎪⎫63,-63,0,C ⎝⎛⎭⎪⎫63,263,0,D ⎝ ⎛⎭⎪⎫0,263,0,P ⎝ ⎛⎭⎪⎫0,0,63,故PC →=⎝ ⎛⎭⎪⎫63,263,-63,BC →=(0,6,0),CD =⎝ ⎛⎭⎪⎫-63,0,0. 设平面BPC 的一个法向量为n 1=(x ,y ,1),则由n 1⊥PC →,n 1⊥BC →,得⎩⎪⎨⎪⎧63x +2 63y -63=0,6y =0,解得x =1,y =0,则n 1=(1,0,1). 同理可求出平面DPC 的一个法向量为n 2=⎝ ⎛⎭⎪⎫0,12,1.设平面BPC 与平面DPC 的夹角为θ,则cos θ=|n 1·n 2||n 1||n 2|=12·14+1=105. 19.、[2014·辽宁卷] 如图15所示,△ABC 和△BCD 所在平面互相垂直,且AB =BC =BD =2,∠ABC =∠DBC =120°,E ,F 分别为AC ,DC 的中点.(1)求证:EF ⊥BC ;(2)求二面角E BF C 的正弦值.19.解:(1)证明:方法一,过点E 作EO ⊥BC ,垂足为O ,连接OF .由△ABC ≌△DBC 可证出△EOC ≌△FOC ,所以∠EOC =∠FOC =π2,即FO ⊥BC .又EO ⊥BC ,EO ∩FO =O ,所以BC ⊥平面EFO .又EF ⊂平面EFO ,所以EF ⊥BC .方法二,由题意,以B 为坐标原点,在平面DBC 内过B 作垂直BC 的直线,并将其作为x 轴,BC 所在直线为y 轴,在平面ABC 内过B 作垂直BC 的直线,并将其作为z 轴,建立如图所示的空间直角坐标系,易得B (0,0,0),A (0,-1,3),D (3,-1,0),C (0,2,0),因而E (0,12,32),F (32,12,0),所以EF →=(32,0,-32),BC →=(0,2,0),因此EF →·BC →=0,从而EF →⊥BC →,所以EF ⊥BC .(2)方法一,在图1中,过点O 作OG ⊥BF ,垂足为G ,连接EG .因为平面ABC ⊥平面BDC ,所以EO ⊥面BDC ,又OG ⊥BF ,所以由三垂线定理知EG ⊥BF ,因此∠EGO 为二面角E BF C 的平面角.在△EOC 中,EO =12EC =12BC ·cos 30°=32.由△BGO ∽△BFC 知,OG =BOBC ·FC =34,因此tan ∠EGO =EO OG =2,从而得sin ∠EGO =255,即二面角E BF C 的正弦值为2 55. 方法二,在图2中,平面BFC 的一个法向量为n 1=(0,0,1). 设平面BEF 的法向量n 2=(x ,y ,z ),又BF →=(32,12,0),BE →=(0,12,32),所以⎩⎪⎨⎪⎧n 2·BF →=0,n 2·BE →=0,得其中一个n 2=(1,-3,1).设二面角E BF C 的大小为θ,且由题知θ为锐角,则cos θ=|cos 〈n 1,n 2〉|=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1||n 2|=15,因此sin θ=25=2 55,即所求二面角正弦值为2 55.19.G 5、G 11[2014·新课标全国卷Ⅰ] 如图15,三棱柱ABC A 1B 1C 1中,侧面BB 1C 1C 为菱形,AB ⊥B 1C .图15(1)证明:AC =AB 1;(2)若AC ⊥AB 1,∠CBB 1=60°,AB =BC ,求二面角A A 1B 1 C 1的余弦值.19.解:(1)证明:连接BC 1,交B 1C 于点O ,连接AO ,因为侧面BB 1C 1C 为菱形,所以B 1C ⊥BC 1,且O 为B 1C 及BC 1的中点.又AB ⊥B 1C ,所以B 1C ⊥平面ABO . 由于AO ⊂平面ABO ,故B 1C ⊥AO . 又B 1O =CO ,故AC =AB 1.(2)因为AC ⊥AB 1,且O 为B 1C 的中点,所以AO =CO .又因为AB =BC ,所以△BOA ≌ △BOC .故OA ⊥OB ,从而OA ,OB ,OB 1两两垂直. 以O 为坐标原点,OB 的方向为x 轴正方向,|OB |为单位长,建立如图所示的空间直角坐标系O xyz .因为∠CBB 1=60°,所以△CBB 1为等边三角形,又AB =BC ,则A ⎝ ⎛⎭⎪⎫0,0,33,B (1,0,0),B 1⎝ ⎛⎭⎪⎫0,33,0,C ⎝ ⎛⎭⎪⎫0,-33,0. AB 1→=⎝ ⎛⎭⎪⎫0,33,-33, A 1B 1→=AB =⎝⎛⎭⎪⎫1,0,-33, B 1C →1=BC =⎝ ⎛⎭⎪⎫-1,-33,0.设n =(x ,y ,z )是平面AA 1B 1的法向量,则 ⎩⎨⎧n ·AB 1=0,n ·A 1B 1→=0,即⎩⎪⎨⎪⎧33y -33z =0,x -33z =0. 所以可取n =(1,3,3).设m 是平面A 1B 1C 1的法向量, 则⎩⎪⎨⎪⎧m ·A 1B 1→=0,m ·B 1C 1→=0,同理可取m =(1,-3,3).则cos 〈n ,m 〉=n ·m |n ||m |=17.所以结合图形知二面角A A 1B 1 C 1的余弦值为17.18.,,,[2014·四川卷] 三棱锥A BCD 及其侧视图、俯视图如图14所示.设M ,N 分别为线段AD ,AB 的中点,P 为线段BC 上的点,且MN ⊥NP .(1)证明:P 是线段BC 的中点;(2)求二面角A NP M 的余弦值.图1418.解:(1)如图所示,取BD 的中点O ,连接AO ,CO . 由侧视图及俯视图知,△ABD ,△BCD 为正三角形,所以AO ⊥BD ,OC ⊥BD .因为AO ,OC ⊂平面AOC ,且AO ∩OC =O , 所以BD ⊥平面AOC .又因为AC ⊂平面AOC ,所以BD ⊥AC . 取BO 的中点H ,连接NH ,PH .又M ,N ,H 分别为线段AD ,AB ,BO 的中点,所以MN ∥BD ,NH ∥AO , 因为AO ⊥BD ,所以NH ⊥BD . 因为MN ⊥NP ,所以NP ⊥BD .因为NH ,NP ⊂平面NHP ,且NH ∩NP =N ,所以BD ⊥平面NHP . 又因为HP ⊂平面NHP ,所以BD ⊥HP .又OC ⊥BD ,HP ⊂平面BCD ,OC ⊂平面BCD ,所以HP ∥OC . 因为H 为BO 的中点,所以P 为BC 的中点.(2)方法一:如图所示,作NQ ⊥AC 于Q ,连接MQ .由(1)知,NP ∥AC ,所以NQ ⊥NP .因为MN ⊥NP ,所以∠MNQ 为二面角A NP M 的一个平面角. 由(1)知,△ABD ,△BCD 为边长为2的正三角形,所以AO =OC = 3. 由俯视图可知,AO ⊥平面BCD .因为OC ⊂平面BCD ,所以AO ⊥OC ,因此在等腰直角△AOC 中,AC = 6. 作BR ⊥AC 于R因为在△ABC 中,AB =BC ,所以R 为AC 的中点, 所以BR =AB 2-⎝ ⎛⎭⎪⎫AC 22=102. 因为在平面ABC 内,NQ ⊥AC ,BR ⊥AC ,所以NQ ∥BR .又因为N 为AB 的中点,所以Q 为AR 的中点,所以NQ =BR 2=104.同理,可得MQ =104. 故△MNQ 为等腰三角形, 所以在等腰△MNQ 中, cos ∠MNQ =MN 2NQ =BD4NQ =105.故二面角A NP M 的余弦值是105. 方法二:由俯视图及(1)可知,AO ⊥平面BCD . 因为OC ,OB ⊂平面BCD ,所以AO ⊥OC ,AO ⊥OB . 又OC ⊥OB ,所以直线OA ,OB ,OC 两两垂直.如图所示,以O 为坐标原点,以OB ,OC ,OA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O xyz .则A (0,0,3),B (1,0,0),C (0,3,0),D (-1,0,0). 因为M ,N 分别为线段AD ,AB 的中点, 又由(1)知,P 为线段BC 的中点,所以M ⎝ ⎛⎭⎪⎫-12,0,32,N ⎝ ⎛⎭⎪⎫12,0,32,P ⎝ ⎛⎭⎪⎫12,32,0,于是AB =(1,0,-3),BC =(-1,3,0),MN =(1,0,0),NP =⎝ ⎛⎭⎪⎫0,32,-32. 设平面ABC 的一个法向量n 1=(x 1,y 1,z 1), 由⎩⎪⎨⎪⎧n 1⊥AB ,n 1⊥BC ,得⎩⎪⎨⎪⎧n 1·AB =0,n 1·BC =0,即⎩⎨⎧(x 1,y 1,z 1)·(1,0,-3)=0,(x 1,y 1,z 1)·(-1,3,0)=0, 从而⎩⎨⎧x 1-3z 1=0,-x 1+3y 1=0.取z 1=1,则x 1=3,y 1=1,所以n 1=(3,1,1). 设平面MNP 的一个法向量n 2=(x 2,y 2,z 2),由,⎩⎪⎨⎪⎧n 2⊥MN ,n 2⊥NP ,得⎩⎪⎨⎪⎧n 2·MN =0,n 2·NP =0,即⎩⎪⎨⎪⎧(x 2,y 2,z 2)·(1,0,0)=0,(x 2,y 2,z 2)·⎝⎛⎭⎪⎫0,32,-32=0, 从而⎩⎪⎨⎪⎧x 2=0,32y 2-32z 2=0. 取z 2=1,则y 2=1,x 2=0,所以n 2=(0,1,1). 设二面角A NP M 的大小为θ,则cos θ=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=⎪⎪⎪⎪⎪⎪(3,1,1)·(0,1,1)5×2=105.故二面角A NP M 的余弦值是105. 17.、[2014·天津卷] 如图14所示,在四棱锥P ABCD 中,PA ⊥底面ABCD, AD ⊥AB ,AB ∥DC ,AD =DC =AP =2,AB =1,点E 为棱PC 的中点.(1)证明:BE ⊥DC ;(2)求直线BE 与平面PBD 所成角的正弦值;(3)若F 为棱PC 上一点,满足BF ⊥AC ,求二面角F AB P 的余弦值.图1417.解:方法一:依题意,以点A 为原点建立空间直角坐标系(如图所示),可得B (1,0,0),C (2,2,0),D (0,2,0),P (0,0,2).C 由E 为棱PC 的中点,得E (1,1,1).(1)证明:向量BE =(0,1,1),DC =(2,0,0), 故BE ·DC =0, 所以BE ⊥DC .(2)向量BD =(-1,2,0),PB =(1,0,-2). 设n =(x ,y ,z )为平面PBD 的法向量,则⎩⎪⎨⎪⎧n ·BD =0,n ·PB =0,即⎩⎪⎨⎪⎧-x +2y =0,x -2z =0. 不妨令y =1,可得n =(2,1,1)为平面PBD 的一个法向量.于是有cos 〈n ,BE 〉=n ·BE |n |·|BE |=26×2=33,所以直线BE 与平面PBD 所成角的正弦值为33. (3) 向量BC =(1,2,0),CP =(-2,-2,2),AC =(2,2,0),AB =(1,0,0).由点F 在棱PC 上, 设CF =λCP →,0≤λ≤1.故BF =BC +CF =BC +λCP →=(1-2λ,2-2λ,2λ).由BF ⊥AC ,得BF ·AC =0,因此2(1-2λ)+2(2-2λ)=0,解得λ=34,即BF =⎝ ⎛⎭⎪⎫-12,12,32.设n 1=(x ,y ,z )为平面FAB 的法向量,则⎩⎪⎨⎪⎧n 1·AB =0,n 1·BF =0,即⎩⎪⎨⎪⎧x =0,-12x +12y +32z =0.不妨令z =1,可得n 1=(0,-3,1)为平面FAB 的一个法向量.取平面ABP 的法向量n 2=(0,1,0),则cos 〈,〉=n 1·n 2|n 1|·|n 2|=-310×1=-31010.易知二面角F AB P 是锐角,所以其余弦值为31010.方法二:(1)证明:如图所示,取PD 中点M ,连接EM ,AM .由于E ,M 分别为PC ,PD 的中点,故EM ∥DC ,且EM =12DC .又由已知,可得EM ∥AB 且EM =AB ,故四边形ABEM 为平行四边形,所以BE ∥AM .因为PA ⊥底面ABCD ,故PA ⊥CD ,而CD ⊥DA ,从而CD ⊥平面PAD .因为AM ⊂平面PAD ,所以CD ⊥AM .又BE ∥AM ,所以BE ⊥CD .(2)连接BM ,由(1)有CD ⊥平面PAD ,得CD ⊥PD .而EM ∥CD ,故PD ⊥EM .又因为AD =AP ,M 为PD 的中点,所以PD ⊥AM ,可得PD ⊥BE ,所以PD ⊥平面BEM ,故平面BEM ⊥平面PBD ,所以直线BE 在平面PBD 内的射影为直线BM .而BE ⊥EM ,可得∠EBM 为锐角,故∠EBM 为直线BE 与平面PBD 所成的角.依题意,有PD =22,而M 为PD 中点,可得AM =2,进而BE = 2.故在直角三角形BEM 中,tan ∠EBM =EM BE =AB BE =12,因此sin ∠EBM =33,所以直线BE 与平面PBD 所成角的正弦值为33. (3)如图所示,在△PAC 中,过点F 作FH ∥PA 交AC 于点H .因为PA ⊥底面ABCD ,所以FH ⊥底面ABCD ,从而FH ⊥AC .又BF ⊥AC ,得AC ⊥平面FHB ,因此AC ⊥BH .在底面ABCD 内,可得CH =3HA ,从而CF =3FP .在平面PDC 内,作FG ∥DC 交PD 于点G ,于是DG =3GP .由于DC ∥AB ,故GF ∥AB ,所以A ,B ,F ,G 四点共。
2014高考汇编立体几何
数学G单元立体几何G1 空间几何体的结构20.、、[2014·安徽卷] 如图15,四棱柱ABCDA1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.图15(1)证明:Q为BB1的中点;(2)求此四棱柱被平面α所分成上下两部分的体积之比;(3)若AA1=4,CD=2,梯形ABCD的面积为6,求平面α与底面ABCD所成二面角的大小.20.解:(1)证明:因为BQ∥AA1,BC∥AD,BC∩BQ=B,AD∩AA1=A,所以平面QBC∥平面A1AD,从而平面A1CD与这两个平面的交线相互平行,即QC∥A1D.故△QBC与△A1AD的对应边相互平行,于是△QBC∽△A1AD,所以BQ BB 1=BQ AA 1=BCAD =12,即Q 为BB 1的中点.(2)如图1所示,连接QA ,QD .设AA 1=h ,梯形ABCD 的高为d ,四棱柱被平面α所分成上下两部分的体积分别为V 上和V 下,BC =a ,则AD =2a .图1V 三棱锥Q A 1AD =13×12·2a ·h ·d =13ahd ,V 四棱锥Q ABCD =13·a +2a 2·d ·⎝ ⎛⎭⎪⎫12h =14ahd ,所以V 下=V 三棱锥Q A 1AD +V 四棱锥Q ABCD =712ahd .又V 四棱柱A 1B 1C 1D 1 ABCD =32ahd ,所以V 上=V 四棱柱A 1B 1C 1D 1 ABCD -V 下=32ahd -712ahd =1112ahd ,故V 上V 下=117.(3)方法一:如图1所示,在△ADC 中,作AE ⊥DC ,垂足为E ,连接A 1E . 又DE ⊥AA 1,且AA 1∩AE =A , 所以DE ⊥平面AEA 1,所以DE ⊥A 1E .所以∠AEA 1为平面α与底面ABCD 所成二面角的平面角. 因为BC ∥AD ,AD =2BC ,所以S △ADC =2S △BCA . 又因为梯形ABCD 的面积为6,DC =2,所以S △ADC =4,AE =4.于是tan ∠AEA 1=AA 1AE =1,∠AEA 1=π4.故平面α与底面ABCD 所成二面角的大小为π4.方法二:如图2所示,以D 为原点,DA ,DD 1→分别为x 轴和z 轴正方向建立空间直角坐标系.设∠CDA =θ,BC =a ,则AD =2a . 因为S 四边形ABCD =a +2a2·2sin θ=6,所以a =2sin θ.图2从而可得C (2cos θ,2sin θ,0),A 1⎝ ⎛⎭⎪⎫4sin θ,0,4, 所以DC =(2cos θ,2sin θ,0),DA 1→=⎝ ⎛⎭⎪⎫4sin θ,0,4. 设平面A 1DC 的法向量n =(x ,y ,1), 由⎩⎪⎨⎪⎧DA 1→·n =4sin θ x +4=0,DC→·n =2x cos θ+2y sin θ=0,得⎩⎪⎨⎪⎧x =-sin θ,y =cos θ,所以n =(-sin θ,cos θ,1).又因为平面ABCD 的法向量m =(0,0,1), 所以cos 〈n ,m 〉=n ·m|n||m|=22,故平面α与底面ABCD 所成二面角的大小为π4.8.[2014·湖北卷] 《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:“置如其周,令相乘也.又以高乘之,三十六成一.”该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式V ≈136L 2h .它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈275L 2h 相当于将圆锥体积公式中的π近似取为( ) A.227 B.258 C.15750 D.355113 8.B7.、[2014·辽宁卷] 某几何体三视图如图11所示,则该几何体的体积为( ) A .8-2π B .8-π C .8-π2 D .8-π4图117.BG2 空间几何体的三视图和直观图7.[2014·安徽卷] 一个多面体的三视图如图12所示,则该多面体的表面积为( ) A.21+ 3 B.8+ 2C.21 D.18图127.A2.[2014·福建卷] 某空间几何体的正视图是三角形,则该几何体不可能是( )A.圆柱B.圆锥C.四面体D.三棱柱2.A5.[2014·湖北卷] 在如图11所示的空间直角坐标系Oxyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的正视图和俯视图分别为( )图11A.①和②B.①和③5.D7.、[2014·湖南卷] 一块石材表示的几何体的三视图如图12所示,将该石材切削、打( )图12A.1 B.2 C.3 D.47.B5.[2014·江西卷] 一几何体的直观图如图11所示,下列给出的四个俯视图中正确的是( )图11A B C D图125.B7.、[2014·辽宁卷] 某几何体三视图如图11所示,则该几何体的体积为( )A .8-2πB .8-πC .8-π2D .8-π4图117.B3.[2014·浙江卷] 几何体的三视图(单位:cm)如图11所示,则此几何体的表面积是( )图11A .90 cm 2B .129 cm 2C .132 cm 2D .138 cm 23.D12.[2014·新课标全国卷Ⅰ] 如图13,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )图13A .6 2B .6C .4 2D .412.B6.[2014·新课标全国卷Ⅱ] 如图11,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm ,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )图11A.1727B.59C.1027D.13 6.C17.[2014·陕西卷] 四面体ABCD 及其三视图如图14所示,过棱AB 的中点E 作平行于AD ,BC 的平面分别交四面体的棱BD ,DC ,CA 于点F ,G ,H .(1)证明:四边形EFGH 是矩形;(2)求直线AB 与平面EFGH 夹角θ的正弦值.图1417.解:(1)证明:由该四面体的三视图可知,BD ⊥DC ,BD ⊥AD ,AD ⊥DC , BD =DC =2,AD =1.由题设,BC ∥平面EFGH , 平面EFGH ∩平面BDC =FG , 平面EFGH ∩平面ABC =EH , ∴BC ∥FG ,BC ∥EH ,∴FG ∥EH . 同理EF ∥AD ,HG ∥AD ,∴EF ∥HG . ∴四边形EFGH 是平行四边形.又∵AD ⊥DC ,AD ⊥BD ,∴AD ⊥平面BDC , ∴AD ⊥BC ,∴EF ⊥FG , ∴四边形EFGH 是矩形.(2)方法一:如图,以D 为坐标原点建立空间直角坐标系,则D (0,0,0),A (0,0,1),B (2,0,0),C (0,2,0),DA =(0,0,1),BC =(-2,2,0), BA =(-2,0,1).设平面EFGH 的法向量n =(x ,y ,z ), ∵EF ∥AD ,FG ∥BC , ∴n ·DA =0,n ·BC =0,得⎩⎪⎨⎪⎧z =0,-2x +2y =0,取n =(1,1,0),∴sin θ=|cos 〈BA →,n 〉|=⎪⎪⎪⎪⎪⎪BA ·n |BA ||n |=25×2=105.方法二:如图,以D 为坐标原点建立空间直角坐标系, 则D (0,0,0),A (0,0,1),B (2,0,0),C (0,2,0),∵E 是AB 的中点,∴F ,G 分别为BD ,DC 的中点,得E ⎝⎛⎭⎪⎫1,0,12,F (1,0,0),G (0,1,0).∴FE →=⎝⎛⎭⎪⎫0,0,12,FG =(-1,1,0), BA =(-2,0,1).设平面EFGH 的法向量n =(x ,y ,z ), 则n ·FE =0,n ·FG =0,得⎩⎪⎨⎪⎧12z =0,-x +y =0,取n =(1,1,0), ∴sin θ=|cos 〈BA →,n 〉|=⎪⎪⎪⎪⎪⎪⎪⎪BA ·n |BA →||n |=25×2=105. 10.[2014·天津卷] 一个儿何体的三视图如图13所示(单位:m),则该几何体的体积为________m 3.图1310.20π37.[2014·重庆卷] 某几何体的三视图如图12( )12A .54B .60C .66D .72 7.BG3 平面的基本性质、空间两条直线4.[2014·辽宁卷] 已知m ,n 表示两条不同直线,α表示平面.下列说法正确的是( ) A .若m ∥α,n ∥α,则m ∥n B .若m ⊥α,n ⊂α,则m ⊥n C .若m ⊥α,m ⊥n ,则n ∥α D .若m ∥α,m ⊥n ,则n ⊥α 4.B17.、、[2014·福建卷] 在平面四边形ABCD 中,AB =BD =CD =1,AB ⊥BD ,CD ⊥BD .将△ABD 沿BD 折起,使得平面ABD ⊥平面BCD ,如图15所示.(1)求证:AB ⊥CD ;(2)若M 为AD 中点,求直线AD 与平面MBC 所成角的正弦值.图1517.解:(1)证明:∵平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,AB ⊂平面ABD ,AB ⊥BD ,∴AB ⊥平面BCD .又CD ⊂平面BCD ,∴AB ⊥CD . (2)过点B 在平面BCD 内作BE ⊥BD .由(1)知AB ⊥平面BCD ,BE ⊂平面BCD ,BD ⊂平面BCD ,∴AB ⊥BE ,AB ⊥BD . 以B 为坐标原点,分别以BE →,BD →,BA →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图所示).依题意,得B (0,0,0),C (1,1,0),D (0,1,0),A (0,0,1),M ⎝ ⎛⎭⎪⎫0,12,12.则BC →=(1,1,0),BM →=⎝ ⎛⎭⎪⎫0,12,12,AD →=(0,1,-1).设平面MBC 的法向量n =(x 0,y 0,z 0),则⎩⎨⎧n ·BC →=0,n ·BM →=0,即⎩⎪⎨⎪⎧x 0+y 0=0,12y 0+12z 0=0, 取z 0=1,得平面MBC 的一个法向量n =(1,-1,1). 设直线AD 与平面MBC 所成角为θ,则sin θ=⎪⎪⎪⎪cos 〈n ,AD →〉=|n ·AD →||n |·|AD →|=63.即直线AD 与平面MBC 所成角的正弦值为63.11.[2014·新课标全国卷Ⅱ] 直三棱柱ABC A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为( )A.110B.25C.3010D.2211.C [解析] 如图,E 为BC 的中点.由于M ,N 分别是A 1B 1,A 1C 1的中点,故MN ∥B 1C 1且MN =12B 1C 1,故MN 綊BE ,所以四边形MNEB 为平行四边形,所以EN 綊BM ,所以直线AN ,NE 所成的角即为直线BM ,AN 所成的角.设BC =1,则B 1M =12B 1A 1=22,所以MB =1+12=62=NE ,AN =AE =52,在△ANE 中,根据余弦定理得cos ∠ANE =64+54-542×62×52=3010.18.,,,[2014·四川卷] 三棱锥A BCD 及其侧视图、俯视图如图14所示.设M ,N 分别为线段AD ,AB 的中点,P 为线段BC 上的点,且MN ⊥NP .(1)证明:P是线段BC的中点;(2)求二面角ANPM的余弦值.图1418.解:(1)如图所示,取BD的中点O,连接AO,CO.由侧视图及俯视图知,△ABD,△BCD为正三角形,所以AO⊥BD,OC⊥BD.因为AO,OC⊂平面AOC,且AO∩OC=O,所以BD⊥平面AOC.又因为AC⊂平面AOC,所以BD⊥AC.取BO的中点H,连接NH,PH.又M,N,H分别为线段AD,AB,BO的中点,所以MN∥BD,NH∥AO,因为AO⊥BD,所以NH⊥BD.因为MN⊥NP,所以NP⊥BD.因为NH,NP⊂平面NHP,且NH∩NP=N,所以BD⊥平面NHP.又因为HP⊂平面NHP,所以BD⊥HP.又OC⊥BD,HP⊂平面BCD,OC⊂平面BCD,所以HP∥OC.因为H为BO的中点,所以P为BC的中点.(2)方法一:如图所示,作NQ ⊥AC 于Q ,连接MQ.由(1)知,NP ∥AC ,所以NQ ⊥NP .因为MN ⊥NP ,所以∠MNQ 为二面角A NP M 的一个平面角. 由(1)知,△ABD ,△BCD 为边长为2的正三角形,所以AO =OC = 3.由俯视图可知,AO ⊥平面BCD .因为OC ⊂平面BCD ,所以AO ⊥OC ,因此在等腰直角△AOC 中,AC = 6. 作BR ⊥AC 于R因为在△ABC 中,AB =BC ,所以R 为AC 的中点,所以BR =AB 2-⎝ ⎛⎭⎪⎫AC 22=102.因为在平面ABC 内,NQ ⊥AC ,BR ⊥AC , 所以NQ ∥BR .又因为N 为AB 的中点,所以Q 为AR 的中点, 所以NQ =BR2=104.同理,可得MQ =104.故△MNQ 为等腰三角形, 所以在等腰△MNQ 中,cos ∠MNQ =MN2NQ =BD4NQ =105.故二面角A NP M 的余弦值是105.方法二:由俯视图及(1)可知,AO ⊥平面BCD . 因为OC ,OB ⊂平面BCD ,所以AO ⊥OC ,AO ⊥OB . 又OC ⊥OB ,所以直线OA ,OB ,OC 两两垂直.如图所示,以O 为坐标原点,以OB ,OC ,OA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O xyz .则A (0,0,3),B (1,0,0),C (0,3,0),D (-1,0,0).因为M ,N 分别为线段AD ,AB 的中点, 又由(1)知,P 为线段BC 的中点,所以M ⎝ ⎛⎭⎪⎪⎫-12,0,32,N ⎝ ⎛⎭⎪⎪⎫12,0,32,P ⎝ ⎛⎭⎪⎪⎫12,32,0,于是AB =(1,0,-3),BC =(-1,3,0),MN =(1,0,0),NP =⎝ ⎛⎭⎪⎪⎫0,32,-32. 设平面ABC 的一个法向量n 1=(x 1,y 1,z 1),由⎩⎪⎨⎪⎧n 1⊥AB ,n 1⊥BC ,得⎩⎪⎨⎪⎧n 1·AB =0,n 1·BC =0,即 ⎩⎪⎨⎪⎧(x 1,y 1,z 1)·(1,0,-3)=0,(x 1,y 1,z 1)·(-1,3,0)=0, 从而⎩⎪⎨⎪⎧x 1-3z 1=0,-x 1+3y 1=0.取z 1=1,则x 1=3,y 1=1,所以n 1=(3,1,1).设平面MNP 的一个法向量n 2=(x 2,y 2,z 2),由,⎩⎪⎨⎪⎧n 2⊥MN ,n 2⊥NP ,得⎩⎪⎨⎪⎧n 2·MN =0,n 2·NP =0,即⎩⎪⎨⎪⎧(x 2,y 2,z 2)·(1,0,0)=0,(x 2,y 2,z 2)·⎝ ⎛⎭⎪⎪⎫0,32,-32=0, 从而⎩⎪⎨⎪⎧x 2=0,32y 2-32z 2=0. 取z 2=1,则y 2=1,x 2=0,所以n 2=(0,1,1).设二面角A NP M 的大小为θ,则cos θ=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=⎪⎪⎪⎪⎪⎪⎪⎪(3,1,1)·(0,1,1)5×2=105. 故二面角A NP M 的余弦值是105.G4 空间中的平行关系20.、、[2014·安徽卷] 如图15,四棱柱ABCD A 1B 1C 1D 1中,A 1A ⊥底面ABCD ,四边形ABCD 为梯形,AD ∥BC ,且AD =2BC .过A 1,C ,D 三点的平面记为α,BB 1与α的交点为Q .图15(1)证明:Q 为BB 1的中点;(2)求此四棱柱被平面α所分成上下两部分的体积之比;(3)若AA 1=4,CD =2,梯形ABCD 的面积为6,求平面α与底面ABCD 所成二面角的大小.20.解: (1)证明:因为BQ ∥AA 1,BC ∥AD ,BC ∩BQ =B ,AD ∩AA 1=A ,所以平面QBC ∥平面A 1AD ,从而平面A 1CD 与这两个平面的交线相互平行, 即QC ∥A 1D .故△QBC 与△A 1AD 的对应边相互平行, 于是△QBC ∽△A 1AD ,所以BQ BB 1=BQ AA 1=BCAD =12,即Q 为BB 1的中点.(2)如图1所示,连接QA ,QD .设AA 1=h ,梯形ABCD 的高为d ,四棱柱被平面α所分成上下两部分的体积分别为V 上和V 下,BC =a ,则AD =2a .图1V 三棱锥Q A 1AD =13×12·2a ·h ·d =13ahd ,V 四棱锥Q ABCD =13·a +2a 2·d ·⎝ ⎛⎭⎪⎫12h =14ahd ,所以V 下=V 三棱锥Q A 1AD +V 四棱锥Q ABCD =712ahd .又V 四棱柱A 1B 1C 1D 1 ABCD =32ahd ,所以V 上=V 四棱柱A 1B 1C 1D 1 ABCD -V 下=32ahd -712ahd =1112ahd ,故V 上V 下=117.(3)方法一:如图1所示,在△ADC 中,作AE ⊥DC ,垂足为E ,连接A 1E . 又DE ⊥AA 1,且AA 1∩AE =A , 所以DE ⊥平面AEA 1,所以DE ⊥A 1E .所以∠AEA 1为平面α与底面ABCD 所成二面角的平面角. 因为BC ∥AD ,AD =2BC ,所以S △ADC =2S △BCA . 又因为梯形ABCD 的面积为6,DC =2, 所以S △ADC =4,AE =4.于是tan ∠AEA 1=AA 1AE =1,∠AEA 1=π4.故平面α与底面ABCD 所成二面角的大小为π4.方法二:如图2所示,以D 为原点,DA ,DD 1→分别为x 轴和z 轴正方向建立空间直角坐标系.设∠CDA =θ,BC =a ,则AD =2a . 因为S 四边形ABCD =a +2a2·2sin θ=6,所以a =2sin θ.图2从而可得C (2cos θ,2sin θ,0),A 1⎝ ⎛⎭⎪⎫4sin θ,0,4, 所以DC =(2cos θ,2sin θ,0),DA 1→=⎝ ⎛⎭⎪⎫4sin θ,0,4. 设平面A 1DC 的法向量n =(x ,y ,1), 由⎩⎪⎨⎪⎧DA 1→·n =4sin θ x +4=0,DC→·n =2x cos θ+2y sin θ=0,得⎩⎪⎨⎪⎧x =-sin θ,y =cos θ,所以n =(-sin θ,cos θ,1).又因为平面ABCD 的法向量m =(0,0,1), 所以cos 〈n ,m 〉=n ·m|n||m|=22,故平面α与底面ABCD 所成二面角的大小为π4.17.、[2014·北京卷] 如图13,正方形AMDE 的边长为2,B ,C 分别为AM ,MD 的中点.在五棱锥P ABCDE 中,F 为棱PE 的中点,平面ABF 与棱PD ,PC 分别交于点G ,H .(1)求证:AB ∥FG ;(2)若PA ⊥底面ABCDE ,且PA =AE ,求直线BC 与平面ABF 所成角的大小,并求线段PH 的长.图1317.解:(1)证明:在正方形AMDE 中,因为B 是AM 的中点,所以AB ∥DE . 又因为AB ⊄平面PDE , 所以AB ∥平面PDE .因为AB ⊂平面ABF ,且平面ABF ∩平面PDE =FG , 所以AB ∥FG .(2)因为PA ⊥底面ABCDE , 所以PA ⊥AB ,PA ⊥AE .建立空间直角坐标系Axyz ,如图所示,则A (0,0,0),B (1,0,0),C (2,1,0),P (0,0,2),F (0,1,1),BC →=(1,1,0).设平面ABF 的法向量为n =(x ,y ,z ),则 ⎩⎨⎧n ·AB →=0,n ·AF →=0,即⎩⎪⎨⎪⎧x =0,y +z =0.令z =1,则y =-1.所以n =(0,-1,1). 设直线BC 与平面ABF 所成角为α,则 sin α=|cos 〈n ,BC →〉|=⎪⎪⎪⎪⎪⎪n ·BC →|n ||BC →|=12.因此直线BC 与平面ABF 所成角的大小为π6.设点H 的坐标为(u ,v ,w ).因为点H 在棱PC 上,所以可设PH →=λPC →(0<λ<1).即(u ,v ,w -2)=λ(2,1,-2),所以u =2λ,v =λ,w =2-2λ. 因为n 是平面ABF 的一个法向量, 所以n ·AH →=0,即(0,-1,1)·(2λ,λ,2-2λ)=0,解得λ=23,所以点H 的坐标为⎝ ⎛⎭⎪⎫43,23,23.所以PH =⎝ ⎛⎭⎪⎫432+⎝ ⎛⎭⎪⎫232+⎝ ⎛⎭⎪⎫-432=2. 19.、、、[2014·湖北卷] 如图14,在棱长为2的正方体ABCD A 1B 1C 1D 1中,E ,F ,M ,N 分别是棱AB ,AD ,A 1B 1,A 1D 1的中点,点P ,Q 分别在棱DD 1,BB 1上移动,且DP =BQ =λ(0<λ<2).(1)当λ=1时,证明:直线BC 1∥平面EFPQ .(2)是否存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.19.解:方法一(几何方法):(1)证明:如图①,连接AD 1,由ABCD A 1B 1C 1D 1是正方体,知BC 1∥AD 1. 当λ=1时,P 是DD 1的中点,又F 是AD 的中点,所以FP ∥AD 1,所以BC 1∥FP . 而FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ ,故直线BC 1∥平面EFPQ .(2)如图②,连接BD .因为E ,F 分别是AB ,AD 的中点,所以EF ∥BD ,且EF =12BD .又DP =BQ ,DP ∥BQ ,所以四边形PQBD 是平行四边形,故PQ ∥BD ,且PQ =BD ,从而EF ∥PQ ,且EF =12PQ .在Rt △EBQ 和Rt △FDP 中,因为BQ =DP =λ,BE =DF =1, 于是EQ =FP =1+λ2,所以四边形EFPQ 也是等腰梯形.同理可证四边形PQMN 也是等腰梯形.分别取EF ,PQ ,MN 的中点为H ,O ,G ,连接OH ,OG , 则GO ⊥PQ ,HO ⊥PQ ,而GO ∩HO =O ,故∠GOH 是面EFPQ 与面PQMN 所成的二面角的平面角.若存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角,则∠GOH =90°. 连接EM ,FN ,则由EF ∥MN ,且EF =MN 知四边形EFNM 是平行四边形. 连接GH ,因为H ,G 是EF ,MN 的中点, 所以GH =ME =2.在△GOH 中,GH 2=4,OH 2=1+λ2-⎝ ⎛⎭⎪⎪⎫222=λ2+12, OG 2=1+(2-λ)2-⎝ ⎛⎭⎪⎪⎫222=(2-λ)2+12, 由OG 2+OH 2=GH 2,得(2-λ)2+12+λ2+12=4,解得λ=1±22, 故存在λ=1±22,使面EFPQ 与面PQMN 所成的二面角为直二面角.方法二(向量方法):以D 为原点,射线DA ,DC ,DD 1分别为x ,y ,z 轴的正半轴建立如图③所示的空间直角坐标系.由已知得B (2,2,0),C 1(0,2,2),E (2,1,0),F (1,0,0),P (0,0,λ).BC 1→=(-2,0,2),FP =(-1,0,λ),FE =(1,1,0).(1)证明:当λ=1时,FP =(-1,0,1), 因为BC 1→=(-2,0,2), 所以BC 1→=2FP →,即BC 1∥FP .而FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ ,故直线BC 1∥平面EFPQ .(2)设平面EFPQ 的一个法向量为n =(x ,y ,z ),则由⎩⎨⎧FE →·n =0,FP →·n =0可得⎩⎪⎨⎪⎧x +y =0,-x +λz =0.于是可取n =(λ,-λ,1).同理可得平面MNPQ 的一个法向量为m =(λ-2,2-λ,1). 若存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角, 则m ·n =(λ-2,2-λ,1)·(λ,-λ,1)=0, 即λ(λ-2)-λ(2-λ)+1=0,解得λ=1±22.故存在λ=1±22,使面EFPQ 与面PQMN 所成的二面角为直二面角.18.、[2014·新课标全国卷Ⅱ] 如图13,四棱锥P ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(1)证明:PB ∥平面AEC ;(2)设二面角D AE C 为60E ACD 的体积.18.解:(1)证明:连接BD 交AC 于点O ,连接EO . 因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点,所以EO ∥PB .因为EO ⊂平面AEC ,PB ⊄平面AEC , 所以PB ∥平面AEC .(2)因为PA ⊥平面ABCD ,ABCD 为矩形, 所以AB ,AD ,AP 两两垂直.如图,以A 为坐标原点,AB →,AD ,AP 的方向为x 轴、y 轴、z 轴的正方向,|AP →|为单位长,建立空间直角坐标系A xyz ,则D ()0,3,0,E ⎝ ⎛⎭⎪⎪⎫0,32,12,AE →=⎝⎛⎭⎪⎪⎫0,32,12.设B (m ,0,0)(m >0),则C (m ,3,0),AC =(m ,3,0).设n 1=(x ,y ,z )为平面ACE 的法向量,则⎩⎨⎧n 1·AC →=0,n 1·AE →=0,即⎩⎪⎨⎪⎧mx +3y =0,32y +12z =0, 可取n 1=⎝ ⎛⎭⎪⎪⎫3m ,-1,3. 又n 2=(1,0,0)为平面DAE 的法向量, 由题设易知|cos 〈n 1,n 2〉|=12,即33+4m 2=12,解得m =32.因为E 为PD 的中点,所以三棱锥E ACD 的高为12.三棱锥E ACD 的体积V =13×12×3×32×12=38. 17.,[2014·山东卷] 如图13所示,在四棱柱ABCD A 1B 1C 1D 1中,底面ABCD 是等腰梯形,∠DAB =60°,AB =2CD =2,M 是线段AB 的中点.图13(1)求证:C1M∥平面A1ADD1;(2)若CD1垂直于平面ABCD且CD1=3,求平面C1D1M和平面ABCD所成的角(锐角)的余弦值.17.解:(1)证明:因为四边形ABCD是等腰梯形,且AB=2CD,所以AB∥DC,又M是AB的中点,所以CD∥MA且CD=MA.连接AD1.因为在四棱柱ABCDA1B1C1D1中,CD∥C1D1,CD=C1D1,所以C1D1∥MA,C1D1=MA,所以四边形AMC1D1为平行四边形,因此,C1M∥D1A.又C1M⊄平面A1ADD1,D1A⊂平面A1ADD1,所以C1M∥平面A1ADD1.(2)方法一:连接AC ,MC . 由(1)知,CD ∥AM 且CD =AM , 所以四边形AMCD 为平行四边形, 所以BC =AD =MC .由题意∠ABC =∠DAB =60°, 所以△MBC 为正三角形, 因此AB =2BC =2,CA =3,因此CA ⊥CB .设C 为坐标原点,建立如图所示的空间直角坐标系C xyz .所以A (3,0,0),B (0,1,0),D 1(0,0,3).因此M ⎝ ⎛⎭⎪⎪⎫32,12,0,所以MD 1→=⎝ ⎛⎭⎪⎪⎫-32,-12,3,D 1C 1→=MB →=⎝ ⎛⎭⎪⎪⎫-32,12,0.设平面C 1D 1M 的一个法向量n =(x ,y ,z ),由⎩⎨⎧n ·D 1C 1→=0,n ·MD1→=0,得⎩⎪⎨⎪⎧3x -y =0,3x +y -23z =0,可得平面C 1D 1M 的一个法向量n =(1,3,1).又CD 1→=(0,0,3)为平面ABCD 的一个法向量.因此cos 〈CD 1→,n 〉=CD 1→·n|CD 1→||n |=55,所以平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值为55.方法二:由(1)知,平面D 1C 1M ∩平面ABCD =AB ,点过C 向AB 引垂线交AB 于点N ,连接D 1N.由CD 1⊥平面ABCD ,可得D 1N ⊥AB , 因此∠D 1NC 为二面角C 1 AB C 的平面角. 在Rt △BNC 中,BC =1,∠NBC =60°, 可得CN =32,所以ND 1=CD 21+CN 2=152. 在Rt △D 1CN 中,cos ∠D 1NC =CND 1N=32152=55,所以平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值为55.18.,,,[2014·四川卷] 三棱锥A BCD 及其侧视图、俯视图如图14所示.设M ,N 分别为线段AD ,AB 的中点,P 为线段BC 上的点,且MN ⊥NP .(1)证明:P是线段BC的中点;(2)求二面角ANPM的余弦值.图1418.解:(1)如图所示,取BD的中点O,连接AO,CO.由侧视图及俯视图知,△ABD,△BCD为正三角形,所以AO⊥BD,OC⊥BD.因为AO,OC⊂平面AOC,且AO∩OC=O,所以BD⊥平面AOC.又因为AC⊂平面AOC,所以BD⊥AC.取BO的中点H,连接NH,PH.又M,N,H分别为线段AD,AB,BO的中点,所以MN∥BD,NH∥AO,因为AO⊥BD,所以NH⊥BD.因为MN⊥NP,所以NP⊥BD.因为NH,NP⊂平面NHP,且NH∩NP=N,所以BD⊥平面NHP.又因为HP⊂平面NHP,所以BD⊥HP.又OC⊥BD,HP⊂平面BCD,OC⊂平面BCD,所以HP∥OC.因为H为BO的中点,所以P为BC的中点.(2)方法一:如图所示,作NQ ⊥AC 于Q ,连接MQ.由(1)知,NP ∥AC ,所以NQ ⊥NP .因为MN ⊥NP ,所以∠MNQ 为二面角A NP M 的一个平面角. 由(1)知,△ABD ,△BCD 为边长为2的正三角形,所以AO =OC = 3.由俯视图可知,AO ⊥平面BCD .因为OC ⊂平面BCD ,所以AO ⊥OC ,因此在等腰直角△AOC 中,AC = 6. 作BR ⊥AC 于R因为在△ABC 中,AB =BC ,所以R 为AC 的中点,所以BR =AB 2-⎝ ⎛⎭⎪⎫AC 22=102.因为在平面ABC 内,NQ ⊥AC ,BR ⊥AC , 所以NQ ∥BR .又因为N 为AB 的中点,所以Q 为AR 的中点, 所以NQ =BR2=104.同理,可得MQ =104.故△MNQ 为等腰三角形, 所以在等腰△MNQ 中,cos ∠MNQ =MN2NQ =BD4NQ =105.故二面角A NP M 的余弦值是105.方法二:由俯视图及(1)可知,AO ⊥平面BCD . 因为OC ,OB ⊂平面BCD ,所以AO ⊥OC ,AO ⊥OB . 又OC ⊥OB ,所以直线OA ,OB ,OC 两两垂直.如图所示,以O 为坐标原点,以OB ,OC ,OA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O xyz .则A (0,0,3),B (1,0,0),C (0,3,0),D (-1,0,0).因为M ,N 分别为线段AD ,AB 的中点, 又由(1)知,P 为线段BC 的中点,所以M ⎝ ⎛⎭⎪⎪⎫-12,0,32,N ⎝ ⎛⎭⎪⎪⎫12,0,32,P ⎝ ⎛⎭⎪⎪⎫12,32,0,于是AB =(1,0,-3),BC =(-1,3,0),MN =(1,0,0),NP =⎝ ⎛⎭⎪⎪⎫0,32,-32. 设平面ABC 的一个法向量n 1=(x 1,y 1,z 1),由⎩⎪⎨⎪⎧n 1⊥AB ,n 1⊥BC ,得⎩⎪⎨⎪⎧n 1·AB =0,n 1·BC =0,即 ⎩⎪⎨⎪⎧(x 1,y 1,z 1)·(1,0,-3)=0,(x 1,y 1,z 1)·(-1,3,0)=0, 从而⎩⎪⎨⎪⎧x 1-3z 1=0,-x 1+3y 1=0.取z 1=1,则x 1=3,y 1=1,所以n 1=(3,1,1).设平面MNP 的一个法向量n 2=(x 2,y 2,z 2),由,⎩⎪⎨⎪⎧n 2⊥MN ,n 2⊥NP ,得⎩⎪⎨⎪⎧n 2·MN =0,n 2·NP =0,即⎩⎪⎨⎪⎧(x 2,y 2,z 2)·(1,0,0)=0,(x 2,y 2,z 2)·⎝ ⎛⎭⎪⎪⎫0,32,-32=0, 从而⎩⎪⎨⎪⎧x 2=0,32y 2-32z 2=0. 取z 2=1,则y 2=1,x 2=0,所以n 2=(0,1,1).设二面角A NP M 的大小为θ,则cos θ=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=⎪⎪⎪⎪⎪⎪⎪⎪(3,1,1)·(0,1,1)5×2=105. 故二面角A NP M 的余弦值是105.G5 空间中的垂直关系17.、、[2014·福建卷] 在平面四边形ABCD 中,AB =BD =CD =1,AB ⊥BD ,CD ⊥BD .将△ABD 沿BD 折起,使得平面ABD ⊥平面BCD ,如图15所示.(1)求证:AB ⊥CD ;(2)若M 为AD 中点,求直线AD 与平面MBC 所成角的正弦值.图1517.解:(1)证明:∵平面ABD ⊥平面BCD ,平面ABD ∩平面BCD =BD ,AB ⊂平面ABD ,AB ⊥BD ,∴AB ⊥平面BCD .又CD ⊂平面BCD ,∴AB ⊥CD . (2)过点B 在平面BCD 内作BE ⊥BD .由(1)知AB ⊥平面BCD ,BE ⊂平面BCD ,BD ⊂平面BCD ,∴AB ⊥BE ,AB ⊥BD . 以B 为坐标原点,分别以BE →,BD →,BA →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系(如图所示).依题意,得B (0,0,0),C (1,1,0),D (0,1,0),A (0,0,1),M ⎝ ⎛⎭⎪⎫0,12,12.则BC →=(1,1,0),BM →=⎝ ⎛⎭⎪⎫0,12,12,AD →=(0,1,-1).设平面MBC 的法向量n =(x 0,y 0,z 0),则⎩⎨⎧n ·BC →=0,n ·BM →=0,即⎩⎪⎨⎪⎧x 0+y 0=0,12y 0+12z 0=0, 取z 0=1,得平面MBC 的一个法向量n =(1,-1,1). 设直线AD 与平面MBC 所成角为θ,则sin θ=⎪⎪⎪⎪cos 〈n ,AD →〉=|n ·AD →||n |·|AD →|=63.即直线AD 与平面MBC 所成角的正弦值为63.18.、[2014·广东卷] 如图14,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.(1)证明:CF⊥平面ADF;(2)求二面角DAFE的余弦值.图1419.、[2014·湖南卷] 如图16所示,四棱柱ABCDA1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.(1)证明:O1O⊥底面ABCD;(2)若∠CBA=60°,求二面角C1OB1D的余弦值.19.解:(1)如图(a),因为四边形ACC1A1为矩形,所以CC1⊥AC.同理DD1⊥BD.因为CC1∥DD1,所以CC1⊥BD.而AC∩BD=O,因此CC1⊥底面ABCD.由题设知,O1O∥C1C.故O1O⊥底面ABCD.(2)方法一:如图(a),过O1作O1H⊥OB1于H,连接HC1.由(1)知,O1O⊥底面ABCD,所以O1O⊥底面A1B1C1D1,于是O1O⊥A1C1.图(a)又因为四棱柱ABCD A 1B 1C 1D 1的所有棱长都相等,所以四边形A 1B 1C 1D 1是菱形, 因此A 1C 1⊥B 1D 1,从而A 1C 1⊥平面BDD 1B 1,所以A 1C 1⊥OB 1,于是OB 1⊥平面O 1HC 1. 进而OB 1⊥C 1H .故∠C 1HO 1是二面角C 1OB 1D 的平面角. 不妨设AB =2.因为∠CBA =60°,所以OB =3,OC =1,OB 1=7.在Rt △OO 1B 1中,易知O 1H =OO 1·O 1B 1OB 1=237.而O 1C 1=1,于是C 1H =O 1C 21+O 1H 2=1+127=197. 故cos ∠C 1HO 1=O 1H C 1H=237197=25719.即二面角C 1OB 1D 的余弦值为25719.方法二:因为四棱柱ABCD A 1B 1C 1D 1的所有棱长都相等,所以四边形ABCD 是菱形,因此AC ⊥BD .又O 1O ⊥底面ABCD ,从而OB ,OC ,OO 1两两垂直.如图(b),以O 为坐标原点,OB ,OC ,OO 1所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系O xyz ,不妨设AB =2.因为∠CBA =60°,所以OB =3,OC =1,于是相关各点的坐标为O (0,0,0),B 1(3,0,2),C 1(0,1,2).易知,n 1=(0,1,0)是平面BDD 1B 1的一个法向量. 设n 2=(x ,y ,z )是平面OB 1C 1的一个法向量,则⎩⎨⎧n 2·OB →1=0,n 2·OC→1=0,即⎩⎪⎨⎪⎧3x +2z =0,y +2z =0.取z =-3,则x =2,y =23,所以n 2=(2,23,-3).设二面角C 1OB 1D 的大小为θ,易知θ是锐角,于是cos θ=|cos 〈,〉|=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=2319=25719.故二面角C 1OB 1D 的余弦值为25719.19.、、[2014·江西卷] 如图16,四棱锥P ABCD 中,ABCD 为矩形,平面PAD ⊥平面ABCD .图16(1)求证:AB ⊥PD . (2)若∠BPC =90°,PB =2,PC =2,问AB 为何值时,四棱锥P ABCD 的体积最大?并求此时平面BPC 与平面DPC 夹角的余弦值.19.解:(1)证明:因为ABCD 为矩形,所以AB ⊥AD . 又平面PAD ⊥平面ABCD , 平面PAD ∩平面ABCD =AD , 所以AB ⊥平面PAD ,故AB ⊥PD .(2)过P 作AD 的垂线,垂足为O ,过O 作BC 的垂线,垂足为G ,连接PG . 故PO ⊥平面ABCD ,BC ⊥平面POG ,BC ⊥PG . 在Rt △BPC 中,PG =2 33,GC =263,BG =63. 设AB =m ,则OP =PG 2-OG 2=43-m 2,故四棱锥P ABCD 的体积为 V =13×6·m ·43-m 2=m38-6m 2.因为m 8-6m 2=8m 2-6m 4=-6⎝⎛⎭⎪⎫m 2-232+83,所以当m =63,即AB =63时,四棱锥P ABCD 的体积最大.此时,建立如图所示的空间直角坐标系,各点的坐标分别为O (0,0,0),B ⎝ ⎛⎭⎪⎪⎫63,-63,0,C ⎝ ⎛⎭⎪⎪⎫63,263,0,D ⎝ ⎛⎭⎪⎪⎫0,263,0,P ⎝ ⎛⎭⎪⎪⎫0,0,63,故PC→=⎝ ⎛⎭⎪⎪⎫63,263,-63,BC →=(0,6,0),CD =⎝ ⎛⎭⎪⎪⎫-63,0,0.设平面BPC 的一个法向量为n 1=(x ,y ,1),则由n 1⊥PC →,n 1⊥BC →,得⎩⎪⎨⎪⎧63x +2 63y -63=0,6y =0,解得x =1,y =0,则n 1=(1,0,1).同理可求出平面DPC 的一个法向量为n 2=⎝ ⎛⎭⎪⎫0,12,1.设平面BPC 与平面DPC 的夹角为θ,则cos θ=|n 1·n 2||n 1||n 2|=12·14+1=105.19.、[2014·辽宁卷] 如图15所示,△ABC 和△BCD 所在平面互相垂直,且AB =BC =BD =2,∠ABC =∠DBC =120°,E ,F 分别为AC ,DC 的中点.(1)求证:EF ⊥BC ;(2)求二面角E BF C 的正弦值.19.解:(1)证明:方法一,过点E 作EO ⊥BC ,垂足为O ,连接OF .由△ABC ≌△DBC 可证出△EOC ≌△FOC ,所以∠EOC =∠FOC =π2,即FO ⊥BC .又EO ⊥BC ,EO ∩FO =O ,所以BC ⊥平面EFO .又EF ⊂平面EFO ,所以EF ⊥BC .方法二,由题意,以B 为坐标原点,在平面DBC 内过B 作垂直BC 的直线,并将其作为x 轴,BC 所在直线为y 轴,在平面ABC 内过B 作垂直BC 的直线,并将其作为z 轴,建立如图所示的空间直角坐标系,易得B (0,0,0),A (0,-1,3),D (3,-1,0),C (0,2,0),因而E (0,12,32),F (32,12,0),所以EF →=(32,0,-32),BC →=(0,2,0),因此EF →·BC →=0,从而EF →⊥BC →,所以EF ⊥BC .(2)方法一,在图1中,过点O 作OG ⊥BF ,垂足为G ,连接EG .因为平面ABC ⊥平面BDC ,所以EO ⊥面BDC ,又OG ⊥BF ,所以由三垂线定理知EG ⊥BF ,因此∠EGO 为二面角E BF C 的平面角. 在△EOC 中,EO =12EC =12BC ·cos 30°=32.由△BGO ∽△BFC 知,OG =BOBC ·FC =34,因此tan ∠EGO =EOOG =2,从而得sin ∠EGO=255,即二面角E BF C 的正弦值为2 55. 方法二,在图2中,平面BFC 的一个法向量为n 1=(0,0,1). 设平面BEF 的法向量n 2=(x ,y ,z ), 又BF →=(32,12,0),BE →=(0,12,32),所以⎩⎨⎧n 2·BF→=0,n 2·BE →=0,得其中一个n 2=(1,-3,1).设二面角E BF C 的大小为θ,且由题知θ为锐角,则cos θ=|cos 〈n 1,n 2〉|=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1||n 2|=15,因此sin θ=25=2 55,即所求二面角正弦值为2 55.19.G 5、G 11[2014·新课标全国卷Ⅰ] 如图15,三棱柱ABC A 1B 1C 1中,侧面BB 1C 1C 为菱形,AB ⊥B 1C .图15(1)证明:AC =AB 1;(2)若AC ⊥AB 1,∠CBB 1=60°,AB =BC ,求二面角A A 1B 1 C 1的余弦值. 19.解:(1)证明:连接BC 1,交B 1C 于点O ,连接AO ,因为侧面BB 1C 1C 为菱形,所以B 1C ⊥BC 1,且O 为B 1C 及BC 1的中点.又AB ⊥B 1C ,所以B 1C ⊥平面ABO . 由于AO ⊂平面ABO ,故B 1C ⊥AO . 又B 1O =CO ,故AC =AB 1.(2)因为AC ⊥AB 1,且O 为B 1C 的中点,所以AO =CO .又因为AB =BC ,所以△BOA ≌ △BOC .故OA ⊥OB ,从而OA ,OB ,OB 1两两垂直. 以O 为坐标原点,OB 的方向为x 轴正方向,|OB |为单位长,建立如图所示的空间直角坐标系O xyz.因为∠CBB 1=60°,所以△CBB 1为等边三角形,又AB =BC ,则A ⎝ ⎛⎭⎪⎪⎫0,0,33,B (1,0,0),B 1⎝ ⎛⎭⎪⎪⎫0,33,0,C ⎝ ⎛⎭⎪⎪⎫0,-33,0.AB 1→=⎝ ⎛⎭⎪⎪⎫0,33,-33,A 1B 1→=AB =⎝ ⎛⎭⎪⎪⎫1,0,-33,B 1C →1=BC =⎝ ⎛⎭⎪⎪⎫-1,-33,0. 设n =(x ,y ,z )是平面AA 1B 1的法向量,则 ⎩⎪⎨⎪⎧n ·AB 1=0,n ·A 1B 1→=0,即⎩⎪⎨⎪⎧33y -33z =0,x -33z =0.所以可取n =(1,3,3).设m 是平面A 1B 1C 1的法向量,则⎩⎨⎧m ·A 1B 1→=0,m ·B 1C 1→=0,同理可取m =(1,-3,3).则cos 〈n ,m 〉=n ·m|n ||m |=17.所以结合图形知二面角A A 1B 1 C 1的余弦值为17.18.,,,[2014·四川卷] 三棱锥A BCD 及其侧视图、俯视图如图14所示.设M ,N 分别为线段AD ,AB 的中点,P 为线段BC 上的点,且MN ⊥NP .(1)证明:P 是线段BC 的中点; (2)求二面角A NP M 的余弦值.图1418.解:(1)如图所示,取BD 的中点O ,连接AO ,CO . 由侧视图及俯视图知,△ABD ,△BCD 为正三角形,所以AO ⊥BD ,OC ⊥BD .因为AO ,OC ⊂平面AOC ,且AO ∩OC =O , 所以BD ⊥平面AOC .又因为AC ⊂平面AOC ,所以BD ⊥AC .取BO 的中点H ,连接NH ,PH .又M ,N ,H 分别为线段AD ,AB ,BO 的中点,所以MN ∥BD ,NH ∥AO , 因为AO ⊥BD ,所以NH ⊥BD . 因为MN ⊥NP ,所以NP ⊥BD .因为NH ,NP ⊂平面NHP ,且NH ∩NP =N ,所以BD ⊥平面NHP . 又因为HP ⊂平面NHP ,所以BD ⊥HP .又OC ⊥BD ,HP ⊂平面BCD ,OC ⊂平面BCD ,所以HP ∥OC . 因为H 为BO 的中点,所以P 为BC 的中点. (2)方法一:如图所示,作NQ ⊥AC 于Q ,连接MQ .由(1)知,NP ∥AC ,所以NQ ⊥NP .因为MN ⊥NP ,所以∠MNQ 为二面角A NP M 的一个平面角. 由(1)知,△ABD ,△BCD 为边长为2的正三角形,所以AO =OC = 3.由俯视图可知,AO ⊥平面BCD .因为OC ⊂平面BCD ,所以AO ⊥OC ,因此在等腰直角△AOC 中,AC = 6. 作BR ⊥AC 于R因为在△ABC 中,AB =BC ,所以R 为AC 的中点,所以BR =AB 2-⎝ ⎛⎭⎪⎫AC 22=102. 因为在平面ABC 内,NQ ⊥AC ,BR ⊥AC , 所以NQ ∥BR .又因为N 为AB 的中点,所以Q 为AR 的中点, 所以NQ =BR2=104.同理,可得MQ =104.故△MNQ 为等腰三角形, 所以在等腰△MNQ 中,cos ∠MNQ =MN2NQ =BD4NQ =105.故二面角A NP M 的余弦值是105.方法二:由俯视图及(1)可知,AO ⊥平面BCD . 因为OC ,OB ⊂平面BCD ,所以AO ⊥OC ,AO ⊥OB . 又OC ⊥OB ,所以直线OA ,OB ,OC 两两垂直.如图所示,以O 为坐标原点,以OB ,OC ,OA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系O xyz .则A (0,0,3),B (1,0,0),C (0,3,0),D (-1,0,0).因为M ,N 分别为线段AD ,AB 的中点, 又由(1)知,P 为线段BC 的中点,所以M ⎝ ⎛⎭⎪⎪⎫-12,0,32,N ⎝ ⎛⎭⎪⎪⎫12,0,32,P ⎝ ⎛⎭⎪⎪⎫12,32,0,于是AB =(1,0,-3),BC =(-1,3,0),MN =(1,0,0),NP =⎝ ⎛⎭⎪⎪⎫0,32,-32. 设平面ABC 的一个法向量n 1=(x 1,y 1,z 1),由⎩⎪⎨⎪⎧n 1⊥AB ,n 1⊥BC ,得⎩⎪⎨⎪⎧n 1·AB =0,n 1·BC =0,即 ⎩⎪⎨⎪⎧(x 1,y 1,z 1)·(1,0,-3)=0,(x 1,y 1,z 1)·(-1,3,0)=0, 从而⎩⎪⎨⎪⎧x 1-3z 1=0,-x 1+3y 1=0.取z 1=1,则x 1=3,y 1=1,所以n 1=(3,1,1).设平面MNP 的一个法向量n 2=(x 2,y 2,z 2),由,⎩⎪⎨⎪⎧n 2⊥MN ,n 2⊥NP ,得⎩⎪⎨⎪⎧n 2·MN =0,n 2·NP =0,即⎩⎪⎨⎪⎧(x 2,y 2,z 2)·(1,0,0)=0,(x 2,y 2,z 2)·⎝ ⎛⎭⎪⎪⎫0,32,-32=0, 从而⎩⎪⎨⎪⎧x 2=0,32y 2-32z 2=0. 取z 2=1,则y 2=1,x 2=0,所以n 2=(0,1,1).设二面角A NP M 的大小为θ,则cos θ=⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|=⎪⎪⎪⎪⎪⎪⎪⎪(3,1,1)·(0,1,1)5×2=105. 故二面角A NP M 的余弦值是105.17.、[2014·天津卷] 如图14所示,在四棱锥P ABCD 中,PA ⊥底面ABCD, AD⊥AB ,AB ∥DC ,AD =DC =AP =2,AB =1,点E 为棱PC 的中点.(1)证明:BE ⊥DC ;(2)求直线BE 与平面PBD 所成角的正弦值;(3)若F 为棱PC 上一点,满足BF ⊥AC ,求二面角F AB P 的余弦值.图1417.解:方法一:依题意,以点A 为原点建立空间直角坐标系(如图所示),可得B (1,0,0),C (2,2,0),D (0,2,0),P (0,0,2).C 由E 为棱PC 的中点,得E (1,1,1).(1)证明:向量BE =(0,1,1),DC =(2,0,0), 故BE ·DC =0, 所以BE ⊥DC .(2)向量BD =(-1,2,0),PB =(1,0,-2). 设n =(x ,y ,z )为平面PBD 的法向量,则⎩⎪⎨⎪⎧n ·BD =0,n ·PB =0,即⎩⎪⎨⎪⎧-x +2y =0,x -2z =0.不妨令y =1,可得n =(2,1,1)为平面PBD 的一个法向量.于是有cos 〈n ,BE 〉=n ·BE |n |·|BE |=26×2=33, 所以直线BE 与平面PBD 所成角的正弦值为33.(3) 向量BC =(1,2,0),CP =(-2,-2,2),AC =(2,2,0),AB =(1,0,0).由点F 在棱PC 上,设CF =λCP →,0≤λ≤1.故BF =BC +CF =BC +λCP →=(1-2λ,2-2λ,2λ).由BF ⊥AC ,得BF ·AC =0,因此2(1-2λ)+2(2-2λ)=0,解得λ=34,即BF =⎝ ⎛⎭⎪⎫-12,12,32.设n 1=(x ,y ,z )为平面FAB 的法向量,则⎩⎪⎨⎪⎧n 1·AB =0,n 1·BF =0,即⎩⎪⎨⎪⎧x =0,-12x +12y +32z =0.不妨令z =1,可得n 1=(0,-3,1)为平面FAB 的一个法向量.取平面ABP 的法向量n 2=(0,1,0),则cos 〈,〉=n 1·n 2|n 1|·|n 2|=-310×1=-31010.易知二面角F AB P 是锐角,所以其余弦值为31010.方法二:(1)证明:如图所示,取PD 中点M ,连接EM ,AM .由于E ,M 分别为PC ,PD 的中点,故EM ∥DC ,且EM =12DC .又由已知,可得EM ∥AB 且EM =AB ,故四边形ABEM 为平行四边形,所以BE ∥AM .因为PA ⊥底面ABCD ,故PA ⊥CD ,而CD ⊥DA ,从而CD ⊥平面PAD .因为AM ⊂平面PAD ,所以CD ⊥AM .又BE ∥AM ,所以BE ⊥CD .(2)连接BM ,由(1)有CD ⊥平面PAD ,得CD ⊥PD .而EM ∥CD ,故PD ⊥EM .又因为AD =AP ,M 为PD 的中点,所以PD ⊥AM ,可得PD ⊥BE ,所以PD ⊥平面BEM ,故平面BEM ⊥平面PBD ,所以直线BE 在平面PBD 内的射影为直线BM .而BE ⊥EM ,可得∠EBM为锐角,故∠EBM 为直线BE 与平面PBD 所成的角.依题意,有PD =22,而M 为PD 中点,可得AM =2,进而BE =2.故在直角三角形BEM 中,tan ∠EBM =EM BE=AB BE=12,因此sin ∠EBM =33,所以直线BE 与平面PBD 所成角的正弦值为33.(3)如图所示,在△PAC 中,过点F 作FH ∥PA 交AC 于点H .因为PA ⊥底面ABCD ,所以FH ⊥底面ABCD ,从而FH ⊥AC .又BF ⊥AC ,得AC ⊥平面FHB ,因此AC ⊥BH .在底面ABCD 内,可得CH =3HA ,从而CF =3FP .在平面PDC 内,作FG ∥DC 交PD 于点G ,于是DG =3GP .由于DC ∥AB ,故GF ∥AB ,所以A ,B ,F ,G 四点共面.由AB ⊥PA ,AB ⊥AD ,得AB ⊥平面PAD ,故AB ⊥AG ,所以∠PAG 为二面角F AB P 的平面角.在△PAG 中,PA =2,PG =14PD =22,∠APG =45°.由余弦定理可得AG =102,cos∠PAG =31010,所以二面角F AB P 的余弦值为31010.。
2014高考数学迎考重要锦囊立体几何知识整合
2014高考数学迎考重要锦囊:立体几何知识整合高考立体几何试题一般共有4道(选择、填空题3道,解答题1道),共计总分27分左右,考查的知识点在20个以内。
选择填空题考核立几中的计算型问题,而解答题着重考查立几中的逻辑推理型问题,当然,二者均应以正确的空间想象为前提。
随着新的课程改革的进一步实施,立体几何考题正朝着“多一点思考,少一点计算”的发展。
从历年的考题变化看,以简单几何体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题。
知识整合1.有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的内容,因此在主体几何的总复习中,首先应从解决“平行与垂直”的有关问题着手,通过较为基本问题,熟悉公理、定理的内容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律--充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能力和空间想象能力。
2. 判定两个平面平行的方法:(1)根据定义--证明两平面没有公共点;(2)判定定理--证明一个平面内的两条相交直线都平行于另一个平面;(3)证明两平面同垂直于一条直线。
3.两个平面平行的主要性质:⑴由定义知:“两平行平面没有公共点”。
⑵由定义推得:“两个平面平行,其中一个平面内的直线必平行于另一个平面。
⑶两个平面平行的性质定理:”如果两个平行平面同时和第三个平面相交,那么它们的交线平行“。
⑷一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
⑸夹在两个平行平面间的平行线段相等。
⑹经过平面外一点只有一个平面和已知平面平行。
以上性质⑵、⑷、⑸、⑹在课文中虽未直接列为”性质定理“,但在解题过程中均可直接作为性质定理引用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014高考数学必考知识点:立体几何考试内容平面及其基本性质.平面图形直观图的画法.平行直线.对应边分别平行的角.异面直线所成的角.异面直线的公垂线.异面直线的距离.直线和平面平行的判定与性质.直线和平面垂直的判定与性质.点到平面的距离.斜线在平面上的射影.直线和平面所成的角.三垂线定理及其逆定理.平行平面的判定与性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定与性质.多面体.正多面体.棱柱.棱锥.球.考试要求(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图;能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想像它们的位置关系.(2)掌握两条直线平行与垂直的判定定理和性质定理,掌握两条直线所成的角和距离的概念,对于异面直线的距离,只要求会计算已给出公垂线时的距离.(3)掌握直线和平面平行的判定定理和性质定理;掌握直线和平面垂直的判定定理和性质定理;掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念掌握三垂线定理及其逆定理.(4)掌握两个平面平行的判定定理和性质定理,掌握二面角、二面角的平面角、两个平行平面间的距离的概念,掌握两个平面垂直的判定定理和性质定理.(5)会用反证法证明简单的问题.(6)了解多面体、凸多面体的概念,了解正多面体的概念.(7)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图.(8)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图.(9)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.9(B).直线、平面、简单几何体考试内容:平面及其基本性质.平面图形直观图的画法.平行直线.直线和平面平行的判定与性质.直线和平面垂直的判定.三垂线定理及其逆定理.两个平面的位置关系.空间向量及其加法、减法与数乘.空间向量的坐标表示.空间向量的数量积.直线的方向向量.异面直线所成的角.异面直线的公垂线.异面直线的距离.直线和平面垂直的性质.平面的法向量.点到平面的距离.直线和平面所成的角.向量在平面内的射影.平行平面的判定和性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定和性质.多面体.正多面体.棱柱.棱锥.球.考试要求:(1)掌握平面的基本性质。
会用斜二测的画法画水平放置的平面图形的直观图:能够画出空间两条直线、直线和平面的各种位置关系的图形.能够根据图形想像它们的位置关系.(2)掌握直线和平面平行的判定定理和性质定理;理解直线和平面垂直的概念.掌握直线和平面垂直的判定定理;掌握三垂线定理及其逆定理.(3)理解空间向量的概念,掌握空间向量的加法、减法和数乘.(4)了解空间向量的基本定理;理解空间向量坐标的概念.掌握空间向量的坐标运算.(5)掌握空间向量的数量积的定义及其性质:掌握用直角坐标计算空间向量数量积的公式;掌握空间两点间距离公式.(6)理解直线的方向向量、平面的法向量、向量在平面内的射影等概念.(7)掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念.对于异面直线的距离,只要求会计算已给出公垂线或在坐标表示下的距离掌握直线和平面垂直的性质定理掌握两个平面平行、垂直的判定定理和性质定理.(8)了解多面体、凸多面体的概念。
了解正多面体的概念.(9)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图.(10)了解棱锥的概念,掌握正棱锥的性质。
会画正棱锥的直观图.(11)了解球的概念.掌握球的性质.掌握球的表面积、体积公式.(考生可在9(A )和9(B )中任选其一)立体几何知识要点一、 平面. 1. 经过不在同一条直线上的三点确定一个面.注:两两相交且不过同一点的四条直线必在同一平面内.2. 两个平面可将平面分成3或4部分.(①两个平面平行,②两个平面相交)3. 过三条互相平行的直线可以确定1或3个平面.(①三条直线在一个平面内平行,②三条直线不在一个平面内平行)[注]:三条直线可以确定三个平面,三条直线的公共点有0或1个.4. 三个平面最多可把空间分成 8 部分.(X 、Y 、Z 三个方向)二、 空间直线.1. 空间直线位置分三种:相交、平行、异面. 相交直线—共面有反且有一个公共点;平行直线—共面没有公共点;异面直线—不同在任一平面内[注]:①两条异面直线在同一平面内射影一定是相交的两条直线.(×)(可能两条直线平行,也可能是点和直线等)②直线在平面外,指的位置关系:平行或相交③若直线a 、b 异面,a 平行于平面α,b 与α的关系是相交、平行、在平面α内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线.(×)(射影不一定只有直线,也可以是其他图形)⑥在同一平面内的射影长相等,则斜线长相等.(×)(并非是从平面外一点..向这个平面所引的垂线段和斜线段)⑦b a ,是夹在两平行平面间的线段,若b a =,则b a ,的位置关系为相交或平行或异面.2. 异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)3. 平行公理:平行于同一条直线的两条直线互相平行.4. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(如下图).(二面角的取值范围[) 180,0∈θ) (直线与直线所成角(] 90,0∈θ)(斜线与平面成角() 90,0∈θ)(直线与平面所成角[] 90,0∈θ)12方向相同12方向不相同(向量与向量所成角])180,0[ ∈θ推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.5. 两异面直线的距离:公垂线的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. (1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面)三、 直线与平面平行、直线与平面垂直.1. 空间直线与平面位置分三种:相交、平行、在平面内.2. 直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)[注]:①直线a 与平面α内一条直线平行,则a ∥α. (×)(平面外一条直线) ②直线a 与平面α内一条直线相交,则a 与平面α相交. (×)(平面外一条直线) ③若直线a 与平面α平行,则α内必存在无数条直线与a 平行. (√)(不是任意一条直线,可利用平行的传递性证之)④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×)(可能在此平面内)⑤平行于同一直线的两个平面平行.(×)(两个平面可能相交)⑥平行于同一个平面的两直线平行.(×)(两直线可能相交或者异面)⑦直线l 与平面α、β所成角相等,则α∥β.(×)(α、β可能相交)3. 直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)4. 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直.● 若PA ⊥α,a ⊥AO ,得a ⊥PO (三垂线定理), 得不出α⊥PO . 因为a ⊥PO ,但PO 不垂直OA .● 三垂线定理的逆定理亦成立. 直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,那么这两条直线平行.[注]:①垂直于同一平面....的两个平面平行.(×)(可能相交,垂直于同一条直线.....的两个平面平行)②垂直于同一直线的两个平面平行.(√)(一条直线垂直于平行的一个平面,必垂直于另一个平面)③垂直于同一平面的两条直线平行.(√)5. ⑴垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.[注]:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]⑵射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上P O Aa四、 平面平行与平面垂直.1. 空间两个平面的位置关系:相交、平行.2. 平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,哪么这两个平面平行.(“线面平行,面面平行”)推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行.[注]:一平面间的任一直线平行于另一平面.3. 两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行,线线平行”)4. 两个平面垂直性质判定一:两个平面所成的二面角是直二面角,则两个平面垂直.两个平面垂直性质判定二:如果一个平面与一条直线垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直,面面垂直”)注:如果两个二面角的平面对应平面互相垂直,则两个二面角没有什么关系.5. 两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.推论:如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面. 证明:如图,找O 作OA 、OB 分别垂直于21,l l ,因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,. 6. 两异面直线任意两点间的距离公式:θcos 2222mn d n m l +++=(θ为锐角取加,θ为钝取减,综上,都取加则必有⎥⎦⎤ ⎝⎛∈2,0πθ) 7. ⑴最小角定理:21cos cos cos θθθ=(1θ为最小角,如图)⑵最小角定理的应用(∠PBN 为最小角) 简记为:成角比交线夹角一半大,且又比交线夹角补角一半长,一定有4条.成角比交线夹角一半大,又比交线夹角补角小,一定有2条.成角比交线夹角一半大,又与交线夹角相等,一定有3条或者2条.成角比交线夹角一半小,又与交线夹角一半小,一定有1条或者没有.五、 棱锥、棱柱. 1. 棱柱.⑴①直棱柱侧面积:Ch S =(C 为底面周长,h 是高)该公式是利用直棱柱的侧面展开图为矩形得出的.②斜棱住侧面积:l C S 1=(1C 是斜棱柱直截面周长,l 是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.⑵{四棱柱}⊃{平行六面体}⊃{直平行六面体}⊃{长方体}⊃{正四棱柱}⊃{正方体}. {直四棱柱}⋂{平行六面体}={直平行六面体}.四棱柱平行六面体直平行六面体长方体正四棱柱正方体底面是平行四边形侧棱垂直底面底面是矩形底面是正方形侧面与底面边长相等⑶棱柱具有的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;直棱柱的各个侧面都是矩形........;正棱柱的各个侧面都是全等的矩形...... ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形. ③过棱柱不相邻的两条侧棱的截面都是平行四边形.注:①棱柱有一个侧面和底面的一条边垂直可推测是直棱柱. (×)图1θθ1θ2图2P αβθM A B O(直棱柱不能保证底面是钜形可如图)②(直棱柱定义)棱柱有一条侧棱和底面垂直.⑷平行六面体:定理一:平行六面体的对角线交于一点.............,并且在交点处互相平分. [注]:四棱柱的对角线不一定相交于一点.定理二:长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和.推论一:长方体一条对角线与同一个顶点的三条棱所成的角为γβα,,,则1c o s c o s c o s 222=++γβα.推论二:长方体一条对角线与同一个顶点的三各侧面所成的角为γβα,,,则2c o s c o s c o s 222=++γβα.[注]:①有两个侧面是矩形的棱柱是直棱柱.(×)(斜四面体的两个平行的平面可以为矩形) ②各侧面都是正方形的棱柱一定是正棱柱.(×)(应是各侧面都是正方形的直.棱柱才行) ③对角面都是全等的矩形的直四棱柱一定是长方体.(×)(只能推出对角线相等,推不出底面为矩形) ④棱柱成为直棱柱的一个必要不充分条件是棱柱有一条侧棱与底面的两条边垂直. (两条边可能相交,可能不相交,若两条边相交,则应是充要条件)2. 棱锥:棱锥是一个面为多边形,其余各面是有一个公共顶点的三角形.[注]:①一个棱锥可以四各面都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以棱柱棱柱3V Sh V ==.⑴①正棱锥定义:底面是正多边形;顶点在底面的射影为底面的中心.[注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形)ii. 正四面体是各棱相等,而正三棱锥是底面为正△侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形. ②正棱锥的侧面积:'Ch 21S =(底面周长为C ,斜高为'h ) ③棱锥的侧面积与底面积的射影公式:αcos 底侧S S =(侧面与底面成的二面角为α) 附: 以知c ⊥l ,b a =⋅αcos ,α为二面角b l a --.则l a S ⋅=211①,b l S ⋅=212②,b a =⋅αcos ③ ⇒①②③得αcos 底侧S S =.注:S 为任意多边形的面积(可分别多个三角形的方法).⑵棱锥具有的性质:①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.⑶特殊棱锥的顶点在底面的射影位置:①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面多边形内心. ④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心.⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心.⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径;⑧每个四面体都有内切球,球心I 是四面体各个二面角的平分面的交点,到各面的距离等于半径.[注]:i. 各个侧面都是等腰三角形,且底面是正方形的棱锥是正四棱锥.(×)(各个侧面的等腰三角形不知是否全等)ii. 若一个三角锥,两条对角线互相垂直,则第三对角线必然垂直.简证:A B ⊥CD ,AC ⊥BD ⇒ BC ⊥AD. 令b AC c AD a AB ===,, 得c a c b AD BC c AD a b AB AC BC -=⋅⇒=-=-=,,已知()()0,0=-⋅=-⋅c a b b c a0=-⇒c b c a 则0=⋅AD BC . iii. 空间四边形OABC 且四边长相等,则顺次连结各边的中点的四边形一定是矩形. iv. 若是四边长与对角线分别相等,则顺次连结各边的中点的四边是一定是正方形. 简证:取AC 中点'O ,则⊥⇒⊥'⊥'AC AC O B AC o o ,平面=∠⇒⊥⇒'FGH BO AC B O O 90°易知EFGH 为平行四边形⇒EFGH 为长方形.若对角线等,则EFGH FG EF ⇒=为正方形.3. 球:⑴球的截面是一个圆面.①球的表面积公式:24R S π=. ②球的体积公式:334R V π=.⑵纬度、经度:①纬度:地球上一点P 的纬度是指经过P 点的球半径与赤道面所成的角的度数.②经度:地球上B A ,两点的经度差,是指分别经过这两点的经线与地轴所确定的二个半平面的二面角的度数,特别地,当经过点A 的经线是本初子午线时,这个二面角的度数就是B 点的经度.附:①圆柱体积:h r V 2π=(r 为半径,h 为高) ②圆锥体积:h r V 231π=(r 为半径,h 为高) ③锥形体积:Sh V 31=(S 为底面积,h 为高)4. ①内切球:当四面体为正四面体时,设边长为a ,a h 36=,243a S =底,243a S =侧得a a a R R a R a a a 46342334/424331433643222=⋅==⇒⋅⋅+⋅=⋅. 注:球内切于四面体:h S R S 313R S 31V 底底侧A CD B ⋅=⋅+⋅⋅⋅=- ②外接球:球外接于正四面体,可如图建立关系式.六. 空间向量.1. (1)共线向量:共线向量亦称平行向量,指空间向量的有向线段所在直线互相平行或重合. 注:①若a 与b 共线,b 与c 共线,则a 与c 共线.(×) [当0=b 时,不成立] ②向量c b a ,,共面即它们所在直线共面.(×) [可能异面] ③若a ∥b ,则存在小任一实数λ,使b a λ=.(×)[与0=b 不成立] ④若a 为非零向量,则00=⋅a .(√)[这里用到)0(≠b b λ之积仍为向量](2)共线向量定理:对空间任意两个向量)0(,≠b b a ,a ∥b 的充要条件是存在实数λ(具有唯一性),使b a λ=.(3)共面向量:若向量a 使之平行于平面α或a 在α内,则a 与α的关系是平行,记作a ∥α.(4)①共面向量定理:如果两个向量b a ,不共线,则向量P 与向量b a ,共面的充要条件是存在实数对x 、y 使b y a x P +=.②空间任一点...O .和不共线三点......A .、.B .、.C .,则)1(=++++=z y x OC z OB y OA x OP 是PABC 四点共面的充要条件.(简证:→+==++--=AC z AB y AP OC z OB y OA z y OP )1(P 、A 、B 、C 四点共面)注:①②是证明四点共面的常用方法.2. 空间向量基本定理:如果三个向量....c b a ,,不共面...,那么对空间任一向量P ,存在一个唯一的有序实数组x 、y 、z ,使c z b y a x p ++=.推论:设O 、A 、B 、C 是不共面的四点,则对空间任一点P , 都存在唯一的有序实数组x 、y 、z 使 OC z OB y OA x OP ++=(这里隐含x+y+z≠1).注:设四面体ABCD 的三条棱,,,,d AD c AC b AB ===其中Q 是△BCD 的重心,则向量)(31c b a AQ ++=用MQ AM AQ +=即证.3. (1)空间向量的坐标:空间直角坐标系的x 轴是横轴(对应为横坐标),y 轴是纵轴(对应为纵轴),z 轴是竖轴(对应为竖坐标). ①令a =(a 1,a 2,a 3),),,(321b b b b =,则),,(332211b a b a b a b a ±±±=+))(,,(321R a a a a ∈=λλλλλ332211b a b a b a b a ++=⋅ a ∥)(,,332211R b a b a b a b ∈===⇔λλλλ332211b a b a b a ==⇔ 0332211=++⇔⊥b a b a b a b a 222321a a a a a a ++=⋅=(用到常用的向量模与向量之间的转化:a a a a a a ⋅=⇒⋅=2) 232221232221332211||||,cos b b b a a a b a b a b a b a b a b a ++⋅++++=⋅⋅>=< ②空间两点的距离公式:212212212)()()(z z y y x x d -+-+-=.(2)法向量:若向量a 所在直线垂直于平面α,则称这个向量垂直于平面α,记作α⊥a ,如果α⊥a 那么向量a 叫做平面α的法向量.(3)用向量的常用方法:①利用法向量求点到面的距离定理:如图,设n 是平面α的法向量,AB 是平面α的一条射线,其中α∈A ,则点B 到平面α的距离为||||n n AB ⋅.②利用法向量求二面角的平面角定理:设21,n n 分别是二面角βα--l 中平面βα,的法向量,则21,n n 所成的角就是所求二面角的平面角或其补角大小(21,n n 方向相同,则为补角,21,n n 反方,则为其夹角).③证直线和平面平行定理:已知直线≠⊄a 平面α,α∈⋅∈⋅D C a B A ,,且CDE 三点不共线,则a ∥α的充要条件是存在有序实数对μλ⋅使CE CD AB μλ+=.(常设CE CD AB μλ+=求解μλ,若μλ,存在即证毕,若μλ,不存在,则直线AB 与平面相交). α▲n BC A αβ▲n 2n 1αC E D ABII. 竞赛知识要点一、四面体.1. 对照平面几何中的三角形,我们不难得到立体几何中的四面体的类似性质:①四面体的六条棱的垂直平分面交于一点,这一点叫做此四面体的外接球的球心;②四面体的四个面组成六个二面角的角平分面交于一点,这一点叫做此四面体的内接球的球心;③四面体的四个面的重心与相对顶点的连接交于一点,这一点叫做此四面体的重心,且重心将每条连线分为3︰1;④12个面角之和为720°,每个三面角中任两个之和大于另一个面角,且三个面角之和为180°.2. 直角四面体:有一个三面角的三个面角均为直角的四面体称为直角四面体,相当于平面几何的直角三角形. (在直角四面体中,记V 、l 、S 、R 、r 、h 分别表示其体积、六条棱长之和、表面积、外接球半径、内切球半径及侧面上的高),则有空间勾股定理:S 2△ABC +S 2△BCD +S 2△ABD =S 2△ACD.3. 等腰四面体:对棱都相等的四面体称为等腰四面体,好象平面几何中的等腰三角形.根据定义不难证明以长方体的一个顶点的三条面对角线的端点为顶点的四面体是等腰四面体,反之也可以将一个等腰四面体拼补成一个长方体.(在等腰四面体ABCD 中,记BC = AD =a ,AC = BD = b ,AB = CD = c ,体积为V ,外接球半径为R ,内接球半径为r ,高为h ),则有 ①等腰四面体的体积可表示为22231222222222c b a b a c a c b V -+⋅-+⋅-+=; ②等腰四面体的外接球半径可表示为22242c b a R ++=; ③等腰四面体的四条顶点和对面重心的连线段的长相等,且可表示为22232c b a m ++=; ④h = 4r.二、空间正余弦定理.空间正弦定理:sin ∠ABD/sin ∠A-BC-D=sin ∠ABC/sin ∠A-BD-C=sin ∠CBD/sin ∠C-BA-D 空间余弦定理:cos ∠ABD=cos ∠ABCcos ∠CBD+sin ∠ABCsin ∠CBDcos ∠A-BC-D立体几何知识要点一、知识提纲(一)空间的直线与平面⒈平面的基本性质 ⑴三个公理及公理三的三个推论和它们的用途. ⑵斜二测画法. ⒉空间两条直线的位置关系:相交直线、平行直线、异面直线.⑴公理四(平行线的传递性).等角定理.⑵异面直线的判定:判定定理、反证法.⑶异面直线所成的角:定义(求法)、范围.⒊直线和平面平行 直线和平面的位置关系、直线和平面平行的判定与性质. ⒋直线和平面垂直⑴直线和平面垂直:定义、判定定理.⑵三垂线定理及逆定理.5.平面和平面平行两个平面的位置关系、两个平面平行的判定与性质.6.平面和平面垂直互相垂直的平面及其判定定理、性质定理.(二)直线与平面的平行和垂直的证明思路(见附图)(三)夹角与距离7.直线和平面所成的角与二面角⑴平面的斜线和平面所成的角:三面角余弦公式、最小角定理、斜线和平 面所成的角、直线和平面所成的角.⑵二面角:①定义、范围、二面角的平面角、直二面角.②互相垂直的平面及其判定定理、性质定理.8.距离⑴点到平面的距离.⑵直线到与它平行平面的距离.⑶两个平行平面的距离:两个平行平面的公垂线、公垂线段.⑷异面直线的距离:异面直线的公垂线及其性质、公垂线段.(四)简单多面体与球9.棱柱与棱锥⑴多面体.⑵棱柱与它的性质:棱柱、直棱柱、正棱柱、棱柱的性质.⑶平行六面体与长方体:平行六面体、直平行六面体、长方体、正四棱柱、 正方体;平行六面体的性质、长方体的性质.⑷棱锥与它的性质:棱锥、正棱锥、棱锥的性质、正棱锥的性质.⑸直棱柱和正棱锥的直观图的画法.10.多面体欧拉定理的发现⑴简单多面体的欧拉公式.⑵正多面体.11.球⑴球和它的性质:球体、球面、球的大圆、小圆、球面距离.⑵球的体积公式和表面积公式.二、常用结论、方法和公式1.从一点O 出发的三条射线OA 、OB 、OC ,若∠AOB=∠AOC ,则点A 在平面∠BOC 上的射影在∠BOC 的平分线上;2. 已知:直二面角M -AB -N 中,AE ⊂ M ,BF ⊂ N,∠EAB=1θ,∠ABF=2θ,异面直线AE 与BF 所成的角为θ,则;cos cos cos 21θθθ=3.立平斜公式:如图,AB 和平面所成的角是1θ,AC 在平面内,BC 和AB 的射影BA 1成2θ,设∠ABC=3θ,则cos 1θcos 2θ=cos 3θ;4.异面直线所成角的求法:(1)平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;(2)补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;5.直线与平面所成的角斜线和平面所成的是一个直角三角形的锐角,它的三条边分别是平面的垂线段、斜线段及斜线段在平面上的射影。
