9-3 单摆和复摆
单摆复摆的区别

单摆和复摆最本质的区别应该是摆动所绕的轴不一样(单摆是绕点),从而导致了一系列的差异,详述如下:单摆simplependulum质点振动系统的一种,是最简单的摆。
绕一个悬点来回摆动的物体,都称为摆,但其周期一般和物体的形状、大小及密度的分布有关。
但若把尺寸很小的质块悬于一端固定的长度为l 且不能伸长的细绳上,把质块拉离平衡位置,使细绳和过悬点铅垂线所成角度小于5°,放手后质块往复振动,可视为质点的振动,其周期T只和l和当地的重力加速度g有关,即T=2π√(L/g),而和质块的质量、形状和振幅的大小都无关系,其运动状态可用简谐振动公式表示,称为单摆或数学摆。
如果振动的角度大于5°,则振动的周期将随振幅的增加而变大,就不成为单摆了。
如摆球的尺寸相当大,绳的质量不能忽略,就成为复摆(物理摆),周期就和摆球的尺寸有关了。
伽利略第一个发现摆的振动的等时性,并用实验求得单摆的周期随长度的二次方根而变动。
惠更斯制成了第一个摆钟。
单摆不仅是准确测定时间的仪器也可用来测量重力加速度的变化。
惠更斯的同时代人天文学家J.里希尔曾将摆钟从巴黎带到南美洲法属圭亚那,发现每天慢2.5分钟,经过校准,回巴黎时又快2.5分钟。
惠更斯就断定这是由于地球自转引起的重力减弱。
I.牛顿则用单摆证明物体的重量总是和质量成正比的。
直到20世纪中叶,摆依然是重力测量的主要仪器。
复摆compoundpendulum在重力作用下,能绕通过自身某固定水平轴摆动的刚体。
又称物理摆。
复摆的转轴与过刚体质心C并垂直于转轴的平面的交点O称为支点或悬挂点。
摆动过程中,复摆只受重力和转轴的反作用力,而重力矩起着回复力矩的作用。
设质量为m的刚体绕转轴的转动惯量为I,支点至质心的距离为s,则复摆微幅振动的周期T=2π√(I/mgs),式中g为重力加速度。
它相当于摆长l=I/ms的单摆作微幅振动的周期。
在OC的延长线上取O′点使OO′=l(l称等价摆长)则此点称为复摆的摆动中心。
简谐振动演示09

2 A2
2 A1 A2 cos( 2 1 )
o
2 2 2
60
0
A
x
A A A 5 10 (m)
平衡位置 x = 0
55
关于谐振动的合成的计算
教材
下册书 P38 9-5 9-28 9-30
56
(二)、 同一直线上两个不同频率谐振动的合成
当 2 1时 2 1 2 1 x1
9-6
9-7
基训:P93 例1 习题:A卷:一 1. 2. B卷:一 1.
17
9-2、旋转矢量
1.设一矢量 OM 逆时针方向 匀速转动,角速为
OM A
y
y
M
A
t 0
2. t 时刻矢端 M 点的位
o
t 0 x
置(坐标) x A cos(t 0 ) y A sin( t 0 )
由此可见: 旋转矢量的端点在坐标轴上投影点的运 动为谐振动 旋转矢量旋转一周 投影点全振动一次
19
X
例1
一谐振动的相位为
3 3 3 画旋转矢量,指出其投影点 的位置
, 2
,
60
x
o
60
例2
质点在平衡位置向 x 轴正向运动,
画对应的旋矢,指出其相位是多 少? 3 ( )
t=0时与x轴
正方向夹角 t时刻与x轴
x
正方向夹角
t=0时 刻 与t时 夹角
相位 t +
平衡位置 x=0 t
简谐振动的解题方法:
1. 解析法 2. 图示法
x A cos(t )
3。旋转矢量法(几何法) x x
《单摆和复摆》课件

如何设计一个实验来验证单摆 和复摆的周期公式?
THANKS
感谢观看
复摆的回复力由重力和支点的 支持力合成,方向始终指向平 衡位置。
单摆和复摆的能量转换
单摆和复摆在运动过程中,动能 和势能之间相互转换。
当摆角较小时,单摆的运动近似 简谐振动,能量转换呈现周期性
变化。
复摆在运动过程中,由于支点摩 擦和空气阻力等因素,能量会有
所损失,导致运动周期变长。
03
单摆和复摆的应用
02
4. 启动计时器,记录复摆完成一 个周期的时间。
实验结果和实验分析
实验结果
通过实验测量得到单摆和复摆的运动周期,并记录在表格中。
实验分析
根据测量结果,分析单摆和复摆的运动特性,比较两者之间的差异。通过计算单摆的振动周期公式 T=2π√(L/g) ,其中L为单摆的长度,g为重力加速度,验证理论公式是否与实验结果相符。对于复摆,分析其转动惯量、质量 等因素对周期的影响。
钟表和计时器中的应用
钟表的核心机制
复摆在高级钟表中的应用
单摆被用作钟表的核心计时机制。其 规律的周期性运动被转换成时间单位 ,如秒、分、小时。
在高级机械钟表中,复摆常用于更精 确地调节和平衡钟表的运行。
精确度与稳定性
由于单摆的简单运动模式和自然频率 的稳定性,它为钟表提供了高精度的 时间基准。
振动隔离和减震中的应用
实验步骤和实验操作
3. 开始计时,记录单摆和复摆的运动周期。 4. 重复实验多次,求平均值。
5. 分析实验数据,得出结论。
实验步骤和实验操作
实验操作 1. 调整单摆的长度,使小球能够自由摆动。
2. 启动计时器,记录单摆完成一个周期的时间。
单摆与复摆的区别

2014-11-11
单摆测G和复摆测G哪个更精确
2014-10-07
单摆复摆问题
2014-12-03
复摆跟单摆有什么区别
2014-09-24
蛇蝎美人°RB1
2014-12-11
为您推荐:
其他类似问题
单摆的周期很短,怎样操作才能比较准确的测出这个单摆的周期
2014-11-08
凸轮式颚式破碎机与复摆式颚式破碎机的区别
优质解答
单摆是质点振动系统的一种,是最简单的摆.绕一个悬点来回摆动的物体,都称为摆,但其周期一般和物体的形状、大小及密度的分布有关.但若把尺寸很小的质块悬于一端固定的长度为l且不能伸长的细绳上,把质块拉离平衡位置,使细绳和过悬点铅垂线所成角度小于5°,放手后质块往复振动,可视为质点的振动,其周期T只和l和当地的重力加速度g有关,即T=2π√(L/g),而和质块的质量、形状和振幅的大小都无关系,其运动状态可用简谐振动公式表示,称为单摆或数学摆.如果振动的角度大于5°,则振动的周期将随振幅的增加而变大,就不成为单摆了.如摆球的尺寸相当大,绳的质量不能忽略,就成为复摆(物理摆),周期就和摆球的尺寸有关了.复摆是在重力作用下,能绕通过自身某固定水平轴摆动的刚体.又称物理摆.复摆的转轴与过刚体质心C并垂直于转轴的平面的交点O称为支点或悬挂点.摆动过程中,复摆只受重力和转轴的反作用力,而重力矩起着回复力矩的作用.
《单摆和复摆》课件

定义:复摆是一类特殊的摆动装置,由刚体绕一固定点在平面内或空间内作周期性摆动形成
原理:复摆的摆动可看作是两个或多个单摆的组合运动,通过调整各单摆的参数和相对位置,实现特定的运动规律和特性
复摆的周期公式
公式推导:根据单摆周期公式推导复摆周期公式
解决方法:减小空气阻力和机械摩擦,采用高精度材料制作摆轴等。
单摆和复摆的实验研究
单摆实验的设计和操作
实验目的:研究单摆的周期与摆长、摆角的关系
实验器材:支架、细线和重物
实验步骤:将细线悬挂在支架上,固定好重物并使其自然下垂;释放重物,使其开始摆动;使用秒表记录摆动的周期
实验数据记录:记录不同摆长和摆角下单摆的周期,分析数据并得出结论
环保领域:用于测量风速、风向等。
总结与展望
单摆和复摆的重要性和应用前景
重要性和应用前景:单摆和复摆在物理学和工程学中具有重要地位,其应用前景广泛,包括测量、控制、仿真等领域。
未来研究方向:随着科技的发展,单摆和复摆的研究方向将更加深入,未来将会有更多的应用场景和新的研究领域。
挑战与机遇:虽然单摆和复摆的研究面临一些挑战,但也存在许多机遇,需要更多的研究和探索。
单击此处输入你的项正文,请尽量言简意阐述观点。
单摆的分类
单击此处输入你的项正文,请尽量言简意阐述观点。
单击此处输入你的项正文,请尽量言简意阐述观点。
复摆的定义和分类
单摆和复摆的应用场景
物理实验:单摆和复摆是物理学中重要的实验装置,用于研究力学、振动和波动等现象。
精密测量:单摆和复摆可以用于测量重力加速度、时间等精密参数,具有高精度和高稳定性。
影响因素:摆长、质量、重力加速度等对复摆周期的影响
简谐运动
准弹性力
系统本身决定的常数
动力学方程:
在水平方向上:
弹簧振子
F kx
由牛顿第二定律
d 2x kx m 2 dt
k 令 2 m
则有
d x 2 x 0 2 dt
二阶齐次常 微分方程
2
一般写成: 或:
x A sin t x A cost
振动和波动
共同特征:运动在时间、空间上的周期性
振动: 任何物理量在某一定值附近随时间周期性变化
波动: 振动在空间的传播
振动
机械振动:物体在某一位置附近作周期往复运动 电磁振荡:电场、磁场随时间作周期性变化
简谐振动(简谐运动):最简单、最基本的振动
9-1简谐振动
一、简谐振动的基本特征
弹簧振子
轻弹簧 k + 刚体 m (平动~质点) 集中弹性 集中惯性
解得
2 2 v v 2 A x0 02 x 2 2
的状态如何就决定了系 统未来的振 但计算A的大小时不一定非用初 始 条件,只要同时告诉某 时刻的x与
幅A的大小。所以A由初始条件决定。
相应的v,又知道,就可以求出A。
3、初相位
初相:
由 t = 0时
x0 A cos v0 A sin
(1)、相位 t 是确定振动状态的物理量
(2) ( t )与状态参量 x,v有一一对应的关系
x A cos(t ); v A sin(t )
当 t 例:
3
时:
A x , 2
A x , 2
3 v A 2
质点在 x A 2 处以速率 v向 x方向运动
单摆与复摆

单摆与复摆读书报告一、知识点简介绕一个悬点来回摆动的物体,都称为摆,其周期一般和物体的形状、大小及密度的分布有关。
但若把尺寸很小的质块悬于一端固定的长度为l且不能伸长的细绳上,把质块拉离平衡位置,使细绳和过悬点铅垂线所成角度小于︒5,放手后质块往复振动,可视为质点的振动,其周期T只和绳长l和当地的重力加速度g 有关,而与质块的质量、形状和振幅的大小都无关。
其运动状态可用简谐振动公式表示,称为单摆或数学摆。
如果振动的角度大于︒5,则摆不再做简谐振动,振动的周期将随振幅的增加而变大。
复摆是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系,又称物理摆。
复摆的周期与摆球的尺寸有关。
二、该知识点提出的背景摆与其性质是由伽利略发现并进行初步研究的。
在意大利的比萨城里,17岁的大学生伽利略在教堂时无意中观察到悬在天花板上的挂灯摆动逐渐平息的过程中,每次摆动所用的时间并不改变。
这一发现引起了伽利略的思考:是不是其他的摆动也跟吊灯相似,摆动一次的时间跟摆动幅度没关系?吊灯的轻重是否会影响摆动一次的时间?伽利略通过脉搏计时,数着吊灯的摆动次数。
吊灯的摆动幅度、摆动速度不同,但两次测量的时间是相同的。
回家后,他继续研究,发现并提出了单摆的等时性,即小角度振动的单摆的周期与质块的质量、形状和振幅无关,并通过实验求得单摆的周期随摆线长度的二次方根而变动。
在此基础上,荷兰数学家、物理学家惠更斯经过长期的研究,发现了单摆的周期规律,确定了单摆做简谐运动的周期公式,此公式为单摆做简谐运动时的周期T与摆长l、重力加速度g之间的定量关系。
如摆球的尺寸相当大,绳的质量不能忽略,在重力作用下,摆球为绕通过自身某固定水平轴摆动,视为刚体运动,当摆角不同时其运动方程的解也不同。
三、建立该知识点所经历的困难首先,伽利略实验所用的大小不同的木球、铁球、石块、铜球,体积都较大,并不能很好地视其为质点,且绳子与小球连接起来也有困难,对摆线的长度也有误差影响。
9-3单摆和复摆
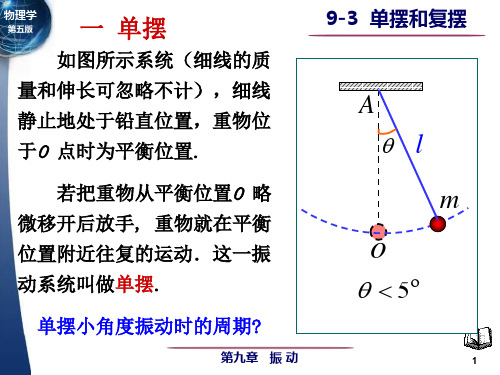
dt
θ l
v FT m
o
J = ml
振 动
θ = θ m cos( ω t + ϕ )
T = 2π l g
v P
2
2
第九章
物理学
第五版
二
复摆 (θ < 5 )
o
9-3
单摆和复摆 转动正向
振动时的周期? 振动时的周期
v v v M =l ×F M = −mgl sin θ
d 2θ = Jβ = J 2 dt
第九章 振 动
A
θ
l
m
o
θ <5
o
1
物理学
第五版
动力学分析: 动力学分析:
9-3
单摆和复摆
转动 正向
θ < 5 时 , sinθ ≈ θ M = − mgl sin θ ≈ − mglθ d 2θ − mglθ = J 2
o
A
dθ g g 2 = − θ 令ω = 2 dt l l d 2θ 2 = −ω θ 2 dt
F = − kx 平衡位置 x = 0
d x 2 = −ω x 2 dt
2
x = A cos(ωt + ϕ )
单摆 弹簧振子 ω = k m 由振动系统本身性质决定) (由振动系统本身性质决定)
第九章 振 动
a = −ω x
2
v = − A ω sin( ω t + ϕ )
ω= g l
ω = mgl
π 2
Q0 I 0
O
﹡ π
2π
﹡
(ωt +ϕ)
π q = Q0 cos(ωt +ϕ) i = I0 cos(ωt +ϕ + ) 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、对单摆做受力分析:总力矩=惯性力力矩+重力矩
M mal cos( 0 ) mgl sin( 0 )
M
J
ml 2
d 2 dt 2
mal
cos(
0 ) mgl
sin(
0 )
4、数学分析: sin( 0) sin cos0 cos sin0
弹簧振子 k m
单摆
g l
复摆
mgl
J
第九章 振动
2 20
2
22
F k k1 k2 x k1k2 x
2 k1 k2 2
k1 k2
系统的振动频率:
即系统仍然做简谐运动,两个弹簧串联
后的等效劲度系数k k1k2 k k
v
1 T
1
2
k1
m 2
1
2
1 k1k2 m k1 k2
9-3 单摆和复摆(Simple Pendulum and Compound Pendulum)
正 向
FT m
r O
Fg sin
Fg cos
Fg
第九章 振动
9-3 单摆和复摆(Simple Pendulum and Compound Pendulum)
5 0.0873rad, sin5 0.0875
M J
转
A
动
正
向
v FT m
O
r J ml 2 Fg
第九章 振动
9-3 单摆和复摆( Simple Pendulum and Compound Pendulum)
g
l
转
A
动
l
正 向
FT m
O
J
ml 2
P
第九章 振动
挂灯与摆钟
9-3-1 (受力和力矩两种分析方法) (1) 摆长为2m的单摆频率为多少? (2) 假定单摆的振幅很小,将它放在以加速度2.0 m/ s2
复摆(物理摆)
一个质量分布复杂,形状任意的实 际物体,摆动是否也进行简谐运动? 如果是,它的周期又是多少呢?
1、0点为支点,C点为复摆的质心, l 为支点与质心的距离
2、O点为平衡位置,定义正方向
3、 受力分析得运动方程
转动正向 O
l
*C
r Fg
(C点为质心)
第九章 振动
9-3 单摆和复摆( Simple Pendulum and Compound Pendulum)
9-3 单摆和复摆( Simple Pendulum and Compound Pendulum)
单摆
1、O点为平衡位置:因为摆在 不摆动是就停止在该处。
2、定义正方向
3、力矩关系式:
r M
r rF
(通过转轴的力分量不影响转动)
M l Fg sin( ) l Fg sin
转
A
动
l v
向上运动的电梯中,其频率为多少?
(1) v 1 1 g 0.35Hz
T 2 l
(2) 平衡位置 =0, 将单摆离开平衡位置x处 0
T cos ma mg
T
sin
m
d2x dt 2
= 1
T ma mg
T
x l
m
d2x dt 2
弹簧一端固定,则弹簧振子的频率为:
v= 1 k
2 m
设原来弹簧系数为k,弹簧减掉一半后,劲度系数为:
设变为k : 1
mg k
mg mg
k1 k1
kk 1
k
k1
11 k1Fra bibliotek2 k1
k1 2k 增加为原来的两倍
9-3-3两个轻弹簧的劲度系数为k1和k2 ,则物体在光滑斜面上振动。 (1)证明其运动仍是简谐运动。 (2)求系统的振动频率。
转动正向
O
l
*C
(C点为质心)
第九章 振动
9-3 单摆和复摆(Simple Pendulum and Compound Pendulum)
如果复摆的支点通过质心,它就不会摆
动,因为 l 0, T,意味着这样一
个摆永远无法完成一次摆动。
转动正向
O
l
*C
角谐振动
(C点为质心)
第九章 振动
9-3 单摆和复摆(Simple Pendulum and Compound Pendulum)
区别:单摆是细线的长度, 复摆是支点到质心的距离。
第九章 振动
物理攻略
1.确定平衡位置,建立坐标。
2.偏离一点平衡位置, 做受力分析
3.利用牛顿定律列出运动方程。
4.通过判断加速度是否与位移成 正比且方向相反来确定是否是简 谐运动,能否得到简谐振动微分方 程。 5.是简谐运动,确定角频率。
9-3-2 如图所示,一质量为m、直径为D的塑料圆柱体一部分浸入密度为
v 1 ag
2 l
d2x a g x 0 dt 2 l
=0.386Hz
思考题:若火车沿水平轨道以加速度a直线运动, 则车厢中摆长为l 的单摆周期为:
g2 a2
l
1、在非惯性参考系中进行受力分析,设平衡位置单摆与垂直 方向夹角0,绳子拉力T。则: T cos0 mg; T sin0 ma
的液体中,另一部分浮在液面上。如果用手轻轻向下按动圆柱体,放手后 圆柱体将上下振动。试证明该振动为简谐运动,并求振动周期(圆柱体表面 与液体的摩擦力忽略不计)。
1、以圆柱体平衡时为坐标原点,向下建立Ox轴。
平衡时所受合力:F gV mg 0
O
2、离开平衡位置移动一微小距离x, 受合力:
对于平衡状态,设物体质量为m,有: 当离开平衡位置x处,有
mg sin
kx 2 20
k2 x20 k1x10
k (x x ) k (x x )
22
20
11
10
k x kx
22
11
物体在非平衡位置上所受合力为: 物体在非平衡位置上所受合力为:
F mg sin k (x x ) k x
cos( 0) cos cos0 sin sin0
sin ;cos 1;sin0
a a2
g2
; cos0
g a2 g2
5、运动方程:
d 2
a2 g2
0
dt 2
l
6、单摆周期: T 2
l
g2 a2
a ma 0
a
0
9-3 单摆和复摆(Simple Pendulum and Compound Pendulum)
所受合力:F mg [V ( D)2 x] g
2
F g( D)2 x
2
kx
x
T 2 m
k
T 4 m D g
9-3-3 两个轻弹簧的劲度系数为k1和k2,则物体在光滑斜面上振动。 (1)证明其运动仍是简谐运动。 (2)求系统的振动频率。
k1 k2
弹簧振子放在倾角为的光滑斜面上,
