2.数制和编码(第1章)
数字电子技术 (佘新平 著) 华中科技大学出版社 课后答案

第一章数制与编码1.1 自测练习1.1.1、模拟量数字量1.1.2、(b)1.1.3、(c)1.1.4、(a)是数字量,(b)(c)(d)是模拟量1.2 自测练习1.2.1. 21.2.2. 比特bit1.2.3. 101.2.4. 二进制1.2.5. 十进制1.2.6. (a)1.2.7. (b)1.2.8. (c)1.2.9. (b)1.2.10. (b)1.2.11. (b)1.2.12. (a)1.2.13. (c)1.2.14. (c)1.2.15. (c)1.2.16. 1001001 1.2.17. 111.2.18. 110010 1.2.19. 1101 1.2.20. 8进制1.2.21. (a)1.2.22. 0,1,2,3,4,5,6,71.2.23. 十六进制1.2.24. 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F 1.2.25. (b)1.3 自测练习1.3.1. 1221.3.2. 675.521.3.3. 011111110.011.3.4. 521.3.5. 1BD.A81.3.6. 1110101111.11101.3.7. 38551.3.8. 28.3751.3.9. 100010.111.3.10. 135.6251.3.11. 570.11.3.12. 120.51.3.13. 2659.A1.4 自测练习1.4.1. BCD Binary coded decimal 二—十进制码1.4.2. (a)1.4.3. (b)1.4.4. 8421BCD码,4221BCD码,5421BCD 1.4.5. (a)1.4.6. 011001111001.10001.4.7. 111111101.4.8. 101010001.4.9. 111111011.4.10. 61.051.4.11. 01011001.01110101 1.4.12. 余3码1.4.13. XS31.4.14. XS31.4.15. 1000.10111.4.16. 1001100000111.4.17. 521.4.18. 110101.4.19. 0101111.4.20. (b)1.4.21. ASCII1.4.22. (a)1.4.23. ASCII American Standard Code for Information Interchange美国信息交换标准码EBCDIC Extended Binary Coded Decimal Interchange Code 扩展二-十进制交换吗1.4.24. 10010111.4.25. ASCII1.4.26. (b)1.4.27. (b)1.4.28. 110111011.4.29. -1111.4.30. +231.4.31. -231.4.32. -861.5 自测练习1.5.1 略1.5.2 110111011.5.3 010001011.5.4 11100110 补码形式1.5.5 011111011.5.6 10001000 补码形式1.5.7 11100010 补码形式习题1.1 (a)(d)是数字量,(b)(c)是模拟量,用数字表时(e)是数字量,用模拟表时(e)是模拟量1.2 (a)7, (b)31, (c)127, (d)511, (e)40951.3 (a),(b),(c)(d)522104108×+×+320410910×+×+×26108108×+×+321102105100×+×+×+21+1.4 (a), (b), (c)(d)3212121×+×+984+12+12+×××4311212121×+×+×+212×64212+12+12+12+1××××1212+×2220110327.15310210710110510..=×+×+×+×+×3210-1-221011.0112+02+12+12+02+12=××××××210-18437.448+38+78+48=××××10-1-2163A.1C316+A16+116+C16=××××,,,1.6 (a)11110, (b)100110,(c)110010, (d)10111.7 (a)1001010110000, (b)10010111111.8 110102 = 2610, 1011.0112 = 11.37510,57.6438 = 71.81835937510,76.EB16 = 118. 91796875101.9 1101010010012 = 65118 = D4916,0.100112 = 0.468 = 0.9816,1011111.011012 = 137.328 = 5F.68161.10 168 = 1410,1728 = 12210,61.538 = 49.671875,126.748 = 86.9375101.11 2A16 = 4210 = 1010102 = 528,B2F16 = 286310 = 1011001011112 = 54578,D3.E16= 211.87510 = 11010011.11102 = 323.78,1C3.F916 = 451.9726562510 =111000011.111110012 = 703.76281.12 (a)E, (b)2E, (c)1B3, (d)3491.13 (a)22, (b)110, (c)1053, (d)20631.14 (a)4094, (b)1386, (c)492821.15 (a)23, (b)440, (c)27771.16 198610 = 111110000102 = 00011001100001108421BCD,67.31110 = 1000011.010012 =01100111.0011000100018421BCD, 1.183410 = 1.0010112 = 0001.00011000001101008421BCD ,0.904710 = 0.1110012 = 0000.10010000010001118421BCD1.17 1310 = 000100118421BCD = 01000110XS3 = 1011Gray, 6.2510 = 0110.001001018421BCD =1001.01011000 XS3 = 0101.01Gray,0.12510 = 0000.0001001001018421BCD =0.010*********XS3 = 0.001 Gray1.18 101102 = 11101 Gray,0101102 = 011101 Gray1.19 110110112 = 0010000110018421BCD,45610 = 0100010101108421BCD,1748=0010011101008421BCD,2DA16 = 0111001100008421BCD,101100112421BCD = 010*********BCD,11000011XS3 = 100100008421BCD1.20 0.0000原= 0.0000反= 0.0000补,0.1001原= 0.1001反= 0.1001补,11001原= 10110反= 10111补1.21 010100原= 010100补,101011原= 110101补,110010原= 101110补,100001原= 111111补1.22 1310 = 00001101补,11010 = 01101110补,-2510 = 11100111补,-90 =10100110补1.23 01110000补= 11210,00011111补= 3110,11011001补= -3910,11001000补= -56101.24 1000011 1000001 1010101 1010100 1001001 1001111 1001110 0100001 0100000 1001000 1101001 1100111 1101000 0100000 1010110 1101111 1101100 1110100 1100001 1100111 11001011.25 0100010 1011000 0100000 0111101 0100000 0110010 0110101 0101111 1011001 01000101.26 BEN SMITH1.27 00000110 100001101.28 01110110 10001110第二章逻辑门2.1 自测练习2.1.1. (b)2.1.2. 162.1.3. 32, 6 2.1.4. 与2.1.5. (d)2.1.6. 162.1.7. 32, 6 2.1.8. 或2.1.9. 非2.1.10. 12.2 自测练习2.2.1. FAB=.2.2.2. (b)2.2.3. 高2.2.4. 322.2.5. 16,52.2.6. 12.2.7. 串联2.2.8. (d)2.2.9. 不相同2.2.10. 高2.2.11. 相同2.2.12. (a)2.2.13. (c)2.2.14. 奇2.3 自测练习2.3.1. OC,上拉电阻2.3.2. 0,1,高阻2.3.3. (b)2.3.4. (c)2.3.5. ,FAB=. 高阻2.3.6. 不能2.4 自测练习2.4.1. TTL,CMOS2.4.2. Transisitor Transistor Logic2.4.3. Complementary Metal Oxide Semicoductor2.4.4. 高级肖特基TTL,低功耗和高级低功耗肖特基TTL 2.4.5. 高,强,小2.4.6. (c)2.4.7. (b)2.4.8. (c)2.4.9. 大2.4.10. 强2.4.11. (a)2.4.12. (a)2.4.13. (b)2.4.14. 高级肖特基TTL2.4.15. (c)习题2.1 与,或,与2.2 与门,或门,与门2.3 (a)F=A+B, F=AB (b)F=A+B+C, F=ABC (c)F=A+B+C+D, F=ABCD 2.4 (a)0 (b)1 (c)0 (d)02.5 (a)0 (b)0 (c)1 (d)02.6 (a)1 (b)1 (c)1 (d)12.7 (a)4 (b)8 (c)16 (d)322.8 (a)3 (b)4 (c)5 (d)6ABCF0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 11111112.9 (a)(b)ABCDF1110 1 1 1 0 1 0 0 00 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 0 0 0 0 1 00 1 1 1 0 1 0 1 1 0 1 1 0 1 1 0 0 1 1 1 0 111111112.10 YABAC=+ 2.11ABCY0 0 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 11111112.122.13F1 = A(B+C), F2=A+BCA B C F1 F2 0 0 0 0 0 0 0 1 0 0 0 1 0 00 0 1 1 0 1 1 0 1 1 1 1 0 0 0 1 1 1 0 1 1 111112.142.15 (a)0 (b)1 (c)1 (d)02.16 (a)1 (b)0 (c)0 (d)12.17 (a)0 (b)02.182.19 CDEF.2.20 CY ABDF.2.21 102.22 402.23 当TTL反相器的输出为3V,输出是高电平,红灯亮。
数字电路_2数制和编码

? 区位码——GB 2312的所有字符分布在一个94行×94列的二维平面内,行号称为区号,列号称 为位号。区号和位号的组合就可以作为汉字字符的编码,称为汉字的区位码。
加法
减法
十六进制
? 由于二进制数在使用时位数太长,不容易记忆,所以又推出了十六进制数。 ? 十六进制数有两个基本特点:
? 它由十六个字符 0~9以及A,B,C,D,E,F组成(它们分别表示十进制数 10~15);
? 十六进制数运算规律是逢十六进一,即基 R=16=2 4,通常在表示时用尾部标志 H或下标 16以示区别。 例如:十六进制数 4AC8可写成( 4AC8 )16,或写成 4AC8H 。
B表示。 例如:二进制数 10110011 可以写成( 10110011 )2,或写成 10110011B ? 对于十进制数可以不加注基数;
十进制
(D) 0 1 2 3 4
56
7
8
9 10
二进制 (B) 0 1 10 11 100 101 110 111 1000 1001 1010
计算机采用二进制数
(101.11)B= 1×22 +0×21+1×20+1×2-1+1×2-2 =(5.75)D
各数位的权是2的幂
十进制数 →二进制数 将整数部分和小数部分分别进行转换。
整数部分 ---除2取余,逆序排列 ; 合并
小数部分 ---乘2取整,顺序排列。
? 十进制数 44.375 转换成二进制等于多少?
(44.375)D=(?)B
十六进制数 →二进制数
? 十六进制数转换为二进制数时正好与上面所述相反,只要将每位的十六进制数对应的 4 位二进制写出来就行了。
数制与编码专题教案

数制与编码专题教案第一章:数制的基本概念1.1 教学目标让学生了解数制的概念和分类让学生掌握不同数制之间的转换方法让学生理解数制在计算机科学中的应用1.2 教学内容数制的定义和分类不同数制之间的转换方法(十进制与二进制、八进制、十六进制的转换)数制在计算机科学中的应用实例(二进制与计算机硬件)1.3 教学方法采用讲授法,讲解数制的定义和分类,以及不同数制之间的转换方法通过举例和练习,让学生掌握数制的转换技巧利用多媒体演示数制在计算机硬件中的应用实例1.4 教学评估课堂练习:让学生完成不同数制之间的转换练习题课后作业:布置相关的数制转换练习题,巩固所学知识第二章:二进制与计算机硬件2.1 教学目标让学生了解二进制的概念和特点让学生掌握二进制在计算机硬件中的应用让学生了解不同进制之间的优缺点比较2.2 教学内容二进制的概念和特点二进制在计算机硬件中的应用实例(如CPU的寄存器、内存地址等)不同进制之间的优缺点比较(如十进制、八进制、十六进制)2.3 教学方法采用讲授法,讲解二进制的概念和特点,以及其在计算机硬件中的应用通过举例和练习,让学生了解不同进制之间的优缺点比较利用多媒体演示二进制在计算机硬件中的应用实例2.4 教学评估课堂练习:让学生完成二进制与不同进制之间的转换练习题课后作业:布置相关的进制比较练习题,巩固所学知识第三章:字符编码3.1 教学目标让学生了解字符编码的概念和分类让学生掌握常见字符编码方案(如ASCII、Uni)让学生了解字符编码在计算机中的应用3.2 教学内容字符编码的概念和分类常见字符编码方案(ASCII、Uni)的介绍和使用方法字符编码在计算机中的应用实例(如文本文件的编码、网页内容的编码)3.3 教学方法采用讲授法,讲解字符编码的概念和分类,以及常见字符编码方案的使用方法通过举例和练习,让学生了解字符编码在计算机中的应用实例利用多媒体演示字符编码的转换过程3.4 教学评估课堂练习:让学生完成字符编码的转换练习题课后作业:布置相关的字符编码应用实例练习题,巩固所学知识第四章:数据压缩与编码4.1 教学目标让学生了解数据压缩与编码的概念和分类让学生掌握常见数据压缩编码算法(如Huffman编码、LZ77)让学生了解数据压缩与编码在计算机中的应用4.2 教学内容数据压缩与编码的概念和分类常见数据压缩编码算法(Huffman编码、LZ77)的介绍和使用方法数据压缩与编码在计算机中的应用实例(如文件压缩、图像压缩)4.3 教学方法采用讲授法,讲解数据压缩与编码的概念和分类,以及常见数据压缩编码算法的使用方法通过举例和练习,让学生了解数据压缩与编码在计算机中的应用实例利用多媒体演示数据压缩与编码的转换过程4.4 教学评估课堂练习:让学生完成数据压缩与编码的转换练习题课后作业:布置相关的数据压缩与编码应用实例练习题,巩固所学知识第五章:编码实践与应用5.1 教学目标让学生了解编码实践的意义和目的让学生掌握编码实践的方法和技巧让学生了解编码实践在实际应用中的重要性5.2 教学内容编码实践的意义和目的编码实践的方法和技巧(如编码规范、编码优化)编码实践在实际应用中的实例(如软件开发、数据通信)5.3 教学方法采用讲授法,讲解编码实践的意义和目的,以及编码实践的方法和技巧通过举例和练习,让学生了解编码实践在实际应用中的重要性利用多媒体演示编码实践的实例和应用5.4 教学评估第六章:编码错误与校验6.1 教学目标让学生了解编码过程中可能出现的错误类型让学生掌握常见校验码的原理和应用让学生理解校验码在保证数据传输正确性中的作用6.2 教学内容编码过程中可能出现的错误类型(比特错误、位错误、字符错误等)常见校验码(奇偶校验、循环冗余校验CRC、校验和)的原理和方法校验码在数据传输和存储中的应用实例6.3 教学方法采用讲授法,讲解编码过程中可能出现的错误类型和校验码的原理通过示例和练习,让学生学会和使用校验码利用多媒体演示校验码在数据传输中的应用过程6.4 教学评估课堂练习:让学生完成校验码的和使用练习题课后作业:布置相关的校验码应用实例练习题,巩固所学知识第七章:生物特征编码7.1 教学目标让学生了解生物特征编码的基本概念让学生掌握常见生物特征编码技术(如指纹识别、面部识别)让学生理解生物特征编码在身份验证和安防中的应用7.2 教学内容生物特征编码的基本概念和原理常见生物特征编码技术(指纹识别、面部识别、虹膜识别等)的工作原理和应用生物特征编码在身份验证和安防领域的应用实例7.3 教学方法采用讲授法,讲解生物特征编码的基本概念和常见编码技术通过示例和练习,让学生了解生物特征编码技术的工作原理和应用利用多媒体演示生物特征编码在身份验证和安防中的应用过程7.4 教学评估课堂练习:让学生完成生物特征编码技术的工作原理和应用练习题课后作业:布置相关的生物特征编码应用实例练习题,巩固所学知识第八章:编码与隐私保护8.1 教学目标让学生了解编码与隐私保护的关系让学生掌握常见编码技术在隐私保护中的应用(如加密算法)让学生理解编码技术在保障信息安全中的作用8.2 教学内容编码与隐私保护的关系和重要性常见编码技术(对称加密、非对称加密、哈希算法等)在隐私保护中的应用编码技术在信息安全领域的应用实例8.3 教学方法采用讲授法,讲解编码与隐私保护的关系和编码技术在隐私保护中的应用通过示例和练习,让学生学会使用编码技术来保护隐私利用多媒体演示编码技术在信息安全中的应用过程8.4 教学评估课堂练习:让学生完成编码技术在隐私保护和信息安全应用的练习题课后作业:布置相关的编码技术应用实例练习题,巩固所学知识第九章:编码发展趋势与未来9.1 教学目标让学生了解编码领域的发展趋势让学生掌握前沿编码技术(如辅助编码、量子编码)让学生理解编码技术在未来的发展和应用前景9.2 教学内容编码领域的发展趋势和未来挑战前沿编码技术(辅助编码、量子编码、边缘计算编码等)的原理和应用编码技术在未来的发展和应用前景的实例9.3 教学方法采用讲授法,讲解编码领域的发展趋势和前沿编码技术通过示例和讨论,让学生了解编码技术在未来的发展和应用前景利用多媒体演示前沿编码技术的应用过程和未来发展趋势9.4 教学评估课堂讨论:让学生参与讨论编码领域的发展趋势和未来前景课后作业:布置相关的编码技术发展趋势研究作业,巩固所学知识第十章:综合实践与案例分析10.1 教学目标让学生综合运用所学编码知识和技能让学生掌握实际项目中编码实践的方法和技巧让学生理解编码技术在解决实际问题中的作用10.2 教学内容综合实践的目的和要求实际项目中编码实践的方法和技巧编码技术在解决实际问题中的案例分析10.3 教学方法采用案例分析法,讲解实际项目中编码技术的应用和方法通过小组讨论和实际项目模拟,让学生综合运用所学知识进行编码实践利用多媒体演示实际项目中编码技术的应用过程10.4 教学评估小组项目:让学生分组完成重点和难点解析重点环节一:不同数制之间的转换方法需要重点关注的原因:数制转换是计算机科学中的基础,对于后续学习计算机硬件、字符编码等章节有重要影响。
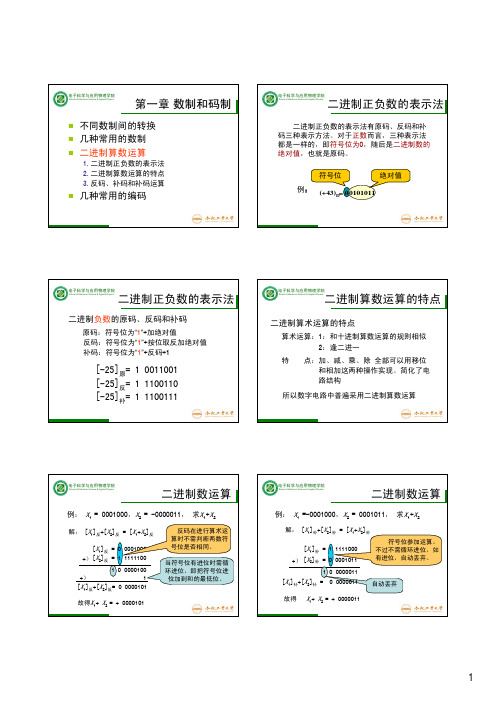
第一章数制和码制二进制正负数的表示法二进制正负数的表示法
电子科学与应用物理学院School of Electronic Science & Applied Physics 电子科学与应用物理学院School of Electronic Science & Applied Physics电子科学与应用物理学院School of Electronic Science & Applied Physics 电子科学与应用物理学院School of Electronic Science & Applied Physics电子科学与应用物理学院School of Electronic Science & Applied Physics 电子科学与应用物理学院School of Electronic Science & Applied Physics电子科学与应用物理学院School of Electronic Science & Applied Physics 电子科学与应用物理学院School of Electronic Science & Applied Physics电子科学与应用物理学院School of Electronic Science & Applied Physics-循环二进制码(2m-1→0 仅一位之差)电子科学与应用物理学院School of Electronic Science & Applied Physics循环二进制码电子科学与应用物理学院School of Electronic Science & Applied Physics十进制符号“8”电子科学与应用物理学院School of Electronic Science & Applied Physics电子科学与应用物理学院School of Electronic Science & Applied Physics 电子科学与应用物理学院School of Electronic Science & Applied Physics电子科学与应用物理学院School of Electronic Science & Applied Physics。
数制与编码

8421BCD码和十进制的之间的转化
例:将十进制数768用8421BCD码表示。 十进制数 7 6 8 8421码 0111 0110 1000 (768)10=(0111 0110 1000)8421
注意:
1.编码是一种符号表示某个具体的实物,所以编码不能比较大小。 2.8421BCD码是使用最广泛的 一种编码,在用4位二进制数码来表示1位十制 数时,每1位二进制数的位权依次为23、22、21、20,即8421,所以称为8421码 8421码选取0000—1001前十种组合来表示十进制数,而后六种组合舍去不用,称 为伪码。
可将每个八进数用3位二进制数表示,然后按八进制的排序将这些3位二进
制数排列好,就可得到相应的二进制数。
例:将八进制数475转化为二进制数。
解: 八进制数 4
7
5
二进制数 100 111
101
所以(475)8=(100111101)8
二进制数换为十六进制数
可将二进制整数自右向左每4位分为一组,最后不足4位的,高位用零补
6、将下列的二进制转化为十进制
(1011)2
(11011)2
(110110)2
(110011110)2
7、将下列的十进制转化为二进制
(20) (38)
(100) (184)
8、完成下列二进制的运算
101+11
11111+101
110-11
1101-111
9、什么是二进制代码? 什么是8421编码?列出8421BCD码的真 值表?
二进制数换为八进制数
可将二进制整数自右向左每3位分为一组,最后不足3位的,高位用零补足,
再把每3位二进制数对应的八进制数写出即可。
数字逻辑2014-2015(2)复习资料

第一章数制与编码1、二、八、十、十六进制数的构成特点及相互转换;2、有符号数的编码;3、格雷码的特点;各种进制如何用BCD码表示;4、有权码和无权码有哪些?例:一、选择题1、(1100110)B=()8421BCD=()D=()H=()O (178)10=()2=()8421BCD=()16=()82、将数1101.11B转换为十六进制数为( A )A. D.C HB. 15.3HC. 12.E HD. 21.3H3、在下列一组数中,最大数是()。
A.(258)DB.(100000001 )BC.(103)HD.(001001010111 )8421BCD4、若用8位字长来表示,(-62)D=( )原5、属于无权码的是()A.8421 码B.余3 码C.2421 码D.自然二进制码6、分别用842lBCD码表示(10011000)2为()A.230B.98C.9807、十进制数33的余3码为()。
A.00110110B.110110C.01100110D.1001008、数字电路中使用的数制是()。
A.二进制B.八进制C.十进制D.十六进制9、二进制数[101101]2和下列数中()相等A.[46]10B.[2D]16C.[54]8D.[101101]BCD10、在时间和数值上都断续变化的离散信号叫做()。
A.数字信号B.断续信号C.模拟信号D.连续信号二、判断题1、格雷码具有任何相邻码只有一位码元不同的特性。
()2、8421BCD码、5421BCD码、2421BCD码都是有权的二-十进制编码。
()3、BCD码是一种人为选定的0~9十个数字的代码,可以有许多种。
()4、8421BCD码是有权的二-十进制编码。
( )第二章逻辑代数基础1、基本逻辑运算和复合逻辑运算的运算规律、电路符号;2、逻辑代数的基本定律及三个规则;3、逻辑函数表达式、逻辑图、真值表及相互转换;4、最小项、最大项的性质;5、公式法化简;卡诺图法化简(有约束的和无约束的)。
计算机第一章

2. 数制间的转换(输入计算机的数都要被转换为二进制)
(1)各进位制数转换为十进制数
将各进位制数按照其通式展开(个位为0位),计算出结果即可。
(2)十进制数换成二、八、十六进制数
10→?采用“?除 — 倒取余数法”(一直除到商为0,将得出的余数倒排即为转换结果。)
(3)二进制数与八进制数转换
1.逻辑与规则(当A和B同时为真时,A AND B 的值为真,否则为假。)
0 AND 0=0,n,0 AND 1=0 nn1 AND 0=0 nn1 AND 1=1(或 0?0=0 0?1=0 1?0=0 1?1=1)
2.逻辑或规则(当A和B有一个为真时,A OR B 的值为真,否则为假。)
0 OR 0=0 nn0 OR 1=1nn1 OR 0=1 nn1 OR 1=1(或 0+0=0 0+1=1 1+0=1 1+1=1)
主板上最主要的部件是主机,即CPU和内存,图1-9是CPU和内存条的外形。
CPU
CPU的两个重要指标是字长和时钟频率。字长反映了PC能同时处理的数据的长度,其标志计算机的运算精度;时钟频率则反映了PC的运行速度。CPU的性能指标决定了计算机的档次。
内存
PC的内存主要有ROM、RAM和Cache三种:
(3)八进制计数制:有0-7共8个数码,逢八进一。(7+1=10)
(4)十六进制计数制:有0-9、A、B、C、D、E、F共十六个数码,逢十六进一。(F+1=10)
(5)数的表示:(数值)计数制 例:(2BF)16 (十进制数默认,可不加下标。)
(6)各进制数的对应关系:如图1-1所示。(试写出?处相应的数)
1数制与编码

二进制数的特点:
• 只有两个数码, 很容易用物理器件来实现。
• 运算规则简单。
• 可使用逻辑代数这一数学工具。
• 节省设备
例:如需表示数字0~999,共有1000个信息量。
十进制:用3位,每位10个数字,共需30个数字设备。
二进制:用10位,每位2个数字,共需20个数字设备。
⒈真值:在数值前加“+”号表示正数; 在数值前加“-”号表示负数。 ⒉机器数:把符号数值化的表示方法称~。 用“0”表示正数,用“1”表示负数。 例: 真值 机器数 +9 +1001 01001 -9 -1001 11001
符号位
常用的机器数有:原码、反码、补码 其符号位规则相同,数值部分的表示形式有差异。
几种常用数制的 表示方法(P5)
R=10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
二进制 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000
八进制 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20
X ⑷数值范围 [X]反= n 1 (2 1) X ;0 X 2n ;-2n X 0
00000 [0]反= 11111
⒉ 特点(续)
⑸两数和的反码等于两数反码之和; ⑹符号位参与运算,有进位时循环相加。
循环相 加
例:已知 X1=1100 X2=1010 求 Y1= X1- X2 ; Y2= X2- X1
⑴等精度转换
设α进制有 i位小数,转换后β进制有 j位小数。 (0.0…01)α= (1×α-i)10 i位 (0.01)2= (1×2-2)10 (0.0…01)β = (1×β-j)10 j位 (0.1)4= (1×4-1)10
