实验2 利用SIMULINK进行制导弹道仿真

合集下载

导弹最优导引律仿真分析(例子)

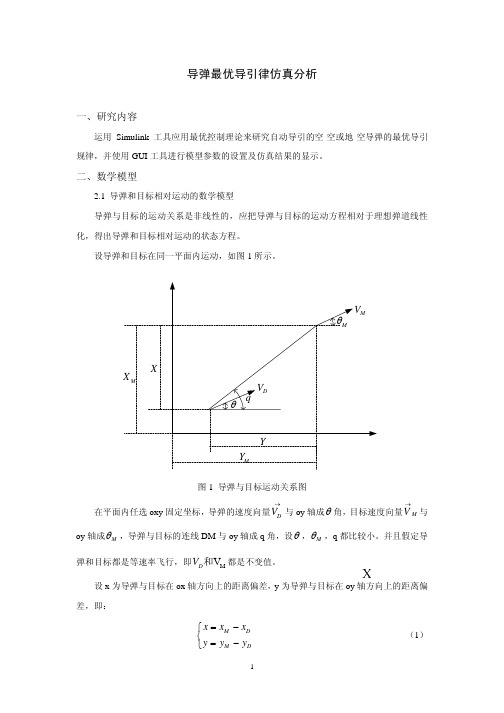
到限制，导弹结构能承受的最大过载也受到限制，所以控制信号 u 应该受到限制，因此，选
择下列形式的二次型指标函数
( ) ( ) ∫ ( ) J = 1 X T 2
tf
CX t f
+ 1 tf 2 t0
X T QX + U T RU dt
⎡c1 0 0 0 ⎤ ⎡0 0 0 0⎤
式中，
C
=
⎢ ⎢
0
c2
0
0
⎥ ⎥
,
Q
=
⎢⎢0
0
0
0⎥⎥
⎢0
⎢ ⎣
0
0 0
c3 0
0⎥
c4
⎥ ⎦
⎢0 0 0 0⎥ ⎢⎣0 0 0 0⎥⎦
2.2.2 最优导引律
（11）
完全考虑弹体二阶振荡环节时，假定目标不机动，导弹运动的状态方程见式（8），即
•
X = AX + Bu
（12）
⎡0 1 0 0 ⎤ ⎡ 0 ⎤
式中， A = ⎢⎢0 0 VD ⎢0 0 0
]
2(t f − t)2 + 6(t f − t)
ω
ω2
−
15 4ω
2
3
]
K3 (t) =
KDVD [(t f
− t)3
3 ω2 3 −
(t f
−t −
3 )2 ω
2(t f ω
− t)2
+
6(t f − t) ω2
−
15 4ω
2
3
]
最优导引方框图如图 3 所示。
6
u(σ )
KDω 2
+
1 s x4 1 s x3 VD +

基于Simulink的高空空投AUV全弹道仿真系统研究

基于Simulink的高空空投AUV全弹道仿真系统研究潘常军;郭迎清【摘要】High altitude Air-Launched AUV(AL-AUV)is a new kind of underwater vehicle that integrates high gliding and underwater, and designed on High Altitude ASW Weapons Conception(HAAWC). The simulation of the complete trajectory of AL-AUV is an important part and theoretical basic for conceptual design. The 6(or 9)DOF(Degree Of Freedom)simulation models of gliding, decelerating and underwater stages are established based on the movement and environment characteristics of high altitude AL-AUV trajectory’s steady stages. The AL-AUV’s free gliding trajectory and decelerating trajectory are simulated respectively with the effort of wing unit and circle parachute. The AUV underwater stage yaw and depth controllers are designed and system closed loop control simulation is completed which validates the AUV moving along the specified path under control. The simulations indicate that the simulation system applicable to AL-AUV complete trajectory unit design, characteristics analysis and controller design.% 高空空投AUV(Autonomous Underwater Vehicle,自主水下航行器)是一种基于“高空反潜武器概念”而设计的基高空滑翔与水下自主航行于一体的新型水下航行器,对其全弹道的仿真是其概念设计阶段的重要内容和理论基础。

基于Matlab／Simulink的火箭深弹水中弹道可视化仿真

一
爹ｃｏｓ
ｄ￡
㈩
＝ｚ０Ｏ，ｓｃ：ｉ０ｓｎ
ｔ
积分初始条件取为空中弹道落点Ｃ的弹道诸元：￡ｃ，ｃＹｙ，Ｃ０。＝ｔ时＝，ｃ＝Ｘ，＝上式是深弹在水中任意时刻的运动方程，随着深弹在水中的运动，角一直在改变，０最后趋于９￣０，所以在一定时刻后，火箭深弹垂直向下运动。当深弹正面阻力与浮力之和等于重力时，深弹以一定的速度匀速下沉，此时的速度称为极限下沉速度。极限速度可用下面公式计算
、
３６３６３７３７３８３８３９４０，５４Ｏ１４５４０４５４０
１２１３３５１４３５１５３５３０１６３０３５３０１３３０１４３０１５Ｉ６３５１７
距离（ｍ）
距离（）ｍ
关键词：箭深弹；ｄｂＳｌｋ弹道仿真火Ｍａａ／ｉｉ；ｍｕｎ中图分类号：Ｊ；Ｐ９．Ｔ６Ｔ３１９文献标识码：Ａ文章编号：６２５５２１０ — ０３０１７ — ４Ｘ（０２）７０３ — ３
不同的射角人水后，在水中垂直段的射角均变为９。０；
航天大学出版社。０９２０．
ＢａｅｎｔｅＭａｌｂ／ｍｕｉｋＲｏｋｔｐｈＣｈｒｅＵｎｅｗａｅｓｄｏｈｔａＳｉｌｃｅｎＤｅｔａｇｄｒｔｒ
ｌ・６以某火箭深弹为例，初始射角分别为４。和５１５・１ｏ行弹道仿真和分析。２进曼１．３３１速度变化规律．火箭深弹以一定的初速和射角到达水面，进入水中，深弹首先作减速运动，然后进人极限下潜段。以某火箭深弹为例，以两种不同的初始射角，经过仿真系统得到的速度变化图如图２所示。

MATLAB实验SIMULINK仿真

实验九SIMULINK仿真一、实验目的SIMULINK是一个对动态系统（包括连续系统、离散系统和混合系统）进行建模、仿真和综合分析的集成软件包，是MA TLAB的一个附加组件，其特点是模块化操作、易学易用，而且能够使用MATLAB提供的丰富的仿真资源。

在SIMULINK环境中，用户不仅可以观察现实世界中非线性因素和各种随机因素对系统行为的影响，而且也可以在仿真进程中改变感兴趣的参数，实时地观察系统行为的变化。

因此SIMULINK已然成为目前控制工程界的通用软件，而且在许多其他的领域，如通信、信号处理、DSP、电力、金融、生物系统等，也获得重要应用。

对于信息类专业的学生来说，无论是学习专业课程或者相关课程设计还是在今后的工作中，掌握SIMULINK，就等于是有了一把利器。

本次实验的目的就是通过上机训练，掌握利用SIMULINK对一些工程技术问题（例如数字电路）进行建模、仿真和分析的基本方法。

二、实验预备知识1. SIMULINK快速入门在工程实际中，控制系统的结构往往很复杂，如果不借助专用的系统建模软件，则很难准确地把一个控制系统的复杂模型输入计算机，对其进行进一步的分析与仿真。

1990年，Math Works软件公司为MATLAB提供了新的控制系统模型图输入与仿真工具，并命名为SIMULAB，该工具很快就在控制工程界获得了广泛的认可，使得仿真软件进入了模型化图形组态阶段。

但因其名字与当时比较著名的软件SIMULA类似，所以1992年正式将该软件更名为SIMULINK。

SIMULINK的出现，给控制系统分析与设计带来了福音。

顾名思义，该软件的名称表明了该系统的两个主要功能：Simu（仿真）和Link（连接），即该软件可以利用系统提供的各种功能模块并通过信号线连接各个模块从而创建出所需要的控制系统模型，然后利用SIMULINK提供的功能来对系统进行仿真和分析。

⏹SIMULINK的启动首先启动MATLAB，然后在MA TLAB主界面中单击上面的Simulink按钮或在命令窗口中输入simulink命令。

基于MATLAB／Simulink的弹道仿真模块化设计

ＴｈｅＩｎｃｏｒｐｏｒａｔｅＳｉｍｕｌａｔｉｏｎｏｆｔｈｅＭｉｓｓｉｌｅＴｒａｊｅｃｔｏｒｙＢａｓｅｄｏｎＭＡＴＬＡＢ／Ｓｉｍｕｌｉｎｋ
ＺＨＡ（）Ｊｕｎ－ｍｉｎ．ＨＥＹａ—ｊｕａｎ（Ｎｏ．２０３ＲｅｓｅａｒｃｈＩｎｓｔｉｔｕｔｅｏｆＣｈｉｎａＯｒｄｎａｎｃｅＩｎｄｕｓｔｒｉｅｓ．Ｘｉ’ａｎ７１００６５．Ｃｈｉｎａ）Ａｂｓｔｒａｃｔ：Ｉｎｔｈｉｓｐａｐｅｒ．ｔｈｅｉｎｃｏｒｐｏｒａｔｅｂａｌｌｉｓｔｉｃｓｉｍｕｌａｔｉｏｎｍｏｄｅｌｏｆｍｉｓｓｉｌｅｔｒａｊｅｃｔｏｒｙｉｓｂａｓｅｄｏｎｔｈｅＳｉｍｕｌｉｎｋｔｏｏｌｂｏｘｉｎｔｈｅＭａｔｌａｂｌａｎｇｕａｇｅ．Ｕｓｉｎｇｔｈｉｓｍｅｔｈｏｄ，ｔｈｅｄｙｎａｍｉｃｓｙｓｔｅｍｓｉｍｕｌａｔｉｏｎｂｅｃｏｍｅｓｅａｓｙａｎｄｖｉｓｕａ１．ｉｎｃｒｅａｓｉｎｇｔｈｉｓｍｏｄｅｌｔｒａｎｓｐｌａｎｔ．ＴｈｅｒｅｌｅｖａｎｔｒｅｓｕｌｔｓａｒｅｇｉｖｅｎｔＯａｄｅｔｅｒｍｉｎａｔｅｃｏｎｄｉｔｉｏｎ．ｔｈｅｒｅｓｕｌｔｓｈａｖｅｂｅｅｎｖａｌｉｄａｔｅｄ．Ｋｅｙｗｏｒｄｓ｛ＭＡＴＬＡＢ／Ｓｉｍｕｌｉｎｋ；ｓｉｍｕｌａｔｉｏｎｏｆｍｉｓｓｉｌｅｔｒａｊｅｃｔｏｒｙ；ｉｎｃｏｒｐｏｒａｔｅ
Ｓｉｍｕｌｉｎｋ完成某型号制导导弹的弹道模块化设
计，为总体性能及控制系统的分析提供平台。
３弹道பைடு நூலகம் 真模块化设计
２弹道仿真模块化设计思想
弹道仿真模块的设计分三步：（１）根据弹道仿真系统的任务及功能，将系统分为若干个模块，确定各模块的输入输出信号流；（２）分别构建各模块的内容；（３）模块封装，闭合大回路。

基于SIMULINK的某型反坦克导弹攻顶弹道方案设计研究

方程中各参数变化对攻顶弹道效果的影响。
Ａｂｓｔｒａｃｔ：Ｂａｌｌｉｓｔｉｃｓｓｃｈｅｍｅｉｓｖｅｒｙｉｍｐｏｒｔａｎｔｉｎｒｅｓｅａｒｃｈｉｎｇａｎｔｉ — ｔａｎｋｍｉｓｓｉｌｅ．Ｔｈｉｓｐａｐｅｒｄｅｓｉｇｎｅｄｂａｌｌｉｓｔｉｃｓｓｃｈｅｍｅｏｆａｋｉｎｄｏｆａｎｔｉ — ｔａｎｋｍｉｓｓｉｌｅｐｒｅｌｉｍｉｎａｒｉｌｙａｎｄｐｒｏｐｏｓｅｄａｋｉｎｄｏｆｂａｌｌｉｓｔｉｃｓｓｃｈｅｍｅｔｈａｔｃａｎａｃｈｉｅｖｅｔｏａｔｔａｃｋｔｏｐａｒｍｏｒｂａｓｅｄｏｎｔｈｅＳＩＭＵＬＩＮＫａｎｄｆｕｎｃｔｉｏｎｓｏｆｍｏｔｉｏｎ．ａｎｄａｎａｌｙｓｅｓｈｏｗｈｅｔｃｈａｎｇｅｄｐａｒａｍｅｔｅｒｓｉｎｆｕｎｃｔｉｏｎｓｏｆｍｏｔｉｏｎｉｎｆｌｕｅｎｃｅｈｅｔａｔｔａｃｋｉｎｇｔｏｐａｌＴａｏｒａｃｃｏｒｄｉｎｇｔｏｔｈｅｒｅｓｕｌｔｏｆｓｉｍｕｌａｔｉｏｎ．
摘要：在反坦克导弹的研制中，弹道方案的设计具有重要地位。本文基于ＳＩＭＵＬＩＮＫ仿真平台，在导弹外弹道运动方程的基础上，对某型反坦克导弹攻顶弹道方案进行了初步设计，提出了一种能够实现有效攻顶打击的弹道方案，并通过仿真结果分析了各运动

Matlab和Simulink通信与系统仿真实验指导书

通信与系统仿真实验指导书
昆明理工大学信息工程与自动化学院通信工程系邵玉斌撰
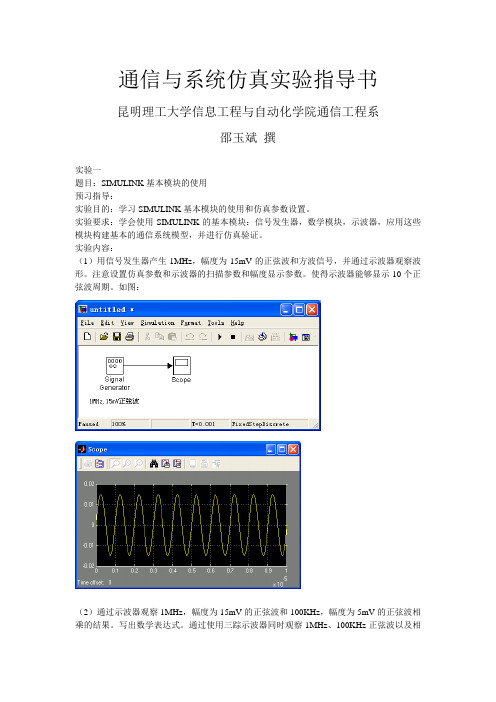
实验一题目：SIMULINK 基本模块的使用预习指导：实验目的：学习 SIMULINK 基本模块的使用和仿真参数设置。实验要求：学会使用 SIMULINK 的基本模块：信号发生器，数学模块，示波器，应用这些模块构建基本的通信系统模型，并进行仿真验证。实验内容：（1）用信号发生器产生 1MHz，幅度为 15mV 的正弦波和方波信号，并通过示波器观察波形。注意设置仿真参数和示波器的扫描参数和幅度显示参数。使得示波器能够显示 10 个正弦波周期。如图：
（3）请用 simulink 模型实现课本 p252 程序 6-21 的建模和计算。比较编程和图形建模的各
自特点。（4）使用频谱仪测量正弦信号的功率频谱。分别测量 800Hz，振幅为 1V 的正弦信号和方波信号的频谱，比较两者的区别。频谱仪模块在 DSP 工具箱中的 sinks 中。
注意设置频谱仪的 FFT 长度为 2048（可设其它长度试试）。显示特性设置为幅度显示，而不要设置为分贝方式。（5）学有余力的同学，可设计一个系统观察双边带调制输出信号的波形和频谱。
（5）用 sim 指令在命令空间启动模型进行仿真：对（4）中的模型采样命令 open 打开，采用 sim 指令进行仿真。请给出指令语句。实验报告内容和要求： 1. 对（1）～（5）作出实验记录，特别是遇到的问题和解决办法。（20 分） 2. 画出（1）的仿真模型方框图，说明参数设置情况，画出所得到的波形示意图。（20 分） 3. 画出（2）的仿真模型方框图，说明参数设置情况，画出所得到的波形示意图。（20 分） 4. 画出（3）的仿真模型方框图，说明参数设置情况，画出所得到的波形示意图。（10 分） 5. 给出（5）的程序代码和运行结果描述。（20 分） 6. 完成思考题。（10 分） 7. 实验报告必须使用实验报告用纸，必须手写。实验报告请在实验完成后一周内提交。思考题： 1. 谈谈用 sim 指令进行仿真和在 SIMULINK 中用菜单进行仿真这两种方式各自特点和优点？ 2. 利用信号与系统的知识计算 H(s)=5/(2s+1)的冲激响应 h(t)。是否符合（1）a 中的仿真结果？ 3. 说明封装子系统的过程。

Simulink方法及仿真实验

《现代机械工程基础实验》之机械工程控制基础综合实验报告姓名学号班级山东建筑大学机电工程学院2012.06.04~06第二部分Simulink方法及仿真实验一、开环系统1、如图所示，开环系统是积分环节的开环系统。

当输入信号分别是方波信号和正弦信号时，分析输出信号的波形。

积分环节的特点是输出量为输入量对时间的累积，输出幅值呈线性增长。

经过时间的累积后，当输入信号为零时，输出量不再增加且该值保持不变，即是具有记忆的功能。

（a）输入信号是方波信号输入信号波形图输出信号波形图分析：当输入信号时方波信号时，输出信号等于对方波信号时间的累积。

当方波信号在高电位时，输出为线性增长；当方波信号在零电位时，输出信号不增加，并且是保持不变的，因此是一条直线，在时间的积累下，输出信号就是如图所示的波形。

(b) 输入信号是正弦信号输入信号波形图输出信号波形图分析：当输入信号时正弦波信号时，输出信号也是输入信号对时间的累积。

当正弦波在上半部分时，输出信号不断增大；当在1/2周期时，输出信号达到最大值；当正弦波在下半周期时，输出信号因为对负值的不断累积而减小，在一个周期时为0。

因为可以得出输出信号的波形图如上图所示。

2、如图所示，开环系统是一阶惯性环节的开环系统。

当输入信号分别是方波信号和正弦信号时，分析输出信号的波形。

一阶惯性环节逇输出需要延迟一段时间才能够接近所要求的输出量，但是它也是从输入开始的时候就有了输出。

如图所示的一阶惯性环节，因此输出量的最大值应该时输出量的1/2。

（a）输入信号是方波信号输入信号波形图输出信号波形图分析：当输入信号是方波信号时，输出量一开始就有了，且从0开始逐渐增大，当达到1/2周期时，输出量达到了最大值；当方波信号为零电位时，输出量有不断减小，在一个周期时变为0，如此周期变化下去，因此可以得到输出信号的波形图如图所示。

（b）输入信号是阶跃信号输入信号波形图输出信号波形图分析：当输入信号是阶跃信号时，在输入信号时零电位时，输出量为0；当输入信号阶跃变为高电位时，输出信号不立刻变化，而是缓慢的变化达到最大值，最后保持不变。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实验2 利用SIMULINK 进行制导弹道仿真实验目的
利用Simulink 进行仿真建模，通过以鱼雷追踪目标的制导弹道仿真过程，初步掌握系统数学仿真方法。

实验内容
图5 系统的结构框图
其中目标模型为：
cos sin T T T T T T
T T w X V Y V ψψ⎧ψ=⎪=⎨⎪=-⎩ 式中，,,,T T T T W X Y ψ分别为目标弹道偏角、回旋角速度、纵向距离和侧向距离；
假设：当20t <时，(0)0.4T T ψψ==弧度，目标做匀速运动；
当20t ≥时，0.1/T w rad s =，目标开始做回旋运动；
其鱼雷模型为：
5.80.19 3.6192.42515119.84cos sin y r y y r
y w w w w Xe Vm Ye Vm ββδδψψβ⎧=-+-⎪=--⎪⎪=⎪⎨=ψ⎪⎪=-ψ⎪ψ=-⎪⎩
式中，,,,,,,,y w r Vm Xe Ye βδψψ分别为鱼雷的侧滑角、回旋角速度、直舵角、航向角、弹道偏角、速度，地面坐标系中的X 轴和Z 轴坐标。

Vm=25m/s 。

鱼雷与目标的相对距离为，,T T X X Xe Y Z Ze ∆=-∆=-。

q 为地球视线角，q ηψ
=-为雷体系中的提前角。

操舵规律,0.5,10r K K r δηδ=-=≤。

终端脱靶量定义为
t f r =鱼雷模型仿真初值为：
(0)(0)(0)(0)(0)(0)0.25/y w r Xe Ze Vm m s βδψ=======。

目标模型仿真初值为：(0)5/,(0)(0)1500,(0)0T T T T V m s X Z m w ====
实验步骤
由图5所示的系统控制结构图可知，该系统大致可以分为三个部分：目标模型，鱼雷模型以及观察模块。

1.根据目标模型和鱼雷模型的数学方程组，调用Simulink 工具箱模块库中的所需模块建立目标模型和鱼雷模型。

2.根据系统结构框图完成整个系统仿真模型的搭建，如图6 所示。

3.设置各模块的参数，并按照题目给定的初值条件设置好各模块的初值。

4.设置仿真器的参数，这里选择起始时间为0s ，终止时间为100s ，变步长解法器ode45，最大步长为0.05，最小步长自动调整。

5.对已经建立好的系统仿真模型进行运行调试，并对仿真结果进行分析。

图6 系统仿真模型结构图
图7 目标的弹道曲线
图8 鱼雷追踪曲线为了绘制绘制鱼雷跟踪弹道曲线，运行以下程序代码：plot(xe,ze)
hold on
plot(xt,zt)
图9 鱼雷跟踪弹道曲线
实验结果分析
由上图可以发现利用Simulink 建立系统仿真模型可以实现鱼雷跟踪目标的功能，达到了预期的目的，验证了实验的正确性。

与此同时，由图9可以发现鱼雷跟踪目标后还会继续运行，与实际情况并不相符，为了更好的绘制绘制鱼雷跟踪弹道曲线，仿真结构图中结合了stop 模块用来使终端脱靶量即终端时刻所对应的最小距离22tf r x z =∆+∆以给出仿真结束的时间停止仿真。

通过反复的调试，观测工作空间tf r 的值发现终端脱靶量不可能为零，最小为3.3左右。

将tf r 设置为小于等于3.3时绘制的鱼雷跟踪目标弹道曲线如图10所示。

可见数学模型并不能完全深刻的描述出物理模型，所以仿真结果也与实际鱼雷弹道并不完全吻合，但作为一个仿真软件，在其精度允许范围内并不影响其仿真效果和实验的有效性和正确性。

图10 鱼雷跟踪弹道曲线。