AP微积分AB2008年选择题真题答案
经济数学-微积分答案 2008年-2009年第一学_武汉理工大学考试试题纸(A卷)

六、证明题(本题满分4分)
、 设在[0,1]上连续,在(0,1)内可导,且,
试证:在(0,1)内存在一点,使.
、重要的不是知识的数量,而是知识的质量,有些人知道很多很多,但却不知道最有用的东西。 —— 托尔斯泰
、重要的不是知识的数量,而是知识的质量,有些人知道很多很多,但却不知道最有用的东西。 —— 托尔斯泰
武汉理工大学考ቤተ መጻሕፍቲ ባይዱ试题纸(A卷)
课程名称 高等数学B(上) 专业班级:工商t 0704
题号 一 二 三 四 五 六 总分 题分 15 15 30 24 12 4 100 备注: 学生不得在试题纸上答题(含填空题、选择题等客观题)
(1) . (2) .
(3) 设,求.
(4) , 其中具有一阶导数,求 .
(5) 已知,求.
四、计算题(本题共4小题,每小题6分,共24分)
(1) . (2) .
(3) . (4) .
(3)是函数的( )
A.连续点 B.跳跃间断点 C.可去间断点 D.无穷间断点
(4)函数的单调增加区间为( )
A. B. C. D.
(5)若广义积分收敛,则( )
A.>1 B.≥1 C.<1 D.≤1
二、填空题(本题共5小题,每小题3分,共15分)
(1) = .
(2)若=1,则 .
(3)曲线上经过点(1,0)处的切线方程为 .
(4)已知, 则 .
(5)已知, 则= . 三、计算题(本题共5小题,每小题6分,共30分)
五、应用题(本题共2小题,每小题6分,共12分)
(1) 某商品的需求函数为(P为价格,Q为需求量),
2008级微积分上(A)试题及其参考答案

2008级微积分(上)A理工课程试题及其参考答案1.求下列极限(每小题5分,共20分)
1.
其中,
二.求解下列各题(每小题5分,共20分).
1.设,其中为连续函数,求
解:.
2.设函数由方程确定,其中具有一阶连续导数,求
解:方程两边同时关于求导,得:
(1)
所以, (2)
故
3.设求
解:两边取对数,得:
上式两边同时关于求导,得:
所以
4.求方程的通解.
解:特征方程为,特征根为,故通解为
三.求下列积分(每小题6分,共30分)
另解:令则
原式
3.
其中
;
所以,
4.设求
解:因为
故
5
四.求解下列各题(共10分)
讨论方程的根的个数.
解:令
令得唯一驻点
因为当时,而当时,
因此为函数的最大值.
又
综合以上信息可以画出函数之草图.
从图易见方程恰有两根.
五.设有连续导数,且(1),求(共10分)
解:由(1)式显然得
(2)
(2)式两边关于求导,得
即
即,
也就是(3)
此为一阶线性微分方程,故其通解为
(4)
将代入(4)式,得,所以.
六.求曲线与与轴及直线所围图形分别绕轴、轴旋转一周所生成的立体的体积.(10分)
解:(一)
(二)。
08级微积分Ⅲ 题目及答案

4、 设曲面 ∑ 为上半球面 x 2 + y 2 + z 2 = R 2 ( z ≥ 0) , 曲面 ∑1 为曲面 ∑ 在第一卦限中的部分, 则下面正确的是 ( ) (A) (C)
∫∫ xdS = 4∫∫ xdS
∑ ∑1
(B) (D)
பைடு நூலகம்
∫∫ zdS = 4∫∫ zdS
∑ ∑1
∫∫ ydS = 4∫∫ ydS
08 级微积分Ⅲ题目及参考答案
一、填空题(本大题共 5 小题,每小题 4 分,共计 20 分) 1、设曲线 L 为圆周 x = a cos t , y = a sin t , (0 ≤ t ≤ 2π ) ,则
Ñ ∫ (x
L
2
+ y 2 ) n ds =____________________.
解:一代二换三定限
PDF 文件使用 "pdfFactory Pro" 试用版本创建
且 L1 的方向取顺时针方向,记 L1 和 L 所围区域为 D ,则有:
p=
−y x ,Q = 2 2 x +y x + y2
2
∂P y2 − x2 ∂Q , x2 + y 2 ≠ 0 = 2 = 2 2 ∂y ( x + y ) ∂x ∴Ñ ∫ Pdx + Qdy =Ñ ∫
Ò ∫∫ x dS 的值为(
2 ∑
) (D)4π a 4
4π 4 a 3
(B) 3π a 4
2 2 2
(C)2π a 4
解:利用轮换对称性
Ò ∫∫ x dS = Ò ∫∫ y dS = Ò ∫∫ z dS ,
∑ ∑ ∑
Ò ∫∫ x dS = 3 Ò ∫∫ ( x
2008考研数二真题及解析
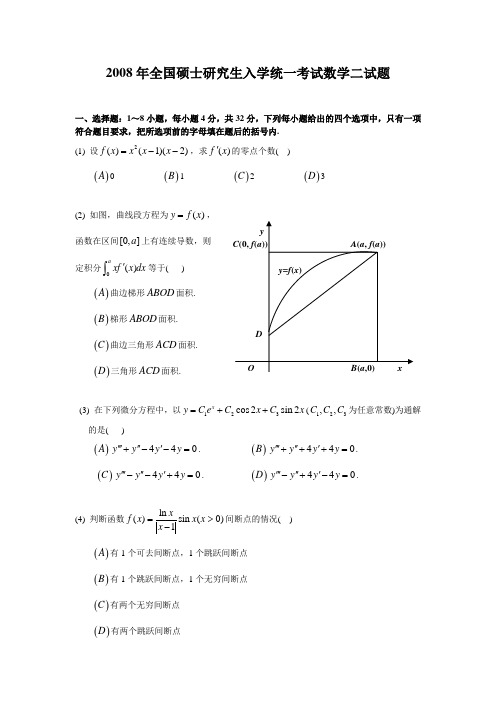
2008年全国硕士研究生入学统一考试数学二试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1) 设2()(1)(2)f x x x x =--,求()f x '的零点个数( )()A 0()B 1 ()C 2()D 3(2) 如图,曲线段方程为()y f x =, 函数在区间[0,]a 上有连续导数,则 定积分()axf x dx '⎰等于( )()A 曲边梯形ABOD 面积.()B 梯形ABOD 面积. ()C 曲边三角形ACD 面积.()D 三角形ACD 面积.(3) 在下列微分方程中,以123cos 2sin 2xy C e C x C x =++(123,,C C C 为任意常数)为通解的是( )()A 440y y y y ''''''+--=. ()B 440y y y y ''''''+++=. ()C 440y y y y ''''''--+=.()D 440y y y y ''''''-+-=.(4) 判断函数ln ()sin (0)1xf x x x x =>-间断点的情况( ) ()A 有1个可去间断点,1个跳跃间断点 ()B 有1个跳跃间断点,1个无穷间断点 ()C 有两个无穷间断点 ()D 有两个跳跃间断点yC (0, f (a )) A (a , f (a ))y =f (x )O B (a ,0) xD(5) 设函数()f x 在(,)-∞+∞内单调有界,{}n x 为数列,下列命题正确的是( )()A 若{}n x 收敛,则{}()n f x 收敛. ()B 若{}n x 单调,则{}()n f x 收敛. ()C 若{}()n f x 收敛,则{}n x 收敛.()D 若{}()n f x 单调,则{}n x 收敛.(6) 设函数f 连续. 若()()2222,uvD f x y F u v dxdy x y+=+⎰⎰,其中区域uv D 为图中阴影部分,则Fu∂=∂( ) ()A ()2vf u()B ()2vf u u()C ()vf u()D ()vf u u(7) 设A 为n 阶非零矩阵,E 为n 阶单位矩阵. 若3A O =,则( )()A E A -不可逆,E A +不可逆.()B E A -不可逆,E A +可逆. ()C E A -可逆,E A +可逆.()D E A -可逆,E A +不可逆.(8) 设1221A ⎛⎫=⎪⎝⎭,则在实数域上与A 合同的矩阵为( ) ()A 2112-⎛⎫⎪-⎝⎭.()B 2112-⎛⎫⎪-⎝⎭.()C 2112⎛⎫ ⎪⎝⎭.()D 1221-⎛⎫⎪-⎝⎭.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9) ()f x 连续,21cos(sin )lim1(1)()x x x e f x →-=-,则(0)f =(10) 微分方程2()0xy x e dx xdy -+-=的通解是y =O xvx 2+y 2=u 2 x 2+y 2=1 D uvy(11) 曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 . (12) 求函数23()(5)f x x x =-的拐点______________. (13) 已知xyy z x ⎛⎫=⎪⎝⎭,则(1,2)_______z x ∂=∂. (14) 矩阵A 的特征值是,2,3λ,其中λ未知,且248A =-,则λ=_______.三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求极限()40sin sin sin sin limx x x x x →-⎡⎤⎣⎦.(16) (本题满分10分)设函数()y y x =由参数方程20()ln(1)t x x t y u du =⎧⎪⎨=+⎪⎩⎰确定,其中()x t 是初值问题 020|0xt dx te dtx -=⎧-=⎪⎨⎪=⎩的解. 求22d y dx .(17)(本题满分9分)计算212arcsin 1x x dx x-⎰(18)(本题满分11分)计算{}max ,1,Dxy dxdy ⎰⎰其中{(,)02,02}D x y x y =≤≤≤≤(19)(本题满分11分)设()f x 是区间[0,)+∞上具有连续导数的单调增加函数,且(0)1f =. 对于任意的[0,)t ∈+∞,直线0,x x t ==,曲线()y f x =以及x 轴所围成曲边梯形绕x 轴旋转一周生成一旋转体. 若该旋转体的侧面面积在数值上等于其体积的2倍,求函数()f x 的表达式.(20)(本题满分11分)(I) 证明积分中值定理:若函数()f x 在闭区间[,]a b 上连续,则至少存在一点[,]a b η∈,使得()()()baf x dx f b a η=-⎰;(II) 若函数()x ϕ具有二阶导数,且满足,32(2)(1),(2)()x dx ϕϕϕϕ>>⎰,则至少存在一点(1,3)ξ∈,()0ϕξ''<使得.(21)(本题满分11分)求函数222u x y z =++在约束条件22z x y =+和4x y z ++=下的最大和最小值.(22)(本题满分12分)设n 元线性方程组Ax b =,其中2221212n n a a a A a a ⨯⎛⎫ ⎪ ⎪= ⎪⎪⎝⎭,12n x x x x ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,100b ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭(I) 证明行列式()1nA n a =+(II) 当a 为何值时,该方程组有唯一解,并求1x (III) 当a 为何值时,该方程组有无穷多解,并求通解(23)(本题满分10分)设A 为3阶矩阵,12,αα为A 的分别属于特征值1,1-的特征向量,向量3α满足323A ααα=+,(I) 证明123,,ααα线性无关; (II) 令()123,,P ααα=,求1P AP -2008年全国硕士研究生入学统一考试数学二试题解析一、选择题 (1)【答案】D【详解】因为(0)(1)(2)0f f f ===,由罗尔定理知至少有1(0,1)ξ∈,2(1,2)ξ∈使12()()0f f ξξ''==,所以()f x '至少有两个零点. 由于()f x '是三次多项式,三次方程()0f x '=的实根不是三个就是一个,故D 正确.(2)【答案】C 【详解】00()()()()()()aa a aaxf x dx xdf x xf x f x dx af a f x dx '==-=-⎰⎰⎰⎰其中()af a 是矩形ABOC 面积,0()af x dx ⎰为曲边梯形ABOD 的面积,所以0()axf x dx '⎰为曲边三角形的面积.(3)【答案】D【详解】由微分方程的通解中含有xe 、cos2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2r r i ==±,所以特征方程为(1)(2)(2)0r r i r i --+=,即32440r r r -+-=. 故以已知函数为通解的微分方程是440y y y ''''''-+-=(4) 【答案】A【详解】0,1x x ==时()f x 无定义,故0,1x x ==是函数的间断点因为 000ln 11lim ()lim lim lim csc |1|csc cot x x x x x xf x x x x x++++→→→→=⋅=-- 200sin lim lim 0cos cos x x x xx x x++→→=-=-=同理 0lim ()0x f x -→= 又 1111ln 1lim ()lim lim sin lim sin1sin11x x x x x f x x x x ++++→→→→⎛⎫=⋅== ⎪-⎝⎭ 111ln lim ()lim lim sin sin11x x x xf x x x --+→→→=⋅=--所以 0x =是可去间断点,1x =是跳跃间断点.(5)【答案】B【详解】因为()f x 在(,)-∞+∞内单调有界,且{}n x 单调. 所以{()}n f x 单调且有界. 故{()}n f x 一定存在极限.(6)【答案】A【详解】用极坐标得 ()()222()22211,()vu uf r r Df u v F u v dudv dv rdr v f r dr u v +===+⎰⎰⎰⎰⎰所以()2Fvf u u∂=∂(7) 【答案】C【详解】23()()E A E A A E A E -++=-=,23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆.(8) 【答案】D 【详解】记1221D -⎛⎫=⎪-⎝⎭,则()2121421E D λλλλ--==---,又()2121421E A λλλλ---==----所以A 和D 有相同的特征多项式,所以A 和D 有相同的特征值.又A 和D 为同阶实对称矩阵,所以A 和D 相似.由于实对称矩阵相似必合同,故D 正确.二、填空题 (9)【答案】2【详解】222220001cos[()]2sin [()2]2sin [()2]()lim lim lim ()[()2]4(1)()x x x x xf x xf x xf x f x x f x xf x e f x →→→-⋅==⋅- 011lim ()(0)122x f x f →=== 所以 (0)2f =(10)【答案】()xx eC --+【详解】微分方程()20xy x edx xdy -+-=可变形为x dy yxe dx x--= 所以 111()dx dx x x xx x y e xe e dx C x xe dx C x e C x ----⎡⎤⎛⎫⎰⎰=+=⋅+=-+⎢⎥ ⎪⎝⎭⎣⎦⎰⎰(11)【答案】1y x =+【详解】设(,)sin()ln()F x y xy y x x =+--,则1cos()11cos()x y y xy F dy y x dx F x xy y x--'-=-=-'+-,将(0)1y =代入得01x dy dx==,所以切线方程为10y x -=-,即1y x =+(12)【答案】(1,6)-- 【详解】53235y xx =-⇒23131351010(2)333x y x x x -+'=-=⇒134343101010(1)999x y x x x--+''=+= 1x =-时,0y ''=;0x =时,y ''不存在在1x =-左右近旁y ''异号,在0x =左右近旁0y ''>,且(1)6y -=- 故曲线的拐点为(1,6)--(13)【答案】2(ln 21)2- 【详解】设,y xu v x y==,则v z u = 所以121()ln v v z z u z v y vu u u x u x v x x y-∂∂∂∂∂=⋅+⋅=-+⋅∂∂∂∂∂ 2ln 11ln x yv vy u y y u ux y x y x ⎛⎫⎛⎫⎛⎫=-+=⋅-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ 所以(1,2)2(ln 21)2z x ∂=-∂(14)【答案】-1【详解】||236A λλ =⨯⨯= 3|2|2||A A =32648λ∴ ⨯=- 1λ⇒=-三、解答题 (15)【详解】 方法一:4300[sin sin(sin )]sin sin sin(sin )limlim x x x x x x x x x→→--= 22220001sin cos cos(sin )cos 1cos(sin )12lim lim lim 3336x x x xx x x x x x x →→→--==== 方法二:331sin ()6x x x o x =-+ 331sin(sin )sin sin (sin )6x x x o x =-+4444400[sin sin(sin )]sin sin (sin )1lim lim 66x x x x xx o x x x x →→⎡⎤-∴ =+=⎢⎥⎣⎦(16)【详解】方法一:由20x dx te dt--=得2x e dx tdt =,积分并由条件0t x =得21x e t =+,即2l n (1)x t =+所以 2222ln(1)2(1)ln(1)21dydy t tdt t t dxt dx dt t +⋅===+++222222[(1)ln(1)]2ln(1)221dt t d y d dy t t tdt dx t dx dx dx dt t ++++⎛⎫=== ⎪⎝⎭+ 22(1)[ln(1)1]t t =+++方法二:由20x dx te dt--=得2x e dx tdt =,积分并由条件0t x =得21x e t =+,即2l n (1)x t =+所以 2222ln(1)2(1)ln(1)21x dydy t tdt t t e x dxt dx dt t +⋅===++=+所以 22(1)x d ye x dx=+(17)【详解】 方法一:由于221arcsin lim 1x x x x-→=+∞-,故212arcsin 1x x dx x-⎰是反常积分.令arcsin x t =,有sin x t =,[0,2)t π∈22122222000arcsin sin cos 2cos sin ()cos 221x x t t t t t dx tdt t tdt dt t x πππ===--⎰⎰⎰⎰2222220001sin 21sin 2sin 2441644tt t td t tdt πππππ=-=-+⎰⎰ 222011cos 2168164t πππ=-=+ 方法二:212arcsin 1x x dx x -⎰12201(arcsin )2x d x =⎰ 121122220001(arcsin )(arcsin )(arcsin )28x x x x dx x x dx π=-=-⎰⎰令arcsin x t =,有sin x t =,[0,2)t π∈12222200011(arcsin )sin 2cos 224x x dx t tdt t d t ππ==-⎰⎰⎰ 222200111(cos 2)cos 242164t t t tdt πππ=-+=-⎰故,原式21164π=+(18)【详解】 曲线1xy =将区域分成两 个区域1D 和23D D +,为了便于计算继续对 区域分割,最后为()max ,1Dxy dxdy ⎰⎰123D D D xydxdy dxdy dxdy =++⎰⎰⎰⎰⎰⎰112222211102211x xdx dy dx dy dx xydy =++⎰⎰⎰⎰⎰⎰1512ln 2ln 24=++-19ln 24=+(19)【详解】旋转体的体积20()tV f x dx π=⎰,侧面积22()1()tS f x f x dx π'=+⎰,由题O 0.5 2 xD 1D 3 D 2设条件知220()()1()ttf x dx f x f x dx '=+⎰⎰上式两端对t 求导得 22()()1()f t f t f t '=+, 即 21y y '=-由分离变量法解得 21l n (1)y y t C+-=+, 即 21t y y C e+-= 将(0)1y =代入知1C =,故21t y y e +-=,1()2t t y e e -=+于是所求函数为 1()()2t ty f x e e -==+(20)【详解】(I) 设M 与m 是连续函数()f x 在[,]a b 上的最大值与最小值,即()m f x M ≤≤ [,]x a b ∈由定积分性质,有 ()()()bam b a f x dx M b a -≤≤-⎰,即 ()baf x dx m M b a≤≤-⎰由连续函数介值定理,至少存在一点[,]a b η∈,使得 ()()b af x dx f b aη=-⎰即()()()baf x dx f b a η=-⎰(II) 由(I)的结论可知至少存在一点[2,3]η∈,使32()()(32)()x dx ϕϕηϕη=-=⎰又由 32(2)()()x d x ϕϕϕη>=⎰,知 23η<≤对()x ϕ在[1,2][2,]η上分别应用拉格朗日中值定理,并注意到(1)(2)ϕϕ<,()(2)ϕηϕ<得 1(2)(1)()021ϕϕϕξ-'=>- 112ξ<<2()(2)()02ϕηϕϕξη-'=<- 123ξη<<≤在12[,]ξξ上对导函数()x ϕ'应用拉格朗日中值定理,有2121()()()0ϕξϕξϕξξξ''-''=<- 12(,)(1,3)ξξξ∈⊂(21)【详解】方法一:作拉格朗日函数22222(,,,,)()(4)F x y z x y z x y z x y z λμλμ=++++-+++-令 2222022020040x y z F x x F y y F z F x y z F x y z λμλμλμλμ'=++=⎧⎪'=++=⎪⎪'=-+=⎨⎪'=+-=⎪'=++-=⎪⎩解方程组得111222(,,)(1,1,2),(,,)(2,2,8)x y z x y z ==-- 故所求的最大值为72,最小值为6.方法二:问题可转化为求2242242u x y x x y y =++++在224x y x y +++=条件下的最值 设44222222(,,)2(4)F x y u x y x y x y x y x y λλ==++++++++-令 323222442(12)0442(12)040x y F x xy x x F y x y y y F x y x y λλλ'⎧=++++=⎪'=++++=⎨⎪'=+++-=⎩解得1122(,)(1,1),(,)(2,2)x y x y ==--,代入22z x y =+,得122,8z z == 故所求的最大值为72,最小值为6.(22)【详解】(I)证法一:2222122212132101221221122a a a a a a aa aA r ar aaa a =-=121301240134(1)2(1)3231(1)0n n n a a a n a a n ar ar a n a nnn a n--+-=⋅⋅⋅=++ 证法二:记||n D A =,下面用数学归纳法证明(1)nn D n a =+.当1n =时,12D a =,结论成立.当2n =时,2222132a D a a a==,结论成立.假设结论对小于n 的情况成立.将n D 按第1行展开得2212102121212n n a a a aD aD a a-=-21221222(1)(1)n n n n n aD a D ana a n a n a ---- =-=--=+故 ||(1)nA n a =+证法三:记||n D A =,将其按第一列展开得 2122n n n D aD a D --=-, 所以 211212()n n n n n n D aD aD a D a D aD ------=-=-222321()()n n n n a D aD a D aD a ---=-==-=即 12122()2n n n n n n n n D a aD a a a aD a a D ----=+=++=++2121(2)(1)n n n n n a a D n a a D --==-+=-+1(1)2(1)n n n n a a a n a -=-+⋅=+(II)因为方程组有唯一解,所以由Ax B =知0A ≠,又(1)nA n a =+,故0a ≠. 由克莱姆法则,将n D 的第1列换成b ,得行列式为2221122(1)(1)112102*********n n n nn n a a a aa aa aD na a a a a --⨯-⨯-===所以 11(1)n n D nx D n a-==+(III)方程组有无穷多解,由0A =,有0a =,则方程组为12101101001000n n x x x x -⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 此时方程组系数矩阵的秩和增广矩阵的秩均为1n -,所以方程组有无穷多解,其通解为()()10000100,TTk k +为任意常数.(23)【详解】(I)证法一:假设123,,ααα线性相关.因为12,αα分别属于不同特征值的特征向量,故12,αα线性无关,则3α可由12,αα线性表出,不妨设31122l l ααα=+,其中12,l l 不全为零(若12,l l 同时为0,则3α为0,由323A ααα=+可知20α=,而特征向量都是非0向量,矛盾)11,A αα=-22A αα=∴32321122A l l αααααα=+=++,又311221122()A A l l l l ααααα=+=-+ ∴112221122l l l l ααααα-+=++,整理得:11220l αα+=则12,αα线性相关,矛盾. 所以,123,,ααα线性无关.证法二:设存在数123,,k k k ,使得1122330k k k ααα++= (1)用A 左乘(1)的两边并由11,A αα=-22A αα=得1123233()0k k k k ααα-+++= (2)(1)—(2)得 113220k k αα-= (3) 因为12,αα是A 的属于不同特征值的特征向量,所以12,αα线性无关,从而130k k ==,代入(1)得220k α=,又由于20α≠,所以20k =,故123,,ααα线性无关.(II) 记123(,,)P ααα=,则P 可逆,123123(,,)(,,)AP A A A A αααααα==1223(,,)αααα=-+123100(,,)011001ααα-⎛⎫ ⎪= ⎪ ⎪⎝⎭100011001P -⎛⎫ ⎪= ⎪ ⎪⎝⎭所以 1100011001P AP --⎛⎫ ⎪= ⎪ ⎪⎝⎭.。
2008级下期微积分A期末考试试题评分标准

2008级下期微积分期末考试试题(A)评分标准二、填空题(每题3分,合计15分)1.{}(2,4,1)2,4,1--或;2.121cos sin x C e C x C x ++;3.11)3;4.32R π;5., 00, 0/2, x x x x ππππ--<≤⎧⎪<<⎨⎪=±⎩.三、(9 分)[解] 令 (,,) 2--=-+-x y zF x y z x ex y z ①(1)1,--=+-x y z x F x e 1,--=-+x y z y F xe 2,--=--x y z z F xe ②(1)1,2,----∂+-=-=-∂-x y z x x y z z F z x e x F xe ②, 1,2,----∂+=-=-∂-x y z y x y z z F zxe y F xe ② 3(0,2,1)(0,2,1)11(1), .22-∂∂=-=∂∂z z e x y ②四、(9分)[解] 椭圆2244+=x y 上点(,)x y 到直线2360+-=x y 的距离=d ① 令222(,,)(236)(44)λλ=+-++-F x y x y x y ②,224(236)206(236)80440λλλ=+-+=⎧⎪=+-+=⎨⎪=+-=⎩x xF x y x F x y y F x y ③, 解得88553355⎧⎧==-⎪⎪⎪⎪⎨⎨⎪⎪==-⎪⎪⎩⎩x x y y , ② 代入距离公式知所求点为83(,)55①五. (9分) [解] 收敛区间为[1,1)- ②,令 110011()() (0)11+∞∞=====≠++∑∑n n n n x x S x S x x n x n x ①()11001()11+∞∞=='⎛⎫'===⎪+-⎝⎭∑∑n n n n x S x x n x ② 1111001()()(0)()d d ln(1)1'=-===---⎰⎰xxS x S x S S x x x x x② 11ln(1)0:()() (1001)-≠==--≤<<<x x S x S x x x x x或 ① 0:() 1.==x S x① 六、(9分) [解] 将函数()f x 作偶延拓,周期为2π.① 0.n b = ①,002d ,a x x πππ==⎰①,2022cos d [cos 1]n a x nx x n n ππππ==-⎰②224, 2[(1)1] (1,2,)0, nn n n n n ππ⎧-⎪=--==⎨⎪⎩为奇数为偶数② 2141()cos(21), [,]2(21)n f x n x x n ππππ∞==--∈--∑ ②七、( 9分) [解] 22222()∂-∂==∂+∂Q y x Px x y y② 记L 所围成的区域为D ,选取适当小的0>ε,在D 内作圆周2221:+=L x y ε,取顺时针方向. ②在L 与1L 所围成区域1D 上用格林公式得=+-⎰+122d d L L y x xy y x 1()0∂∂-=∂∂⎰⎰D Q Pd x y σ ②故 ⎰+-L y x xy y x 22d d =-=+-⎰122d d L y x x y y x ⎰--121L ydx xdy ε222211(2)(2)2=--==⎰⎰D d σπεπεε③其中2D 为1L 所围成的区域.八、( 9 分) [解] 取1S 为圆盘:2210⎧+≤⎨=⎩x y z ,方向取下侧 ①,则⎰⎰⎰⎰⎰++=++++++VS S V z y x y x y z x z x y z y z x )d (3d )d (d )d (d )d (2222323231②2122200063d sin d d 5=⋅=⎰⎰⎰ππθϕϕρρρπ ② ⎰⎰+++++1d )d (d )d (d )d (232323S y x y z x z x y z y z x=⎰⎰-xyD y x y d d 2①2122001d sin d 4r r πθθπ=-=-⎰⎰ ② =-=⎰⎰⎰⎰⎰⎰+11S S S S6129()5420=--=πππ ①九、( 9分)[解] 由对称性,所求面积是第一卦限的4倍:44xyxyD D S σσ==⎰⎰⎰⎰③cos 2004d d r πθθ=⎰⎰ ③204(1sin )d πθθ=-⎰ ② =2(2)π- ①十、( 7分)[证] (,,)(,),=x y G x y y F z z 令12122211, , ,=⋅=⋅=-⋅-⋅x y z x yG F G F G F F z z z zn 12122211, , ⎛⎫=⋅⋅-⋅-⋅ ⎪⎝⎭x y F F F F z z z z ()121221, , =--zF zF xF yF z ③在任一点(), , x y z 处的切平面方程为1212() ()()()0-+-+---=zF X x zF Y y xF yF Z z 即 1212()0+-+=zF X zF Y xF yF Z ③显然,0===X Y Z 满足方程,即任意一点处的切平面都通过原点. ①。
ap微积分真题答案

ap微积分真题答案【篇一:ap 微积分bc 选择题样卷一】version - section i - part a calculators are not permitted on this portion of the exam28 questions - 55 minutes1) givenfind dy/dx. a) b) c) d) e)2) give the volume of the solid generated by revolving the region bounded by the graph of y = ln(x), the x-axis, the lines x = 1 and x = e, about the y-axis. a) b) c) d)e)3) the graph of the derivative of fis shown below.find the area bounded between the graph of f and the x-axis over the interval [-2,1], given that f(0) = 1. a) b) c) d) e)4) determine dy/dt, given thatanda)b)c)d)e)5) the function-1is invertible. give the slope of the normal line to the graph of f atx = 3.a) b) c)d)e)6) determinea) b)c) d) e)7) give the polar representation for the circle of radius 2 centered at ( 0 , 2 ). a)b)c)d)e)8) determinea)b)c) d)e)9) determinea) b) c) d) e)10) give the radius of convergence for the seriesa)b)c) d)e)11) determinea)b)【篇二:ap 微积分bc选择题样卷二】17 questions - 50 minutes1) the limit of the sequenceas n approaches is -3. what is the value of c? a)b)c)d)e)2) ifand y = 3 when x = -2, then what is y? a) b) c)d) e)3) the graph of the derivative of fis given below.which of the following is false about the function f?a) f is increasing on [1,4].b) f is concave down on [1,5/2].c) f is concave down on [-3,0).d) f is not differentiable at 0. e) the funciton is constant on (-,-3].4) determinea)b)c) d) e)5) give the area that lies below the x-axis and is contained within theregion bounded by the polar curvea) b) c) d) e)6) give the error that occurs when the area between the curve and the x-axis over the interval [0,1] is approximated by the trapezoid rule with n = 4. a)b)c)d)e)7) letdetermine f(2/3). a)b)c) d) e)8) give the length of the curve determined byfor t from 0 to 2. a)b)c)d)e)9) particles a and b leave the origin at the same time and move along the y-axis. their positions are determined by the functionsfor t between 0 and 8. what is the velocity of particle b when particlea stops for the first time? a) b)c)d) e)10) the base of a solid is the region in the xy plane enclosed by thecurvesover the interval[0,/4]. cross sections of the solid perpendicular to the x-axis are squares. determine the volume of the solid. a)b)c)d)e)11) give the minimum value of the functionfor x 0. a)b)c)d)e)12) select the true statement associated with the function【篇三:ap微积分考试详解】>微积分ap课程包括微积分ab (calculus ab) 和微积分bc(calculus bc)两门课。
2008年微积分(上册)期终考试试卷 含答案

1---○---○------○---○---……… 评卷密封线…………… 密封线内不要答题,密封线外不准填写考生信息,违者考试成绩按0分处理…………… 评卷密封…………中南大学考试试卷2008级(第一学期)期终考试试卷(2009年1月7日,10:10—12:00)时间110分钟2008~2009学年第一学期《微积分A 》课程88学时,5.5学分,闭卷,总分100分,平时成绩占30%一、填空题(本题共5小题,每题3分,共15分)1.已知212)1(lim2334-=-++++∞→x x bx x a x ,则a = ,b = .2.设)2008()2)(1(---=x x x x y ,则)2009(y = .3.dxxx x ⎰++421)1(= .4.设)(x f 是以周期为6的周期函数,且在一个周期内的表达式为)33(,1)(2<≤-++=x x xx f ,则其Fourier 级数的系数3b = .5.点)3,4,2(--到平面0322=++-z y x 的距离为 .二、选择题(本题共5小题,每小题3分,共15分)→x 11211---x e x x ∞22.设函数)(x f 在),(b a 内连续,则必有( ).(A ))(x f 为),(b a 内的有界函数;(B ))(x f 在),(b a 内必有最大值和最小值; (C )若0)(lim,0)(lim<>-→+→x f x f b x a x ,则)(x f =0至少有一根;(D ))(x f 必取得介于)(a f 和)(b f 之间的任何值.3.积分dx tx f t I t s)(0⎰=与( )有关. (A )x t s ,,(B )t s ,(C )t x ,(D )s4.广义积分()收敛.(A )dx xx ⎰∞+2ln (B )dx x x ⎰∞+2ln 1(C )dxx x ⎰∞+22)(ln 1(D )dxxx ⎰∞+2ln 15.设∑∞=1n n u ,∑∞=1n n v 均为正项级数,下列结论正确的是().(A )若),2,1(1 =≥+n u u n n 且0lim =∞→n n u ,则∑∞=1n n u 收敛(B ) 若0lim ≠=∞→k u n n pn ,则当1>p 时,∑∞=1n n u 收敛,1≤p 时∑∞=1n n u 发散(C )若+∞=∞→nn n v u lim,且∑∞=1n n v 收敛,则∑∞=1n n u 发散(D )若0lim=∞→nn n v u ,且∑∞=1n n v 发散,则∑∞=1n n u 发散3三、求解下列各题(每小题7分,共28分)1.设()(1)f x x x =-,11<<-x ,求()f x 的极值点和拐点.2.设⎩⎨⎧+=+=tt y t t x 6arctan 3,求22dx y d 。
AP 微积分 AB 2008 (Form B) 真题及解析

(c) Let T be the time at which the car’s speed reaches 80 kilometers per hour.
Then, r(T ) = 80 or T = 0.331453 hours.
At time T, the car has gone
∫ x(T ) = T r (t ) dt = 10.794097 kilometers 0
AP® Calculus AB 2008 Scoring Guidelines
Form B
The College Board: Connecting Students to College Success
The College Board is a not-for-profit membership association whose mission is to connect students to college success and opportunity. Founded in 1900, the association is composed of more than 5,400 schools, colleges, universities, and other educational organizations. Each year, the College Board serves seven million students and their parents, 23,000 high schools, and 3,500 colleges through major programs and services in college admissions, guidance, assessment, financial aid, enrollment, and teaching and learning. Among its best-known programs are the SAT®, the PSAT/NMSQT®, and the Advanced Placement Program® (AP®). The College Board is committed to the principles of excellence and equity, and that commitment is embodied in all of its programs, services, activities, and concerns.
