关于复数的乘幂与方根
复变函数第一章(2)复数的乘幂与方根

n
n
注: (1)复数z的n次方根共有n个。
(2)几何意义:n z的n个值就在以原点为圆心,
n r为半径的圆内接正n边形的n个顶点。
例3:计算4 1 i
解:
因为
1i
2(cos i sin )
4
4
2k
2k
所以 4 1 i 8 2 (cos 4
i sin 4
复变函数w f (z)涉及4个变量x, y,u, v
我们需要两个平面去描述函数的图像。
我们取两个平面,分别称为z平面与w平面。
如果在z 平面上函数w f (z)的定义域D内取一点z0 ,
通过w f (z)在w平面上有相应的点w0对应。
当z取遍点集D时,w平面上有相应的点集G与之对应。
例7 两类常见的复变函数
n次多项式函数 P(z) a0 a1z a2 z 2 an z n
其中,a0 , a1, a2 , , an (an 0)为复常数,n为非负整数
有理函数 P(z) 其中,P(z), Q(z)为多项式函数。 Q(z)
1.4.2 复变函数的几何解释—映照
)
4
4
(k 0,1,2,3)
即
w0
8
2(cos i sin )
16
16
w1
8
2 (c os 9
16
i sin
9 )
16
w2
8
17
2 (c os 16
i sin 17
16
)
w2
w3
8
2 (c os 25
16
i sin
(完整word版)1.3复数的乘幂与方根
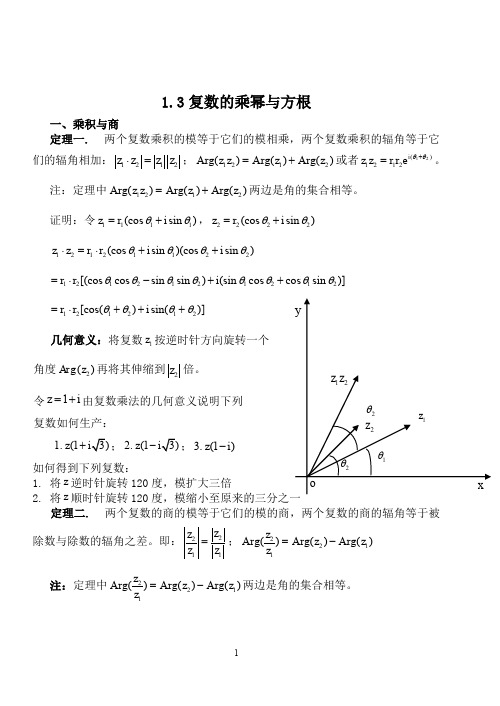
1.3复数的乘幂与方根一、乘积与商定理一.两个复数乘积的模等于它们的模相乘,两个复数乘积的辐角等于它们的辐角相加:1212z z z z ⋅=;1212rg()rg()rg()A z z A z A z =+或者12()1212i z z r r e θθ+=。
注:定理中1212rg()rg()rg()A z z A z A z =+两边是角的集合相等。
证明:令1111(cos sin )z r i θθ=+,2222(cos sin )z r i θθ=+12121122(cos sin )(cos sin )z z r r i i θθθθ⋅=⋅++1212121212[(cos cos sin sin )(sin cos cos sin )]r r i θθθθθθθθ=⋅-++ 121212[cos()sin()]r r i θθθθ=⋅+++几何意义:将复数1z 按逆时针方向旋转一个 角度2()Arg z 再将其伸缩到2z 倍。
令1z i =+由复数乘法的几何意义说明下列 复数如何生产:1.(1z +;2.(1z -;3.(1)z i -如何得到下列复数:1. 将z 逆时针旋转120度,模扩大三倍2. 将z 顺时针旋转120定理二.两个复数的商的模等于它们的模的商,两个复数的商的辐角等于被除数与除数的辐角之差。
即:2211z z z z =;2211rg()rg()rg()z A A z A z z =-注:定理中2211rg()rg()rg()z A A z A z z =-两边是角的集合相等。
证明:由除法定义21z z z =,即:21z zz =。
由定理一得:11z z z z ⋅=;11rg()rg()rg()A zz A z A z =+2211z z z z ∴=;2211rg()rg()rg()z A A z A z z =-定理一和定理二如果用复数的指数形式证明则更简单。
1.3复数的乘幂与方根
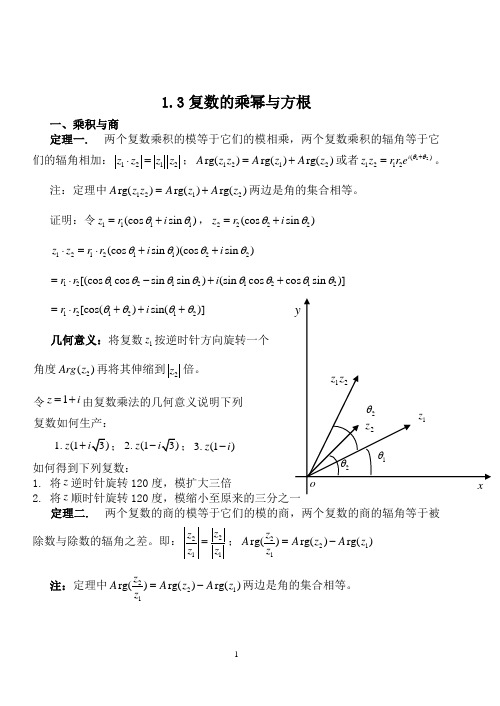
1.3复数的乘幂与方根一、乘积与商定理一.两个复数乘积的模等于它们的模相乘,两个复数乘积的辐角等于它们的辐角相加:1212z z z z ⋅=;1212rg()rg()rg()A z z A z A z =+或者12()1212i z z rr eθθ+=。
注:定理中1212rg()rg()rg()A z z A z A z =+两边是角的集合相等。
证明:令1111(cos sin )z r i θθ=+,2222(cos sin )z r i θθ=+12121122(cos sin )(cos sin )z z r r i i θθθθ⋅=⋅++1212121212[(cos cos sin sin )(sin cos cos sin )]r r i θθθθθθθθ=⋅-++ 121212[cos()sin()]r r i θθθθ=⋅+++几何意义:将复数1z 按逆时针方向旋转一个 角度2()Arg z 再将其伸缩到2z 倍。
令1z i =+由复数乘法的几何意义说明下列 复数如何生产:1.(1z +;2.(1z -;3.(1)z i -如何得到下列复数:1. 将z 逆时针旋转120度,模扩大三倍2. 将z 顺时针旋转120定理二.两个复数的商的模等于它们的模的商,两个复数的商的辐角等于被除数与除数的辐角之差。
即:2211z z z z =;2211rg()rg()rg()zA A z A z z =- 注:定理中2211rg()rg()rg()z A A z A z z =-两边是角的集合相等。
证明:由除法定义21z z z =,即:21z zz =。
由定理一得:11z z z z ⋅=;11rg()rg()rg()A zz A z A z =+2211z z z z ∴=;2211rg()rg()rg()zA A z A z z =- 定理一和定理二如果用复数的指数形式证明则更简单。
第一章3复数的乘幂与方根

第二节
复数的运算
一、复数的代数运算及共轭复数的运算法则
二、复数的代数运算的几何表示
三、复数的乘幂与方根
三、复数的乘幂与方根
1. 乘幂
设复数 ≠ 0, = (cos+sin),
则 = (cosn+sinn) ,为正整数.
规定 z
−n
1
= n.
z
), w3 = 2 (cos
+ i sin
),
16
16
16
16
1
8
1
8
这四个根是内接于以原点为圆心,半径为 2的圆的正方形的顶点
8
谢谢观看!
当 = , + 1, ⋯ 时,这些根又重复出现.
=
=
1
[cos
2 在几何上,
+ 2
+ 2
+ sin
], = 0,1,2, ⋯ , − 1
1
的个值是以原点为圆心, 为
半径的圆的内接正边形的个顶点.
例3.求 1 + .
4
解: 1 + = 2(cos + sin )
特别地,当 = 1时,得到棣莫弗公式
(cos+sin) = cosn+sinn.
2. 方根
z 称为的次方根.
设 z = r (cos + i sin ), w = (cos + i sin )
方程 wn = z 的根 w ,即 w =
n
n
有 (cos n + i sin n ) = r (cos + i sin )
1.2复数的运算及其几何意义

x1 ) y1 )
参数 t (, ),
上式可以借助复数合并为一个式子,即:
z x(t ) iy(t ) x1 t( x2 x1 ) + i [y1 t( y2 y1 )]. 过z1 , z2的直线方程是: z z(t ) z1 ), 0 t 1.
则将向量OZ1按逆时针方向
•z
y
旋转一个角 2 ,
r • z1
再伸长(缩短)到原来的 r2 倍,
所得向量OZ就表示乘积z1 z2.
1
o
r1
2
•
r2
z2
x
z1z2 r1r2[cos(1 2 ) i sin(1 2 )]
10
可将结论推广到 n 个复数相乘的情况:
设 zk rk (cosk i sink ) rkeik , (k 1,2,, n)
28
cos
π 4
2kπ 4
i sin
π 4
2kπ 4
w3
(k 0,1,2,3).
即 0
1
28
cos
π 16
i
sin
π 16
,
1
1
28
cos
9π 16
i
sin
9π 16
,
2
1
28
cos
17π 16
i
sin
17π 16
,
3
1
28
cos
25π 16
i sin
25π 16
.
15
;
(2) z z;
(3) z z z 2 ;
(4) z z 2 Re(z), z z 2i Im(z).
复数和、差、共轭的几何意义
复数的乘幂与方根

复数的乘幂与方根教学目的:掌握复数的乘幂与方根的计算方法,了解乘幂、方根的几何意义教学重点:掌握利用复数的三角表示式求解复数的乘幂与方根教学难点:理解乘幂与方根的几何解释,方根的计算方法教学类型:板书教学时数:1学时教学过程:1、乘幂的计算定义1 n 个相同的复数 z 的乘积称为 z 的 n 次幂,记为 z n.显然由定理1 及其推广可知,|z n|=|z|n; Arg z n=nArg z,即若 z=r(cosθ+i sinθ),则有z n=r n(cos nθ+i sin nθ).思考:若是用代数形式 z=x+iy 计算 z n难度有多大?例:计算 (1+i)100.,解:|1+i|=2+12=√2,θ=π4因此,(1+i)100=(√2)100(cos25π+i sin25π)=250(−1+i∙0)=−250.2、方根的计算n.定义2 若 w=z n,称 z 为 w 的 n 次方根,记为 z=√w分析:已知复数 w =r (cos θ+i sin θ),求复数z =ρ(cos φ+i sin φ),使得 w =z n 成立,即有r (cos θ+i sin θ)= ρn (cos nφ+i sin nφ).从上式中可以得到r = ρn ,θ+2kπ=nφ,k ∈Z .因此,ρ= r 1n , φ=θ+2kπn ⁄, k ∈Z ,z =√w n =r 1n (cos θ+2kπ+i sin θ+2kπ) 究竟有几个?k =0,1,2,⋯,n −1时,得到 n 个互异的值z 0=r 1n (cos θn +i sin θn ); z 1=r 1n (cos θ+2πn +i sin θ+2πn); ⋯⋯z n−1=r 1n (cos θ+2(n −1)πn +i sin θ+2(n −1)πn) 由三角函数的周期性,可知当 k 取其他整数值时,方根的值重复出现,因此可知 n 次方根有且仅有 n 个!综上所述,n 次方根的计算方法为(1) 将复数w =x +iy 表示成三角表示式w =r (cos θ+i sin θ)(2) √w n =r 1n (cos θ+2kπn +i sin θ+2kπn )(3) k =0,1,2,⋯,n −1例:计算√i 3.解:(1)r =|i |=1,θ=π2, w =i =r (cos θ+i sin θ);(2)√w 3=r 1(cosθ+2kπ3+i sin θ+2kπ3) =cos (1+4k)π6+i sin (1+4k)π6;(3)k =0,1,2.即√i 3 分别为z 0=cos π6+i sin π6;z 1=cos 5π+i sin 5π; z 2=cos 9π6+i sin 9π6. 注解 n 次方根的几何解释上述例子中的3个3次方根正好是以原点为中心以1为半径的圆的内接正三角形的三个顶点。
复数概念表示法乘幂与方根区域
背景
复数是十六世纪人们在解代数方程时引进的。 为使负数开方有意义,需要再一次扩大数系,使实 数域扩大到复数域。但在十八世纪以前,由于对复 数的概念及性质了解得不清楚,用它们进行计算又 得到一些矛盾,所以,在历史上长时期人们把复数 看作不能接受的“虚数”。直到十八世纪, J.D’Alembert(1717-1783)与L.Euler(17071783)等人逐步阐明了复数的几何意义和物理意义, 澄清了复数的概念,并且应用复数和复变函数研究 了流体力学等方面的一些问题。复数才被人们广泛 承认接受,复变函数论才能顺利建立和发展。
邻域复平面上以内部的点的集合称为点的折线连接属于中任意两点均可用完全区域边界与边界点已知点的任何邻域中都包含有界区域与无界区域若存在闭区域区域为圆点表示以re轴的直线几个点只是边界增加了一个或它仍然是区域几个点如果在其中去掉一个或组成它的边界由两个圆周而且是有界的表示一个圆环re表示下半复平面表示右半复平面实变函数表示为
2 2
• 判断复数相等
z z x x , y y , 其 z x 中 iy , z x iy 1 2 1 2 1 2 1 1 1 2 2 2 z 0 Re z ) Im ( z ) 0 (
一般, 任意两个复数不能比较大小。
2. 代数运算
•四则运算
3
例 2 : 求 1
3
解 : 1 co 0 i s 0 s i n
i i 1 2 设 z r e , z r e 1 1 2 2
证明
由复数除法的定义 z=z2 /z1,即 z1z = z2 ∵|z||z1|=|z2|及Argz1+Argz=Arg z2( z1≠0)
Argz=Argz2-Argz1 即:
复数的乘幂与方根
(15 8) (10 12)i 23 2
2
2
5 4
i 41 41
z 23 2 i 41 41
2
arg
z
arctan
41 23
41
+ arctan 2 +,
23
故 Argz arg z 2k arctan 2 (2k 1)
23 (k 0,1,2, ).
2.复数的乘幂
当 k=0,1,…,n-1 时,可得n 个不同的 根,而 k 取其它整数时,这些根又会重复出现。
几何上, n z 的 n个值是以原点为中心,n r 为半 径的圆周上 n个等分点,即它们是内接于该圆周 的正 n边形的 n个顶点。
例1 求 4 1 i
1 y
1 i
解: 1 i 2 ,
arg(1 i) , 2
定义
zn
1 zn
.
由定义:
z n
1 zn
1
r n (cos n i sin n )
r
n
cos n i sinn cos2 n sin2 n
r n[cos(n ) i sin(n )] r e n n .
3.复数的方根 (开方)——乘方的逆运算
问题 给定复数 z = re i ,求所有的满足ωn = z 的 复数ω。
1. 乘积与商
定理1 两个复数乘积的模等于它们的模相乘, 两个复数乘积的幅角等于它们的幅角相加。
即 z1 z2 z1 z2 Arg(z1 z2 ) Argz1 Argz2 .
证明 设 z1=r1(cosθ1+ isinθ1)= r1e iθ1 z2=r2(cosθ2+ isinθ2)= r2e iθ2
则 z1z2 = r1r2(cosθ1+ isinθ1)( cosθ2+ isinθ2)
复数的乘幂与方根
8 2(cos 4 4
i sin 4 4
)
(k 0,1, 2, 3)
解:将向量
z1
z2逆时针旋转
3
后得到的向量
z1
z3
学
或z1z3的终点即为所求.
复 变 函 数
z3
z1
(cos
3
i sin
3
)( z2
y
z1
)
与 积 分
( 1 i 3 )(1 i)
变 换
22
13 13
z3 z2
3 z2 z1
( ) ( )i
22 22
复
1 4
4
变 函 数
w2 r n (cos n i sin n )
与
积 分 变 换
wn1
1
r n (cos
2(n 1)
n
i sin
2(n 1)
n
)
而k取其它整数时,这些根又会重复出现。
哈
例1 求 3 1
尔
滨
工
程
大
学
例2 设z 1 i,求z4和4 z
z1
x
哈 尔
所以
z3
3 ( 2
31 )(
22
3 )i
2
滨 工 程
同理,若转角为 ,可得
大 学
3
y
复 变 函
z3
(3 2
3)(1 22
3 )i 2
数
与
积
分
1.1复数的乘幂(2)
π π − + 2kπ − 4 + 2kπ + i sin 4 1 − i = 6 2 cos 3 3 ( k = 0,1,2).
13
π π 即 w0 = 2 cos − + i sin − , 12 12
∴它的三个三次方单根为:
( −8i ) = 2e
也就是 k = 0, ⇒ ω0 = 2e
i(− ) 6
1 3
i(
− π 2 + 2 kπ ) 3
= 2e
π
π 2 i ( − + kπ ) 6 3
(k = 0,1, 2)
π
π
k = 1, ⇒ ω1 = 2e
i( ) 2
π
= 2(cos(− ) + i sin(− )) = 3 − i 6 6
6
当 k = 0,1,2,L, n − 1 时, 得到 n 个相异的根 :
θ θ w0 = r cos + i sin , n n
1 n
θ + 2π θ + 2π w1 = r cos + i sin , n n LLLLL,
1 n
θ + 2( n − 1)π θ + 2( n − 1)π wn−1 = r cos + i sin . n n
于是 ρ n = r , cos nϕ = cosθ , sin nϕ = sinθ , 显然 nϕ = θ + 2kπ,
故 ρ =r , ϕ =
1 n
( k = 0, ± 1, ± 2,L)
,
θ + 2kπ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
所得向量 z 就表示积 z1 ⋅ z2 .
o
y
[证毕 证毕] 证毕
从几何上看, 从几何上看 两复数对应的向量分别为 z1 , z2 ,
z ρ
ρ1
z1 z ρ 22
x
两复数相乘就是把模相乘, 辐角相加. 两复数相乘就是把模相乘, 辐角相加.
3
z 特别地, 2 = 1时,只需旋转一个角度ϕ 2就行了,
( k = 0, ±1, ±2,⋯ , )
12
当 k = 0,1,2,⋯, n − 1 时, 得到 n 个相异的根 :
w0 = ρ e n ,
1 n
i
ϕ
w1 = ρ e
1 n
i[
ϕ + 2π
n
]
⋯⋯⋯⋯⋯,
w n −1 = ρ e
1 n
i[
ϕ + 2( n −1)π
n
]
以其他整数值代入时, 当k以其他整数值代入时 这些根又重复出现 以其他整数值代入时 这些根又重复出现.
10
(1 + i )n + (1 − i )n =
cos π i sin π π π n ( 2) + + ( 2 ) cos − 4 + i sin − 4 4 4
n n
n
nπ nπ nπ nπ = ( 2 ) cos + i sin + cos − i sin 4 4 4 4
三
复数的乘幂与方根
1、乘积与商 2、幂与根 3、小结与思考
1、乘积与商 两个复数乘积的模等于它们的模的乘积; 两个复数乘积的模等于它们的模的乘积 两个复数乘积的辐角等于它们的辐角的和. 两个复数乘积的辐角等于它们的辐角的和 证
设复 数z1和z2的指数形式分别 为
z1 = ρ1e , z 2 = ρ 2 e
若 m = n = 0,
则k = 1
5
Argz 注意: 即辐角主值, 注意: 可以换成 argz 即辐角主值,此时
的整数倍。 大家应该注意两端允许相差 2π 的整数倍。即
arg(z1z2 ) = argz1 + argz2 + 2kπ.
由此可将结论推广到 n 个复数相乘的情况 个复数相乘的情况:
设 zk = ρk (cos ϕk + i sin ϕk ) = ρk e iϕk , (k = 1, 2,⋯, n)
z1 ⋅ z2 ⋅⋯⋅ zn = ρ 1 ⋅ ρ 2 ⋅ ⋯ ⋅ ρ n e i ( ϕ
1 +ϕ 2
+⋯ϕ n )
.
6
两个复数的商的模等于它们的模的商; 两个复数的商的模等于它们的模的商 两个复 数的商的辐角等于被除数与除数的辐角之差. 数的商的辐角等于被除数与除数的辐角之差 证 设复数 z1和 z 2的指数形式分别为
应熟练掌握复数乘积与商的运算. 应熟练掌握复数乘积与商的运算 在各种 形式中以三角形式、指数形式最为方便 形式中以三角形式、指数形式最为方便:
z1 ⋅ z2 = ρ1 ⋅ ρ 2 e
i (ϕ1 + ϕ 2 )
z 2 ρ 2 i (ϕ 2 −ϕ1 ) e . = z1 ρ1
棣莫佛( 棣莫佛(de Moivre)公式
n
=2
n+ 2 2
nπ cos . 4
11
(2) n次方根 次方根
已知z =ρ e ,求z的n次方根
iϕ
相当于求方程 w = z 的根 w , 其中 z =ρ e
n
iϕ
wk = z = ρ e
n 1 n1 nຫໍສະໝຸດ i(ϕ + 2 kπ
n
)
ϕ + 2kπ ϕ + 2kπ = ρ cos + i sin n n
则z1 ⋅ z2 = ρ1e
iϕ1
iϕ1
iϕ 2
,
⋅ ρ 2e
iϕ 2
= ρ1 ρ 2 e
i ( ϕ1 + ϕ 2 )
2
z1 ⋅ z2 = ρ1 ⋅ ρ 2 e
i ( ϕ1 + ϕ 2 )
Arg( z1 z2 ) = Argz1 + Argz2 .
先把 z1 按逆时针方向 旋 转一个 角 ϕ 2 ,
8
17
cos 17 π i sin 17 π , w2 = 2 + 16 16
8
cos 25π i sin 25π . w3 = 2 + 16 16
8
w1
y
这四个根是内接于中 心在原点半径为 2 的
8
w0
w2
o
x
圆的正方形的四个顶点 .
w3
18
三、小结与思考
iz相当于将z所对应的向量 OZ 沿逆时针方向旋转
→
→
π
2
-z相当于将z所对应的向量 OZ 沿逆时针方向旋转π
-iz相当于将z所对应的向量 OZ 沿顺时针方向旋转
→
π
2
4
说明 由于辐角的多值性 Arg( z1 z2 ) = Argz1 + Argz2 由于辐角的多值性, 两端都是无穷多个数构成的两个数集. 两端都是无穷多个数构成的两个数集 对于左端的任一值, 右端必有值与它相对应. 对于左端的任一值 右端必有值与它相对应 例如, 例如,设 z1 = −1, z2 = i , 则 z1 ⋅ z2 = − i , Argz1 = π + 2nπ, ( n = 0, ± 1, ± 2,⋯), π Argz2 = + 2m π, ( m = 0, ± 1, ± 2,⋯), 2 π Arg( z1 z2 ) = − + 2kπ, ( k = 0, ± 1, ± 2,⋯), 2 3π π 故 + 2( m + n)π = − + 2kπ, 只须 k = m + n + 1. 2 2 若 k = −1, 则 m = 0, n = −2 或 m = −2, n = 0.
8
i
−
π
6
i
2、幂与根 、 (1). n次幂 次幂: 次幂 n 个相同复数 z 的乘积称为 z 的 n 次幂 ,
记作 z n , z n = z ⋅ z ⋅ ⋯ ⋅ z .
n个
对 于 任 何 整 数 n, n n 有 z = [ ρ (cos ϕ + i sin ϕ )] = [ ρ e iϕ ]n
=ρ n e inϕ =ρ n (cos nϕ + i sin nϕ ). 当 z 的模 ρ = 1, 即 z = cos ϕ + i sin ϕ , n (cos ϕ + i sin ϕ ) = cos nϕ + i sin nϕ .
棣莫佛公式
9
例2 解
化简 (1 + i )n + (1 − i )n .
(cos ϕ + i sin ϕ )n = cos nϕ + i sin nϕ .
放映结束, Esc退出. 放映结束,按Esc退出. 退出
19
1 1 1 + i = 2 i + 2 2 cos π i sin π = 2 + 4 4 1 1 1 − i = 2 i − 2 2
π π = 2 cos − + i sin − 4 4
6
cos 7 π i sin 7 π , w1 = 2 + 12 12
6
cos 5π i sin 5π . w2 = 2 + 4 4
6
16
例5
计算 4 1 + i 的值.
cos π i sin π 解 1 + i = 2 + 4 4 π π + 2kπ + 2kπ 8 4 1 + i = 2 cos 4 + i sin 4 ( k = 0,1,2,3). 4 4 cos π i sin π , 8 即 w0 = 2 + 16 16 cos 9π i sin 9π , w1 = 2 + 16 16
z1 = ρ1e , z2 = ρ 2 e ,
iϕ1
iϕ 2
z 2 ρ 2 i ( ϕ 2 − ϕ1 ) e . [证毕 则 = 证毕] 证毕 z1 ρ1
7
1 π π 例1 已知 z1 = (1 − 3i ), z2 = sin − i cos , 2 3 3 z1 求 z1 ⋅ z2 和 . π z2 π − i π =e 3 解 因 为 z 1 = cos − + i sin −
z 的 n 个值就是以原点为中心 ,
ρ 为半径的圆的内接正 n 边形的 n 个顶点.
14
例4 解
计算 3 1 − i 的值. 1 1 1 − i = 2 i − 2 2
π π = 2 cos − + i sin − 4 4
3 3 π π π − i z 2 = cos − + i sin − = e 6 6 6
π π − 3− 6 i
z1 ⋅ z 2 = e
z1 =e z2
π π − 3+ 6
=e =e
−
π
2
i
= −i ,
3 1 = − i. 2 2
13
例如 k = n 时,
wn = ρ e
1 n
1 n
i[
