粘性流体运动微分方程(了解性学习)讲解
第七章粘性流体动力学

D
x
三边长为dx, , , 点坐标为 点坐标为( 三边长为 ,dy,dz,A点坐标为(x,y,z) ) 对微小平面可以为其上面具有相同的应力 由于τ的存在 表面力不垂直表面, 的存在, 由于 的存在,表面力不垂直表面,为τ 的合力方向。 和p的合力方向。 的合力方向 外法线方向为正, 设p外法线方向为正,过A点三个平面上切 外法线方向为正 点三个平面上切 力方向与坐标轴相同。 力方向与坐标轴相同。 在直角坐标系下, 上的相关应力可以 在直角坐标系下,AC上的相关应力可以 分解为 pxx τ xy τ xz
N—S方程的说明: 方程的说明: 方程的说明 a. 对理想流体 对理想流体ν=0,N—S变成欧拉微分方 , 变成欧拉微分方 对于静止流体, 程 。 对于静止流体 , N—S方程中的惯性 方程中的惯性 力项为0,变为欧拉平衡方程。 力项为 ,变为欧拉平衡方程。 b. N—S方程适用于不可压缩流体 方程适用于不可压缩流体 c. N—S方程适用于牛顿流体 方程适用于牛顿流体 d. 对真实流体 对真实流体N—S适用于不同流态,对 适用于不同流态, 适用于不同流态 紊流时,转变为时均流场的雷诺方程。 紊流时,转变为时均流场的雷诺方程。 e. N—S方程有 p vx v y vz 四个未知量,补 四个未知量, 方程有 充连续方程理论上可以解
p yy τ yx τ yz AD面上的应力为 pzz τ zx τ zy 面上的应力为
AB面上的应力为 面上的应力为
τ,p下标中, 第一个表示与平面垂直的 , 下标中 下标中, 坐标轴, 坐标轴, 第二个表示与应力作用线平行 的坐标轴,这样,六个面上有18个应力 的坐标轴 , 这样 , 六个面上有 个应力 将六面体向A点缩小 三个面上的9个 点缩小, 若 将六面体向 点缩小,三个面上的 个 应力就表示A点的应力 因此, 点的应力, 应力就表示 点的应力 , 因此 , 粘性流 体中任一点的应力由9个分量组成 个分量组成。 体中任一点的应力由 个分量组成。 以过六面体中心M及平行 轴的直线为准 以过六面体中心 及平行x轴的直线为准 及平行 ,对该直线取力矩 定义:逆时针力矩为正,顺时针为负, 定义:逆时针力矩为正,顺时针为负, 对该直线力矩和为
粘性流体运动微分方程(了解性学习)讲解

一、粘性流体的特点
粘性流体运动微分方程
(1)粘性流体的表面力包括:压应力和粘性引起的切应力。
xy ( yz ( zx (
u x y u y z u z x
u y x u z y
) yx ) zy ) xz
二阶非线性非齐次偏微分方程组
四个未知量ux,uy,uz和 p
N-S方程与连续性微分方程4个
理论上可 以求解
只能对一些简单的流动问题,如圆管中的层流 等,求得精确解。 对于大多数较复杂的不可压缩粘性流体的流动问 题,难以用该方程求出精确解。
计算流体力学的发展,可以用该方程求得许多复 杂流动的近似解。
无法求解
z方向
9个应力,3个速度分量,共12个未知数
3个方程加上连续性方程,共4个方程
补充关系式: 1、切应力和角变形速度的关系
yz zx xy
u z u y zy y z u x u z xz x z u y u x yx x y
u x t u y t u z t
u u u
u x x x
u u u
u x y y
u u u
u x z z
v u y
2
u y x x
u y y y
u y z z
v u
2
u z x x
u z y y
u z z z
zx z
dz )dxdy]
化简后得 x方向 y方向
1 pxx 1 yx zx dux X x y z dt 1 p yy 1 zy xy duy Y y z x dt 1 pzz 1 xz yz duz Z z x y dt
5-粘性流体力学基础

fm
1
p v2u
v ( u) 3
式(7—5d)是在 Const 条件下对一切牛顿流体都普遍
适用的运动微分方程式,亦称之为纳维—斯托克斯方程。
14
方程的物理意义:
左边 du 为流体质点加速度(单位质量流体的惯性力); dt
右边
f
为作用在流体微团上单位质量的质量力;
m
- 1 p为作用在流体微团上单位质量流体的压强合力;
0.3
将已知数据代入前式得 Q 0.016 cm2 s ,与按同心环形缝隙
流动计算结果相同。
29
§7-5 绕流圆球的小雷诺数流动
在工程实际中,我们经常要研究固体微粒和液体细滴在流体
中的缓慢运动,这里,圆球是经常遇到的几何形状。如炉膛空气
流中的煤粉颗粒,油滴,烟道烟气中的灰尘,水蒸气中的水滴以
及水中沉降的泥砂等,都可以近似看作小圆球。对这些小圆球的
2 z
u y x
ux y
yz
zy
2 x
uz y
u y z
(7—3)
zx
xz
2 y
ux
z
uz x
式(7—3)称为广义牛顿内摩擦定律。
8
在粘性流体中,与角变形速度产生切应力一样,线变形 速度产生附加切应力。根据牛顿内摩擦定律
xx
2
ux x
yy
2
u y y
zz
2
uz z
(7—4)
式(7—3)、(7—4)为本构方程。
2 r2
ur
2 r2
u
2 r2
u
cos
2
r 2 cos
u
ur t
ur
ur r
不可压缩粘性流体的运动微分方程名师优质资料

2 v x ~1 2 x
v 1 x ~ y
2 vx 1 ~ y2 2
然后,再来求出其它各量的数量级,由连续方程
,于是又得到以下数量级: 因此 v y ~
v y ~ x 2 v y ~ 2 x v y ~1 y 2 v 1 y ~ 2 y
边界层内,这是由于层外的流体质点不断地穿入到边界层里 去的缘故。
总结上面所述,边界层的基本特征有:
• 与物体的长度相比,边界层的厚度很小; •边界层内沿边界层厚度的速度变化非常急剧,即速
度梯度很大;
•边界层沿着流体流动的方向逐渐增厚;
•由于边界层很薄,因而可近似地认为,边界层中各
截面上的压强等于同一截面上边界层外边界上的压强;
o 图8-2 分析切向应力之间的关系用图
x
根据达朗伯原理,作用于微元平行六面体上的各力对通过中心 M并与z轴相平行的轴的力矩之和应等于零。又由于质量力和 惯性力对该轴的力矩是四阶无穷小量,可以略去不计,故有
yx xy dz dy dx dx yx dxdz yx dy dxdy xy dydz xy dx dydz 0 2 y 2 2 x 2
(8-37)
v v y x 0 x y 1 1
式中 Re l vl 。很显然,在边界层内, vx与v、x与l 以及y 与 是同一数量级,于是可取 v , x ~ 1和y ~ x ~1
(符号~表示数量级相同),所以得到如下一些数量级:
v x ~1 x
现将切向应力和法向应力的关系式代入 式(8-1),化简可得不可压缩粘性流体的运动微 分方程:
纳维-斯托克斯(Navier-Stokes)方程
最新传递过程原理讲课提纲04粘性流体运动的微分方程及其应用2

传递过程原理讲课提纲04粘性流体运动的微分方程及其应用2仅供学习与交流,如有侵权请联系网站删除 谢谢36§2—4 N —S 方程在柱坐标及球坐标中的表示 1. 柱坐标中的表示x= rcos αy= rsin αz= z在r 分量方向 zuu r u u r u r u u u r z r r r r ∂∂+-∂∂+∂∂+∂∂2αααθ = ()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂+∂∂-2222222111z u u r u r ru r r r r p X r rr r ααυρα 在α分量方向zuu r u u u r u r u u u z r r ∂∂++∂∂+∂∂+∂∂αααααααθ = ()⎭⎬⎫⎩⎨⎧∂∂+∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂+∂∂-2222222111z u r u r u r ru r r r p r X r αααααυαρ 在z 分量方向zuu u r u r u u u z z z z r z ∂∂+∂∂+∂∂+∂∂αθα = ]1)(1[122222z u u r r u r r r z p X zz z z ∂∂+∂∂+∂∂∂∂+∂∂-αυρ 2. 球坐标中的表示x= (rsin α)cos φ y= (rsin α)sin φ z= rcos α r 分量:yy图 19仅供学习与交流,如有侵权请联系网站删除 谢谢36ru u u r u u r u r u u u r r r r r 22sin φαφαφααθ+-∂∂⋅+∂∂+∂∂+∂∂ ]sin 1)(2sin 1sin sin 11[122222222φαααφαααααυρφαα∂∂++∂∂+-∂∂+⎪⎭⎫⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂-u ctg u u u r u r u r r u r r r r p X r r rr r =α分量:rctg u r u u u r u u r u r u u u r r αφααθφααφαααα2sin -+∂∂⋅+∂∂+∂∂+∂∂]sin cos 2sin 2sin 1sin sin 11[11222222222222φααααφαααααυαρφααααα∂∂--∂∂+∂∂+⎪⎭⎫⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂-u r r u u r u r u r r u r r r p r X r =φ分量:r ctg u u r u u u r u u r u ru u u r r rθφααθφφφφφαφφ++∂∂⋅+∂∂+∂∂+∂∂sin ]sin cos 2sin sin 2sin 1sin sin 11[sin 112222222222222φαααφαφαααααυφαραφφφφφ∂∂+-∂∂+∂∂+⎪⎪⎭⎫⎝⎛∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂-u r r u u r u r u r r u r r r p r X r =§3 流体运动方程的应用§3-1 平壁间的稳定层流设平板无限大,相互平行,作层流运动一维稳定流动,不可压缩于是 u y =u z=0 (1)x图 20仅供学习与交流,如有侵权请联系网站删除 谢谢36由连续性方程有0=∂∂xu x(2) 又对稳定流动0=∂∂θxu (3) 故N —S 方程简化为:)(12222zu y u X x px x ∂∂+∂∂+=∂∂υρ 对无限大平板可认为 0=∂∂z u x故022=∂∂zu x , 又在x 方向 X = 0于是 222211dy u d dx dpy u x p x x υρυρ=⇒∂∂=∂∂ 边界条件(Boundary Condition) y=y 0, u x =0 初始条件(Initial condition) y=0,0=dydu x于是 ()22021y y dx dp u --=μ 及 ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛-=2max 1y y u u 式中: dxdpy u ⋅-=20max 21μ 又设平板的宽度为w ,则流体流过二平行平板间的体积流量为⎰⎰⎪⎭⎫ ⎝⎛-===Ay v y dx dp w udy w udA Q 0300322μ 另一方面,若设平板间的主体流速(即截面平均流速)A图 21仅供学习与交流,如有侵权请联系网站删除 谢谢36为u b 则有Q V =u b ·B ·(2y 0) 可得: 2031y dx dp u b ⎪⎭⎫ ⎝⎛-=μ 故32=x b u u 及 203y u dx dp b μ-= §3-2 圆形直管内的稳定层流 化工原理中已得出了相应的结论。
粘性流体-PPT

现在,我们将考虑定常流。例如,若讨论绕固体得流动(为 确定起见,下面我们将讨论这种情况),则来流速度应为常数。 此外还假设流体就是不可压缩得。
在流体动力学方程组(纳维-斯托克斯方程组)里,就表征流
体本身特性得参数而言,只出现运动粘性系数
。还有,求
解这个方程组所必须确定得未知函数就是速度 和 ,这里
类似得,我们可以写出流体中得压力分布公式。为此, 我们必须由参数 和 作出某个量纲为压力除以密度得 量,比如,这个量可以就是 。于就是, 就是无量纲变 量 和无量纲参数R得函数,所以
最后,类似得考虑也可适用于这样一些量:她们描写流
动得特性,但不就是坐标得函数。例如作用在物体上得阻力
F就就是这样一个量。我们可以说,阻力F与用
不难写出周围流体作用于固体表面得力得表达式。 一个面元上所受得作用力恰等于通过这个面元得动量通 量。通过面元 得动量通量就是
把 写成
得形式,这里 就是沿法线得单位
矢量,并考虑到在固体表面上
,我们得到作用在单位
面积上得力 为
其中等式右边第一项就是普通得流体压力,而第二项就是由 于粘性引起得作用在固体表面上得摩擦力。式中 就是单 位矢量,她沿流体界面得外法线,即沿固体表面得内法线。
组成得并具有力得量纲得某个量之比必定只就是雷诺数得
函数。比如,
组合成力得量纲可以就是
。
因而
若重力对流动有重要作用,则流动不就是由三个参数确
定,而就是由
和重力加速度 这四个参数确定。由
这四个参数可构成两个独立得无量纲量,而不就是一个。比
如,这两个量可以就是雷诺数和弗劳德数,弗劳德数为
最后,提一下非定常流。要描述一个确定类型得非定常
第四节 两个旋转圆柱面之间得流动
5.1 粘性流体运动微分方程式

xy x
dx
yy
yy y
dy
惯性力: dv y dxdydz dt
x
zy
y D
o
二.以应力形式表示的运动微分方程: 列平行六面体流体微元y方向的力平衡方程:
dvy xy yy zy f y dxdydz dxdydz 0 dxdydz y z dt x 同理可得x方向和z方向的运动微分方程: 1 xx yx zx dvx fx x y z dt
不可压缩粘性流体的N-S方程
2.法向应力与应变速度的关系:
vx xx p 2 x v y yy p 2 y vz zz p 2 z
粘性流体法向应力与应变速度关系的本构方程
四.纳维-斯托克斯方程(N-S方程): 1 xx yx zx dvx fx x y z dt x方向的微分方程式:
z
A
zy
y D
o
二.以应力形式表示的运动微分方程: 平行六面体流体微元y方向受力情况: 表面力:
xy yy zy dxdydz y z x
B C
zy
zy z
dz
xy
yy
A
质量力:
f y dxdydz
z
xy
C
边长:dx,dy,dz
中心:M点
B M A z dy dz dx y D
o
x
在流场中取微小平行六面体流体微元ABCD,分析其受力情况: 顶点:A(x,y,z)
C
边长:dx,dy,dz
中心:M点
第五讲 粘性流动NS方程
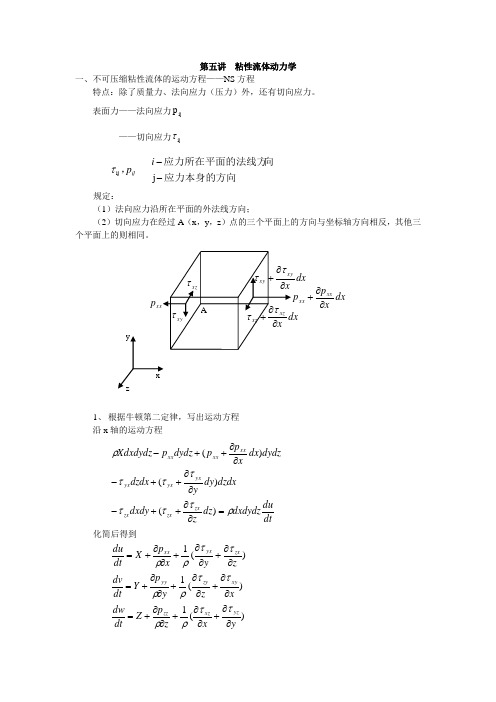
第五讲 粘性流体动力学一、不可压缩粘性流体的运动方程——NS 方程特点:除了质量力、法向应力(压力)外,还有切向应力。
表面力——法向应力ij p——切向应力ij τ应力本身的方向向应力所在平面的法线方,--j ij i p ij τ规定:(1)法向应力沿所在平面的外法线方向;(2)切向应力在经过A (x ,y ,z )点的三个平面上的方向与坐标轴方向相反,其他三个平面上的则相同。
1、 根据牛顿第二定律,写出运动方程沿x 轴的运动方程 dt du dxdydz dz z dxdy dzdx dy y dzdx dydz dx x p p dydz p Xdxdydz zx zxzx yxyx yx xx xx xx ρττττττρ=∂∂++-∂∂++-∂∂++-)()()( 化简后得到 )(1)(1)(1yx z p Z dt dw xz y p Y dt dv zy x p X dt du yz xz zz xy zy yy zx yx xx ∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+=ττρρττρρττρρdx x p xx xx ∂∂+九个应力和三个速度分量均为未知数,四个方程。
2、 切向应力之间的关系由达朗伯原理,对M 点力矩之和为0;质量力和惯性力对该轴的力矩是四阶小量,略去不计,得到02)(22)(2=∂∂+++∂∂+--dx dydz dx x dx dydz dy dxdz dy y dy dxdz xy xy xy yx yx yx ττττττ 再略去四阶小量,得到xzzx zx yz yxxy ττττττ===则九个应力中只有六个是独立变量。
3、 广义牛顿内摩擦定律速度梯度等于流体微团的角变形速率,则有y xz x yzz xy e xw z u e z v y w e y u x v μμτμμτμμτ2)(2)(2)(=∂∂+∂∂==∂∂+∂∂==∂∂+∂∂=4、 法向应力对于理想流体 p p p p zz yy xx -===对于粘性流体,有线变形,使法向应力有变化,产生附加的法向应力,关系式如下。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
补充了3个方程,多 一个未知数 pt
粘性流体中,任意点的动压强 p 是过该点三个 相互正交平面上法向应力的平均值。
1 2 ux u y uz p (p xx p yy pzz ) p t 3 3 x y z
对于不可压缩粘性流体
广义牛顿内摩 擦定律
u x z
应力符号的第一个脚标表示作用面的外法线方向;第二个 脚标表示应力的方向。 (2)粘性流体任一点的动压强,由于粘性切应力的存在,各 方向大小不等,即pxx pyy pzz。
二、以应力表示的粘性流体运动微分方程
z
'zy
xy xz
dz
pxx
dy dx
yx pyy yz p'xx 'xz p'yy 'yz 'xy 'yx pzz zx zy
二阶非线性非齐次偏微分方程组
四个未知量ux,uy,uz和 p
N-S方程与连续性微分方程4个
理论上可 以求解
只能对一些简单的流动问题,如圆管中的层流 等,求得精确解。 对于大多数较复杂的不可压缩粘性流体的流动问 题,难以用该方程求出精确解。
计算流体力学的发展,可以用该方程求得许多复 杂流动的近似解。
补充了6个方程
2、法向应力和线变形速度的关系
u x p xx pt p ' xx pt 2 x pt——理想流体压强 u y p yy pt p ' yy pt 2 理想流体中,同一点各方向的法 y 向应力相等 pxx= pyy = pzz=pt uz pzz pt p ' zz pt 2 z
xHale Waihona Puke p'zz’zx
x方向(牛顿第二运动定律)
y
p xx Xdxdydz [ pxx dydz ( pxx x dx )dydz ]
[ yx dxdz ( yx
x dxdydz du dt
yx y
dy )dxdz] [ zxdxdy ( zx
p =p t
三、不可压缩粘性流体运动微分方程
——纳维一斯托克斯方程(N-S方程) 将补充的关系式代入以应力表示的粘性流体 运动微分方程,整理后得到
X Y Z
1 p x 1 p y 1 p z
v u x
2
du x dt du y dt du z dt
zx z
dz )dxdy]
化简后得 x方向 y方向
1 pxx 1 yx zx dux X x y z dt 1 p yy 1 zy xy duy Y y z x dt 1 pzz 1 xz yz duz Z z x y dt
无法求解
z方向
9个应力,3个速度分量,共12个未知数
3个方程加上连续性方程,共4个方程
补充关系式: 1、切应力和角变形速度的关系
yz zx xy
u z u y zy y z u x u z xz x z u y u x yx x y
第八节
一、粘性流体的特点
粘性流体运动微分方程
(1)粘性流体的表面力包括:压应力和粘性引起的切应力。
xy ( yz ( zx (
u x y u y z u z x
u y x u z y
) yx ) zy ) xz
u x t u y t u z t
u u u
u x x x
u u u
u x y y
u u u
u x z z
v u y
2
u y x x
u y y y
u y z z
v u z
2
u z x x
u z y y
u z z z
