高中物理竞赛第12章气体动理论(共56张PPT)
合集下载
高二物理竞赛课件：气体动理学理论
统计规律：对大量偶然事件整体起作用的稳定的规律.
例： 1. 掷骰子
2.伽尔顿板实验
一个小球落在哪里
有偶然性；少量小球 的分布每次都可能不
同；当小球数 N 足
够大时小球的分布具 有统计规律。
............ ........... ............ ........... ............ ........... ............
6.1 气体动理学的基本概念
一. 热力学系统
➢ 热力学系统：是一个由大量的微观 粒子（原子、分子）组成的宏观系 统，简称系统。
➢ 外界（环境）: 系统以外的部分。系 统与外界之间可通过交换能量(做功， 热传递)和交换物质而相互作用。
外 界
热力学系统
孤立系统：系统与外界不发生任何相互作用。 （既无能量交换、又无物质交换）
利用扫描隧道显 微镜技术，把一个个 原子排列成 IBM 字 母的照片.
对于由大量分子组成的热力学系统从微观上加 以研究时, 必须用统计的方法.
(1) 分子的数密度和线度
阿伏伽德罗常数：1 mol 物质所含的分子（或原 子）的数目均相同 .
NA 6.0221367(36) 1023 mol1
n 分子数密度（ ）：单位体积内的分子数目.
封闭系统：系统与外界只有能量交换而无物质交换。 开放系统：系统与外界既有能量交换又有物质交换。
二. 宏观量和微观量
宏观状态与宏观量：描述一个系统宏观性质的可观测物 理量，称为宏观量，它表征大量分子无规则运动的集体 效果和平均效果。如：温度（T）、压强（p）、体积 （V）、内能（E）、热容量（C）等。用宏观量表征 的系统状态，称为宏观状态。 微观状态与微观量：在一定的宏观状态下, 系统内大量 分子仍在不停地进行无规则运动(热运动), 对应于每个 时刻系统处于不同的力学状态(位置、速度)，称为微观 状态。任一时刻, 表征系统中个别分子或整体性质的物 理量称为微观量，如每个分子的瞬时速度、瞬时动能 或系统的瞬时总动能(所有分子动能之和)等. 宏观与微观的关系：一个宏观状态, 对应着大量的不同 的微观状态。宏观量等于微观量的统计平均值。
12气体动理论 (1)
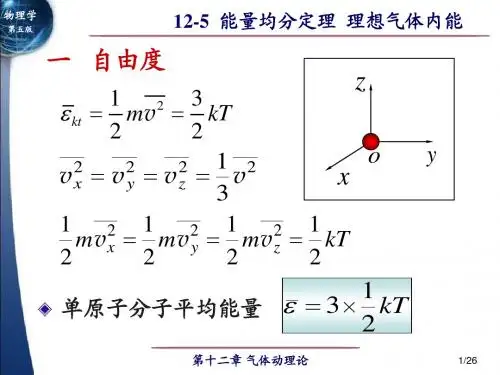
1 T 一定时 λ ∝ p p 一定时 λ ∝ T
25/26
第十二章 气体动理论
物理学
第五版
12-8 分子平均碰撞次数和平均自由程 试估计下列两种情况下空气分子的平均自由程: 例 试估计下列两种情况下空气分子的平均自由程 （1）273 K、1.013 ×105 Pa 时； ） （2） 273 K、1.333 × 10 −3 Pa 时。 ） d = 3.10×10−10 m） （空气分子有效直径
第十二章 气体动理论
1/26
z
物理学
第五版
12-5 能量均分定理 理想气体内能
刚性双原子分子 分子平均平动动能
ε kt
1 1 1 2 2 2 = m v Cx + m v Cy + m v Cz 2 2 2
分子平均转动动能
1 1 2 ε kr = J ω y + J ω z2 2 2
第十二章 气体动理论
第十二章 气体动理论
4/26
物理学
第五版
12-5 能量均分定理 理想气体内能
刚性分子能量自由度 刚性分子能量自由度 自由度 分子 单原子分子 双原子分子 多原子分子
t 平动
3 3 3
r
转动 0 2 3
i
总 3 5 6
第十二章 气体动理论
5/26
物理学
第五版
12-5 能量均分定理 理想气体内能
能量均分定理（玻耳兹曼假设） 二 能量均分定理（玻耳兹曼假设）
∆S
o
v1 v2
v
∆N = N
∫
v2 v1
f ( v )d v
12/26
第十二章 气体动理论
物理学
第五版
气体动理论
上一张 下一张 返回
三Hale Waihona Puke 、 压 强 推 导上一张 下一张
返回
具有速度 vi 的Ni 个分子作用：
上一张 下一张 返回
上一张 下一张 返回
压强公式的推导过程：
• 对象：理想气体的微观模型。
• 状态：平衡态。
• 方法：个别分子服从力学规律，
•
大量分子服从统计规律。
• 结论：P = n m v 2/ 3
即:
（1） f (v) dN Ndv
f (v)表示在速率v 附近 单位速率间隔内的分子数 占总分子数的比率.
（2） f (v)dv dN N
表示速率在 v~v+dv 区间 内的分子数占总分子数的比 率，即阴影1 面积。
（3） v2 f (v)dv N
v1
N
表示速率在 v1~ v2 区间 内的分子数占总分子数的 比率， 即阴影2 面积。
• Q：系统与外界的热交换。 Q>0表示系统从外界吸热；Q<0表示系统向外 界放热。
• E：系统内能的改变量。 E>0表示系统内能增加（若是理想气体，则 温度升高)；E<0表示系统内能减少。
• A：系统对外界的做功情况。 A>0表示系统对外界作正功，如体积膨胀的过 程；A<0表示系统对外界作负功，亦即外界对 系统做功。
不可逆 可逆.
上一张 下一张 返回
有关物质结构与运动规律的 三条基本定理
• 宏观物体有大量微粒组成。 • 分子间存在相互作用力。 • 分子永不停息地无规运动。
上一张 下一张 返回
气体分子运动的特点：
• 看作是惯性支配下的自由运动。 • 分子间存在频繁碰撞。 • 服从统计规律。
三Hale Waihona Puke 、 压 强 推 导上一张 下一张
返回
具有速度 vi 的Ni 个分子作用：
上一张 下一张 返回
上一张 下一张 返回
压强公式的推导过程：
• 对象：理想气体的微观模型。
• 状态：平衡态。
• 方法：个别分子服从力学规律，
•
大量分子服从统计规律。
• 结论：P = n m v 2/ 3
即:
（1） f (v) dN Ndv
f (v)表示在速率v 附近 单位速率间隔内的分子数 占总分子数的比率.
（2） f (v)dv dN N
表示速率在 v~v+dv 区间 内的分子数占总分子数的比 率，即阴影1 面积。
（3） v2 f (v)dv N
v1
N
表示速率在 v1~ v2 区间 内的分子数占总分子数的 比率， 即阴影2 面积。
• Q：系统与外界的热交换。 Q>0表示系统从外界吸热；Q<0表示系统向外 界放热。
• E：系统内能的改变量。 E>0表示系统内能增加（若是理想气体，则 温度升高)；E<0表示系统内能减少。
• A：系统对外界的做功情况。 A>0表示系统对外界作正功，如体积膨胀的过 程；A<0表示系统对外界作负功，亦即外界对 系统做功。
不可逆 可逆.
上一张 下一张 返回
有关物质结构与运动规律的 三条基本定理
• 宏观物体有大量微粒组成。 • 分子间存在相互作用力。 • 分子永不停息地无规运动。
上一张 下一张 返回
气体分子运动的特点：
• 看作是惯性支配下的自由运动。 • 分子间存在频繁碰撞。 • 服从统计规律。
物理竞赛热学气体动理论 固体 液体 物态变化
积分可以求出速率范围在v1－v2内分子数占总 分子数的比率为
N v2 f v dv v1 N
归一化条件
f ( v ) dv 1
0
平均值
v vf ( v)dv
0
v v f ( v)dv
2 2 0
二、麦克斯韦速率分布 早在1859年，英国物 理学家麦克斯韦利用平衡 态理想气体分子在三个方 向上作独立运动的假设导 出了麦克斯韦速率分布， 其表达式如下：
因而分子的每一个平动自由度的平均动能都为
1 1 1 1 1 2 1 2 2 2 mv x mv y mv z ( mv ) kT 2 2 2 3 2 2
按照统计力学的基本原理，可将上述结论推广 到分子的转动和振动，因为无论是平动、转动还是 振动，都没有哪一个自由度是特别优越的，或者说 跟任何一个自由度相对应的运动出现的机会都是均 等的。可由此推出一个普遍的定理——能量按自由 度均分定理:在温度为T的平衡态下，气体分子的每 一个自由度都具有相同的平均动能，其大小都等于
W E S S
例：在一大水杯的水中，有一半径为R的大油滴，现 将此大油滴打散成多个半径均为r的小油滴，问此过 程要做多少功？已知油和水的表面张力系数为σ
解：设最后大油滴被打散成N个半径均为r的小油滴
3
4 4 3 3 R N r 3 3
油滴表面积增加
2 2
R N r
df (v) dv
v v p
0
可得
2kT 2 RT RT vp 1.41 m M M
2．平均速率
8kT 8RT v vf ( v)dv m M 0
3．方均根速率
应用物理课件：气体动理论
气体动理论
容器内有大量分子，这些分子不断地与A1面碰撞，因 而使A1面受到一个持续的作用力。把容器中N个分子对器壁 的作用都考虑进去，则A1面受到各个分子的平均冲力之和 为
F F1 F2 FN
N
Fi
m12x
L
m22x
L
m
2 Nx
L
i 1
N
mx
i 1
i 1
(2-6)
大小不变，分子与A2面碰撞后又以vix飞向A1面，再次对A1
面碰撞。由图2-5知，第i个分子与A1面发生两次连续的碰撞，
在x轴上运动的距离为2L，所需时间是
t 。2根L 据动量定
vix
理F·t=ΔP，得在该段时间内第i个分子作用于A1面的平均冲
力为
Fi
Pi t
2mix 2L ix
mi2x
L
(2-5)
ΔPi=－mvix－mvix=－2mvix
(2-4)
F·t=ΔP知，这一动量的改变等于此次碰撞
中A1面施于第i个分子的冲量，其方向指向X轴的负方向。根 据牛顿第三定律，该分子在此次碰撞中施于A1面的冲量为 2mvix，方向指向X
气体动理论
忽略分子间相互作用的情况下，第i个分子与A1面碰撞
后被弹回，将以－vix飞向A2面。由于x方向速度分量的数值
2 x
nm
2 x
(2-9)
气体动理论
式中 n N 表示单位体积内的分子数，它也是统计平均值。
由于分子L速3 率的平方可表示为i2
2 ix
2 iy
2 iz
，所以，N
个分子的速率均方值为
N
N
N
N
2 i
2 ix
高二物理竞赛课件气体分子运动理论的基本概念.pptx
理想气体压强公式的物理意义
• 把宏观量 p 和统计平均值（ n,t ,v2 ）联系起来， 典型地显示了宏观量和微观量的关系。
• 气体压强具有统计意义，在推导压强公式的过程 中所取的 dA, dt 都是“宏观小微观大”的量，使 得压强有个稳定的数值。
•
气体压强
p
2 3
nt
是个统计规律，而不是一个力学
公式。它与分子的平均平动动能有关，反映了气
体分子运动的剧烈程度，这个关系可以和热力学
系统温度相联系起来。
2.3 温度的微观解释
由 p 2 n t
3
和理想气体物态方程 pV m RT M
可得 3 1 m RT .
2nM V
因为
n
N V
, 而N
m M
N A , 且N A
6.0220451023 mol 1
2)当距离r r0时，势能Ep最小，动能Ek最大。
3)当距离r r0时，排斥力随距离减小急剧增加，势能Ep急剧增大，动能Ek
不断减小。
4)当距离r
d时，势能E
p
增加至Ek
，分子速度为零，不再趋近。
0
2.5 范德瓦尔斯气体的压强
问题: 1）分子力的有效作用距离 2）分子间的平衡距离 3）分子的有效直径 4）分子之间的吸引力和排斥力各有什么特点? 5）气体状态方程考虑分子的体积后如何修正? 6）考虑分子之间的吸引力后又如何修正? 7）什么是分子的内压强? 8）为什么说分子的内压强与分子数密度平方成正比? 9）范德瓦耳斯等温线.
3. 理想气体定律的推证
1） 阿伏伽德罗定律
由（2.5）式 p 2 n 和 （2.6）式 3 kT 可得
3
2
高中物理奥林匹克竞赛专题--气体动理论(共50张PPT)
假定：分子的速度按方向均匀分布
vy
v x v y v z 0?
v x 2v y 2v z 2
~1 3
v2
vx
1 2 m fv x 2 = 1 31 2 m k,t = fv 1 3y (2 2 3 k1 2 T )m =1 2fkv z T 2 1 2 m f(1 3 v 2 )k,t 12mf v2
现气体中有N个分子，N m M
N0
R k=
N0
气体内能记以 E EN M m N 01 2(tRr2s)kT
EM m1 2(tr2s)RTMm
1摩尔气体的内能 pV mRT
Emol 1 2(tr2s)RT
M 特别：s=0时
tri
E
m i RT M2
i 2
pV
n N V
p 13nmf v2
为分子数密度； m f 为一个分子的质量
v 2 为分子速度平方的平均值
v 2 N 1 (v 1 2 v 2 2 v N 2) N 1 v i2
v i 为第i个分子的 速度
引入分子的平均平动动能：k,t (1 2mfv2)1 2mfv2
于是有：
12mf
vx2
1kT 2
12mf
vy2
1kT 2
12mf vz2
1kT 2
t3
结论：分子的平均平动动能 3 kT 是均匀分配在每个平动
自由度上的（ 1 kT ）
2
？当分子还兼有2 转动.振动自由度时，是否应该每个自由
度上都有 1 kT 的平均动能？
2
19
可以证明：分子的每个自由度上都有 1 kT 的平均动能——
b.双原子分子 非刚性分子（高温时） 转动自由度
气体的等容变化和等压变化(课件)(共56张PPT)
一、气体的等容变化
1、等容变化：一定质量的气体在体积不变时， 压强随温度的变化叫做等容变化。
2 ．查理定律：一定质量的某种 气体，当体积不变时，各种气 B 体的压强 p 与温度 之间都有线 性关系，如图所示，我们把它 0 叫做查理定律．
PAt/0C Nhomakorabea注：B点纵坐标是0摄氏度的压强，并非大 气压。
3．热力学温标的建立： 建立背景：由查理定律中压强p与与摄氏温度t的变化 关系图甲可以看出，在等容过程中，压强跟摄氏温度 是一次函数关系，而不是简单的正比例关系。 P P A A
B
B
t/0C
273.15 T/K 如果把该图的AB直线延长至与横轴相交，把交点当 做坐标原点，建立新的坐标系（图乙）此时压强与温度 的关系就是正比例关系了。图乙坐标原点的意义“气体 压强为零时其温度为零”，由此可见，为了使一定质量 的气体在体积不变的情况下，压强与体积成正比，只需 要建立一种新的温标就可以了。
（4）成立条件及适用范围： 成立条件：质量不变，体积不变 适用范围：压强不太大，温度不太低
（5）注意事项：
①查理定律是实验定律，由法国科学家查理通过实验发 现的． ②在p/T=C中的C与气体的种类、质量、体积有关． 注意：p与热力学温度T成正比，不与摄氏温度成正比， 但压强的变化p与摄氏温度t的变化成正比．
摄氏温标描述：
（1）.文字描述：一定质量的气体，在体积不变的情况 下，温度每升高（或降低） 1℃，增加（或减少）的压 强等于它0℃时压强的1/273．
pt－ p0 1 t . 1＋ （ 2 ）．表达式： p0t ＝273或 pt＝p0 273
p1 p2 pn p = t1 273 t2 273 tn 273 t
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
k
3 2
kT
6.211021J
1m3
Ek nk 1.65105 J/m3
H2 : vrms= 1920ms-1 O2 : vrms= 483ms-1
注
a. P、T、 k 、vrms… — 统计量(平衡态,系统)
对少数粒子 无意义
b. 不同气体(m 、v 2不同) k 相同 — T 相同
15 .
氢( H2 )
2.02
氦( He )
4.0
氮( N2 )
28.0
水蒸气( H2O )
18.0
氧( O2 )
32.0
二氧化硫(SO2)
64.0
1 920
1 370 517 645 483
324
14 .
[讨论] 系统( V=1m3 ,t =27ºC,P=1atm) 的分子微观量的平均值
n P 2.661025 m3 kT
17 .
二 能量均分定理（玻耳兹曼假设）
气体处于平衡态时，分子任何一个能量 自由度的平均值都相等，均为 1 kT ，这就 是能量按自由度均分定理 . 2
分子的平均能量
1 (t r 2s)kT 1 (t r v)kT i kT
2
2
2
对于个别分子来说,每一种形式的能量不一定 按自由度均分.能均分定理是关于分子热运动 动能的统计规律.
系统状态了,其它的宏观物理
性质则是这两个物态参量的函数 o
A ( p1,V1,T1)
B ( p2 ,V2 ,T2 ) V
— T =f (P 、V ) (与气体性质有关)
如果过程进行的充分缓慢,过程进行的每一个
中间态都可以近似看成平衡态,这就是准静态过程
4.
2. 理想气体物态方程
(1) 定量,平衡态 m M
注
种类(相互作用)
a. 刚性与非刚性 温度
低温
现代量子理论 常温 以及实验 高温
b. 常温（本教材）
转动、振动 振动
“冻结”
所有自由度均存在
单原子分子 i = 3
刚性双原子分子 i = 3 +2 = 5
刚性多原子分子 i = 3 +3 = 6
18 .
三. 理想气体的内能 ( 不计分子间势能 )
气体内所有分子的动能和分子内原子间势能之和,不计分子间的相互作用能.Βιβλιοθήκη v2xv2yv2z
1 v2 3
单个分子: vix viy viz
vi2 vi2x vi2y vi2z
二. 理想气体压强公式
设 边长分别为 x、y 及 z 的长方体中有 N 个全同
的质量为 m 的气体分子，计算 A1 壁面所受压强.
气体处于平衡态,各处压强 相等,以A1面为例 单个分子遵循力学规律.
一个分子一次碰撞
分子动量改变量
(mvix ) mvix 2mvix vx
对器壁冲量 2mvix
vx
y
A2
o
z
v
- mmvvvxx
x vy
v
A1
xvz
o
A1 y
zx
v
vx
11 .
两次碰撞间隔时间: 2 x vix
单位时间碰撞次数: vix 2x
单个分子单位时间 施于器壁的冲量:
mvi2x x
注
............
...........
当小球数 N 足够大时小
............ ...........
球的分布具有统计规律.
............ ...........
............
9.
12－3 理想气体压强公式
气体压强 — 大量分子碰撞宏观效果 ,热运动一种表现
大量分子作热运动时具有统计规律性,我们利用 力学规律+统计方法求出与大量分子运动有关 的一些物理量的平均值,从而对与分子热运动相 联系的宏观量(现象)给出微观解释
力平衡 P1= P2 =… 热平衡 T1=T2 =… 物质分布“均匀”
可用P、T
描述系统性质
a. 绝热自由膨胀
b. 热传导
绝
热
刚 p,V ,T 真空
性
0ºC
100ºC
p,V ,T
“稳定态”而非平衡态
3.
注 a. P、 T 、 V — 平衡态参量 b. 平衡态 — “无序” 非平衡态 — “有序” c. 热动平衡
vx
vix ? N
N
vi2x
vx2
、v
2 y
、vz2
之间关系(
vx2
i 1
N
)
气体处于平衡态时,不管个别分子的运动具有何种偶然性,但大量
分子的整体表现却是有规律的.
在大量的偶然,无序的分子运动中,包含的一种规律性,称统计规律.
牛顿力学的决定性和统计力学的概率性相结合
8.
[讨论] a. 抛硬币，抛骰子— 等概率事件 b. 伽尔顿板实验—不等概率事件
空间自由度=t+r+s
加入限制条件后将减少空间自由度.
17 .
分子能量自由度 i(运动自由度)
分子(平均)能量构成
平动能
1 mv2 2
1 2
mvx2
、
1 2
mv
2 y
、
1 2
mvz2
转动能
1 J2
2
每两个原子间有振动动能和振动势能
谐振动一个周期内的平均动能和平均势能相等
分子平均能量 kt kr V
单位: K(开尔文). T 273 t
2.
注 系统 — 大量粒子(分子)
外界(环境)
系统
边 (工质) 界
能量交换 物质交换
孤立系统 — 无能量物质交换
绝热系统 — 无热量交换
开放系统 —与周围环境可有物质交换,也可有
能量交换的系统
2.
二.平衡态
无外界的影响、宏观性质不随时间变化
特征:
内部各处
[讨论]
研究方法 1 气体动理论 —— 微观描述 力学规律+统计方法
单个分子: 无序、具有偶然性、遵循力学规律. 整体(大量分子): 服从统计规律 .
分子微的观m 量，v 等 统计平均
宏观量 p，V，T
用概率论的方法研究大量微观粒子的热运动规律
2 热力学 —— 宏观描述 唯象方法(实验)+能量观点
不涉及所研究物质的分子结构和分子的微观运动, 从热力学三大基本定律出发,以逻辑演绎与实验结果相结合, 来研究宏观可测量之间关系及其系统运动形态的变化
d. 理想概念
无外界影响
e. 非平衡态
平衡态
t 足够大
反之 有外界影响永远到不了平衡态
改变系统状态的方法:作功,热传递,物质转移
4.
三. 理想气体物态方程
1. 物态方程(定量气体、平衡态)
物态方程: 理想气体平衡态宏观参量间的函数关系 .
对于固定质量的均匀系统,
p
在没有外力场情况下,只需要
两个物态参量就可以完全决定
单个分子碰撞特性 ：偶然性 、不连续性. 大量分子碰撞的总效果 ：恒定的、持续的力的作用.
10 .
一. 理想气体的微观模型
单个分子满足
1. 分子—”质点” 分子的运动遵从经典力学的规律 .
2 .除碰撞瞬间外, 无相互作用(匀速直线运动,分子势能不计)
3.碰撞—完全弹性
与器壁碰撞— 只改变速度方向,不改变速率
（A） pV m （B） pV (kT )
（C） pV (RT ) （D） pV (mT )
解 p nkT
N nV pV kT
在00C和标准大气压下,分子数密度n=2.686x1025m-3
四 热力学第零定律
两系统接触：
有温差 — 热量传递
如不作功
无热量传递 — 热平衡(温度相同)
热平衡
A
C
o r0
r
r 109 m时 F 0
在气体的分子数密度很低的情况下,分子间作用力可以不计 7 .
三. 分子热运动无序性及统计规律
1. 分子热运动无序性
分子力 聚集 热运动 散开
“状态”（固、液、气） 分子热运动无序性 平衡态
[讨论] 系统平衡态时微观量算术统计平均值
热运动无序性
2. 统计规律
48ºC
A
48ºC
B 绝热板 A B
(a)
(b)
12－2 物质的微观模型 统计规律性
一.分子的线度和分子力
分子间的平均距离 l 3 1/ n
1.分子线度
占有体积
自身体积
有效体积 (相互作用)
2.分子力 — 短程力、电磁相互作用力
r0 引力>斥力 r r0 分子力为零
r0 斥力>引力
F r0 ~ 1010 m
pV N k T 或 pV RT
N NA k R / NA 1.381023J K1 Boltzmann常数 摩尔气体常量 R 8.31 J mol1 K1
m系统总质量，M 摩尔质量，m 单个分子质量
理想气体宏观定义: 遵守三个实验定律和阿伏伽德罗定律的气体. 温度不太低,压强不太大时
大量分子总效应
单位时间 N 个粒子对器壁总冲量:
mvi2x ix
m x
i
vi2x
Nm vi2x x iN
Nm x
v
2 x
器壁A1 所受平均冲力:
F
v
2 x
Nm
x
气体压强
p
F yz
Nm xyz
v
2 x
n N xyz
统计规律
v
2 x
1 v2 3