向量加减法数乘的坐标运算习题
向量运算法则练习题(附答案)

向量运算法则练习题(附答案)以下是向量运算法则的练题及其答案。
1. 向量相加已知向量A = (3, 4) 和向量B = (5, -2),求向量C = A + B 的值。
解答:向量C的值为:(3+5, 4+(-2)) = (8, 2)2. 向量相减已知向量D = (6, 2) 和向量E = (3, -1),求向量F = D - E 的值。
解答:向量F的值为:(6-3, 2-(-1)) = (3, 3)3. 向量数量乘法已知向量G = (2, -3),求向量H = 3G 的值。
解答:向量H的值为:(3 * 2, 3 * (-3)) = (6, -9)4. 向量点乘已知向量I = (1, -2) 和向量J = (3, 4),求向量K = I · J 的值。
解答:向量K的值为:(1 * 3) + (-2 * 4) = 3 - 8 = -55. 向量夹角已知向量L = (2, 2) 和向量M = (-1, 3),求向量L和向量M的夹角的余弦值。
解答:设向量L和向量M的夹角为θ,则向量L·向量M = |L| * |M| * cos(θ)向量L·向量M = (2 * -1) + (2 * 3) = -2 + 6 = 4|L| = √(2^2 + 2^2) = √(4 + 4) = √8|M| = √((-1)^2 + 3^2) = √(1 + 9) = √104 = √8 * √10 * cos(θ)cos(θ) = 4 / (√8 * √10) ≈ 0.89以上是向量运算法则的练习题及其答案。
希望对你的学习有所帮助!如有任何疑问,请随时提出。
高中试卷-6.3.3 平面向量加、减运算坐标表示(含答案)

第六章平面向量及其应用6.3.3平面向量加、减运算坐标表示一、基础巩固等于 【详解】因为12AB AD AD DE AE +=+=uuu r uuu r uuu r uuu r uuu r ,6.已知(5,4)a =r ,(3,2)b =r ,则与23a b -r r 平行的单位向量为( )A .525,55æöç÷ç÷èøB .525,55æöç÷ç÷èø或525,55æö--ç÷ç÷èøC .(1,2)或(1,2)--D .(1,2)【答案】B【详解】解:∵(5,4)a =r ,(3,2)b =r ,23(1,2)a b \-=r r ,22|23|125a b \-=+=r r ,则与23a b -r r 平行的单位向量为15(23)(1,2)5|23|a b a b ±×-=±-r r r r ,化简得,525,55æöç÷ç÷èø或525,55æö--ç÷ç÷èø.7.在矩形ABCD 中, 5AB =,3BC =,P 为矩形内一点,且52AP =,若(),AP AB AD R l m l m =+Îuuu r uuu r uuu r ,则53l m +的最大值为( )A .52B .102C .334+D .6324+【答案】B【详解】由题意,以点A 为坐标原点,以AB 所在直线为x 轴,AD 所在直线为y 轴,建立如图所示的平面直角坐标系,则()0,0A ,()5,0B ,()0,3D ,设(),P x y ,则(),AP x y =uuu r ,()5,3AB AD l m l m +=uuu r uuu r ,8.已知点P 分12PP uuuu v 的比为23-,设A .2-B .3(7,8),u u u r解得432x y ì=ïíï=î,所以4,23P æöç÷èø,当点P 靠近点2P 时,122PPPP =uuu r uuur ,则()()24124x x y y ì=-ïí-=-ïî,解得833x y ì=ïíï=î,所以8,33P æöç÷èø,11.(多选)已知向量1(1,2)e =-u r ,2(2,1)e =u u r ,若向量1122a e e l l =+r u r u u r ,则可使120l l <成立的a r 可能是 ( )A .(1,0)B .(0,1)C .(−1,0)D .(0,−1)【答案】AC【详解】11221212=(2,2)a e e l l l l l l =+-++r u r u u r 若(1,0)a =r ,则12122120l l l l -+=ìí+=î,解得1212,55l l =-=,120l l <,满足题意;若(0,1)a =r ,则12122021l l l l -+=ìí+=î,解得1221,55l l ==,120l l >,不满足题意;因为向量(1,0)-与向量(1,0)共线,所以向量(1,0)-也满足题意.12.(多选)已知向量(,3)a x =v ,(3,)b x =-v ,则下列叙述中,不正确是( )A .存在实数x ,使a bv v P B .存在实数x ,使()a b a +v v P v C .存在实数x ,m ,使()ma b a+v P v v D .存在实数x ,m ,使()ma b b +v P vv 【答案】ABC【详解】由a b r r P ,得29x =-,无实数解,故A 中叙述错误;(3,3)a b x x +=-+r r ,由()a b a +r r r ∥,得3(3)(3)0x x x --+=,即29x =-,无实数解,故B 中叙述错误;(3,3)ma b mx m x +=-+r r ,由()ma b a +r r r ∥,得(3)3(3)0m x x mx +--=,即29x =-,无实数解,故心中叙述错误;由()ma b b +r r r ∥,得3(3)(3)0m x x mx -+--=,即()290m x +=,所以0m =,x ÎR ,故D 中叙述正确.二、拓展提升13.如图,已知ABCD Y 的三个顶点A ,B ,C 的坐标分别是(2,1)-,(1,3)-,(3,4),求顶点D 的坐标.【答案】(2,2)【详解】解:设顶点D 的坐标为(,)x y .(2,1)A -Q ,(1,3)B -,(3,4)C ,(1(2),31)(1,2)AB \=----=uuu r ,(3,4)DC x y =--uuu r ,又AB DC =uuu r uuur,所以(1,2)(3,4)x y =--.即13,24,x y =-ìí=-î解得2,2.x y =ìí=î所以顶点D 的坐标为(2,2).由平行线分线段成比例得:1234h MB h AB ==,1122132142MNC ABC h NC S h NC NC S h BC BC h BC D D ´´==×=×´´89NC BC \=,89NC BC \=uuu r uuu r ,8(1)求点B,点C的坐标;(2)求四边形OABC的面积.【答案】(1)533,,,222 B Cæöæç÷çç÷çèøè。
人教A版高中数学必修第二册课后习题第六章 平面向量加、减运算的坐标表示 平面向量数乘运算的坐标表示

6.3.3 平面向量加、减运算的坐标表示6.3.4 平面向量数乘运算的坐标表示A 级必备知识基础练1.向量a=(2,3),b=(1,-1),则2a+b=( ) A.10B.(5,5)C.(5,6)D.(5,7)2.已知a=(-5,6),b=(-3,2),c=(x,y),若a-3b+2c=0,则c 等于( ) A.(-2,6) B.(-4,0) C.(7,6)D.(-2,0)3.(多选题)下列各对向量不共线的是( ) A.a=(2,3),b=(3,-2) B.a=(2,3),b=(4,-6) C.a=(√2,-1),b=(1,√2) D.a=(1,√2),b=(√2,2)4.已知四边形ABCD 的三个顶点为A(0,2),B(-1,-2),C(3,1),且BC ⃗⃗⃗⃗⃗ =2AD ⃗⃗⃗⃗⃗ ,则顶点D 的坐标为( ) A.(2,72)B.(2,-12)C.(3,2)D.(1,3)5.已知向量a=(1,2),b=(2,-2),c=(1,λ).若c ∥(2a+b),则λ= .6.已知OA ⃗⃗⃗⃗⃗ =(-2,m),OB ⃗⃗⃗⃗⃗ =(n,1),OC ⃗⃗⃗⃗⃗ =(5,-1),若点A,B,C 在同一条直线上,且m=2n,则m+n= .7.已知a=(x+3,x 2-3x-4),A(1,2),B(3,2). (1)若AB ⃗⃗⃗⃗⃗ =a,求x 的值; (2)若AB ⃗⃗⃗⃗⃗ ∥a,求x 的值.8.如图,已知在△AOB 中,A(0,5),O(0,0),B(4,3),OC ⃗⃗⃗⃗⃗ =14OA ⃗⃗⃗⃗⃗ ,OD ⃗⃗⃗⃗⃗ =12OB⃗⃗⃗⃗⃗ ,AD 与BC 相交于点M,求点M 的坐标.B 级关键能力提升练9.已知点A(√3,1),B(0,0),C(√3,0),∠BAC 的平分线AE 与BC 相交于点E,设BC ⃗⃗⃗⃗⃗ =λCE ⃗⃗⃗⃗ ,则实数λ等于( ) A.2B.12C.-3D.-1310.设向量a=(a 1,b 1),b=(a 2,b 2),定义一种运算“ ”,向量a b=(a 1,b 1) (a 2,b 2)=(a 2b 1,a 1b 2).已知m=2,12,n=(π3,0),点P(x,y)在y=sin x 的图象上运动,点Q 在y=f( OP ⃗⃗⃗⃗⃗ +n(其中O 为坐标原点),则y=f(x)的最小值为 ( )A.-1B.-2C.2D.1211.在平面直角坐标系xOy 中,已知点A(3,1),B(-2,2),C(-1,4). (1)以线段AB,AC 为邻边作平行四边形ACDB,求向量AD ⃗⃗⃗⃗⃗ 的坐标; (2)设实数t 满足(AB ⃗⃗⃗⃗⃗ -t OC⃗⃗⃗⃗⃗ )∥BC ⃗⃗⃗⃗⃗ ,求t 的值.12.如图所示,设点P(x,y)是线段P 1P 2上不同于P 1,P 2的点,且满足|P 1P ⃗⃗⃗⃗⃗⃗⃗⃗ ||PP 2⃗⃗⃗⃗⃗⃗⃗⃗ |=λ,即P 1P ⃗⃗⃗⃗⃗⃗ =λPP 2⃗⃗⃗⃗⃗⃗ ,λ叫做点P 分有向线段P 1P 2⃗⃗⃗⃗⃗⃗⃗⃗ 所成的比,点P 叫做有向线段P 1P 2⃗⃗⃗⃗⃗⃗⃗⃗ 的以λ为定比的定比分点.求点P 的坐标,并思考P 1,P 2中点的坐标公式.参考答案6.3.3 平面向量加、减运算的坐标表示 6.3.4 平面向量数乘运算的坐标表示1.B ∵向量a=(2,3),b=(1,-1),∴2a+b=(5,5),故选B.2.D ∵a-3b+2c=0,∴(-5,6)-(-9,6)+(2x,2y)=(0,0),即{2x -5+9=0,2y +6-6=0,∴{x =-2,y =0,即c=(-2,0).故选D. 3.ABC A,B,C 中各对向量均不满足向量共线定理,D 中b=√2a,两个向量共线.4.A 设顶点D 的坐标为(x,y).因为BC ⃗⃗⃗⃗⃗ =(4,3),AD ⃗⃗⃗⃗⃗ =(x,y-2),且BC ⃗⃗⃗⃗⃗ =2AD ⃗⃗⃗⃗⃗ ,所以{2x =4,2y -4=3,所以{x =2,y =72,所以选A. 5.122a+b=2(1,2)+(2,-2)=(4,2),c=(1,λ),由c ∥(2a+b),得4λ-2=0,得λ=12.6.9或92AB ⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ =(n,1)-(-2,m)=(n+2,1-m),BC ⃗⃗⃗⃗⃗ =OC⃗⃗⃗⃗⃗ −OB⃗⃗⃗⃗⃗ =(5,-1)-(n,1)=(5-n,-2). 因为A,B,C 共线,所以AB ⃗⃗⃗⃗⃗ 与BC ⃗⃗⃗⃗⃗ 共线, 所以-2(n+2)=(1-m)(5-n).①又m=2n,②解①②组成的方程组得{m =6,n =3或{m =3,n =32. 所以m+n=9或m+n=92.7.解(1)AB ⃗⃗⃗⃗⃗ =(2,0),因为AB ⃗⃗⃗⃗⃗ =a, 所以{x +3=2,x 2-3x -4=0,解得x=-1.(2)因为AB ⃗⃗⃗⃗⃗ ∥a,所以x 2-3x-4=0,解得x=-1或4.8.解因为OC ⃗⃗⃗⃗⃗ =14OA ⃗⃗⃗⃗⃗ =14(0,5)=(0,54),所以C (0,54). 因为OD ⃗⃗⃗⃗⃗⃗ =12OB ⃗⃗⃗⃗⃗ =12(4,3)=(2,32),所以D (2,32).设M(x,y),则AM ⃗⃗⃗⃗⃗⃗ =(x,y-5),CM ⃗⃗⃗⃗⃗⃗ =(x ,y -54),CB ⃗⃗⃗⃗⃗ =(4,74),AD ⃗⃗⃗⃗⃗ =(2,32)-(0,5)=(2,-72).因为AM ⃗⃗⃗⃗⃗⃗ ∥AD ⃗⃗⃗⃗⃗ ,所以-72x-2(y-5)=0,即7x+4y=20. ①因为CM ⃗⃗⃗⃗⃗⃗ ∥CB⃗⃗⃗⃗⃗ , 所以74x-4(y -54)=0,即7x-16y=-20. ②联立①②,解得的坐标为(127,2).9.C 如图,由已知得,∠ABC=∠BAE=∠EAC=30°,∠AEC=60°,|AC ⃗⃗⃗⃗⃗ |=1,∴|EC⃗⃗⃗⃗⃗ |=1tan60°=√33.∵BC ⃗⃗⃗⃗⃗ =λCE ⃗⃗⃗⃗⃗ ,λ<0,∴|λ|=|BC ⃗⃗⃗⃗⃗||CE ⃗⃗⃗⃗⃗|=√3√33=3.∴λ=-3.10.B 由题意知,点P 的坐标为(x,sin OP⃗⃗⃗⃗⃗ +n=(12x ,2sinx)+(π3,0)=(12x +π3,2sinx).又因为点Q 在y=f(x)的图象上运动,所以点Q 的坐标满足y=f(x)的解析式,即y=2sin (2x -2π3).所以函数y=f(x)的最小值为-2.11.解(1)由向量加法的平行四边形法则知, AD ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +AC⃗⃗⃗⃗⃗ =(-5,1)+(-4,3)=(-9,4). (2)AB ⃗⃗⃗⃗⃗ -t OC ⃗⃗⃗⃗⃗ =(-5,1)-(-t,4t)=(t-5,1-4t),BC ⃗⃗⃗⃗⃗ =(-1,4)-(-2,2)=(1,2). 因为(AB ⃗⃗⃗⃗⃗ -t OC ⃗⃗⃗⃗⃗ )∥BC ⃗⃗⃗⃗⃗ , 所以(t-5)×2=1-4t, 解得t=116.12.解设P(x,y),P 1(x 1,y 1),P 2(x 2,y 2),则根据题意,得(x-x 1,y-y 1)=λ(x 2-x,y 2-y), 即{x -x 1=λ(x 2-x ),y -y 1=λ(y 2-y ),当λ≠-1时,解得{x=x1+λx21+λ,y=y1+λy21+λ.则点P的坐标为x1+λx21+λ,y1+λy21+λ.当λ=1时,点P的坐标为x1+x22,y1+y22,这就是线段P1P2的中点坐标公式.。
(整理版)平面向量的坐标运算(典型例题)

平面向量的坐标运算〔典型例题〕[教学重点]理解平面向量的坐标表示及它们之间的一一对应关系;掌握平面向量的加法、减法、实数与向量积的坐标运算法那么;能够判断向量的平行或由向量的平行求解向量的坐标.[教学难点]理解平面向量的坐标表示是几何问题代数化的根底,将求解的几何图形问题,放置在直角坐标系下,通过向量的坐标运算到达求解的目的,是本章内容的重要思想方法和具体应用.[典型例题]例1、A、B、C、D是平面直角坐标系中任意位置上四个不同点,求证:.解:设A、B、C、D四点的坐标分别为(x1,y1), (x2,y2), (x3, y3), (x4, y4),那么由向量的坐标表示可得:再由向量和的坐标运算得例2.ΔABC内一点G,使得,D是BC中点,求证:点G是ΔABC的重心,且.解:如下图建立直角坐标系:设A(x1, y1), B(x2, y2), C(x3, y3), G(x, y)那么由∴即∴即(x-x1, y-y1)=(x2+x3-2x, y2+y3-2y)∴x-x1=x2+x3-2x, y-y1=y2+y3-2y∴x2+x3=3x-x1, y2+y3=3y-y1由∴∴即将x2+x3=3x-x1,y2+y3=3y-y1代入∴∴即,且必有∴A、G、D三点共线,即中线AD过G点.同理可证AC、AB边上中线也必过G点.故G是ΔABC的重心.例3.设向量,假设,求使成立的实数λ和x的值.解:由向量的坐标运算法那么∵∴∴由∴,即.例4.如图,直角ΔABE的直角边为AB、AE,以AB、AE为边在ΔABE外部作正方形ABCD 和正方形AEFG,连结CE交AB于N点,连结BF交AE于M点,证明AM=AN.解:此题除了用平面几何的方法求证,可用平面向量知识及运算求证.如图建立坐标系设AE边长为a,AB边长为b, 那么E(a, 0), B(0, -b), F(a, a),C(-b, -b).设M(x, 0), N(0, y)那么,∵,∴ab-(a+b)x=0∴,即,由,且,∴(a+b)(y+b)-b2=0, ∴,即,∴,∴AM=AN.课外练习:1.假设点P(2,3),Q(3,a),R(4,b)共线,那么有〔〕.A、a=4,b=5B、b-a=1C、2a-b=3D、a-2b=32.点A(-1,-2), ,那么C点坐标为〔〕.A、(0, 1)B、(1, 3) C 、(0, -1) D、(3, 1)3.ΔABC中,顶点B(1,1), C(2, -6), D是BC边上一点,假设ΔABD的面积是ΔABC面积的,那么点D的坐标为〔〕.A、B、C、D、4.a、b、c是两两不相等的实数,那么点A(a+b,c), B(b+c,a), C(c+a,b)的位置关系满足〔〕.A、在同一条直线上B、是RtΔ的三个顶点C、是等边Δ的三个顶点D、是钝角Δ的三个顶点5.ΔABC中,A(3, 6), B(0, 0), C(6,2),过AB边上一点D作BC的平行线,交AC于E点,假设ΔADE的面积是梯形DECB面积的,求D、E两点坐标.参考答案:1.C2.A3.D4.A5. 解:由DE//BC,∴ΔADE∽ΔABC,∵ΔADE面积是梯形DECB面积∴ΔADE面积是ΔABC面积,∴,∴,设D(x1, y1), E(x2, y2)∴,,,由x1-3=-1, y1-6=-2∴x1=2, y1=4.由x2-3=1, , ∴x2=4, ,∴.。
空间向量的加减和数乘运算

分配律
$k(overset{longrightarrow}{a} + overset{longrightarrow}{b}) = koverset{longrightarrow}{a} + koverset{longrightarrow}{b}$。
单调性
当$k > 0$时,数乘会使向量增大;当$k < 0$时,数乘会使向量缩小。
在线性代数中,向量组的线性组合可以通过数乘运算来实现,从而研究向量组之间的关系。
向量组的线性组合
向量空间是由向量构成的集合,通过向量的加减和数乘运算可以研究向量空间的结构和性质。
向量空间
04
空间向量加减和数乘运算的注意事项
01
02
零向量的特殊性
零向量与任意向量数乘,结果仍然是零向量。
零向量与任意向量相加或相减,结果仍然是该任意向量。
解析
根据空间向量加法和减法的定义,$(overset{longrightarrow}{a} + overset{longrightarrow}{b}) + (overset{longrightarrow}{a} - overset{longrightarrow}{b})$的坐标等于两个向量的对应坐标相加和相减。即,$(overset{longrightarrow}{a} + overset{longrightarrow}{b}) + (overset{longrightarrow}{a} - overset{longrightarrow}{b}) = ( - 1 + 3,5 + ( - 1),2 + 4) = (2,4,6)$。
计算方法
根据定义,数乘的计算方法为将向量的每个分量分别乘以该实数。
向量的数乘运算题型练习-高一下学期数学人教A版(2019)必修第二册

第六章 6.2.3向量的数乘运算【基础篇】题型1 向量的数乘的定义与运算法则 1.已知λ∈R ,则下列结论正确的是( ) A .|λa |=λ|a | B .|λa |=|λ|a C .|λa |=|λ||a |D .|λa |>02.若a ,b 为已知向量,且 23(4a -3c )+3(5c -4b )=0,则c =________.题型2 向量的数乘的应用3.如图,在△ABC 中,D 是边BC 的中点,AG →=2GD →,则用向量AB →,AC →表示BG →为( )A .BG →=-23AB →+13AC →B .BG →=-13AB →+23AC →C .BG →=23AB →-13AC →D .BG →=23AB →+13AC →4.如图,在平面四边形ABCD 中,E ,F 分别为AB ,DC 的中点,AD →=m ,BC →=n ,则EF →=( ) A .12m +12n B .23m +13n C.34m +14nD .13m +23n题型3 向量共线的判定5.已知AB →=a +5b ,BC →=-2a +8b ,CD →=3(a -b ),且a ,b 不共线,则( ) A .A ,B ,C 三点共线 B .A ,B ,D 三点共线 C .A ,C ,D 三点共线D .B ,C ,D 三点共线6.在四边形ABCD 中,对角线AC 与BD 交于点O.若2OA →+3OC →=2OD →+3OB →,则四边形ABCD 一定是( ) A .矩形B .梯形C .平行四边形D .菱形7.已知向量a =2e 1-3e 2,b =2e 1+3e 2,c =2e 1-9e 2,其中e 1,e 2不共线.问是否存在实数λ,μ,使向量d =λa +μb 与c 共线?题型4 向量共线定理的应用8.如图,在△ABC 中,AN →=14NC →,P 是BN 上一点.若AP →=mAB →+211AC →,则实数m 的值为( )A .911B .211C .311D .1119.在△ABC 中,点D 在边BC 的延长线上,且BC →=3CD →.若AO →=xAB →+(1-x)AC →,-13<x<0,则点O 在( ) A .线段BC 上 B .线段CD 上 C .线段AC 上D .线段AD 上10.在△ABC 中,点D 满足AD →=16AB →+12AC →,直线AD 与BC 交于点E ,则|CE →||CB →|的值为( ) A .12 B .13 C .14D .1511.设e 1,e 2是空间内两个不共线的向量,已知AB →=e 1+ke 2,BC →=5e 1+4e 2,DC →=-e 1-2e 2,且A ,B ,D 三点共线,则实数k =________.【提升篇】1.在平行四边形ABCD 中,AC ,BD 交于点O ,则( ) A .AO →=AB →+AD → B .AO →=12(AB →+AD →)C .AO →=AB →-AD → D .AO →=12(AB →-AD →)2.已知向量a ,b 不共线.若向量a +λb 与b +λa 的方向相反,则λ的值为( ) A .1 B .0C .-1D .±13.庄严美丽的国旗和国徽上的五角星是革命和光明的象征,正五角星是一个非常优美的几何图形,且与黄金分割有着密切的联系,在如图所示的正五角星中,以A ,B ,C ,D ,E 为顶点的多边形为正五边形,已知PTAP =5-12,则( )A .CT →=3-52CA →+3-52CE →B .CT →=5-12CA →+5-12CE →C .CT →=3-54CA →+3-54CE →D .CT →=3-54CA →+5-12CE →4.已知O 是平面内一定点,A ,B ,C 是平面上不共线的三个点,动点P 满足OP →=OA →+λ⎝ ⎛⎭⎪⎫AB →|AB →|+AC →|AC →|(λ∈[0,+∞)),则点P 的轨迹一定通过△ABC 的( ) A .外心 B .内心C .重心D .垂心5.(多选)[重庆南开中学2022质量检测]已知点P 是△ABC 的中线BD 上一点(不包含端点)且AP →=xAB →+yAC →,则下列说法正确的是( ) A .x +2y =1B .2x +y =1C .2x +4y ≥2 2D .log 2x +log 2y≥-36.(多选)[山东师范大学附属中学2022高一月考]已知点P 为△ABC 所在平面内一点,且PA →+2PB →+3PC →=0.若E 为AC 的中点,F 为BC 的中点,则下列结论正确的是( ) A .向量PA →与PC →可能平行 B .点P 在线段EF 的延长线上 C .点P 在线段EF 上 D .PE ∶PF =2∶17.已知M 是△ABC 所在平面内的一点.若满足6AM →-AB →-2AC →=0,且S △ABC =λS △ABM ,则实数λ的值是________.8.[山东历城二中、章丘四中等校2022高一联考]在△ABC 中,点P 满足BP =2PC ,过点P 的直线与AB ,AC 所在的直线分别交于点M ,N ,若AB →=λAM →,AC →=μAN →(λ>0,μ>0),求1λ+1μ的最小值.9.已知e 1,e 2是平面上两个不共线的向量,且AB →=k e 1-4e 2,CD →=-e 1+k e 2,BD →=e 1+2e 2.(1)若AB →,CD →方向相反,求k 的值; (2)若A ,C ,D 三点共线,求k 的值.答案及解析1.【答案】C【详解】当λ<0时,|λa |=λ|a |不成立,A 错误;|λa |是一个非负实数,而|λ|a 是一个向量,B 错误;当λ=0或a =0时,|λa |=0,D 错误.故选C. 2.【答案】1213b -839a【详解】∵23(4a -3c )+3(5c -4b )=0,∴83a -2c +15c -12b =0,化简得13c =12b -83a ,∴c =1213b -839a . 3.【答案】A【详解】由题意可得BG →=BA →+AG →=BA →+23AD →=BA →+23×12(AB →+AC →)=BA →+13AB →+13AC →=13AC→-23AB →.故选A. 4.【答案】A【详解】由已知可得CF →+DF →=0,EA →+EB →=0,由平面向量的加法可得⎩⎪⎨⎪⎧EF →=EA →+AD →+DF →,EF →=EB →+BC →+CF →,上述两个等式相加可得2EF →=AD →+BC →=m +n ,则EF →=12(m +n ).故选A. 5.【答案】B【详解】∵AB →=a +5b ,BC →=-2a +8b ,CD →=3(a -b ),且a ,b 不共线,∴BD →=BC →+CD →=-2a +8b +3(a -b )=a +5b .∵AB →=a +5b ,∴BD →=AB →,即BD →与AB →共线,则A ,B ,D 三点共线,故选B. 6.【答案】B【详解】∵2OA →+3OC →=2OD →+3OB →,∴2(OA →-OD →)=3(OB →-OC →),∴2DA →=3CB →,∴四边形ABCD 一定是梯形.故选B.7.【答案】由题意得d =λa +μb =(2λ+2μ)e 1+(-3λ+3μ)e 2, 若d 与c 共线,则存在实数k ≠0,使d =kc , 即(2λ+2μ)e 1+(-3λ+3μ)e 2=2ke 1-9ke 2,即⎩⎪⎨⎪⎧2λ+2μ=2k ,-3λ+3μ=-9k ,解得λ=-2μ. 故存在实数λ,μ,且λ=-2μ,使d 与c 共线. 8.【答案】D【详解】由题意可得AC →=5AN →,则AP →=mAB →+211×5AN →=mAB →+1011AN →.因为B ,P ,N 三点共线,所以m +1011=1,即m =111.9.【答案】B【详解】由向量共线定理可知O ,B ,C 三点共线. ∵BC →=3CD →,∴AC →-AB →=3AD →-3AC →,∴AD →=-13AB →+43AC →.又∵-13<x <0,∴点O 在线段CD 上,且不与C ,D 两点重合.10.【答案】C【解析】设AE →=λAD →=λ6AB →+λ2AC →,则CE →=AE →-AC →=λAD →-AC →=λ6AB →+λ2AC →-AC →=λ6AB →+⎝⎛⎭⎫λ2-1AC →, CB →=AB →-AC →,且CE →,CB →共线,设CE →=kCB →, 则λ6AB →+⎝⎛⎭⎫λ2-1AC →=k (AB →-AC →), 所以⎩⎨⎧λ6=k ,λ2-1=-k ,所以λ6=1-λ2,解得λ=32,此时CE →=14AB →-14AC →,所以CE →=14CB →,故|CE →||CB →|=14.故选C. 11.【答案】1【详解】依题意,CD →=e 1+2e 2, 故AD →=AB →+BC →+CD →=7e 1+(k +6)e 2. 已知A ,B ,D 三点共线,可设AD →=λAB →, 则7e 1+(k +6)e 2=λ(e 1+ke 2),所以⎩⎪⎨⎪⎧7=λ,k +6=kλ,解得k =1.1.【答案】B【详解】如图,在平行四边形ABCD 中,AC ,BD 交于点O ,由平行四边形法则得AB →+AD→=AC →=2AO →,所以AO →=12(AB →+AD →).故选B.2.【答案】C【详解】∵向量a +λb 与b +λa 的方向相反,∴(a +λb )∥(b +λa ).由向量共线的充要条件可知,存在一个实数m ,使得a +λb =m (b +λa ),即(1-mλ)a =(m -λ)b .∵a 与b 不共线,∴1-mλ=m -λ=0,可得m =λ.∴1-λ2=0,λ=±1.当λ=1时,向量a +b 与b +a 是相等向量,其方向相同,不符合题意,故舍去.∴λ=-1.3.【答案】A【详解】设AP =1,则PT =5-12=TS ,CP =1+5-12=5+12=CS , CT →=CA →+AT →=CA →+25-1TS →=CA →+25-1(CS →-CT →)=CA →+25-1(1+5-122+5-12CE →-CT →)=CA→+CE →-5+12CT →,所以5+32CT →=CA →+CE →,所以CT →=3-52CA →+3-52CE →. 故选A. 4.【答案】B【详解】AB →|AB →|为AB →上的单位向量,AC →|AC →|为AC →上的单位向量,设∠BAC 的平分线为AD ,则AB →|AB →|+AC →|AC →|的方向为AD → 的方向. 又∵λ∈[0,+∞),∴λ⎝ ⎛⎭⎪⎫AB →|AB →|+AC →|AC →|的方向与AB →|AB →|+AC →|AC →|的方向相同.∵OP →=OA →+λ⎝ ⎛⎭⎪⎫AB →|AB →|+AC →|AC →|,∴点P 在射线AD 上移动. ∴点P 的轨迹一定通过△ABC 的内心. 5.【答案】AC【详解】因为AP →=xAB →+yAC →,所以AP →=xAB →+2yAD →.又B ,P ,D 三点共线,所以x +2y =1,所以选项A 正确,选项B 错误.x +2y =1,所以2x +4y =2x +22y ≥2 2x ·22y =2 2x+2y=2 2(当且仅当x =12,y =14时等号成立),所以选项C 正确.因为x +2y =1≥2 2xy ,所以xy ≤18⎝⎛⎭⎫当且仅当x =12,y =14时等号成立, 所以log 2x +log 2y =log 2(xy )≤log 218=-3,所以选项D 错误.故选AC. 6.【答案】CD【详解】点P 为△ABC 所在平面内一点,E 为AC 的中点,F 为BC 的中点,则P A →+PC →=2PE →,PB →+PC →=2PF →,而P A →+2PB →+3PC →=0,即(PA →+PC →)+2(PB →+PC →)=0,于是得2PE →+4PF →=0,即EP →=2PF →,所以点P 在线段EF 上,且PE ∶PF =2∶1,即点P ,A ,C 不共线,则向量PA →与PC →不可能平行,A 不正确,B 不正确,C 正确,D 正确.故选CD .7.【答案】3【详解】如图,记2AM →=AN →.∵AN →-AB →+2AN →-2AC →=0, ∴BN →=2NC →,S △ABC =32S △ABN .又∵S △ABM =12S △ABN ,∴S △ABC =3S △ABM ,∴λ=3.8.【答案】【详解】连接AP ,如图.∵△ABC 中,BP →=BA →+AP →,PC →=PA →+AC →, 点P 满足BP →=2PC →, ∴-AB →+AP →=2(AC →-AP →), ∴AP →=23AC →+13AB →.又∵AB →=λAM →,AC →=μAN →(λ>0,μ>0), ∴AP →=2μ3AN →+λ3AM →.又∵M ,P ,N 三点共线, ∴2μ3+λ3=1,λ>0,μ>0, ∴1λ+1μ=⎝⎛⎭⎫1λ+1μ·⎝⎛⎭⎫2μ3+λ3=2μ3λ+λ3μ+1≥2 2μ3λ·λ3μ+1=2 23+1, 当且仅当2μ3λ=λ3μ,即⎩⎪⎨⎪⎧μ=3(2-2)2,λ=3(2-1) 时取“=”,则1λ+1μ的最小值为2 23+1. 9.【答案】(1)由题意知,AB →∥CD →,则存在λ∈R ,使得AB →=λCD →,即k e 1-4e 2=λ(-e 1+k e 2),整理得(k +λ)e 1=(kλ+4)e 2. 由e 1,e 2是不共线的向量,得⎩⎪⎨⎪⎧k +λ=0,kλ+4=0,解得⎩⎪⎨⎪⎧λ=2,k =-2或⎩⎪⎨⎪⎧λ=-2,k =2. 又AB →,CD →方向相反,则λ=-2,k =2,故k 的值为2.(2)由题意知,AD →=AB →+BD →=(k +1)e 1-2e 2.由A ,C ,D 三点共线得,存在μ∈R ,使得AD →=μCD →,即(k +1)e 1-2e 2=μ(-e 1+k e 2),整理得(k +μ+1)e 1=(kμ+2)e 2. 由e 1,e 2是不共线的向量,得⎩⎪⎨⎪⎧k +μ+1=0,kμ+2=0, 解得⎩⎪⎨⎪⎧k =1,μ=-2或⎩⎪⎨⎪⎧k =-2,μ=1.综上,k =1或k =-2.。
(完整版)高中数学向量的加减与数乘知识总结+题库
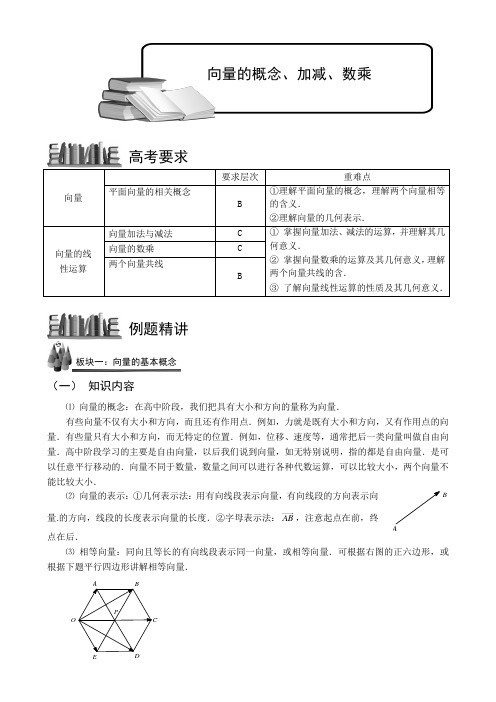
向量要求层次重难点平面向量的相关概念B①理解平面向量的概念,理解两个向量相等的含义.②理解向量的几何表示.向量的线 性运算向量加法与减法C ① 掌握向量加法、减法的运算,并理解其几何意义.② 掌握向量数乘的运算及其几何意义,理解两个向量共线的含.③ 了解向量线性运算的性质及其几何意义.向量的数乘 C 两个向量共线B(一) 知识内容⑴ 向量的概念:在高中阶段,我们把具有大小和方向的量称为向量.有些向量不仅有大小和方向,而且还有作用点.例如,力就是既有大小和方向,又有作用点的向量.有些量只有大小和方向,而无特定的位置.例如,位移、速度等,通常把后一类向量叫做自由向量.高中阶段学习的主要是自由向量,以后我们说到向量,如无特别说明,指的都是自由向量.是可以任意平行移动的.向量不同于数量,数量之间可以进行各种代数运算,可以比较大小,两个向量不能比较大小.⑵ 向量的表示:①几何表示法:用有向线段表示向量,有向线段的方向表示向量.的方向,线段的长度表示向量的长度.②字母表示法:AB ,注意起点在前,终点在后.⑶ 相等向量:同向且等长的有向线段表示同一向量,或相等向量.可根据右图的正六边形,或根据下题平行四边形讲解相等向量.POE DCBA例题精讲高考要求板块一:向量的基本概念向量的概念、加减、数乘B已知E、F、G、H分别是平行四边形ABCD边AB、DC、BC、AD的中点,O为对角线AC与BD的交点,分别写图中与DF,BH,AO相等的向量.解:DF FC GO OH AE EB========BH HC AG GD=AO OC⑷向量共线或平行:通过有向线段AB的直线,叫做向量AB的基线.如果向量的基线互相平行或重合,则称这些向量共线或平行.向量a平行于向量b,记作a∥b.说明:共线向量的方向相同或相反,注意:这里说向量平行,包含向量基线重合的情形,与两条直线平行的概念有点不同.事实上,在高等数学中,重合直线是平行直线的特殊情形.⑸零向量:长度等于零的向量,叫做零向量.记作:0.零向量的方向不确定,零向量与任意向量平行.⑹用向量表示点的位置:任给一定点O和向量a,过点O作有向线段OA a=,则点A相对于点O 位置被向量a所唯一确定,这时向量OA又常叫做点A相对于点O的位置向量.⋅=.AB AC3(二)典例分析:【例1】给出命题⑴零向量的长度为零,方向是任意的.⑵若a,b都是单位向量,则a=b.⑶向量AB与向量BA相等.⑷若非零向量AB与CD是共线向量,则A,B,C,D四点共线.以上命题中,正确命题序号是()A.⑴ B.⑵ C.⑴⑶ D.⑴⑷【例2】下列命题中正确的有:( )⑴四边形ABCD是平行四边形当且仅当AB DC=;⑵向量AB与BA是两平行向量;⑶向量AB与CD是共线向量,则A,B,C,D四点必在同一直线上;⑷单位向量不一定都相等;⑸a 与b 共线,b 与c 共线,则a 与c 也共线; ⑹平行向量的方向一定相同;【变式】 平面向量a ,b 共线的充要条件是( )A .a ,b 方向相同B .a ,b 两向量中至少有一个为零向量C .λ∃∈R ,b a λ=D .存在不全为零的实数1λ,2λ,120a b λλ+=【例3】 ⑴设0a 为单位向量,①若a 为平面内的某个向量,则0a a a =⋅;②若a 与0a 平行,则0a a a =⋅;③若a 与0a 平行且1a =,则0a a =.上述命题中,假命题个数是( ) A .0B .1C .2D .3⑵若非零向量a ,b 满足a b b -=,则( )A .22b a b >-B .22b a b <-C .22a a b >-D .22a a b <-【变式】 给出下列命题:①若a b =,则a b =;②若A B C D ,,,是不共线的四点,则AB DC =是四边形ABCD 为平行四边形的充要条件; ③若a b =,b c =,则a c =; ④a b =的充要条件是a b =且a b ∥; ⑤若a b ∥,b c ∥,则a c ∥;其中正确的序号是 .【例4】 如图所示,1A ,2A ,3A ,…,8A 是O 的8个等分点,以1A ,2A ,…,8A 及O 这9个点中任意两个为起始点和终点的向量中,模等于半倍的向量有多少个?【变式】 (海淀区2008-2009学年度第一学期期末试卷)如图,在正方形ABCD 中,下列描述中正确的是( )A .AB BC =B .AB CD =C .2AC AB = D.AB BC AB BC +=-A 35A D CBA(一) 知识内容1. 向量的加法:a+babbabb aba a+b CCOBa+b b+ccbaa+b+c⑴ 向量加法的三角形法则:已知向量,a b ,在平面上任取一点A ,作AB a =,BC b =,再作向量AC ,则向量AC 叫做a 和b 的和(或和向量),记作a b +,即a b AB BC AC +=+=. ⑵ 向量求和的平行四边形法则:① 已知两个不共线的向量a ,b ,作AB a =,AD b =,则A ,B ,D 三点不共线,以AB ,AD 为邻边作平行四边形ABCD ,则对角线上的向量AC a b =+,这个法则叫做向量求和的平行四边形法则. ② 向量的运算性质:向量加法的交换律:a b b a +=+ 向量加法的结合律:()()a b c a b c ++=++关于0:00a a a +=+= ⑶ 向量求和的多边形法则:已知n 个向量,依次把这n 个向量首尾相连,以第一个向量的始点为始点,第n 个向量的终点为终点的向量叫做这n 个向量的和向量.这个法则叫做向量求和的多边形法则.2. 向量的减法:dcbaa+b+c+dbacda-b baO⑴ 相反向量:与向量a 方向相反且等长的向量叫做a 的相反向量,记作a -. 零向量的相反向量仍是零向量.⑵ 差向量定义:如果把两个向量的始点放在一起,则这两个向量的差是以减向量的终点为始点,被减向量的终点为终点的向量.推论:一个向量BA 等于它的终点相对于点O 的位置向量OA 减去它的始点相对于点O 的位置向量OB ,或简记“终点向量减始点向量”.⑶ 一个向量减去另一个向量等于加上这个向量的相反向量板块二:向量的加减运算(三)典例分析:【例5】 设P 是ABC △所在平面内的一点,2BC BA BP +=,则( )A .0PA PB += B .0PC PA += C .0PB PC +=D .0PA PB PC ++=【变式】 如图,在平行四边形ABCD 中,下列结论中错误的是( )A .AB DC = B .AD AB AC += C .AB AD BD -= D .0AD CB +=【例6】 D 是ABC ∆的边AB 上的中点,则向量CD =( )A .12BC BA -B .12BC BA -- C .12BC BA -+D .12BC BA +.【例7】 设D ,E ,F ,分别是ABC ∆的三边BC 、CA 、AB 上的点,且2,DC BD =2,CE EA =2,AF FB =则AD BE CF ++与BC ( ) A.反向平行B.同向平行C.互相垂直D.既不平行也不垂直【例8】 根据图示填空:⑴ a b += ;⑵ e b d ++= .【例9】 化简下列各式:⑴ 7()8()a b a b +--; ⑵ 12(2)(432)6a b c a b c +---+【例10】 如图,D ,E ,F 分别是ABC ∆的边AB ,BC ,CA 的中点,则( )A .0AD BE CF ++=B .0BD CF DF -+=C .0AD CE CF +-= D .0BD BE FC --=DCBAFE DCBA【例11】 已知O A B ,,是平面上的三个点,直线AB 上有一点C ,满足20AC CB +=,则OC =( )A .2OA OB - B .2OA OB -+C .2133OA OB -D .1233OA OB -+【例12】 如图所示,E F 、是四边形ABCD 的对角线AC BD 、的中点,已知,AB a CD c ==,求向量EF .【例13】 已知O A B ,,是平面上的三个点,直线AB 上有一点C ,满足20AC CB +=,则OC =( )A .2OA OB - B .2OA OB -+C .2133OA OB -D .1233OA OB -+【例14】 已知任意四边形ABCD 中,,E F 分别是,AD BC 的中点,求证:1()2EF AB DC =+.【例15】 ⑴ 已知ABCD □的两条对角线交于点O ,设AB a =,AD b =,用向量a 和b 表示向量BD ,AO .⑵ 已知ABCD □的两条对角线交于点O ,设对角线AC =a ,BD =b ,用a ,b 表示BC ,AB .CAAC【例16】 设P 是正六边形OABCDE 的中心,若OA a =,OE b =,试用向量a ,b 表示OB 、OC 、ODOE .【例17】 在ABC △中,AB c =,AC b =.若点D 满足2BD DC =,则AD =( )A .2133b c +B .5233c b -C .2133b c -D .1233b c +⑵在平行四边形ABCD 中,E 和F 分别是边CD 和BC 的中点.若AC AE AF λμ=+,其中λ,μ∈R ,则λμ+= .【变式】 证明:若向量,,OA OB OC 的终点A B C 、、共线,当且仅当存在实数,λμ满足等式1λμ+=,使得OC OB OA λμ=+.OCA【变式】 如图,在ABC △中,点O 是BC 的中点,过点O 的直线分别交直线AB ,AC 于不同的两点M N ,,若AB mAM =,AC nAN =,则m n +的值为.ONM CBA【变式】 在平行四边形ABCD 中,E 和F 分别是边CD 和BC 的点.且1BF a FC a =-,1DE bEC b=-, 若AC AE AF λμ=+,其中λ,μ∈R ,则λμ+= .FB【变式】 设正六边形ABCDEF 的对角线,AC CE 分别被内点,M N 分成为AM CNr AC CE==,如果,,B M N 共线,求r 的值.【变式】 证明:若向量,,OA OB OC 的终点A B C 、、共线,当且仅当存在实数,λμ满足等式1λμ+=,使得OC OB OA λμ=+.(一) 知识内容3. 数乘向量:定义:实数λ和向量a 的乘积是一个向量,记作a λ,且a λ的长a a λλ=<教师备案> 判断正误:已知λμ∈R ,.①()a b a b λλλ+=+;(√) ②()a a a λμλμ+=+;(√) ③()()a a λμλμ=;(√) ④()()a b a b λμλμ+=++.(×)4. 向量共线的条件⑴ 平行向量基本定理:如果a b λ=,则a ∥b ;反之,如果a ∥b ,且0b ≠,则一定存在唯一的一个实数λ,使a b λ=.⑵ 单位向量:给定一个非零向量a ,与a 同方向且长度等于1的向量,叫做向量a 的单位向量.如果a 的单位向量记作0a ,由数乘向量的定义可知0a a a =或0a a a=.(三)典例分析:【例18】 设12,e e 是不共线的向量,已知向量1212122,3,2AB e ke CB e e CD e e =+=+=-,若A B D 、、三点共线,求k 的值.OCBA板块三:向量的数乘与共线【变式】 设a ,b ,c 为非零向量,其中任意两个向量不共线,已知a b +与c 共线,且b c +与a 共线,则b a c ++= .【变式】 已知,a b 是不共线的向量,25AB a b =+,8BC a b =-+,3()CD a b =-,则A B D 、、C 、四点中共线的三点是___________【变式】 设,a b 是不共线的两个向量,已知22(2)AB ka k b =+-,BC a b =+,2CD a b =-,若A B D、、三点共线,求k 的值.【变式】 证明对角线互相平分的四边形是平行四边形.ODCBA【例19】 如图,平行四边形ABCD 中,E F 、分别是BC DC 、的中点,G 为DE BF 、的交点,若AB =a ,AD =b ,试以a ,b 为基底表示DE 、BF 、CG .F CBA【变式】 如图,在∆ABC 中,AD 、BE 、CF 分别是BC 、CA 、AB 上的中线,它们交于点G ,则下列各等式中不正确的是( ) A .23BG BE = B .2CG GF =C .12DG AG =D .121332DA FC BC +=【变式】 已知五边形ABCDE ,M 、N 、P 、Q 分别是边AB 、CD 、BC 、DE 的中点,K 、H 分别是MN 和PQ 的中点,求证:KH 平行且等于14AE .ED CBA MNP Q K HGFEDC BA【变式】 如图,E 、F 分别是平行四边形ABCD 的边AD 、CD 的中点,BE 、BF 与对角线AC 分别交于点R 和点T .求证AR RT TC ==.(向量法)TRF E D CB A【变式】 四边形ABCD 中,E ,F ,M ,N 分别为BC ,AD ,BD ,AC 的中点,O 为MN 的中点,试用向量的方法证明:O 也是EF 的中点.FEO MNDCB A【变式】 ⑴在平行四边形ABCD 中,AC 与BD 交于点O E ,是线段OD 的中点,AE 的延长线与CD 交于点F .若AC a =,BD b =,则AF =( )A .1142a b +B .2133a b +C .1124a b +D .1233a b +⑵如图,两块斜边长相等的直角三角板拼在一起.若AD xAB y AC =+, 则x = ,y = .OF E DCBA【变式】 若等边ABC ∆的边长为23,平面内一点M 满足1263CM CB CA =+,则MA = ,MB = .(用CB ,CA 向量表示) FECBA M三角形有五心:内心、外心、垂心、重心和旁心,这里我们用向量这个工具来研究三角形的前四心,有些地方涉及到数量积,老师可以根据情况先补充数量积的知识,或将这些地方跳过去以后再讲.板块四:三角形有五心相关证明60︒45︒EDBCA⑴内心:过点A ,方向平行于向量()(0)||||AB ACAB AC λλ+≠的直线过ABC ∆的内心(BAC ∠的角分线所在直线);||||||0AB PC BC PA CA PB P ++=⇔为ABC ∆的内心;⑵外心:PA PB PC ==⇔P 为ABC ∆的外心;⑶垂心:PA PB PB PC PC PA P ⋅=⋅=⋅⇔为ABC ∆的垂心(先补充数量积的相关知识) ⑷重心:0PA PB PC P ++=⇔为ABC ∆的重心.另外:在ABC ∆中,G 为平面上任意一点,有1()3GO GA GB GC =++⇔O 为ABC ∆的重心1()()()()03GO GA GB GC GA GO GB GO GC GO =++⇒-+-+-=,即0OA OB OC ++=,知O 为ABC ∆的重心;若O 为ABC ∆的重心,则11()(3)33GA GB GC GO OA OB OC ++=+++20OA OB OC OA OE ++=+=,故1()3GA GB GC GO ++=.【例20】 在OAB ∆中,M 为OB 的中点,N 为AB 的中点,P 为,ON AM 交点,利用向量证明23AP AM =,即重心为中线的一个三等分点.【变式】 ⑴已知3()2(2)4()0m a m a m a b -++-+-=,则m =⑵已知a ,b 方向相同,且3a =,7b =,则2a b -=【变式】 若O 是ABC ∆内一点,0OA OB OC ++=,则O 是ABC ∆的( )A.内心 B .外心 C .垂心 D .重心【变式】 (2003年天津)O 是平面内一定点,A ,B ,C 是平面上不共线的三个点,动点P 满足AB AC OP OA AB AC λ⎛⎫ ⎪=++ ⎪⎝⎭,[0,)λ∈+∞,则P 的轨迹一定通过ABC ∆的( ) A .外心 B .内心 C .重心 D .垂心【变式】 若点O 是ABC △的外心,且0OA OB CO ++=,则内角C 的大小为____OEDC BA【变式】 已知点G 是ABC ∆的重心,过G 作直线与AB 、AC 两边分别交于M 、N 两点,且设AM xAB =,AN y AC =,则113x y+=.NMGCBA【变式】 非正ABC △的外接圆的圆心为O ,两条边上的高的交点为H ,()OH m OA OB OC =++,求实数m 的值.【变式】 如图,设G 为OAB ∆的重心,过G 的直线与,OA OB 分别交于P 和Q ,已OP hOA =,OQ kOB =,OAB ∆与OPQ ∆的面积分别为S 和T .求证:⑴113h k+=;⑵4192S T S ≤≤.【例21】 已知任意四边形ABCD 中,,E F 分别是,AD BC 的中点,求证:1()2EF AB DC =+.E BBAMG QP O【例22】 如图所示,E F 、是四边形ABCD 的对角线AC BD 、的中 点,已知,AB a CD c ==,求向量EF .A【变式】 在平行四边形ABCD 中,AC 与BD 交于点O ,E 是线段OD 的中点,AE 的延长线与CD 交于点F .若AC a =,BD b =,则AF =( )A . 1142a b +B . 2133a b +C . 1124a b +D . 1233a b +【变式】 已知点M 是ABC ∆的重心,,MA a MB b ==,用,a b 表示,,AB AC BC .FEDCBAM【变式】 M 、N 分别是ABC ∆的边AB 、AC 的靠近A 的三等分点.求证:13MN BC =,且MN ∥BC .【变式】 已知矩形ABCD 中,宽为2,长为AB a =,BC b =,AC c =,试作出向量a b c ++,并求其长度.OFE DCBA【变式】 如图,在ABC △中,点O 是BC 的中点,过点O 的直线分别交直线AB ,AC 于不同的两点M N ,,若AB mAM =,AC nAN =,则m n +的值为 .ONMCBA。
(整理)向量的加减法实数与向量的乘积.

高中学生学科素质训练高一数学同步测试(9)—向量的加减法、实数与向量的乘积一、选择题(每小题5分,共60分,请将所选答案填在括号内)1.如图,已知四边形ABCD 是梯形,AB ∥CD ,E 、F 、G 、H 分别是AD 、BC 、AB 与CD 的中点,则EF 等于( )A .+B .+C .DH +D .GH +2.下列说法正确的是 ( ) A .方向相同或相反的向量是平行向量 B .零向量的长度为0C .长度相等的向量叫相等向量D .共线向量是在同一条直线上的向量3.在△ABC 中,D 、E 、F 分别BC 、CA 、AB 的中点,点M 是△ABC 的重心,则 -+等于( )A .B .4C .4D .4 4.已知向量与反向,下列等式中成立的是( ) A .||||||-=- B .||||-=+C .||||||-=+D .||||||+=+5.在 ABCD 中,设====,,,,则下列等式中不正确的是( )A .=+B .=-C .=-D .=-6.下列各量中是向量的是( ) A .质量 B .距离C .速度D .电流强度7.在矩形ABCD 中,O 是对角线的交点,若OC e DC e BC 则213,5=== ( )A .)35(2121e e + B .)35(2121e e - C .)53(2112e e - D .)35(2112e e - 8.若),,(,,,R ∈=+μλμλ不共线则( )A .==,B .o ==μ,C .o ==,λD .o o ==μλ, 9.化简)]24()82(21[31--+的结果是( )A .-2B .-2C .-D .-10.下列三种说法:①一个平面内只有一对不共线向量可作为表示该平面所有向量的基底 ②一个平面内有无数对不共线向量可作为该平面的所有向量的基底 ③零向量不可作为基底中的向量。
其中正确的是 ( )A .①②B .②③C .①③D .①②③11.若2121,,PP P OP λ===,则等于 ( )A .b a λ+B .b a +λC .)1(λλ-+D .λλλ+++111 12.已知ABCD 为菱形,则下列各式中正确的个数为 ( )①=②||||=③||||+=-④||4||||22=+2A .1个B .2个C .3个D .4个二、填空题(每小题4分,共16分,答案填在横线上)13.21,e e 不共线,当k= 时,2121,e k e b e e k a +=+=共线. 14.非零向量||||||,b a b a b a +==满足,则b a ,的夹角为 . 15.在四边形ABCD 中,若||||,,-=+==且,则四边形ABCD 的形状是 .16.已知,,的模分别为1、2、3,则||++的最大值为 .三、解答题(本大题共74分,17—21题每题12分,22题14分)17.设21,e e 是两个不共线的向量,2121212,3,2e e e e e k e -=+=+=,若A 、 B 、D 三点共线,求k 的值.18.已知△ABC 及一点O ,求证:O 为△ABC 的重心的充要条件是.=++19.已知向量,,32,32212121e e e e e e 与其中+=-=不共线向量,9221e e -=,问是否存在这样的实数,,μλ使向量与μλ+=共线?20.试证:以三角形三边上的中线为边可以作一个三角形.21.如图,在△ABC 中,P 是BC 边上的任一点,求证:存在,1)1,0(,2121=+∈λλλλ且使 21λλ+=.22.一架飞机从A 地按北偏西30°方向飞行3000千米到达13地,然后向C 地飞行,设C 地恰在A 地的北偏东30°,并且A 、C 两地相距3000千米,求飞机从B 地向C 地飞行 的方向和B 、C 两地的距离.高一数学同步测试(9)参考答案一、1.C 2.B 3.C 4.C 5.B 6.C 7.A 8.D 9.B 10.B 11.D 12.C二、13.1± 14.120° 15.菱形 16.6三、17.k=-818.设P 、Q 、R 分别是BC 、CA 、AB 的中点,则.3,,3231,3231,3231000000重合与故可知则为重心设反之故O O OC OB OA OO O O O O =++==++=++=+++=+=+=19.μλμλμλμλμλ2.,,2933222-=∈-=⎩⎨⎧-=+-=+只要故存在解之R k k即可.20.如图,=++===则,,λ)()(21=+++++=++故证21.如图,作PE ∥AB ,PD ∥AC ,则21==λλ=+=+=+∴21λλ 22.(1)3000千米 (2)正东方向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∴kλ= =-λ 1, 故选 D.
答案:D
8.在平面直角坐标系 xOy 中,四边形 ABCD 的边 AB∥ DC,AD∥BC,已知点 A(-2,0),B(6,8),C(8,6),则 D 点的 坐标为________.
解析:在平行四边形 ABCD 中,O→B+O→D=O→A+O→C, ∴O→D=O→A+O→C-O→B=(-2,0)+(8,6)-(6,8)=(0,-2),即 D 点坐标为(0,-2).
思路分析:利用向量坐标运算的各公式.
1 已知 a=(3,-2),b=(-10,9).试问当 k 为何值时, ka+b 与 2a-3b 平行?平行时它们同向还是反向?
解:ka+b=k(3,-2)+(-10,9) =(3k-10,-2k+9), 2a-3b=2(3,-2)-3(-10,9) =(6+30,-4-27)=(36,-31), ∵ka+b 与 2a-3b 平行, ∴(3k-10)×(-31)-(-2k+9)×36=0. 解得 k=-1241=-32, 此时 ka+b 与 2a-3b 平行,且反向.
A2
A
A1
1.向量共线的坐标表示 设 a=(x1,y1),b=(x2,y2),其中 b≠0. 那么当且仅当 x1y2-x2y1=0 时,向量 a、b(b≠0)共线, 即 a∥b⇔x1y2-x2y1=0.
2.证明三点共线的方法 设 A(x1,y1)、B(x2,y2)、C(x3,y3), 只要证明向量A→B与B→C共线,便可证得 A、B、C 三点共 线.
三点共线问题 【例 2】 向量P→A=(k,12),P→B=(4,5),P→C=(10,k), 当 k 为何值时,A、B、C 三点共线?
思路分析:A、B、C 三点要共线,则必有B→A∥C→A.
2 已知向量O→A=(k,12)、O→B=(4,5)、O→C= (-k,10),且 A、B、C 三点共线,则 k=________.
三、解答题 10.已知O→A=(1,1),O→B=(3,-1),O→C=(a,b). (1)若 A,B,C 三点共线,求 a,b 的关系;
自测自评
1.已知向量 a=(2,4),b=(-3,-6),则 a 和 b( )
A.共线且方向相同 B.共线且方向相反
C.是相反向量
D.不共线
解析:a=-23b 且-23<0,∴a 和 b 共线且方向相反. 答案:B
2.若三点 P(1,1)、A(2,-4)、B(x,-9)共线,则( )
A.x=-1 C.x=92
10 10 )
解D析.:(-与3A→1B01共0,线的1100单)或位(向3 1量010是,±-A→→B11.00)
|AB|
答案:D
4.已知|a|=2 3,b=(-1, 3),且 a∥b,则 a=________.
解析:∵a∥b,b=(-1, 3), 可设 a=(-λ, 3λ), 又∵|a|=2 3,∴(-λ)2+3λ2=12,λ=± 3. 当 λ= 3时,a=(- 3,3).当 λ=- 3时,a=( 3,-3)
B.x=3 D.x=51
解析:P→A=(1,-5),P→B=(x-1,-10). ∵P→A∥P→B,∴1×(-10)-(-5)×(x-1)=0,x=3.
答案:BBiblioteka 3.已知两点 A(2,3),B(-4,5),则与A→B共线的单位向量
是( )
A.(-6,12)
B.(-6,2)或(6,-2)
C.(-3
1010,
当
P1P PP2
=λ时,点P的坐标是什么?
3 已知向量A→B=(4,3)、A→D=(-3,-1),点 A(-1,-2). (1)求线段 BD 的中点 M 的坐标; (2)若点 P(2,y)满足P→B=λB→D(λ∈R),求 y 与 λ 的值.
基础达标
一、选择题 1.已知平面向量 a=(x,1),b=(-x,x2),则向量 a+ b( ) A.平行于 x 轴 B.平行于第一、三象限的角平分线 C.平行于 y 轴 D.平行于第二、四象限的角平分线
解析:由 a+b=(0,1+x2),且 1+x2≠0 及向量的性质可 知选 C.
答案:C
4.已知向量 a,b 不共线,c=ka+b(k∈R),d=a-b, 如果 c∥d,那么( )
A.k=1 且 c 与 d 同向 B.k=1 且 c 与 d 反向 C.k=-1 且 c 与 d 同向 D.k=-1 且 c 与 d 反向
解析:A→B=O→B-O→A=(4-k,-7),B→C=O→C-O→B=(- 4-k,5),由A→B∥B→C,所以 7(k+4)-5(4-k)=0,得 k=-32.
答案:-23
向量平行的应用 【例 3】 如下图,已知点 A(4,0),B(4,4),C(2,6),求 AC 与 OB 的交点 P 的坐标.
答案:(0,-2)
9.已知 A(-1,0),B(3,1),C(4,3),D(0,2),则四边形 ABCD 的形状为________.
解析:由于A→B=(3,1)-(-1,0)=(4,1),D→C=(4,3)-(0,2) =(4,1),所以A→B=D→C,所以四边形 ABCD 为平行四边形.
答案:平行四边形
rr
r r r ur
例1:如图,分别用基底 i ,j 表示向量 a 、b 、 c 、d ,
并求出它们的坐标.
解:如图可知
r uuuur uuuur r r a = Ar A1 + AA2 = 2i +3j
a = (2, 3) 同理 r r r
b = -2i + 3j = (-2, 3); r rr c = -2i - 3j = (-2, -3); r rr d = 2i - 3j = (2, -3).
答案:(- 3,3)或( 3,-3)
5.已知 A(-2,-3),B(2,1),C(1,4),D(-7,-4), 试问:(1)A→B与C→D是否共线?
解:(1)A→B=(4,4),C→D=(-8,-8), ∴C→D=-2A→B.∴A→B与C→D共线.
平面向量共线的坐标运算 【例 1】 向量 a=(1,1),b=(x,1),u=a+2b,v=2a -b. (1)若 u=3v,求 x; (2)若 u∥v,求 x,并判断 u 与 v 同向还是反向.
