4.1平面向量的加法减法运算
02-第二节 平面向量的运算-课时1 向量的加法运算、减法运算高中数学必修第二册人教版

= = ,所以四边形和四边形都是平行四边形,所以
= , = .
A √ 由平行四边形法则,得 + = .
B √ || = || = 1,|| = || = 1,所以|| = ||.
C × − = − = + ≠ .
D.
【解析】 + ( + ) + = + + + = .
)
2.如图所示的方格纸中有定点,,,,,
,,则 + =( C )
A.
B.
C.
D.
【解析】 设 = + ,利用向量加法的平行四
边形法则作出向量,再平移即可发现 = .
1.(多选)如图,在等腰梯形中,//, = 2,
= = = 1,为的中点,则( ABD
A. + =
B.|| = ||
C. − =
D. + =
)
【解析】 由题意得|| = || = || = 1,//,//,所以
所以△是以∠为直角的直角三角形,
从而 ⊥ ,所以平行四边形是矩形.
根据矩形的对角线相等,知|| = ||,因此| + | = 4.
(2)若|| = || = | −
|+|
|,求
.
|−|
【解析】 如图所示,平行四边形中,设 = ,
(1)若|| = 7 + 1,|| = 7 − 1,且| − | = 4,求| + |;
【解析】 如图所示,设 = , = ,以,为邻边作
平行四边形,则|| = | − | = | − |,|| = |
+| = | + |.
平面向量的加法与减法

平面向量的加法与减法在数学中,平面向量是用来描述平面上的位移和力的工具。
平面向量具有大小和方向两个特征,可以通过数学运算来完成加法和减法操作。
本文将详细介绍平面向量的加法和减法运算,并探讨其应用。
一、平面向量的表示方法平面向量通常用字母加箭头来表示,如AB→表示从点A到点B的位移向量。
平面向量还可以用坐标表示,如向量→AB的坐标表示为(ABx , ABy)。
其中,ABx表示向量在x轴上的分量,ABy表示向量在y轴上的分量。
二、平面向量的加法两个平面向量的加法是指将两个向量的对应分量相加的操作。
设有两个向量→AB和→CD,其坐标分别为(ABx , ABy)和(CDx , CDy)。
那么,向量→AB与→CD的和为→AB + →CD,其坐标为(ABx + CDx , ABy + CDy),即两个向量的横坐标分量相加得到新向量的横坐标,纵坐标分量相加得到新向量的纵坐标。
三、平面向量的减法平面向量的减法是指将一个向量减去另一个向量的操作。
设有两个向量→AB和→CD,其坐标分别为(ABx , ABy)和(CDx , CDy)。
那么,向量→AB减去向量→CD的差为→AB - →CD,其坐标为(ABx - CDx , ABy - CDy),即两个向量的横坐标分量相减得到新向量的横坐标,纵坐标分量相减得到新向量的纵坐标。
四、平面向量的应用平面向量的加法与减法在数学中有广泛的应用。
以下列举几个常见的应用场景:1. 位移问题:平面向量的加法可用于求解物体在空间中的位移问题。
通过将各个位移向量进行加法运算,可以得到物体的总位移向量。
2. 力的合成:力的合成是指多个力的作用下,合成后产生的力。
通过将各个力向量进行加法运算,可以得到合成力的大小和方向。
3. 航空航天:在航空航天领域中,平面向量的加法与减法被广泛运用于导航和控制系统中,用以计算飞行器的位置和速度。
4. 平面几何:平面向量的加法与减法在平面几何中也有重要应用。
平面向量加减法口诀
向量的加法口诀: 首尾相连,首连尾,方向指向末向量。
以第一个向量的起点为起点,以第二个向量的终点为终点的向量是两向量的和向量。
二、向量的减法两向量做减法运算,图像如下图所示:向量的减法口诀: 首首相连,尾连尾,方向指向被减向量。
以第一个向量的终点为起点,以第二个向量的终点为终点的向量是两向量的差向量。
向量的学习是高一数学必修四第二章的内容,要求同学们会向量的基本运算,其中就包括加法、减法、数乘。
要求大家能根据运算法则解决基本的向量运算,学会运用图像解决向量加减法,向量的数乘等问题。
向量的相关题目难度也不是很大,只要大家认真学习,认真做好笔记,认真做做题目,总结做题规律,那么当我们遇到类似题目时就会似曾相识,做起来也很顺手,再细心点的话,得满分也没有问题。
学习方法很多,重要的事找到适合自己的方法,当然适合自己方法就是最好的方法。
附一;三角形定则解决向量加减的方法将各个向量依次首尾顺次相接,结果为第一个向量的起点指向最后一个向量的终点。
注:两个向量相减,则表示两个向量起点的字母必须相同;差向量的终点指向被减向量的终点。
平行四边形定则解决向量加法的方法实数λ叫做向量a的系数,乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩.当∣λ∣>1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上伸长为原来的λ∣倍;当∣λ∣<1时,表示向量a的有向线段在原方向(λ>0)或反方向(λ<0)上缩短为原来的λ∣倍.数与向量的乘法满足下面的运算律结合律:(λa)·b=λ(a·b)=(a·λb).向量对于数的分配律(第一分配律):(λ+μ)a=λa+μa.数对于向量的分配律(第二分配律):λ(a+b)=λa+λb.数乘向量的消去律:① 如果实数λ≠0且λa=λb,那么a=b.② 如果a≠0且λa=μa,那么λ=μ 3、向量的的数量积定义:已知两个非零向量a,b.作OA=a,OB=b,则角AOB称作向量a和向量b的夹角,记作〈a,b〉并规定0≤〈a,b〉≤π定义:两个向量的数量积(内积、点积)是一个数量,记作a·b.若a、b不共线,则a·b=|a|·|b|·cos〈a,b〉;若a、b共线,则a·b=+-∣a∣∣b∣.向量的数量积的坐标表示:a·b=x·x'+y·y'.向量的数量积的运算律a·b=b·a(交换律);(λa)·b=λ(a·b)(关于数乘法的结合律);(a+b)·c=a·c+b·c(分配律);向量的数量积的性质a·a=|a|的平方.a⊥b 〈=〉a·b=0.|a·b|≤|a|·|b|.向量的数量积与实数运算的主要不同点1、向量的数量积不满足结合律,即:(a·b)·c≠a·(b·c);例如:(a·b)^2≠a^2·b^2.2、向量的数量积不满足消去律,即:由 a·b=a·c (a≠0),推不出 b=c.3、|a·b|≠|a|·|b|4、由 |a|=|b| ,推不出 a=b或a=-b.4、向量的向量积定义:两个向量a和b的向量积(外积、叉积)是一个向量,记作a×b.若a、b不共线,则a×b的模是:∣a×b∣=|a|·|b|·sin〈a,b〉;a×b的方向是:垂直于a和b,且a、b和a×b按这个次序构成右手系.若a、b共线,则a×b=0.向量的向量积性质:∣a×b∣是以a和b为边的平行四边形面积.。
平面向量加法

平面向量加法
两个向量做加法运算就是向量的加法,是一种向量的运算。
向量的加法口诀:首尾相连,首连尾,方向指向末向量。
向量的减法口诀:首首相连,尾连尾,方向指向被减向量。
平面向量是在二维平面内既有方向(direction)又有大小(magnitude)的量,物理学中也称作矢量,与之相对的是只有大小、没有方向的数量(标量)。
平面向量用a,b,c上面加一个小箭头表示,也可以用表示向量的有向线段的起点和终点字母表示。
向量的加法满足平行四边形法则和三角形法则。
AB+BC=AC。
a+b=(x+x',y+y')。
a+0=0+a=a。
向量加法的运算律:交换律:a+b=b+a;结合律:(a+b)+c=a+(b+c)。
如果a、b是互为相反的向量,那么a=-b,b=-a,a+b=0. 0的反向量为0,AB-AC=CB. 即“共同起点,指向被减”,a=(x,y) b=(x',y') 则 a-b=(x-x',y-y')。
平面向量的基本概念与运算法则

平面向量的基本概念与运算法则平面向量是在平面中具有大小和方向的量,由有序数对表示。
在数学中,平面向量是研究平面几何和代数的基础。
本文将介绍平面向量的基本概念和运算法则,以帮助读者更好地理解和应用平面向量。
一、平面向量的基本概念平面向量通常用有向线段表示,其中起点和终点之间的位置表示向量的方向。
一个平面向量可由其终点的坐标减去起点的坐标得到。
例如,向量AB可以表示为向量a = (x2-x1, y2-y1),其中A(x1, y1)和B(x2, y2)是向量的起点和终点。
平面向量的大小通常用向量的长度来表示,也称为向量的模。
向量a = (x, y)的长度表示为|a|或||a||,可以通过勾股定理计算得到:|a| =√(x^2+y^2)。
向量的长度是一个非负数。
二、平面向量的运算法则1. 加法运算平面向量的加法运算定义为将两个向量的对应分量相加。
例如,对于向量a = (x1, y1)和向量b = (x2, y2),它们的和可以表示为向量c = (x1+x2, y1+y2)。
2. 减法运算平面向量的减法运算定义为将两个向量的对应分量相减。
例如,对于向量a = (x1, y1)和向量b = (x2, y2),它们的差可以表示为向量c =(x1-x2, y1-y2)。
3. 数乘运算平面向量的数乘运算定义为将向量的每个分量与一个标量相乘。
例如,对于向量a = (x, y)和标量k,它们的数乘可以表示为向量b = (kx, ky)。
4. 乘法运算平面向量的乘法运算有两种形式:数量积和向量积。
4.1 数量积数量积(又称点积或内积)定义为两个向量的对应分量相乘后再相加。
数量积的结果是一个标量。
对于向量a = (x1, y1)和向量b = (x2,y2),它们的数量积表示为a · b = x1x2 + y1y2。
4.2 向量积向量积(又称叉积或外积)定义为两个向量的乘积是一个新的向量,它垂直于原来两个向量组成的平面,并且方向遵循右手法则。
平面向量的加减法

[精解详析] 因为 a+b= BA ,c-d= DC , 所以 a= OA ,b= BO ,c= OC ,d= OD ;如图所示,作 平行四边形 OBEC,平行四边形 ODFA,根据平行四边形法则 可得:b-c= EO ,a+d= OF .
跟踪练习
1.如图,已知正方形 ABCD 的边长等于 1,
An1 An A0 An ,这可以称为向量加法
例题讲解
[例1] 如图所示,
已知向量a,b,c试作出向量a+b+c.
[精解详析] 法一:如图 1 所示, 首先在平面内任取一点 O,作向量 OA = a,再作向量 AB =b,则得向量 OB =a+b; 然后作向量 BC = c,则向量 OC = (a+ b)+ c =a+b+c 即为所求.
AB =a, BC =b, AC =c,试作以下
向量并分别求模. (1)a+b+c; (2)a-b+c.
解:(1)如图,由已知得:a+b= AB + BC = AC ,又 AC =c, 延长AC到E, 使| CE |=| AC |. 则a+b+c= AE ,且| AE |=2 2. (2)作 BF = AC ,连接CF, 则D、C、F共线, 则 DB + BF = DF , 而 DB = AB - AD =a- BC =a-b, ∴a-b+c= DB + BF = DF 且| DF |=2.
例题讲解
[例 2] 化简或计算:
(1) CD + BC + AB ; (2) AB + DF + CD + BC + FA .
[精解详析] (1) CD + BC + AB =( AB + BC )+ CD = AC + CD = AD . (2) AB + DF + CD + BC + FA =( AB + BC )+( CD + DF )+ FA = AC + CF + FA = AF + FA =0.
平面向量的加法减法与数乘运算课件

数乘的运算性 质
结合律
$\lambda(\mu\mathbf{a})=(\lambda\mu)\mathbf{a}$。
分配律
$\lambda(\mathbf{a}+\mathbf{b})=\lambda\mathbf{a}+\lambd a\mathbf{b}$。
反交换律
$\lambda\mathbf{a}\cdot\mathbf{b}=\lambda(\mathbf{a}\cdot \mathbf{b})$。
2023
PART 04
平面向量的加法减法与数 乘运算的应用
REPORTING
在物理学中的应用
力的合成
电磁学中的向量表示
在物理中,向量加法可以应用于力的 合成,例如两个力的向量和可以表示 为它们的加法运算。
在电磁学中,向量加法可以用于表示 电磁场中的向量,例如电场强度和磁 场强度。
速度和加速度
速度和加速度是物理学中重要的向量 概念,通过向量加法可以计算出物体 在不同方向上的速度和加速度。
详细描述
2. 这类题目需要学生灵活运用所学知识,进行深入思考 和细致计算。
2023
REPORTING
THANKS
感谢观看
求解向量与轴的夹角
通过数乘运算可以求得向量与 轴之间的夹角。
投影问题
通过数乘运算可以求得一个向 量在另一个向量上的投影。来自 2023PART 03
平面向量的加法减法与数 乘运算的几何意 义
REPORTING
平面向量的几何意 义
01
02
03
04
向量表示为有向线段
向量的起点为线段的起点,终 点为线段的终点
向量的长度和方向
平面向量的加法与减法

平面向量的加法与减法在平面向量的运算中,加法和减法是两个基本且重要的运算操作。
通过合适的方法进行向量相加或相减,可以获得新的向量,进而帮助我们解决实际问题和优化计算过程。
本文将重点探讨平面向量的加法和减法,并介绍它们的性质和运算规则。
一、向量的表示平面上的向量可以用有序数对表示,我们通常以大写字母加箭头(→)来表示向量,例如向量A可以表示为A→ = (x,y)。
其中,x和y分别表示向量在x轴和y轴上的分量。
二、向量的加法向量的加法是指将两个向量相加,得到一个新的向量。
向量的加法满足以下几个性质:1. 交换律:对于任意向量A和B,有A + B = B + A。
2. 结合律:对于任意向量A、B和C,有(A + B) + C = A + (B + C)。
3. 零向量:零向量的表示为O→ = (0,0),对于任意向量A,有A +O→ = A。
根据以上性质,我们可以通过向量的对应分量相加的方式来进行向量的加法运算。
例如,向量A→ = (x1,y1)和向量B→ = (x2,y2),它们的和A→ + B→ = (x1+x2,y1+y2)。
三、向量的减法向量的减法是指将一个向量减去另一个向量,得到一个新的向量。
向量的减法同样满足交换律和结合律,减法的规则可以通过相应的加法来表示。
对于向量A和向量B,向量的减法可以表示为A→ - B→ = A→ + (-B→),其中-A→表示向量B→的反向量。
向量的反向量的表示为-A→ = (-x,-y),即将向量的每个分量取反。
根据向量的加法运算规则,我们可以将向量的减法转化为相应的加法运算。
例如,向量A→ = (x1,y1)和向量B→ = (x2,y2),它们的差A→ - B→ = A→ + (-B→) = (x1,y1) + (-x2,-y2) = (x1-x2,y1-y2)。
四、几何意义向量的加法和减法在平面几何中具有重要的几何意义。
对于向量的加法,可以将两个向量的起点放在同一个位置,然后将终点相连,所得的新向量即为其和向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
即 令 于是
AAaBBbaAD,bADaAD
b
AB
这就是向量的加法交换律.(与数量的加法交换律相似)
例2.如图所示是平行四边形ABCD ,化
简下列各式:
D
C
(1) AB BC
(2) AB AD
(3) AD CD
A
B
解:(1) AB BC AC
(2) AB AD AC
(3) 因为 AD BC , 所以 AD CD BC CD BD 即 AD CD BD
ab ba
热身运动:拔河
热身运动:拔河
1、相反向量: 与非零向量a 长度相等,且方向相
反的向量叫做向量 a的相反向量,记作 。 a
说明: ① 规定 0 0
② 性质 a a
a
a
a
a
0
2、向量的减法:
向量a与向量b的负向量的和定义为向量 a
与向量 b的差,即
a
b
a
b
求两个向量差的运算叫作向量的减法
⑶ 方向指向被减向量
同起点,连终点,指向被减
2、小试牛刀
已知向量
a 和
b(如下图),请分别画出
a
b
和
b
a
b
a
b
a
3、动脑思考
若 a、b共线时,怎样作 a
b
?
① 共线同向
a a
bbaara
br b
b
AC
B
a
b
AB
AC
CB
② 共线反向
a a a a
a
r a
bbbbrb
B
a
b
AB
注意:两个向量的和仍然是一个向量
首
向量加法的三角形法则
尾 相
连
作平移,首尾相连,由起点指向终点.
rr
rr
练习:已知向量a, b,求作向量 a b
r
rc
首
b
尾 相
r连Biblioteka acab
例1:在平行四边形ABCD中,求作 AB +AD
我们先来找一找在这个平行四边形中相等的向量: AB DC AD BC BA CD DA CB
共起点、连终点、指向被减
作业:
• 教材P89,课堂练习第1、2题
A
AC
C
CB
例1
已知如图所示向量
a
、b,请画出向量
a
b
a
b
a O
A
b
a
b
B
例2 化简:
⑴ OD OA
⑵ AB AC BD DC
解:⑴ OD OA AD ⑵ AB AC BD DC CB BD DC
CD DC CC 0
1、已知
a、b
,求作
a
b
b
b
a
b
首 相
D
C
连
练一练
如图,已知 a, b 用向量加法的平行四边形法则 作出 a b
(1) b
ab
首
ba
首 相
(2)
b
a
ab
连
a
回顾例1:平行四边形ABCD中,AB AD AC
问: 能否不移动向
量 AD , 而移动向 量 AB ?结果是否和
原来一样呢?
解:因为 AB DC , 所以 AD AB AD DC AC
§§24..21 .平1面向向量量加的加法法运运算算 及其几何意义
以前,乘车从慈溪去嘉兴要先从慈溪到杭州 再由杭州到嘉兴,则两次位移的总效果如何?
嘉兴
杭州
慈溪
如果我们把北京、上海、临港分别用字母 A、B、C表示,那么两种方法可以看成:
临港
1、位移 AB 与位移 BC 的和
uuur
2、位移 AC
结论:动点从点A直接位
AB BC AD DB _B_C___ MD MN MP DP _M__N__
AM AN MGGE _N__E__ ABCD AC BD __0____
备选题:
如图所示,在平行四边形ABCD中,设
AB
a,AD
b,试用
a,b表示向量
AC、
BD、 D。B
D
C
b
A
a B
1、向量减法的定义及其几何意义 2、正确熟练地掌握向量减法法则:
1、向量减法法则:已知向量 a,b不共线,求作
向量作OOAA法c,:O使a在B,平cOB面Oa内Ab任b,取则O一B点O,作bbbObabbaaaBa
a
A
b
OA BO BO OA BA
向量减法法则
OA OB BA
O
a
A
b
a
b
B
归纳概括: ⑴ 将两向量移到共同起点
⑵ 连接两向量的终点,
移到点C ,与两次连续位
北京
上海 移的效果相同.即
AB BC AC
问:位移求和时,两次位移的位置关系是什么? 如何求出他们的和位移?
向量的加法
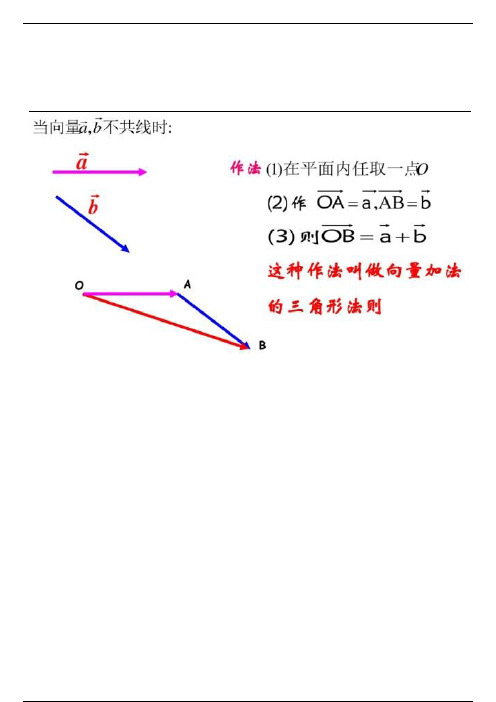
定义:求两个向量和的运算,叫做向量的加法.
a
作法:1在平面内任取一点 A
C
a+b
2作AB a,BC b
b
3则向量AC a b
A
B
a+b=AB+BC=AC
这种求不共线的两个向量和的方法叫做 首
向量加法的平行四边形法则
首 相
作平移,共起点,四边形,对角线
连
向量的加法
已知向量a,b,用向量加法的平行四边形法则 求作向量a+b.
作法: (1)在平面内任取一点A
b
a
(2)作 AB a, AD b
B
(3)以AB,AD为邻边
A
作平行四边形ABCD 首
则 AC a b
a
a
b
a
2、快速抢答:
AB AD __D_B___
OB OC DB _C__D__
BA BC ___C_A__
OA OC BO CO __B_A__
OAOB __B_A__
AB AC BD DC __0___
NQ QP MN MP __0___ AB BC DC DA __0___
解:因为 AD BC , 所以 AB AD AB BC AC.
例1:在平行四边形ABCD中,AB AD AC
1.说一说两个相加向量的位置特点; 2. 两个向量相加的和向量与这两个向量的 位置关系;
例1:在平行四边形ABCD中,AB AD AC
AB AD 的和正好是以向量 AB 、AD 为邻 边的平行四边形的对角线AC 表示的向量.
