2017-2018学年广东省广州市天河区普通高中高一数学上10月月考试题(04)(含答案)
广东天河区普通高中上学期高一数学10月月考试题 01 Wo

上学期高一数学10月月考试题01一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若集合{}0,1,2A =,则集合A 的子集共有 ( ) A .3个 B .6个 C .7个 D .8个 2. 如果函数()f x kx b =+在R 上单调递减,则( ) A. 0k > B. 0k < C. 0b > D. 0b <3.已知集合}01|{2=-=x x A ,则下列式子表示正确的有( ) ①A ∈1 ②A ∈-}1{ ③A ⊆φ ④A ⊆-}1,1{A .1个B .2个C .3个D .4个4.下列四个函数中,与y x =表示同一函数的是 ( ) A .2)(x y = B .33x y = C .2x y =D .xx y 2=5.下列函数中在区间(,0)-∞上是增函数的是 ( ) A .2xy = B . y x =- C .xy 1=D .2y x =. 6.如图,I 是全集,M 、P 、S 是I 的3个子集,则阴影部分所表示的集合是( )A. (M∩P )∩SB. (M∩P )∪SC. (M∩P )∩S I CD. (M∩P )∪S I C7.函数y = ).A .{|1}x x ≤B .{|0}x x ≥C .{|10}x x x ≥或≤D .{|01}x x ≤≤8.已知函数()f x =m 的取值范围是( ) A. 04m <≤B. 01m ≤≤C. 4m ≥D. 04m ≤≤9. 设,a b R ∈,集合{}1,,0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭,则b a -= ( ) A .1B .1-C .2D .2-10.如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上单调递减,那么实数a 的取值范围是( )A 、3a -≤B 、3a -≥C 、a ≤5D 、a ≥5二、填空题(每小题4分,共16分,请将答案填在题中的横线上)11. 函数xx x f -++=211)(的定义域为______________________ 12. 已知)(x f 是奇函数,且当0>x 时,12)(2-=x x f ,那么)1(-f =_______________。
广东天河区普通高中2017-2018学年上学期高一数学10月月考试题 08 Word版含答案

上学期高一数学10月月考试题08一、选择(每题只有一个正确选项,共计15题,3×15=45分) 1.设集合A={1,2,3,4,5},B={2,4}则正确的是A .AB ⊆ B .A B ∉C .B A ⊆D .B A ∉ 2. 下列5个关系式,其中正确的有①{a ,b }={b ,a };②{a ,b }⊆{b ,a };③{0}=∅;④∅{0};⑤0∈{0}.A .6个B .5个C .4个D .3个3. 设集合B 满足条件{1,3}∪B={1,3,5},则满足条件的集合B 的个数是A .1B .2C .3D .44.已知集合P={(x ,y )| x + y=3},集合Q={(x ,y )|x-y=5},那么P ∩Q= A .{(4,-1)} B .(4,-1) C .{4、-1} D .∅5. 函数y =1-x +x 的定义域是A .{x |x ≤1}B .{x |x ≥0}C .{x |x ≥1或x ≤0} D.{x |0≤x ≤1}6.下列各图中,不能是函数f (x )图象的是()7. 已知集合A ={a ,b },集合B ={0,1},下列对应不是A 到B 的映射的是()8.若()⎪⎩⎪⎨⎧<+=>-=0,10,00,22x x x x x x f ,则)]1([f f 的值为A .2B .1C .0D .-1 9.下列函数中,在区间()0,1上是增函数的是 A .||y x = B .3y x =- C .1y x= D .22y x =-+10.设函数()f x 是定义在R 上的奇函数,当0x ≤时,2()2f x x x =-,则(2)f =A . 0B . 8C .-8D . -211.已知函数31()f x x x=+的图象关于 A .原点对称 B .y 轴对称 C .y =x 对称D .y =-x 对称12. 下列函数为偶函数的是( )A .()||f x x x =+B .21()f x x x=+C .2()f x x x =+D .2||()x f x x=13. 若奇函数()x f 在[]5,2上为增函数,且有最小值0,则它在[]2,5--上 A.是减函数,有最小值0 B.是增函数,有最小值0 C.是减函数,有最大值0 D.是增函数,有最大值014.函数2()22f x x ax a =-++在[0,a ]上取得最大值3,最小值2,则实数a 为A .0或1B .1C .2D .以上都不对15.定义在R 上的偶函数f (x )在[0,+∞)上是增函数,若f (a )<f (b ),则一定可得A .a <bB .a >bC .|a |<|b |D .0≤a <b 或a >b ≥0二、填空(每题4分,共计4×6=24分)16某工厂8年来某产品产量y 与时间t 年的函数关系如下图,则:t①前3年总产量增长速度越来越快; ②前3③第3年后,这种产品停止生产;④第3年后,这种产品年产量保持不变. 以上说法中正确的是_______.17.若{}{}21,4,,1,A x B x ==且AB B =,则x = .18. 已知函数⎩⎨⎧>≤-=0,30,1)(2x x x x x f , 若15)(=x f ,则=x .19.函数0y =的定义域是________.20. 设集合A ={x |x +m ≥0},B ={x |-2<x <4},全集U =R ,且(∁U A )∩B =∅,求实数m 的取值范围为________.21. 已知函数2()4f x x ax =+-在[]1,10-上具有单调性,则a 的范围是_________.三、解答题(写出必要的解答过程,共计31分)22.(本小题满分6分)已知集合{}36A x x =≤<,{}29B x x =<<.求()R C AB ,()R C B A .23.(本小题满分6分)若集合{}{}2|60,|10M x x x N x ax =+-==-=,且N M ⊆,求实数a 的值.24.(本小题满分10分)求函数12-=x y 在区间[2,5]上的最大值和最小值.25. (本小题满分9分)已知2(11)()1(11)x x f x x x ⎧-≤≤=⎨><-⎩或,(1)画出f (x )的图像;(2)求f (x )的定义域和值域.答案二、填空16. ① ③ 17. 0或2± 18.-4或 5 19. 3|,12x x x ⎧⎫<≠-⎨⎬⎩⎭且 20. 2m ≥ 21. 220a a ≥≤-或三、解答题 22. (){}|36R C AB x x x =<≥或(){}|269R C B A x x x x =≤≤<≥或3或23.0,11,23- 24.解:任取1212,[2,5],.x x x x ∈<且211212122()2211(1)(1)x x y y x x x x --=-=---- 1212,[2,5],.x x x x ∈<且211212120,(1)(1)00x x x x y y y y ∴->-->∴->∴>所以函数12-=x y 在区间[2,5]上是减函数. 所以函数的最大值是2,最小值是12.25.定义域是R值域是[0,1] (图略)。
广东省天河区普通高中2017_2018学年高一数学10月月考试题02201712090123
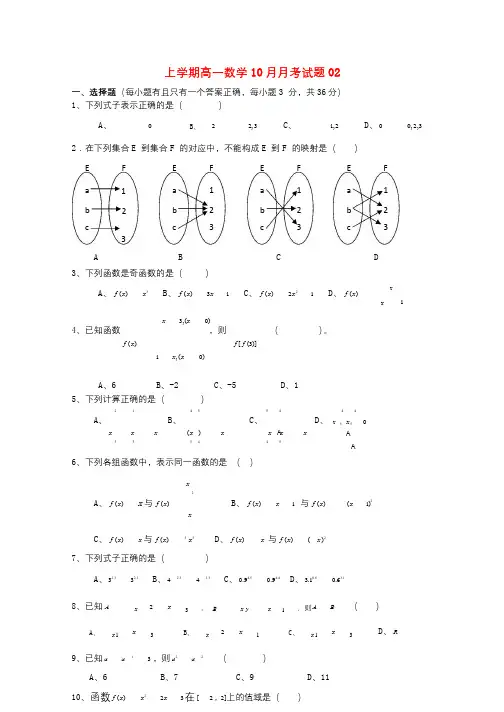
上学期高一数学10月月考试题02一、选择题(每小题有且只有一个答案正确,每小题3分,共36分)1、下列式子表示正确的是()A、0B 、22,3C、1,2D、00,2,32.在下列集合E到集合F的对应中,不能构成E到F的映射是()E F E F E F E Fa a 1 a 1 a 11b b 2 b 2 b 22c c 3 c 3 c 33A B C D3、下列函数是奇函数的是()A、f(x)x3B、f(x)3x 1C、f(x)2x21D、f(x)xx1x 3,(x 0)4、已知函数,则()。
f(x)f[f(3)]1x,(x0)A、6B、-2C、-5D、15、下列计算正确的是()214554A、B、C、D、x x x(x)x x A x x 33544544x5x50AA6、下列各组函数中,表示同一函数的是()x2A、f(x)x与f(x)B、f(x)x 1与f(x)(x 1)2xC、f(x)x与f(x)3x3D、f(x)x与f(x)(x)27、下列式子正确的是()A、32.332.1B、4 2.34 1.3C、0.94.50.94.4D、3.10.60.63.18、已知Ax 2x 3、Bx y x 1,则A B ()A 、x 1x 3B 、x 2x 1C 、x 1x 3D、R9、已知a a13,则a2a2()A、6B、7C、9D、1110、函数f(x)x22x3在[2,2]上的值域是()A、[4,5]B、[4,)C、[4,3]D、[3,5]- 1 -11、若 f (x ) 在 R 上是偶函数,且在[0,+∞)上是减函数,则下列结论正确的是()。
A 、 f (3) f (1) f (2)B 、 f (2) f (3) f (1)C 、 f (1)f (2) f (3)D 、 f (2) f (1)f (3)12、已知奇函数 f (x ) 是 [1,1]上的增函数,且 (3 ) (1 ) 0 ,则 的取值范围是f t f tt3( )1 241 1ttt t ttA 、B 、C 、D 、6 6 3332 1 t t3 3二、填空题(请把正确答案填在相应的横线上,每小题 4分,共 16分)1 f (x ) x 3 x 113、函数的定义域是 ;x 2 2x (x 0)14、已知,若,则 =;f (x )f (x ) 3 xx 1 (x0)15、已知 f (x ) 是 R 上的奇函数,当 x0 时 f (x ) 2x1 ,则 f (2) f (0);e exxxxee 16.设f (x ), g (x ) 它们有如下性质:(1)[g (x )]2[ f (x )]2 122(2) f (x y ) f (x )g (y ) g (x ) f (y )等,请你再写出一个类似的性质:g (x y )。
广东省天河区普通高中2017_2018学年高一数学10月月考试题03201712090124

上学期高一数学 10月月考试题 03一、选择题:本大题共 10个小题,每小题 5分,满分 50分。
在每小题的四个选项中,只有一项符合要求。
1、已知集合 A1, 2,3, B2, 4,则 AUB 为( )A .1, 2,4B .2,3,4C .0, 2,4D .{1, 2,3, 4}2、图中阴影部分表示的集合是( )A 、 (C A )B B 、 A (C B )UUC 、C (AB ) D 、C (AB ) uu2 ,[1, 1)x x3、已知则().f (x ); f (2)x , x [1,6]A .4B .2C .0D .14、( )log 8log 27 log 25235A.5B.6C.7D.85、函数 y lg(x 2) 的定义域是( ) A .(2,)B .[2,) C . (2,) D .[2,)1.51y4 , y 8 , y 0.90.486、设,则 ()1232A. y 3y 1 y 2 B. C.D.yy y yyy A. y 3y 1y 2B.C.D.21 3 1 3 2yyy12391x21x7、函数y= 是()A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶数8、已知0<a<1,则函数y a x和y(a1)x2在同坐标系中的图象只能是图中的- 1 -9、函数f(x)ln x2x8的零点一定位于区间( )A. (1, 2)B. (2 , 3)C. (3, 4)D. (4, 5)10、函数()log(222)的单调增区间为()f x x x0.5A.(,1)B.(2,)C. (1,)D.(2,)二、填空题:本大题共4个小题,每小题5分,满分20分。
11、用列举法表示“大于1且小于6的整数”的集合:_________12、下列4组函数:①y x2;②y2x;③y log x;④y2x2那个函数增长速度最快_______(填序号)13、若x log41,则4x4x______314、函数f(x)=x3+ax+1,f(1)=3,则f(-1)=________.三、解答题:本大题共6个小题,满分80分。
广东省天河区普通高中2017_2018年高二数学月月考试题0

上学期高二数学 11 月月考试题 01一、选择题(每题只有一个选项正确,每题4 分,共 40 分)1 以下四个命题中,正确的选项是 ()A 第一象限的角必是锐角B 锐角必是第一象限的角C 终边同样的角必相等D 第二象限的角必大于第一象限的角2.若会合={ | y =2x },={ | y = x 1 } ,则 ∩ 等于()M yP yM PA { y | y >1}B { y | y ≥ 1}C { y | y >0}D { y | y ≥ 0}3.若 , , c 成等比数列 , 则函数 =2+ +c 的图象与 x 轴交点的个数是()a by ax bxA 0B 1C 2D 0或 24 不等式11的解集是()xA . x x 1B . x x 1C . x 0 x 1D . x x 1或 x 05.函数 y=cosx (sinx+cosx )的最小正周期为()AB2CD246 将函数 ysin 2x 的图像向左平移6个单位 , 再向上平移 1 个单位后所得图像对应的函数分析式是 ()A . ysin( 2x) 1B .3C . ysin( 2x) 1 D .6ysin( 2x) 13ysin( 2x) 167 . 已 知 空 间 直 角 坐 标 系 O xyz 中 有 一 点 A 1, 1,2 , 点 B 是 xOy 平 面 内 的 直 线xy 1上的动点,则 A, B 两点的最短距离是 ()INPUT x3417 A6C 3DIF x<0 THENB22y=x+1 8.在右侧的程序中输入 3,运转结果是 ( )ELSEA 4 B 9IF x>5 THENC5D y =5y=3*x ELSEy=2*x-1 END IFEND IFPRINT y END(第 8 题 )9.若直线x y 2 被圆 (x a)2 y 2 4 所截得的弦长为 2 2 , 则实数 a 的值为( )A – 1 或 3B 1 或 3C –2 或 6D 0或 410设 P 是 60的二面角l内一点, PA 平面 , PB平面 , A,B 为 垂足,PA4, PB 2, 则 AB 的长为()A2 3B2 5C2 7D4 2二、填空题(每题 4 分,共 20 分)11.已知 cos1 , 为第三象限角,则 sin() =________2312y(log 1 a) x 在 R 上为减函数,则 aks5*/u213 已知等差数列a n 的公差 d 0 ,且 a 1 , a 3 , a 9 成等比数列,则 a 1a 3 a 9 的值是a 2a 4a1014.已知向量 a =(2,x) , b =(3,4) ,且 a 、 b 的夹角为锐角, 则 x 的取值范围是 _________15. 若函数 f (x) 为奇函数,且当0时, ( ) 10 x , 则 的值是 xf x f ( 2)_________三、解答题(每题8 分,共 40 分;写出必需的演算步骤和推理过程)16.( 8 分)如图,从参加环保知识比赛的学生中抽出60 名,将其成绩(均为整数)整理后画出的频次散布直方图以下:察看图形,回答以下问题:( 1) 79.5 到 89.5 这一组的频数、频次分别是多少? ( 2)预计此次环保知识比赛的及格率(60 分及以上为及格) .17 ( 8 分) 已知函数 f ( x)Asin( x ) b ( A 0, 0,0 2 ) 在同一周期内有最高点 ( ,1) 和最低点 (7, 3) ,( 1)求此函数 f ( x) 的分析式;( 2)函数 y f ( x) 的图像1212怎样由函数 y2 sin 2x 的图像变换获取 ?18.(8 分) 如图,已知四棱锥 P ABCD 的底面 ABCD 是菱形 ,PA 平面 ABCD , PAAD AC , 点 F 为 PC 的中点 .(Ⅰ)求证 : PA // 平面 BFD ;(Ⅱ)求二面角 CBF D 的正切值 .PFADBC19. ( 8 分)已知数列 { a n } 的前 n 项和为 S n ,且知足 a n2S n S n 10(n1 2), a 12(Ⅰ)求证: { 1} 是等差数列; ks5*/uS n(Ⅱ)求 a n 的表达式20. (8 分)某化工厂生产的某种化工产品,当年产量在150 吨至 250 吨以内,其年生产的总成本 y (万元)与年产量 x (吨)之间的关系可近似地表示为x 2 30x 4000y10( 1)当年产量为多少吨时,每吨的均匀成本最低,并求每吨最低均匀成本;( 2)若每吨均匀出厂价为16 万元,求年生产多少吨时,可获取最大的年收益,并求最大年收益 .参照答案一、选择题(每题只有一个选项正确,每题 4 分,共 40 分)1 至 5: B C A C C ; 6 至 10: A B C D C。
天河普通高中2012018学年高一数学10月月考试题02

上学期高一数学10月月考试题02一、选择题(每小题有且只有一个答案正确,每小题3分,共36分) 1、下列式子表示正确的是( )A 、{}0φ⊆B 、{}{}22,3∈C 、{}1,2φ∈D 、{}00,2,3⊆ 2.在下列集合E 到集合F 的对应中,不.能构成E 到F 的映射是( )3、下列函数是奇函数的是( )A 、3()f x x =B 、()31f x x =-C 、2()21f x x =- D 、()1x f x x =- 4、已知函数3,(0)()1,(0)x x f x x x +≤⎧=⎨->⎩,则[(3)]f f =( )。
A 、6B 、-2C 、-5D 、15、下列计算正确的是( )A 、2133x x x ÷= B 、4554()x x = C 、4554x x x = D 、44550xx -=6、下列各组函数中,表示同一函数的是 ( )A 、()f x =x 与()f x =2x xB 、()1f x x =- 与()f x =C 、()f x x =与()f x =、()f x x =与2()f x =7、下列式子正确的是( )A 、 2.32.133< B 、 2.3 1.344--> C 、 4.5 4.40.90.9> D 、0.6 3.13.10.6>8、已知{}23A x x =-<≤、 {B x y ==,则A B =( )A 、{}13x x << B 、{}21x x -<< C 、{}13x x ≤≤ D 、R 9、已知13a a-+=,则22a a -+=( )A 、6B 、7C 、9D 、11 10、2()23f x x x =+-函数在[2-,2]上的值域是( )A 、[4,5]-B 、[4,)-+∞C 、[4,3]--D 、[3,5]-11、若()f x 在R 上是偶函数,且在[0,+∞)上是减函数,则下列结论正确的是( )。
【中小学资料】广东省天河区普通高中2017-2018学年高一数学10月月考试题01
上学期高一数学10月月考试题01一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若集合{}0,1,2A =,则集合A 的子集共有 ( ) A .3个 B .6个 C .7个 D .8个 2. 如果函数()f x kx b =+在R 上单调递减,则( ) A. 0k > B. 0k < C. 0b > D. 0b <3.已知集合}01|{2=-=x x A ,则下列式子表示正确的有( ) ①A ∈1 ②A ∈-}1{ ③A ⊆φ ④A ⊆-}1,1{A .1个B .2个C .3个D .4个4.下列四个函数中,与y x =表示同一函数的是 ( ) A .2)(x y = B .33x y = C .2x y =D .xx y 2=5.下列函数中在区间(,0)-∞上是增函数的是 ( ) A .2xy = B . y x =- C .xy 1=D .2y x =. 6.如图,I 是全集,M 、P 、S 是I 的3个子集,则阴影部分所表示的集合是( )A. (M∩P)∩SB. (M∩P)∪SC. (M∩P)∩S I CD. (M∩P)∪S I C7.函数y = ).A .{|1}x x ≤B .{|0}x x ≥C .{|10}x x x ≥或≤D .{|01}x x ≤≤8.已知函数()f x =m 的取值范围是( ) A. 04m <≤B. 01m ≤≤C. 4m ≥D. 04m ≤≤9. 设,a b R ∈,集合{}1,,0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭,则b a -= ( )A .1B .1-C .2D .2-10.如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上单调递减,那么实数a 的取值范围是( )A 、3a -≤B 、3a -≥C 、a ≤5D 、a ≥5二、填空题(每小题4分,共16分,请将答案填在题中的横线上)11. 函数xx x f -++=211)(的定义域为______________________ 12. 已知)(x f 是奇函数,且当0>x 时,12)(2-=x x f ,那么)1(-f =_______________。
广东省天河区普通高中高一数学10月月考试题08
上学期高一数学10月月考试题08一、选择(每题只有一个正确选项,共计15题,3×15=45分) 1.设集合A={1,2,3,4,5},B={2,4}则正确的是A .AB ⊆ B .A B ∉C .B A ⊆D .B A ∉ 2. 下列5个关系式,其中正确的有①{a ,b }={b ,a };②{a ,b }⊆{b ,a };③{0}=∅;④∅{0};⑤0∈{0}.A .6个B .5个C .4个D .3个3. 设集合B 满足条件{1,3}∪B={1,3,5},则满足条件的集合B 的个数是A .1B .2C .3D .44.已知集合P={(x ,y )| x + y=3},集合Q={(x ,y )|x-y=5},那么P ∩Q= A .{(4,-1)} B .(4,-1) C .{4、-1} D .∅5. 函数y =1-x +x 的定义域是A .{x |x ≤1}B .{x |x ≥0}C .{x |x ≥1或x ≤0} D.{x |0≤x ≤1}6.下列各图中,不能是函数f (x )图象的是()7. 已知集合A ={a ,b },集合B ={0,1},下列对应不是A 到B 的映射的是()8.若()⎪⎩⎪⎨⎧<+=>-=0,10,00,22x x x x x x f ,则)]1([f f 的值为 A .2 B .1 C .0 D .-1 9.下列函数中,在区间()0,1上是增函数的是 A .||y x = B .3y x =- C .1y x= D .22y x =-+10.设函数()f x 是定义在R 上的奇函数,当0x ≤时,2()2f x x x =-,则(2)f =A . 0B . 8C .-8D . -211.已知函数31()f x x x=+的图象关于 A .原点对称B .y 轴对称C .y =x 对称D .y =-x 对称12. 下列函数为偶函数的是( )A .()||f x x x =+B .21()f x x x=+C .2()f x x x =+ D .2||()x f x x=13. 若奇函数()x f 在[]5,2上为增函数,且有最小值0,则它在[]2,5--上 A.是减函数,有最小值0 B.是增函数,有最小值0 C.是减函数,有最大值0 D.是增函数,有最大值014.函数2()22f x x ax a =-++在[0,a ]上取得最大值3,最小值2,则实数a 为A .0或1B .1C .2D .以上都不对15.定义在R 上的偶函数f (x )在[0,+∞)上是增函数,若f (a )<f (b ),则一定可得A .a <bB .a >bC .|a |<|b |D .0≤a <b 或a >b ≥0二、填空(每题4分,共计4×6=24分)16某工厂8年来某产品产量y 与时间t 年的函数关系如下图,则:①前3年总产量增长速度越来越快; ②前3年中总产量增长速度越来越慢; ③第3年后,这种产品停止生产;④第3年后,这种产品年产量保持不变. 以上说法中正确的是_______. 17.若{}{}21,4,,1,A x B x ==且AB B =,则x = .18. 已知函数⎩⎨⎧>≤-=0,30,1)(2x x x x x f , 若15)(=x f ,则=x .19.函数0y =的定义域是________.20. 设集合A ={x |x +m ≥0},B ={x |-2<x <4},全集U =R ,且(∁U A )∩B =∅,求实数m 的取值范围为________.21. 已知函数2()4f x x ax =+-在[]1,10-上具有单调性,则a 的范围是_________.三、解答题(写出必要的解答过程,共计31分)22.(本小题满分6分)已知集合{}36A x x =≤<,{}29B x x =<<.求()R C AB ,()R C B A .23.(本小题满分6分)若集合{}{}2|60,|10M x x x N x ax =+-==-=,且N M ⊆,求实数a 的值.24.(本小题满分10分)求函数12-=x y 在区间[2,5]上的最大值和最小值.25. (本小题满分9分)已知2(11)()1(11)x x f x x x ⎧-≤≤=⎨><-⎩或,(1)画出f (x )的图像;(2)求f (x )的定义域和值域.答案二、填空16. ① ③ 17. 0或2± 18.-4或 5 19. 3|,12x x x ⎧⎫<≠-⎨⎬⎩⎭且 20. 2m ≥ 21. 220a a ≥≤-或三、解答题 22. (){}|36R C AB x x x =<≥或(){}|269R C B A x x x x =≤≤<≥或3或23.0,11,23- 24.解:任取1212,[2,5],.x x x x ∈<且211212122()2211(1)(1)x x y y x x x x --=-=---- 1212,[2,5],.x x x x ∈<且211212120,(1)(1)00x x x x y y y y ∴->-->∴->∴>所以函数12-=x y 在区间[2,5]上是减函数. 所以函数的最大值是2,最小值是12.25.定义域是R值域是[0,1] (图略)。
天河区一中2018-2019学年上学期高三数学10月月考试题
天河区一中2018-2019学年上学期高三数学10月月考试题班级__________ 座号_____ 姓名__________ 分数__________一、选择题1. 设l ,m ,n 表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m ∥l ,m ⊥α,则l ⊥α;②若m ∥l ,m ∥α,则l ∥α;③若α∩β=l ,β∩γ=m ,γ∩α=n ,则l ∥m ∥n ;④若α∩β=l ,β∩γ=m ,γ∩α=n ,n ∥β,则l ∥m .其中正确命题的个数是( )A .1B .2C .3D .42. 复数z=(其中i 是虚数单位),则z 的共轭复数=()A .﹣iB .﹣﹣iC . +iD .﹣ +i3. 若关于的不等式的解集为,则参数的取值范围为( )x 07|2||1|>-+-++m x x R m A .B .C .D .),4(+∞),4[+∞)4,(-∞]4,(-∞【命题意图】本题考查含绝对值的不等式含参性问题,强化了函数思想、化归思想、数形结合思想在本题中的应用,属于中等难度.4. 在《张邱建算经》中有一道题:“今有女子不善织布,逐日所织的布比同数递减,初日织五尺,末一日织一尺,计织三十日”,由此推断,该女子到第10日时,大约已经完成三十日织布总量的( )A .33%B .49%C .62%D .88%5. 已知双曲线kx 2﹣y 2=1(k >0)的一条渐近线与直线2x+y ﹣3=0垂直,则双曲线的离心率是( )A .B .C .4D .6. 设抛物线C :y 2=2px (p >0)的焦点为F ,点M 在C 上,|MF|=5,若以MF 为直径的圆过点(0,2),则C 的方程为( )A .y 2=4x 或y 2=8xB .y 2=2x 或y 2=8xC .y 2=4x 或y 2=16xD .y 2=2x 或y 2=16x7. 数列{a n }满足a n+2=2a n+1﹣a n ,且a 2014,a 2016是函数f (x )=+6x ﹣1的极值点,则log 2(a 2000+a 2012+a 2018+a 2030)的值是( )A .2B .3C .4D .58. 方程x=所表示的曲线是()A .双曲线B .椭圆C .双曲线的一部分D .椭圆的一部分9. 某几何体的三视图如图所示,且该几何体的体积是,则正视图中的x 的值是()A .2B .C .D .310.已知数列为等差数列,为前项和,公差为,若,则的值为( ){}n a n S d 201717100201717S S -=d A .B .C .D .120110102011.若函数()y f x =的定义域是[]1,2016,则函数()()1g x f x =+的定义域是( )A .(]0,2016B .[]0,2015C .(]1,2016D .[]1,201712.抛物线y=﹣8x 2的准线方程是( )A .y=B .y=2C .x=D .y=﹣2二、填空题13.在中,已知角的对边分别为,且,则角ABC ∆C B A ,,c b a ,,B c C b a sin cos +=B 为.14.下列四个命题:①两个相交平面有不在同一直线上的三个公交点②经过空间任意三点有且只有一个平面③过两平行直线有且只有一个平面④在空间两两相交的三条直线必共面其中正确命题的序号是 . 15.已知函数,,则 ,的值域21,0()1,0x x f x x x ⎧-≤=⎨->⎩()21xg x =-((2))f g =[()]f g x 为.【命题意图】本题考查分段函数的函数值与值域等基础知识,意在考查分类讨论的数学思想与运算求解能力.16.已知直线:()被圆:所截的弦长是圆心到直线的043=++m y x 0>m C 062222=--++y x y x C 距离的2倍,则 .=m 17.将一张坐标纸折叠一次,使点与点重合,且点与点重合,则的()0,2()4,0()7,3(),m n m n +值是.三、解答题18.如图的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm ).(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连结BC ′,证明:BC ′∥面EFG .19.在平面直角坐标系中,过点的直线与抛物线相交于点、两点,设xOy (2,0)C 24y x =A B ,.11(,)A x y 22(,)B x y (1)求证:为定值;12y y (2)是否存在平行于轴的定直线被以为直径的圆截得的弦长为定值?如果存在,求出该直线方程y AC 和弦长,如果不存在,说明理由.20.已知函数,.3()1xf x x =+[]2,5x ∈(1)判断的单调性并且证明;()f x (2)求在区间上的最大值和最小值.()f x []2,521.(本小题满分12分)数列满足:,,且.{}n b 122n n b b +=+1n n n b a a +=-122,4a a ==(1)求数列的通项公式;{}n b (2)求数列的前项和.{}n a n S 22.已知函数f (x )=ax 2+2x ﹣lnx (a ∈R ).(Ⅰ)若a=4,求函数f (x )的极值;(Ⅱ)若f ′(x )在(0,1)有唯一的零点x 0,求a 的取值范围;(Ⅲ)若a ∈(﹣,0),设g (x )=a (1﹣x )2﹣2x ﹣1﹣ln (1﹣x ),求证:g (x )在(0,1)内有唯一的零点x 1,且对(Ⅱ)中的x 0,满足x 0+x 1>1.23.(本题满分15分)已知函数,当时,恒成立.c bx ax x f ++=2)(1≤x 1)(≤x f (1)若,,求实数的取值范围;1=a c b =b (2)若,当时,求的最大值.a bx cx x g +-=2)(1≤x )(x g 【命题意图】本题考查函数单调性与最值,分段函数,不等式性质等基础知识,意在考查推理论证能力,分析问题和解决问题的能力.24.已知cos (+θ)=﹣,<θ<,求的值.天河区一中2018-2019学年上学期高三数学10月月考试题(参考答案)一、选择题1.【答案】B【解析】解:∵①若m∥l,m⊥α,则由直线与平面垂直的判定定理,得l⊥α,故①正确;②若m∥l,m∥α,则l∥α或l⊂α,故②错误;③如图,在正方体ABCD﹣A1B1C1D1中,平面ABB1A1∩平面ABCD=AB,平面ABB1A1∩平面BCC1B1=BB1,平面ABCD∩平面BCC1B1=BC,由AB、BC、BB1两两相交,得:若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n不成立,故③是假命题;④若α∩β=l,β∩γ=m,γ∩α=n,n∥β,则由α∩γ=n知,n⊂α且n⊂γ,由n⊂α及n∥β,α∩β=m,得n∥m,同理n∥l,故m∥l,故命题④正确.故选:B.【点评】本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养. 2.【答案】C【解析】解:∵z==,∴=.故选:C.【点评】本题考查了复数代数形式的乘除运算,是基础题.3.【答案】A4.【答案】B【解析】5.【答案】A【解析】解:由题意双曲线kx2﹣y2=1的一条渐近线与直线2x+y+1=0垂直,可得渐近线的斜率为,又由于双曲线的渐近线方程为y=±x故=,∴k=,∴可得a=2,b=1,c=,由此得双曲线的离心率为,故选:A.【点评】本题考查直线与圆锥曲线的关系,解题的关键是理解一条渐近线与直线2x+y+1=0垂直,由此关系求k,熟练掌握双曲线的性质是求解本题的知识保证.6.【答案】C【解析】解:∵抛物线C方程为y2=2px(p>0),∴焦点F坐标为(,0),可得|OF|=,∵以MF为直径的圆过点(0,2),∴设A(0,2),可得AF⊥AM,Rt△AOF中,|AF|==,∴sin∠OAF==,∵根据抛物线的定义,得直线AO切以MF为直径的圆于A点,∴∠OAF=∠AMF,可得Rt△AMF中,sin∠AMF==,∵|MF|=5,|AF|=∴=,整理得4+=,解之可得p=2或p=8因此,抛物线C的方程为y2=4x或y2=16x.故选:C.方法二:∵抛物线C方程为y2=2px(p>0),∴焦点F(,0),设M(x,y),由抛物线性质|MF|=x+=5,可得x=5﹣,因为圆心是MF的中点,所以根据中点坐标公式可得,圆心横坐标为=,由已知圆半径也为,据此可知该圆与y轴相切于点(0,2),故圆心纵坐标为2,则M点纵坐标为4,即M(5﹣,4),代入抛物线方程得p2﹣10p+16=0,所以p=2或p=8.所以抛物线C的方程为y2=4x或y2=16x.故答案C.【点评】本题给出抛物线一条长度为5的焦半径MF,以MF为直径的圆交抛物线于点(0,2),求抛物线的方程,着重考查了抛物线的定义与简单几何性质、圆的性质和解直角三角形等知识,属于中档题.7. 【答案】C【解析】解:函数f (x )=+6x ﹣1,可得f ′(x )=x 2﹣8x+6,∵a 2014,a 2016是函数f (x )=+6x ﹣1的极值点,∴a 2014,a 2016是方程x 2﹣8x+6=0的两实数根,则a 2014+a 2016=8.数列{a n }中,满足a n+2=2a n+1﹣a n ,可知{a n }为等差数列,∴a 2014+a 2016=a 2000+a 2030,即a 2000+a 2012+a 2018+a 2030=16,从而log 2(a 2000+a 2012+a 2018+a 2030)=log 216=4.故选:C .【点评】熟练掌握利用导数研究函数的极值、等差数列的性质及其对数的运算法则是解题的关键. 8. 【答案】C 【解析】解:x=两边平方,可变为3y 2﹣x 2=1(x ≥0),表示的曲线为双曲线的一部分;故选C .【点评】本题主要考查了曲线与方程.解题的过程中注意x 的范围,注意数形结合的思想. 9. 【答案】C解析:由三视图可知:原几何体是一个四棱锥,其中底面是一个上、下、高分别为1、2、2的直角梯形,一条长为x 的侧棱垂直于底面.则体积为=,解得x=.故选:C .10.【答案】B 【解析】试题分析:若为等差数列,,则为等差数列公差为, {}n a ()()111212nn n na S d a n nn -+==+-⨯n S n ⎧⎫⎨⎬⎩⎭2d ,故选B. 2017171100,2000100,201717210S S d d ∴-=⨯==考点:1、等差数列的通项公式;2、等差数列的前项和公式.11.【答案】B 【解析】12.【答案】A【解析】解:整理抛物线方程得x 2=﹣y ,∴p=∵抛物线方程开口向下,∴准线方程是y=,故选:A .【点评】本题主要考查抛物线的基本性质.解决抛物线的题目时,一定要先判断焦点所在位置. 二、填空题13.【答案】4π【解析】考点:正弦定理.【方法点晴】本题考查正余弦定理,根据正弦定理,将所给的含有边和角的等式化为只含有角的等式,再利用三角形的三角和是,消去多余的变量,从而解出角.三角函数题目在高考中的难度逐渐增加,以考查三︒180B 角函数的图象和性质,以及三角形中的正余弦定理为主,在年全国卷( )中以选择题的压轴题出2016现.14.【答案】 ③ .【解析】解:①两个相交平面的公交点一定在平面的交线上,故错误;②经过空间不共线三点有且只有一个平面,故错误;③过两平行直线有且只有一个平面,正确;④在空间两两相交交点不重合的三条直线必共面,三线共点时,三线可能不共面,故错误,故正确命题的序号是③,故答案为:③ 15.【答案】,. 2[1,)-+∞【解析】16.【答案】9【解析】考点:直线与圆的位置关系【方法点睛】本题考查了直线与圆的位置关系,属于基础题型,涉及一些最值问题,当点在圆的外部时,圆上的点到定点距离的最小值是圆心到直线的距离减半径,当点在圆外,可做两条直线与圆相切,当点在圆上,可做一条直线与圆相切,当点在圆内,过定点做圆的弦时,过圆心即直径最长,当定点是弦的中点时,弦最短,并且弦长公式是,R 是圆的半径,d 是圆心到直线的距离.222d R l -=17.【答案】345【解析】考点:点关于直线对称;直线的点斜式方程.三、解答题18.【答案】【解析】解:(1)如图(2)它可以看成一个长方体截去一个小三棱锥,设长方体体积为V1,小三棱锥的体积为V2,则根据图中所给条件得:V1=6×4×4=96cm3,V2=••2•2•2=cm3,∴V=v1﹣v2=cm3(3)证明:如图,在长方体ABCD﹣A′B′C′D′中,连接AD′,则AD′∥BC′因为E,G分别为AA′,A′D′中点,所以AD′∥EG,从而EG∥BC′,又EG⊂平面EFG,所以BC′∥平面EFG;2016年4月26日19.【答案】(1)证明见解析;(2)弦长为定值,直线方程为.1x =【解析】(2 ,进而得时为定值.1a =试题解析:(1)设直线的方程为,由AB 2my x =-22,4,my x y x =-⎧⎨=⎩得,∴,2480y my --=128y y =-因此有为定值.111]128y y =-(2)设存在直线:满足条件,则的中点,,x a =AC 112(,22x y E +AC =因此以为直径圆的半径,点到直线的距离AC 12r AC ===E x a =,12||2x d a +=-所以所截弦长为==.=当,即时,弦长为定值2,这时直线方程为.10a -=1a =1x =考点:1、直线与圆、直线与抛物线的位置关系的性质;2、韦达定理、点到直线距离公式及定值问题.20.【答案】(1)增函数,证明见解析;(2)最小值为,最大值为.2.5【解析】试题分析:(1)在上任取两个数,则有,所以在[]2,512x x <1212123()()()0(1)(1)x x f x f x x x --=<++()f x []2,5上是增函数;(2)由(1)知,最小值为,最大值为.(2)2f =5(5)2f =试题解析:在上任取两个数,则有[]2,512x x <,12121233()()11x x f x f x x x -=-++12123()(1)(1)x x x x -=++0<所以在上是增函数.()f x []2,5所以当时,,2x =min ()(2)2f x f ==当时,.5x =max 5()(5)2f x f ==考点:函数的单调性证明.【方法点晴】本题主要考查利用定义法求证函数的单调性并求出单调区间,考查化归与转化的数学思想方法.先在定义域内任取两个数,然后作差,利用十字相乘法、提公因式法等方法化简式子成12x x <12()()f x f x -几个因式的乘积,判断最后的结果是大于零韩式小于零,如果小于零,则函数为增函数,如果大于零,则函数为减函数.121.【答案】(1);(2).122n n b +=-222(4)n n S n n +=-++【解析】试题分析:(1)已知递推公式,求通项公式,一般把它进行变形构造出一个等比数列,由等比122n n b b +=+数列的通项公式可得,变形形式为;(2)由(1)可知,n b 12()n n b x b x ++=+122(2)nn n n a a b n --==-≥这是数列的后项与前项的差,要求通项公式可用累加法,即由{}n a 112()()n n n n n a a a a a ---=-+-+求得.211()a a a +-+试题解析:(1),∵,112222(2)n n n n b b b b ++=+⇒+=+1222n n b b ++=+又,121224b a a +=-+=∴.2312(21)(2222)22222221n nn n a n n n +-=++++-+=-+=-- ∴.224(12)(22)2(4)122n n n n n S n n +-+=-=-++-考点:数列的递推公式,等比数列的通项公式,等比数列的前项和.累加法求通项公式.22.【答案】【解析】满分(14分).解法一:(Ⅰ)当a=4时,f (x )=4x 2+2x ﹣lnx ,x ∈(0,+∞),.…(1分)由x ∈(0,+∞),令f ′(x )=0,得.当x 变化时,f ′(x ),f (x )的变化如下表:xf ′(x )﹣0+f (x )↘极小值↗故函数f (x )在单调递减,在单调递增,…(3分)f (x )有极小值,无极大值.…(4分)(Ⅱ),令f ′(x )=0,得2ax 2+2x ﹣1=0,设h (x )=2ax 2+2x ﹣1.则f′(x)在(0,1)有唯一的零点x0等价于h(x)在(0,1)有唯一的零点x0当a=0时,方程的解为,满足题意;…(5分)当a>0时,由函数h(x)图象的对称轴,函数h(x)在(0,1)上单调递增,且h(0)=﹣1,h(1)=2a+1>0,所以满足题意;…(6分)当a<0,△=0时,,此时方程的解为x=1,不符合题意;当a<0,△≠0时,由h(0)=﹣1,只需h(1)=2a+1>0,得.…(7分)综上,.…(8分)(说明:△=0未讨论扣1分)(Ⅲ)设t=1﹣x,则t∈(0,1),p(t)=g(1﹣t)=at2+2t﹣3﹣lnt,…(9分),由,故由(Ⅱ)可知,方程2at2+2t﹣1=0在(0,1)内有唯一的解x0,且当t∈(0,x0)时,p′(t)<0,p(t)单调递减;t∈(x0,1)时,p′(t)>0,p(t)单调递增.…(11分)又p(1)=a﹣1<0,所以p(x0)<0.…(12分)取t=e﹣3+2a∈(0,1),则p(e﹣3+2a)=ae﹣6+4a+2e﹣3+2a﹣3﹣lne﹣3+2a=ae﹣6+4a+2e﹣3+2a﹣3+3﹣2a=a(e﹣6+4a﹣2)+2e﹣3+2a>0,从而当t∈(0,x0)时,p(t)必存在唯一的零点t1,且0<t1<x0,即0<1﹣x1<x0,得x1∈(0,1),且x0+x1>1,从而函数g(x)在(0,1)内有唯一的零点x1,满足x0+x1>1.…(14分)解法二:(Ⅰ)同解法一;…(4分)(Ⅱ),令f′(x)=0,由2ax2+2x﹣1=0,得.…(5分)设,则m∈(1,+∞),,…(6分)问题转化为直线y=a与函数的图象在(1,+∞)恰有一个交点问题.又当m∈(1,+∞)时,h(m)单调递增,…(7分)故直线y=a 与函数h (m )的图象恰有一个交点,当且仅当.…(8分)(Ⅲ)同解法一.(说明:第(Ⅲ)问判断零点存在时,利用t →0时,p (t )→+∞进行证明,扣1分)【点评】本题考查函数与导数等基本知识,考查推理论证能力和运算求解能力,考查函数与方程的思想、化归与转化的思想、数形结合的思想,考查运用数学知识分析和解决问题的能力. 23.【答案】【解析】(1);(2).]0222[-2(1)由且,得,1=a c b =42()(222b b b x b bx x x f -++=++=当时,,得,…………3分1=x 11)1(≤++=b b f 01≤≤-b 故的对称轴,当时,,………… 5分 )(x f 21,0[2∈-=b x 1≤x 2min max ()(124()(1)11b b f x fb f x f ⎧=-=-≥-⎪⎨⎪=-=≤⎩解得,综上,实数的取值范围为;…………7分222222+≤≤-b b ]0222[-,…………13分112≤+=且当,,时,若,则恒成立,2a =0b =1c =-1≤x 112)(2≤-=x x f 且当时,取到最大值.的最大值为2.…………15分0=x 2)(2+-=x x g 2)(x g 24.【答案】 【解析】解:∵<θ<,∴+θ∈(,),∵cos(+θ)=﹣,∴sin(+θ)=﹣=﹣,∴sin(+θ)=sinθcos+cosθsin=(cosθ+sinθ)=﹣,∴sinθ+cosθ=﹣,①cos(+θ)=cos cosθ﹣sin sinθ=(cosθ﹣cosβ)=﹣,∴cosθ﹣sinθ=﹣,②联立①②,得cosθ=﹣,sinθ=﹣,∴====.【点评】本题考查函数值的求法,是中档题,解题时要认真审题,注意三角函数诱导公式、加法定理和同角三角函数关系式的合理运用.。
广东省天河区普通高中2017-2018学年高一数学10月月考试题07
DCBA 上学期高一数学10月月考试题07一:选择题(60分=12小题×5分/小题。
) 1.设全集}6,5,4,3,2,1{=U,集合{1,3,5}A =,集合{3,5}B =,则A .U AB = B .()U U A B =ð C .()U U AB =ð D .()()U U U A B =痧2.与函数x y =的图象相同的函数是A .2)(x y = B. 2x y = C .33x y = D .2xx y =3.函数]1,3[,12--∈-=x x y 的值域是 A .]1,(--∞ B. ),1[+∞ C .]1,21[ D. ]21,1[-- 4.将函数)(x f y =的图象沿x 轴向右平移2个单位,所得的图象为2-=x y ,则)(x f y =的函数式为A.2+=x y B. x y = C. x y =+2 D. x y =-25.如果{}210A x axax =-+<=∅,则实数a 的集合为A .{}04a a << B .{}04a a ≤< C .{}04a a <≤ D .{}04a a ≤≤6. 函数]2,2[,1)(-∈=x x f 的奇偶性是A 奇函数B 偶函数C 既奇又偶函数D 非奇非偶函数7.函数122--=x y 的单调增区间是A )1,(-∞B ),1(+∞C ),1()1,(+∞⋃-∞D ),1(),1,(+∞-∞8. 某同学到长城旅游,他租自行车由宾馆骑行前往长城,前进了akm ,觉得有点累,休息后沿原路返回bkm(b<a)。
想起“不到长城非好汉”,便调转车头继续前进。
则该同学离起点的距离s 与时间t 的图象大致为9. 不等式7142≤-<x 的解集是A )41,23[)2,43[--⋃-B )41,23[]2,43(--⋃ C ]41,23()2,43[--⋃ D ]41,23()2,43[--⋃- 10. 满足条件⊆}3,2,1{M ⊂≠{}1,2,3,4,5,6的集合M 的个数是A 7B 8C 9D 1011. 设全集}7,6,5,4,3,2,1{=U,∁U }3,1{)(=B A , A (∁U B )}5,2{=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上学期高一数学10月月考试题04
第Ⅰ卷 一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.设集合{2012,0,2012},{0,2012,2013}M N =-=,若集合,A M
N B M N ==,则A C B =( )
A.φ
B. {-2012,0,2012,2013}
C.{2012,2013}-
D.{0,2012} 2.下列函数中与函数2()f x x =相等的是(
) A .
4()g x = B . ()2x g x = C . ()g x D . 3
()x g x x
= 3.下列四个集合中,表示空集的是( )
A.{0}
B.22{(,)|,,}x y y x x y R =-∈
4.定义在R 上的偶函数f (x )满足:对任意的x 1,x 2∈[0,+∞)(x 1≠x 2),有
f (x 2)-f (x 1)x 2-x 1<0,则( ) A .f (3)<f (-2)<f (1)
B .f (1)<f (-2)<f (3)
C .f (-2)<f (1)<f (3)
D .f (3)<f (1)<f (-2)
5.已知函数2()2f x x x =--+,则函数()y f x =-的图象为( )
6.已知P ={0,1},Q ={-1,0,1},f 是从P 到Q 的映射,则满足f (0)>f (1)的映射有( )个
A.2
B.3
C.4
D.5
7.设集合A=10,2⎡⎫⎪⎢⎣⎭, B=1,12⎡⎤⎢⎥⎣⎦, 函数f (x )=()1,221,
,x x A x x B ⎧+∈⎪⎨⎪-∈⎩
若0x A ∈, 且[]0()f f x A ∈,
则0x 的取值范围是( ) A.10,4⎛⎤ ⎥⎝⎦ B.11,42⎛⎤ ⎥⎝⎦ C.11,42⎛⎫ ⎪⎝⎭ D.30,8⎡⎤⎢⎥⎣⎦
8.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“孪生函数”, 那么函数解析式为221y x =-,值域为{1,7}的“孪生函数”共有
( ) A .10个 B .9个 C .8个 D .4个
9
.函数y = ( ) A .奇函数 B .偶函数 C .非奇非偶函数 D .是奇函数又是偶函数
10
.函数y =的单减区间是( )
A.(),1-∞-
B.()1,-+∞
C.()3,1--
D.()1,1-
11.一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示. 某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)
给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水. 则正确论断的个数是( )
A . 0 B. 1 C. 2 D. 3
12.已知()32||f x x =-,2
()2g x x x =-,(),()()()(),()()g x f x g x F x f x f x g x ≥⎧=⎨<⎩当时当时,则()F x 的最值是( )
A.最大值为3
,最小值 B.
最大值为,无最小值
C.最大值为3,无最小值
D.既无最大值,也无最小值
二、填空题:本题共4小题,共20分
.
13.已知函数f (x +1)=3x +2,则f (x )的解析式为()f x =_________
14. 设集合A={23≤≤-x x },B={x 1212+≤≤-k x k },且A ⊇B ,则实数k 的取值范围是
15.已知函数2()48f x x kx =--在[2,10]上具有单调性,则实数k 的取值范围是_______.
16.给出下列说法:
①集合{1,2,3}A =,则它的真子集有8个; ②2(),((0,1))f x x x x
=+∈的值域为(3,)+∞; ③若函数()f x 的定义域为[0,2],则函数(2)()2f x g x x =
-的定义域为[)0,2; ④函数()f x 的定义在R 上的奇函数,当0x >时,()1f x x =-+,则当0x <时,()1f x x =-
⑤设53()=5f x ax bx cx +++(其中,,a b c 为常数,x R ∈),若(2012)3f -=-,则(2012)13f =;其中正确的是 (只写序号)。
三、解答题:本大题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤。
17.设{|11}A x Z x =∈-≤≤,{}{}
430,1,2,|()1B C a f x x ax ===++为偶函数, 求:(1)()A
B C ; (2)()A B C B C 。
18.已知2{|280}A x x x =--=},22{|120}B x x ax a =++-=,若A
B B =,求实数a
的取值集合。
19.商店出售茶壶和茶杯,茶壶单价为每个20元,茶杯单价为每个5元,该店推出两种促销优惠办法:
(1)买1个茶壶赠送1个茶杯;
(2)按总价打9.2折付款。
某顾客需要购买茶壶4个,茶杯若干个,(不少于4个),若设购买茶杯数为x 个,付款数为y (元),试分别建立两种优惠办法中y 与x 之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更省钱?
20.已知函数2()1ax b f x x +=+是定义在(1,1)-上的奇函数,且12()25
f =。
(1)求函数()f x 的解析式;
(2)用单调性的定义证明()f x 在(1,1)-上是增函数; (3)解不等式2
(1)()0f t f t -+<。
21.已知函数2()21f x x ax =--在区间[0,2]上的最大值为()g a ,最小值为(),()h a a R ∈。
(1)求()g a 和()h a ;
(2)作出()g a 和()h a 的图像,并分别指出()g a 的最小值和()h a 的最大值各为多少?
22.已知定义域为[]0,1的函数()f x 同时满足:
①对于任意的[]0,1x ∈,总有()0f x ≥; ②(1)1f =;
③若12120,0,1x x x x ≥≥+≤,则有1212()()()f x x f x f x +≥+成立。
(1)求(0)f 的值;
(2)求()f x 的最大值;
(3)若对于任意[]0,1x ∈,总有[]2
()()1a f x f x >++恒成立,求实数a 的取值范围。
答案。
