信号与系统习题答案
信号与系统习题与答案

【填空题】(为任意值)是________ (填连续信号或离散信号),若是离散信号,该信号____(填是或不是)数字信号。
【填空题】是________ (填连续信号或离散信号),若是离散信号,该信号____(填是或不是)数字信号。
【填空题】信号________ (填是或不是),若是周期信号,周期为__pi/5__。
【填空题】系统为____(填线性或非线性)系统、____(填时变或非时变)系统、____(填因果或非因果)系统。
【填空题】系统为____(填线性或非线性)系统、____(填时变或非时变)系统、____(填因果或非因果)系统。
【简答题】判断下图波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号。
连续时间信号【简答题】判断下图波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号。
离散时间信号且为数字信号【简答题】判断信号是功率信号还是能量信号,若是功率信号,平均功率是多少?若是能量信号,能量为多少?功率信号平均功率为4.5【简答题】线性时不变系统具有哪些特性?均匀性、叠加性、时不变性、微分性、因果性。
【填空题】的函数值为____。
2【填空题】的函数值为____。
【填空题】假设,的函数值为____。
1【填空题】假设,的函数值为____。
【填空题】的函数值为____。
我的答案:第一空:e^2-26【填空题】已知,将____(填左移或右移)____可得。
右移个单位7【简答题】计算的微分与积分。
8【简答题】什么是奇异信号?我的答案:奇异信号是指函数本身或其导数或高阶导数具有不连续点(跳变点)。
9【简答题】写出如下波形的函数表达式。
我的答案:f(t)=u(t)+u(t-1)+u(t-2)10【简答题】已知信号的图形如图所示,画出的波形。
我的答案:【简答题】信号微分运算具有什么特点?举一个应用实例。
特点:微分凸显了信号的变化部分。
微分方程(包括偏微分方程和积分方程)把函数和代数结合起来,级数和积分变换解决数值计算问题。
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
(完整word版)信号与系统专题练习题及答案

信号与系统专题练习题一、选择题1.设当t 〈3时,x(t)=0,则使)2()1(t x t x -+-=0的t 值为 C 。
A t>-2或t>-1 B t=1和t=2 C t>—1 D t 〉-22.设当t 〈3时,x (t)=0,则使)2()1(t x t x -⋅-=0的t 值为 D 。
A t>2或t 〉-1 B t=1和t=2 C t>—1 D t>—23.设当t<3时,x(t )=0,则使x (t/3)=0的t 值为 C 。
A t>3 B t=0 C t<9 D t=34.信号)3/4cos(3)(π+=t t x 的周期是 C 。
A π2 B π C 2/π D π/2 5.下列各表达式中正确的是 BA. )()2(t t δδ= B 。
)(21)2(t t δδ= C. )(2)2(t t δδ= D 。
)2(21)(2t t δδ=6. 已知系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B . A 线性时不变系统 B 线性时变系统 C 非线性时不变系统 D 非线性时变系统 7。
已知 系统的激励e(t )与响应r (t)的关系为:)()(2t e t r = 则该系统为 C .A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统8。
⎰∞-=t d ττττδ2sin )( A 。
A 2u (t ) B )(4t δ C 4 D 4u (t) 10. dt t t )2(2cos 33+⋅⎰-δπ等于 B 。
A 0 B —1 C 2 D —211.线性时不变系统输出中的自由响应的形式由 A 决定A 系统函数极点的位置;B 激励信号的形式;C 系统起始状态;D 以上均不对。
12.若系统的起始状态为0,在x (t)的激励下,所得的响应为 D . A 强迫响应;B 稳态响应;C 暂态响应;D 零状态响应。
信号与系统--完整版答案--纠错修改后版本
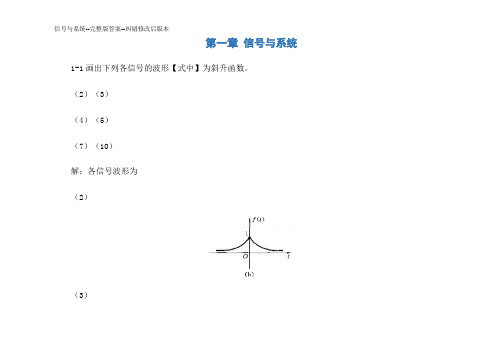
1)
3)
5)
3.8、求下列差分方程所描述的离散系统的单位序列响应。
2)5)
3.9、求图所示各系统的单位序列响应。
(a)
(c)
3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示,求下列卷积和。
(1)(2)(3)(4)
4.34 某LTI系统的频率响应,若系统输入,求该系统的输出。
4.35 一理想低通滤波器的频率响应
4.36 一个LTI系统的频率响应
若输入,求该系统的输出。
4.39 如图4-35的系统,其输出是输入的平方,即(设为实函数)。该系统是线性的吗?
(1)如,求的频谱函数(或画出频谱图)。
(2)如,求的频谱函数(或画出频谱图)。
(1) (2) (3) (4) (5)
4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-23
4.20 若已知,试求下列函数的频谱:
(1)(3) (5)
(8)(9)
4下列方式求图4-25示信号的频谱函数 (1)利用xx和线性性质(门函数的频谱可利用已知结果)。
(1)
5-18 已知系统函数和初始状态如下,求系统的零输入响应。
(1),
(3),
5-22 如图5-5所示的复合系统,由4个子系统连接组成,若各子系统的系统函数或冲激响应分别为,,,,求复合系统的冲激响应。
5-26 如图5-7所示系统,已知当时,系统的零状态响应,求系数a、b、c。
5-28 某LTI系统,在以下各种情况下起初始状态相同。已知当激励时,其全响应;当激励时,其全响应。
(7)(8)
1-7 已知序列的图形如图1-7所示,画出下列各序列的图形。
信号与系统课后习题答案(金波 华中科技大学出版社)

1-3 解 周期 T=7 ,一个周期的能量为 信号的功率为
P
E 56 8W T 7
1-5 解 (a) (3t 2 2) ( ) 4 (t ) ; (b) e
3t
t 2
(5 2t ) 0.5e 3t (t 2.5) 0.5e 7.5 (t 2.5)
2
1-10 已知一线性非时变系统,系统的初始状态为零,当输入信号为 f1 (t ) ,其输出信号为
y1 (t ) ,对应的波形如题图 1.10(a)(b)所示。试求: (a) 当输入信号为 f 2 (t ) 时,其波形如题图 1.15(c)所示,画出对应的输出 y 2 (t ) 的波形。 (b) 当输入信号为 f 3 (t ) 时,其波形如题图 1.10(d)所示,画出对应的输出 y 3 (t ) 的波形。
(b) 波形如图1.2(b)所示。显然是能量信号。
E 1 1 6 2 1 37 J
(c) 能量信号
E lim (e 5t ) 2 dt e 10t dt
T 0 0
T
1 10t e 0.1 J 10 0
(d) 功率信号,显然有
P 1W
习
基本练习题
题 一
1-1 判断下列信号是否是周期的,如果是周期的,求出它的基频和公共周期。 (a) f (t ) 4 3 sin(12 t ) sin(30 t ) ; (b) f (t ) cos(10 t ) cos(20 t ) ; (c) f (t ) cos(10 t ) cos(20t ) ; (d) f (t ) cos(2t ) 2 cos(2t
2
信号与系统第六章习题答案

第六章 离散系统的Z域分析 6.1学习重点 1、离散信号z 域分析法—z变换,深刻理解其定义、收敛域以及基本性质;会根据z变换的定义以及性质求常用序列的z变换;理解z变换与拉普拉斯变换的关系。
2、熟练应用幂级数展开法、部分分式法及留数法,求z 反变换。
3、离散系统z 域分析法,求解零输入响应、零状态响应以及全响应。
4、z 域系统函数()z H 及其应用。
5、离散系统的稳定性。
6、离散时间系统的z 域模拟图。
7、用MATLAB 进行离散系统的Z 域分析。
6.2 教材习题同步解析 6.1 求下列序列的z 变换,并说明其收敛域。
(1)n 31,0≥n (2)n−−31,0≥n(3)nn−+ 3121,0≥n (4)4cos πn ,0≥n(5)+42sin ππn ,0≥n 【知识点窍】本题考察z 变换的定义式 【逻辑推理】对于有始序列离散信号[]n f 其z 变换的定义式为()[]∑∞=−=0n nzn f z F解:(1)该序列可看作[]n nε31()[][]∑∑∞=−∞=− == =010313131n n n nn n z z n n Z z F εε对该级数,当1311<−z ,即31>z 时,级数收敛,并有 ()13331111−=−=−z zz z F其收敛域为z 平面上半经31=z 的圆外区域 (2)该序列可看作[]()[]n n nnεε331−=−−()()[][]()[]()∑∑∞=−∞=−−=−=−=010333n nn nnnzzn n Z z F εε对该级数,当131<−−z ,即3>z 时,级数收敛,并有()()33111+=−−=−z zz z F 其收敛域为z 平面上半经3=z 的圆外区域(3)该序列可看作[][]n n nn n n εε+ = + −3213121()[][]()∑∑∑∞=−∞=−∞=−+ =+ = + =01010*********n nn n n nn n n n z z z n n Z z F εε对该级数,当1211<−z 且131<−z ,即3>z 时,级数收敛,并有 ()3122311211111−+−=−+−=−−z zz z z zz F 其收敛域为z 平面上半经3=z 的圆外区域(4)该序列可看作[]n n επ4cos()[]∑∑∑∑∞=−−∞=−−∞=−∞=−+=+== =0140140440*******cos 4cos n nj n nj nn j j n n z e z e z e e z n n n Z z F πππππεπ对该级数,当114<−ze j π且114<−−zejπ,即1>z 时,级数收敛,并有()122214cos 24cos 21112111212222441414+−−=+−−=−+−=−×+−×=−−−−z z zz z z z z e z z e z z z eze z F j j j j ππππππ其收敛域为z 平面上半经1=z 的圆外区域 (5)该序列可看作[][][]n n n n n n n n εππεππππεππ+=+= +2cos 2sin 222sin 4cos 2cos 4sin 42sin()[]()122212212212cos 22cos 2212cos 22sin 222cos 222sin 222cos 2sin 222222222200++=+++=+−−++−=+=+=∑∑∞=−∞=−z z z z z z z z z z z z z z z n z n n n n Z z F n nn n ππππππεππ 其收敛域为z 平面上半经1=z 的圆外区域 6.2 已知[]1↔n δ,[]a z z n a n −↔ε,[]()21−↔z z n n ε, 试利用z 变换的性质求下列序列的z 变换。
信号与系统课后习题答案

习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD (15,6)=3 Hz 。
因此,公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD (5, 15)=5 Hz 。
因此,公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数,因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的,基频 =0f 1/π Hz 。
因此,公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号,显然有 1=P W1-3 解 周期T=7 ,一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+; (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
信号与系统(应自炉)习题答案第1章 习题解重点

(222222j t k j t j t j k f t k e
e
e
e
f t π
π
π
πππ+++++==⨯==
∴原函数是周期函数,令1k =,则基波周期为2π。
1-2.
求信号( 14sin( 110cos(2--+=t t t f的基波周期。
解:cos(101 t +的基波周期为15
π,s i n (4
1-8.
用阶跃函数写出题图1-8所示各波形的函数表达式。
t
t
t
(a (
bc
题图1-8
解:(a)((((((3[31]2[11]f t t u t u t u t u t =++-+++-- (((3[13]t u t u t +-+---
(((((
(3 3(1 1(1 1(3 3f
t t u t t u t t u t t u t =+++--++-+-+--(b)([( (1]2[(1 (2]4(2 f t u t u t u t u t u t =--+---+-
1 t -的基波周期为
1
2
π二者的最小公倍数为π,故( 14sin( 110cos(2--+=t t t f的基波周期为π。
1-3.
设(3, 0<=tt f ,对以下每个信号确定其值一定为零的t值区间。
(1)(t f -1(2)((t f t f -+-21(3)((t f t f --21(4)(t f 3(5)(f
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.1求下列序列的z 变换)(z X ,并标明收敛域,绘出)(z X 的零极点图。
(1))()21(k kε (2))()41(k kε−(3))()31(k kε−−(4))()31(k k−ε(5))1(21(−−−k kε(6))1(+k δ(7))]10()([)21(−−k k k εε (8))()31()()21(k k kk εε+(9))3(81)(−−k k δδ6.2求下列序列的z 变换,并标注收敛区。
(1))3()3(−−k k ε (2))()3(k k ε− (3))(3k k ε−6.3用z 变换的性质和常用z 变换求下列信号的双边z 变换。
(1))1(2)()21(−−+k k k kεε; (2))(31()21(k kkε⎥⎦⎤⎢⎣⎡+−; (3))3(+k akε;(4))()31(2k k ε+;(5))1()32(+−−k k kε;(6))2()1(−−k a kkε;(7))1(+k ekj επ;(8))()21()(2k k k k−+−−εε;(9))1()1(−−−k k k ε。
6.4已知)(n f 的z 变换为)(z F ,求下列序列的z 变换。
(1)∑=nk k k f a 0)(; (2))2(n f ; (3))(n nf ;(4)∑=nk k kf 0)(;(5)∑=nk k f a)(。
6.5已知信号)(n f 的z 变换)(z F 如下,试求)(n f 的初值)0(f 和终值)(∞f 。
(1)2225.0)(+=z z z F(2)21)(22−−++=z z z z z F(3)12222)(22−−++=z z z z z F (4)1322)(22+−=z z z z F (5)NN z z z z F )5.0)(1()(1−−=+ (6)231)(22+−++=z z z z z F(7)16)(2−−=z z zz F(8)612)(2−−−=z z z z F6.6若序列的z 变换如下,求该序列的前三项。
(1)2,)1)(2()(2>−−=z z z z z F(2),1,)5.0)(1(1)(2>+−++=z z z z z z F(3)1,)1()(32>−−=z z zz z F ,6.7用部分分式展开法或长除法,留数法求下列)(z F 的逆z 变换 (1)12111)(−+=z z F 21>z (2)21181431211)(−−−++−=z z z z F 21<z(3) 21411211)(−−−−=z z z F 21<z (4) az az z F −−=−−111)( a z 1>6.8直接从下列z 变换看出它们所对应的序列。
(1)1)(=z X )(∞≤z (2)3)(z z X = )(∞≤z (3)1)(−=zz X )0(∞≤<z(4)122)(2++−=−z z z X )0(∞≤<z(5)111)(−−=az z X )(a z >(6)111)(−−=azz X )(a z < 6.9求下列)(z F 的单边z 变换: (1))3)(2)(1()(−−−=z z z zz F ,3>z ;(2))21()1()(2+−=z z z z F ,1>z ;(3) 32)3(2)(−+=z z z F ,3>z ; (4)1)(2+=z zz F ,1>z ; (5))1)(1()(2−+=z z zz F ,1>z ;(6))2(1)(2−−=z z z z F ,2>z ; (7))1(1)(441−−=−−z z z z F ,1>z 。
6.10已知双边z 变换为)4)(3)(2(2)(−−−=z z z zz F(1)4>z ,求原函数)(k f ; (2)2<z ,求原函数)(k f ; (3)43<<z ,求原函数)(k f 。
6.11画出2112523)(−−−+−−=zz z z X 的零极点图,在下列三种收敛域下,那种情况对应左边序列,右边序列,双边序列?并求各对应序列。
(1)2>z (2)5.0<z(3)25.0<<z6.12已知)(*)()(21k f k f k y =,用卷积性质求下列情况下的)(k f ;(1))()(1k a k f kε=,)1()(2−=k k f δ; (2))(2)(1k k f kε=,)1()()(2−−=k k k f εε;(3))()21()(1k k f kε=,)()(2k k k f ε=。
6.13用z 变换与拉普拉斯变换的关系:(1)由)()(t tet f atε−=的2)(1)(α+=s s F ,求变换的z k ke t)(εα−。
(2)由)()(2t tt f ε=的32)(ss F =,求)(2k k ε的z 变换。
6.14求下列差分方程描述的因果离散系统的零输入响应。
(1))1()2(2)1(3)(−=−+−+k f k y k y k y , 1)1(=−y ,0)2(=−y ;(2))1()()2(2)1()(−+=−−−−k f k f k k y k y ,2)1(=−y ,1)2(=−y ;(3))(2)2(4)1(4)(k f k y k y k y =−+−+,0)1(=−y ,1)2(=−y 。
6.15用z 变换方法计算下列系统的零输入响应、零状态响应和全响应。
(1))(3)1(25.0)(k k y k y kε−=−−,8)1(=−y(2))()5.0(4)2(25.0)1()(k k y k y k y kε=−+−+,6)1(=−y ,12)2(−=−y6.16描述某离散时间系统的差分方程为)1(2)(7)2(1.0)1(7.0)(−−=−+−−k f k f k y k y k y(1)求系统函数)(z H ; (2)求单位序列响应)(k h ;(3)若)()(,4)1()2(k k f y y ε==−=−,分别求此系统的零输入响应)(k y zi 和零状态响应)(k y zs 。
6.17求下列系统的全响应:(1))(1.0)1(9.0)(k k y k y ε=−− , 2)1(=−y(2))()2(2)1()(k k y k y k y ε=−−−− ,1)1(−=−y 41)2(=−y (3))()(2)1(3)2(k n y k y k y ε=++++ ,0)0(=y ,1)1(=y 6.18用z 变换求下列系统的响应)(k y(1))(2)2(3.0)1(1.0)(k n y k y k y ε=−−−+ 0)1(=−y 0)2(=−y(2))()5.0()2(2.0)1(9.0)(k n y k y k y kε=−+−− 1)1(=−y 4)2(−=−y (3))()5.0()2(1.0)1(7.0)(k k y k y k y kε=−+−+ 0)1(=−y 3)2(=−y(4))()4.0()2(25.0)(k k y k y kε=−− 0)1(=−y 3)2(=−y (5))()5.0()2(25.0)(k n y k y kε=−− 0)1(=−y 0)2(=−y6.19已知因果离散系统的系统函数如下。
分别用串连形式和并联形式信号流图模拟系统。
(1))3)(2)(1(3)(++++=z z z z z F ;(2))25.06.0)(5.0()1)(1()(22+−−+−−=z z z z z z z F 。
6.20求图P6.1所示系统的系统函数并粗略绘其频响。
图P6.16.21绘出以下系统的极零点图和幅频响应。
(1)5.02)(−−=z z z H(2))2()()(−−=k k k h δδ(3)5.02)(++=z z z H6.22已知离散系统差分方程表示式)()1(31)(k x k y k y =−−(1)求系统函数和单位样值响应;(2)若系统的零状态响应为)()31()21(3)(k k y k kε⎥⎦⎤⎢⎣⎡−=,求激励信号)(k x ;(3)画出系统函数的零、极分布图;(4)粗略画出幅频响应特性曲线; (5)画系统的结构框图。
6.23已知离散系统差分方程表示式)1(31)()2(81)1(43)(−+=−+−−k x k x k y k y k y (1)求系统函数和单位样值响应;(2)画出系统函数的零、极分布图; (3)粗略画出幅频响应特性曲线; (4)画系统的结构框图。
6.24求图P6.2所示三阶段非递归滤波器的系统函数,并绘出其极零图与粗略的幅频响应曲线。
假设输入信号的取样间隔为1ms 。
图P6.26.25描述某离散时间系统的差分方程为)1(31)()2(81)1(43)(−+=−+−−k f k f k y k y k y 分别以直接形式、级联形式和并联形式画出系统的信号流程图。
