函数y=Asin(ωx+φ)的图象 作业 高中数学 必修四 苏教版 含答案
高中数学必修四第一章 (三)正弦型函数y=Asin(ωx+φ)的图象

人大附中分校高一数学导学学案题目 1.3.1正弦型函数y =A sin (ωx +φ)的图象课型 新授课 教材 数学B 版必修4§1.3.1学 习 要 求 1.理解振幅、周期、频率、初相的定义;2.理解振幅变换、相位变换和周期变换的规律;3.会用“五点法”画出y =A sin(ωx +φ)的简图,明确A 、ω和φ对函数图象的影响作用;重 点 难 点重点:熟练地对y =sin x 进行振幅、周期和相位变换。
难点:理解振幅变换、周期变换和相位变换的规律。
导 学 学 案一.自学课本P44~45,通过观察、考虑观缆车,得出振幅、周期、频率、初相的概念。
在函数)sin(φω+=t R y 中,点P 旋转一周所需要的时间ωπ2=T ,叫做点P 的转动周期。
在1秒内,点P 转动的周数πω21==T f ,叫做转动的频率。
0OP 与x 轴正方向的夹角φ叫做初相。
二.归纳总结:函数y =A sin(ωx +φ),其中0,0>>ωA 表示一个振动量时,A 就表示这个量振动时离开平衡位置的最大距离,通常称为这个振动的振幅; 往复一次所需的时间ωπ2=T ,称为这个振动的周期;单位时间内往复振动的次数πω21==T f ,称为振动的频率; φω+x 称为相位; 0=x 时的相位φ称为初相。
三.例题:例1.在同一坐标系中,画出函数y =2sin x x ∈R ;y =21sin x x ∈R 的图象(简图) (比较它们的振幅的大小与A 的关系)y =sin x -112ππyxO结论:一般地,函数x A y sin =的值域是[],,A A -最大值是A ,最小值是A -,由此可知,A 的大小,反映曲线x A y sin =波动幅度的大小。
因此A 也称为振幅。
Asin(ωx+φ)的图像与性质练习(含解析)
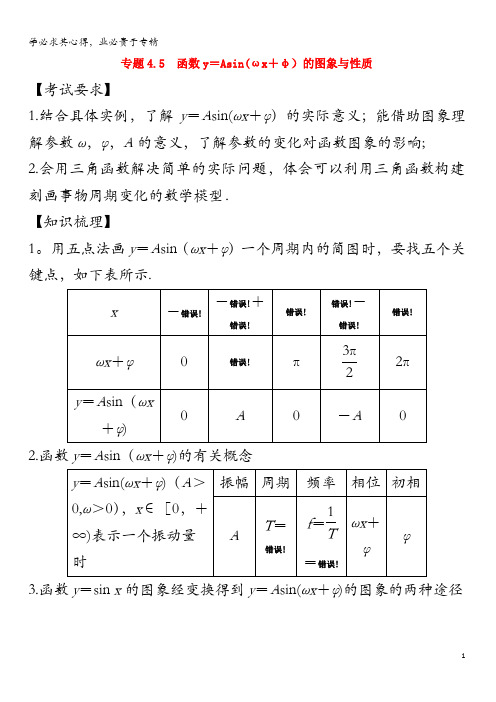
专题4.5 函数y=Asin(ωx+φ)的图象与性质【考试要求】1.结合具体实例,了解y=A sin(ωx+φ)的实际意义;能借助图象理解参数ω,φ,A的意义,了解参数的变化对函数图象的影响;2.会用三角函数解决简单的实际问题,体会可以利用三角函数构建刻画事物周期变化的数学模型.【知识梳理】1。
用五点法画y=A sin(ωx+φ)一个周期内的简图时,要找五个关键点,如下表所示.2.函数y=A sin(ωx+φ)的有关概念3.函数y=sin x的图象经变换得到y=A sin(ωx+φ)的图象的两种途径4。
三角函数应用(1)用正弦函数可以刻画三种周期变化的现象:简谐振动(单摆、弹簧等),声波(音叉发出的纯音),交变电流。
(2)三角函数模型应用题的关键是求出函数解析式,可以根据给出的已知条件确定模型f(x)=A sin(ωx+φ)+k中的待定系数。
(3)把实际问题翻译为函数f(x)的性质,得出函数性质后,再把函数性质翻译为实际问题的答案。
【微点提醒】1。
由y=sin ωx到y=sin(ωx+φ)(ω>0,φ〉0)的变换:向左平移错误!个单位长度而非φ个单位长度。
2。
函数y=A sin(ωx+φ)的对称轴由ωx+φ=kπ+错误!(k∈Z)确定;对称中心由ωx+φ=kπ(k∈Z)确定其横坐标。
3.音叉发出的纯音振动可以用三角函数表达为y=A sin ωx,其中x表示时间,y表示纯音振动时音叉的位移,错误!表示纯音振动的频率(对应音高),A表示纯音振动的振幅(对应音强)。
4。
交变电流可以用三角函数表达为y=A sin(ωx+φ),其中x表示时间,y表示电流,A表示最大电流,错误!表示频率,φ表示初相位。
【疑误辨析】1.判断下列结论正误(在括号内打“√"或“×”)(1)将函数y=3sin 2x的图象左移错误!个单位长度后所得图象的解析式是y=3sin错误!.()(2)利用图象变换作图时“先平移,后伸缩"与“先伸缩,后平移”中平移的长度一致.()(3)函数y=A cos(ωx+φ)的最小正周期为T,那么函数图象的两个相邻对称中心之间的距离为错误!.( )(4)由图象求解析式时,振幅A的大小是由一个周期内图象中最高点的值与最低点的值确定的。
2018年高中数学必修四专题y=Asin(ωx+φ)函数的图象和性质(附答案)

2018年高中数学必修四专题y=Asin(ωx+φ)函数的图象和性质(附答案)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.要想得到函数的图像,只须将的图像()A.向右平移个单位B.向左平移个单位C.向右平移个单位D.向左平移个单位【答案】A【解析】试题分析:函数向左或右平移个单位(向左平移,向右平移)得到,令,得,故选A.2.将函数的图像向左平移个单位,则平移后的函数图像()(A)关于直线对称(B)关于直线对称(C)关于点对称(D)关于点对称【答案】A3.将函数的图像向右平移个单位后,所得的图像对应的解析式为()A.B.C.D.【答案】C4.要得到的图象只需将的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位【答案】C5.要得到函数的图象,只需将的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【答案】B6.函数的图像经过下列平移,可以得到偶函数图像的是()A.向右平移个单位 B.向左平移个单位C.向右平移个单位D.向左平移个单位【答案】C7.函数的部分图象如图所示,为了得到的图象,只需将的图象( )A.向右平移个单位B.向右平移个单位C.向左平移个单位D.向左平移个单位【答案】B8. 若将函数图象上各点的横坐标伸长到原来的3倍(纵坐标不变),再将所得图象沿轴向右平移个单位长度,则所得图象的一个对称中心是()A. B.C. D.【答案】D9.为了得到函数的图象,可以将函数的图象()A.向左平移个单位长度B.向左平移个单位长度C.向右平移个单位长度D.向右平移个单位长度【答案】D10.为得到函数的图象,可将函数的图象()A.向左平移个单位B.向左平移个单位[来源:学&科&网]C.向右平移个单位D.向右平移个单位【答案】C11.将函数的图象向右平移个单位,再纵坐标不变,横坐标变为原来的2倍,所得新图象的函数解析式是()A.y=sin4x B.y=sinxC.y=sin(4x﹣)D.y=sin(x﹣)【答案】D12.将函数图象上所有点的横坐标伸长到原来的2倍,再向右平移个单位长度,得到函数的图象.则图象一条对称轴是()A. B. C. D.【答案】C二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 将函数的图象向右平移个单位后,所得图象关于轴对称,则的值为____________.【答案】14. 将函数的图象向左平移个单位后,得到的图象对应的函数为奇函数,则的最小值为.【答案】15.设函数的部分图象如图所示.则=【答案】16.对于函数给出下列四个命题:①该函数是以为最小正周期的周期函数;②当且仅当时,该函数取得最小值-1;③该函数的图象关于对称;④当且仅当时,.其中正确命题的序号是___________.(请将所有正确命题的序号都填上)【答案】③④三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知函数(其中)的周期为,其图象上一个最高点为.(Ⅰ)求的解析式;(Ⅱ)当时,求的最值及相应的的值.【答案】(Ⅰ);(Ⅱ)时,取得最小值1,时,取得最大值.18. 已知函数的图象(部分)如图所示.(1)求函数的解析式;(2)若,且,求.【答案】(1)(2)19. 某同学用“五点法”画函数(,)在某一个周期内的图象时,列表并填入了部分数据,如下表:0 0(1)请将上表空格中所缺的数据填写在答题卡的相应位置上,并直接写出函数的解析式;(2)把函数图象上所有点的横坐标缩短到原来的倍(纵坐标不变),再把所得图象向左平移个单位,得到函数的图象,求函数的单调递增区间.【答案】(1)(2),.20. 某同学用“五点法”画函数在某一个周期内的图象时,列表并填入了部分数据,如下表:(1)请将上表数据补充完整,填写在答题卡上相应位置...........,并直接写出函数f(x)的解析式;(2)将图象上所有点向左平行移动个单位长度,得到的图象,求的图象离原点O最近的对称中心.【答案】(1);(2).21. 设函数(为常数,且)的部分图象如图所示.(1)求的值;(2)当时,求的取值范围.【答案】(1),,;(2)的取值范围为.22. 设+.(1)求在上的最大值和最小值;(2)把的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移个单位,得到函数的图象,求g(x)的单调减区间.【答案】(1)的最大值是4+,最小值是;(2)单调减区间是。
【高考复习】2018年高考数学 必修4 三角函数y=Asin(ωx+φ)的图象性质 复习题(含答案)

2018年高考数学 必修4 三角函数y=Asin(ωx +φ)的图象性质复习题1.求函数sin()y A x ωϕ=+的值域,最值,周期,单调区间,对称轴、对称中心等 ,会用五点法作sin()y A x ωϕ=+简图:五点分别为:、 、 、 、 。
2.图象的基本变换:相位变换:sin sin()y x y x ϕ=⇒=+ 周期变换:sin()sin()y x y x ϕωϕ=+⇒=+ 振幅变换:sin()sin()y x y A x ωϕωϕ=+⇒=+ 3.函数sin()y A x ωϕ=+的解析式:即求A 由最值确定,ω有周期确定,φ有特殊点确定。
4.函数sin y x =象到函数sin()(0,0)y A x A ωϕω=+>>的图象变换.5.三角函数最值类型:(1)y =a sin x +b cos x 型函数最值的求法:常转化为:y =x +ϕ)(2)y =a sin 2x +b sin x +c 型:常通过换元法(令sinx=t ,[]1,1t ∈-)转化为y =at 2+bt +c 型: (3)同一问题中出现sin cos ,sin cos ,sin cos x x x x x x +-∙,求它们的范围时,一般是令sin cos x x t +=或21sin cos sin cos 2t x x t x x --=⇒∙=或21sin cos 2t x x -∙=-,转化为关于t 的二次函数来解决例1.基础练习: 1、函数2sin(3)7y x π=+的振幅是 ,相位是 ,初相是 ,周期是 .2、为了得到函数R x x y ∈+=),3cos(的图象,只需把余弦曲线上所有的点向 (左或右)平行移动 个单位长度.3、要得到函数sin(2)3y x π=-的图象,只要sin 2y x =的图象向 (左或右)平行移动 个单位长度.4、把函数sin(2)6y x π=+的图象向右平移3π个单位后,所得图象对应函数解析式为 .5、要得到函数sin()26x y π=-+的图象,可由sin()2xy =-的图象向 (左或右)平行移动 个单位长度.6、把函数sin y x =的图象上所有的点的纵坐标变为原来的13倍(横坐标不变)所得图象的解析式为 .7、将函数sin y x =的图象上所有点向左平移3π个单位长度,再把所得图象上各点横坐标变为原来的5倍,则最后所得图象的解析式为 .例2.已知函数f(x)=sin(3π-2x) (x ∈R ).(1)求f(x)的单调减区间;(2)经过怎样的图象变换使f(x)的图象关于y 轴对称?(仅叙述一种方案即可).例3.如图为函数y 1=Asin(ωx +φ) (|φ|<2π)的一个周期内的图象.(1)写出y 1的解析式;(2)若y 2与y 1的图象关于直线x=2对称,写出y 2的解析式; (3)指出y 2的周期、频率、振幅、初相.例4.已知函数)32sin(21)(π-+=x x f ,x ∈[2,4ππ,].(1)求f(x)的最大值和最小值;(2)若不等式f(x)-m<2在x ∈[2,4ππ,]上恒成立,求实数m 的取值范围.例5.已知函数f(x)=Asin(ωx +φ)(A >0,ω>0)的一个周期的图象如图所示. (1)求f(x)的解析式;(2)若函数g(x)与f(x)的图象关于直线x=2对称,求g(x)的解析式; (3)求函数g(x)的单调区间.三角函数y =Asin(ωx +φ)的图象性质 测试题一、选择题:1.函数y=2sin(421π-x )的振幅、周期和初相分别是( )A.2,π41,-4πB.2,π41,4π C.2,4π,-4π D.±2,4π,-4π2.函数y=sin(2x-3π)在区间[-2π,π]的简图是( )3.函数y=2sin(2x+3π)图象的一条对称轴方程为( ) A.x=-6π B.x=-125ππ C.x=2π D.x=6π4.将函数y=sin x 的图象上所有的点向右平移10π个单位长度,再把所得各点的横坐标变为原来的2倍(纵坐标不变),所得图象的函数解析式是( )A.y=sin(2x-10π)B.y=sin(2x-20π)C.y=sin(1021π-x )D.y=sin(2021π-x )5.将函数y=sin4x 的图像向左平移12π个单位,得到函数y=sin(4x+ϕ)的图像,则ϕ的值为( ) A.12π- B.3π- C.3π D.12π6.将函数y=sin x 的图象向左平移2π个单位长度,得到函数y=f(x)的图象,则下列说法正确的是( )A.y=f(x)是奇函数B.y=f(x)的周期为πC.y=f(x)的图象关于直线x=2π对称D.y=f(x)的图象关于点(-2π,0)对称7.函数y=2sin(1x 23π+)在一个周期内的三个零点可能是( ) A.511,,333πππ- B.2410,,333πππ- C.1123,,666πππ- D.25,,333πππ- 二、填空题: 8.函数 y=51sin(3x-3π) 的定义域是_________,值域是________,周期是________,振幅是________,频率是________,初相是_________.9.要得到y=sin2x-cos2x 的图象,只需将函数y=sin2x+cos2x 的图象沿x 轴向____移___________个单位.10.设函数y=1-3sin(2x+3π)(其中2π-≤x ≤0),当x=_______时,函数的最大值为4.11.把函数y=sin(3x+6π)的图像向左平移3π个单位,再将图像上各点的横坐标缩短为原来的12,那么所得的图像的函数表达式为_______.12.已知函数f(x)=Atan(ωx+ ϕ)(ω>0, ||2πϕ<),y=f(x)的部分图像如下图,则f(24π)=_____.13.已知ω>0,0<φ<π,直线x=4π和x=45π是函数f(x)=sin(ωx +φ)图象的两条相邻的对称轴,则φ=________.三、解答题:14.已知函数f(x)=Asin(ωx+ ϕ)(A>0,ω>0,| ϕ |<π,x ∈R)的部分图像如图所示. (1)求函数f(x)的解析式;(2)求函数y=f(-x)的单调区间及在x ∈[-2,2]上的最值,并求出相应的x 的值.15.已知曲线y=Asin(ωx +φ) (A>0,ω>0)上的一个最高点的坐标为(2,8,π),此点到相邻最低点间的曲线与x 轴交于点(83π,0),若φ∈(-2π,2π).(1)试求这条曲线的函数表达式;(2)用“五点法”画出(1)中函数在[0,π]上的图象.16.已知函数f(x)=sin(ωx +φ) (ω>0,0≤φ≤π)是R 上的偶函数,其图象关于点M(43π,0)对称,且在区间[0,2π]上是单调函数,求φ和ω的值.17.已知函数f(x)=-2asin(2x+6π)+2a+b,x ∈[3,44ππ],是否存在常数a,b ∈Z ,使得f(x)的值域为[].若存在,求出a,b 的值;若不存在,请说明理由.参考答案例2.解:例3.解:例4.解:例5.测试题参考答案1.答案为:C2.答案为:A3.答案为:B4.答案为:C5.选C.【解析】将函数y=sin4x 的图像向左平移12π个单位,得到函数y=sin [4(x+12π)]=sin(4x+3π)的图像,所以ϕ的值为3π. 6.答案为:D 7.选B.【解析】23π-是y=2sin(1x 23π+)的一个零点,y=2sin(1x 23π+)周期T=4π,T2=2π, 所以410,33ππ也是零点. 8.答案为:(-∞,+ ∞),(-15 ,15 ), 2π3 ,15 ,15 ,32π ,-π3 ;9.答案为:右,π2;10.答案:512π-;【解析】由2π-≤x ≤0知22x 333πππ-≤+≤, 当2x 32ππ+=-, 即5x 12π=-时,y=sin(2x+3π)取最小值-1,故y=1-3sin(2x+3π)取最大值4.11.答案:y=-sin(6x+6π);【解析】把函数y=sin(3x+6π)的图像向左平移3π个单位长度,得到函数y sin 3(x )sin(3x )366πππ=++=-+[]的图像,再将图像上各点的横坐标缩短为原来的12,纵坐标不变,得到函数y=-sin(6x+6π)的图像.12.答案【解析】如图可知T 3288ππ=-,即24ππ=ω,所以ω=2, 再结合图像可得2k 82ππ⨯+ϕ=π+,k ∈Z ,即|k |42ππϕ=π+<,所以31k 44-<<,只有k=0,所以4πϕ=,又图像过点(0,1),代入得Atan 4π=1,所以A=1,函数的解析式为f(x)=tan(2x+ 4π),则f ()tan 243ππ==13.答案为:4π;14.解:(1)由图像知A=2.T=8,∵2T 8π==ω,∴4πω=,又图像经过点(1,2), ∴2sin(4π+ϕ)=2,2k 42ππ+ϕ=π+,(k ∈Z),即2k 4πϕ=π+,(k ∈Z).∵|ϕ|<π,∴4πϕ=,∴f(x)=2sin(x 44ππ+).(2)y=f(-x)=2sin(x 44ππ-+)=-2sin(x 44ππ-)由2k x 2k 2442πππππ-≤-≤π+,得8k-1≤x ≤8k+3,k ∈Z ,故y=f(-x)在[8k-1,8k+3],k ∈Z 上是减少的;同理,函数在[8k+3,8k+7],k ∈Z 上是增加的.∵x ∈[-2,2],由上可知当x=-1时,y=f(-x)取最大值2;当x=2时,y=f(-x)取最小值15.解:16.解:17.解:∵3x 44ππ≤≤∴3252x 2x 22363πππππ≤≤≤+≤,∴1sin(2x )62π-≤+≤ (1)当a>0时-2a<0由题意得2a 2a b 12a 2a b 32⎧++=⎪⎨-++=-⎪⎩ ,解得a 1b 5=⎧⎪⎨=⎪⎩.∵a,b ∈Z 舍去. (2)当a<0时-2a>0由题意得2a 2a b 32a 2a b 1++=-⎧⎪⎨-++=⎪⎩解得a 1b 1=-⎧⎨=⎩符合题意.。
2019-2020学年高中数学苏教版必修四 课下能力提升:(十一) 函数y=Asin(ωx+φ)的图象 Word版含答案

课下能力提升(十一) 函数y =A sin(ωx +φ)的图象一、填空题1.电流I (单位:A)随时间t (单位:s)变化的函数关系是I =50sin ⎝ ⎛⎭⎪⎫100πt +π3,t ∈[0,+∞),则电流I 变化的周期是________,频率是________,振幅是________,初相是________.2.函数y =sin x 的图象上所有点的纵坐标不变,将横坐标缩短为原来的12倍,然后将图象沿y 轴向上平移2个单位长度,再沿x 轴向右平移π6个单位长度,得到的函数图象所对应的函数解析式是________________.3.设函数f (x )=cos ωx (ω>0),将y =f (x )的图象向右平移π3个单位长度后,所得的图象与原图象重合,则ω的最小值是________.4.已知函数y =sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,0<φ ≤π2的部分图象如图所示,则点(ω,φ)的坐标是________.5.把函数y =f (x )的图象上各点向右平移π6个单位,再把横坐标变为原来的2倍,再把纵坐标变为原来的23倍,所得图象的解析式是y =2sin ⎝ ⎛⎭⎪⎫12x +π3,则f (x )的解析式为________.二、解答题6.已知函数y =3sin ⎝ ⎛⎭⎪⎫12x -π4.(1)用“五点法”画函数的图象;(2)说出此图象是由y =sin x 的图象经过怎样的变换得到的? (3)求此函数的周期、振幅、初相;(4)求此函数的对称轴、对称中心、单调递增区间.7.已知函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫A>0,ω>0,|φ|<π2的部分图象如图所示.(1)求函数f (x )的解析式;(2)令g (x )=f ⎝⎛⎭⎪⎫x +7π6,试判断函数g (x )的奇偶性,并说明理由.8.已知函数f (x )=sin(ωx +φ)(ω>0,0≤φ≤π)是R 上的偶函数,其图象关于点M ⎝⎛⎭⎪⎫3π4,0对称,且在区间⎣⎢⎡⎦⎥⎤0,π2上是单调函数,求φ和ω的值.答 案1.150 50 50 π32.解析:由题意知,y =sin x 12−−−−−−−→坐原的倍横标变为来y =sin 2x ――→向上平移2 个单位长度y =sin 2x +26π−−−−−−−→向右平移位度个单长y =sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π6+2=sin ⎝⎛⎭⎪⎫2x -π3+2.答案:y =sin ⎝⎛⎭⎪⎫2x -π3+2 3.解析:由已知得,cos ⎣⎢⎡⎦⎥⎤ω⎝⎛⎭⎪⎫x -π3=cos ωx ,所以cos ⎝ ⎛⎭⎪⎫ωx -ωπ3=cos ωx ,则ωx -ω3π=ωx +2k π,k ∈Z , ∴ω=-6k ,又ω>0,∴ω的最小值是6. 答案:64.解析:由图象可得周期T =2⎝ ⎛⎭⎪⎫7π8-3π8=π=2πω,即得ω=2,将点⎝ ⎛⎭⎪⎫3π8,0代入y =sin(2x +φ)得sin ⎝ ⎛⎭⎪⎫3π4+φ=0,令3π4+φ=π,得φ=π4,∴(ω,φ)的坐标为⎝⎛⎭⎪⎫2,π4.答案:⎝⎛⎭⎪⎫2,π45.解析:y =2sin ⎝ ⎛⎭⎪⎫12x +π332−−−−−−−→坐原的倍纵标变为来y =3sin ⎝ ⎛⎭⎪⎫12x +π312−−−−−−−→坐原的倍横标变为来 y =3sin ⎝⎛⎭⎪⎫x +π36π−−−−−−→向左平移位个单 y =3sin ⎝⎛⎭⎪⎫x +π6+π3=3sin ⎝ ⎛⎭⎪⎫x +π2=3cos x .∴f (x )=3cos x . 答案:f (x )=3cos x 6.解:(1)列表:描点连线;将所得五点用光滑的曲线连接起来,得到所求函数一个周期内的图象,如图所示,再将这部分图象左右平移4k π(k ∈Z )个单位长度,得函数y =3sin ⎝ ⎛⎭⎪⎫12x -π4的图象.(2)法一:①把y =sin x 图象上所有的点向右平移π4个单位长度,得到y =sin ⎝⎛⎭⎪⎫x -π4的图象;②把y =sin ⎝ ⎛⎭⎪⎫x -π4图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y =sin ⎝ ⎛⎭⎪⎫12x -π4的图象;③将y =sin ⎝ ⎛⎭⎪⎫12x -π4图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),就得到y =3sin ⎝ ⎛⎭⎪⎫12x -π4的图象.法二:①把y =sin x 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y =sin 12x 的图象;②把y =sin 12x 图象上所有的点向右平移π2个单位长度,得到y =sin 12⎝⎛⎭⎪⎫x -π2=sin ⎝⎛⎭⎪⎫12x -π4的图象; ③将y =sin ⎝ ⎛⎭⎪⎫12x -π4的图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),就得到y =3sin ⎝ ⎛⎭⎪⎫12x -π4的图象.(3)周期T =2πω=2π12=4π,振幅A =3,初相是-π4.(4)令12x -π4=π2+k π,k ∈Z ,解得x =3π2+2k π,k ∈Z ,即函数的对称轴是直线x =3π2+2k π,k ∈Z . 令12x -π4=k π,k ∈Z ,解得x =2k π+π2,k ∈Z , 即函数的对称中心为⎝⎛⎭⎪⎫π2+2k π,0,k ∈Z .令-π2+2k π≤12x -π4≤π2+2k π,k ∈Z .解得-π2+4k π≤x ≤3π2+4k π,k ∈Z ,即函数的单调递增区间为⎣⎢⎡⎦⎥⎤-π2+4k π,3π2+4k π,k ∈Z .7.解:(1)由图象知A =2.f (x )的最小正周期T =4×⎝⎛⎭⎪⎫5π12-π6=π,故ω=2πT =2. 将点(π6,2)代入f (x )的解析式得sin ⎝ ⎛⎭⎪⎫π3+φ=1,又|φ|<π2,所以φ=π6.故函数f (x )的解析式为f (x )=2sin ⎝⎛⎭⎪⎫2x +π6.(2)g (x )=f ⎝ ⎛⎭⎪⎫x +7π6=2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x +7π6+π6 =2sin ⎝⎛⎭⎪⎫2x +5π2=2cos2x ,因为g (x )的定义域为R ,且g (-x )=g (x ),故g (x )为偶函数. 8.解:∵f (x )在R 上是偶函数, ∴当x =0时,f (x )取得最大值或最小值, 即sin φ=±1,得φ=k π+π2,k ∈Z ,又0≤φ≤π,∴φ=π2.由图象关于M ⎝ ⎛⎭⎪⎫3π4,0对称可知,sin ⎝ ⎛⎭⎪⎫3π4ω+π2=0,∴3π4ω+π2=k π,k ∈Z ,解得ω=43k -23,k ∈Z . 又f (x )在⎣⎢⎡⎦⎥⎤0,π2上是单调函数,所以T ≥π,即2πω≥π,∴ω≤2,又ω>0,∴当k =1时,ω=23,当k =2时,ω=2.。
函数y=Asin(ωx+φ)的图象与性质 作业 高中数学 必修四 苏教版 含答案

学业分层测评(十二)函数y =A sin(ωx +φ)的图象与性质(建议用时:45分钟)学业达标]一、填空题1.已知f (x )=sin(3x +φ)⎝ ⎛⎭⎪⎫|φ|<π2的图象的一个对称中心是⎝ ⎛⎭⎪⎫-7π12,0,则φ=________.【解析】 把x =-712π代入sin(3x +φ)=0, 得sin ⎣⎢⎡⎦⎥⎤3×⎝ ⎛⎭⎪⎫-712π+φ=0, ∴φ-74π=k π,又|φ|<π2,所以令k =-2,得φ=-2π+74π=-π4. 【答案】 -π4 2.三角函数式:①y =3sin ⎝ ⎛⎭⎪⎫2x -5π6;②y =3sin ⎝ ⎛⎭⎪⎫2x +7π6;③y =3sin ⎝ ⎛⎭⎪⎫2x -5π12;④y =3cos ⎝ ⎛⎭⎪⎫2x +2π3.其中在⎣⎢⎡⎦⎥⎤π6,2π3上的图象如图1-3-11所示的函数是________.图1-3-11【解析】 代入⎝ ⎛⎭⎪⎫π6,-3,⎝ ⎛⎭⎪⎫23π,3检验.【答案】 ①②④3.(2016·南京高一检测)函数f (x )=2sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,-π2<φ<π2的部分图象如图1-3-12所示,则ω=________;φ=________.图1-3-12【解析】 34T =5π12-⎝ ⎛⎭⎪⎫-π3=3π4,∴T =2πω=π,∴ω=2.当x =5π12时,2×5π12+φ=π2,∴φ=-π3. 【答案】 2 -π34.点P ⎝ ⎛⎭⎪⎫-π6,2是函数f (x )=sin(ωx +φ)+m (ω>0,|φ|<π2)的图象的一个对称中心,且点P 到该图象的对称轴的距离的最小值为π2,则正确的序号有________.【导学号:06460035】①f (x )的最小正周期是π;②f (x )的值域为0,4];③f (x )的初相φ=π3;④f (x )在⎣⎢⎡⎦⎥⎤4π3,2π上单调递增. 【解析】 由题意,⎩⎪⎨⎪⎧-π6ω+φ=k π(k ∈Z )①,m =2,且函数的最小正周期为T =4×π2=2π,故ω=2πT =1.代入①式得φ=k π+π6(k ∈Z ),又|φ|<π2,所以φ=π6,所以f (x )=sin ⎝ ⎛⎭⎪⎫x +π6+2.故函数f (x )的值域为1,3],初相为π6,排除①②③项,选④项.【答案】 ④5.已知函数f (x )=A cos(ωx +φ)的图象如图1-3-13所示,f ⎝ ⎛⎭⎪⎫π2=-23,则f (0)=________.图1-3-13【解析】 由图象可得最小正周期为23π,于是f (0)=f ⎝ ⎛⎭⎪⎫2π3,注意到23π与π2关于7π12对称,所以f ⎝ ⎛⎭⎪⎫2π3=-f ⎝ ⎛⎭⎪⎫π2=23.【答案】 236.设函数f (x )=2sin ⎝ ⎛⎭⎪⎫π2x +π5.若对任意x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为________.【解析】 f (x )的周期T =4,|x 1-x 2|的最小值为2. 【答案】 27.(2016·南通高一检测)若函数f (x )=3sin(ωx +φ)对任意x 都有f ⎝ ⎛⎭⎪⎫π3+x =f (-x ),则f ⎝ ⎛⎭⎪⎫π6=________.【解析】 由于函数f (x )=3sin(ωx +φ)对任意x 都有f ⎝ ⎛⎭⎪⎫π3+x =f (-x ),则函数f (x )的图象关于直线x =π6对称,则f ⎝ ⎛⎭⎪⎫π6是函数f (x )的最大值或最小值,则f ⎝ ⎛⎭⎪⎫π6=-3或3.【答案】 ±38.(2016·苏州高一检测)设函数y =sin(ωx +φ)⎝ ⎛⎭⎪⎫ω>0,φ∈⎝ ⎛⎭⎪⎫-π2,π2的最小正周期为π,且其图象关于直线x =π12对称,则在下面四个结论:①图象关于点⎝ ⎛⎭⎪⎫π4,0对称;②图象关于点⎝ ⎛⎭⎪⎫π3,0对称;③在⎣⎢⎡⎦⎥⎤0,π6上是增函数;④在⎣⎢⎡⎦⎥⎤-π6,0上是增函数,所有正确结论的编号为________.【解析】 ∵T =π,∴ω=2.又2×π12+φ=k π+π2, ∴φ=k π+π3.∵φ∈⎝ ⎛⎭⎪⎫-π2,π2,∴φ=π3,∴y =sin ⎝ ⎛⎭⎪⎫2x +π3.由图象及性质可知②④正确.【答案】 ②④ 二、解答题9.(2016·无锡高一检测)已知函数f (x )=A sin(ωx +φ),x ∈R ⎝ ⎛⎭⎪⎫其中A >0,ω>0,0<φ<π2的周期为π,且图象上一个最低点为M ⎝ ⎛⎭⎪⎫2π3,-2. (1)求f (x )的解析式;(2)当x ∈⎣⎢⎡⎦⎥⎤0,π12时,求f (x )的最值. 【解】 (1)由最低点为M ⎝ ⎛⎭⎪⎫2π3,-2得A =2.由T =π,得ω=2πT =2ππ=2.由点M ⎝ ⎛⎭⎪⎫2π3,-2是图象的一个最低点,得2sin ⎝ ⎛⎭⎪⎫4π3+φ=-2,即sin ⎝ ⎛⎭⎪⎫4π3+φ=-1,4π3+φ=2k π-π2(k ∈Z ),φ=2k π-11π6(k ∈Z ).又φ∈⎝ ⎛⎭⎪⎫0,π2,∴φ=π6,∴f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π6.(2)∵x ∈⎣⎢⎡⎦⎥⎤0,π12,∴2x +π6∈⎣⎢⎡⎦⎥⎤π6,π3,∴当2x +π6=π6,即x =0时,f (x )取得最小值1;当2x +π6=π3,即x =π12时,f (x )取得最大值 3.能力提升]1.(2016·南通高一检测)方程2sin ⎝ ⎛⎭⎪⎫x +π3+2a -1=0在0,π]上有两个不相等的实数根,则实数a 的取值范围是________.【解析】 ∵x ∈0,π],x +π3∈⎣⎢⎡⎦⎥⎤π3,4π3,2sin x +π3∈-3,2].画出函数图象可知,当3≤1-2a <2时,原方程有两个不相等的实数根,故-12<a ≤1-32.【答案】 ⎝ ⎛⎦⎥⎤-12,1-32 2.(2016·常州高一检测)函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫A >0,ω>0,|φ|<π2的一段图象如图1-3-14所示.图1-3-14(1)求f (x )的解析式;(2)把f (x )的图象向左至少平移多少个单位长度,才能使得到的图象对应的函数为偶函数?【解】 (1)A =3,2πω=43⎝ ⎛⎭⎪⎫4π-π4=5π,故ω=25. 由f (x )=3sin ⎝ ⎛⎭⎪⎫25x +φ的图象过点⎝ ⎛⎭⎪⎫π4,0得sin ⎝ ⎛⎭⎪⎫π10+φ=0,又|φ|<π2,故φ=-π10,∴f (x )=3sin ⎝ ⎛⎭⎪⎫25x -π10.(2)设把f (x )的图象向左至少平移m (m >0)个单位长度,才能使得到的图象对应的函数为偶函数.由f (x +m )=3sin ⎣⎢⎡⎦⎥⎤25(x +m )-π10=3sin ⎝ ⎛⎭⎪⎫25x +2m 5-π10为偶函数,知2m 5-π10=k π+π2,即m =52k π+3π2.∵m >0,∴m 取最小值3π2. 故至少把f (x )的图象向左平移3π2个单位长度,才能使得到的图象对应的函数是偶函数.。
高中数学必修四北师大版 8 函数y=Asin(ωx+φ)的图像(一) 作业 含答案

§8 函数y =A sin(ωx +φ)的图像(一)课时目标 1.了解φ、ω、A 对函数f (x )=A sin(ωx +φ)的图像的影响.2.掌握y =sin x 与f (x )=A sin(ωx +φ)图像间的变换关系.用“图像变换法”作y =A sin(ωx +φ) (A >0,ω>0)的图像 1.φ对y =sin(x +φ),x ∈R 的图像的影响y =sin(x +φ) (φ≠0)的图像可以看作是把正弦曲线y =sin x 上所有的点______(当φ>0时)或______(当φ<0时)平行移动______个单位长度而得到.2.ω(ω>0)对y =sin(ωx +φ)的图像的影响函数y =sin(ωx +φ)的图像,可以看作是把y =sin(x +φ)的图像上所有点的横坐标______(当ω>1时)或______(当0<ω<1时)到原来的______倍(纵坐标________)而得到.3.A (A >0)对y =A sin(ωx +φ)的图像的影响函数y =A sin(ωx +φ)的图像,可以看作是把y =sin(ωx +φ)图像上所有点的纵坐标______(当A >1时)或______(当0<A <1时)到原来的______(横坐标不变)而得到,函数y =A sin x 的值域为________,最大值为____,最小值为____.4.函数y =sin x 的图像到函数y =A sin(ωx +φ)的图像的变换过程.y =sin x 的图像――→向左(φ>0)或向右(φ<0)平移|φ|个单位______________的图像10ωω>−−−−−−−−−→横坐标变为原来的()倍纵坐标不变__________的图像――→纵坐标变为原来的A (A >0)倍横坐标不变______________的图像.一、选择题1.要得到y =sin ⎝⎛⎭⎫x -π3的图像,只要将y =sin x 的图像( ) A .向左平移π3个单位长度B .向右平移π3个单位长度C .向左平移π6个单位长度D .向右平移π6个单位长度2.为得到函数y =cos(x +π3)的图像,只需将函数y =sin x 的图像( )A .向左平移π6个单位长度B .向右平移π6个单位长度C .向左平移5π6个单位长度D .向右平移5π6个单位长度3.把函数y =sin ⎝⎛⎭⎫2x -π4的图像向右平移π8个单位,所得图像对应的函数是( ) A .非奇非偶函数 B .既是奇函数又是偶函数 C .奇函数 D .偶函数4.将函数y =sin 2x 的图像向左平移π4个单位,再向上平移1个单位,所得图像的函数解析式是( )A .y =cos 2xB .y =1+cos 2xC .y =1+sin(2x +π4) D .y =cos 2x -15.为了得到函数y =sin ⎝⎛⎭⎫2x -π3的图像,只需把函数y =sin ⎝⎛⎭⎫2x +π6的图像( ) A .向左平移π4个长度单位B .向右平移π4个长度单位C .向左平移π2个长度单位D .向右平移π2个长度单位6.把函数y =sin x (x ∈R )的图像上所有的点向左平行移动π3个单位长度,再把所得图像上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图像所表示的函数是( )A .y =sin ⎝⎛⎭⎫2x -π3,x ∈R B .y =sin ⎝⎛⎭⎫x 2+π6,x ∈RC .y =sin ⎝⎛⎭⎫2x +π3,x ∈R D .y =sin ⎝⎛⎭⎫2x +2π3,x-Ray二、填空题7.函数y =sin 2x 图像上所有点的横坐标变为原来的2倍,纵坐标不变,所得图像的函数解析式为f (x )=____________.8.将函数y =sin ⎝⎛⎭⎫2x +π6的图像向左平移π6个单位,所得函数的解析式为____________. 9.为得到函数y =cos x 的图像,可以把y =sin x 的图像向右平移φ个单位得到,那么φ的最小正值是____.10.某同学给出了以下论断:①将y =cos x 的图像向右平移π2个单位,得到y =sin x 的图像;②将y =sin x 的图像向右平移2个单位,可得到y =sin(x +2)的图像; ③将y =sin(-x )的图像向左平移2个单位,得到y =sin(-x -2)的图像;④函数y =sin ⎝⎛⎭⎫2x +π3的图像是由y =sin 2x 的图像向左平移π3个单位而得到的. 其中正确的结论是______(将所有正确结论的序号都填上).三、解答题11.怎样由函数y =sin x 的图像变换得到y =sin ⎝⎛⎭⎫2x -π3的图像,试叙述这一过程.12.已知函数f (x )=sin ⎝⎛⎭⎫π3-2x (x ∈R ). (1)求f (x )的单调减区间;(2)经过怎样的图像变换使f (x )的图像关于y 轴对称?(仅叙述一种方案即可).能力提升13.要得到y =cos ⎝⎛⎭⎫2x -π4的图像,只要将y =sin 2x 的图像( ) A .向左平移π8个单位 B .向右平移π8个单位C .向左平移π4个单位D .向右平移π4个单位14.使函数y =f (x )图像上每一点的纵坐标保持不变,横坐标缩小到原来的12倍,然后再将其图像沿x 轴向左平移π6个单位得到的曲线与y =sin 2x 的图像相同,则f (x )的表达式为( )A .y =sin ⎝⎛⎭⎫4x -π3B .y =sin ⎝⎛⎭⎫x -π6 C .y =sin ⎝⎛⎭⎫4x +π3 D .y =sin ⎝⎛⎭⎫x -π31.由y =sin x 的图像,通过变换可得到函数y =A sin(ωx +φ)的图像,其变化途径有两条:(1)y =sin x ――→相位变换y =sin(x +φ)――→周期变换y =sin(ωx +φ)――→振幅变换y =A sin(ωx +φ).(2)y =sin x ――→周期变换y =sin ωx ――→相位变换y =sin[ω(x +φω)]=sin(ωx +φ)――→振幅变换y =A sin(ωx +φ).注意:两种途径的变换顺序不同,其中变换的量也有所不同:(1)是先相位变换后周期变换,平移|φ|个单位.(2)是先周期变换后相位变换,平移|φ|ω个单位,这是很易出错的地方,应特别注意.2.类似地y =A cos(ωx +φ) (A >0,ω>0)的图像也可由y =cos x 的图像变换得到.§8 函数y =A sin(ωx +φ)的图像(一) 答案知识梳理1.向左 向右 |φ| 2.缩短 伸长 1ω不变 3.伸长 缩短 A 倍 [-A ,A ] A -A 4.y =sin(x +φ) y =sin(ωx +φ)y =A sin(ωx +φ) 作业设计1.B 2.C 3.D4.B [将函数y =sin 2x 的图像向左平移π4个单位,得到函数y =sin2(x +π4),即y =sin(2x+π2)=cos 2x 的图像,再向上平移1个单位,所得图像的函数解析式为y =1+cos 2x .] 5.B [y =sin(2x +π6) 4π→向右平移个长度单位y =sin[2(x -π4)+π6]=sin(2x -π3).]6.C [把函数y =sin x 的图像上所有的点向左平行移动π3个单位长度后得到函数y =sin ⎝⎛⎭⎫x +π3的图像,再把所得图像上所有的点的横坐标缩短到原来的12倍,得到函数 y =sin ⎝⎛⎭⎫2x +π3的图像.] 7.sin x8.y =cos 2x 9.32π 解析 y =sin x =cos ⎝⎛⎭⎫π2-x =cos ⎝⎛⎭⎫x -π2向右平移φ个单位后得y =cos ⎝⎛⎭⎫x -φ-π2, ∴φ+π2=2k π,k ∈Z ,∴φ=2k π-π2,k ∈Z .∴φ的最小正值是32π.10.①③11.解 由y =sin x 的图像通过变换得到函数y =sin ⎝⎛⎭⎫2x -π3的图像有两种变化途径: ①y =sin x ――→向右平移π3个单位y =sin ⎝⎛⎭⎫x -π3――→纵坐标不变横坐标缩短为12y =sin ⎝⎛⎭⎫2x -π3 ②y =sin x ――→纵坐标不变横坐标缩短为12y =sin 2x ――→向右平移π6个单位y =sin ⎝⎛⎭⎫2x -π3. 12.解 (1)由已知函数化为y =-sin ⎝⎛⎭⎫2x -π3.欲求函数的单调递减区间,只需求 y =sin ⎝⎛⎭⎫2x -π3的单调递增区间. 由2k π-π2≤2x -π3≤2k π+π2 (k ∈Z ),解得k π-π12≤x ≤k π+512π (k ∈Z ),∴原函数的单调减区间为⎣⎡⎦⎤k π-π12,k π+512π (k ∈Z ). (2)f (x )=sin ⎝⎛⎭⎫π3-2x =cos ⎣⎡⎦⎤π2-⎝⎛⎭⎫π3-2x。
数学苏教版必修4 第1章1.3.3函数y=Asin(ωx+φ)的图象 作业 Word版含解析

[学业水平训练].为了得到函数=(+),∈的图象,只需把函数=,∈的图象上所有的点:①向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍(纵坐标不变);②向右平移个单位长度,再把所得各点的横坐标缩短到原来的倍(纵坐标不变);③向左平移个单位长度,再把所得各点的横坐标伸长到原来的倍(纵坐标不变);④向右平移个单位长度,再把所得各点的横坐标伸长到原来的倍(纵坐标不变).其中正确的是.解析:==(+)=(+).答案:③.已知函数=(),()图象上每个点的纵坐标保持不变,将横坐标伸长到原来的倍,然后再将整个图象沿轴向左平移个单位,得到的曲线与=的图象相同,则=()的函数表达式为.解析:==(-)=(-).答案:=(-). 在同一平面直角坐标系中,画出三个函数()=(+),()=(+),()=(-)的部分图象(如图),则,,对应的函数依次是.解析:由于函数()、()、()的最大值分别是、、,因此结合图形可知,曲线为()的图象;又()、()的最小正周期分别是π、π,因此结合图形可知,曲线、分别是()、()的图象.答案:(),(),().要得到=(+)的图象,需将函数=至少向左平移个单位长度.解析:将=的图象向左平移φ(φ>)个单位长度得=(+)的图象.令=π+,∈,∴φ=π+,∈.∴当=时,φ=π是φ的最小正值.答案:π.函数=(--)(∈[,π])的增区间是.解析:原式可化为=-(+).令+π≤+≤+π,∈,得+π≤≤+π,∈,又∈[,π],则增区间为[,].答案:[,π].已知函数=(ω+φ)(ω>,<φ≤),且此函数的图象如图所示,则点(ω,φ)的坐标是.解析:由图可知=π-π=,∴=π.又=,∴ω=.又图象过(,),此点可看作“五点法”中函数的第三个点,故有×+φ=π,∴φ=.∴点(ω,φ)的坐标是(,).答案:(,).(·日照高一期末)作出函数=(+),∈的简图,并说明它与=的图象之间的关系.利用函数的周期性,可以把=的图象向左、右扩展,就得到=(+),∈的简图.法一:=的图象=(+)的图象=(+)的图象=(+)的图象.法二:=的图象=的图象=[(+)]=(+)的图象=(+)的图象..已知()=(+)+,∈.()求函数()的最小正周期和单调增区间;()函数()的图象可以由函数= (∈)的图象经过怎样的变换得到?解:()函数()的最小正周期为==π.由π-≤+≤π+(∈)知π-≤≤π+(∈).所以所求的单调递增区间为[π-,π+](∈).()变换情况如下:==[(+)]=(+)+.[高考水平训练].若函数=(ω+φ)(ω>,φ>)的图象的一个最高点为(,),它到相邻的最低点之间的图象与轴交于点(,),则这个函数的解析式为.解析:由题知=,且有得所以函数的解析式为=(+).答案:=(+).若函数=()同时具有下列三个性质:()最小正周期为π;()在=时取得最大值;()在区间[-,]上是增函数.则=()的解析式可以是(填序号).①=(+);②=(+);③=(-);④=(-).解析:由()排除①.由()可知函数在=时取得最大值,代入可知③满足,而且在区间[-,]上,③是增函数.答案:③。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学业分层测评(十一) 函数y =A sin(ωx +φ)的图象
(建议用时:45分钟)
学业达标]
一、填空题
1.函数y =cos x 图象上各点的纵坐标不变,把横坐标变为原来的2倍,得到图象的解析式为y =cos ωx ,则ω的值为________.
【解析】 y =cos x ―――――――――→
横坐标变为原来的2倍y =cos 12x .
【答案】 1
2
2.将y =cos 2x 的图象向右平移π
3个单位,得到的图象对应的解析式为________.
【解析】 y =cos 2x →y =cos 2⎝ ⎛⎭⎪⎫x -π3=cos ⎝ ⎛
⎭⎪⎫2x -2π3.
【答案】 y =cos ⎝ ⎛
⎭
⎪⎫2x -2π3
3.将函数y =cos ⎝ ⎛⎭⎪⎫
x -π3向右平移________个单位长度得到y =sin x 的图象.
【解析】 y =sin x =cos ⎝ ⎛⎭⎪⎫π2-x =cos ⎝ ⎛⎭
⎪⎫
x -π2,
y =cos ⎝ ⎛⎭⎪⎫x -π3的图象变换为y =cos ⎝ ⎛⎭⎪⎫
x -π2的图象应向右平移π6个单位. 【答案】 π6
4.将函数y =sin 2x 的图象向左平移π
4个单位,再向上平移1个单位,所得图象的函数解析式是________.
【解析】 y =sin 2x
y =sin 2⎝ ⎛⎭
⎪⎫
x +π4
=sin ⎝ ⎛
⎭⎪⎫2x +π2=cos 2x ―――→向上平移1个单位
y =cos 2x +1.
【答案】 y =cos 2x +1 5.某同学给出了以下论断:
①将y =cos x 的图象向右平移π
2个单位,得到y =sin x 的图象; ②将y =sin x 的图象向右平移2个单位,可得到y =sin(x +2)的图象; ③将y =sin(-x )的图象向左平移2个单位,得到y =sin(-x -2)的图象; ④函数y =sin ⎝ ⎛
⎭⎪⎫2x +π3的图象是由y =sin 2x 的图象向左平移π3个单位而得到
的.
其中正确的结论是________(将所有正确结论的序号都填上). 【解析】 由图象平移变换可知①③正确. 【答案】 ①③
6.用“五点法”画函数y =2sin ⎝ ⎛
⎭⎪⎫ωx +π3(ω>0)在一个周期内的简图时,五
个关键点是⎝ ⎛⎭⎪⎫-π6,0,⎝ ⎛⎭⎪⎫π12,2,⎝ ⎛⎭⎪⎫π3,0,⎝ ⎛⎭⎪⎫712π,-2,⎝ ⎛⎭
⎪⎫
5π6,0,则ω=________.
【解析】 周期T =5π6-⎝ ⎛⎭⎪⎫-π6=π,∴2π
ω=π,ω=2. 【答案】 2
7.函数y =3sin ⎝ ⎛
⎭
⎪⎫-x +π6的相位和初相分别是________.
【解析】 y =3sin ⎝ ⎛⎭⎪⎫-x +π6化为y =3sin ⎝ ⎛⎭⎪⎫
x +5π6,相位x +5π6,初相5π6.
【答案】 x +5π6,5π
6
8.(2016·南京高一检测)设ω>0,函数y =sin ωx +π3+2的图象向右平移4
3π个单位后与原图象重合,则ω的最小值为________.
【解析】 由题意知4π
3是函数周期的整数倍,又ω>0, ∴2πω·k =43π,∴ω=32k (k ∈Z ), ∴ω的最小值为32.
【答案】 3
2 二、解答题
9.用“五点法”画函数y =3sin ⎝ ⎛⎭⎪⎫2x +π3,x ∈⎣⎢⎡⎦
⎥⎤
-π6,5π6的图象.
【导学号:06460032】
【解】 ①列表:
⎝ ⎛⎭⎪⎫-π6,0,⎝ ⎛⎭⎪⎫π12,3,⎝ ⎛⎭⎪⎫π3,0,⎝ ⎛⎭⎪⎫7π12,-3,⎝ ⎛⎭
⎪⎫5π6,0. ③连线:用光滑曲线将所描五个点顺次连接起来,得函数y =3sin ⎝ ⎛
⎭⎪⎫2x +π3,x
∈⎣⎢⎡⎦
⎥⎤
-π6,5π6的简图,如图所示.
10.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫
π3-2x (x ∈R ).
(1)求f (x )的单调减区间.
(2)经过怎样的图象变换使f (x )的图象关于y 轴对称?(仅叙述一种方案即可) 【解】 (1)由已知函数化为y =-sin ⎝ ⎛
⎭
⎪⎫2x -π3. 欲求函数的单调递减区间,只需求y =sin2x -π
3的单调递增区间. 由2k π-π2≤2x -π3≤2k π+π
2(k ∈Z ), 解得k π-π12≤x ≤k π+5
12π(k ∈Z ),
∴原函数的单调减区间为⎣⎢⎡
⎦⎥⎤k π-π12,k π+512π(k ∈Z ).
(2)f (x )=sin ⎝ ⎛⎭⎪⎫
π3-2x =cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π3-2x =cos ⎝ ⎛⎭⎪⎫2x +π6=cos 2⎝ ⎛
⎭
⎪⎫x +π12.
∵y =cos 2x 是偶函数,图象关于y 轴对称, ∴只需把y =f (x )的图象向右平移π
12个单位长度即可.
[能力提升]
1.将函数f (x )的图象向右平移π
3个单位长度后,再向上平移1个单位长度得函数y =2sin ⎝ ⎛
⎭
⎪⎫4x -π4的图象,则f (x )=________.
【解析】 将y =2sin ⎝ ⎛
⎭⎪⎫4x -π4的图象向左平移π3个单位长度,得函数y =
2sin ⎣⎢⎡⎦⎥⎤
4⎝
⎛⎭⎪⎫x +π3-π4=2sin4x +13π12的图象,再向下平移一个单位长度,得函数y =2sin ⎝ ⎛
⎭
⎪⎫4x +13π12-1的图象,即f (x )=2sin4x +13π12-1.
【答案】 2sin ⎝ ⎛
⎭
⎪⎫4x +13π12-1
2.某同学用“五点法”画函数y =A sin(ωx +φ)(A >0,ω>0)在一个周期内简图时,列表如下:
则A =【解析】 由表格得A =2,34π-π12=2π
ω, ∴ω=3,∴ωx +φ=3x +φ.
当x =π12时,3x +φ=π4+φ=0,∴φ=-π4.
【答案】 2 3 -π
4
3.要得到函数y =2cos x 的图象,只需将函数y =2sin ⎝ ⎛
⎭⎪⎫2x +π4图象上的所
有点的________.
①横坐标缩短到原来的12(纵坐标不变),再向左平行移动π
8个单位长度; ②横坐标缩短到原来的12(纵坐标不变),再向左平行移动π
4个单位长度; ③横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动π
4个单位长度; ④横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动π
8个单位长度. 【解析】 y =2cos x =2sin ⎝ ⎛⎭⎪⎫
x +π2.
法一:y =2sin ⎝ ⎛
⎭⎪⎫2x +π4=2sin 2(x +π8
)y =2sin 2⎝ ⎛⎭
⎪⎫
x +π2――――→横坐标缩短为原来的1
2
y =2sin ⎝ ⎛⎭⎪⎫x +π2. 法二:y =2sin ⎝ ⎛⎭⎪⎫2x +π4―――――→横坐标缩短为原来的1
2y =2sin ⎝ ⎛⎭⎪⎫x +π
4y =2
sin ⎝ ⎛⎭⎪⎫
x +π2.
【答案】 ②
4.已知f (x )=2sin 2x ,将函数y =f (x )的图象向左平移π
6个单位,再向上平移1个单位,得到函数y =g (x )的图象,区间[a ,b ](a ,b ∈R 且a <b )满足:y =g (x )在[a ,b ]上至少含有30个零点,在所有满足上述条件的[a ,b ]中,求b -a 的最小值.
【解】 f (x )=2sin 2x ,
g (x )=2sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π6+1=2sin ⎝ ⎛
⎭⎪⎫2x +π3+1.
g (x )=0⇒sin ⎝ ⎛
⎭
⎪⎫2x +π3=-12⇒
x=kπ-π
4或x=kπ-
7
12π,k∈Z,
即g(x)的零点相离间隔依次为π
3和
2π
3,
故若y=g(x)在[a,b]上至少含有30个零点,则b-a的最小值为14×2π3+
15×π
3=
43π
3.。
