浙江省余姚市三中2015-2016学年高二上学期期中考试数学试卷(无答案)
浙江省余姚市高风中学2015-2016学年高二上学期期中考试化学试题

余姚市高风中学2015学年第一学期期中试题高二化学试卷总分:100分考试时间:60分钟第Ⅰ卷(选择题,共50分)一、选择题(共13小题,每小题2分,共26分.每小题只有一个选项符合题意)1.下列物质全部属于纯净物的是A.福尔马林、白酒、食醋B.甘油、硬脂酸、乙醇钠C.苯、汽油、无水乙醇D.二氯乙烷、聚氯乙烯、苯酚2.下列化学用语正确的是A.乙烯的结构简式:CH2CH2 B.聚丙烯的结构简式为:C.乙炔、苯和苯乙烯的最简式都为为CH D.四氯化碳分子的电子式为3.化学与人类生活密切相关。
下列说法正确的是A.乙醇和乙酸都是常用调味品的主要成分 B.苯酚有一定毒性,不能用作消毒剂和防腐剂C.能将工业酒精兑水后饮用,因为其中含有甲醇,它具有醇香味D.制作航天服的聚酯纤维和用于光缆通信的光导纤维都是新型无机非金属材料4.下列各对物质中,互为同系物的是A.甲苯和二甲苯 B.C.CH3-CH=CH2与 D.5.一些治感冒的药物含有PPA成分,PPA对感冒有比较好的对症疗效,但也有较大的副作用,我国药监局禁止使用含有PPA成分的感冒药,PPA是盐酸苯丙醇胺(pheng pro panolamine缩写),从其名称看,其有机成分的分子结构中肯定不含下列中的A.-OH B. -COOH C.-C6H5D、-NH26.下列用系统命名法命名的有机物名称正确的是A.2–甲基–4–乙基戊烷B.3, 4, 4–三甲基己烷C.2, 3–二乙基–1–戊烯D. 1, 2, 4–三甲基–1–丁醇7、下列各组中的反应,属于同一反应类型的是A.由溴丙烷水解制丙醇;由丙烯与水反应制丙醇 B.由甲苯硝化制对硝基甲苯;由甲苯氧化制苯甲酸C.由1—氯环己烷消去制环己烯;由丙烯加溴制1,2 二溴丙烷D.由苯甲酸乙酯水解制苯甲酸和乙醇;由乙酸和乙醇制乙酸乙酯8、分子式为C5H12O的某醇与溴化钠、硫酸混合加热得卤代烃,该卤代烃与强碱醇溶液共热后,不能发生消去反应,该醇可能是:A. 2,2-二甲基-1-丙醇B. 2-甲基-2-丁醇C. 1-戊醇D. 3-戊醇9、在核磁共振氢谱中出现三组峰的化合物是10.下列关于蛋白质的说法不正确的是( )A .重金属盐能使蛋白质变性,所以误食重金属盐时,可以喝牛奶解毒B .阿胶的主要成分是蛋白质,蚕丝的主要成份是纤维素C .蛋白质溶液中加入饱和硫酸铵溶液,蛋白质析出,再加水,重新溶解D .浓硝酸溅到皮肤上,会使皮肤呈现黄色11、0.1 mol 阿斯匹林(其学名为乙酰水杨酸,结构简式为 与足量的NaOH 溶液反应,最多消耗NaOH 的物质的量 A .0.1 molB .0.2 molC .0.3 molD .0.4 mol12.在苯和苯酚组成的混合物中,碳元素的质量分数为90% 则混合物中氧元素的质量分数为 A .2.5%B .5%C .6.5%D .7.5%13.下列的叙述中,正确的是A .检验溴乙烷中的溴元素,加入NaOH 溶液共热,冷却后加入AgNO 3溶液,观察有无浅黄色沉淀生成B .苯酚钠溶液中通入少量二氧化碳:2C 6H 5O -+ CO 2 + H 2O 2C 6H 5OH + CO2-3C .苯酚能与FeCl 3溶液反应生成紫色沉淀D .苯酚有强腐蚀性,沾在皮肤上可用酒精清洗二、选择题(共24小题,每小题3分,共24分.每小题只有一个选项符合题意)14.欲从苯酚的乙醇溶液中回收苯酚,有下列操作:①蒸馏;②过滤;③分液;④加入足量的金属钠;⑤通入过量的CO 2;⑥加入足量的NaOH 溶液;⑦加入足量的FeCl 3溶液;⑧加入足量浓溴水;⑨加入适量盐酸。
浙江省宁波市余姚中学2016届高三上学期期中数学试卷(理科) 含解析

2015-2016学年浙江省宁波市余姚中学高三(上)期中数学试卷(理科)一、选择题(本大题共8个小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.)1.下列说法正确的是()A.若命题p,¬q都是真命题,则命题“p∧q”为真命题B.命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0则x≠0或y≠0”C.命题“∀x∈R,2x>0"的否定是“∃x0∈R,2≤0”D.“x=﹣1"是“x2﹣5x﹣6=0"的必要不充分条件2.已知函数f(x)=Asin(ωx+φ)( A≠0,ω>0,)在时取得最大值,且它的最小正周期为π,则()A.f(x)的图象过点(0,)B.f(x)在上是减函数C.f(x)的一个对称中心是D.f(x)的图象的一条对称轴是x=3.已知数列{a n}满足:a n=,且S n=,则n的值为()A.8 B.9 C.10 D.114.若α、β是两个相交平面,则在下列命题中,真命题的序号为()①若直线m⊥α,则在平面β内,一定不存在与直线m平行的直线.②若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直.③若直线m⊂α,则在平面β内,不一定存在与直线m垂直的直线.④若直线m⊂α,则在平面β内,一定存在与直线m垂直的直线.A.①③B.②③C.②④D.①④5.已知函数f(x)=﹣kx2(k∈R)有四个不同的零点,则实数k的取值范围是()A.k<0 B.k<1 C.0<k<1 D.k>16.若直线+=1通过点M(cosα,sinα),则()A.a2+b2≤1 B.a2+b2≥1 C.D.7.已知双曲线与抛物线y2=8x有一个公共的焦点F,且两曲线的一个交点为P,若|PF|=5,则双曲线的离心率为()A.2 B.2C.D.8.设a<0,(3x2+a)(2x+b)≥0在(a,b)上恒成立,则b﹣a的最大值为()A.B.C.D.二、填空题(每题5分,满分35分,将答案填在答题纸上)9.设全集为R,集合M={x∈R|x2﹣4x+3>0},集合N={x∈R|log2x<1},则M∪N=;M∩N=;∁R(M∩N)=.10.已知曲线+=1,当曲线表示圆时k的取值是,当曲线表示焦点在y轴上的椭圆时k的取值范围是,当曲线表示双曲线时k的取值范围是.11.已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.则该几何体的表面积是;体积是.12.已知实数x,y,实数a>1,b>1,且a x=b y=2,(1)若ab=4,则+=;(2)a2+b=8,则+的最大值是.13.已知向量,的夹角60°,||=2,||=2,=λ+μ,若λ+μ=2,则||的最小值是,此时,夹角大小为.14.已知f(x)=x2﹣3x+4,若f(x)的定义域和值域都是[a,b],则a+b=.15.正方体ABCD﹣A1B1C1D1的棱长为1,底面ABCD的对角线BD在平面α内,则正方体在平面α内的影射构成的图形面积的取值范围是.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤。
浙江省余姚市第三中学2015-2016学年高二下学期期中考

第二部分 通用技术(共35分)一、选择题(本大题共10小题,每小题2分,共20分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.如图所示的奶嘴式电子体温计,依据婴儿口腔来设计口含部分的形状与尺寸;含部分材料采用食品级硅胶;部件全部采用圆滑弧线设计;液晶显示屏显示温度以提醒家长注意。
从人机关系的角度分析,以下说法中不合理...的是 A .口含部分尺寸的确定,考虑了静态的人和动态的人 B .体温计采用奶嘴式造型,考虑人的生理需求和心理需求 C .口含部分材料采用食品级硅胶,符合健康的目标 D .液晶显示屏通过显示温度提醒家长注意,体现安全的目标2.如图所示为一款热熔胶枪,可以用于材料涂胶,使用时只用按压扳机,就可从喷嘴挤出熔胶;暂不使用时,还可以打开支架将胶枪斜立放置。
下列对该热熔胶枪的评价中,不是从功能角度进行评价的是 A .通过按压扳机,可轻松挤出熔胶 B .外壳采用隔热、绝缘材料,确保安全 C .设有支架,不用时可有效防止喷嘴与桌面接触D .切换电源开关,实现方便通、断电 3.如图所示为一款活动扶手,扶手与支座之间通过两颗销钉连接。
扶手水平放置时(如图甲),扶手与支座之间连接牢固可靠,扶手前端能承受由上至下的力;翻折扶手时,只需将扶手往前方拉动,再向下翻下(如图乙)。
以下扶手的设计方案中最合理的是A BCD第1题图图甲 图乙扶手支座第3题图喷嘴支架电源开关第2题图4.用厚度为3mm 的扁钢手工加工如图所示的连接件,请问加工左侧的凹槽时,下列工具中不需要...的是 A .台钻 B .样冲 C .圆锉 D .手锯5.以下关于金属材料加工工艺的说法中正确的是 A .锯割之前需要对锉刀表面添加润滑油B .钻孔时应该先将钻头对准钻孔中心,再启动台钻C .钻孔时应将工件夹持在台虎钳上D .锯割时应双手握柄用力推拉6.如图所示是某同学绘制的零件加工图纸,其中漏标的尺寸有A .一处B .两处C .三处D .四处7.在使用指甲剪剪指甲(对C 端施加向下作用力)时,构件AB 与构件AC 的主要受力形式是 A .AB 受拉,AC 受弯曲 B .AB 受拉,AC 受拉 C .AB 受压,AC 受弯曲 D .AB 受压,AC 受压8.如图所示为垃圾处理厂的垃圾处理工艺流程。
浙江省余姚中学高二数学下学期期中试题(无答案)

浙江省余姚中学2015-2016学年高二数学下学期期中试题(无答案)一.选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.集合{}{}2,1,0,1xA y R yB =∈==-,则下列结论正确的是( # )A .{}0,1AB ⋂=B .{}0,A B ⋃=+∞C .()(),0R C A B ⋃=-∞D .(){}1,0R C A B ⋂=-2.已知函数=)(x f 32x ax bx c +++),,(R c b a ∈,则下列结论中错误的是( # ) A.∃0x R ∈,)(0x f =0B.函数)(x f y =的图像是中心对称图形C.若0x 是)(x f 的极小值点,则)(x f 在区间(-∞, 0x )单调递减 D.若0x 是)(x f 的极值点,则 'f (0x )=03.有一段演绎推理是这样的:“有些有理数是真分数,整数是有理数,则整数是真分数”,结论显然是错误的,是因为 ( # )A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误 4.设()f x 为定义在R 上的奇函数,且0x >时,()()12xf x =,则函数()()sin F x f x x =-在[]ππ-,上的零点个数为( # ) A .2B .3C .4D .55.“已知R d c b a ∈,,,,且1=+=+d c b a ,1>+bd ac ,则d c b a ,,,中至少有一个是负数.”用反证法证明此命题的假设应该是( # )A.d c b a ,,,中至多有一个是负数 B.d c b a ,,,都是非负数 C.d c b a ,,,都是负数 D.d c b a ,,,都是正数 6.在平面直角坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0,2).延长CB 交x 轴于点1A ,作第2个正方形111A B C C ;延长11C B 交x 轴于点2A ,作第3个正方形2221A B C C …按这样的规律进行下去,第2016个正方形的面积为( # )A.2015235⎪⎭⎫⎝⎛⨯B.2015495⎪⎭⎫⎝⎛⨯C.2016235⎪⎭⎫⎝⎛⨯D.2016495⎪⎭⎫⎝⎛⨯7.已知函数()y xf x='的图象如右图所示(其中()f x'是函数)(xf的导函数).下面四个图象中,)(xfy=的图象大致是(#)A. B.C.D.8.设函数)(xf的定义域为R,)0(≠xx是)(xf的极大值点,以下结论一定正确的是(#)A.x-是)(xf--的极小值点B.x-是)(xf-的极小值点C.x-是)(xf-的极小值点D.()()0,x R f x f x∀∈≤二.填空题(本大题共7小题,多空题每题6分,单空题每题5分,共36分)9.已知函数()()222, 1,2, 1,x xf xx x⎧--+≤⎪=⎨->⎪⎩则()()3f f=▲,()f x的单调递减区间是▲.10.在等差数列{}n a中,若010=a,则有等式nnaaaaaa-+++=+++192121ΛΛ),19(*Nnn∈<成立.类比上述性质,相应地:在等比数列{}n b中,若19=b,则有等式▲成立.11.若函数21()f x x axx=++在),2(+∞上不单调,则实数a的取值范围是▲.12.设函数221)(+=xxf,则(6)(5)(0)(6)(7)f f f f f-+-+++++=L L▲.(提示:参考课本中等差数列前n项求和公式的推导)-11O xy13.已知函数)(x f 在R 上满足88)2(2)(2-+--=x x x f x f ,则曲线)(x f y =在点())1(,1f 处的切线方程是 ▲ .14.设()g x 是定义在R 上以1为周期的函数,若()()f x x g x =+在区间[0,1]上的值域为[2,5]-,则()f x 在区间[]10,0上的值域为 ▲ .15.若在曲线0),(=y x f 上两个不同点处的切线重合,则称这条切线为曲线0),(=y x f 的“自公切线”.下列方程:①221x y -=;②2||y x x =-,③2||14x y +=-;④3sin 4cos y x x =+对应的曲线中存在“自公切线”的有 ▲ .(写出所有符合条件的序号)三.解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤) 16.(本小题满分14分)函数2()lg(23)f x x x =--的定义域为集合A ,函数()2(2)x g x a x =-≤的值域为集合B .(1)求集合A ,B ;(2)若集合A ,B 满足A B B =I ,求实数a 的取值范围.17.(本小题满分15分)已知()||,=-+∈R f x x x a b x .(1)当1,1a b ==时,若45)(=x f ,求x 的值; (2)若21-=b ,且对任何]1,0(∈x 不等式()0f x <恒成立,求实数a 的取值范围.18.(本小题满分15分)已知{}n b 是等差数列,且11b =,1210100b b b +++=L .(1)求数列{}n b 的通项公式; (2)设数列{}n a 的通项为1lg 1n n a b ⎛⎫=+⎪⎝⎭,记n S 为数列{}n a 的前n 项的和.试比较n S 与11lg 2n b +的大小,并证明你的结论.19.(本小题满分15分)已知函数232211(),()3222a a f x x x g x x ax =-=-+.(1)当函数()y f x =在区间[0,1]上的最小值为13-时,求实数a 的值;(2)若函数()f x 与()g x 的图象有三个不同的交点,求实数a 的取值范围.20.(本小题满分15分)设函数2()ln 2f x x x x =-+.(1)求()f x 的单调区间;(2)若存在区间1[,][,)2a b ⊆+∞,使()f x 在[,]a b 上的值域是[(2),(2)]k a k b ++,求实数k的取值范围.。
浙江省余姚中学2015-2016学年高二上学期开学考试化学试卷.pdf

2015学年 余姚中学高质量检测 第学 期 必考题(70分) 一、选择题(本大题共20小题,每小题2分,共40分) 1.下列物质在生活中应用时,起还原作用的是( )A.明矾作净水剂B.甘油作护肤保湿剂C.漂粉精作消毒剂D.铁粉作食品袋内的脱氧剂 2.下列有关氯元素及其化合物的表示正确的是( )A.质子数为17、中子数为20的氯原子:B.氯离子(Cl-)的结构示意图:C.氯分子的电子式:D.氯乙烯分子的结构简式:H3C-CH2Cl 3.下列说法错误的是( )A. FeO是碱性氧化物B. 用加热法分离泥沙中的碘单质是化学变化C. 丁达尔效应可用于区分胶体和溶液D. Fe2O3 + 3CO 2Fe +3CO2 是复分解反应 4.下列除去杂质(括号的物质为杂质)的方法中,错误的是( ) A.FeCl3溶液(FeCl2):通入适量Cl2 B.CO(CO2):通过NaOH溶液洗气后干燥 C.MnO2(KCl):加水溶解后过滤、洗涤、烘干 D.SO2(HCl):通过饱和Na2CO3溶液洗气后干燥 5.向四支试管中分别加入少量不同的无色溶液进行如下操作,结论正确的是( ) 操作现象结论A滴加BaCl2溶液生成白色沉淀原溶液中有SOB滴加氯水和CCl4,振荡、静置下层溶液显紫色原溶液中有I-C用洁净铂丝蘸取溶液进行焰色反应火焰呈黄色原溶液中有Na+,无K+D滴加稀NaOH溶液,将湿润红色石蕊试纸置于试管口试纸不变蓝原溶液中无NH. 短周期主族元素X、Y、Z、W原子序数依次增大,X原子最外层有6个电子,Y是至今 发现的非金属性 最强的元素,Z在周期表中处于周期序数等于族序数的位置,W的单质广泛用作半导体材料。
下列叙述正确的是( ) A.原子最外层电子数由多到少的顺序:Y、X、W、Z B.原子半径由大到小的顺序:W、Z、Y、X C.元素非金属性由强到弱的顺序:Z、W、X D.简单气态氢化物的稳定性由强到弱的顺序:X、Y、W .下列说法正确的是 ( ) A.H2、D2互为同位素 B.碘晶体、碘蒸气是同素异形体 C.NH4OCN、CO(NH2)2互为同分异构体 D.C2H4与C3H6一定是同系物 .下列有关实验的选项正确的是( ) A.配制0.10mol/L NaOH溶液B.除去CO中的CO2C.苯萃取碘水中的I2分出水层后的操作D.用量筒量取26.00mL的液体.设NA为阿伏加德罗常数的值,下列说法正确的是( ) A.2.0gH218O与D2O的混合物中所含中子数为NA B.常温常压下,4.4g乙醛所含σ键数目为0.7NA C.标准状况下,5.6LCO2与足量Na2O2反应转移的电子数为0.5 NA D.50ml 12mol/L盐酸与足量MnO2共热,转移的电子数为0. 3NA .某同学用下列装置制备并检验Cl2的性质。
浙江省余姚中学2016届高三上学期期中考试理数试题 含解析

一、选择题(本大题共8个小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.)1.下列说法正确的是( )A .若命题p ,q ⌝都是真命题,则命题“p q ∧”为真命题B .命题“若0xy =,则0x =或0y ="的否命题为“若0xy ≠,则0x ≠或0y ≠"C .命题“R x ∀∈,20x>”的否定是“0R x ∃∈,020x ≤"D .“1x =-”是“2560x x --="的必要不充分条件【答案】C .考点:1、命题及其关系;2、充分条件;3、必要条件.2。
已知函数()()sin f x x ωϕ=A +(0A ≠,0ω>,22ππϕ-<<)在23x π=时取得最大值,且它的最小正周期为π,则( )A .()f x 的图象过点10,2⎛⎫ ⎪⎝⎭B .()f x 在2,63ππ⎡⎤⎢⎥⎣⎦上是减函数C .()f x 的一个对称中心是5,012π⎛⎫ ⎪⎝⎭D .()f x 的图象的一条对称轴是512x π=【答案】C .【解析】考点:1、求函数()()sin f x x ωϕ=A +的解析式;2、三角函数的图像及其性质。
3.已知数列{}na 满足:21nan n=+,且1011nS=,则n 的值为( )A .8B .9C .10D .11【答案】C . 【解析】试题分析:因为21111(1)1nan n n n n n ===-+++,所以 11111110(1)()()12231111n S n n n =-+-++-=-=++,所以10n =,故应选C 。
考点:1、裂项求和.4.若α、β是两个相交平面,则在下列命题中,真命题的序号为( ) ①若直线m α⊥,则在平面β内一定不存在与直线m 平行的直线. ②若直线m α⊥,则在平面β内一定存在无数条直线与直线m 垂直. ③若直线m α⊂,则在平面β内不一定存在与直线m 垂直的直线. ④若直线m α⊂,则在平面β内一定存在与直线m 垂直的直线. A .①③ B .②③ C .②④D .①④ 【答案】C .考点:1、直线与平面之间的位置关系。
2015-2016学年浙江省普通高中高二(上)学业水平测试数学试卷及答案

2015-2016学年浙江省普通高中高二(上)学业水平测试数学试卷一、选择题(本大题共18小题,每小题3分,共54分.每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.(3分)函数f(x)=3的定义域为()A.(﹣∞,0)B.[0,+∞)C.[2,+∞)D.(﹣∞,2)2.(3分)下列数列中,构成等比数列的是()A.2,3,4,5 B.1,﹣2,﹣4,8 C.0,1,2,4 D.16,﹣8,4,﹣2 3.(3分)任给△ABC,设角A,B,C所对的边分别为a,b,c,则下列等式成立的是()A.c2=a2+b2+2abcosC B.c2=a2+b2﹣2abcosCC.c2=a2+b2+2absinC D.c2=a2+b2﹣2absinC4.(3分)如图,某简单组合体由一个圆锥和一个圆柱组成,则该组合体三视图的俯视图为()A. B.C.D.5.(3分)要得到余弦曲线y=cosx,只需将正弦曲线y=sinx向左平移()A.个单位B.个单位C.个单位D.个单位6.(3分)在平面直角坐标系中,过点(0,1)且倾斜角为45°的直线不经过()A.第一象限B.第二象限C.第三象限D.第四象限7.(3分)已知平面向量=(1,x),=(y,1).若∥,则实数x,y一定满足()A.xy﹣1=0 B.xy+1=0 C.x﹣y=0 D.x+y=08.(3分)已知{a n}(n∈N*)是以1为首项,2为公差的等差数列.设S n是{a n}的前n项和,且S n=25,则n=()A.3 B.4 C.5 D.69.(3分)设抛物线y2=2px(p>0)的焦点为F.若F到直线y=x的距离为,则p=()A.2 B.4 C.2 D.410.(3分)在空间直角坐标系Oxyz中,若y轴上点M到两点P(1,0,2),Q (1,﹣3,1)的距离相等,则点M的坐标为()A.(0,1,0)B.(0,﹣1,0)C.(0,0,3)D.(0,0,﹣3)11.(3分)若实数x,y满足,则y的最大值为()A.B.1 C.D.12.(3分)设a>0,且a≠1,则“a>1”是“log a<1”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件13.(3分)如图,在正方体ABCD﹣A1B1C1D1中,M为棱D1C1的中点.设AM与平面BB1D1D的交点为O,则()A.三点D1,O,B共线,且OB=2OD1B.三点D1,O,B不共线,且OB=2OD1C.三点D1,O,B共线,且OB=OD1D.三点D1,O,B不共线,且OB=OD114.(3分)设正实数a,b满足a+λb=2(其中λ为正常数).若ab的最大值为3,则λ=()A.3 B.C.D.15.(3分)在空间中,设l,m为两条不同直线,α,β为两个不同的平面,则下列命题正确的是()A.若l⊂α,m不平行于l,则m不平行于αB.若l⊂α,m⊂β,且α,β不平行,则l,m不平行C.若l⊂α,m不垂直于l,则m不垂直于αD.若l⊂α,m⊂β,l不垂直于m,则α,β不垂直16.(3分)设a,b,c∈R,下列命题正确的是()A.若|a|<|b|,则|a+c|<|b+c|B.若|a|<|b|,则|a﹣c|<|b﹣c|C.若|a|<|b﹣c|,则|a|<|b|﹣|c|D.若|a|<|b﹣c|,则|a|﹣|c|<|b| 17.(3分)已知F1,F2分别是双曲线﹣=1(a,b>0)的左、右焦点,l1,l2为双曲线的两条渐近线.设过点M(b,0)且平行于l1的直线交l2于点P.若PF1⊥PF2,则该双曲线的离心率为()A.B.C.D.18.(3分)如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是()A.(,) B.(,]C.(,]D.(,)二、填空题(本大题共4小题,每空3分,共15分)19.(6分)设,为平面向量.若=(1,0),=(3,4),则||=,•=.20.(3分)设全集U={2,3,4},集合A={2,3},则A的补集∁U A=.21.(3分)在数列{a n}(n∈N*)中,设a1=a2=1,a3=2.若数列{}是等差数列,则a6=.22.(3分)已知函数f(x)=,g(x)=ax+1,其中a>0.若f(x)与g(x)的图象有两个不同的交点,则a的取值范围是.三、解答题(本大题共3小题,共31分)23.(10分)已知函数f(x)=2sinxcosx,x∈R.(Ⅰ)求f()的值;(Ⅱ)求函数f(x)的最小正周期;(Ⅲ)求函数g(x)=f(x)+f(x+)的最大值.24.(10分)设F1,F2分别是椭圆C:+y2=1的左、右焦点,过F1且斜率不为零的动直线l与椭圆C交于A,B两点.(Ⅰ)求△AF1F2的周长;(Ⅱ)若存在直线l,使得直线F2A,AB,F2B与直线x=﹣分别交于P,Q,R 三个不同的点,且满足P,Q,R到x轴的距离依次成等比数列,求该直线l的方程.25.(11分)已知函数f(x)=ax++,a∈R.(Ⅰ)判断函数f(x)的奇偶性,并说明理由;(Ⅱ)当a<2时,证明:函数f(x)在(0,1)上单调递减;(Ⅲ)若对任意的x∈(0,1)∪(1,+∞),不等式(x﹣1)[f(x)﹣]≥0恒成立,求a的取值范围.2015-2016学年浙江省普通高中高二(上)学业水平测试数学试卷参考答案与试题解析一、选择题(本大题共18小题,每小题3分,共54分.每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.(3分)函数f(x)=3的定义域为()A.(﹣∞,0)B.[0,+∞)C.[2,+∞)D.(﹣∞,2)【解答】解:要使函数f(x)=3有意义,可得x﹣2≥0,解得x≥2.函数的定义域为:[2,+∞).故选:C.2.(3分)下列数列中,构成等比数列的是()A.2,3,4,5 B.1,﹣2,﹣4,8 C.0,1,2,4 D.16,﹣8,4,﹣2【解答】解:由等比数列的定义以及性质可知,A,B,C都不是等比数列.故选:D.3.(3分)任给△ABC,设角A,B,C所对的边分别为a,b,c,则下列等式成立的是()A.c2=a2+b2+2abcosC B.c2=a2+b2﹣2abcosCC.c2=a2+b2+2absinC D.c2=a2+b2﹣2absinC【解答】解:式子c2=a2+b2﹣2abcosC符合余弦定理,正确;故选:B.4.(3分)如图,某简单组合体由一个圆锥和一个圆柱组成,则该组合体三视图的俯视图为()A. B.C.D.【解答】解:简单组合体由一个圆锥和一个圆柱组成,左侧是圆锥,右侧是圆柱,俯视图为:三角形与矩形组成,故选:D.5.(3分)要得到余弦曲线y=cosx,只需将正弦曲线y=sinx向左平移()A.个单位B.个单位C.个单位D.个单位【解答】解:∵cosx=sin(x﹣)∴余弦函数y=cosx的图象可看作正弦y=sinx图象向左平移个单位得到.故选:A6.(3分)在平面直角坐标系中,过点(0,1)且倾斜角为45°的直线不经过()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:过点(0,1)且倾斜角为45°的直线为y﹣1=x,即x﹣y+1=0,当x=0时,y=1,当y=0时,x=﹣1,所以直线x﹣y+1=0过第一,二,三象限,不过第四象限,故选:D.7.(3分)已知平面向量=(1,x),=(y,1).若∥,则实数x,y一定满足()A.xy﹣1=0 B.xy+1=0 C.x﹣y=0 D.x+y=0【解答】解:平面向量=(1,x),=(y,1).若∥,则xy=1.即xy﹣1=0.故选:A.8.(3分)已知{a n}(n∈N*)是以1为首项,2为公差的等差数列.设S n是{a n}的前n项和,且S n=25,则n=()A.3 B.4 C.5 D.6【解答】解:S n=25=n+,化为n2=25,解得n=5.故选:C.9.(3分)设抛物线y2=2px(p>0)的焦点为F.若F到直线y=x的距离为,则p=()A.2 B.4 C.2 D.4【解答】解:抛物线y2=2px(p>0)的焦点为F(,0).F到直线y=x的距离为,可得:=,解得p=4.故选:B.10.(3分)在空间直角坐标系Oxyz中,若y轴上点M到两点P(1,0,2),Q (1,﹣3,1)的距离相等,则点M的坐标为()A.(0,1,0)B.(0,﹣1,0)C.(0,0,3)D.(0,0,﹣3)【解答】解:根据题意,设点M(0,y,0),∵|MP|=|MQ|,∴=,即y2+5=y2+6y+11,∴y=﹣1,∴点M(0,﹣1,0).故选:B.11.(3分)若实数x,y满足,则y的最大值为()A.B.1 C.D.【解答】解:做出直线y=x,y=x与圆(x﹣1)2+y2=1的图象,得出不等式组对应的可行域,如图阴影部分所示,根据题意得:y的最大值为1,故选:B.12.(3分)设a>0,且a≠1,则“a>1”是“log a<1”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解答】解:∵log a<1=log a a,当a>1时,函数是一个增函数,不等式成立,当0<a<1时,函数是一个减函数,根据函数的单调性有a<,综上可知a的取值是(0,)∪(1,+∞),故“a>1”是“log a<1”的充分不必要条件,故选:A.13.(3分)如图,在正方体ABCD﹣A1B1C1D1中,M为棱D1C1的中点.设AM与平面BB1D1D的交点为O,则()A.三点D1,O,B共线,且OB=2OD1B.三点D1,O,B不共线,且OB=2OD1C.三点D1,O,B共线,且OB=OD1D.三点D1,O,B不共线,且OB=OD1【解答】解:【解法一】如图1,连接AD1,BC1,利用公理2可直接证得,并且由D1M∥AB且D1M=AB,∴OD1=BO,∴D1,O,B三点共线,且OB=2OD1.【解法二】以正方体ABCD﹣A1B1C1D1的顶点D为坐标原点,DA所在的直线为x 轴,DC所在的直线为y轴,DD1所在的直线为z轴建立空间直角坐标系,如图所示,设正方体的棱长为1,则A(1,0,0),B(1,1,0),D1(0,0,1),M(0,,1);设点O(x,x,z),∴=(x﹣1,x,z),=(﹣1,,1);又与共线,∴=λ,∴(x﹣1,x,z)=(﹣λ,λ,λ),即,解得,∴点O(,,);∴=(﹣,﹣,),又=(﹣1,﹣1,1),∴=,∴D1,O,B三点共线,且OB=2OD1.故选:A.14.(3分)设正实数a,b满足a+λb=2(其中λ为正常数).若ab的最大值为3,则λ=()A.3 B.C.D.【解答】解:设正实数a,b满足a+λb=2(其中λ为正常数)若ab的最大值为3,则2≤2,当ab=3时:=1,解得:λ=,故选:D.15.(3分)在空间中,设l,m为两条不同直线,α,β为两个不同的平面,则下列命题正确的是()A.若l⊂α,m不平行于l,则m不平行于αB.若l⊂α,m⊂β,且α,β不平行,则l,m不平行C.若l⊂α,m不垂直于l,则m不垂直于αD.若l⊂α,m⊂β,l不垂直于m,则α,β不垂直【解答】解:若l⊂α,m不平行于l,则m⊂α,m平行于α,m与α相交都有可能,故不正确;若l⊂α,m⊂β,且α,β不平行,则l,m可以与交线平行,故不正确;若l⊂α,m不垂直于l,则m不垂直于α,利用反证法可得正确;若l⊂α,m⊂β,l不垂直于m,α,β垂直时也成立,故不正确.故选:C.16.(3分)设a,b,c∈R,下列命题正确的是()A.若|a|<|b|,则|a+c|<|b+c|B.若|a|<|b|,则|a﹣c|<|b﹣c|C.若|a|<|b﹣c|,则|a|<|b|﹣|c|D.若|a|<|b﹣c|,则|a|﹣|c|<|b|【解答】解:根据不等式的基本性质,对各选项考察如下:对于A选项:若|a|<|b|,不一定有|a+c|<|b+c|成立,如a=﹣2,b=3,c=﹣1,此时|a+c|>|b+c|,故A不正确;对于B选项:若|a|<|b|,不一定有|a﹣c|<|b﹣c|成立,如a=﹣2,b=3,c=1,此时|a﹣c|>|b﹣c|,故B不正确;对于C选项:若|a|<|b﹣c|,不一定有|a|<|b|﹣|c|,如a=2,b=2,c=﹣3,此时|a|>|b|﹣|c|,故C不正确;对于D选项:若|a|<|b﹣c|,则必有|a|﹣|c|<|b|成立,因为,|a|<|b﹣c|≤|b|+|c|,所以,|a|﹣|c|<|b|,故D正确.故答案为:D.17.(3分)已知F1,F2分别是双曲线﹣=1(a,b>0)的左、右焦点,l1,l2为双曲线的两条渐近线.设过点M(b,0)且平行于l1的直线交l2于点P.若PF1⊥PF2,则该双曲线的离心率为()A.B.C.D.【解答】解:根据题意可得F1(﹣c,0)、F2(c,0),双曲线的渐近线为:y=x,直线PM的方程为:y=﹣(x﹣b),联立,可得x=,∴P(,)∴=(+c,),=(﹣c,)∵PF1⊥PF2,∴•=0,∴(+c,)•(﹣c,)=0∴=0∴b2=4a2,∴c2=5a2,∴e==,故选:B.18.(3分)如图,在菱形ABCD中,∠BAD=60°,线段AD,BD的中点分别为E,F.现将△ABD沿对角线BD翻折,则异面直线BE与CF所成角的取值范围是()A.(,) B.(,]C.(,]D.(,)【解答】解:可设菱形的边长为1,则BE=CF=,BD=1;线段AD,BD的中点分别为E,F;∴,=;∴===;∴=;由图看出;∴;∴;即异面直线BE与CF所成角的取值范围是.故选:C.二、填空题(本大题共4小题,每空3分,共15分)19.(6分)设,为平面向量.若=(1,0),=(3,4),则||=1,•= 3.【解答】解:||==1,•=1×3+0×4=3.故答案1,3.20.(3分)设全集U={2,3,4},集合A={2,3},则A的补集∁U A={4} .【解答】解:∵全集U={2,3,4},集合A={2,3},∴∁U A={4},故答案为:{4}21.(3分)在数列{a n}(n∈N*)中,设a1=a2=1,a3=2.若数列{}是等差数列,则a6=120.【解答】解:∵数列{}是等差数列,∴公差d=.则.则,….累积得:,∴a6=120.故答案为:120.22.(3分)已知函数f(x)=,g(x)=ax+1,其中a>0.若f(x)与g(x)的图象有两个不同的交点,则a的取值范围是(0,1).【解答】解:f(x)=,(1)若a<0,作出f(x)和g(x)的图象如图,显然f(x)与g(x)只有一个交点.(2)若a=0,作出f(x)和g(x)的图象如图,显然f(x)与g(x)只有一个交点.(3)若a>1,作出f(x)和g(x)的图象如图,显然f(x)与g(x)只有一个交点.(4)若0<a<1,作出f(x)和g(x)的图象如图,显然f(x)与g(x)有两个交点.(5)若a=1,作出f(x)和g(x)的图象如图,显然f(x)与g(x)只有一个交点.综上,a的取值范围是(0,1).故答案为(0,1).三、解答题(本大题共3小题,共31分)23.(10分)已知函数f(x)=2sinxcosx,x∈R.(Ⅰ)求f()的值;(Ⅱ)求函数f(x)的最小正周期;(Ⅲ)求函数g(x)=f(x)+f(x+)的最大值.【解答】解:(Ⅰ)由题意得f()=2sin cos=1,(Ⅱ)∵f(x)=sin2x,∴函数f(x)的最小正周期为T==π,(Ⅲ)∵g(x)=sin2x+sin(2x+)=sin2x+cos2x=sin(2x+),∴当x=k,k∈Z时,函数g(x)的最大值为.24.(10分)设F1,F2分别是椭圆C:+y2=1的左、右焦点,过F1且斜率不为零的动直线l与椭圆C交于A,B两点.(Ⅰ)求△AF1F2的周长;(Ⅱ)若存在直线l,使得直线F2A,AB,F2B与直线x=﹣分别交于P,Q,R 三个不同的点,且满足P,Q,R到x轴的距离依次成等比数列,求该直线l的方程.【解答】解:(Ⅰ)因为椭圆的长轴长2a=2,焦距2c=2.又由椭圆的定义得|AF1|+|AF2|=2a所以△AF1F2的周长为|AF1|+|AF2|+|F1F2|=2+2(Ⅱ)由题意得l不垂直两坐标轴,故设l的方程为y=k(x+1)(k≠0)于是直线l与直线x=﹣交点Q的纵坐标为y Q=设A(x1,y1),B(x2,y2),显然x1,x2≠1,所以直线F2A的方程为y=(x﹣1)故直线F2A与直线x=﹣交点P的纵坐标为y P=同理,点R的纵坐标为y R=因为P,Q,R到x轴的距离依次成等比数列,所以|y P|•|y R|=|y Q|2即|×|=整理得9|x1x2+(x1+x2)+1|=|x1x2﹣(x1+x2)+1|.(*)联立y=k(x+1)与椭圆方程,消去y得(1+2k2)x2+4k2x+2k2﹣2=0所以x1+x2=,x1x2=代入(*)化简得|8k2﹣1|=9解得k=±经检验,直线l的方程为y═±(x+1).25.(11分)已知函数f(x)=ax++,a∈R.(Ⅰ)判断函数f(x)的奇偶性,并说明理由;(Ⅱ)当a<2时,证明:函数f(x)在(0,1)上单调递减;(Ⅲ)若对任意的x∈(0,1)∪(1,+∞),不等式(x﹣1)[f(x)﹣]≥0恒成立,求a的取值范围.【解答】(Ⅰ)解:∵f(﹣x)=﹣ax=﹣(ax++)=﹣f(x),又∵f(x)的定义域为{x∈R|x≠﹣1且x≠1},∴函数f(x)为奇函数;(Ⅱ)证明:任取x1,x2∈(0,1),设x1<x2,则f(x1)﹣f(x2)=a(x1﹣x2)+==.∵0<x1<x2<1,∴2(x1x2+1)>2,0<(x12﹣1)(x22﹣1)<1,∴>2>a,∴a﹣<0.又∵x1﹣x2<0,∴f(x1)>f(x2).∴函数f(x)在(0,1)上单调递减;(Ⅲ)解:∵(x﹣1)[f(x)﹣]=(x﹣1)[ax]==.∴不等式(x﹣1)[f(x)﹣]≥0恒成立化为不等式ax2(x2﹣1)+2≥0对任意的x∈(0,1)∪(1,+∞)恒成立.令函数g(t)=at2﹣at+2,其中t=x2,t>0且t≠1.①当a<0时,抛物线y=g(t)开口向下,不合题意;②当a=0时,g(t)=2>0恒成立,∴a=0符合题意;③当a>0时,∵g(t)=a(t﹣)2﹣+2.∴只需﹣+2≥0,即0<a≤8.综上,a的取值范围是0≤a≤8.。
浙江省余姚市高二数学上学期期中试题 理(无答案) 新人教A版
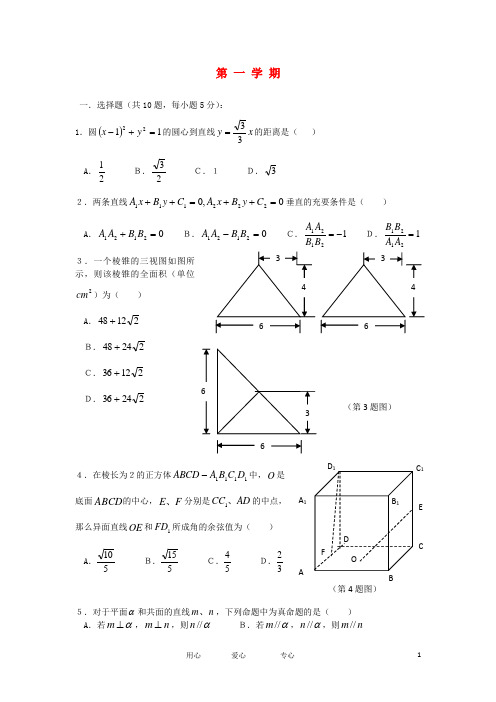
用心 爱心 专心1第 一 学 期一.选择题(共10题,每小题5分):1.圆()1122=+-y x 的圆心到直线x y 33=的距离是( ) A .21B.23 C.1 D.32.两条直线0,0222111=++=++C y B x A C y B x A 垂直的充要条件是( ) A .02121=+B B A A B.02121=-B B A A C.121-=A AD.121=BB 3.一个棱锥的三视图如图所示,则该棱锥的全面积(单位2cm )为( )A .21248+B.22448+ C.21236+ D.22436+4.在棱长为2的正方体1111D C B A ABCD -中,O 是底面ABCD 的中心,F E 、分别是AD CC 、1的中点,那么异面直线OE 和1FD 所成角的余弦值为( )A .510 B.515 C.54 D.325.对于平面α和共面的直线n m 、,下列命题中为真命题的是( ) A .若α⊥m ,n m ⊥,则α//n B.若α//m ,α//n ,则n m //(第3题图)6666ABCDA 1B 1C 1D 1OFE(第4题图)用心 爱心 专心 2C.若α⊂m ,α//n ,则n m // D.若n m 、与α所成角相等,则n m // 6.平面内到两定点的距离之比为1:2的动点的轨迹是( ) A .线段 B.直线 C.圆 D.椭圆7.已知直线l 方程为()0,=y x f ,点),(111y x P 、),(222y x P 分别在l 上和l 外,则方程()()()0,,,2211=--y x f y x f y x f 表示( )A .过点1P 且与l 垂直的直线 B.与l 重合的直线 C.过点2P 且与l 平行的直线 D.不过点2P ,但与l 平行的直线 8.多面体ABCDEF 中,已知面ABCD 是边长为3的正方形,AB EF //,23=EF ,EF 与面AC 的距离为2,则该多面体的体积为( )A .29 B.5 C.6 D.2159.若直线1=+by a x 与圆122=+y x 有公共点,则( )A .122≤+b a B.122≥+b a C.11122≤+b a D.11122≥+b a10.给出命题:①设l 、m 位直线,α为平面,若直线m l //,且α⊂m ,则α//l ; ②若一个角的两边分别平行于另一个角的两边,则这两个角相等或互补; ③设n m 、是一对异面直线,则存在平面α,使α⊂m 且α//n ; ④若一个二面角的两个面分别垂直于另一个二面角的两个面,则这两个二面角的平面角相等或互补.上述命题中真命题的个数为( ) A .1 B.2 C.3 D.4 二.填空题(共7题,每小题4分):11.已知1F 、2F 为椭圆192522=+y x 的两个焦点,过1F 的直线交椭圆于B A 、两点,若1222=+B F A F ,则=AB _________.12.正方体1111D C B A ABCD -中,直线B A 1与平面CD B A 11所成的角为_________. 13.已知集合{}0103|2≤--=x x x A ,{}121|-≤≤+=m x m x B ,若B 是A 的充分条件,则m 的取值范围是_________.14.已知球O 的面上四点D C B A 、、、,⊥DA 平面ABC ,ABCD(第14题图)ABCDE F(第8题图)用心 爱心 专心 3BC AB ⊥,3===BC AB DA ,则球O 的体积为_________.15.直线b x y +=与曲线21y x -=有且仅有一个公共点,则b 的取值范围是_________. 16.正三棱柱111C B A ABC -中,底面边长和侧棱长都为2,过底面上一边AB 作平面α,使α与底面ABC 成︒60的二面角,则正三棱柱被平面α截得的截面面积为_________. 17.过点()3,2P 作圆122=+y x 的两条切线PB PA 、,B A 、为切点,则直线AB 的方程为_________.三.解答题(共5大题,共72分):18.(14分)在△ABC 中,已知()2,5-A ,()3,7B ,且AC 边的中点M 在y 轴上,BC 边的中点N 在x 轴上.求: (1)顶点C 的坐标; (2)直线MN 的方程.19.(14分)已知0>c ,设P :函数xc y =在R 上单调递减;Q :不等式12>-+c x x 的解集为R .若P 和Q 有且仅有一个正确,求c 的取值范围.20.(14分)某几何体的一棱长为7,它在正视图中的射影长为6,它在侧视图、俯视图中的投影分别为a 、b .联想长方体…… (1)求22b a +的值;(2)求b a +的最大值. 21.(15分)在四棱锥ABCD P -中,△PBC 为正三角形,⊥AB 平面PBC ,CD AB //,DC AB 21=,BC DC 3=,E 为PD 中点.(1)求证:直线//AE 平面PBC ;(2)求证:平面⊥APD 平面PDC ;(3)求平面PAD 与平面PBC 所成锐二面角的大小. 22.(15分)设二次函数()m x x x f ++=22的图象与两坐标轴有三个交点,经过这三个交点的圆记为C . (1)求实数m 的取值范围;(2)求圆C 的方程.问圆C 是否经过定点?若有,求出定点的坐标,并证明你的结论.A DB CEP(第21题图)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
余姚三中2015学年第一学期高二期中数学测试卷
一.选择题:每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的。
1.直线10x +=的倾斜角是( )
A.00
B.090
C.045
D.不存在
2.若直线x y a 3++=0过圆x y x y 22
++2-4=0的圆心,则a 的值为( ) A .-1 B.1 C. 3 D.-3 3.如果0,0AC BC <<,那么直线0Ax By C ++=不通过( )
A .第一象限
B .第二象限
C .第三象限
D .第四象限 4.已知正方体1111D C B A ABCD -中,F
E ,分别为棱BC 和 棱1CC 的中点,则异面直线AC 和E
F 所成的角为( ) A. 030 B. 045 C. 060 D. 090 5.在空间,下列命题正确的是 ( )
A .平行于同一平面的两条直线平行
B .平行于同一直线的两个平面平行
C .垂直于同一平面的两个平面平行
D .垂直于同一平面的两条直线平行 6.直线x-y+3=0被圆()2
2x+2(2)2y +-=截得的弦长等于 ( ) A .
2
6 B .3 C .23 D .6
7. 若实数y x ,满足不等式组330,230,10,x y x y x y +-≥⎧⎪
--≤⎨⎪-+≥⎩
则y x +的最大值为 ( )
A.9
B.
15
7
C.1
D.
715
8.过点()4,2-且在两坐标轴上截距相等的直线有 ( ) A.1条 B.2条 C.3条 D.4条
9.若直线10ax by ++=与圆2
2
1x y +=相离,则点(,)P a b 的位置是 ( ) A.在圆上
B.在圆外
C.在圆内
D.以上都有可能
10.已知圆C 的方程是0104422
=---+y x y x ,直线l :x y -=,则圆C 上有几个点到直线l 的距离为 22 ( )
A.1 个
B. 2个
C.3个
D.4个 二.填空题:本大题共7小题,每小题4分,共28分。
11.
0y m -+=与圆22220x y x +--=相切,则实数m 等于____________
12.圆2220x y +=的弦AB 的中点为(2,3)P -,则弦AB 所在直线的方程是 13.若点(,3)P m 到直线4310x y -+=的距离为4,且点P 在不等式230x y +-<表示的平面区域内,则实数m 的值为_______________
14.若直线21:60l x a y ++=与直线2:(2)320l a x ay a -++=平行,则实数a 的值为______
15.过点(1,1)P 的直线与圆22
(2)(3)9x y -+-=相交于,A B 两点,则AB 的最小值为
________
16.已知线段PQ 两端点的坐标分别为)1,1(-P 和)2,2(Q ,若直线0:=-+m y mx l 与线段
PQ 有交点,则实数m 的取值范围是______________
17.设n m ,是两条不重合的直线,γβα,,是三个两两不重合的平面,给出下列四个命题: ① βαγβγα//,,则若⊥⊥ ② βαβα//,,则若⊥⊥m m
③ βααββα//,//,,//,则是异面直线,、若n n m m n m ⊂⊂
④ βαβα//,//,,则若n m n m ⊂
⊂.其中正确的命题的序号是 .
三.解答题:本大题共5小题,共72分。
解答应写出文字说明、证明过程或演算步骤。
18. (本题满分12分)已知直线l 的倾斜角为0135,且经过点)1,1(P (1)求直线l 的方程;
(2)求点)4,3(A 关于直线l 的对称点B 的坐标.
19. (本题满分15分)如图,在直三棱柱111ABC A B C -中,1AB BB =,1AC ⊥平面1A BD ,
D 为的AC 中点.
(1)求证:1B C //平面1A BD ;
(2)求证:11B C ⊥平面11ABB A ;
(3)设E 是1CC 上一点,试确定E 的位置,使平面1A BD ⊥平面BDE ,并说明理由.
20. (本题满分15分)如图,已知BCD ∆中,90BCD ∠=︒,AB ⊥平面BCD ,1,BC CD ==
AB E F =、分别为AC AD 、的中点.
(1)求证:平面BEF ⊥平面ABC ;
(2)求直线AD 与平面BEF 所成角的正弦值.
21. (本题满分15分)已知平面区域0
240x y x y ≥⎧⎪≥⎨⎪+-≤⎩
A
C
B
1A
1C
D
1B
恰好被面积最小的圆222
:()()C x a y b r -+-=及其内部所覆盖. (1)作出该不等式组所确定的平面区域试,并求圆C 的方程.
(2)若斜率为1的直线l 与圆C 交于不同两点,.A B 满足CA CB ⊥,求直线l 的方程.
22. (本题满分15分)已知圆C :224
20(,0)x y tx y t R t t
+--=∈≠与x 轴交于点O 、A ,与y 轴交于点O 、B ,其中O 为原点. (1)求证:OAB ∆的面积为定值;
(2)设直线42+-=x y 与圆C 交于点M 、N ,若OM ON =,求圆C 的方程.。
