人教版高中数学必修二直线的点斜式方程 (1)ppt模板
合集下载
人教A版高二数学必修二第三章3.2.1 直线的点斜式方程(共23张ppt)

y=-x+3的斜率为-1,在y轴上的截距为3.
思考8
若直线l的斜率为k,在x轴上的截距为
a,则直线l的方程是什么?
解:y=k(x-a)
例2 已知直线l1:y=k1x b1,l2:y=k 2x+b 2,试讨论: (1)l1 //l2的条件是什么?(2)l1 l2的条件是什么?
分析:回忆用斜率判断两条直线平行、垂直的结论.思考 (1)l1 //l2时,k1,k2,b1,b2 有何关系? (2)l1 ⊥l2时,k1,k2,b1,b2 有何关系?
1.直线方程可表示成点斜式方程的条件是
( A )
A.直线的斜率存在
B.直线的斜率不存在
C.直线不过原点
D.不同于上述选项
2.经过点 且倾斜角是30°的直线的方程是 ( 2, 2) ( C )
A. y 2
3 ( x 2) 3
B. y 2 3( x 2)
D. y 2 3( x 2)
y - y0 当x≠x0时,则k = ,即P(x,y)在过点P(x 0 0 ,y0 ), x - x0 斜率为k的直线l上.
直线的点斜式方程 由直线上一定点和直线的斜率确定的直线 方程,叫直线的点斜式方程.
过点P(x 斜率为k的直线l的方程为: 0 0 ,y0 ),
y y0 k ( x x0).
成立的条件:直线的斜率存在.
y
l
P0 (x0 , y 0 )
O
x
思考3
已知直线l经过已知点P0(x0,y0),且它
的斜率不存在,直线l的方程是什么? y
l
P 0 ( x0 , y0 )
x x0 0或x x0
O
x
2.2.1直线的点斜式方程(教学课件(人教版))

(1) : =
(2) : =
, :
+ , : =
=
− .
− ;
平行
垂直
练习5 直线y=kx-3k+2(k∈R)必过定点(
A.(3,2)
B.(-3,2)
C.(-3,-2)
A )
D.(3,-2)
练习6 若直线l过点P(2,1),且与直线y-1=2x-3垂直,则直
(1) l1 / / l2的条件是什么?
(2)l1 l2的条件是什么?
(1) 若l1 // l2 , 则k1 k2 , 此时, l1 , l2与y轴的交点不同, 即b1 b2 ;
反之, 若k1 k2 , 且b1 b2 , 则l1 // l2 .
(2) 若l1 l2 , 则k1k2 1;
已知直线 l 经过点(x0, y0),
(1)当直线 l 的倾斜角为0°时,直线 l 的方程是什么?
(2)当直线 l 的倾斜角为90°时,直线 l 的方程如何表示?
y
当倾斜角为0°时,k=0,代入点斜式
P(x,y)
l
P0(x0,y0)
O
x
已知直线 l 经过点(x0, y0),
(1)当直线 l 的倾斜角为0°时,直线l的方程是什么?
我们已经学习了直线的点斜式方程的表示,那么若
直线经过点P0(0,b),斜率为k,此时直线方程如何表示?
将点P0(0,b)和斜率k代入点斜式方程,得 y-b=k(x-0) 即 y=kx+b
我们把直线l与y 轴的交点(0,b)的纵坐标 b 叫做直线l
在y轴上的截距,这样,方程y=kx+b由直线的斜率k与它
高中数学《直线的点斜式方程》课件(共16张PPT)

直线的点斜式、斜截式方程
1.直线的点斜式方程和斜截式方程
名称
点斜式
斜截式
已知条件 点 P(x0,y0)和斜率 k 斜率 k 和直线在 y 轴上的截距 b
图示
方程 ___y-___y0_=__k_(_x_-__x_0_) __
_y_=__k_x_+__b____
适用范围
斜率存在
2.直线 l 在 y 轴上的截距 定义:直线 l 与 y 轴交点(0,b)的__纵__坐__标__b__叫作直线 l 在 y 轴上的截距. [化解疑难] 解读直线的点斜式方程 直线的点斜式方程的前提条件是:(1)已知一点 P(x0,y0)和斜率 k;(2)斜率 必须存在.只有这两个条件都具备,才可以写出点斜式方程.
二、特点
斜率:直线的斜率是直线在某一点上的变化率,反映了直线在该点上的陡峭程度。斜率越大, 直线越陡峭;斜率越小,直线越平缓。
截距:直线的截距是直线与y轴的交点坐标,反映了直线在y轴上的位置。截距越大,直线离y 轴越远;截距越小,直线离y轴越近。
方程的适用范围:直线的点斜式方程适用于已知一点和斜率的直线,不适用于斜率不存在的直 线。
1.过点 P(-2,0),斜率是 3 的直线的方程是( )
A.y=3x-2
B.y=3x+2
C.y=3(x-2)
D.y=3(x+2)
答案: D
自主练习
2.直线方程为 y+2=2x-2,则( )
自主练习
A.直线过点(2,-2),斜率为 2
B.直线过点(-2,2),斜率为 2
C.直线过点(1,-2),斜率为12
精准例题
直线的点斜式方程 课后总结 直线的点斜式方程是描述直线的一种重要方式,它表达了直线在某一点上的斜率和截距,是解
3.2.1 直线的点斜式方程(共26张PPT)

栏目 导引
第三章
直线与方程
跟踪训练
1.写出下列直线的方程
(1)经过点A(2,5),斜率是4; (2)经过点B(2,3),倾斜角是45°;
(3)经过点C(-1,1),与x轴平行;
(4)经过点D(1,1),与x轴垂直. 解:(1)y-5=4(x-2); (2)k=tan 45°=1,所以y-3=x-2; (3)y=1; (4)x=1.
栏目 导引
第三章
直线与方程
(3)∵直线的倾斜角为 60° , ∴其斜率 k=tan 60° = 3. ∵直线与 y 轴的交点到原点的距离为 3, ∴直线在 y 轴上的截距 b= 3 或 b=- 3. ∴所求直线方程为 y= 3x+ 3 或 y= 3x- 3.
【名师点评】 利用斜截式写直线方程时, 首先要考虑斜率 是否存在,其次要注意截距与距离的区别与联系.
栏目 导引
第三章
直线与方程
题型四
例4
直线在平面直角坐标系中位置的确定
)
1 方程 y= ax+ 表示的直线可能是 ( a
栏目 导引
第三章
直线与方程
1 1 【解析】 直线 y= ax+ 的斜率是 a, 在 y 轴上的截距是 , a a 1 当 a>0 时,斜率 a>0,在 y 轴上的截距是 >0,则直线 y= a 1 ax+ 过第一、 二、 三象限, 四个选项都不符合; 当 a<0 时, a 1 1 斜率 a<0, 在 y 轴上的截距是 <0, 则直线 y= ax+ 过第二、 a a 三、四象限,仅有选项 B 符合.
第三章
直线与方程
3.2
直线的方程
3.2.1 直线的点斜式方程
第三章
直线与方程
人教版高中数学必修二3.2.1直线的点斜式方程ppt模板

解:这条直线经过点P1(-2,3), 斜率是 k=tan450=1 代入点斜式得 y-3 = x + 2
画图时, 再找出直线l上另一点, 例如p1 ( 1,4) 过p1 , p0的直线即为所求,
y P1
° -5
°
O
°5
x
练习
1、写出下列直线的点斜式方程:
(1)经过A(3,1), 斜率是 2 (2)经过B( 2 ,2),倾斜角是 30
思考2: 下列直线:y=-2x+1,y=x-4,y=3x,y=-3在y轴上的截 距分别是什么?
思考3: 如何求直线y-y0=k(x-x0)在x轴、y轴上的截距?
斜截式方程的应用:
例2:斜率是5,在y轴上的截距是4的直线方程。
解:由已知得k =5, b= 4, 代入斜截式方程 y= 5x + 4
练习
P0(x0,y0) x
y y0 k x x0
y y0 k ( x x0 )
点斜式
(1)直线上任意一点的坐标是方程的解(满足方程) (2)方程的任意一个解是直线上点的坐标
思考:
方程k=
y-y1 与 y-y1=k(x-x1) 有何不同? x-x1
思考6:经过点P0(x0,y0)的任意一条直线的方程都能
一个关于x,y的方程,化为整式即为 y y0 k ( x ,x 那么直线 l上每一点的坐标都满 0) 足这个方程吗?
y y0 k ( x x0 ) 的所有点P(x,y)是否都在直线l上? 为什么?
思考5:满足方程
点斜式方程
y
a
设直线任意一点(P0除外)的坐标为
P(x,y)。
例题分析:
例3 已知直线l1 : y k1 x b1 , l2 : y k 2 x b2 试讨论 : (1)l1∥ l 2的条件是什么 ? (2)l1 l 2的条件是什么 ?
画图时, 再找出直线l上另一点, 例如p1 ( 1,4) 过p1 , p0的直线即为所求,
y P1
° -5
°
O
°5
x
练习
1、写出下列直线的点斜式方程:
(1)经过A(3,1), 斜率是 2 (2)经过B( 2 ,2),倾斜角是 30
思考2: 下列直线:y=-2x+1,y=x-4,y=3x,y=-3在y轴上的截 距分别是什么?
思考3: 如何求直线y-y0=k(x-x0)在x轴、y轴上的截距?
斜截式方程的应用:
例2:斜率是5,在y轴上的截距是4的直线方程。
解:由已知得k =5, b= 4, 代入斜截式方程 y= 5x + 4
练习
P0(x0,y0) x
y y0 k x x0
y y0 k ( x x0 )
点斜式
(1)直线上任意一点的坐标是方程的解(满足方程) (2)方程的任意一个解是直线上点的坐标
思考:
方程k=
y-y1 与 y-y1=k(x-x1) 有何不同? x-x1
思考6:经过点P0(x0,y0)的任意一条直线的方程都能
一个关于x,y的方程,化为整式即为 y y0 k ( x ,x 那么直线 l上每一点的坐标都满 0) 足这个方程吗?
y y0 k ( x x0 ) 的所有点P(x,y)是否都在直线l上? 为什么?
思考5:满足方程
点斜式方程
y
a
设直线任意一点(P0除外)的坐标为
P(x,y)。
例题分析:
例3 已知直线l1 : y k1 x b1 , l2 : y k 2 x b2 试讨论 : (1)l1∥ l 2的条件是什么 ? (2)l1 l 2的条件是什么 ?
高中数学必修二《直线的两点式方程》PPT (1)
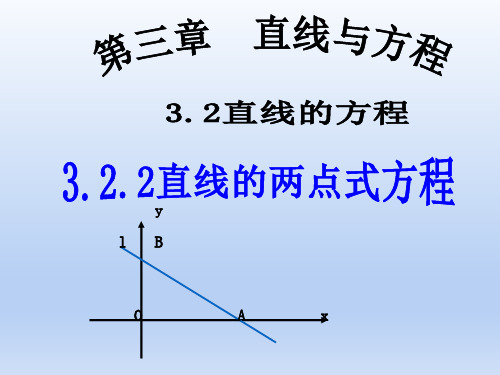
示意图
方程
使用范围
x
a≠0,
b≠0
a
y
+ =1
b
谢谢!
解答有关问题.
思 维 脉 络
1.直线方程的两点式
名称
两
点
式
已知条件
P1(x1,y1),
P2(x2,y2),
其中 x1≠x2,
y1≠y2
示意图
方程
y-y 1
=
x-x1
x2 -x1
y 2 -y 1
使用范围
斜率存在
且不为 0
2.直线方程的截距式
名称
已知条件
截
距
式
在 x,y 轴上
的截距为 a,
b 且 ab≠0
P1(x1,y1 ),P2(x2 ,y 2 )的 点 的 直 线
都 可 以 用 方 程 (yyபைடு நூலகம் )(x2 x1 ) (x x1 )(y2 y1 )表 示 ;
x y
C.不 经 过 原 点 的 直 线
都 可 以 用 方 程 1表 示 ;
a b
D.经 过 定 点 的 直 线 都
可 以 用 y kx b表 示 .
M(
,
),即M( , )
2
2
2 2
3 1
y0
x5
过A(-5,
0),M( , )的直线方程为
1
3
2 2
0
5
2
2
整理得:x+13y+5=0
这就是BC边上中线所在的直线的方程。
练习1:求过下列两点的直线方程
(1)M(-1,4),N(1,10)
(2)P1(2,1),P2(0,-3)
新人教A版必修二《直线的点斜式方程》ppt课件

课前探究学习
课堂讲练互动
活页限时训练
(4)过点 P(-2,3),Q(5,-4)的直线的斜率 -4-3 -7 kPQ= = 7 =-1. 5--2 又∵直线过点 P(-2,3), ∴由直线方程的点斜式可得直线方程为 y-3=-1×(x+2),即 x+y-1=0.
课前探究学习
课堂讲练互动
活页限时训练
二:问题的提出
问题1:过点P(-1,3)的直线有多少条?
问题2:过点P(-1,3)且倾斜角为 30 的直线有 多少条
问题的探究:, 给定一个定点A(-1,3)和斜率为-2就可以
决定一条直线l .
(1) 如果直线l上一点B的横坐标为2,你能求出它的纵 坐标吗? (2) 如果直线上一点B的横坐标为x,你能求出它的纵坐 标吗?
l 的方程就是
y y0 0 ,或 y y0
y
P0 l
O x
(2)与
y 轴平行或重合的直线的方程是什么?
当直线 l 的倾斜角为 90 时,直线没有斜率,这 时,直线 l 与 y 轴平行或重合,它的方程不能用点斜
式表示.这时,直线 l 上每一点的横坐标都等于 x0, 所以它的方程就是 y l
②斜率不存在时: x x0
练习:课本95页1,2
题型一
直线的点斜式方程
【例 1】 求满足下列条件的直线方程. (1)过点 P(-4,3),斜率 k=-3; (2)过点 P(3,-4),且与 x 轴平行; (3)过点 P(5,-2),且与 y 轴平行; (4)过 P(-2,3),Q(5,-4)两点. [思路探索] 利用直线方程的点斜式,以及数形结合的思想,
x x0 0 ,或 x x0
O
P0
x
人教版数学必修二3.《直线的点斜式方程》同步PPT课件

4
解:设直线的方程为 y 3x b
4
则它与两坐标轴的交点分别为(3b/4,0)和(0,b).
由题意知
|
3b 4
||b|
9b2 16
b2
9
整理得 |b|=3
∴b=±3.
所以直线得方程为y
3x 4
3
或y
3x 3 4
.
人 教 版 数 学 必修二 3.《直 线的点 斜式方 程》同 步PPT课 件
例二
.已知直线l过A(3,-5)和B(-2,5),求直 线l的方程。
解:∵直线l过点A(3,-5)和B(-2,5)
5 5
k L 2 3 2 将A(3,-5),k=-2代入点斜式,得
y-(-5) =-2(x-3),即 2x+y-1=0
x轴所在直线的方程是什么?y轴所在直线的方
程是什么?
y
O
x
x轴所在直线的方程为y=0, y轴所在直线的方程为x=0。
人 教 版 数 学 必修二 3.《直 线的点 斜式方 程》同 步PPT课 件
人 教 版 数 学 必修二 3.《直 线的点 斜式方 程》同 步PPT课 件
倾斜角为0°的直线的方程是什么? y
y
P0
P1
O
x1 x0
x
(2)若x1≠x0,则 y1 y0 kx1 x0, 这说明过
点P1和点 P0 的直线的斜率为k,可得点 P1在过点 P0(x0,y0),斜率为k的直线l上.
人 教 版 数 学 必修二 3.《直 线的点 斜式方 程》同 步PPT课 件
人 教 版 数 学 必修二 3.《直 线的点 斜式方 程》同 步PPT课 件
(5)斜率为
3 2
,在y轴上的截距是-2。
解:设直线的方程为 y 3x b
4
则它与两坐标轴的交点分别为(3b/4,0)和(0,b).
由题意知
|
3b 4
||b|
9b2 16
b2
9
整理得 |b|=3
∴b=±3.
所以直线得方程为y
3x 4
3
或y
3x 3 4
.
人 教 版 数 学 必修二 3.《直 线的点 斜式方 程》同 步PPT课 件
例二
.已知直线l过A(3,-5)和B(-2,5),求直 线l的方程。
解:∵直线l过点A(3,-5)和B(-2,5)
5 5
k L 2 3 2 将A(3,-5),k=-2代入点斜式,得
y-(-5) =-2(x-3),即 2x+y-1=0
x轴所在直线的方程是什么?y轴所在直线的方
程是什么?
y
O
x
x轴所在直线的方程为y=0, y轴所在直线的方程为x=0。
人 教 版 数 学 必修二 3.《直 线的点 斜式方 程》同 步PPT课 件
人 教 版 数 学 必修二 3.《直 线的点 斜式方 程》同 步PPT课 件
倾斜角为0°的直线的方程是什么? y
y
P0
P1
O
x1 x0
x
(2)若x1≠x0,则 y1 y0 kx1 x0, 这说明过
点P1和点 P0 的直线的斜率为k,可得点 P1在过点 P0(x0,y0),斜率为k的直线l上.
人 教 版 数 学 必修二 3.《直 线的点 斜式方 程》同 步PPT课 件
人 教 版 数 学 必修二 3.《直 线的点 斜式方 程》同 步PPT课 件
(5)斜率为
3 2
,在y轴上的截距是-2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例一 直线l经过点P(1,2),且倾斜角α=135°,求 直线l的点斜式方程,并画出直线l。 y 解:直线经过点P(1,2),斜率 k=tan 120°=-1,代入点斜式方 4 程得 Q 3 2 P y-2=-1×(x-1) 1 画图时,只需取直线上的另 一点Q(x1,y1),例如取x1=0,y1=3, 得Q的坐标为(0,3)过点P,Q 的直线即为所求。
倾斜角为0°的直线的方程是什么? y
P0ቤተ መጻሕፍቲ ባይዱ
O
l
x
此时,tan 0°=0 即k=0,这时直线与 x轴平 行或重合,直线的方程就是y-y0=0或y=y0。
倾斜角为90°的直线的方程是什么? y l
P0
O
x
此时,直线没有斜率,直线与y轴平行或重 合,它的方程不能用点斜式表示。直线的方程为 y-y0=0或y=y0。
2.一条直线经过点A(0,5),倾斜角为0°,求 这直线方程。 y 5
O
x
解:这条直线经过点A(0,5),斜率是k=tan0°=0 代入点斜式,得y - 5 = 0
3 y2 ( x 1) 则直线n的方程为_______________ 。 3
(2) 直线n的倾斜角为直线m的倾斜角的一半, 则 直线n的斜率也是直线m的斜率的一半。对吗? 错
(3)直线m的方程为 y=ax+2a+1, 则直线m必过定点
_________ ( -2,1) 。
(4)已知直线的点斜式方程是 y-2=x-1,那么此直线 的斜率是_______ ,倾斜角是__________ 1 45° 。
O
1
2
3
x
已知直线l的斜率是k,与y轴的交点是P (0,b),求直线方程。 代入点斜式方程,得l的直线方程:y-b=k(x-0) 即 y = kx + b。 y P(0,b)
O
x
我们把直线l与y轴交点(0,b)的纵坐标b叫 做直线l在y轴上的截距,方程 y=kx+b,由直线k与 它在y轴上的截距b确定,所以,该方程叫做直线的 斜截式方程,简称斜截式。 y (0,b) O x
P0
l
O
x
(1)若x1=x0,则y1=y0,说明点P1与点P0重合, 可得点P1在直线l上.
y
P0
P1
O
x1
x0
x
(2)若x1≠x0,则 y y 0 k x x0 ,这说明过 点P1和点 P0 的直线的斜率为k,可得点 P1在过点 P0(x0,y0),斜率为k的直线l上.
以上分析说明:方程恰为过点P0(x0,y0),斜率 为k的直线l上的任一点的坐标所满足的关系式,我们 称方程 y y k x x 为过点P0(x0,y0),斜率为k 0 0 的直线l的方程. 这个方程由直线上一点及其斜率决定,我们叫 做直线的点斜式方程,简称点斜式.
课堂小结
1.直线方程的两种形式: 点斜式: y y1 k ( x x1 ) 斜截式: y kx b. 2.两种特殊情况:过点P(x0,y0)且与坐标轴平行的 直线的方程分别是:y=y0和x=x0。
随堂练习
1.填空 (1)直线m的方程为 y 2 3( x 1) 则直线m所过 (-1,-2) 倾斜角是______ 定点P的坐标是______, 60° 。如果直 线n也过P点,且倾斜角为直线m 的倾斜角的一半,
. .
O
x
设点P(x,y)是直线l上不同于P0的任意 一点.根据经过两点的直线斜率公式,得
y y0 k x x0
可化为y y 0 k x x0
由以上推导可知:
过点P(x0,y0),斜率为k的直线l上的每一点 的坐标都满足方程 y-y0=k(x-x0)。
思考
坐标满足上面方程的每一点是否都在过点P (x0,y0),斜率为k的直线上? y
y kx b.
左端y的系数恒为1,右端x的系数k和常数项 b均有明显的几何意义.k是直线的斜率,b是直线 在y轴上的截距。
例二 斜率是5,在y轴上的截距是4的直线的点斜 式和斜截式。 解:由已知得k=5,b=4,代入斜截式方程 y=kx+b 。 得到y=5x+4——斜截式 变形得到y+1=5(x+1)——点斜式
情感态度与价值观
通过让学生体会直线的斜截式方程与一次函数 的关系,进一步培养学生数形结合的思想,渗透数 学中普遍存在相互联系,相互转化等观点,使学生 能用联系的观点看问题。
教学重难点
重点
直线的点斜式方程和斜截式方程。
难点
直线的点斜式方程和斜截式方程的应用。
已知直线l经过已知点P0(x0,y0),并且它 的斜率是k,求直线l的方程。 y l P P1
新课导入
在直角坐标系内确定一条直线的几何 要素有哪些?
1.已知直线上的一点和直线的倾斜角(斜率)可 以确定一条直线。 2.已知两点可以确定一条直线。
给定一个点P0(x0,y0)和斜率k,或给 定两点P1(x1,y1),P2(x2,y2),就能确定一 条直线.能否将直线上所有点的坐标(x, y)满 足的关系表示出来?
思考
截距是距离吗? y (0,b) y
O
x
O
(0,b)
x
截距等于b,可能为正值,也可能为负值。 所以,截距不是距离。
直线 l 在 x 轴上的截距是什么? y (a,0) x
O
直线l与x轴交点(a ,0)的横坐标a叫做 直线l在x轴上的截距。
观察方程y=kx+b,它的形式有什么特点? 斜率
y轴上的截距
y y 0 k x x0
思考
直角坐标系中所有直线都能用点斜式表示吗? y l
O
x
y y 0 k x x0 所以,斜率不存在,即倾
斜角为90°的直线不能用点斜式表示.
x轴所在直线的方程是什么?y轴所在直线的方 程是什么? y
O
x
x轴所在直线的方程为y=0, y轴所在直线的方程为x=0。
3.2.1 直线的点斜式方程
教学目标
知识与能力
理解直线方程的点斜式,斜截式的形式特点和适 用范围。
能正确利用直线的点斜式,斜截式公式求直线方 程。
体会直线的斜截式方程与一次函数的关系。
过程与方法
在已知直角坐标系内确定一条直线的几何要 素——直线上的一点和直线的倾斜角的基础上, 通过师生探讨,得出直线的点斜式方程;学生通过 对比理解“截距”与“距离”的区别。
