电磁学_稳恒磁场
大学物理 稳恒磁场

第十一章稳恒磁场磁场由运动电荷产生。
磁场与电场性质有对称性,学习中应注意对比.§11-1 基本磁现象磁性,磁力,磁现象;磁极,磁极指向性,N极,S极,同极相斥,异极相吸。
磁极不可分与磁单极。
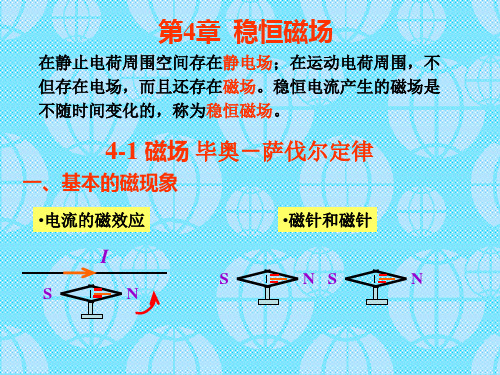
一、电流的磁效应1819年,丹麦科学家奥斯特发现电流的磁效应;1820年,法国科学家安培发现磁场对电流的作用。
二、物质磁性的电本质磁性来自于运动电荷,磁场是电流的场。
注:1932年,英国物理学家狄拉克预言存在“磁单极”,至今科学家一直在努力寻找其存在的证据。
§11-2 磁场磁感强度一、磁场磁力通过磁场传递,磁场是又一个以场的形式存在的物质。
二、磁感强度磁感强度B 的定义:(1)规定小磁针在磁场中N 极的指向为该点磁感强度B 的方向。
若正电荷沿此方向运动,其所受磁力为零。
(2)正运动电荷沿与磁感强度B 垂直的方向运动时,其所受最大磁力F max 与电荷电量q 和运动速度大小v 的乘积的比值,规定为磁场中某点磁感强度的大小。
即:qvF B max=磁感强度B 是描写磁场性质的基本物理量。
若空间各点B 的大小和方向均相等,则该磁场为均匀磁场....;若空间各点B 的大小和方向均不随时间改变,称该磁场为稳恒磁场....。
磁感强度B 的单位:特斯拉(T)。
§11-3 毕奥-萨伐尔定律 一、毕-萨定律电流元: l Id电流在空间的磁场可看成是组成电流的所有电流元l Id 在空间产生元磁感强度的矢量和。
式中μ0:真空磁导率, μ0=4π×10-7NA 2 dB 的大小: 20sin 4rIdl dB θπμ=d B 的方向: d B 总是垂直于Id l 与r 组成的平面,并服从右手定则.一段有限长电流的磁场: ⎰⎰⨯==l l r r l Id B d B 304πμ二、应用1。
一段载流直导线的磁场 )cos (cos 42100θθπμ-=r IB 说明:(1)导线“无限长":002r I B πμ=(2)半“无限长”: 00004221r I r IB πμπμ==2.圆电流轴线上的磁场 磁偶极矩232220)(2x R R IB +=μ讨论:(1)圆心处的磁场:x = 0 RIB 20μ=;(2)半圆圆心处的磁场: RIR I B 422100μμ==(3)远场:x >>R ,引进新概念 磁偶极矩0n IS m =则: m xB 3012πμ=3.载流螺线管轴线上的磁场)cos (cos 2120ββμ-=nIB讨论:(1)“无限长”螺线管:nI B 0μ=(2)半“无限长”螺线管:nI B 021μ=例:求圆心处的B .§11-4 磁通量 磁场的高斯定理 一、磁感线作法类似电场线。
稳恒磁场
例1 如图载流长直导线的电流为 , 试求通过矩形面积的磁通量(导线与矩 形共面)。
I
B
解 先求 出
,对变磁场给
dΦ
I
l
d1 d2
0 I B 2π x
后积分求 m
B
Φm
B // dS
dΦm BdS
0 I
o
x
2π x 0 Il d2 dx Φm dΦm S 2 π d1 x 0 I l d 2 Φm ln 2π d1
B I
B
I
圆电流
I
载流长螺线管
载流长直导线
3、磁感应线特性
•磁感应线是环绕电流的无头尾的闭合曲线,无起点无终 点; •磁感应线不相交。
二、磁通量
1、磁通量定义:
通过磁场中某一曲面的磁感应线的数目,定义为磁通量, 用Ф表示。
2、计算
通过任意S面的磁通量Ф,其数学 表达式:
3、说明
B B d S
ldx
22
4-3 安培环路定理
安培 (Ampere, 1775-1836)
法国物理学家,电动力学的创始人。1805年 担任法兰西学院的物理教授,1814年参加了 法国科学会,1818年担任巴黎大学总督学, 1827年被选为英国皇家学会会员。他还是柏 林科学院和斯德哥尔摩科学院院士。 安培在电磁学方面的贡献卓著,发现了一系 列的重要定律、定理,推动了电磁学的迅速 发展。1827年他首先推导出了电动力学的基 本公式,建立了电动力学的基本理论,成为 电动力学的创始人。
28
(3)电流在回路之外
0 I 0 I B1 , B2 2 π r 2 π r 1 2 B2 B1 I 0 d d dl B1 dl1 B2 dl2 2 2π dl1 I r1 r2 B1 dl1 B2 dl2 0
电磁学教学资料 电磁学第五章 稳恒磁场的基本性质---高斯和环路定理

L
F jdV B
V
F idS B
S
•
其中B为外磁场的磁感应强度。外磁场是指 除受力电流之外的其他电流产生的磁场。
30
• 这些电流(即载流导体)在外磁场B中所受的 力矩分别为:
L r ( Id l B )
L
L r ( j B)dV
求 此段载流导线受的磁力。
y
dFx IBdl sin IBdy
dFy IBdl cos IBdx
Fx IBdy 0
0 0
dF
B
Idl
I
F
O L A x
Fy IBdx IBL
0
L
相当于载流直导线 OA 在匀强磁场中受的力,方向沿 y 向。
19
例4 求无限大平面电流的磁场 解 面对称
B dl B dl B dl ab bc B d l B dl
cd da
i
b
B
P
a
B dl B dl
a c
b
d
2 Bab 0 abi B 0i / 2
m d
S
S
m
B dS
S
dS
B n
B cos dS
规定 磁力线穿入
单位: 1T•m2 =1Wb(韦伯) 磁力线穿出
m 0 m 03
例 在真空中有一无限长载流直导线, 试求:通过其右侧矩形线框的磁通量。
解:
dΦm= B . dS
1 s E dS 0 qi
1.大学物理-稳恒磁场概念

思路: 思路: 实验
理论
应用
磁现象
1)磁体间有相互作用力 1)磁体间有相互作用力 同性相斥, 同性相斥,异性相吸 磁极不能单独存在 2)奥斯特: 奥斯特: 奥斯特 电流 3)安培: 磁体 3)安培: 安培 磁体 4) 洛仑兹: 洛仑兹: 5) 载流导线 磁体 电流 运动电荷 载流导线 –
S S N S N
磁感应强度
一. 磁感应强度概念
r r Fe r →B= 参照:电场强度: 参照:电场强度: E = q0
磁感应强度: 磁感应强度: 运动点电荷: 运动点电荷: 电流元: 电流元:
1. 定义: 定义:
r r Fe = q0 E
r r Fm r Fm r r , B= q0v0 I 0dl0
?
r r r dFm = ( I 0 dl 0 ) × B
3. 画 B x曲线 r 0 IR 2 r B= 3 i 2 2 2( R + x ) 2 练习: 练习:
B
o
x
Bo = ?
I
R
o
R o
I
B0 =
0 I
8R
30 I 0 I B0 = + 8R 4πR
亥姆霍兹圈: 例4.亥姆霍兹圈:实验室用近似均匀磁场 亥姆霍兹圈 两个完全相同的N匝共轴密绕短线圈 匝共轴密绕短线圈, 两个完全相同的 匝共轴密绕短线圈,其中心间距 与线圈半径R相等 相等, 与线圈半径 相等,通同向平行等大电流 I. . 求轴线上 o1 .
磁场 如何作用—通过磁场 1.磁场概念: 磁力如何作用 通过磁场: 1.磁场概念: 磁力如何作用 通过磁场: 磁场概念 电流或运动电荷周围,除了电场, 电流或运动电荷周围,除了电场,还有磁场
第11章 稳恒磁场

z
D
无限长载流长直导线的磁场 无限长载流长直导线的磁场. 载流长直导线的磁场
θ2
v B
B=
4 π r0
(cosθ 1 − cosθ 2 )
B=
I
o
µ0 I
2 π r0
θ1 → 0 θ2 → π
x
C
θ1
P y
无限长载流长直导线的磁场
B=
µ0I
2πr
I B
I
X
B
电流与磁感应 电流与磁感应强度成右螺旋关系 半无限长载流长直导线的磁场
=
I
2π R
v B
o
l
R
v v ∫ B ⋅ dl =
l
∫ 2πR
µ0 I
v dl
dl
v v µ0 I ∫l B ⋅ d l = 2 π R ∫l d l v v 设闭合回路 l 为圆形 ∫l B ⋅ dl = µ0 I 回路( 成右螺旋) 回路( l 与 I 成右螺旋)
I
o
v B
R
若回路绕向为顺时针时, 若回路绕向为顺时针时,则
z
带电粒子在磁场中沿其他方向运动时 F 垂直于 v 与特定直线所组成的平面 与特定直线所组成的平面. 当带电粒子在磁场中垂直于此特定直线运动 时受力最大. 时受力最大
F = Fmax = F⊥
Fmax ∝ qv
Fmax q , v 无关 qv 大小与
磁感应 的定义: 磁感应强度 B 的定义:当 正电荷垂直于 特定直线运动 时,受力 Fmax 将 Fmax ×v 方向 的方向. 定义为该点的 B 的方向
I I I
I S S N I N
磁通量 磁场的高斯定理
v ∆S B
第7章稳恒磁场

o
L
P
x
结论 任意平面载流导线在均匀磁场 中所受的力,与其始点和终点相同的载流 直导线所受的磁场力相同.
42
二 物理学 均匀磁场对载流线圈的作用力矩
将平面载流线圈放入均匀磁场中,
da边受到安培力大小:
Fda
Il
2
B
sin(
2
)
bc边受到安培力大小:
Fbc
Il 2 B
sin(
2
)
o
Fda
d
a
I
l1
qvB m v2 R
m qBR v
70 72 73 74 76
质谱仪的示意图
锗的质谱
30
物理学
霍耳效应
31
物理学
B
霍耳电压 Fm
UH
RH
IB d
b
d
vd+
+ ++
+q
+
- - - - - I
UH
Fe
qEH qvd B I qnvd S qnvdbd
EH vd B U H vd Bb
× ×
××0
粒子做匀速圆周运动
物理学
(3)
0与B成角
// 0 cos
0 sin
R m m0 sin
qB
qB
•
0 //
B
B
T 2R 2m qB
螺距 h : h //T 0 cos T 2m0 cos
qB
h //
0
q R
物理学
例题1 :请根据磁感应强度的方向规定,给 出下列情况运动电荷的受力方向:
B
c
en
大学物理磁场稳恒磁场理论1

求解电流磁场分布基本思路: 电流元磁场公式 磁场叠加原理 电流磁场分布
毕 — 沙定律:电流元产生磁场的规律,与点电荷电场 公式作用地位等价 I dB
P
.
r
Idl
0 Idl r dB 4r 3
讨论: 无限长直电流
讨论:
0 I B (cos 1 cos 2 ) 4a
I
1. 无限长直电流
1 0 ,
0 I B 2a
B
R,无限长半圆柱金属面通电流I,求轴线上 练习:半径
解:通电半圆柱面 电流线(无限长直电流)集合
B
R
dI
dB ' dB
I B 2a
0
2. 圆电流轴线上磁场: 2 0 IR i 0 Pm B 3 3 2 2 2 2 2 2( R x ) 2 ( R x ) 2
I 圆电流圆心处磁场: B 2R
0 0
B 0nI
电流的磁矩:
P I Sn m
第二节磁场的高斯定理和安培环路定理
2) 在垂直于导线平面内围绕电流的任意闭合路径
0 I rd LB dl LB cosdl L 2 r 0 I 2 0 d 0 I 2 若电流反向,则为 0 I
描述空间 矢量场一般方法
一. 磁场高斯定理 用场线描述场的分布 用高斯定理,环路定理揭示场的 基本性质
1.磁感应线
切向:该点 B 方向 疏密:正比于该点 B 的大小
闭合, 或两端伸向无穷远; 与载流回路互相套联; 互不相交。
特点
2. 磁通量
通过磁场中某给定面的磁感应线的总条数
电磁学——稳恒磁场g

方向:规定为正电荷运动方向。
dq 大小: I dt
单位(SI):安培(A)
电流密度
当通过任一截面的电量不均匀时,用电流强度 来描述就不够用了,有必要引入一个描述空间不同 点电流的大小的物理量。
dI j n dS
dI dS
导体中某点的电流密度,数值上等于通过该点 场强方向垂直的单位截面积的电流强度。
2( R 2 x 2 )3 2
大小: B 2( R 2 x 2 )3 2
0 IR 2
x
X
x
结论
方向:
右手螺旋法则
0 IR 2 B 2( R 2 x 2 )3 2
1. x R B ?
B
0 IR 2
2x 3
2. x 0 B ?
载流圆环
B
圆心角 2
A1
p
A2
B
I
0 R 2 Indl R2 R2 l 2 csc2 B dB 3 sin 2 2 2 2 2 (R l ) 2 0 0 B ( nI sin )d nI (cos 2 cos 1 ) 1 2 2
讨论:
1、若 R L 即无限长的螺线管, 1 , 2 0 则有 B 0 nI
2、对长直螺线管的端点(上图中A1、A2点) 1 , 2 0 2 1 则有A1、A2点磁感应强度 B 0 nI 2
练 习
求圆心O点的 B 如图,
I
I
B
O R
Bc
b
c
B
通电螺线管
I
I
I
I
1、每一条磁力线都是环绕电流的闭合曲线,因此 磁场是涡旋场。磁力线是无头无尾的闭合回线。 2、任意两条磁力线在空间不相交。 3、磁力线的环绕方向与电流方向之间可以分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、环外部空间的磁场?为什么? 2、如果不是密绕,但保持对称, 则内、外部空间的磁场?
§4
磁场的高斯定理和磁矢势
一、磁通量的定义及计算:
v v dΦ B = B ⋅ dS = BcosθdS v v Φ B = ∫ B ⋅ dS
S
单位: 1Wb = 1T × 1m 2 S
v B v B
二、高斯定理
v ω = Ω '− Ω = dΩ = dl2 ⋅ ∇Ω
v v μ0 I B ⋅ dl 2 = dl2 ⋅ ∇Ω 4π
v μ0 I B= ∇Ω 4π
3.2 安培环路定理的表述和证明
∫
L
v v B ⋅d l = μ 0
∑I
i
安培环路定理表述如下:磁感应强度 沿任何闭合环路L 的线积分,等于穿 过这环路所有电流的代数和的μ0倍
Ω '−Ω = ω
∂Ω ∂Ω ∂Ω )dx + ( )dy + ( )dz + O ( dl 2 ) ∂x ∂y ∂z v Ω ( x , y, z ) = Ω ( x0 , y0 , z0 ) + dl ⋅ ∇Ω + O ( dl 2 )
v v v v dl = dxi + dyj + dzk
v Ω '−Ω = ω = dl2 ⋅ ∇Ω
12
4π r12 dF12
2
μ 0 dl1 dl2
若:
r12 = C >> 1 dl1dl2
dF12 = 10 −7 / C ( N )
则
I = 1A
2.1 磁感应强度矢量----毕奥—萨伐尔定律
两电流元之间的相互作用是通过磁场进行的! 电流元在空间 p 处产生的磁场:
p
v I 1dl1
v v μ o Idl × r ˆ dB = ⋅ 4π r2
v dB
v B
r0
μ 0 Idl sin θ dB = 4π r2
θ = π
R 2I B = ∫ dB cos α = 2 ( R 2 + r0 2 ) 3 / 2
1、圆心处: 2、轴上远处: 3、其他地方?
B =
2
, sin θ = 1, r0 = r sin α
α
μ0
I
R
μ0 I
2 R
B =
μ0 R 2I
v v ∫∫ B ⋅ d S = 0
S
即通过任意闭合曲面的磁通量为 0,
如何理解?
例:半无限长螺线管, 求:x=0处磁场强度B的径向分量。
带电环轴线上某点的磁 场强度为 dB =
μ0
R 2 Indx
2 2 3/ 2
2 (R + x )
图中 x = l
x = R cot β ; dx = − R csc 2 β ; R 2 + x 2 = R 2 csc 2 β ; dB = −
2 r3
例题4:一对相同、共轴、半径为 R、相距为 a 、载流各为 I 的圆线圈, (1)求轴线上的磁场分布;(2)a 多大时两线圈间轴线中点O 处附近 的磁场最均匀? 1、轴线上的磁场分布:
RI B= 2 [ R + ( x + a / 2) ] μ RI + 2 [ R + ( x − a / 2) ]
∫∫ B ⋅ dS = ∫∫ B ⋅ dS − ∫∫ B ⋅ dS = 0
S1 S2
∫∫ B ⋅ dS = ∫∫ B ⋅ dS
S1 S2
既然通过曲面S 的磁通量仅由它的边界线L 所决定,我们就可能找到一个 矢量A ,它沿L 作线积分等于通过S 的磁通量:
dF12 = q2 E1
例:载流螺线管磁感应线的分布:
N
S
N S
1、磁场在管内外的方向; 2、磁感应线密度(场强)的分布?
2.3
载流回路的磁场
实例:直线电流的磁场的求解。 v v ˆ v μ o Idl sin θ μ0 Id l × r B= B = L 4π 4π r 2 r2
∫
∫
v θ dl l
v pm = qm l
H = −∇U m
磁偶极子在外磁场中受到的力矩
v v v L = pm × H
1819-1820年丹麦科学家奥斯特发现电流产生磁场效应
现已知磁铁与磁铁,磁铁与电流 之间的相互作用都是通过磁场进行 的
磁铁 电流
磁场
磁铁 电流
1820年 奥斯特
磁针的一跳 电流的磁效应
奥斯特实验
0
L/2
2
−L / 2
dl ∫ [R + ( x − l )
2
2
3/ 2
B=
μ nI
0
2
(cos β − cos β )
1 2
0
1、无限长管:B = μ nI
B 2、半无限长管: =
μ nI
0
2
3、无限长管内非轴线处场强? 4、无限长管外场强?
§3
安培环路定理
3.1 载流线圈与磁偶极层的等价性
v ˆ dl1 × r12
方向与AB所构成的平面垂直,并满足右手定则。
矢量运算 v v v v (1) a ⋅ b = b ⋅ a = ab cos θ
v v v v v (2) a × b = ab sin θ ⋅ e n = − b × a
(3)
v en
v v v v v v v v v a ⋅ (b × c ) = b ⋅ (c × a ) = c ⋅ (a × b )
2 r12
∫
L1
v v v a×b = c
• 安培环路定理的应用举例 例题1:求圆截面的无限长直导线的磁场分布,设导线的 半径为 R ,电流 I 均匀地通过横截面
v v ∫ B ⋅d l = B ⋅ 2 π r = μ ∑ I
L 0
'
I
R
r > R,∑ I
'
= I
B(r )
B
=
I 2 π r
0
μ
'
v r
v v dB1 ( r )
磁感应强度单位? 1T = 1N /( A ⋅ m ) 则安培定律可写为:
v μ d F 12 = 0 4π v v ˆ I 2 d l 2 × ( I 1 d l 1 × r12 )
2 r12
1T = 10 4 Gs
v v = I 2 d l 2 × d B 12
与静电场比较?
dx
作近似:
r
B( x + Δx ) − B( x ) S = B⊥ 2π r dx
π r 2 dB( x ) 2π r dx
x =0
= B⊥
B⊥ =
μ 0 nIr
4R
4.2 磁矢势
运用磁场的“高斯定理”更根本的意义在于能引入另一个矢量
—磁矢势
v A( r , t )
∫∫
r r B ⋅ dS = 0
∫
L1
v v v μ I B( r2 ) ⋅ ( − dl2 ) = 0 4π
∫
L1
v v ˆ ( − dl2 × dl1 ) ⋅ r12
2 r12
=−
μ0 I 4π
∫
L1
dω = −
μ0 I ω 4π
Ω + ( −Ω ' ) + ω = 0
Ω ( x , y, z ) = Ω ( x0 , y0 , z0 ) + (
μ o I ⋅ ro d θ ⋅ sin θ μoI B=∫ = 2 2 2 L 4π ro 4π sin θ ⋅ ro / sin θ θ 1 μoI = (cos θ 1 − cos θ 2 ) θ 2 4π ro
∫θ
v B
I
∫θ
θ2
1
sin θ ⋅ d θ
0
=
=
π
μoI B = 2π ro
2.4 载流圆线圈轴线上的磁场 电流 I 、半径 R 、场点 r0.
v v v v v v v v v a × (b × c ) = b ⋅ (a ⋅ c ) − c ⋅ (a ⋅ b )
v i
v k
(4)
v v v i×j =k
v v v j ×k = i
v j
v v v k ×i = j
v v v k × j = −i
例题1:求一对平行电流元间的相互作用力,二者都与连线垂直。
I
v r
v B
因为各电流元产生的磁场方向相同,磁场方向垂直纸 面向里所以只求标量积分。磁场方向垂直纸面向里。
Q l = − r cos θ Q ro = r sin θ
∴ l = −ro ctgθ
∴ dl = ro dθ / sin 2 θ
θ2
1
ro
sin θ ⋅ d θ
μ o I ⋅ ro d θ ⋅ sin θ μoI B=∫ = 2 2 2 L 4π ro 4π sin θ ⋅ ro / sin θ
2 r12
v v μ I B( r2 ) = 0 1 4π
∫
L1
v v v r12 = r2 − r1
1
v μ0 I v v B( r2 ) ⋅ dl2 = 4π
o•
2 r12 L1 v v ˆ μ 0 I ( dl2 × dl1 ) ⋅ r12 = 2 4π r12
∫
v v ˆ ( dl1 × r12 ) ⋅ dl2
0 1 2 1 21 2
r
21
v I dl
2
2
2
v dF
牛顿第三定培
国际电磁学单位制是MKSA制,M长度、K质量、S时间、A安培
