直言命题及其推理完整版本
合集下载
第三章_简单命题(直言命题)及其推理(上)
在自然语言中说“有些东西是什么”，还暗含 着“有些东西不是什么”；说“有些东西不是 什么”，还暗含着“有些东西是什么”。
逻辑学中说“有些S是P”没有暗含着“有些S不 是P”；说“有些S不是P”也没有暗含着“有些S 是P”。
逻辑学中所说的“有些”是“至少有一个”的 意思，至多可以多到全体。
第一节 命题概述
一、命题和判断 二、命题和语句 三、命题的种类
一、命题和判断
命题是表达判断的语句。命题的基本特 征是真和假。
判断是对事物情况有所断定的思维形式， 亦即被断定了的命题。
联系：命题当被思维主体断定之后，它 便成为判断。
区别：作为命题，它是对事物情况的陈 述；作为判断，它带有主体断定的性质， 有时还带有情感色彩。
2、直言命题的凡恩图解
凡恩图解（Venn diagrams）是英国逻辑学 家、数学家J•凡恩（John Venn，1834-1923 年）于1880年创造的。
凡恩图解用两个相交叉的圆圈构成的图形 表示在直言命题（A、E、I、O）中，主项 “S”与谓项“P”在外延间的各种关系。
可以用文恩图解来刻画直言命题的四种形式
一、什么是直言命题
1、含义：直言命题是一个主谓结构，它 断定了某个数量的对象具有或者不具有 某种性质，因此也叫做“性质命题”。
2、结构：主项、谓项、量项、联项。 主项和谓项统称为词项。 直言命题的质：肯定命题、否定命题。 直言命题的量：全称、特称、单称。
特别提醒注意的是：
逻辑学中的特称量词“有些”与自然语言中的 “有些”的含义是不同的。
四种直言命题连续变形推理
（1）SAP→SEP→PES→PAS→SIP→SOP （2）SAP→PIS→POS （3）SEP→SAP→PIS→POS （4）SEP→PES→PAS→SIP→SOP （5）SIP→SOP （6）SIP→PIS→POS （7）SOP→SIP→PIS→POS （8）SOP（不能先换位）
逻辑学中说“有些S是P”没有暗含着“有些S不 是P”；说“有些S不是P”也没有暗含着“有些S 是P”。
逻辑学中所说的“有些”是“至少有一个”的 意思，至多可以多到全体。
第一节 命题概述
一、命题和判断 二、命题和语句 三、命题的种类
一、命题和判断
命题是表达判断的语句。命题的基本特 征是真和假。
判断是对事物情况有所断定的思维形式， 亦即被断定了的命题。
联系：命题当被思维主体断定之后，它 便成为判断。
区别：作为命题，它是对事物情况的陈 述；作为判断，它带有主体断定的性质， 有时还带有情感色彩。
2、直言命题的凡恩图解
凡恩图解（Venn diagrams）是英国逻辑学 家、数学家J•凡恩（John Venn，1834-1923 年）于1880年创造的。
凡恩图解用两个相交叉的圆圈构成的图形 表示在直言命题（A、E、I、O）中，主项 “S”与谓项“P”在外延间的各种关系。
可以用文恩图解来刻画直言命题的四种形式
一、什么是直言命题
1、含义：直言命题是一个主谓结构，它 断定了某个数量的对象具有或者不具有 某种性质，因此也叫做“性质命题”。
2、结构：主项、谓项、量项、联项。 主项和谓项统称为词项。 直言命题的质：肯定命题、否定命题。 直言命题的量：全称、特称、单称。
特别提醒注意的是：
逻辑学中的特称量词“有些”与自然语言中的 “有些”的含义是不同的。
四种直言命题连续变形推理
（1）SAP→SEP→PES→PAS→SIP→SOP （2）SAP→PIS→POS （3）SEP→SAP→PIS→POS （4）SEP→PES→PAS→SIP→SOP （5）SIP→SOP （6）SIP→PIS→POS （7）SOP→SIP→PIS→POS （8）SOP（不能先换位）
第三章直言命题及其推理第一、二、三节
如：上述例子中的“发展变化的”、“唯物主义者”、 “经济发达的国家”、“固体”、“中国的首都”、“直辖
市”。
2021/6/28
4
联项：又称为直言命题的质，是联结主项和谓项的语词， 表示“具有”还是“不具有”的差别。决定这个命题
是肯 定命题还是否定命题。 肯定联项：是；否定联项：不是。
量项：又称命题的量，是表示主项外延被断定的范围的语词。 如：上述例子中的“所有” 、 “有的” 。
2021/6/28
23
A、E、I、O中主项与谓项的周延情况：
就主项而言：全称命题的主项都周延，特称命题的 主项都不周延；
就谓项而言：否定命题的谓项都周延，肯定命题的 谓项都不周延。
2021/6/28
24
注：
周延性问题是命题的形式问题，而不是命题的 真假问题，它与命题的具体内容没有关系。所以， 要确定一个命题的主、谓项周延与否，只要看它是 命题A、E、I、O中哪一种命题形式即可，而与主谓 项具体是什么概念没有关系。
直言命题的谓项是否周延，是由命题的质（联项）来决定 的。即否定命题确定的断定了谓项的全部外延，它的谓项是 周延的。也就是说当我们在断定某对象不是P的时候，实际 上断定它被排斥在P的全部外延之外。而肯定命题SAP、SIP 没有对谓项的全部外延确定的作出断定，所以其谓项是不周 延的。我们从肯定命题概括反映的S与P之间外延关系可以看 出，当我们断定某对象是P的时候，并没有确定的断定它是P 的全部。
主项 周延 周延 不周延 不周延
谓项 不周延 周延 不周延 周延
22
A、E、I、O四种直言命题主项和谓项的周延情况：
直言命题的主项是否周延，是由命题的量（量项）来决 定的。即，全称命题（全称肯定和全称否定命题）确定地断 定了主项的全部外延，所以其主项是周延的。特称命题没有 确定的断定主项的全部外延，所以它的主项是不周延的。
直言命题的推理规则
直言命题的推理规则
1. 嘿，所有的 A 都是 B 呀，就像所有的苹果都是水果一样。
比如说，
所有的猫都是动物，那只要是猫，就肯定是动物呀！
2. 哇塞，有些 A 是 B 哦，就好像有些花是红色的。
想想看，有些学生
是很勤奋的，对吧？这就是这样的道理呀！
3. 不是所有的 A 都是 B 呢，这不就跟不是所有的天都是蓝色的一样嘛。
比如，不是所有的人都喜欢运动呀！
4. 所有的 A 都不是 B ，这多明显呀！就好比所有的三角形都不是圆形。
你看，所有的石头都不是植物，是不是很容易理解？
5. 有些 A 不是 B 呀，这就如同有些动物不是哺乳动物一样。
比如说，
有些衣服不是红色的，很正常嘛！
6. 哎呀，如果 A 是 B，那么 C 是 D 呀！就像是如果今天下雨，那么地面会湿一样。
要是你考试得了满分，那肯定会很开心呀！
7. 要是 A 不是 B，那么 C 也不是 D 呢，好比如果这不是手机，那它也不能打电话呀。
你想想，如果这不是钥匙，那它也打不开这把锁呀！
结论：这些直言命题的推理规则真的很有趣也很实用呢，能帮我们更好地理解和思考很多事情呀！。
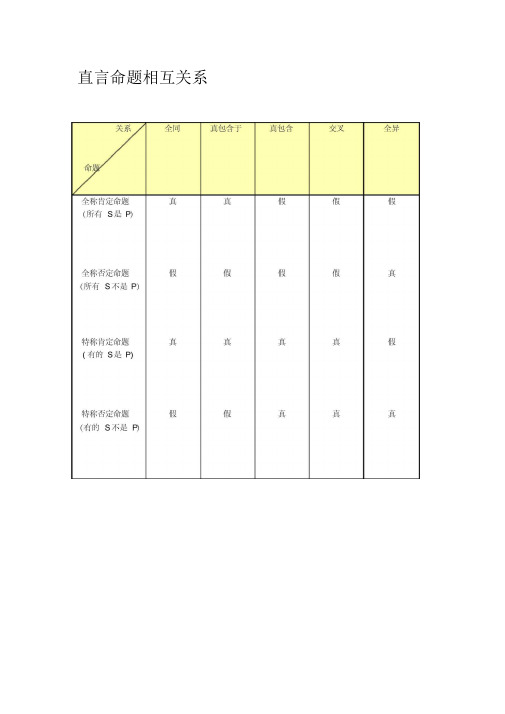
直言命题关系
充分条件假言连锁推理
必要条件假言连锁推理
如果P,那么Q
只有P,才Q
如果Q,那么R
只有Q,才R
7如果P,那么R
7只有P,才R
二难推理
简单构成式
简单破坏式
复杂构成式
复杂破坏式
如果P,那么Q
如果P,那么Q
如果P,那么Q
如果P,那么Q
如果R,那么Q
如果Q那么R
如果R,那么S
如果R,那么S
P或者R
非Q或者非R
非P且非Q
不相容选言 命题（要么P,要么Q）
有且只有一真才为真
肯定一个选言支，就否定 其余的选言支；否定一个 选言支意外的所有选言 支，可以冃疋未否疋的选 言支
“P且Q”或 者“非P且非Q”
充分条件假 言命题（如果P,那么Q）
只有前件真后件假才为 假
肯定前件就否定后件， 否定后件就能否定前件 否定前件不能否定后件 肯定后件不能肯定前件
“非P且Q或“P且非Q
负命题（并非
P）
原命题为真则为假；原 命题为假则为真
肯定原命题就否定负命题 否定原命题就肯定负命题
P
复言命题转换关系
“如果P,那么Q=“只有Q,才P” = “非P或Q
“只有P,才Q=“如果Q那么P”二“P或者非Q
“除非P,否则Q=“若果非P,那么Q”=“只有P,才非Q
假言命题连锁推理
一假）但可同假
“所有S都是P”与“某个S不是P”
“所有S都不是P”与“某个S是P”
下 反 对 关 系
“有些S是P”与“有些S不是P”
不能同假（必有
一真）可同真
“某个S不是P”与“有些S是P”
“某个S是P”与“有些S不是P”
必要条件假言连锁推理
如果P,那么Q
只有P,才Q
如果Q,那么R
只有Q,才R
7如果P,那么R
7只有P,才R
二难推理
简单构成式
简单破坏式
复杂构成式
复杂破坏式
如果P,那么Q
如果P,那么Q
如果P,那么Q
如果P,那么Q
如果R,那么Q
如果Q那么R
如果R,那么S
如果R,那么S
P或者R
非Q或者非R
非P且非Q
不相容选言 命题（要么P,要么Q）
有且只有一真才为真
肯定一个选言支，就否定 其余的选言支；否定一个 选言支意外的所有选言 支，可以冃疋未否疋的选 言支
“P且Q”或 者“非P且非Q”
充分条件假 言命题（如果P,那么Q）
只有前件真后件假才为 假
肯定前件就否定后件， 否定后件就能否定前件 否定前件不能否定后件 肯定后件不能肯定前件
“非P且Q或“P且非Q
负命题（并非
P）
原命题为真则为假；原 命题为假则为真
肯定原命题就否定负命题 否定原命题就肯定负命题
P
复言命题转换关系
“如果P,那么Q=“只有Q,才P” = “非P或Q
“只有P,才Q=“如果Q那么P”二“P或者非Q
“除非P,否则Q=“若果非P,那么Q”=“只有P,才非Q
假言命题连锁推理
一假）但可同假
“所有S都是P”与“某个S不是P”
“所有S都不是P”与“某个S是P”
下 反 对 关 系
“有些S是P”与“有些S不是P”
不能同假（必有
一真）可同真
“某个S不是P”与“有些S是P”
“某个S是P”与“有些S不是P”
法律逻辑直言命题案例题(3篇)
第1篇命题一：甲是盗窃案的犯罪嫌疑人。
命题二：乙和丙至少有一个是盗窃案的犯罪嫌疑人。
命题三：如果甲是盗窃案的犯罪嫌疑人，那么乙和丙都不是盗窃案的犯罪嫌疑人。
分析：1. 命题一分析命题一是一个简单的直言命题，表示甲是盗窃案的犯罪嫌疑人。
根据直言命题的逻辑规则，如果这个命题是真的，那么甲就是盗窃案的犯罪嫌疑人。
这是一个直接的陈述，不需要进一步的分析。
2. 命题二分析命题二是一个复合直言命题，表示乙和丙至少有一个是盗窃案的犯罪嫌疑人。
这个命题可以分解为以下两个简单命题：- 乙是盗窃案的犯罪嫌疑人。
- 丙是盗窃案的犯罪嫌疑人。
根据逻辑规则，复合命题“至少有一个”等价于“或者...或者...”，因此命题二可以表示为：乙是盗窃案的犯罪嫌疑人，或者丙是盗窃案的犯罪嫌疑人。
如果这个命题是真的，那么乙和丙中至少有一个人是盗窃案的犯罪嫌疑人。
3. 命题三分析命题三是一个条件直言命题，表示如果甲是盗窃案的犯罪嫌疑人，那么乙和丙都不是盗窃案的犯罪嫌疑人。
这个命题可以表示为：- 如果甲是盗窃案的犯罪嫌疑人，则乙不是盗窃案的犯罪嫌疑人。
- 如果甲是盗窃案的犯罪嫌疑人，则丙不是盗窃案的犯罪嫌疑人。
这是一个典型的条件命题，其逻辑形式为“如果P，则Q”。
根据条件命题的逻辑规则，这个命题只有在甲是盗窃案的犯罪嫌疑人且乙和丙都不是盗窃案的犯罪嫌疑人时才是真的。
如果甲确实是盗窃案的犯罪嫌疑人，但乙或丙中至少有一个人也是犯罪嫌疑人，那么命题三就是假的。
综合分析：- 如果命题一为真，那么甲是盗窃案的犯罪嫌疑人，这与命题三中的条件相符，但无法确定乙和丙的情况。
- 如果命题二为真，那么乙和丙中至少有一个人是盗窃案的犯罪嫌疑人。
这与命题三的条件相矛盾，因为如果甲是盗窃案的犯罪嫌疑人，根据命题三，乙和丙都不应该是犯罪嫌疑人。
- 如果命题三为真，那么甲是盗窃案的犯罪嫌疑人，且乙和丙都不是盗窃案的犯罪嫌疑人。
这与命题二的条件相矛盾，因为命题二要求乙和丙至少有一个人是犯罪嫌疑人。
【资料】逻辑学简单命题及其推理直言命题汇编
A. 表示至少存在一个的数量词。如“有”、“有 的”、“至少一个”、“不是无”、“不是没有” 等。
例如：
有（有的∕至少一个∕不是无∕不是没有）学 生是大学生。
特称量项“有（有的）”的逻辑含义与其作为 日常语言使用时的含义是不同的。
其逻辑含义是表示存在，是“至少有一个”， 至于有多少是不确定的，可以是一个、几个、乃至 全部。“有（有的）”是什么并不意味“有（有 的）”不是什么，反之，“有（有的）”不是什么 也不意味“有（有的）”是什么。
b.所有的鸟都不是不凭借空气飞翔的。
D.用重叠词表达全称。这种词既表达主项，又表达全称量项。例如 （21）a.人人（村村∕家家∕户户）都要遵纪守法。
b.所有的人（每一个村∕每一个家庭∕每一户人家）都要遵纪守法。
E.用“没有（无并非）……是（不是）……”表达全称。其中“没有（无
并非）……是……”表达全称否定，“没有（无并非）……不是（是不）……”
表达肯定联项的词用“是”，它在特定语境中 可省略；表达否定联项的词语用“不是”，此外还 有“并非”、“非”、“并不”、“并无”、 “没”、“没有”等。否定联项不能省略。
• 桂林山水甲天下。 • 马路并非马走的路。 • 鲸鱼非卵生动物。 • 海南岛的冬天并不太冷。 • 有些蛇并无毒液。 • 赤道附近没有极光。
“有（有的）”与“有些”的逻辑含义也不一 样。“有些”的逻辑含义相当“这些”或“那些”， 则“至少有两个”。
“少数”、“多数”、“部分”、“绝大部分” 等表示相对确定的数量，不表达形式逻辑的特称量 项。
质的概念。用逻辑变项P表示。离开具体语境的谓项 一般不能省略。
3.联项
联项是直言命题的质，是联结主项和谓项、表 示肯定或否定的概念。
第三章直言命题及其推理
第一节 命题和推理概述
一、什么是命题 二、命题与语句
一、什么是命题
北京是中华人民共和国的首都。 中国既是社会主义国家，又是发展中国家。 2＋2＝5。 生态危机可能毁灭人类。 只有年满18周岁，才有选举权。 要么在沉默中爆发，要么在沉默中死亡。
上述语句有这样的特点：
…………
命题是反映事物情况的思维 形式。
第三章 直言命题及其推理
命题与推理概述 直言命题 直言命题的直接推理 三段论
教学目的与要求：
• 通过本章的学习，理解直言命题的定义、种类， 明确什么是合乎逻辑的推理，掌握直言命题直 接推理的方法，掌握三段论的定义、结构、公 理、规则、格与式，学会判别这些推理无效式 的方法。提高正确运用这些推理的能力，为有 关论证知识的学习打下基础。
2、“他或者是工人，或者是干部。”
• 上述判断是以下哪种情况？（ ）
A、无所真假 B、真的 C、假的 D、或者是真的，或者是假的
3、“某体操队有些队员来自湖南。”
• 以上判断的对象是：（ ）
A、某体操队 B、某体操队的有些队员 C、体操队员 D、某体操队的所有队员
四、推理的结构及其种类
推理的定义与 有效性
三、命题推理及其特征
1、命题推理
命题推理 谓词推理
2、命题推理的特征
第二节 直言命题
一、什么是直言命题 二、直言命题的种类 三、直言命题词项的周延性 四、直言命题的真假性质
一、什么是直言命题
1、定义
陈述思维对象具有或不具 有某种性质的命题，也叫 性质命题。
（1）地球不是最大的行星。 （2）所有的经济规律都是客观规律。 （3）所有的金属都是导电的。 （4）有些青年不是文学爱好者。
第三章直言命题及其推理
第三章 直言命题及其推理
第一节 一、什么是判断
判断和推理的概述
肯定 否定
1.判断的定义： 对思维对象有所断定的思维形态。 例： 湖南大学是千年学府。 湖南大学不是世界一流大学。 中国或者是社会主义国家，或者是资本主义国家。 2.判断的逻辑特征： 有两个
(1) 判断必须有所断定 没有任何断定就不是判断 例：湖南大学在哪里？ (2) 判断必然有真或假 不可能既不是真也不是假的
2.同一语句可以表达不同的判断 这是由语句的多义性和语境的差异性造成的。 例： 一个工人的建议被采纳了。 也许只有一个建议，也许有很多建议。 只有一个建议。 小李肩上的担子很重。 也许是重量，也许是责任。 小店关门了。 也则 幽默： 而旅客住的房间漏雨，第二天早上，旅客对旅店
两个特征一个也不能少，而且要么两个特征同时，此时表达 的一定是判断；要么同时都没有，此时表达的就不是判断。
二、判断与语句的关系
判断的语言形式一定是语句，语句的内容则是判断， 但两者的关系不是简单的一对一的关系。 1.所有的判断都要通过语句表达，但不是所有的语句 都直接表达判断。 A. 陈述句直接表达判断，另外反诘疑问句也表达判断。 例：湖南大学难道不是千年学府吗？ B. 因疑而问的问句不直接表达判断。 例：湖南大学在哪里？ C. 祈使句、感叹句通常不直接表达判断。 例：啊，湖南大学！
一个县官画了一只老虎，但看去像猫。他叫了一个衙役来问：“你看这 是个啥？”衙役一看，直率地回答：“是猫，我的老爷。”这下可惹恼 了县官。他破口大骂：“你有眼无珠，把虎看成猫，真是胆大包天！” 他下令把这个衙役重责四十大板。县官又叫另一个衙役来看。这个衙役 一看，画上画的怪象黑猫，可他不敢说。县官问：“你说这是啥？”衙 役答：“老爷，我不敢说！”“你怕啥？”“ 我怕老爷！”县官生气 地质问：“那末我怕谁？”“老爷怕皇帝！”“皇帝又怕谁？”“皇帝 怕老天！”“老天怕什么？”“老天只怕云！”“云怕什么？”“云最 怕风！”“风怕什么？”“风很害怕墙！”“墙怕什么？”“墙怕老 鼠！”“老鼠怕什么？”这时，这个衙役指着老爷的画答道：“老鼠什
第一节 一、什么是判断
判断和推理的概述
肯定 否定
1.判断的定义： 对思维对象有所断定的思维形态。 例： 湖南大学是千年学府。 湖南大学不是世界一流大学。 中国或者是社会主义国家，或者是资本主义国家。 2.判断的逻辑特征： 有两个
(1) 判断必须有所断定 没有任何断定就不是判断 例：湖南大学在哪里？ (2) 判断必然有真或假 不可能既不是真也不是假的
2.同一语句可以表达不同的判断 这是由语句的多义性和语境的差异性造成的。 例： 一个工人的建议被采纳了。 也许只有一个建议，也许有很多建议。 只有一个建议。 小李肩上的担子很重。 也许是重量，也许是责任。 小店关门了。 也则 幽默： 而旅客住的房间漏雨，第二天早上，旅客对旅店
两个特征一个也不能少，而且要么两个特征同时，此时表达 的一定是判断；要么同时都没有，此时表达的就不是判断。
二、判断与语句的关系
判断的语言形式一定是语句，语句的内容则是判断， 但两者的关系不是简单的一对一的关系。 1.所有的判断都要通过语句表达，但不是所有的语句 都直接表达判断。 A. 陈述句直接表达判断，另外反诘疑问句也表达判断。 例：湖南大学难道不是千年学府吗？ B. 因疑而问的问句不直接表达判断。 例：湖南大学在哪里？ C. 祈使句、感叹句通常不直接表达判断。 例：啊，湖南大学！
一个县官画了一只老虎，但看去像猫。他叫了一个衙役来问：“你看这 是个啥？”衙役一看，直率地回答：“是猫，我的老爷。”这下可惹恼 了县官。他破口大骂：“你有眼无珠，把虎看成猫，真是胆大包天！” 他下令把这个衙役重责四十大板。县官又叫另一个衙役来看。这个衙役 一看，画上画的怪象黑猫，可他不敢说。县官问：“你说这是啥？”衙 役答：“老爷，我不敢说！”“你怕啥？”“ 我怕老爷！”县官生气 地质问：“那末我怕谁？”“老爷怕皇帝！”“皇帝又怕谁？”“皇帝 怕老天！”“老天怕什么？”“老天只怕云！”“云怕什么？”“云最 怕风！”“风怕什么？”“风很害怕墙！”“墙怕什么？”“墙怕老 鼠！”“老鼠怕什么？”这时，这个衙役指着老爷的画答道：“老鼠什
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
这句话的诀窍是什么？
思维训练
• 有一年京城举行科举考试，许多 考生路经此地，都要请算命先生算一 算能否考上。算命先生正襟危坐，双 眼微闭，扳起指头算了一会，然后向 三人伸出一个手指，“这是什么意 思？”三个考生不解，“一个，还 是……”“这就是答案！”算命先生 终于开了口，“你们自己思量去吧！ 倘若算错了，本人加倍奉还银子。”
哪些语句 表达命题
1.这份合同是有效的吗？ 2.人生七十古来稀。 3.人非草木，孰能无情。 4.2010年人类将登上火星。 5.1+101=110。 6.我喜欢贝多芬的音乐。 7.哎呀，那还得了！ 8.请把门关上！
3、并非所有的语句都表达命题。
陈述句，直接表达命题。
疑问句、感叹句、祈使 句，一般不直接表达命 题。
直言命题及其推理
命题与推理概述 直言命题 直言命题的直接推理 三段论
教学目的与要求：
• 通过本章的学习，理解直言命题的定义、种类， 明确什么是合乎逻辑的推理，掌握直言命题直 接推理的方法，掌握三段论的定义、结构、公 理、规则、格与式，学会判别这些推理无效式 的方法。提高正确运用这些推理的能力，为有 关论证知识的学习打下基础。
2、命题分类
简单命题
命 题
复合命题
性质命题 关系命题 合取命题 析取命题 蕴涵命题
等值命题
负命题
简单命题
由概念（词项）组成，自身不 包含其他命题的命题。汉语中的单 句常常表达简单命题。如： （1）有的物体是圆的。 （2）法律是一种行为规范。 （3）偶数大于奇数 （4）曹操是曹植的父亲。
复合命题
三、命题形式与种类
1、命题形式 2、命题分类
1、命题形式
• 所有的金属都是导体。 • 法律与道德是相联系的。 • 他或者是医生，或者是教师。 • 如果明天不下雨，那么我们就组织学生去博物馆参观。
• 上述各命题的逻辑形式分别是：
• 所有的S都是P， • a和b有R关系， • p或者q， • 如果p，那么q。
1.定义
2.特征
断定性 真假性
命题的特征
• 第一，断定性。
• 如：“这个周末我们去图书馆吗？”（疑问句，不是 命题。）
• 第二，真假性。
• “所有事物都是命题。）
• 命题的真值：任何命题或者真，或者假，但不能既真 又假。命题的真、假二值，逻辑上统称为命题的真值， 又称为命题的逻辑值。
思维训练
• 清代时京城附近有一算命先生， 算得准极了，大家都称他为活神仙。 张、万两人前来请他算命。他故弄玄 虚地问了张的生辰八字和父母的出生 年月，然后装模作样掐算一番，说： “这位官人是父在母先亡。”然后， 不管谁来算命，他都是这句话。竟被 他打发了各种不同情况的人。
•
问：算命先生玩弄了什么把戏？
由命题组成，自身包含其他命题的命题。汉语中 的复句常常表达复合命题。构成复合命题的命题 叫做支命题。如： (1)李白是诗人，并且杜甫是诗人。 (2)马琳或者王励勤能打入男单4强。 (3)如果你去打水，那我就去买饭。 (4)当且仅当一个三角形是等角三角形，则它是等边 三角形。 (5)并非所有的精神病人都不负刑事责任。
1、同一命题可以用不同的语句来表达。
“一切事物都是运动的。” “没有事物不是运动的。” “没有事物是不运动的。” “难道有不运动的事物吗？” “不运动的事物是没有的。”
思考：试用不同的语句来表达 “一切事物都包 含着矛盾。”
2、同一语句也可以表达不同的命题。
• 如： • “我看见白头翁。” • “小赵在房子里画画。” • “庭前花未发，阁下李先生。” • “无鸡鸭也可无鱼肉也可无萝卜青菜也
• 问：算命先生这回会失算吗？
思维训练
有个媒人给一对男女说媒。 “这个男的过日子真是一把好手。” “这个女的什么都好，就是有点嘴不严。”
• 有个媒人给一对男女说媒。她对那个女的说：“这 个男的过日子真是一把好手。”然后媒人又对那个男的 说：“这个女的什么都好，就是有点嘴不严。”那个男 的也认为“好翻点闲话”也不是什么大毛病。于是两人 都同意相亲。相亲时，只见那个男的倒背一只手，气宇 轩昂；那个女的则拿手帕捂着嘴，显得有点羞羞答答。 俩人都很满意。然而入洞房后，男的才发现那位“羞羞 答答”是个豁唇（俗称兔嘴）；而女的也发现这位“气 宇轩 昂”的一只手有残疾。两人都十分气愤，都去找 媒人要个“说法”。媒人却理直气壮地回答说：“我早 就告清楚你们了，一个是‘一把好手’，一个是‘有点 嘴不严’。并且你们也经过相亲同意了，怎么现在找起
3、命题与判断
• 判断是对思维对象有所断定的 思维形式。
• 所有的判断都是命题。
注意
张三是杀人犯。 李四不是杀人犯。 某甲和某乙是近亲属。
在传统逻辑中，命题与 判断可以不加区别。
二、命题与语句
1. 二者的联系 2. 二者的区别 同一命题可用不同的语句来表达。 同一语句可以表达不同的命题。 并非所有语句都是命题。
第一节 命题和推理概述
一、什么是命题 二、命题与语句
一、什么是命题
北京是中华人民共和国的首都。 中国既是社会主义国家，又是发展中国家。 2＋2＝5。 生态危机可能毁灭人类。 只有年满18周岁，才有选举权。 要么在沉默中爆发，要么在沉默中死亡。
上述语句有这样的特点：
…………
命题是反映事物情况的思维 形式。
可”
※ 日常语言表达的两种情形※
多样性
提供给我们丰 富的表达手段
歧义性
便于他人设 置语言陷阱
黑板是黑色的； The blackboard is black. 你烦不烦？
算命先生说：“桃园三结义，孤 独一枝”，弟兄几个？…… 媒婆说：“那个姑娘眼下没什么， 嘴上也没什么。“ “听话听声，锣鼓听音儿。”
※ 命题的另一种分类模式 ※
模态命题
命 题
非模态命题
命题的分类图示如下：
命题
模态命题
非模态命题
必然命题
可能命题
简单命题
复合命题
性质命题
联言命题
关系命题
假言命题
选言命题
负命题
1、下列语句是否是命题，为什么？
（1）民不畏死，奈何以死惧之。 （2）四个现代化的宏伟目标一定能实现。 （3）欲加之罪，何患无辞？ （4）明天下午上什么课？ （5）雪是黑的。 （6）天空是蓝色的。 （7）如果7大于6，那么6大于7。 （8）毛泽东生于1893年。 （9）你多大了？ （10）我们吃午饭吧。