最新2013届天津高三数学理科试题精选分类汇编7：立体几何

合集下载

2013年天津高考数学(理科)试题及答案

2013年天津市高考数学试卷(理科)(有答案)(Word版)

2013年高考理科数学试题(天津卷)及参考答案

2013年普通高等学校招生全国统一考试(天津卷)理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分, 共150分. 考试用时120分钟. 第Ⅰ卷1至2页, 第Ⅱ卷3至5页.答卷前, 考生务必将自己的姓名、准考证号填写在答题卡上, 并在规定位置粘贴考试用条形码. 答卷时, 考生务必将答案凃写在答题卡上, 答在试卷上的无效. 考试结束后, 将本试卷和答题卡一并交回.祝各位考生考试顺利!第Ⅰ卷注意事项：1. 每小题选出答案后, 用铅笔将答题卡上对应题目的答案标号涂黑. 如需改动, 用橡皮擦干净后, 再选凃其他答案标号.2. 本卷共8小题, 每小题5分, 共40分.参考公式:·如果事件A , B 互斥, 那么·棱柱的体积公式V =Sh ，其中S 表示棱柱的底面面积, h 表示棱柱的高. ·如果事件A , B 相互独立, 那么·球的体积公式其中R 表示球的半径.)()()(B P A P A P B ⋃=+)()(()B P A A P P B =34.3V R π=一．选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的. (1) 已知集合A = {x ∈R | |x |≤2}, A = {x ∈R | x ≤1}, 则(A)(B) [1,2](C) [－2,2](D) [－2,1](2) 设变量x , y 满足约束条件则目标函数z =y －2x 的最小值为 (A) －7 (B) －4 (C) 1 (D) 2(3) 阅读右边的程序框图, 运行相应的程序, 若输入x 的值为1, 则输出S 的值为(A) 64 (B) 73 (C) 512 (D) 585 (4) 已知下列三个命题:①若一个球的半径缩小到原来的, 则其体积缩小到原来的;②若两组数据的平均数相等, 则它们的标准差也相等;③直线x + y + 1 = 0与圆相切. 其中真命题的序号是:(A) ①②③ (B) ①②(C) ①③(D) ②③(5) 已知双曲线的两条渐近线与抛物线的准线分别交于A , B 两点, O 为坐标原点. 若双曲线的离心率为2, △AOB 的面积为, 则p =(A) 1(B)(C) 2 (D) 3(6) 在△ABC 中,则 =(A)(B) (C)(D)(7) 函数的零点个数为 (A) 1 (B) 2 (C) 3 (D) 4(8) 已知函数. 设关于x 的不等式的解集为A , 若,A B ⋂=(,2]-∞360,20,30,x y y x y ≥--≤+-⎧-≤⎪⎨⎪⎩12182212x y +=22221(0,0)x y a b a b -=>>22(0)px p y =>332,2,3,4AB BC ABC π∠===sin BAC ∠101010531010550.5()2|log |1xf x x =-()(1||)f x x a x =+()()f x a f x +<11,22A ⎡⎤-⊆⎢⎥⎣⎦则实数a 的取值范围是(A)(B) (C)(D)2013年普通高等学校招生全国统一考试(天津卷)理科数学第Ⅱ卷注意事项：1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上.2. 本卷共12小题, 共110分. 二．填空题: 本大题共6小题, 每小题5分, 共30分.(9) 已知a , b ∈R , i 是虚数单位. 若(a + i )(1 + i ) = bi , 则a + bi = . (10)的二项展开式中的常数项为 . (11) 已知圆的极坐标方程为, 圆心为C , 点P 的极坐标为, 则|CP | = .(12) 在平行四边形ABCD 中, AD = 1, , E 为CD 的中点.若AC ·BE ＝1, 则AB 的长为 . (13) 如图, △ABC 为圆的内接三角形, BD 为圆的弦, 且BD //AC . 过点A 做圆的切线与DB 的延长线交于点E , AD 与BC 交于点F . 若AB = AC , AE = 6, BD = 5, 则线段CF 的长为 .(14) 设a + b = 2, b >0, 则当a = 时, 取得最小值.三．解答题: 本大题共6小题, 共70分. 解答应写出文字说明, 证明过程或演算步骤. (15) (本小题满分13分)15,02⎛⎫- ⎪ ⎪⎝⎭13,02⎛⎫- ⎪ ⎪⎝⎭15,02130,2⎛⎫+⋃⎛ ⎪ ⎪⎝⎫- ⎪ ⎝⎭⎪⎭52,1⎛⎫-- ⎪ ⎝⎭∞⎪61x x ⎛⎫- ⎪⎝⎭4cos ρθ=4,3π⎛⎫⎪⎝⎭60BAD ︒∠=1||2||a a b +已知函数.(Ⅰ) 求f (x )的最小正周期;(Ⅱ) 求f (x )在区间上的最大值和最小值.(16) (本小题满分13分)一个盒子里装有7张卡片, 其中有红色卡片4张, 编号分别为1, 2, 3, 4; 白色卡片3张, 编号分别为2, 3, 4. 从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同). (Ⅰ) 求取出的4张卡片中, 含有编号为3的卡片的概率.(Ⅱ) 再取出的4张卡片中, 红色卡片编号的最大值设为X , 求随机变量X 的分布列和数学期望.(17) (本小题满分13分)如图, 四棱柱ABCD －A 1B 1C 1D 1中, 侧棱A 1A ⊥底面ABCD , AB //DC , AB ⊥AD , AD = CD = 1, AA 1 = AB = 2, E 为棱AA 1的中点.(Ⅰ) 证明B 1C 1⊥CE ;(Ⅱ) 求二面角B 1－CE －C 1的正弦值.(Ⅲ) 设点M 在线段C 1E 上, 且直线AM 与平面ADD 1A 1所成角的正弦值为, 求线段AM 的长.(18) (本小题满分13分)设椭圆的左焦点为F , 离心率为, 过点F 且与x 轴垂直的直线被椭圆截得的线段长为.(Ⅰ) 求椭圆的方程;(Ⅱ) 设A , B 分别为椭圆的左右顶点, 过点F 且斜率为k 的直线与椭圆交于C , D 两点. 若, 求k 的值.(19) (本小题满分14分)已知首项为的等比数列不是递减数列, 其前n 项和为, 且S 3 + a 3, S 5 + a 5, S 4 + a 4成等差数列.(Ⅰ) 求数列的通项公式;2()2sin 26sin cos 2cos 41,f x x x x x x π⎛⎫=-++- ⎪+⎝⎭∈R0,2π⎡⎤⎢⎥⎣⎦2622221(0)x y a b a b +=>>33433··8AC DB AD CB +=32{}n a (*)n S n ∈N {}n a(Ⅱ) 设, 求数列的最大项的值与最小项的值.(20) (本小题满分14分)已知函数.(Ⅰ) 求函数f (x )的单调区间;(Ⅱ) 证明: 对任意的t >0, 存在唯一的s , 使.(Ⅲ) 设(Ⅱ)中所确定的s 关于t 的函数为, 证明: 当时, 有.2013年普通高等学校夏季招生全国统一考试数学理工农医类(天津卷)第Ⅰ卷一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1．答案：D解析：解不等式|x |≤2，得－2≤x ≤2，所以A ＝{x |－2≤x ≤2}，所以A ∩B ＝{x |－2≤x ≤1}．故选D. 2．答案：A解析：作约束条件360,20,30x y x y y +-≥⎧⎪--≤⎨⎪-≤⎩所表示的可行区域，如图所示，z ＝y －2x 可化为y ＝2x ＋z ，z 表示直线在y 轴上的截距，截距越大z 越大，作直线l 0：y ＝2x ，平移l 0过点A (5,3)，此时z 最小为－7，故选A.3．答案：B解析：由程序框图，得x ＝1时，S ＝1；x ＝2时，S ＝9；x ＝4时，S ＝9＋64＝73，结束循环输出S 的值为73，故选B. 4．答案：C*()1n n nT S n S ∈=-N {}n T 2l ()n f x x x =()t f s =()s g t =2>e t 2ln ()15ln 2g t t <<解析：设球半径为R ，缩小后半径为r ，则r ＝12R ，而V ＝34π3R ，V ′＝33344114πππ33283r R R⎛⎫==⨯ ⎪⎝⎭，所以该球体积缩小到原来的18，故①为真命题；两组数据的平均数相等，它们的方差可能不相等，故②为假命题；圆x 2＋y 2＝12的圆心到直线x ＋y ＋1＝0的距离d＝=，因为该距离等于圆的半径，所以直线与圆相切，故③为真命题．故选C.5．答案：C解析：设A 点坐标为(x 0，y 0)，则由题意，得S △AOB ＝|x 0|·|y 0|.抛物线y 2＝2px 的准线为2p x =-，所以02p x =-，代入双曲线的渐近线的方程b y xa =±，得|y 0|＝2bpa .由2222,,ca abc ⎧=⎪⎨⎪+=⎩得b，所以|y 0|p .所以S △AOB2p =，解得p ＝2或p ＝－2(舍去)． 6．答案：C解析：在△ABC 中，由余弦定理得AC 2＝AB 2＋BC 2－2AB ·BC cos ∠ABC＝2923+-＝5，即得AC.由正弦定理sin sin AC BCABC BAC =∠∠，即3sin BAC=∠，所以sin ∠BAC.7．答案：B解析：函数f (x )＝2x |log 0.5x |－1的零点也就是方程2x |log 0.5x |－1＝0的根，即2x|log 0.5x |＝1，整理得|log 0.5x |＝12x ⎛⎫ ⎪⎝⎭.令g (x )＝|log 0.5x |，h (x )＝12x⎛⎫ ⎪⎝⎭，作g (x )，h (x )的图象如图所示．因为两个函数图象有两个交点，所以f (x )有两个零点．8．答案：A解析：f (x )＝x (1＋a |x |)＝22,0,,0.ax x x ax x x ⎧+≥⎨-+<⎩若不等式f (x ＋a )＜f (x )的解集为A ，且11,22⎡⎤-⎢⎥⎣⎦A ⊆，则在区间11,22⎡⎤-⎢⎥⎣⎦上，函数y＝f(x＋a)的图象应在函数y＝f(x)的图象的下边．(1)当a＝0时，显然不符合条件．(2)当a＞0时，画出函数y＝f(x)和y＝f(x＋a)的图象大致如图．由图可知，当a＞0时，y＝f(x＋a)的图象在y＝f(x)图象的上边，故a＞0不符合条件．(3)当a＜0时，画出函数y＝f(x)和y＝f(x＋a)的图象大致如图．由图可知，若f(x＋a)＜f(x)的解集为A，且11,22⎡⎤-⎢⎥⎣⎦A ⊆，只需1122f a f⎛⎫⎛⎫-+<-⎪ ⎪⎝⎭⎝⎭即可，则有2211112222a a a a⎛⎫⎛⎫⎛⎫--++-+<---⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(a＜0)，整理，得a2－a－1＜0a<<.∵a＜0，∴a∈⎫⎪⎪⎭.综上，可得a的取值范围是⎫⎪⎪⎭.第Ⅱ卷注意事项：1．用黑色墨水的钢笔或签字笔将答案写在答题卡上．2．本卷共12小题，共110分．二、填空题：本大题共6小题，每小题5分，共30分．9．答案：1＋2i解析：由(a＋i)(1＋i)＝a－1＋(a＋1)i＝b i，得10,1,aa b-=⎧⎨+=⎩解方程组，得a＝1，b＝2，则a＋b i＝1＋2i. 10．答案：15解析：二项展开式的通项为3662166C(1)Crrr r r rrT x x--+⎛==-⎝，3602r-=得r＝4，所以二项展开式的常数项为T5＝(－1)446C＝15.11．答案：解析：由圆的极坐标方程为ρ＝4cos θ，得圆心C的直角坐标为(2,0)，点P的直角坐标为(2,)，所以|CP|＝12．答案：1 2解析：如图所示，在平行四边形ABCD 中，AC ＝AB ＋AD ，BE ＝BC ＋CE ＝12-AB ＋AD .所以AC ·BE ＝(AB ＋AD )·12AB AD ⎛⎫-+ ⎪⎝⎭＝12-|AB |2＋|AD |2＋12AB ·AD ＝12-|AB |2＋14|AB |＋1＝1，解方程得|AB |＝12(舍去|AB |＝0)，所以线段AB 的长为12.13．答案：83解析：∵AE 为圆的切线，∴由切割线定理，得AE 2＝EB ·ED . 又AE ＝6，BD ＝5，可解得EB ＝4. ∵∠EAB 为弦切角，且AB ＝AC ， ∴∠EAB ＝∠ACB ＝∠ABC . ∴EA ∥BC .又BD ∥AC ，∴四边形EBCA 为平行四边形． ∴BC ＝AE ＝6，AC ＝EB ＝4. 由BD ∥AC ，得△ACF ∽△DBF ，∴45CF AC BF BD ==. 又CF ＋BF ＝BC ＝6，∴CF ＝83.14．答案：－2解析：因为a ＋b ＝2，所以1＝1||22||a b a a b +⋅+＝||||22||4||4||a ba ab a a b a a b ++=++≥+14||4||a a a a +=，当a ＞0时，5+1=4||4a a ，1||52||4a a b +≥；当a ＜0时，3+1=4||4a a ，1||32||4a a b +≥，当且仅当b ＝2|a |时等号成立．因为b ＞0，所以原式取最小值时b ＝－2a .又a ＋b ＝2，所以a ＝－2时，原式取得最小值．三、解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤． 15．解：(1)f (x )＝sin 2x·ππcossin 44x ⋅＋3sin 2x －cos 2x＝2sin 2x－2cos 2x＝π24x⎛⎫-⎪⎝⎭.所以，f(x)的最小正周期T＝2π2＝π.(2)因为f(x)在区间3π0,8⎡⎤⎢⎥⎣⎦上是增函数，在区间3ππ,82⎡⎤⎢⎥⎣⎦上是减函数．又f(0)＝－2，3π8f⎛⎫=⎪⎝⎭，π22f⎛⎫=⎪⎝⎭，故函数f(x)在区间π0,2⎡⎤⎢⎥⎣⎦上的最大值为，最小值为－2. 16．解：(1)设“取出的4张卡片中，含有编号为3的卡片”为事件A，则P(A)＝1322252547C C+C C6C7=.所以，取出的4张卡片中，含有编号为3的卡片的概率为67.(2)随机变量X的所有可能取值为1,2,3,4.P(X＝1)＝3347C1C35=， P(X＝2)＝3447C4C35=， P(X＝3)＝3547C2C7=， P(X＝4)＝3647C4C7=.所以随机变量X的分布列是随机变量X的数学期望EX＝1×135＋2×435＋3×27＋4×47＝175.17．解：(方法一)(1)证明：如图，以点A为原点建立空间直角坐标系，依题意得A(0,0,0)，B(0,0,2)，C(1,0,1)，B1(0,2,2)，C1(1,2,1)，E(0,1,0)．易得11B C＝(1,0，－1)，CE＝(－1,1，－1)，于是11B C·CE＝0，所以B1C1⊥CE.(2)1B C＝(1，－2，－1)．设平面B1CE的法向量m＝(x，y，z)，则10,0,B CCE⎧⋅=⎪⎨⋅=⎪⎩mm即20,0.x y zx y z--=⎧⎨-+-=⎩消去x，得y＋2z＝0，不妨令z＝1，可得一个法向量为m＝(－3，－2,1)．由(1)，B1C1⊥CE，又CC1⊥B1C1，可得B1C 1⊥平面CEC 1，故11B C＝(1,0，－1)为平面CEC1的一个法向量．于是cos〈m，11B C〉＝1111||||14B CB C⋅==⋅mm，从而sin 〈m ，11B C.所以二面角B 1－CE －C 1.(3)AE ＝(0,1,0)，1EC ＝(1,1,1)．设EM ＝λ1EC ＝(λ，λ，λ)，0≤λ≤1，有AM ＝AE ＋EM ＝(λ，λ＋1，λ)．可取AB ＝(0,0,2)为平面ADD 1A 1的一个法向量．设θ为直线AM 与平面ADD 1A 1所成的角，则sin θ＝|cos 〈AM ，AB 〉|＝AM ABAM AB⋅⋅=.=，解得13λ=，所以AM . (方法二)(1)证明：因为侧棱CC 1⊥底面A 1B 1C 1D 1，B 1C 1⊂平面A1B 1C 1D 1，所以CC1⊥B 1C 1.经计算可得B 1E B 1C 1，EC 1，从而B 1E 2＝22111B C EC +，所以在△B 1EC 1中，B 1C 1⊥C 1E ，又CC 1，C 1E ⊂平面CC 1E ，CC 1∩C 1E ＝C 1，所以B 1C 1⊥平面CC 1E ，又CE ⊂平面CC 1E ，故B 1C 1⊥CE .(2)过B 1作B 1G ⊥CE 于点G ，连接C 1G .由(1)，B 1C 1⊥CE ，故CE ⊥平面B 1C 1G ，得CE ⊥C 1G ，所以∠B 1GC 1为二面角B 1－CE －C 1的平面角．在△CC 1E 中，由CE ＝C 1E ，CC 1＝2，可得C 1G.在Rt △B 1C 1G 中，B 1G ，所以sin ∠B 1GC 1，即二面角B 1－CE －C 1.(3)连接D 1E ，过点M作MH ⊥ED 1于点H ，可得MH ⊥平面ADD 1A 1，连接AH ，AM ，则∠MAH 为直线AM 与平面ADD 1A 1所成的角．设AM ＝x ，从而在Rt △AHM 中，有MHx ，AHx .在Rt △C 1D 1E 中，C 1D 1＝1，ED 1，得EH13x =. 在△AEH 中，∠AEH ＝135°，AE ＝1，由AH 2＝AE 2＋EH 2－2AE ·EHcos 135°，得221711189x x x =++，整理得5x 2－－6＝0，解得x.所以线段AM.18．解：(1)设F (－c,0)，由c a=a =.过点F 且与x 轴垂直的直线为x ＝－c ，代入椭圆方程有2222()1c y a b -+=，解得y ==，解得b =，又a 2－c 2＝b 2，从而ac ＝1，所以椭圆的方程为22=132x y +.(2)设点C (x 1，y 1)，D (x 2，y 2)，由F (－1,0)得直线CD 的方程为y ＝k (x ＋1)，由方程组221,132y k x x y =(+)⎧⎪⎨+=⎪⎩消去y ，整理得(2＋3k 2)x 2＋6k 2x ＋3k 2－6＝0.求解可得x 1＋x 2＝22623k k -+，x 1x 2＝223623k k -+.因为A (3-，0)，B (3，0)，所以AC ·DB ＋AD ·CB＝(x 1y 1－x 2，－y 2)＋(x 2y 2x 1，－y 1)＝6－2x 1x 2－2y 1y 2＝6－2x 1x 2－2k 2(x 1＋1)(x 2＋1)＝6－(2＋2k 2)x 1x 2－2k 2(x 1＋x 2)－2k 2＝22212623k k +++. 由已知得22212623k k +++＝8，解得k ＝. 19．解：(1)设等比数列{a n }的公比为q ，因为S 3＋a 3，S 5＋a 5，S 4＋a 4成等差数列，所以S 5＋a 5－S 3－a 3＝S 4＋a 4－S 5－a 5，即4a 5＝a 3，于是25314a q a ==. 又{a n }不是递减数列且132a =，所以12q =-. 故等比数列{a n }的通项公式为11313(1)222n n n n a --⎛⎫=⨯-=-⋅ ⎪⎝⎭. (2)由(1)得11,121121,.2n n n n n S n ⎧⎫+⎪⎪⎪⎛⎫=--=⎪⎨ ⎪⎝⎭⎪⎪-⎪⎪⎩⎭为奇数，为偶数当n 为奇数时，S n 随n 的增大而减小，所以1＜S n ≤S 1＝32，故11113250236n n S S S S <-≤-=-=. 当n 为偶数时，S n 随n 的增大而增大，所以34＝S 2≤S n ＜1，故221134704312n n S S S S >-≥-=-=-. 综上，对于n ∈N *，总有715126n n S S -≤-≤. 所以数列{T n }最大项的值为56，最小项的值为712-. 20．解：(1)函数f (x )的定义域为(0，＋∞)．f ′(x )＝2x ln x ＋x ＝x (2ln x ＋1)，令f ′(x )＝0，得x =当x－＋所以函数f (x )的单调递减区间是⎛ ⎝，单调递增区间是⎫+∞⎪⎭. (2)证明：当0＜x ≤1时，f (x )≤0.设t ＞0，令h (x )＝f (x )－t ，x ∈[1，＋∞)．由(1)知，h (x )在区间(1，＋∞)内单调递增．h (1)＝－t ＜0，h (e t )＝e 2t ln e t －t ＝t (e 2t －1)＞0.故存在唯一的s ∈(1，＋∞)，使得t ＝f (s )成立．(3)证明：因为s ＝g (t )，由(2)知，t ＝f (s )，且s ＞1，从而2ln ()ln ln ln ln ln ()ln(ln )2ln ln(ln )2ln g t s s s u t f s s s s s u u ====++，其中u＝ln s.要使2ln()15ln2g tt<<成立，只需0ln2uu<<.当t＞e2时，若s＝g(t)≤e，则由f(s)的单调性，有t＝f(s)≤f(e)＝e2，矛盾．所以s＞e，即u＞1，从而ln u＞0成立．另一方面，令F(u)＝ln2uu-，u＞1.F′(u)＝112u-，令F′(u)＝0，得u＝2.当1＜u＜2时，F′(u)＞0；当u＞2时，F′(u)＜0. 故对u＞1，F(u)≤F(2)＜0.因此ln2uu<成立．综上，当t＞e2时，有2ln()15ln2g tt<<.祝福语祝你考试成功!。

天津市2013届最新高三数学精选分类汇编7 立体几何文

最新2013届天津高三数学文科试题精选分类汇编7：立体几何姓名____________班级___________学号____________分数______________一、选择题1 ．（天津市新华中学2012届高三上学期第二次月考文科数学）如图,是一个几何体的正视图、侧视图、俯视图,则该几何体的体积是（）A ．24B ．12C ．8D ．42 ．（天津市天津一中2013届高三上学期第二次月考数学文试题）在正三棱锥P ABC -中,,D E 分别是,AB AC 的中点,有下列三个论断:①PB AC ⊥;②AC //平面PDE ;③AB ⊥平面PDE ,其中正确论断的个数为（）A ．3个B ．2个C ．1个D ．0个 3 ．（天津市天津一中2013届高三上学期第二次月考数学文试题）设,m n 是两条不同的直线,γβα、、是三个不同的平面.给出下列四个命题: ①若m ⊥α,//n α,则m n ⊥; ②若γβγα⊥⊥,,则βα//; ③若//,//m n αα,则//m n ;④若//,//,m αββγα⊥,则m γ⊥.其中正确命题的序号是（）A ．①和②B ．②和③C ．③和④D ．①和④ 4 ．（天津市和平区2013届高三第一次质量调查文科数学）已知正四棱柱ABCD —A 1B 1C l D 1中，AA 1=2AB ，E是AA 1的中点，则异面直线D 1C 与BE 所成角的余弦值为（）A ．15B C D ．35二、填空题5 ．（天津市天津一中2013届高三上学期第三次月考数学文试题）已知某几何体的三视图如图所示,则该几何体的体积为___________.6 ．（天津市天津一中2013届高三上学期第二次月考数学文试题）如图,二面角l αβ--的大小是60°,线段AB α⊂.B l ∈,AB 与l 所成的角为30°.则AB 与平面β所成的角的正弦值是_________.7 ．（天津市天津一中2013届高三上学期第二次月考数学文试题）若某空间几何体的三视图如下图所示,则该几何体的体积是______.8 ．（天津市十二区县重点中学2013届高三毕业班联考（一）数学（文）试题）某几何体的三视图如图所示,则该几何体的体积为.9 ．（天津市六校2013届高三第二次联考数学文试题）若某几何的三视图(单位:cm )如下图所示,此几何体的体积是_____________3cm .10．（天津市滨海新区五所重点学校2013届高三联考试题数学（文）试题(解析版)）一个五面体的三视图如下,正视图与侧视图是等腰直角三角形,俯视图为直角梯形,部分边长如图所示,则此五面体的体积为________.11．（天津市和平区2013届高三第一次质量调查文科数学）已知某几何体的三视图如图所示，根据图中标出的尺寸(单位cm)，可得这个几何体的体积是 cm 3.12．（天津市渤海石油第一中学2013届高三模拟数学（文）试题（2））如图是一个几何体的三视图，则该几何体的体积为13．（2013年普通高等学校招生天津市南开区模拟考试(一)）一个几何体的三视图如右图所示(单位：cm)，则这个几何体的体积为立方厘米．2 2 22 24正视图侧视图俯视图三、解答题14．（天津市耀华中学2013届高三第一次月考文科数学试题）如图,在四棱锥P —ABCD 中,底面ABCD 为正方形,PD ⊥底面ABCD,且AB=PD=1. (1)求证:AC ⊥PB;(2)求异面直线PC 与AB 所成的角; (3)求直线PB 和平面PAD 所成角的正切值.15．（天津市新华中学2012届高三上学期第二次月考文科数学）如图,PAD ∆为等边三角形,ABCD 为矩形,平面⊥PAD 平面ABCD ,2=AB ,E 、F 、G 分别为PA 、BC 、PD 中点,22=AD .(1)求PB 与平面ABCD 所成角; (2)求证:EF AG ⊥;(3)求多面体AGF P -的体积.16．（天津市天津一中2013届高三上学期第三次月考数学文试题）如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧面PAD 是正三角形,且平面PAD ⊥底面ABCD (1)求证:AB ⊥平面PAD(2)求直线PC 与底面ABCD 所成角的余弦值; (3)设1AB =,求点D 到平面PBC 的距离.17．（天津市天津一中2013届高三上学期第二次月考数学文试题）如图,四面体ABCD 中,O 、E 分别是BD 、BC 的中点,2,CA CB CD BD AB AD ======(Ⅰ)求证:AO ⊥平面BCD ;(Ⅱ)求异面直线AB 与CD 所成角的余弦值; (III)求点E 到平面ACD 的距离.BE18．（天津市天津一中2013届高三上学期第二次月考数学文试题）在直三棱柱111ABC A B C -中,1111A B AC =,D E ，分别是棱1BC CC ，上的点(点D 不同于点C ),且AD DE F ⊥，为11B C 的中点.求证:(1)平面ADE ⊥平面11BCCB ; (2)直线1//A F 平面ADE .19．（天津市十二区县重点中学2013届高三毕业班联考（一）数学（文）试题）已知在四棱锥P ABCD-中,//AD BC ,AD CD ⊥,22PA PD AD BC CD ====,,E F 分别是,AD PC 的中点. (Ⅰ)求证AD PBE ⊥平面; (Ⅱ)求证//PA BEF 平面;(Ⅲ)若PB AD =,求二面角F BE C --的大小.20．（天津市六校2013届高三第二次联考数学文试题）如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,//AD BC ,90ADC ∠=,平面PAD ⊥底面ABCD ,E 为AD 的中点,M 是棱PC 的中点,2PA PD ==,112BC AD ==,CD =. (Ⅰ)求证:PE ⊥平面ABCD ;(Ⅱ)求直线BM 与平面ABCD 所成角的正切值; (Ⅲ)求直线BM 与CD 所成角的余弦值.PABCD EMA DFEBC21．（天津市滨海新区五所重点学校2013届高三联考试题数学（文）试题(解析版)）在如图的多面体中,EF ⊥平面AEB ,AE EB ⊥,//AD //EF BC ,24BC AD ==,2AE BE ==,G 是BC 的中点.(Ⅰ)求证://AB 平面DEG ;(Ⅱ)求直线BD 与平面BCFE 所成角的正切值; (Ⅲ)求证:BD EG⊥.22．（天津市和平区2013届高三第一次质量调查文科数学）如图，在直三棱柱ABC —A1BlC1中，，∠ACB=90o．AA 1=2，D 为AB 的中点.(I)求证：AC ⊥BC 1;(II)求证：AC 1//平面B 1CD ：(III)求异面直线AC 1与B 1C 所成角的余弦值23．（天津市渤海石油第一中学2013届高三模拟数学（文）试题（2））如图，在底面为直角梯形的四棱锥P ABCD -中，90AD BC ABC ∠=，∥°，PA ⊥平面ABCD ．326PA AD AB BC ====，，．（Ⅰ）求证：BD ⊥平面PAC ；（Ⅱ）求二面角P BD A --的大小24．（2013年普通高等学校招生天津市南开区模拟考试(一)）如图，四边形ABCD 是矩形，AD=2，DC=1，AB⊥平面BCE ，BE ⊥EC ，EC=1．点F 为线段BE 的中点． ( I )求证：CE ⊥平面ABE ；AEDPCB(Ⅱ)求证：DE∥平面A CF；(Ⅲ)求AC和平面ABE所成角的正弦值。

2013年天津市高考数学试卷(理科)及解析

2013年天津市高考数学试卷（理科）及解析本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分, 共150分. 考试用时120分钟. 第Ⅰ卷1至2页, 第Ⅱ卷3至5页.答卷前, 考生务必将自己的姓名、准考证号填写在答题卡上, 并在规定位置粘贴考试用条形码. 答卷时, 考生务必将答案凃写在答题卡上, 答在试卷上的无效. 考试结束后, 将本试卷和答题卡一并交回.祝各位考生考试顺利!第Ⅰ卷注意事项：1. 每小题选出答案后, 用铅笔将答题卡上对应题目的答案标号涂黑. 如需改动, 用橡皮擦干净后, 再选凃其他答案标号.2. 本卷共8小题, 每小题5分, 共40分.参考公式:·如果事件A , B 互斥, 那么)()()(B P A P A P B ⋃=+·棱柱的体积公式V =Sh ，其中S 表示棱柱的底面面积, h 表示棱柱的高.·如果事件A , B 相互独立, 那么)()(()B P A A P P B =·球的体积公式34.3V R π= 其中R 表示球的半径.一．选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的.(1) 已知集合A = {x ∈R | |x |≤2}, A = {x ∈R | x ≤1}, 则A B ⋂=(A) (,2]-∞ (B) [1,2] (C) [－2,2] (D) [－2,1]解析：本题主要考察不等式的解法，和集合的简单应用，属于简单题。

(2) 设变量x , y 满足约束条件360,20,30,x y y x y ≥--≤+-⎧-≤⎪⎨⎪⎩则目标函数z =y －2x 的最小值为(A) －7 (B) －4(C) 1 (D) 2解析：本题主要考查不等式中的线性规划，属于简单题。

(3) 阅读右边的程序框图, 运行相应的程序, 若输入x 的值为1, 则输出S 的值为(A) 64 (B) 73(C) 512 (D) 585解析：本题主要考察程序框图，属于简单题。

2013年天津市高考数学试卷(理科)答案与解析

2013年天津市高考数学试卷（理科）参考答案与试题解析一．选择题：(每题5分，共40分）在每小题给出的四个选项中，只有一项是符合题目要求的.2．（5分）（2013•天津）设变量x，y满足约束条件，则目标函数z=y﹣2x的，3．（5分）（2013•天津）阅读右边的程序框图，运行相应的程序，若输入x的值为1，则输出S的值为（）4．（5分）（2013•天津）已知下列三个命题：①若一个球的半径缩小到原来的，则其体积缩小到原来的；②若两组数据的平均数相等，则它们的标准差也相等；③直线x+y+1=0与圆相切．V=V=可知，若一个球的半径缩小到原来的；故的圆心到直线=相切，5．（5分）（2013•天津）已知双曲线﹣=1（a＞0，b＞0）的两条渐近线与抛物线y2=2px （p＞0）的准线分别交于O、A、B三点，O为坐标原点．若双曲线的离心率为2，△AOB求出双曲线的渐近线方程与抛物线的面积为，±x，±，双曲线的离心率为，所以则±=的面积为，，得6．（5分）（2013•天津）在△ABC中，，则sin∠BAC=（）BABC=AB=，=得：BAC=x（8．（5分）（2013•天津）已知函数f（x）=x（1+a|x|）．设关于x的不等式f（x+a）＜f（x）的解集为A，若，则实数a的取值范围是（）．﹣﹣|+1≤讨论，可得时，﹣﹣＜时，解得0＞时，解得，时，（﹣）二．填空题：本大题共6小题，每小题5分，共30分.9．（5分）（2013•天津）已知a，b∈R，i是虚数单位．若（a+i）（1+i）=bi，则a+bi=1+2i．，解得10．（5分）（2013•天津）的二项展开式中的常数项为15．=解；设•r=0的二项展开式中的常数项为=1511．（5分）（2013•天津）已知圆的极坐标方程为ρ=4cosθ，圆心为C，点P的极坐标为，则|CP|=．的极坐标为|CP|==2．12．（5分）（2013•天津）在平行四边形ABCD中，AD=1，∠BAD=60°，E为CD的中点．若，则AB的长为．，=+﹣，，∴故答案为13．（5分）（2013•天津）如图，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC．过点A做圆的切线与DB的延长线交于点E，AD与BC交于点F．若AB=AC，AE=6，BD=5，则线段CF的长为．故答案为：．14．（5分）（2013•天津）设a+b=2，b＞0，则当a=﹣2时，取得最小值．=﹣，=，当取得最小值时，取得最小值三．解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤. 15．（13分）（2013•天津）已知函数．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）在区间上的最大值和最小值．2x+）展开，结合二倍角的正余弦公式化简合=2）∈，得﹣﹣≤﹣，）在区间sinxcosx=x=2x+2cos2x=2﹣T==≤，∴﹣≤≤﹣）取得最小值﹣时，﹣）在区间上的最大值为）=216．（13分）（2013•天津）一个盒子里装有7张卡片，其中有红色卡片4张，编号分别为1，2，3，4；白色卡片3张，编号分别为2，3，4．从盒子中任取4张卡片（假设取到任何一张卡片的可能性相同）．（Ⅰ）求取出的4张卡片中，含有编号为3的卡片的概率．（Ⅱ）在取出的4张卡片中，红色卡片编号的最大值设为X，求随机变量X的分布列和数学期望．张的所有可能结果数有=的卡片的概率为====17．（13分）（2013•天津）如图，四棱柱ABCD﹣A1B1C1D1中，侧棱A1A⊥底面ABCD，AB∥DC，AB⊥AD，AD=CD=1，AA1=AB=2，E为棱AA1的中点．（Ⅰ）证明B1C1⊥CE；（Ⅱ）求二面角B1﹣CE﹣C1的正弦值．（Ⅲ）设点M在线段C1E上，且直线AM与平面ADD1A1所成角的正弦值为，求线段AM的长．标系，标出点的坐标后，求出和，由求出（Ⅱ）解：，，即．=．=．的正弦值为（Ⅲ）解：=．所以．的长为．18．（13分）（2013•天津）设椭圆=1（a＞b＞0）的左焦点为F，离心率为，过点F且与x轴垂直的直线被椭圆截得的线段长为．（Ⅰ）求椭圆的方程；（Ⅱ）设A，B分别为椭圆的左，右顶点，过点F且斜率为k的直线与椭圆交于C，D两点．若=8，求k的值．代入求出弦长使其等于，由，再由韦达定理进行求解．求得（Ⅰ）根据椭圆方程为，得±，=∵离心率为，∴=b=；﹣（﹣（，，（k=19．（14分）（2013•天津）已知首项为的等比数列{a n}不是递减数列，其前n项和为S n（n∈N*），且S3+a3，S5+a5，S4+a4成等差数列．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设，求数列{T n}的最大项的值与最小项的值．的方程，结合首项为的等比数列=不是递减数列，且等比数列的首项为﹣（﹣）﹣（﹣）=≤﹣==≥﹣=，总有≤，最小项的值为20．（14分）（2013•天津）已知函数f（x）=x2lnx．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）证明：对任意的t＞0，存在唯一的s，使t=f（s）．（Ⅲ）设（Ⅱ）中所确定的s关于t的函数为s=g（t），证明：当t＞e2时，有．，由导数在（，，一方面由﹣•，，（，，===成立，只需，2+，＜，＜，时，有成立．。

高考真题理科数学解析分类汇编7立体几何

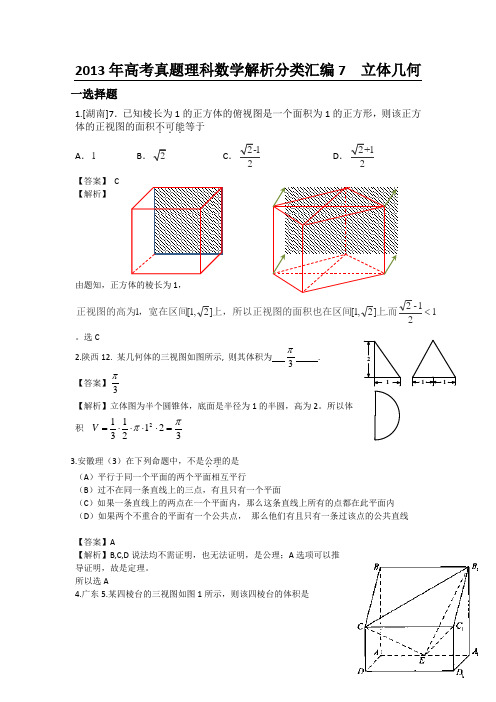
2013年高考真题理科数学解析分类汇编7 立体几何一选择题1.[湖南]7．已知棱长为1的正方体的俯视图是一个面积为1的正方形，则该正方体的正视图的面积不可能．．．等于 A ．1 BCD【答案】 C 【解析】由题知，正方体的棱长为1，1]2,1[1<，宽在区间正视图的高为。

选C2.陕西12. 某几何体的三视图如图所示, 则其体积为 3π. 【答案】3π 【解析】立体图为半个圆锥体，底面是半径为1的半圆，高为2。

所以体积32121312ππ=⋅⋅⋅⋅=V3.安徽理（3）在下列命题中，不是公理．．的是（A ）平行于同一个平面的两个平面相互平行（B ）过不在同一条直线上的三点，有且只有一个平面（C ）如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在此平面内（D ）如果两个不重合的平面有一个公共点，那么他们有且只有一条过该点的公共直线【答案】A【解析】B,C,D 说法均不需证明，也无法证明，是公理；A 选项可以推导证明，故是定理。

所以选A4.广东5.某四棱台的三视图如图1所示，则该四棱台的体积是图1A. 4B.143C.163D. 6解析：显然棱台的上下底的面积分别为1214S S==、，故其体积为121114V=()(124)2333S S h+=++⨯=选B5.广东6.设m，n是两条不同的直线，,αβ是两个不同的平面，下列命题中正确的是A.若,,m nαβαβ⊥⊂⊂，则m⊥n； B. 若//,,m nαβαβ⊂⊂，则//m nC. 若,,m n m nαβ⊥⊂⊂，则αβ⊥； D. 若,//,//m m n nαβ⊥，则αβ⊥解析：选D ∵,//,//m m n nαβ⊥，∴平面β内存在直线α⊥，故αβ⊥其它选项均错。

6.新课标I，6、如图，有一个水平放置的透明无盖的正方体容器，容器高8cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm，如果不计容器的厚度，则球的体积为 ( )A、500π3cm3B、866π3cm3C、1372π3cm3 D、2048π3cm3【解析】设球的半径为R，则由题知球被正方体上面截得圆的半径为4，球心到截面圆的距离为R-2，则222(2)4R R=-+，解得R=5，∴球的体积为3453π⨯=500π3 3cm，故选A.7.新课标I，8、某几何体的三视图如图所示，则该几何体的体积为A.168π+B.88π+C.1616π+D.816π+【命题意图】本题主要考查简单组合体的三视图及简单组合体体积公式，是中档题.【解析】由三视图知，该几何体为放到的半个圆柱底面半径为2高为4，上边放一个长为4宽为2高为2长方体，故其体积为21244222π⨯⨯+⨯⨯ =168π+，故选A .8.新课标II 4、已知m ，n 为异面直线，m ⊥平面α，n ⊥平面β，直线l 满足l ⊥m ，l ⊥n ，l ⊄α， l ⊄β，则（）（A ） α∥β且l ∥α （B ）α⊥β且l ⊥β（C ）α与β相交，且交线垂直于l （D ）α与β相交，且交线平行于l【答案】D设m ∥γ n ∥γ 因为 m ⊥β⟹m ⊥a n ⊥α⟹n ⊥a 所以a ⊥γ又l ⊥m ，l ⊥n 所以l ⊥γ 因此l ∥a新课标II 7、一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到正视图可以为（）(A)(B)(C)(D)【答案】A【解析】在空间直角坐标系中，先画出四面体O ABC -的直观图，以zOx 平面为投影面，则得到正视图(坐标系中红色部分),所以选A.9.江西8.如图，正方体的底面与正四面体的底面在同一平面α上，且AB CD ，正方体的六个面所在的平面与直线CE ，EF 相交的平面个数分别记为,m n ，那么m n +=A.8B.9C.10D.1110.辽宁（10）已知三棱柱1116.34ABC A B C O AB AC -==的个顶点都在球的球面上若，，,AB AC ⊥112AA O =，则球的半径为A B ．．132D ．[答案]C【解析】如图：因为,AB AC ⊥所以BC 是小圆的直径，是小圆的直径，所以球心在的中点R==11.全国（10）已知正四棱柱1111112,ABCD A B C D AA AB CD BDC -=中，则与平面所成角的正弦值等于（A ）23 （B ）3 （C ）3 （D ）13【答案】A【解析】如下图，连接AC 交BD 于点O ，连接1C O ,过C 作1CH C O ⊥于H 为垂足, ⟹⟹CH ⊥平面CD 与平面所成的角为∠CDH设AB=a 则OC=，CH==，sin ∠CDH=12.山东4、已知三棱柱111-ABC A B C 的侧棱与底面垂直，体积为94，的正三角形，若P 为底面111A B C 的中心，则PA 与平面ABC 所成角的大小为(A)512π (B) 3π (C) 4π (D) 6π13.四川3、一个几何体的三视图如图所示，则该几何体的直观图可以是（）14.重庆5、某几何体的三视图如题()5图所示，则该几何体的体积为（）A、5603B、5803C、200D、240【答案】：C15.湖北16.浙江二填空题17.上海13．在x O y平面上，将两个半圆弧22x y x(3)1(3)-+=≥、两条直线x y x(1)1(1)-+=≥和221y =和1y =-围成的封闭图形记为D ，如图中阴影部分．记D 绕y 轴旋转一周而成的几何体为Ω，过(0,)(||1)y y ≤作Ω的水平截面，所得截面面积为48π，试利用祖暅原理、一个平放的圆柱和一个长方体，得出Ω的体积值为__________ 答案2216ππ+[解析]：构造如图所示的圆柱和长方体长方体的长与圆柱的高是2π，圆柱的底面园的直径为2与长方体的侧面长方形的长为4，高为2则水平截面，所得截面面积为48π由祖暅原理得Ω的体积值==2π×4×2+π×2216ππ+18.浙江19. [江苏] 8．如图，在三棱柱ABC C B A -111中，F E D ，，分别是1AA AC AB ，，的中点，设三棱锥ADE F -的体积为1V ，三棱柱ABC C B A -111的体积为2V ，则=21:V V ．【答案】1：24【解析】三棱锥ADE F -与三棱锥ABC A -1的相似比为1：2，故体积之比为1：8．又因三棱锥ABC A -1与三棱柱ABC C B A -111的体积之比为1：3．所以，三棱锥ADE F -与三棱柱ABC C B A -111的体积之比为1：24．20.[全国] （16）已知圆O 和圆K 是球O 的大圆和小圆，其公共弦长等于球O 的半径，3602OK O K =，且圆与圆所在的平面所成角为，则球O 的表面积等于 .答案16π 解析：如图：过两圆相交弦AB 的中点E 分别与两圆圆心O,K 连线，得到两圆直径 CD,和GH 则CD ⊥AB ,和GH ⊥AB ,∠GEC 为两圆的二面角的平面角∠GEC =，O 是大圆圆心即为球心所以OK ⊥圆K 所在平面，AB=OA=OB=OC=R在正三角形AOB 中高OE=R ，在直角三角形OKE 中OK =OE ⟹R=⟹ R= 2⟹ S =16π21.辽宁（13）某几何体的三视图如图所示，则该几何体的体积是 .ABC1A DE F1B1C【答案】1616π-【解析】直观图是圆柱中去除正四棱柱。

2013年高考理科数2013年高考理科数学试题分类汇编：7立体几何

实用文档2013年高考理科数2013年高考理科数学试题分类汇编：7立体几何一、选择题1、（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若34AB AC ==，,AB AC ⊥,112AA =,则球O 的半径为（）AB．C ．132D．2、（2013年高考新课标1（理））如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为（）A ．35003cm πB ．38663cm πC ．313723cm πD ．320483cm π实用文档3、（2013年高考四川卷（理））一个几何体的三视图如图所示,则该几何体的直观图可以是4、（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））在空间中,过点A 作平面π的垂线,垂足为B ,记)(A f B π=.设βα,是两个不同的平面,对空间任意一点P ,)]([)],([21P f f Q P f f Q βααβ==,恒有21PQ PQ =,则（）A ．平面α与平面β垂直B ．平面α与平面β所成的(锐)二面角为045C ．平面α与平面β平行D ．平面α与平面β所成的(锐)二面角为0605、（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））在下列命题中,不是公理．．的是（）A ．平行于同一个平面的两个平面相互平行B ．过不在同一条直线上的三点,有且只有一个平面实用文档C ．如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D ．如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线6、（2013年高考江西卷（理））如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD ,正方体的六个面所在的平面与直线CE,EF 相交的平面个数分别记为,m n ,那么m n +=（）A ．8B ．9C ．10D ．117、高中数学人教版备份2013-10-15.ln8、（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,3的正三角形.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为（）实用文档A ．512πB ．3πC ．4πD ．6π9、（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于（）A ．23BCD ．1310、（2013年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是（）A ．若αβ⊥,m α⊂,n β⊂,则m n ⊥B ．若//αβ,m α⊂,n β⊂,则//m nC ．若m n ⊥,m α⊂,n β⊂,则αβ⊥D ．若m α⊥,//m n ,//n β,则αβ⊥11、（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为实用文档（）A ．B ．C ．D ．12、（2013年上海市春季高考数学试卷(含答案)）若两个球的表面积之比为1:4,则这两个球的体积之比为（）A ．1:2B ．1:4C ．1:8D ．1:1613、（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））已知n m ,为异面直线,⊥m 平面α,⊥n 平面β.直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则（）A ．βα//,且α//lB ．βα⊥,且β⊥lC ．α与β相交,且交线垂直于lD ．α与β相交,且交线平行于l实用文档14、（2013年高考新课标1（理））某几何体的三视图如图所示,则该几何体的体积为（）A ．168π+B ．88π+C ．1616π+D ．816π+15、（2013年高考湖北卷（理））一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有（）A ．1243V V V V <<<B ．1324V V V V <<<C 2134V V V V <<<D ．2314V V V V <<<16、（2013年高考湖南卷（理））已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方等于（）体的正视图的面积不可能．．．A．1B2C2-1D2+117、（2013年普通高等学校招生统一考试广东省数学（理）卷（纯WORD版））某四棱台的三视图如图所示,则该四棱台的体积是实用文档实用文档（）A ．4B ．143 C ．163D ．6二、填空题18、（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））如图,正方体1111ABCD A B C D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P ,Q 的平面截该正方体所得的截面记为S.则下列命题正确的是__①②③⑤___(写出所有正确命题的编号).①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形;③当34CQ =时,S 与11C D 的交点R 满足1113C R =;④当314CQ <<时,S 为六边形;⑤当1CQ =时,S 61 221 1正视俯视侧视第5题图实用文档19、（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））某几何体的三视图如图所示,则该几何体的体积是____________.20、（2013年高考陕西卷（理））某几何体的三视图如图所示, 则其体积为___3_____.112121、实用文档（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知圆O 和圆K是球O 的大圆和小圆,其公共弦长等于球O 的半径,32OK =,且圆O 与圆K 所在的平面所成的一个二面角为60,则球O 的表面积等于______.22、（2013年高考北京卷（理））如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 为BC 的中点,点P在线段D 1E 上,点P 到直线CC 1的距离的最小值为__________.23、（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））如图,在三棱柱ABC C B A -111中,F E D ，，分别是1AA AC AB ，，的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.A B C 1A D E F1B 1C 1B实用文档24、（2013年高考上海卷（理））在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y = 和1y =-围成的封闭图形记为D,如图中阴影部分.记D 绕y 轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为2418y ππ-+,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________25、（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD 版））已知某一多面体内接于一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________26、（2013年上海市春季高考数学试卷(含答案)）在如图所示的正方体1111ABCD A B C D -中,异面直线实用文档1A B 与1B C 所成角的大小为_______27、（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________2cm .三、解答题28、（2013年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））如图1,在等腰直角三角形ABC 中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE ==O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=.DC B ADC AB实用文档(1) 证明:A O '⊥平面BCDE ; (2) 求二面角A CD B '--的平面角的余弦值.29、（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））如图,直棱柱111ABC A B C -中,,D E 分别是1,AB BB 的中点,1AA AC CB AB ===. (1)证明:1//BC 平面1ACD ; (2)求二面角1D AC E --的正弦值.. CO B D EAC D O B E 'A图1图2实用文档 ABC D1A 1C 1B E实用文档30、（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD 版））如图,在四棱柱1111ABCD A B C D -中,侧棱1AA ABCD ⊥底面,//AB DC ,11AA =,3AB k =,4AD k =,5BC k =,6DC k =(0)k >.(1)求证:11;CD ADD A ⊥平面(2)若直线1AA 与平面1AB C 所成角的正弦值为67,求k 的值; (3)现将与四棱柱1111ABCD A B C D -形状和大小完全相同的两个四棱柱拼接成一个新的棱柱,规定:若拼接成的新的四棱柱形状和大小完全相同,则视为同一种拼接方案.问:共有几种不同的方案?在这些拼接成的新四棱柱中,记其中最小的表面积为()f k ,写出()f k 的表达式(直接写出答案,不必要说明理由)实用文档31、（2013年高考湖南卷（理））如图5,在直棱柱1111//ABCD A B C D AD BC -中，,90,,1BAD AC BD BC ∠=⊥=,13AD AA ==.(1)证明:1AC B D ⊥; (2)求直线111B C ACD 与平面所成角的正弦值..32、（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））如图所示,在三棱锥P ABQ-中,PB ⊥平面ABQ ,BA BP BQ ==,,,,D C E F 分别是,,,AQ BQ AP BP 的中点, 2AQ BD =,PD 与EQ 交于点G ,PC 与FQ 交于点H ,连接GH .(1)求证:AB GH ; (2)求二面角D GH E --的余弦值.33、（2013年普通高等学校招生统一考试大纲版数学（理）WORD版含答案（已校对））如图,四棱锥P ABCD-中,902,ABC BAD BC AD PAB∠=∠==∆，与PAD∆都是等边三角形.(I)证明:;PB CD⊥(II)求二面角A PD C--的大小.34、（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD版含附加题））本小题满分10分.如图,在直三棱柱111A B C ABC-中,ACAB⊥,2==ACAB,41=AA,点D是BC的中点(1)求异面直线BA1与DC1所成角的余弦值实用文档实用文档(2)求平面1ADC 与1ABA 所成二面角的正弦值.35、（2013年高考四川卷（理））如图,在三棱柱11ABC A B C -中,侧棱1AA ⊥底面ABC ,12AB AC AA ==,120BAC ∠=,1,D D 分别是线段11,BC B C 的中点,P 是线段AD 的中点.(1)在平面ABC 内,试作出过点P 与平面1A BC 平行的直线l ,说明理由,并证明直线l ⊥平面11ADD A ;(2)设(Ⅰ)中的直线l 交AB 于点M ,交AC 于点N ,求二面角1A A M N --的余弦值. D 1D B A B 1C 1AP36、如图,四棱锥P ABCD-中,PA ,ABCD E BD ⊥平面为的中点,G PD 为的中点，实用文档 3,12DAB DCB EA EB AB PA ∆≅∆====，,连接CE 并延长交AD 于F . (1) 求证:AD CFG ⊥平面; (2) 求平面BCP 与平面DCP 的夹角的余弦值.37、（2013年高考陕西卷（理））如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O ⊥平面ABCD , 12AB AA ==.(1) 证明: A 1C ⊥平面BB 1D 1D ;(2) 求平面OCB 1与平面BB 1D 1D 的夹角θ的大小.O D 1B 1C 1DA C A 1实用文档38、（2013年普通高等学校招生统一考试天津数学（理）试题（含答案））如图, 四棱柱ABCD -A 1B 1C 1D 1中, 侧棱A 1A ⊥底面ABCD , AB //DC , AB ⊥AD , AD = CD = 1, AA 1 = AB = 2, E 为棱AA 1的中点.(1) 证明B 1C 1⊥CE ;(2) 求二面角B 1-CE -C 1的正弦值.(3) 设点M 在线段C 1E 上, 且直线AM 与平面ADD 1A 1所成角的正弦值为26, 求线段AM 的长.39、（2013年高考北京卷（理））如图,在三棱柱ABC -A 1B 1C 1中,AA 1C 1C 是边长为4的正方形,平面ABC ⊥平面AA 1C 1C ,AB=3,BC=5.(1)求证:AA 1⊥平面ABC ;(2)求二面角A 1-BC 1-B 1的余弦值;(3)证明:在线段BC 1存在点D,使得AD ⊥A 1B ,并求1BD BC 的值.实用文档40、（2013年高考湖北卷（理））如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,直线PC ⊥平面ABC ,E ,F 分别是PA ,PC 的中点.(1)记平面BEF 与平面ABC 的交线为l ,试判断直线l 与平面PAC 的位置关系,并加以证明;(2)设(I)中的直线l 与圆O 的另一个交点为D ,且点Q 满足12DQ CP =.记直线PQ 与平面ABC 所成的角为θ,异面直线PQ 与EF 所成的角为α,二面角E l C --的大小为β,求证:sin sin sin θαβ=.41、（2013年高考上海卷（理））如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C,并求直线BC 1到平面D 1AC 的距离.第19题图实用文档 D 1C 1B 1A 1DC B A42、（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））本小题满分14分.如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ，分别是棱SC SA ，的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.43、（2013年上海市春季高考数学试卷(含答案)）如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC 与1AA 所成角的大小为6π,求该三棱柱的体积.B 1A 1C 1 AC B ABC SGF E实用文档44、（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））如图,在四面体BCDA -中,⊥AD 平面BCD ,22,2,==⊥BD AD CD BC .M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且QC AQ 3=.(1)证明://PQ 平面BCD ;(2)若二面角D BM C --的大小为060,求BDC ∠的大小.;45、（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））如图,圆锥顶点为p .底面圆心为o ,其母线与底面所成的角为22.5°.AB 和CD 是底面圆O 上的两条平行的弦,轴OP 与平面PCD 所成的角为60°.(1)证明:平面PAB 与平面PCD 的交线平行于底面; (2)求cos COD ∠.AB CDP QM（第20题图）实用文档46、（2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））如图,四棱锥P ABCD-中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.47、（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD版））如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点.(1)求证:PAC PBC ⊥平面平面；(2)2.AB AC PA C PB A ===--若，1，1，求证：二面角的余弦值48、（2013年高考新课标1（理））如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.(1)证明AB⊥A1C;(2)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C 与平面BB1C1C所成角的正弦值.以下是答案一、选择题1、C2、A3、D4、A5、A6、A实用文档7、C8、B9、A10、D11、A12、C13、D14、A15、C16、C17、D二、填空题18、①②③⑤π-19、1616实用文档实用文档20、3π21、16π2223、1:2424、2216ππ+.25、12π26、23π27、24三、解答题28、(1) 在图1中,易得3,OC AC AD ===实用文档x连结,OD OE ,在OCD ∆中,由余弦定理可得OD == 由翻折不变性可知A D '=所以222A O OD A D ''+=,所以A O OD '⊥,理可证A O OE '⊥, 又OD OE O =,所以A O '⊥平面BCDE .(2) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥,所以A HO '∠为二面角A CD B '--的平面角.结合图1可知,H 为AC 中点,故OH =,从而A H '== 所以cos OH A HO A H '∠=='所以二面角A CD '--向量法:以O 点为原点,建立空间直角坐标系O xyz -则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=-设(),,n x y z =为平面A CD '的法向量,则 CDO B E 'AH实用文档 00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即330230y z x y z ⎧+=⎪⎨-++=⎪⎩,解得3y x z x =-⎧⎪⎨=⎪⎩,令1x =,得()1,1,3n =- 由(Ⅰ) 知,()0,0,3OA '=为平面CDB 的一个法向量, 所以315cos ,535n OA n OA n OA '⋅'===⋅',即二面角A CD B '--的平面角的余弦值为155.29、30、解:(1)取CD 中点E ,连接BE实用文档//AB DE ,3AB DE k ==∴四边形ABED 为平行四边形//BE AD ∴且4BE AD k ==在BCE 中,4,3,5BE k CE k BC k ===222BE CE BC ∴+=90BEC ∴∠=︒,即BE CD ⊥,又//BE AD ,所以CD AD ⊥1AA ⊥平面ABCD ,CD ⊂平面ABCD 1AA CD ∴⊥,又1AA AD A =,CD ∴⊥平面11ADD A(2)以D 为原点,1,,DA DC DD 的方向为,,x y z 轴的正方向建立如图所示的空间直角坐标系(4,0,0)A k ,(0,6,0)C k ,1(4,3,1)B k k ,1(4,0,1)A k所以(4,6,0)AC k k =-,1(0,3,1)AB k =,1(0,0,1)AA =设平面1AB C 的法向量(,,)n x y z =,则由10AC n AB n ⎧⋅=⎪⎨⋅=⎪⎩得46030kx ky ky z -+=⎧⎨+=⎩取2y =,得(3,2,6)n k =-设1AA 与平面1AB C 所成角为θ,则111,sin |cos ,|||||AA n AA n AA n θ=〈〉=⋅26673613k k ==+,解得1k =.故所求k 的值为1 (3)共有4种不同的方案实用文档2257226,018()53636,18k k k f k k k k ⎧+<≤⎪⎪=⎨⎪+>⎪⎩31、(1) AC BB ABCD BD ABCD BB D C B A ABCD ⊥⇒⊂⊥∴-111111,面且面是直棱柱D B AC BDB D B BDB AC B BB BD BD AC 11111,,⊥∴⊂⊥∴=⋂⊥，面。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

最新2013届天津高三数学理科试题精选分类汇编7：立体几何一、选择题1 ．（天津市和平区2013届高三第一次质量调查理科数学）已知正四棱柱ABCD —A 1B 1C l D 1中，AA 1=2AB ，E 是AA 1的中点，则异面直线DC 1与BE 所成角的余弦值为（）A ．15B C D ．352 ．（天津市新华中学2013届高三寒假复习质量反馈数学（理）试题）某几何体的三视图如图所示,则它的体积是（）A ．283π-B ．83π-C ．82π-D ．23π3 ．（天津市天津一中2013届高三上学期第二次月考数学理试题）几何体的三视图如图所示,则该几何体的体积为（）A ．2π+B ．4π+C ．2πD ．4π+4 ．（天津市新华中学2013届高三第三次月考理科数学）已知三棱锥S ABC -的所有顶点都在球O 的球面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =，则此棱锥的体积为（）A B ．C D 5 ．（天津市新华中学2013届高三第三次月考理科数学）设b a ,是两条直线，βα,是两个平面，则b a ⊥的一个充分条件是（）A ．βαβα⊥⊥,//,b aB ．βαβα//,,⊥⊥b aC ．βαβα//,,⊥⊂b aD ．βαβα⊥⊂,//,b a6 ．（天津市新华中学2013届高三第三次月考理科数学）如图，E 、F 分别是三棱锥P-ABC 的棱AP 、BC 的中点，PC=10，AB=6，EF=7，则异面直线AB 与PC 所成的角为（）（）A ．90°B ．60°C ．45°D ．30°二、填空题7 ．（天津市十二区县重点中学2013届高三毕业班联考（一）数学（理）试题）某几何体的三视图如图所示,则该几何体的体积为__________.8 ．（天津市六校2013届高三第二次联考数学理试题（WORD 版））一个几何体的三视图如上图所示,且其侧视图为正三角形,则这个几何体的体积为 .9 ．（天津南开中学2013届高三第四次月考数学理试卷）一个棱锥的三视图如图,则该棱锥的全面积(单位:cm 2)为________.10．（2012-2013-2天津一中高三年级数学第四次月考检测试卷（理））一个几何体的三视图如图所示，则该几何体的表面积与体积分别为___________11．（天津市新华中学2012届高三上学期第二次月考理科数学）如图为一个几何体的三视图，其中俯视为正三角形，A 1B 1=2,AA 1=4，则该几何体的表面积为_______。

12．（天津市滨海新区五所重点学校2013届高三联考试题数学（理）试题）右图是一个空间几何体的三视图,则该几何体的体积大小为___________________.13．（天津市天津一中2013届高三上学期第二次月考数学理试题）已知直线m,n 与平面α,β,给出下列三个命题:①若m∥α,n∥α,则m∥n;②若m∥α,n⊥α,则n⊥m;③若m⊥α,m∥β,则α⊥β.其中真命题的个数是______个14．（天津市天津一中2013届高三上学期第三次月考数学理试题）已知某几何体的三视图如图所示,则该几何体的体积为___________.15．（天津市新华中学2013届高三第三次月考理科数学）已知一个几何体的三视图如下图所示(单位：cm)，其中正视图是直角梯形，侧视图和俯视图都是矩形，则这个几何体的体积是________cm3.16．（天津耀华中学2013届高三年级第三次月考理科数学试卷）一个几何体的三视图如图所示，则该几何体的体积为____________；三、解答题 17．（天津市十二区县重点中学2013届高三毕业班联考（一）数学（理）试题）如图,四棱柱1111D C B A ABCD -的底面A B C 是平行四边形,且1=AB ,2=BC ,060=∠ABC ,E 为BC 的中点, ⊥1AA 平面ABCD .(Ⅰ)证明:平面⊥AE A 1平面DE A 1;(Ⅱ)若E A DE 1=,试求异面直线AE 与D A 1所成角的余弦值; (Ⅲ)在(Ⅱ)的条件下,试求二面角1--C A D E 的余弦值.18．（天津市六校2013届高三第二次联考数学理试题（WORD 版））如图,直三棱柱ABC-A 1B 1C 1中∠ACB=90°,M,N 分别为A 1B,B 1C 1的中点,BC=AA 1=2AC=2,求证:(1)求三棱柱C 1-A 1CB 的体积;(2)求直线A 1C 与直线MB 1所成角的余弦值;(3)求平面B 1MN 与平面A 1CB 所成锐二面角的余弦值.19．（天津市新华中学2013届高三寒假复习质量反馈数学（理）试题）已知四棱锥P-ABCD 的底面为直角梯形,AB∥DC,⊥=∠PA DAB ,90底面ABCD, 且PA=AD=DC=21AB=1,M 是PB 的中点. (Ⅰ)证明:面PAD⊥面PCD; (Ⅱ)求AC 与PB 所成角的余弦值;(Ⅲ)求面AMC 与面BMC 所成二面角的余弦值.ABCDE1A 1B 1C 1D20．（天津南开中学2013届高三第四次月考数学理试卷）如图,已知四棱锥E-ABCD 的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE=2(1)求证:平面EAB⊥平面ABCD(2)求二面角A-EC-D 的余弦值21．（2012-2013-2天津一中高三年级数学第四次月考检测试卷（理））.在长方体1111ABCD A B C D -中，1AB BC ==，12AA =，E 为1BB 中点.（Ⅰ）证明：1AC D E ⊥；（Ⅱ）求DE 与平面1AD E 所成角的正弦值；（Ⅲ）在棱AD 上是否存在一点P ，使得BP ∥平面1AD E ？若存在，求DP 的长；若不存在，说明理由.D 1C 1B 1A 1ED CA22．（天津市耀华中学2013届高三第一次月考理科数学试题）(本小题满分13分)在如图所示的多面体中，EF ⊥平面AEB ，AE ⊥EB ，AD//EF ，EF//BC ．BC=2AD=4，EF=3，AE=BE=2，G 为BC 的中点。

(1)求证：AB//平面DEG ； (2)求证：BD ⊥EG ；(3)求二面角C —DF —E 的正弦值。

23．（天津市滨海新区五所重点学校2013届高三联考试题数学（理）试题）如图在四棱锥P ABCD -中,底面A B C D 是边长为a 的正方形,侧面PAD ⊥底面A B C D ,且PA PD AD ==,设E 、F 分别为PC 、BD 的中点. (Ⅰ) 求证:EF //平面PAD ; (Ⅱ) 求证:面PAB ⊥平面PDC ; (Ⅲ) 求二面角B PD C --的正切值.24．（天津市天津一中2013届高三上学期第二次月考数学理试题）如图,在四棱锥P-ABCD 中,底面为直角梯ABCD,AD∥BC,∠BAD=90O,PA⊥底面ABCD,且PA=AD=AB=2BC,M,N 分别为PC,PB 的中点.(1)求证:PB⊥DM;(2)求CD 与平面ADMN 所成角的正弦值;(3)在棱PD 上是否存在点E,PE∶ED=λ,使得二面角C-AN-E 的平面角为60o.存在求出λ值.BA25．（天津市天津一中2013届高三上学期第三次月考数学理试题）在四棱锥P ABCD -中,底面ABCD 是直角梯形,AB ∥CD ,∠90ABC=, 2AB PB PC BC CD ====,平面PBC ⊥平面ABCD .(1)求证:AB ⊥平面PBC ;(2)求平面PAD 和平面BCP 所成二面角(小于90°)的大小; (3)在棱PB 上是否存在点M 使得CM ∥平面PAD ?若存在,求PMPB的值;若不存在,请说明理由.PABC D26．（天津市新华中学2013届高三第三次月考理科数学）如图，在四棱锥ABCD P -中，底面ABCD 是正方形，侧棱⊥PD 底面ABCD ，DC PD =，E 是PC 的中点，作PB EF ⊥交PB 于点F（1）证明://PA 平面EDB . （2）证明:⊥PB 平面EFD .（3）求二面角D PB C --的大小.27．（天津耀华中学2013届高三年级第三次月考理科数学试卷）（本小题满分13分）在四棱锥P －ABCD 中，底面ABCD 是直角梯形，AB//CD ，︒90=ABC ∠，AB=PB=PC=BC=2CD ，平面PBC ⊥平面ABCD. （1）求证：AB ⊥平面PBC ；（2）求平面ADP 与平面BCP 所成的锐二面角的大小；（3）在棱PB 上是否存在点M 使得CM//平面PAD ？若存在，求PBPM的值；若不存在，请说明理由.最新2013届天津高三数学试题精选分类汇编7：立体几何参考答案一、选择题 1. B 2. A 3. 【答案】C解:由三视图可知,该几何体下面是半径为1,高为2的圆柱.上面是正四棱锥.真四棱锥,底面边长为,所以四棱锥的体积为213⨯=,圆柱的体积为2π,所以该几何体的体积为2π+,选C. 4. 【答案】A【解析】因为ABC ∆为边长为1的正三角形，且球半径为1，所以四面体O ABC -为正四面体，所以ABC ∆的外接圆的半径为3，所以点O 到面ABC 的距离d ==,所以三棱锥的高2SF OE ==,所以三棱锥的体积为11326⨯=，选A.5. 【答案】C【解析】若b β⊥，//αβ，所以b α⊥，又a α⊂，所以b a ⊥，即a b ⊥，所以选C.6. 【答案】B【解析】,取AC 的中点M,连结EM,MF ，因为E,F 是中点，所以16//,322MF AB MF AB ===,110//,522ME PC ME PC ===,所以MF 与ME 所成的角即为AB 与PC 所成的角。

在三角形MEF 中，222537151c o s 253302E MF +--===-⨯⨯，所以120EMF ∠=,所以直线AB 与PC 所成的角为为60，选B.二、填空题 7. π3108+ ; 8.π63334+9. 21248+10. 2，3211. 【答案】24【解析】由三视图可知，该几何体是一个正三棱柱，底面边长为2，高是4.所以该三棱柱的表面积为2122324242⨯⨯+⨯⨯=。

12. 【答案】243π-由三视图可知，该几何体时一个边长为2，2,1的长方体挖去一个半径为1的半球。

所以长方体的体积为2214⨯⨯=，半球的体积为142233ππ⨯=，所以该几何体的体积为243π-。

13. 【答案】2解:①平行于同一平面的两直线不一定平行,所以①错误.②根据线面垂直的性质可知②正确.③根据面面垂直的性质和判断定理可知③正确,所以真命题的个数是2个. 14. 【答案】3π解:由三视图我们可知原几何体是一个圆柱体的一部分,并且有正视图知是一个12的圆柱体,底面圆的半径为1,圆柱体的高为6,则知所求几何体体积为原体积的一半为3π.15. 【答案】32【解析】由三视图可知，该几何体为一个放到的四棱柱，以梯形为低，所以梯形面积为1(12)322⨯+=，四棱柱的高为1，所以该几何体的体积为32。