100测评网高二数学练习卷2008届高三第三次调研测试
数学_2007-2008学年江苏省常州某校高三(上)第三次调研数学试卷(文科)(含答案)

2007-2008学年江苏省常州某校高三(上)第三次调研数学试卷(文科)一、填空题(本大题满分70分)1. 命题“∃x ∈R ,x 2−2x +4>0”的否定为________.2. 已知集合M ={−1, 1},N ={x|12<2x+1<4,x ∈Z},则M ∩N =________.3. 若等比数列{a n }的前三项和S 3=1且a 3=1,则a 2等于________.4. 已知tan(π4+θ)=3,则sin2θ−2cos 2θ+1的值为________.5. 函数f(x)=log 12(2x 2−3x +1)的单调递减区间是________.6. 已知向量a →=(−2, −1)b →=(t, 1),且a →与b →的夹角为钝角,则实数t 的取值范围是________. 7. 设F 1、F 2分别是双曲线x 2−y 29=1的左右焦点,点P 在双曲线上,且PF 1→⋅PF 2→=0,则|PF 1→+PF 2→|=________.8. 已知函数y =log 3(mx +1)在(−∞, 1)上是减函数,则实数 m 的取值范围是________. 9. 已知实数x ,y 满足{y ≤1y ≥|x −1|,则3x −y 的最大值是________.10. 若“a ≥b ⇒c >d“和“a <b ⇒e ≤f“都是真命题,其逆命题都是假命题,则“c ≤d“是“e ≤f“的________条件. 11. 若不等式t t 2+9≤a ≤t+2t 2在t ∈(0, 2]上恒成立,则实数a 的取值范围是________.12. 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.则该几何体的体积为________,用________个这样的几何体就可以拼成一个棱长为6的正方体ABCD −A 1B 1C 1D 1.13. 已知定义在R 上的函数f(x)的图象关于点(−34,0)对称,且满足f(x)=−f(x +32),又f(−1)=1,f(0)=−2,则f(1)+f(2)+f(3)+...+f(2008)=________.14. 如图,第(1)个多边形是由正三角形“扩展”而来,第(2)个多边形是由正方形“扩展”而来…如此类推.设由正n 边形“扩展”而来的多边形的边数为a n ,则a 6=________;1a 3+1a 4+1a 5+⋯+1a 99=________.二、解答题(本大题满分90分)15. 在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,已知tanA +tanC =√3(tanA ⋅tanC −1),且b =72,S △ABC =3√32. 求:(1)角B ;(2)a +c 的值.16.如图,在正方体ABCD −A 1B 1C 1D 1中,E 、F 分别是BB 1、CD 的中点.(1)证明AD ⊥D 1F ;(2)求AE 与D 1F 所成的角.17. 如图所示,我校计划在汉东中学操场北修建一个矩形花坛并在花坛内装置两个相同的喷水器.已知喷水器的喷水区域是半径为5m 的圆.问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?18.如图F 1(−c, 0),F 2(c, 0)为双曲线E 的两焦点,以F 1F 2为直径的圆O与双曲线E 交于M 、N 、M 1、N 1,B 是圆O 与y 轴的交点,连接MM 1与OB 交于H ,且H 是OB 的中点.(1)当c =1时,求双曲线E 的方程;(2)试证:对任意的正实数c ,双曲线E 的离心率为常数;(3)连接F 1M 与双曲线E 交于点A ,是否存在常数λ,使F 1A →=λAM →恒成立,若存在试求出λ的值;若不存在,请说明理由.19. 已知数列{a n }、{b n }、{c n }的通项公式满足b n =a n+1−a n ,c n =b n+1−b n (n ∈N ∗).若数列{b n }是一个非零常数列,则称数列{a n }是一阶等差数列;若数列{c n }是一个非零常数列,则称数列{a n }是二阶等差数列.(1)试写出满足条件a 1=1,b 1=1,c n =1的二阶等差数列{a n }的前五项; (2)求满足条件(1)的二阶等差数列{a n }的通项公式a n ;(3)若数列{a n}的首项a1=2,且满足c n−b n+1+3a n=−2n+1(n∈N∗),求数列{a n}的通项公式.)<20. 已知函数f(x)=ax2+4x−2满足对任意x1,x2∈R且x1≠x2,都有f(x1+x22f(x1)+f(x2).2(1)求实数a的取值范围;(2)试讨论函数y=f(x)在区间[−1, 1]上的零点的个数;(3)对于给定的实数a,有一个最小的负数M(a),使得x∈[M(a), 0]时,−4≤f(x)≤4都成立,则当a为何值时,M(a)最小,并求出M(a)的最小值.2007-2008学年江苏省常州某校高三(上)第三次调研数学试卷(文科)答案1. ∀x∈R,x2−2x+4≤02. {−1}3. −14. 155. (1, +∞)6. (−1,2)∪(2,+∞)27. 2√108. [−1, 0)9. 510. 充分非必要条件11. [2,1]1312. 72,313. 114. 42,9730015. 解:(1)∵ tan(A+C)=tanA+tanC1−tanAtanC∴ tanA+tanC=tan(A+C)⋅(1−tanA⋅tanC)∵ A+C=π−B∴ tan(A+C)=tan(π−B)=−tanB∴ tanA+tanC=−tanB(1−tanAtanC)=tanB(tanAtanC−1)又∵ tanA+tanC=√3(tanA⋅tanC−1),∴ tanB=√3.∵ B∈(0, π)∴ B=π…3(2)∵ S △ABC =12ac ⋅sinB ,且B =π3,S △ABC =3√32, ∴ ac =6.∵ b 2=a 2+c 2−2accosB ,b =72, ∴ (72)2=(a +c)2−2ac(1+cosB),∴ (a +c)2=1214∵ a +c >0 ∴ a +c =112…16. 解:(I)∵ AC 1是正方体, ∴ AD ⊥面DC 1. 又D 1F ⊂面DC 1, ∴ AD ⊥D 1F .(II)取AB 中点G ,连接A 1G ,FG .因为F 是CD 的中点,所以GF 、AD 平行且相等,又A 1D 1、AD 平行且相等,所以GF 、A 1D 1平行且相等,故GFD 1A 1是平行四边形,A 1G // D 1F . 设A 1G 与AE 相交于点H ,则∠AHA 1是AE 与D 1F 所成的角,因为E 是BB 1的中点,所以Rt △A 1AG ≅Rt △ABE ,∠GA 1A =∠GAH ,从而∠AHA 1=90∘,即直线AE 与D 1F 所成角为直角. 17. 花坛的长为10√2m ,宽为5√2m ,两喷水器位于矩形分成的两个正方形的中心,则符合要求.18. 解:(1)由c =1有B(0, 1),H(0,12),M(√32,12), 设E:x 2a 2−y 2b 2=1(a >0,b >0),M 在E 上,则{a 2+b 2=134a 2−14b2=1解得{a 2=12b 2=12, ∴ 当c =1时,双曲线E 的方程E:2x 2−2y 2=1 (2)F 1(−c,0),B(0,c),H(0,c2),M(√3c 2,c2) 设E:x 2a 2−y 2b 2=1(a >0,b >0),{a 2+b 2=c 23c 24a 2−c 24b 2=1,即3e 4−8e 2+4=1,e 2=2或e 2=23(舍), ∴ e =√2为常数 (3)设存在常数λ,使F 1A →=λAM →恒成立, ∴ F 1(−c,0),M(√3c 2,c2), 有A((√3λ−2)c 2(1+λ),λc 2(1+λ)),A 在E 上,则(√3λ−2)2c 24(1+λ)2a 2−λ2c 24(1+λ)2b 2=1,∵ e =√2, 则ca =cb =√2, ∴ λ=√3−14∴ 存在常数λ=√3−14使F 1A →=λAM →恒成立19. 解:(1)a 1=1,a 2=b 1+a 1=2,b 2=c 1+b 1=2∴ a 3=b 2+a 2=4,同样的道理求得a 4=7,a 5=11 (2)依题意b n+1−b n =c n =1,n =1,2,3所以b n =(b n −b n−1)+(b n−1−b n−2)+(b n−2−b n−3)+...+(b 2−b 1)+b 1 =1+1+1+1+...+1=n又a n+1−a n =b n =n ,n =1,2,3,所以a n =(a n −a n−1)+(a n−1−a n−2)+(a n−2−a n−3)+...+(a 2−a 1)+a 1=(n −1)+(n −2)+...+2+1+1=n(n−1)2+1=n 2−n+22(3)由已知c n −b n+1+3a n =−2n+1,可得b n+1−b n −b n+1+3a n =−2n+1, 即b n −3a n =2n+1,整理得:a n+1+2n+1=4(a n +2n ),因而数列{a n +2n }的首项为a 1+2=4,公比为4的等比数列, ∴ a n +2n =4⋅4n−1=4n , 即a n =4n −2n 20. 解:(1)∵ f(x 1+x 22)−f(x 1)+f(x 2)2=a(x 1+x22)2+b(x 1+x 22)+c −ax 12+bx 1+c+ax 22+bx 2+c 2=−a4(x 1−x 2)2<0,4分又∵ x 1≠x 2,∴ 必有a >0,∴ 实数a 的取值范围是(0, +∞).2分(2)△=16+8a ,由(1)知:a >0,所以△>0. 由a >0,f(1)=a +2>0 ①当0<a <6时,总有f(−1)<0,f(0)=−2<0,f(1)>0, 故0<a <6时,f(x)在[−1, 1]上有一个零点;2分②当a >6时,{a >0−1<−42a <1f(1)=a +4−2>0f(−1)=a −4−2>0,即a >6时,f(x)在[−1, 1]上有两个零点;2分③当a =6时,有f(−1)=0,f(0)=−2<0,f(1)>0,故a =6时,f(x)在[−1, 1]上有两个零点.综上:0<a <6时,f(x)在[−1, 1]上有一个零点;a ≥6时,f(x)在[−1, 1]上有两个零点.2分(3)∵ f(x)=ax2+4x−2=a(x+2a )2−2−4a,显然f(0)=−2,对称轴x=−2a<0.①当−2−4a <−4,即0<a<2时,M(a)∈(−2a,0),且f[M(a)]=−4.令ax2+4x−2=−4,解得x=−2±√4−2aa,此时M(a)取较大的根,即M(a)=−2+√4−2aa =√4−2a+2,∵ 0<a<2,∴ M(a)=√4−2a+2>−1.2分②当−2−4a ≥−4,即a≥2时,M(a)<−2a,且f[M(a)]=4.令ax2+4x−2=4,解得x=−2±√4+6aa,此时M(a)取较小的根,即M(a)=−2−√4+6aa =√4+6a+2,∵ a≥2,∴ M(a)=√4+6a−2≥−3.当且仅当a=2时,取等号.3分∵ −3<−1,∴ 当a=2时,M(a)取得最小值−3.1分.。
广东惠州市高三第三次调研考试数学试题(理科卷)及祥解

7 8 994 4 6 4 7 3惠州市2008届高三第三次调研考试数学试题(理科卷 2008.1) 第Ⅰ卷(选择题,共40分)一.选择题:本大题共8小题。
在每小题给出的四个选项中,只有一项是符合题目要求的.每小题5分,满分40分.1.设集合{1,2}A =,则满足{1,2,3}A B ⋃=的集合B 的个数是( ).A .1B .3C .4D .82.如果复数i a a a a z )23(222+-+-+=为纯虚数,那么实数a 的值为( ).A .-2B .1C .2D .1或 -23.计算机是将信息转换成二进制进行处理的. 二进制即“逢二进一”,如2(1101)表示二进制数,将它转换成十进制形式是321012120212⨯+⨯+⨯+⨯= 13,那么将二进制数211611111)(个转换成十进制形式是( ). A .1722- B .1622- C .1621- D .1521- 4.若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计算,其参考数据如下:那么方程32220x x x +--=的一个近似根(精确到0.1)为( ). A .1.2 B .1.3 C .1.4 D .1.55.下图是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( ).A .84,4.84B .84,1.6C .85,1.6D .85,46.定义运算a ⊕b=⎩⎨⎧>≤)()(b a b b a a ,则函数f(x)=1⊕2x的图象是( ).7.椭圆满足这样的光学性质:从椭圆的一个焦点发射光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现在设有一个水平放置的椭圆形台球盘,满足方程:191622=+y x ,点A 、B 是它的两个焦点,当静止的小球放在点A 处,从点A 沿直线出发,经椭圆壁反弹后,再回到点A 时,小球经过的最短路程是( ).A .20B .18C .16D .以上均有可能8.已知函数①x x f ln 3)(=;②x e x f c o s 3)(=;③x e x f 3)(=;④x x f cos 3)(=.其中对于)(x f 定义域内的任意一个自变量1x 都存在唯一个自变量)()(,212x f x f x 使=3成立的函数是( ).A .③B .②③C .①②④D .④第Ⅱ卷(非选择题,共110分)二、填空题:本大题共7小题,其中13~15题是选做题,考生只能选做两题,三题全答的,只计算前两题得分.每小题5分,满分30分.9.已知向量(4,0),(2,2),AB AC ==则BC AC 与的夹角的大小为 . 10.按下列程序框图运算:规定:程序运行到“判断结果是否大于244”为1次运算,若x =5,则运算进行 次才停止。
2008届全国百套高考数学模拟试题分类汇编-130新课程标准内容

2008届全国百套高考数学模拟试题分类汇编13新课程标准内容一、选择题1、(广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)已知命题p: "x ÎR ,cos x ≤1,则( )A .1cos ,:≥∈∃⌝x R x pB .:p Ø" x ∈R,cos x ≥1C . 1cos ,:>∈∃⌝x R x pD .:p Ø" x ∈R,cos x >1答案:C2、(广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)给出下面的程序框图,那么输出的数是 ( )A .2450 B. 2550 C. 5050 D. 4900 答案:C3、(广东省2008届六校第二次联考)如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是( )A. 2(20cm +B. 221cmC. 2(24cm +D. 224cm 答案:A4、(广东省佛山市2008年高三教学质量检测一)如图,水平放置的三棱柱的侧棱长和底边长均为2, 且侧棱1111AA A B C ⊥面,正视图是边长为2的正方形, 该三棱柱的左视图面积为( ).A. 4B. 32C. 22D.3答案:B俯视图左视图_B _1_A _1_B_A_B _1 _A _1_B _A正视图俯视图7 8 994 4 6 4 7 35、(广东省佛山市2008年高三教学质量检测一)为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如,明文1,2,3,4对应密文5,7,18,16. 当接收方收到密文14,9, 23,28时,则解密得到的明文为( ).A .4,6,1,7B .7,6,1,4C .6,4,1,7D .1,6,4,7答案:C6、(广东省惠州市2008届高三第三次调研考试)若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计算,其参考数据如下:那么方程32220x x x +--=的一个近似根(精确到0.1)为( ). A .1.2 B .1.3 C .1.4 D .1.5解析:f (1.40625)=-0.054< 0,f (1.4375)=0.162> 0 且都接近0,由二分法可知其根近似于1.4。
100测评网高三数学复习江苏省镇江市三所省重点高中2008-2009学年第一学期期中

江苏省镇江市三所省重点高中2008-2009学年第一学期期中联考高二数学试卷(文科)江苏省句容高级中学 江苏省大港中学 江苏省扬中高级中学2008年11月 命题人:樊荣良一.填空题:本大题共14小题,每小题5分,共70分.1.方程022=++-+m y x y x 表示一个圆,则m 的范围是_____________ 2.抛物线28x y =的焦点坐标为_________3.已知21F F 、为椭圆192522=+y x 的两个焦点,过1F 的直线交椭圆于A 、B 两点 若1222=+B F A F ,则AB =______________。
4.若双曲线12222=-by a x 的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是______________ 5.设椭圆C 1的离心率为135,焦点在X 轴上且长轴长为26.若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为______________6.如果直线1+=kx y 与圆0422=-+++my kx y x 交于M 、N 两点,且M 、N 关于直线0=+y x 对称,则=+m k _________7.现给出一个算法,算法语句如下图,若其输出值为1,则输入值x 为 8.下图中流程图表示的算法的运行结果是_________9.阅读右框中伪代码,若输入的n 为50,则输出的结果是 .10.若点A 的坐标()2,3,F 为抛物线x y 22=的焦点,点P 在该抛物线上移动,为使得PA PF +取得最小值,则P 点的坐标为________ .11.过点()0,4-作直线l 与圆0204222=--++y x y x 交于A 、B 两点,若AB=8,则直线l 的方程为___________________________12.如图,某人向圆内投镖,如果他每次都投中圆内,那么他投中正方形区域的概率为 (结果用分数表示)13. 设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是14.P 为椭圆22143x y +=上的一点,M 、N 分别是圆22(1)4x y ++= 和22(1)1x y -+=上的点,则|PM | + |PN |的最大值为 .二.解答题:本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤. 15.(本题满分14分)将一颗骰子先后抛掷2次,观察向上的点数,问: (1)共有多少种不同的可能结果?(2)点数之和是5的倍数的可能结果有多少种? (3)点数之和是5的倍数的概率是多少?16.(本题满分15分)抛物线顶点在原点,焦点是圆0422=-+x y x 的圆心。
修改版2008届高三调研考试数学试题(理科)答案及评分标准校对版
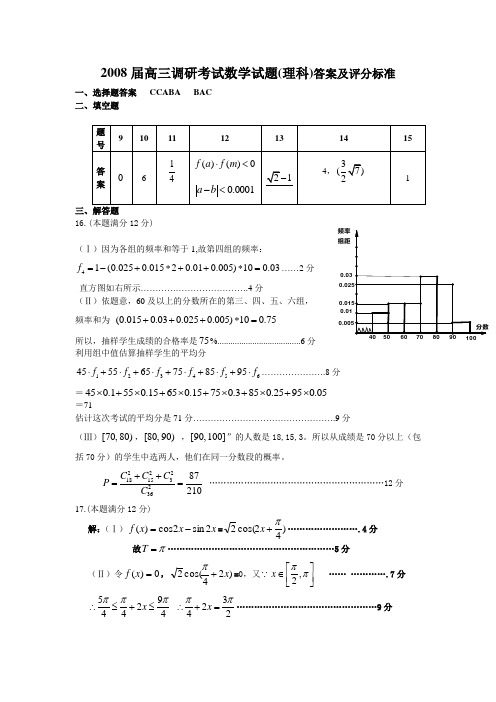
0.030.01频率组距2008届高三调研考试数学试题(理科)答案及评分标准一、选择题答案 CCABA BAC 二、填空题三、解答题16.(本题满分12分)(Ⅰ)因为各组的频率和等于1,故第四组的频率:41(0.0250.01520.010.005)100.03f =-+*++*=……2分直方图如右所示……………………………….4分(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组, 频率和为 (0.0150.030.0250.005)100.75+++*=所以,抽样学生成绩的合格率是75%......................................6分 利用组中值估算抽样学生的平均分123456455565758595f f f f f f ⋅+⋅+⋅+⋅+⋅+⋅………………….8分=450.1550.15650.15750.3850.25950.05⨯+⨯+⨯+⨯+⨯+⨯ =71估计这次考试的平均分是71分………………………………………….9分(Ⅲ)[70,80),[80,90) ,[90,100]”的人数是18,15,3。
所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
22218153236C C C P C ++==87210 ……………………………………………………12分 17.(本题满分12分)解:(Ⅰ)x x x f 2sin 2cos )(-==)42cos(2π+x …………………….4分故π=T …………………………………………………5分 (Ⅱ)令0)(=x f ,)24cos(2x +π=0,又 ,2x ππ⎡⎤∈⎢⎥⎣⎦…… ………….7分 592444x πππ∴≤+≤ 3242x ππ∴+=…………………………………………9分故58x π=函数)(x f 的零点是58x π= ……………. 12分 18.(本题满分12分)证(Ⅰ)因为AB ⊥侧面11BB C C ,故1AB BC ⊥ 在1BC C 中,1111,2,3BC CC BB BCCπ===∠=由余弦定理有1BC == 故有 222111BC BC CC C B BC += ∴⊥而 BC AB B = 且,AB BC ⊂平面ABC∴1C B ABC ⊥平面(Ⅱ)由11,,,,EA EB AB EB ABAE A AB AE ABE ⊥⊥=⊂平面从而1B E ABE ⊥平面 且BE ABE ⊂平面 故1BE B E ⊥不妨设 CE x =,则12C E x =-,则221BE x x =+-又1123B C C π∠= 则2211B E x x =++在1Rt BEB 中有 22114x x x x +++-+= 从而1x =±(舍负)故E 为1CC 的中点时,1EA EB ⊥法二:以B 为原点1,,BC BC BA 为,,x y z 轴,设CE x =,则11(0,0,0),(1),(2B E x B A -- 由1EA EB ⊥得 10EA EB ⋅=即11(1,2)(,0)2211(1)(2)022x x x x x x x --=⎫--=⎪⎪⎭化简整理得 2320x x -+= 1x = 或 x = 当2x =时E 与1C 重合不满足题意EC 1B 1A 1CBA111当1x =时E 为1CC 的中点 故E 为1CC 的中点使1EA EB ⊥(Ⅲ)取1EB 的中点D ,1A E 的中点F ,1BB 的中点N ,1AB 的中点M 连DF 则11//DF A B ,连DN 则//DN BE ,连MN 则11//MN A B 连MF 则//MF BE ,且MNDF 为矩形,//MD AE 又1111,A B EB BE EB ⊥⊥ 故MDF ∠为所求二面角的平面角在Rt DFM 中,111(22DF A B BCE==∆为正三角形)111222MF BE CE === 1tan 2MDF ∴∠== 法二:由已知1111,EA EB B A EB ⊥⊥, 所以二面角11A EB A --的平面角θ的大小为向量11B A与EA 的夹角因为11B A BA ==1(2EA=-- 故 11112cos tan 3EA B A EA B A θθ⋅==⇒=⋅.19. (本题满分14分)解:(Ⅰ)依题意知,直线l 的方程为:1x =-.点R 是线段FP 的中点,且RQ ⊥FP ,∴RQ 是线段FP 的垂直平分线.…………………….2分∴PQ 是点Q 到直线l 的距离.∵点Q 在线段FP 的垂直平分线,∴PQ QF =.…………4分 故动点Q 的轨迹E 是以F 为焦点,l 为准线的抛物线,其方程为:24(0)y x x =>.…………………………………………………….7分(Ⅱ) 设()()B B A A y x B y x A ,,,,()()N N M M y x N y x M ,,,,直线AB 的方程为)1(-=x k y…………………………………………………….8分则⎪⎩⎪⎨⎧==)2(4)1(422BB AA x y x y(1)—(2)得k y y B A 4=+,即ky M 2=,……………………………………9分代入方程)1(-=x k y ,解得122+=kx M .所以点M的坐标为222(1,)k k+.……………………………………10分同理可得:N 的坐标为2(21,2)k k +-.直线MN 的斜率为21kkx x y y k N M N M MN -=--=,方程为 )12(1222---=+k x kkk y ,整理得)3()1(2-=-x k k y ,………………12分 显然,不论k 为何值,(3,0)均满足方程,所以直线MN 恒过定点R (3,0). (14)20. (本题满分14分) .解:11n na kn a +=+ 故2211a a k a ==+,.……………………………………1分 又因为()211111,,2n n n n n a a a a a a n N n +--+==+∈≥则3121a a a a =22a +,即3322221,21,2a aa k a k a a =+=+∴=又.………………………3分 所以212,1k a k k +==∴=, ……………………………………4 (2)11,n na n a +=+ 121121n n n n n a a a a a a a a ---=⋅⋅⋅⋅⋅⋅⋅⋅=()1...21!n n n ⋅-⋅⋅⋅= ……………………………………6 因为()()11!n n a x g x n -=-=1n nx -所以,当1x =时,()()()11123 (2)n n f x f n +==++++=.................................7 当1x ≠时,()21123...n f x x x nx -=++++. (1)()1x ⋅得()()23123...1n n xf x x x x n x nx -=++++-+……(2) ()()()()2112:11...n n x f x x x x nx ---=++++-=11nn x nx x--- ()()2111nn x nx f x xx -∴=--- ……………………………9 综上所述:2(1),12()1,1(1)1n nn n x f x x nx x x x+⎧=⎪⎪=⎨-⎪-≠⎪--⎩ ……………………………10 (3)因为()()()212221211212nnn n f n -∴=-=-+-- 又()333n g n=,易验证当1,2n =,3时不等式不成立; ……………………………11 假设()3n k k =≥,不等式成立,即()3121kkk >-+ 两边乘以3得:()()111331232131222k k k k k k k k k +++>-+=⋅++--+又因为()()()131222233223220k k k k k k k k k +--⋅+=--+=-+>所以()11113213122221k k k k k k k k k ++++>⋅++--+>⋅+即1n k =+时不等式成立.故不等式恒成立. (14)21. (本题满分14分) 解:(Ⅰ)()ln(1)(1),x f x a e a x =+-+(1)()(1)011x xx xae a e f x a e e-+-'∴=-+=<++恒成立,………………………… 所以函数()f x 在(,)-∞+∞上是单调减函数. …………………………4分(Ⅱ) 证明:据题意1,12233(()),(,()),(,())A x f x B x f x C x f x 且x 1<x 2<x 3,由(Ⅰ)知f (x 1)>f (x 2)>f (x 3), x 2=231x x +…………………………6分 12123232(,()()),(,()()BA x x f x f x BC x x f x f x ∴=--=--12321232()()[()()][()()]BA BC x x x x f x f x f x f x ∴⋅=--+--…………………8分123212320,0,()()0,()()0x x x x f x f x f x f x -<->->-<0,(,)2BA BC B ππ∴⋅<∴∠∈即⊿ABC 是钝角三角形……………………………………..9分(Ⅲ)假设⊿ABC 为等腰三角形,则只能是BA BC =即2132()()()f x f x f x =+3212132ln(1)2(1)[ln(1)(1)(1)()x x x a e a x a e e a x x ⇔+-+=++-++ 321222ln(1)2(1)[ln(1)(1)2(1)x x x a e a x a e e a x ⇔+-+=++-+3212ln(1)ln(1)(1)x x x e e e ⇔+=++31332122122(1)(1)(1)2x x x x x x x x x e e e e e e e e +⇔+=++⇔+=++3212x x x e e e ⇔=+ ① …………………………………………..12分而事实上, 3122xx x e e e +≥= ②由于31xxe e <,故(2)式等号不成立.这与(1)式矛盾. 所以⊿ABC 不可能为等腰三角形..14分222212123232()[()()]()[()()]x x f x f x x x f x f x -+-=-+-即:2221321232[()()][()()]x x x x f x f x f x f x -=-∴-=-。
100测评网高二数学练习卷高三第三次调研试题

苏北四市高三第三次调研试题 物理试题 04.28一、单项选择题:本题共5小题,每小题3分,共15分.每小题只有一个....选项符合题意. 1.利用速度传感器与计算机结合,可以自动作出物体运动的图像. 某同学在一次实验中得到的运动小车的速度—时间图像如图所示,以下说法错误的是( )A .小车先做加速运动,后做减速运动B .小车运动的最大速度约为0.8m /sC .小车的位移一定大于8mD .小车做曲线运动2.一质量为m 、带电量为q 的小球用细线系住,线的一端固定在o 点. 若在空间加上匀强电场,平衡时线与竖直方向成60°角。
则电场强度的最小值为( )A .mg/2qB .3mg/2qC .2mg/qD .mg/q3. 如右图所示,曲线C 1、C 2分别是纯电阻直流电路中,内、外电路消耗的电功率随电流变化的图线.由该图可知下列说法中错误的是( ) A .电源的电动势为4VB .电源的内电阻为1ΩC .电源输出功率最大值为8WD .电源被短路时,电源消耗的最大功率可达16W4. 如图所示,相距为d 的两平行金属板水平放置,开始开关S 合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个带电粒子恰能以水平速度v 向右匀速通过两板间.在以下方法中,要使带电粒子仍能匀速通过两板,(不考虑带电粒子所受重力)正确的是 ( )A .把两板间距离减小一倍,同时把粒子速率增加一倍B .把两板的距离增大一倍,同时把板间的磁场增大一倍C .把开关S 断开,两板的距离增大一倍,同时把板间的磁场减小一倍D .把开关S 断开,两板的距离减小一倍,同时把粒子速率减小一倍5.如图所示,P 、Q 是电量相等的两个正电荷,它们的连线中点是O ,A 、B 是PQ 连线的中垂线上的两点,OA <OB ,用E A 、E B 、φA 、φB 分别表示A 、B 两点的场强和电势,则( ) A .E A 一定大于E B ,φA 一定大于φB B .E A 不一定大于E B ,φA 一定大于φB C .E A 一定大于E B ,φA 不一定大于φB D .E A 不一定大于E B ,φA 不一定大于φB.0.1/v s二.多项选择题:本题共 4 小题,每小题 4 分,共16 分.每小题有多个选项....符合题意.全部选对的得 4 分,选对但不全的得 2 分,错选或不答的得 0 分. 6.如图所示,虚线EF 的下方存在着正交的匀强电场和匀强磁场,电场强度为E ,磁感应强度为B .一带电微粒自离EF 为h 的高处由静止下落,从B 点进入场区,做了一段匀速圆周运动,从D 点射出. 下列说法正确的是A .微粒受到的电场力的方向一定竖直向上B .微粒做圆周运动的半径为ghB E 2C .从B 点运动到D 点的过程中微粒的电势能先增大后减小D .从B 点运动到D 点的过程中微粒的电势能和重力势能之 和在最低点C 最小7.如图所示,质量为m 的小球A 沿高度为h 倾角为θ的光滑斜面以初速v 0滑下. 另一质量与A 相同的小球B 自相同高度由静止落下,结果两球同时落地。
100测评网高二数学练习卷普通高中高三教学质量检测

2008年佛山市普通高中高三教学质量检测(二)物理试题本试卷分选择题和非选择题两部分,共10页,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考号填写在答题卡上.用2B铅笔将答题卡试卷类型(A)填涂在答题卡上,并在答题卡右上角的“试室号”和“座位号”栏填写试室号、座位号,将相应的试室号、座位号信息点涂黑.2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答卷上各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁,考试结束后,将答卷和答题卡一并交回.第一部分选择题(共 48 分)一、本题共 12 小题,每小题 4 分,共 48分。
在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确,全部选对的得 4 分,选不全的得 2 分,有错选或不答的得 0 分。
1.下列说法中正确的是A.开普勒通过对天体运动的长期观察,发现了行星运动三定律B.牛顿运动定律可以适应于以接近光速的速度运动的物体C.查德威克通过实验发现了中子D.楞次发现了电磁感应定律2.当氢原子由较高能级跃迁到较低能级时将A .辐射光子,获得能量B.吸收光子,获得能量C.吸收光子,放出能量D.辐射光子,放出能量3.2008年3月24日在希腊点燃了象征着和平、友谊、希望的奥林匹克圣火,罗雪娟成为我国第一个火炬接力手。
某记者拍下固定在地面的旗帜和旗杆下甲、乙两火炬手手中火炬的火焰的照片,如右图所示,下列说法正确的是 A .甲火炬手可能运动,乙火炬手可能静止 B .甲火炬手可能静止,乙火炬手可能向左运动 C .火炬中燃料燃烧将化学能转化为内能与光能D .若火炬手在水平路面上向前跑动且火炬距地面的高度不变,则重力对火炬做正功4.M 、N 为正点电荷Q 的电场中某直线上的两点,距Q 的距离如图所示,一试验电荷q 在Q 的作用下沿该直线由M 向Q 做加速运动。
全国百套高考数学模拟试题分类汇编圆锥曲线解答题c.docx

52、(河南省开封市2008届高三年级第一次质量检)双曲线二-二 = 1(。
〉0,力〉0)的左、右焦点分别为R 、a- b-F 2, 0为坐标原点,点A 在双曲线的右支上,点B 在双曲线左准线上,F\d^AB,OF\OA^OAOB.(1) 求双曲线的离心率e ;(2) 若此双曲线过C (2, V3 ),求双曲线的方程;(3)在(2)的条件下,D" D,分别是双曲线的虚轴端点(D,在y 轴正半轴上),过D 】的直线7交双曲线M 、N, D 2M ± D 2N,求直线Z 的方程。
解:(1) FQ = ABm 四边形住ABO 是平行四边形2008届全国百套高考数学模拟试题分类汇编08圆锥曲线三、解答题(第三部分) 51、(河北省正定中学2008年高三第五次月考)已知直线/过椭圆E: / +2寸=2的右焦点F ,且与E 相交于 两点. (1)设OR = ?(OF + OQ )(。
为原点),求点R 的轨迹方程;(2)若直线/的倾斜角为60° ,求一L + —的值.\PF\ \QF\ 解:⑴设P (m ), GW 况)顼(x,y ) OR = g(OP+。
) n (x,y) = ?[(x,,乂)+ (叫,为)]n <由 工2 +2,2 =2n :+y2 =]易得右焦点尸(1,0)----- (2 分)当直线Zlx 轴时,直线/的方程是:x = l,根据对称性可知R (l,0) 当直线I 的斜率存在时,可设直线I 的方程为y = Rx-1) 4上之 A E w (2k 2+ l)x 2 - 4k 2X + 2Zr 2 - 2 = 0 A = 8^2+8>0; x, +x 2 = (5分)于是R(x,y):x=工1 :工2 = c 艾,; y = *(x — i )2 2k- +1消去参数参得x 2 +2y 2-x = O 而R(l, 0)也适上式,故R 的轨迹方程是7 +2y 2-x = O- (8分)(2)设椭圆另一个焦点为F, 在 APF'F 中 ZPFF' = 120°,| F'F\= 2,设 | PF |= m ,则 | PF' |= 2^2 由余弦定理得(2y/2-m)2 = 22 +m 2-2-2-//z-cosl20° =>m = —%—— 2^2 + 1 同理,在八QF'F,设|涉|=〃,贝\\\QF'\= 2y/2-m 也由余弦定理得(2^2-n)2 =2之 +〃2 -2-2-n-cos60° => 〃 = —%——2^2-1 于是京房—?+旦=2H(12 分)函无-函=0,即函诙2 =0:.~OAL~BF^,.•.四边形F^ABO是菱形..•.函|=|孩|习反|=仁-- * \ A 1^ \ n 4- c 0由双曲线定义得|AR |= 2a + c,e='-^-=^—^- = - + l, \AB\ c e:.e--e -2 = 0,e = 2(e = -1 舍去)(2) e = 2 = ;a2 2c — 2d, 1)2 = 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南通市2008届高三第三次调研测试一、单项选择题.本题共5小题,每小题3分,共15分.每小题只有一个....选项符合题意. 1.关于伽利略对自由落体运动的研究,下列说法中正确的是A .伽利略认为在同一地点,重的物体和轻的物体下落快慢不同B .伽利略猜想运动速度与下落时间成正比,并直接用实验进行了验证C .伽利略通过数学推演并用小球在斜面上验证了位移与时间的平方成正比D .伽利略用小球在斜面上验证了运动速度与位移成正比2.某交流发电机给灯泡供电,产生正弦式交变电流的图象如图所示,下列说法中正确的是 A .交变电流的频率为0.02Hz B .交变电流的瞬时表达式为5c o s 50(Ai t π= C .在t=0.01s 时,穿过交流发电机线圈的磁通量最大 D .若发电机线圈电阻为0.4Ω,则其产生的热功率为5W3.如图所示的电路,闭合开关S ,滑动变阻器滑片P 向左移动,下列结论正确的是A .电流表读数变小,电压表读数变大B .小电泡L 变亮C .电容器C 上电荷量减小D .电源的总功率变大4.如图所示匀强电场E 的区域内,在O 点处放置一点电荷+Q ,a 、b 、c 、d 、e 、f 为以O 点为球心的球面上的点,aecf 平面与电场平行,bedf 平面与电场垂直,则下列说法中正确的是 A .b 、d 两点的电场强度相同 B .a 点的电势等于f 点的电势C .点电荷+q 在球面上任意两点之间移动时,电场力一定做功D .将点电荷+q 在球面上任意两点之间移动,从球面上a 点移动到c 点的电势能变化量一定最大5.如图所示,质量m =1kg 、长L =0.8m 的均匀矩形薄板静止在水平桌面上,其右端与桌子边缘相平.板与桌面间的动摩擦因数为μ=0.4.现用F =5N 的水平力向右推薄板,使它翻下桌子,力F 做的功至少为(g 取10m/s 2) A .1J B .1.6J C .2J D .4J-3s二、多项选择题.本题共4小题,每小题4分,共16分.每小题有多个选项.....符合题意.全部选对的得4分,选对但不全的得2分,有选错或不答的得0分. 6.2007年法国科学家阿尔贝·费尔和德国科学家彼得·格林贝格尔由于发现巨磁电阻(GMR)效应而荣获了诺贝尔物理学奖.如图是利用GMR 设计的磁铁矿探测仪原理示意图,图中GMR 在外磁场作用下,电阻会发生大幅度减小.下列说法正确的是 A .若存在磁铁矿,则指示灯亮 B .若存在磁铁矿,则指示灯不亮C .若电阻R 调大,该探测仪的灵敏度提高D .若电阻R 调小,该探测仪的灵敏度提高7.如图所示,一个金属薄圆盘水平放置在竖直向上的匀强磁场中,下列做法中能使圆盘中产生感应电流的是 A .圆盘绕过圆心的竖直轴匀速转动 B .圆盘以某一水平直径为轴匀速转动 C .圆盘在磁场中向右匀速平移 D .匀强磁场均匀增加8.如图所示,从地面上A 点发射一枚远程弹道导弹,在引力作用下,沿ACB 椭圆轨道飞行击中地面目标B ,C 为轨道的远地点,距地面高度为h .已知地球半径为R ,地球质量为M ,引力常量为G .设距地面高度为h 的圆轨道上卫星运动周期为T 0.下列结论正确的是 A .导弹在CB .导弹在C 点的加速度等于2()GMR h +C .地球球心为导弹椭圆轨道的一个焦点D .导弹从A 点运动到B 点的时间一定小于T 09.如图所示,一网球运动员将球在边界处正上方水平向右击出,球刚好过网落在图中位置(不计空气阻力),相关数据如图,下列说法中正确的是 A .击球点高度h 1与球网高度h 2之间的关系为h 1 =1.8h 2B .若保持击球高度不变,球的初速度0v,一定落在对方界内 C .任意降低击球高度(仍大于2h ),只要击球初速度合适,球一定能落在对方界内 D .任意增加击球高度,只要击球初速度合适,球一定能落在对方界内C三、简答题.本题共3题,共计44分.把答案填在答题卡相应的横线上或按题目要求作答.第10、11题为必做题,第12题有Ⅰ、Ⅱ、Ⅲ三组题,请在其中任选两组题.....作答;若三组题均答,则以Ⅰ、Ⅱ两组题计分. 10.(10分)某实验小组利用如图甲所示的实验装置来验证钩码和滑块所组成的系统机械能守恒.(1)实验前需要调整气垫导轨底座使之水平,利用现有器材如何判断导轨是否水平?▲ . (2)如图乙所示,用游标卡尺测得遮光条的宽度d = ▲ cm ;实验时将滑块从图示位置由静止释放,由数字计时器读出遮光条通过光电门的时间Δt =1.2×10-2s ,则滑块经过光电门时的瞬时速度为 ▲ m/s .在本次实验中还需要测量的物理量有:钩码的质量m 、 ▲ 和 ▲ (文字说明并用相应的字母表示).(3)本实验通过比较 ▲ 和 ▲ 在实验误差允许的范围内相等(用测量的物理量符号表示),从而验证了系统的机械能守恒. 11.(10分)在测定一节干电池的电动势和内阻的实验中,现有下列器材:待测干电池一节,电流表G (满偏电流为2.5mA ,内阻为199Ω),定值电阻R 1=1.0.Ω,定值电阻R 2=99.5.Ω,电阻箱R (0~99.9Ω),开关、导线若干.(1)请在下面所给方框内,画出实验电路图,其中定值电阻应选用 ▲ (选填“R 1”或“R 2”);1h数字计时器(2)某同学实验测出了电阻箱的电阻R 和电流表G 的示数I g ,记录数据(见下表).请在下面坐标图中描点作出1gI -R 图线.(3)根据图线可求得,被测电池的电动势E =___▲___V ,内阻为r =___▲___Ω.12.本题有Ⅰ、Ⅱ、Ⅲ三组题,请在其中任选两组题作答;若三组题均答,则以Ⅰ、Ⅱ两组题计分.Ⅰ.(12分) (选修3-3试题)(1)在以下说法中,正确的是( )A .热量不可能自发地从低温物体传到高温物体B .质量、温度都相同的氢气和氧气,分子平均动能不相同C .液晶既具有液体的流动性,又具有晶体的光学各向异性特点D .饱和汽压随温度的升高而变小(2)用油膜法估测分子大小的实验步骤如下:①向体积为V 1的纯油酸中加入酒精,直到油酸酒精溶液总量为V 2;②用注射器吸取上述溶液,一滴一滴地滴入小量筒,当滴入n 滴时体积为V 0;③先往边长为30~40cm 的浅盘里倒入2cm 深的水;④用注射器往水面上滴1滴上述溶液,等油酸薄膜形状稳定后,将事先准备好的玻璃板放在浅盘上,并在玻璃板上描出油酸薄膜的形状;⑤将画有油酸薄膜轮廓形状的玻璃板,放在画有许多边长为a 的小正方形的坐标纸上,计算出轮廓范围内正方形的总数为N .则上述过程遗漏的步骤是 ▲ ;油酸分子直径的表达式d = ▲ .(3)某风景区有一处约50m 高的瀑布,甚为壮观,请估计瀑布上、下水潭的水温因瀑布的机械能转化成内能而相差多少?[水的比热容34.210c =⨯水J/(kg ﹒℃) ]/ΩⅡ.(12分) (选修3-4试题)(1)在以下说法中,正确的是 ▲A .电磁波谱包括无线电波、微波、红外线、可见光、紫外线、X 射线、γ射线B .牛顿环是簿膜干涉的结果,当用频率更高的单色光照射时,同级牛顿环半径将会变大C .机械波是介质传递波源质点以及振动能量的一种方式D .麦克耳孙-莫雷实验结果表明:不论光源与观察者做怎样的相对运动,光速都是一样的(2)有两个同学利用假期分别去参观北大和南大的物理实验室,各自在那里利用先进的DIS系统较准确地探究了“单摆的周期T 与摆长L 的关系”,他们通过校园网交换实验数据,并由计算机绘制了T 2~L 图象,如图甲所示.去北大的同学所测实验结果对应的图线是 ▲ (选填“A ”或“B ”).另外,在南大做探究的同学还利用计算机绘制了两种单摆的振动图象(如图乙),由图可知,两单摆摆长之比=baL L ▲ .(3)如图所示,半圆玻璃砖的半径R =10cm ,折射率为n =3,直径AB 与屏幕垂直并接触于A 点.激光a 以入射角i =30°射向半圆玻璃砖的圆心O ,结果在水平屏幕MN 上出现两个光斑.求两个光斑之间的距离L .Ⅲ.(12分) (选修3-5试题)(1)下列说法正确的是 ▲A .康普顿效应和电子的衍射现象说明粒子的波动性B .α粒子散射实验可以用来确定原子核电荷量和估算原子核半径C .氢原子辐射出一个光子后能量减小,核外电子的运动加速度减小D .比结合能越大,表示原子核中核子结合得越牢靠,原子核越稳定(2)一个高能γ光子,经过重核附近时与原子核场作用,能产生一对正负电子,请完成相应的反应方程:γ→ ▲ .图甲已知电子质量m e =9.10×10-31kg ,光在真空中的传播速度为速为c =3.00×108m/s ,则γ光子的能量至少为 ▲ J .(3)一质量为M 的航天器远离太阳和行星,正以速度v 0在太空中飞行,某一时刻航天器接到加速的指令后,发动机瞬间向后喷出质量为m 的气体,气体向后喷出的速度大小为v 1,求加速后航天器的速度大小.(v 0 、v 1均为相对同一参考系的速度)四、计算题或推导证明题:本题共3小题,共计45分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分,有数值计算的题,答案中必须明确写出数值和单位. 13.(14分)如图所示,两足够长平行光滑的金属导轨MN 、PQ 相距为L ,导轨平面与水平面夹角α=30°,导轨上端跨接一定值电阻R ,导轨电阻不计.整个装置处于方向竖直向上的匀强磁场中,长为L 的金属棒cd 垂直于MN 、PQ 放置在导轨上,且与导轨保持电接触良好,金属棒的质量为m 、电阻为r ,重力加速度为g ,现将金属棒由静止释放,当金属棒沿导轨下滑距离为s 时,速度达到最大值v m .求: (1)金属棒开始运动时的加速度大小; (2)匀强磁场的磁感应强度大小;(3)金属棒沿导轨下滑距离为s 的过程中,电阻R 上产生的电热.14.(15分)如图Ox 、Oy 、Oz 为相互垂直的坐标轴,Oy 轴为竖直方向,整个空间存在竖直向下的匀强磁场,磁感应强度大小为B .现有一质量为m 、电量为q 的小球从坐标原点O 以速度v 0沿Ox 轴正方向抛出(不计空气阻力,重力加速度为g ).求: (1)若在整个空间加一匀强电场E 1,使小球在xOz平面内做匀速圆周运动,求场强E 1和小球运动的轨道半径; (2)若在整个空间加一匀强电场E 2,使小球沿Ox 轴做匀速直线运动,求E 2的大小;(3)若在整个空间加一沿y轴正方向的匀强电场,求该小球从坐标原点O 抛出后,经过y 轴时的坐标y 和动能E k ;x z o y15.(16分)在水平长直的轨道上,有一长度为L的平板车在外力控制下始终保持速度v0做匀速直线运动.某时刻将一质量为m的小滑块轻放到车面的中点,滑块与车面间的动摩擦因数为μ.(1)证明:若滑块最终停在小车上,滑块和车摩擦产生的内能与动摩擦因数μ无关,是一个定值.(2)已知滑块与车面间动摩擦因数μ=0.2,滑块质量m=1kg,车长L=2m,车速v0=4m/s,取g=10m/s2,当滑块放到车面中点的同时对该滑块施加一个与车运动方向相同的恒力F,要保证滑块不能从车的左端掉下,恒力F大小应该满足什么条件?(3)在(2)的情况下,力F取最小值,要保证滑块不从车上掉下,力F的作用时间应该在什么范围内?南通市2008届高三第三次调研测试物理参考答案及评分标准一、单项选择题.本题共5小题,每小题3分,共15分.每小题只有一个....选项符合题意. 1.C 2.D 3.A 4.D 5.B二、多项选择题.本题共4小题,每小题4分,共16分.每小题有多个选项.....符合题意.全部选对的得4分,选对但不全的得2分,有选错或不答的得0分.6.AC 7.BD 8.BCD 9.AD 三、简答题.本题共3题,共计44分.把答案填在答题卡相应的横线上或按题目要求作答.第10、11题为必做题,第12题有Ⅰ、Ⅱ、Ⅲ三组题,请在其中任选两组题.....作答;若三组题均答,则以Ⅰ、Ⅱ两组题计分. 10.(10分)(1)接通气源,将滑块静置于气垫导轨上,若滑块基本保持静止,则说明导轨是水平的(或轻推滑块,滑块能基本做匀速直线运动).(2分)(2)0,52(2分) 0.43(2分) 滑块上的遮光条初始位置到光电门的距离s (1分)滑块的质量M (1分) mgs (1分)21()()2dm M t+∆(1分) 11.(10分)(1)实验原理图如图所示(2分) R 1(2分)(2)如图所示 (2分)(3)1.38~1.44(2分) 0.40~0.60(2分)12.本题有Ⅰ、Ⅱ、Ⅲ三组题,请在其中任选两组题作答;若三组题均答,则以Ⅰ、Ⅱ两组题计分.Ⅰ.(12分) (选修3-3试题)(1)AC (3分,漏选得1分,错选得0分) (2)将痱子粉均匀撒在水面上(2分) d =1022VV NV a n(2分)(3)设水的的质量为m ,上、下水潭的水温差为Δt ,由能量守恒定律有mgh cm t =∆(3分)代入数据解得 0.12t ∆=℃(2分)Ⅱ.(12分) (选修3-4试题)(1)AD (3分,漏选得1分,错选得0分) (2)B (2分) 4/9(2分) (3)画出如图光路图,设折射角为r ,根据折射定律/Ωsin sin rn i=(1分)解得 60r =︒(1分)由几何知识得,ΔOPQ 为直角三角形,所以两个光斑PQ 之间的距离tan302sin 60L PA AQ R R =+=︒+︒(2分)解得23.1c mL =≈ (1分)Ⅲ.(12分) (选修3-5试题)(1)BD (3分,漏选得1分,错选得0分)(2)0011e e -+(2分) 131.6410J -⨯(2分) (3)设加速后航天器的速度大小为v ,由动量守恒定律有01()Mv mv M m v =-+-(3分) 解得 01Mv mv v M m+=-(2分)四、计算题或推导证明题:本题共3小题,共计45分.解答时请写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分,有数值计算的题,答案中必须明确写出数值和单位. 13.(14分)(1)金属棒开始运动时的加速度大小为a ,由牛顿第二定律有sin mg ma α=① (2分) 解得 s i n a g α=(2分)(2)设匀强磁场的磁感应强度大小为B ,则金属棒达到最大速度时 产生的电动势 c o s m E B L v α= ②(1分) 回路中产生的感应电流 EI R r=+ ③(1分) 金属棒棒所受安培力 F B I L = ④(1分)cd 棒所受合外力为零时,下滑的速度达到最大,则cos sin F mg αα=⑤(1分)由②③④⑤式解得B =(1分)(3)设电阻R 上产生的电热为Q ,整个电路产生的电热为Q 总,则21sin 2m mgs mv Q α=+总 ⑥ (3分) RQ Q R r=+总⑦(1分)由⑥⑦式解得 2()2()m mR gs v Q R r -=+(1分)14.(15分)(1)由于小球在磁场中做匀速圆周运动,设轨道半径为r ,则1qE mg = 解得 1mgE q=(2分) 方向沿y 轴正向(1分) 20v qvB m r = 解得 0mvr qB=(2分)(2) 小球做匀速直线运动,受力平衡,则2qE =(3分)解得2E = (1分)(3)小球在复合场中做螺旋运动,可以分解成水平面内的匀速圆周运动和沿y 轴方向的匀加速运动.做匀加速运动的加速度 32qE mga g m-== (1分) 从原点O 到经过y 轴时经历的时间 t n T =(1分) 212y at =(1分)解得 222224n m gy q B π= (123n =、、)(1分)由动能定理得 2301()2k qE mg y E mv -=-(1分)解得 22322022182k n m g E mv q Bπ=+ (123n =、、)(1分)15.(16分)(1)根据牛顿第二定律,滑块相对车滑动时的加速度mga g mμμ==(1分)欢迎登录100测评网 进行学习检测,有效提高学习成绩.滑块相对车滑动的时间 0v t a=(1分)滑块相对车滑动的距离 2002v s v t a=- (1分) 滑块与车摩擦产生的内能 Q m g s μ=(1分) 由上述各式解得 2012Q m v =(与动摩擦因数μ无关的定值) (1分)(2)设恒力F 取最小值为F 1,滑块加速度为a 1,此时滑块恰好到达车的左端,则 滑块运动到车左端的时间 011v t a = ① 由几何关系有 001122v L v t t -= ② (1分) 由牛顿定律有 11F mg ma μ+=③(1分) 由①②③式代入数据解得 10.5s t =,16N F =(2分)则恒力F 大小应该满足条件是 6N F ≥ (1分)(3)力F 取最小值,当滑块运动到车左端后,为使滑块恰不从右端滑出,相对车先做匀加速运动(设运动加速度为a 2,时间为t 2),再做匀减速运动(设运动加速度大小为a 3).到达车右端时,与车达共同速度.则有12F mg ma μ-=④ (1分) 3mg ma μ=⑤ (1分) 22222223122a t a t L a +=⑥(1分)由④⑤⑥式代入数据解得20.58s t ==(1分) 则力F 的作用时间t 应满足 112t t t t ≤≤+,即0.5s 1.08s t ≤≤(2分)本卷由《100测评网》整理上传,专注于中小学生学业检测、练习与提升.。
