数学建模2010a题
2010“高教社杯”全国大学生数学建模大赛A题论文

基于微元法的变位储油罐罐容表标定问题摘要加油站当地下储油罐发生一定程度变位时,需要重新标定其罐容表,优化“油位计量管理系统”,目的是得到地下储油罐内油量的真实值,所以研究该问题对加油站具有重要意义。
本文主要利用微元法建立积分模型,解决了储油罐的变位识别与罐容表标定的问题,得到了实验储油罐变位后罐容表新的标定值,实际储油罐变位后储油量与油位高度及变位参数之间的关系,以及实际储油罐变位后罐容表新的标定值。
问题一中,首先对纵向倾斜的小椭圆油罐进行分析,将油罐从罐中无油到加满油的过程分为7个部分来分析,分别是:(1)从罐中无油到将油加到刚好不接触油浮子;(2)从油开始接触油浮子到油灌满倾斜角但刚好不接触罐右侧壁;(3)从罐中油开始接触右侧壁到油灌到左侧壁中点水平线;(4)油从左侧壁中点灌到左侧壁终点水平线;(5)油从左侧壁终点灌到右侧壁中点水平线;(6)油从右侧壁中点灌到油浮子刚好显示油满;(7)从油浮子刚好显示油满到将油罐灌满。
分别分析这7个加油的过程,建立模型,用微元法求解每个部分罐中油体积的变化,根据体积的变化得到油面高度的变化,将变位后的油面高度与无变位时的油面高度作比较,分析得出变位对罐容表的影响。
最后由变位后油面的高度,用Matlab编程序得到变位后罐容表新的标定值。
问题二中,经过对实际储油罐的形状与倾斜及偏转角度情况的分析,我们利用割补法建立罐体变位后的数学模型,先分别分析储油罐只纵向倾斜和只横向偏转的情况,用h的函数关系式,再分析储油罐同时纵向倾微元法得到罐中油体积与变位后罐容表刻度斜和横向偏转的情况,我们将模型转变为先将储油罐横向偏转,然后在横向偏转的基础上再纵向倾斜,由所给的实际储油罐的数据,分别结合只进行纵向倾斜和只进行横向偏转的情况,用拟合的方法,利用Simpson公式,近似得到了倾斜角α=4.5230,偏转角β=1.220。
在α和β确定之后,罐内储油量与油位高度及倾斜角α、偏转角β的关系式即转化为油体积与油位高度的关系式,进而计算得到变位后油位间隔为10cm的罐容表新标定值。
2010江西财经大学数学建模竞赛题目A[1]
![2010江西财经大学数学建模竞赛题目A[1]](https://img.taocdn.com/s3/m/f5a926340b4c2e3f572763bd.png)
2010江西财经大学数学建模竞赛题目(2010年5月21日~5月26日)(竞赛前请先仔细阅读“竞赛章程、论文格式规范和交卷要求”)A题:世博会参观线路设计2010年中国上海世界博览会5月1日正式隆重拉开帷幕。
中国的盛情诚邀得到了国际社会积极响应,最终有189个国家、57个国际组织确认参展上海世博会,轻而易举地打破了2000年德国汉诺威世博会保持的177个国家和国际组织参展的纪录,改写了历届世博会国际参展方数量的历史。
截止到5月17日,参观者已经达到295.68万人,其中5月26日一天就达到34万多人,热门场馆出现了排队几个小时的现象。
200多个场馆,使参观者应接不暇。
(1) 如果你作为一个参观者,你将参观哪些场馆?请根据不同情况设计参观线路。
(2) 针对组织者(上海世博局、各参展国或组织),你有什么建议?(3) 针对参观者,你有什么建议?附:2010上海世博会园区介绍上海世博会场地位于南浦大桥和卢浦大桥之间,沿着上海城区黄浦江两岸进行布局。
世博园区规划用地范围为5.28平方公里,其中浦东部分为3.93平方公里,浦西部分为1.35平方公里。
围栏区域(收取门票)范围约为3.28平方公里。
园区规划上海世博会规划方案综合步行适宜距离、人体尺度和参观者的认知度等因素,提出了“园、区、片、组、团”5个层次的结构布局,即:园——5.28平方公里的世博会园区建设用地范围,包括围栏区和围栏区外的配套设施用地,其中浦东3.93平方公里和浦西1.35平方公里;区――3.22平方公里的世博会围栏区,其中浦东2.47平方公里和浦西0.75平方公里;片——5个编号分别是A、B、C、D、E的功能片区,平均用地面积为60公顷;组——12个平均用地规模为10~15公顷的展馆“组”,包括浦东8个组和浦西4个组;团——26个平均用地规模约为2~3公顷的“展馆团”,每个“展馆团”可布置40~45个办展单元,每个“展馆团”的总建筑面积约2~2.5万平方米。
2010全国大学生数学建模大赛本科组A题油罐

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期: 2010 年 9 月 13 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):储油罐的变位识别与罐容表标定摘要加油站的地下储油罐,在使用一段时间后,由于地基变形等原因都会发生变位,本题就是由小椭圆型储油罐的变位模拟,延伸到实际储油罐的变为模型,建立储油量与油位高度及变位参数之间的关系。
对于问题一,是小椭圆型储油罐的模型,用切片法进行积分求体积,由计算无变位的方程推算到有纵向倾角的模型建立,考虑两个突变点,得到三段分段函数;根据函数求出对应的储油量数据,进行误差分析,根据无变位时的拟合误差函数,将模型进行优化处理,然后对新的更加精确的模型方程进行误差分析,对模型进行评估;用建立的数学模型考虑罐体变位后对罐容表的影响,做出倾斜后与无变位的储油量之间的差值,建立其关于油位高度的函数关系;利用修正后的分段函数计算以1cm为油位高度间隔的罐容标定值。
对于问题二,是实际储油罐的模型建立,以问题一中建立的模型为基础,加入横向偏角可求得中间部分的函数关系;对于两端的球冠部分,运用适当的近似进行忽略,简化模型。
2010数学建模竞赛A B题 高教社杯全国大学生数学建模竞赛题目

2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
草根分享论坛 图吧 分享吧 海之南 分享斑竹 share8 好学吧附件1:小椭圆储油罐的实验数据 附件2:实际储油罐的检测数据油油浮子 出油管油位探测装置 注油口 检查口地平线 2m 6m 1m 1m3 m油位高度 图1 储油罐正面示意图 油位探针油位探针α地平线 图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口 检查口水平线α油油浮子出油管油位探针注油口水平线1.2m1.2m1.78m图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线β地平线垂直线油位探针(a )无偏转倾斜的正截面图油位探针油位探测装置地平线 油3m油2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。
2010全国大学生数学建模竞赛A题

2010全国大学生数学建模竞赛A题合作人:何争流,史剑作者:学院:计算机科学与技术;学号:文摘:加油站、燃油生产厂一般都用储油罐来储存燃油,并通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
但许多储油罐在使用一段时间后,罐体位置会因地基变形等原因发生变化,从而导致罐容表发生改变,故需定期对罐容表进行重新标定。
关键词:储油罐,变位,重新标定,几何法,拟合--插值法。
正文:储油罐可能发生纵向倾斜和横向偏转,故需从这两方面研究罐体变位后的标定问题,即罐内储油量与油位高度及变位参数(纵向倾斜角度和横向偏转角度)之间的一般关系,进而对罐容表进行重新标定。
两端平头的小椭圆形储油罐情形拟合—插植法首先我们根据所给的数据,求出拟合函数:设x为测得油位高度,y为罐内油量。
(1)进油情形:1、无变位进油,初值为262L。
设v为测量体积,h为测量高度,对表中数据进行拟合。
2、斜变位进油(θ=4.1),初始值为215L。
设v2为测量体积,h2为测量高度,则由表中数据进行拟合。
对无变位(θ=0)和斜变位(θ=4.1)进油时的数据作图、拟合得到油位高度与罐内储油量的函数关系。
函数的差别为系数不同,而系数不同是由角度不同引起的,所以我们想到对系数关于θ插值,得出θ为变位角,转化为弧度表示则a7 = -2.7165e-005*g-5.5000e-008a6=0.0134*g+2.4000e-005a5= -2.7332*g+0.0043a4=315.3631*g+0.42a3= -2.0587e+004*g-26a2=8.0726e+005*g+1200a1= -1.6824e+007*g+4600a0=1.5337e+008*g+19000当θ=1.8时,g=0.0314,带入上面的式子得到:y=-9.0841e-007*x^7+4.4497e-004*x^6-0.0816*x^5+10.3274*x^4-672.7597*x^3+2.6561e+004*x^2-5.2394e+005*x+4.8373e+006根据这个方程,计算得出罐体变位后油位高度间隔为1cm的实际罐容量。
2010年研究生数学建模A题
这里有个键固定着丆上台应该转不了
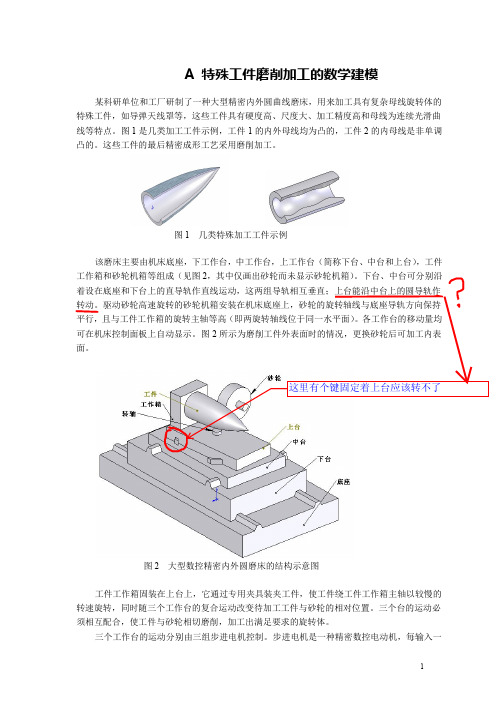
图 2 大型数控精密内外圆磨床的结构示意图 工件工作箱固装在上台上,它通过专用夹具装夹工件,使工件绕工件工作箱主轴以较慢的 转速旋转,同时随三个工作台的复合运动改变待加工工件与砂轮的相对位置。三个台的运动必 须相互配合,使工件与砂轮相切磨削,加工出满足要求的旋转体。 三个工作台的运动分别由三组步进电机控制。步进电机是一种精密数控电动机,每输入一
A 特殊工件磨削加工的数学建模
某科研单位和工厂研制了一种大型精密内外圆曲线磨床,用来加工具有复杂母线旋转体的 特殊工件,如导弹天线罩等,这些工件具有硬度高、尺度大、加工精度高和母线为连续光滑曲 线等特点。图 1 是几类加工工件示例,工件 1 的内外母线均为凸的,工件 2 的内母线是非单调 凸的。这些工件的最后精密成形工艺采用磨削加工。
中台转轴 工件工作箱 夹具基准面
`
中台两对称轴
b
中台 夹具基体 上台
R
螺母 丝杠
传动系统
步进电机
图 4 上台相对中台的转动示意关系 磨床的磨削工具是能磨削高硬度材质的金刚砂轮(指磨削表面含有超高硬度的金刚砂
2
粒) ,磨外圆时根据工件母线的形状,砂轮可采用圆柱体式或轮式,作内圆磨削的砂轮为轮式。 圆柱型砂轮的主要几何参数是砂轮直径 和砂轮厚度 a 。轮式砂轮的主要几何参数有砂轮最大 纵截面(垂直于砂轮转轴的最大截面)的直径 和砂轮厚度 a ,以及其横截面(通过砂轮转轴 的截面)的外端轮廓线参数(理论上它可以是任一凸光滑曲线,但工程上常选用半径为 r 、张 角 不大于 180 的圆弧) ,合理的砂轮几何参数是加工能否实现的关键因素之一(见图 5) 。 在 整个加工过程中工件与砂轮不应脱离接触。
3
3
2010数学建模A题答案论文 储油罐的变位识别与罐容表标定

摘要
储油罐作为加油站常用的贮存设施,对油品在不同液面高度时的贮油量进行精确的 计量变得尤为重要,本文讨论了,加油站卧式储油罐的变位识别与罐容表标定问题。其 主要方法是参考卧式储油罐罐内油品体积标定测量技术,结合几何关系及积分计算,建 立储油罐内储油量,油位高度及变位参数(纵向倾斜角 与横向倾斜角 )之间的关系 模型。然后分析模型,在油位高度一定时,由储油量确定变位参数 与 的值,即为对 储油罐进行变位识别;在变位参数 与 一定时,根据油位高度可确定储油量,即为对 罐容表(罐内油位高度与储油量之间对应的函数关系表达式)进行标定。
地平线
油位探针
油位探测装置
注检 油查 口口
出油管
油浮子
3m
油位
油
高度
1m 2m
6m
1m
图 1 储油罐正面示意图
-2-
地平线 油位探测装置
油位探针
油浮子
注检 油查 口口
出油管
油
α
图 2 储油罐纵向倾斜变位后示意图
水平线
地平线
油位探针
油位探测装置
地平线 油位探针
油 油
β
3m
地平线垂直线
(a)无偏转倾斜的正截面图
-6-
S ' a2 / 2 (a h' )a sin( / 2)
公式(2)
从而求得所求截面面积: S ( a2 / 2 (a h')a sin( / 2)) cos
公式(3)
将式(3)带入式(1)求得: V ( a2 / 2 (a h' )a sin( / 2))l cos
首先,结合上述因素及汽油热膨胀系数,建立模型并对模型进行修正,修正热膨胀 所带来的计算误差。代入附表实际测量数据验证模型。
2010年数学建模a题参考答案(权威)
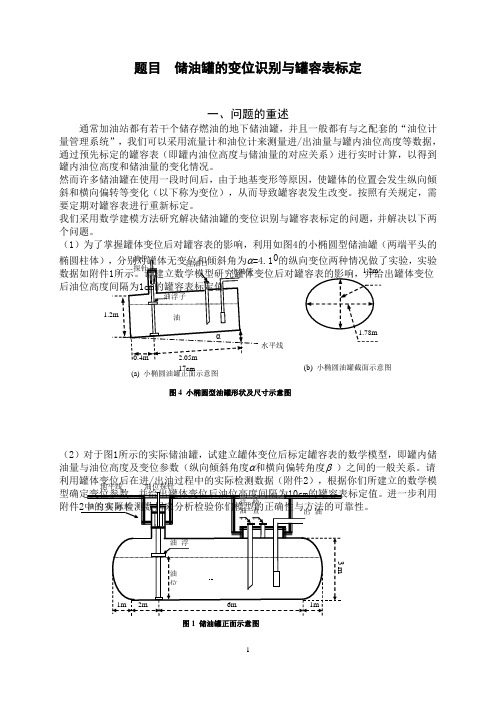
题目 储油罐的变位识别与罐容表标定一、问题的重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,我们可以采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
然而许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
我们采用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题,并解决以下两个问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
(b) 小椭圆油罐截面示意图 α 油 油浮子出油管 油位探针注油口水平线2.05m 17cm 0.4m1.2m 1.2m 1.78m (a) 小椭圆油罐正面示意图 图4 小椭圆型油罐形状及尺寸示意图 油油浮子出油管油位探测装置注油口 检查口 地平线 2m 6m 1m 1m3 m油位图1 储油罐正面示意图 油位探针二、问题的假设(1)向罐内注入的油量数都是通过流量计来完成,是准确的;(2)罐内的储油量只有通过加油机加油流出,并且加油机的计量误差在允许的范围内;(3)不计外部环境的变化对内部油量所产生的影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
储油罐的变位识别与罐容表标定摘要本文主要研究如何识别地下储油罐变位以及对罐容表的重新标定的问题,通过积分和模拟的方法得到储油罐的总油量与油标高度、纵向反转角、横向偏转角之间的关系模型。
根据该模型可根据加油站的出油量以及对应的油标高度来识别储油罐的变位,同时给出变位后的罐容表。
针对问题一,我们用微积分的方法建立油位高度及储油量之间的数学模型。
并给出了罐体变位后油位高度间隔为cm1的罐容表标定值。
针对问题二,同样也用了微积分的方法,将罐容体的体积分成两部分来求解,得到储油量与油位高度及变位参数的理论关系式,将理论值与实际值进行比较,直到得到最符合实际的变位参数值。
但由于计算较复杂,我们没有得到具体的变位参数值。
因此我们又对模型进行了改进,对油面我们假设是水平的,在油面高度上对截面积求积分。
关键词:积分,罐容表1 问题重述通常加油站都有储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生变位,从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐,分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
2 问题分析许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生变位,从而导致罐容表发生改变。
因此我们需要建立模型解决储油罐的变位识别与罐容表标定的问题。
对于问题一,我们用到了数学中的积分方法。
罐体无变位时,沿罐体轴向方向的截面积在各个部分均相等,所以我们只需要用一重积分即可求出是关于油位高度的体积方程;对于罐体倾斜角α=4.10的纵向变位,因为沿罐体轴向方向的截面积在各个部分均不相等,所以需要利用累次积分,将燃油的体积分成无限个极小的椭圆状体,然后在罐体长度上积分求解。
最后对所求得的值进行检验。
对于问题二,在求解罐内储油量时,我们也用数学中的积分方法。
根据储油罐的形状,将体积分成两部分来求解。
中间主体部分体积的求解,需要先找到关于油位高度的截面积方程,然后再在罐体轴向上积分求解;两端球罐体体积的求解,我们假想油面垂直于两端球罐罐面,然后建立积分方程求解。
确定纵向倾斜角度α和横向偏转角度β,对βα、取一个范围,将βα、的不同值代入理论体积公式,将结果与实际值比较,直到找到最适合的值。
3 模型假设(1)罐容体的厚度不计;(2)油位探针、油浮子、流量计、油位计等占有的体积忽略不计; (3)各点处油的密度相同;(4)纵向倾斜角度和横向偏转角度均小于100。
4 符号说明a :小椭圆油罐截面椭圆的长轴;b :小椭圆油罐截面椭圆的短轴;c :油浮子到油罐右端面的距离;d :油浮子到油罐左端面的距离; h :油位高度;R :实际储油罐圆柱截面的半径; V :储油罐的储油量; α:纵向倾斜角度;β:横向偏转角度。
5 模型的建立与求解5.1 问题一的模型建立与求解5.1.1小椭圆油罐罐体无变位的数学模型 当罐体无变位时,沿罐体轴向方向的截面积在各个部分均相等,所以我们只需要用一重积分求出截面积,然后乘以罐体长度,所得乘积即是关于油位高度的体积方程。
为了方便求解,我们简易的画出小椭圆油罐的截面示意图5-1:图5-1小椭圆油罐的截面示意图设:油位高度为h ,椭圆方程为12222=+by a x 。
在y 方向上取椭圆面中的一微元dy 积分得到油的截面积⎰--=bh bxdy s 2, (1)由12222=+by a x by ax 221-=⇒, (2)则积分方程为:dy a s bh bby ⎰---=2212, (3)小椭圆油罐的体积等于截面面积乘以油罐的长度,即l s v ⨯=将dy a s bh bby ⎰---=2212代入上式得dy a l v bh bby⎰---=2212 (4)m a 890.0=,m b 6.0= m b 6.0=,m l 45.2=。
5.1.2小椭圆油罐罐体倾斜1.40纵向变位的数学模型当小椭圆油罐罐体纵向变位时,在罐体轴向上的各截面面积不同,所以我们考虑将燃油体积分成无数个小椭圆体体积,然后积分求解。
画出罐体纵向变位的简易图,见图5-1-2、5-1-3:设:油位高度为h ,油浮距油罐左壁面的距离为d ,距离右壁面的距离为c ;5-1-2小椭圆油罐纵向倾斜的正面示意图 5-1-3小椭圆油罐纵向倾斜的截面示意图我们只考虑油浮子在罐体上表面以下的情况,即:mm d h 1200tan ≤+α 假设在罐体纵向变位时油浮仍然平行于罐体壁面,建立求燃油体积的积分方程:由图1-2可知距离端点z 处的燃油高度:αtan )(d z h --, ……………..(5) 建立截面积的积分方程:dy as bd z h bby ⎰-----=αtan )(2212, (6)在罐体轴向方向上将罐体长度分成无限个极小区域,每个区域的高度为dz ,对每一个极小区域积分,最后求出燃油体积:每一个极小区域体积sdz v =, .……………….(7) 燃油总体积:⎰+=dc v V 0, (8)将(6)、(7)式代入(8)式得dydz aV dc bd z h bby ⎰⎰+-----=0tan )(2212α (9)其中1.40,6.0,4.0,05.2====αm b m d m c ,将各数据代入,求得以下油位高度与燃油体积的关系式:8396.05664.28254899.1)9522.0667.1sin(2562.4)9522.0667.1sin(4497.78396.05664.28250552.0)2449.1667.1sin(4497.70551.21712.795567.5974008622.0)2449.1667.1sin(5645.51712.795567.5974003725.025.125.123210++-+---+++----+-+-⨯+-+-+-=-h h h h h h h h h h h h h h arc arc arc arc V (10)将间隔为值的h cm 1代入(10)式(注:(10)式中h 的单位为m ,计算时要进行单位的换算),即可得到罐体变位后油位高度间隔cm 1的罐容表标定值:见表5-1由于油位探针、油浮子、流量计、油位计、罐体厚度等都占有一定的体积,使得所求的结果存在误差,现对误差进行检验。
将理论标定值与实际标定值做差,所得结果如下图:图5-1-4理论值与实际值的差1的罐容标表标定值表5-1小椭圆罐体变位后油位高度间隔cm5.2 问题二的模型建立与求解5.2.1 实际储油罐变位后的储油量模型中间圆柱体的储油量加上两端球罐体的储油量即是实际储油罐变位后的总储油量。
实际储油罐纵向倾斜变位后中间圆柱体正面示意图如图2-1,截面图如图2-2、2-3。
1)计算中间圆柱体的储油量:设:h为油浮子的高度,x为油面上一点距左端面的距离,油浮距油罐左壁面的距离为d,距离右壁面的距离为c;(a )正面示意图 (b)截面示意图图5-2-1实际储油罐纵向倾斜变位后中间圆柱体的示意图由图5-2-1(a )可以看出距离端点x 处的燃油高度:αtan )(d x h --, (11)当αtan )(d x h -->R 时,我们可以得到实际储油罐纵向变位后的中间圆柱体的截面示意图,见图5-2-1(b )。
由图2-1(b)可以看出阴影部分的截面积s =三角形面积+扇形面积三角形面积s 1:]tan )([222]tan )([2121R d z h R R d z h ----⨯---⨯=⨯⨯αα底高 (12)扇形面积s 2:弧度半径⨯⨯221=]))tan )(arccos((22[21R 2RR d z h ----⨯⨯απ (13)截面积s =三角形面积s 1+扇形面积s 2,即:+-⨯---⨯---]tan )([222]tan )([21R d z h R R d z h αα]))tan )((5.1arccos(22[21R 2Rd z h απ----⨯⨯ …………………………...(14) 燃油体积:在油罐轴向方向上积分得到积分式:当αtan )(d x h --<R 时,我们得到实际储油罐纵向变位后的中间圆柱体的截面示意图如图5-2-2tan)(d z h --图5-2-2实际储油罐纵向变位后的中间圆柱体的截面示意图图中阴影部分的面积=扇形面积—三角形面积,即:]))tan )((arccos(2[21R 2Rd z h R s α---⨯⨯=—]tan )([222)]tan )(([21R d z h R d z h R ----⨯---⨯αα ………(15) 燃油体积:在油罐轴向方向上积分得到积分式⎰=83dz s V (16)2)计算两端球罐体的储油量:我们假设储油罐纵向倾斜后油面仍然平行于地面,此假设对于左右球罐体的倾斜部分的储油量大抵相互抵消。
建立左端球罐体储油量的数学模型:图5-2-3 储油罐截面示意图设:t 1为左端球罐体中燃油面距离地面的垂直高度,t 2为右端球罐体中燃油面距离地面的垂直高度从图中可以以看出αβtan 2cos 1+=h t ,αβtan 6cos 2-=h ttan )(d z h --h图储油罐倾斜变位后示意)(b因为t 1、t2相对于R 分别取不同的值时,积分极限不同,所以我们分四种情况讨论:当R t ≥1时,()()⎰⎰+---=122211625.05.1625.1*2t dy dz z y V (17)当5.11<t时 ()()()⎰⎰+------=t t dz dy z y V 1625.02222215.11625.1*2625.05.1625.1………………………………………(18) 当5.12≥t 时()()⎰⎰+---=10202222625.05.1625.1*2t dy dz z y V (19)当5.12<t时()()()⎰⎰+------=t t dzdy z y V 20625.02222225.12625.1*2625.05.1625.1 (20)3)建立罐内储油量与油位高度及变位参数的数学模型由1)、2)我们得到罐内储油量与油位高度及变位参数之间的理论关系式,将油位高度及变位参数代入关系式,得到不同的理论值,与实际值进行比较,直到找到最合适的变位参数值。
