第十一讲 一线三角模型
初中几何 一线三等角模型
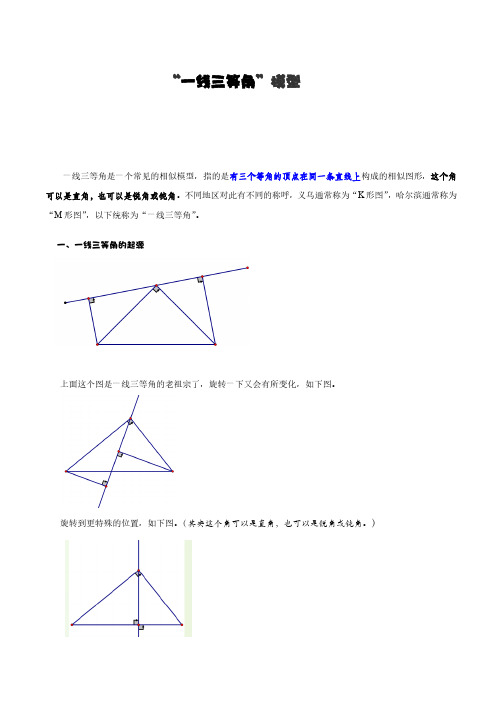
一、一线三等角的起源上面这个图是一线三等角的老祖宗了，旋转一下又会有所变化，如下图。
旋转到更特殊的位置，如下图。
（其实这个角可以是直角，也可以是锐角或钝角。
）“一线三等角”模型一线三等角是一个常见的相似模型，指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。
不同地区对此有不同的称呼，义乌通常称为“K 形图”，哈尔滨通常称为“M 形图”，以下统称为“一线三等角”。
二、一线三等角的两种基本类型1．三等角都在直线的同侧2．三等角分居直线的两侧l三、一线三等角的性质1．一般情况下，由∠1＝∠2＝∠3，易得△AEC∽△BDE. 2．当等角所对的边相等时，两个三角形全等。
如图，当CE＝ED时，易得△AEC≌△BDE.3．“中点型一线三等角”的特殊性质如图，当∠1＝∠2＝∠3且D 是BC 的中点时，△BDE ∽△CFD ∽△DFE .如图，加画两条垂线．．．．．．，“一线三等角”就与“四边形中的半角模型”联系在一起了。
半角模型：EF ＝EM ＋FN . 4．“中点型一线三等角”的变式 如图，当∠1＝∠2且∠AOC ＝90°＋21∠BAC 时，点O 是△ABC 的内心.易证∠4＝∠5＝∠6，以下就省略了。
四、一线三等角的常用构图下面以等腰三角形为例说明一线三等角的常见构图。
由于角顶点位置的改变，或角绕顶点旋转会产生各种各样的变式，但万变不离其宗：构造相似三角形列比例式解决问题。
当然，特殊情况下也可能是全等。
五、一线三等角的应用1．一线三等角应用的三个层次⑴初级阶段：图形中已经存在“一线三等角”，直接应用模型解题；⑵中级阶段：图形中存在“一线二等角”，补上“一等角”构造此模型；⑶高级阶段：图形中只有直线上的一个角，补上“二等角”构造此模型。
2．在张角问题中，构造“一线三等角”是基本手段之一。
对坐标系中的张角问题，在x轴或y轴（也可以是平行于x轴或y轴的直线）上构造“一线三等角”是解决问题的关键。
一线三等角模型及其解法
一线三等角模型及其解法一线三等角模型是将一个图表分解为一线三等角形。
它是一种分解复杂图形的有效方法，可以帮助工程师了解复杂图表中可能存在的规律性和关系。
一、一线三等角模型的定义一线三等角模型是一种通过一条直线和三条重合线将数据进行分解的方法。
它的定义是：原有的数据经过分解、重构后，可以用一线三等角结构或等角三线结构图表示（即用三条线把一条线一分为三），以保证在某一范围内搜索达到最大或最小值。
二、一线三等角模型的特点1、合理性：一线三等角模型由来自原始数据的三角形组成，因此它可以合理地反映数据，以更容易地挖掘数据正确的值和规律。
2、比较性：由于一线三等角模型可以以图形的形式直观地表示数据的相互关系，因此它可以更清晰地显示不同数据之间的差异。
3、趋势性：一线三等角模型可以清楚地显示数据之间的变化趋势，它可以有效地预测某些情况下的发展前景。
三、一线三等角模型的解法1、根据图形上的定义，确定图形线条的表示方式；2、将数据或原始度量根据图形上的定义转换为图形内的点；3、利用拟合算法进行拟合，连接图形上的点与相关的定义；4、使用数学方程求解一线三等角模型，得出不同变量的比例关系及相应的数值；5、根据计算结果绘制图表，解释结果。
四、一线三等角模型的应用1、市场营销：一线三等角模型可以分析市场竞争，从而定位和优化品牌。
2、团队管理：一线三等角模型可以揭示团队的组织关系，以提高团队效率。
3、资源管理：一线三等角模型可以激发和有效地分配资源，以提高生产效率。
4、项目研究：一线三等角模型可以帮助分析市场需求情况，以及项目规划和实施情况。
5、战略管理：一线三等角模型可以提供组织战略发展的方向和衡量标准。
一线三等角模型证明过程
一线三等角模型证明过程1. 认识一线三等角模型说到一线三等角模型，嘿，别急，我们先来点背景知识。
想象一下，数学就像一座神秘的宝藏，里面埋藏着无数的秘密，而一线三等角模型就是其中一个闪闪发光的宝石。
这玩意儿，简单来说，就是把一个三角形分成三部分，然后看看它们之间的关系。
好比把一块美味的蛋糕切成三块，既有视觉的享受，又能品味其中的奥妙。
1.1. 什么是三等角首先，咱们得搞明白“三等角”是什么。
简单来说，就是一个三角形的三个角都是相等的，像极了三个好朋友一起吃冰淇淋，谁都不想多吃一点，公平得很。
这样的三角形叫做“等边三角形”，可别小看它，这可是一切三角形的王者，立马吸引了数学家的目光。
1.2. 一线三等角的妙用一线三等角模型可不仅仅是好看，它的用处可大着呢！比如，咱们在建筑设计、工程测量上，都能看到它的身影。
想象一下，建筑师用它来确保大楼的角度完美无瑕，真是既实用又充满艺术感啊。
2. 证明过程的步骤接下来，就让我们开启证明的旅程吧！首先，咱们得找到一个合适的三角形，当然，选择等边三角形最好，因为它的角度都是60度，简直是稳稳的让人安心。
然后，咱们在这个三角形的底边上画一条线，嘿，这可不是普通的线，它能将三角形分成三部分，每一部分都恰到好处。
2.1. 分割与重组接下来，咱们要用一种很神奇的方法，把这三部分重新组合。
就像把玩具拆散再组装成新的样子，数学的魅力在于这种变化。
我们把每一部分的角度和边长一一对应，最后，嘿，咱们会发现，它们都是相等的！这就像一场精彩的变魔术，大家都惊呼“哇，太神奇了！”2.2. 视觉化证明为了让这个证明更加直观，我们可以用图形来辅助。
画出一个大的等边三角形，再在底边上画出一条平行线，把它分割成几个小三角形。
然后，咱们来个巧妙的观察，发现这些小三角形也是等边的，角度完全相等，真是让人拍手叫绝！这就如同把同一颗星星用不同的角度观察，看到的却是不同的美。
3. 结论与应用最后，经过一番折腾，我们终于证明了一线三等角模型的奥秘。
一线三等角模型结论及证明
一线三等角模型结论及证明
摘要
一线三等角模型是几何学中的重要概念，它指的是在一个给定的直线上，存在三个等角，它们的夹角均为120度。
本文将详细阐述一线三等角模型的结论及证明，以及如何使用它来解决实际问题。
一、定义
一线三等角模型是几何学中的重要概念，它指的是在一个给定的直线上，存在三个等角，它们的夹角均为120度。
二、结论
一线三等角模型的结论如下：
1、如果在一条直线上有三个等角，则它们的夹角均为120度。
2、如果三条直线的夹角均为120度，则它们共线。
三、证明
1、证明一：假设在一条直线上有三个等角，设它们的夹角为α，β，γ，则有
α+β+γ=360°，由等角性质可知α=β=γ=120°，得证。
2、证明二：假设三条直线的夹角均为120°，设它们的夹角分别为α，β，γ，则有α+β+γ=360°，此时α=β=γ=120°，由此可知，三条直线共线，得证。
四、实际应用
一线三等角模型可以用来解决实际问题，比如，在建筑设计中，可以根据一线三等角模型设计出美观的建筑结构，如三角形的屋顶，具有特殊的视觉效果。
结论
一线三等角模型是几何学中的重要概念，它指的是在一个给定的直线上，存在三个等角，
它们的夹角均为120度。
本文详细阐述了一线三等角模型的结论及证明，并且给出了如何使用它来解决实际问题的实例。
一线三等角模型特征及结论
一线三等角模型特征及结论好嘞，咱们来聊聊“一线三等角模型”，这个听起来高大上的名词其实也没那么复杂。
就像一碗热腾腾的面条，虽然看起来简单，但其中却藏着不少讲究。
咱们先说说这“一线三等角”是个啥。
简单来说，就是在某些情况下，我们可以把事情简化成一条线和三个角。
这听起来是不是有点像数学课上学的那些东西？但实际上，它在很多领域里都能派上用场，比如说设计、分析，甚至日常生活中也能找到它的身影。
想象一下，你和朋友们一起去泡温泉，那个水雾缭绕的地方，大家围坐在一起，谈笑风生。
这时候，气氛就像那一条线，大家都聚在这条线上，享受着温暖。
而那些欢声笑语，正是那三个角，分别代表着不同的情感、不同的观点。
你看，一个简单的场景，运用这个模型，就能让我们更好地理解和分析这个过程。
这就是“一线三等角”的魅力所在，能把复杂的事情，变得简单又生动。
再说说这个模型的特征。
这条线就代表着一个核心主题或者主线，围绕着这个主题，大家可以展开不同的讨论。
就像我们在聊天的时候，始终围绕着一个话题，有时候跑偏了，但大家又会很自然地拉回来。
这种核心的连结，让人觉得踏实，也让讨论有了方向。
这三个角嘛，分别代表着不同的视角。
比如说，一个角可能是乐观的，一个是现实的，还有一个可能是有点悲观的。
每个角都有它的价值，咱们不能只看一个角度，这样就会错过很多精彩的细节。
可能有人会想，这种模型有什么用呢？嘿嘿，别急，接下来咱们就来看看它的实际应用。
想想看，在工作中，我们常常需要开会讨论项目。
这个时候，一条主线就是项目的目标，而三个角可以代表不同团队的反馈和建议。
大家围绕着这个目标，分享各自的想法，碰撞出火花，真是热闹得很。
经过这样的讨论，最后能形成一个更完善的方案，让大家都心服口服，简直就像是团队合作的缩影。
在学习上，咱们也能用这个模型。
想象你在复习一门课程，主线就是你要掌握的知识点，而那些角度则可以是不同的例题、应用和理论。
换个角度看问题，会让你豁然开朗，原来原本的难题竟然也能迎刃而解。
一线三角相似模型总结
稿子一：嘿，亲！今天咱们来唠唠“一线三角相似模型”哈！你知道不，这模型可神奇啦！就那么一条线，三个角，就能找出相似来。
先说说啥是“一线三角”哈。
其实就是在一条直线上，有三个顶点，然后这三个顶点分别和另外一个点连线，形成的三个角。
这三个角要是有相等的，那对应的三角形就相似啦！比如说，在一个图形里，有一条直线上依次有 A、B、C 三个点，另外有一个点D，连接 DA、DB、DC，如果角 ADB 和角 BDC 相等，那三角形 ADB 和三角形 BDC 就相似。
这个模型用处可大了！在解决几何问题的时候，能帮咱们快速找到相似三角形，然后通过相似比算出边的长度啊，角度大小啥的。
比如说，给了咱们一个三角形，里面有这么个“一线三角”的情况，还知道一些边的长度，那咱们就能通过相似比，算出其他边的长度，是不是很妙？而且哦，多做几道这种题，你就会发现，其实它经常出现在各种考试里，像是平时的小测验，还有期中期末考。
所以呀，一定要把这个模型弄明白，这样做题的时候才能又快又准，轻松拿高分！怎么样，是不是觉得这个“一线三角相似模型”挺有意思的？稿子二：哈喽呀！今天咱们来好好聊聊“一线三角相似模型”哟！亲，你可别小看这个模型，它可厉害着呢！想象一下，一条线上排着三个点，就像排排坐吃果果似的，然后再加上另外一个点和它们连线，这就构成了“一线三角”。
比如说哈，在一个图形里，直线上的三个点是 E、F、G，另外一个点是 H，连接起来，要是发现角 EHF 和角 FHG 相等，那对应的三角形 EHF 和三角形 FHG 就相似啦。
这个模型在解题的时候，那可真是个宝贝！有时候题目看起来很复杂，但是只要咱们找到了这个“一线三角”，瞬间就柳暗花明又一村啦！它能帮咱们快速找到解题的关键，算出各种边和角的关系。
比如说，知道了其中两个相似三角形的对应边的比例，就能求出其他边的长度啦。
我跟你讲哦，我之前做过好多这样的题，一开始也觉得有点难，但是多练了几次，就发现它其实有规律可循的。
一线三等角模型
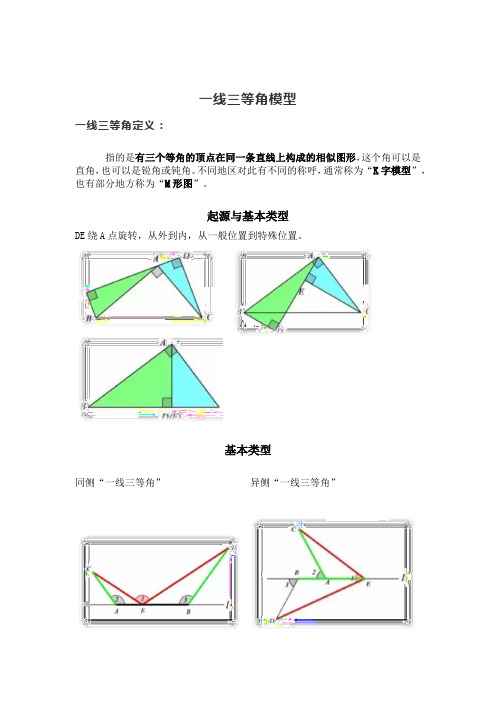
一线三等角模型一线三等角定义：指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。
不同地区对此有不同的称呼，通常称为“K字模型”，也有部分地方称为“M形图”。
起源与基本类型DE绕A点旋转，从外到内，从一般位置到特殊位置。
基本类型同侧“一线三等角”异侧“一线三等角”性质1.一般情况下，如下左图，易得△AEC∽△BDE.2.当等角所对的边相等时，则两个三角形全等。
（若CE=ED，则△AEC≌△BDE）3.中点型“一线三等角”如右上图，当∠1=∠2=∠3，且D是BC中点时，△BDE∽△CFD∽△DFE.4.“一线三等角”的各种变式应用1.“一线三等角”应用的三种情况。
a.图形中已经存在一线三等角，直接应用模型解题；b.图形中存在“一线二等角”，补上“一等角”构造模型解题；c.图形中只有直线上一个角，补上“二等角”构造模型解题.2.在定边对定角问题中，构造一线三等角是基本手段。
3.构造一线三等角的步骤：找角、定线、构相似。
如上图，线上有一特殊角，就考虑构造同侧型一线三等角，当然只加这两条线通常是不够的，为了利用这个特殊角与线段的关系，过C、D两点作直线l的垂线是必不可少的。
模型建立例如图2，已知E是矩形ABCD的边AB上一点，EF⊥DE交BC于点F，试说明：ΔADE∽ΔBFE。
分析：要证明ΔADE与ΔBFE相似，已经知道∠A=∠B=90°，只需要再找出另外一对相等的角即可。
解答：在矩形ABCD中，∠A=∠B=90°∵EF⊥DE∴∠DEF=90°，∠2+∠3=90°又∵∠1+∠3=90°∴∠1=∠2∴ΔADE∽ΔBFE小结：此时，在直线AB上，∠A=∠DEF=∠B=90°，一条线上有3个直角，两边的ΔADE与ΔBFE相似。
这个相似的基本图形像字母K，可以称为“K”型相似，但更因为图形的结构特征是一条线上有3个垂直关系，也常被称为“一线三垂直”。
《一线三等角模型》课件
在建筑设计中，一线三 等角模型可防止建筑形 态过于普通化，同时保 证建筑的美学性与功能 性。
一线三等角模型的应用领域
室内设计
可以用于设计会议室、酒店等 场所。
建筑设计
可以用于设计公共建筑、景观 等。
家具设计
可以用于设计桌椅、灯具等家 具。
建模方法
1
建立坐标系
根据设计需求，建立二维坐标系。
2
构造一线三等角模型的形式
《一线三等角模型》PPT 课件
本PPT课件将介绍一线三等角模型的建模方法和应用，以及如何用Python实 现该模型。
什么是一线三等角模型？
1 基本概念
一条长度为1的线段在 平面上，等分成三段， 依次连接首尾得到一个 三角形，这即为一线三 等角模型。
2 特性
3 优点
等边、等角、狭长、占 用空间小、视觉上飘逸、 新颖。
上海环球金融中心 建筑设计
建筑主体外形线条流畅，中 心部分采用一线三等角模型 造型，整个建筑寓意成长、 挑战和超越。
实战演示
1
怎样运用Python实现一线三等角模型
介绍程序员如何使用Python语言进行一线三等角模型的建模和参数化，方便后 续分析应用。
2
ห้องสมุดไป่ตู้
实战演示案例
通过一线三等角模型和Python语言实现的案例，展示该模型方法和应用的可行 性。
总结
一线三等角模型的应用前景
这一模型的美学和实用性优点促进了其在设计领域中的广泛应用，未来发展前景广阔。
未来的研究与发展方向
未来的研究将着重在拓展该模型的应用领域，提高建模准确性和自动化程度。
在坐标系中，通过角平分线和圆心等方法构造出一线三等角模型。
3
(完整版)几何模型：一线三等角模型
一线三等角模型一.一线三等角概念“一线三等角”是一个常见的相似模型，指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。
不同地区对此有不同的称呼，“K 形图”，“三垂直”，“弦图”等，以下称为“一线三等角”。
二.一线三等角的分类全等篇同侧锐角直角钝角P异侧相似篇A同侧锐角直角钝角P异侧三、“一线三等角”的性质1.一般情况下，如图 3-1，由∠1=∠2=∠3，易得△AEC∽△BDE.2.当等角所对的边相等时，则两个三角形全等.如图 3-1，若 CE=ED，则△AEC≌△BDE.3.中点型“一线三等角”如图 3-2，当∠1=∠2=∠3，且 D 是 BC 中点时，△BDE∽△CFD∽△DFE.4.“中点型一线三等角“的变式(了解) 如图 3-3，当∠1=∠2 且1902BOC BAC ∠=︒+∠时，点 O 是△ABC 的内心.可以考虑构造“一线三等角”.如图 3-4“中点型一线三等角”通常与三角形的内心或旁心相关，1902BOC BAC ∠=︒+∠这是内心的性质，反之未必是内心.在图 3-4（右图）中，如果延长 BE 与 CF ，交于点 P ，则点 D 是△PEF 的旁心.5.“一线三等角”的各种变式（图 3-5，以等腰三角形为例进行说明 ）图 3-5其实这个第 4 图，延长 DC 反而好理解.相当于两侧型的，不延长理解，以为是一种新型的，同侧穿越型？不管怎么变，都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1.“一线三等角”应用的三种情况.a.图形中已经存在“一线三等角”，直接应用模型解题；b.图形中存在“一线二等角”，不上“一等角”构造模型解题；c.图形中只有直线上一个角，不上“二等角”构造模型解题.体会：感觉最后一种情况出现比较多，尤其是压轴题中，经常会有一个特殊角或指导该角的三角函数值时，我经常构造“一线三等角”来解题.2.在定边对定角问题中，构造一线三等角是基本手段，尤其是直角坐标系中的张角问题，在 x 轴或 y 轴（也可以是平行于 x 轴或 y 轴的直线）上构造一线三等角解决问题更是重要的手段.3.构造一线三等角的步骤：找角、定线、构相似坐标系中，要讲究“线”的特殊性如图 3-6，线上有一特殊角，就考虑构造同侧型一线三等角当然只加这两条线通常是不够的，为了利用这个特殊角导线段的关系，过 C、D 两点作直线 l 的垂线是必不可少的。
一线三角模型及例题
相似三角形判定的复习：1.相似三角形的预备定理：平行于三角形一边的直线和其他两边或两边的延长线相交,所截成的三角形与原三角形相似;2.相似三角形的判定定理：1两角对应相等两三角形相似; 2两边对应成比例且夹角相等,两个三角形相似;3三边对应成比例,两个三角形相似;3.直角三角形相似的判定定理：1直角三角形被斜边上的高分成两个直角三角形和原三角形相似;2一直角三角形的斜边和一条直角边与另一直角三角形的斜边和一条直角边对应成比例,那么这两三角形相似;相似三角形的性质：要点1：相似三角形的性质：相似三角形的对应角相等,对应边成比例要点2：相似三角形的性质定理：相似三角形的性质定理1：相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比相似三角形的性质定理2：相似三角形的周长的比等于相似比相似三角形的性质定理3：相似三角形的面积的比等于相似比的平方要点3：知识架构图1、如图,锐角∆ABC的高CD和BE相交于点O,图中相似三角形有多少对请分别写出.2、如图,在锐角∆ABC中,∠ADE=∠ACB,图中相似三角形有多少对请分别写出.3、如图已知∠BAC=∠BDC=90°,8,16==∆∆ADE EBC S S . 问：∠BEC 的大小确定吗 若确定,求期度数；若不确定,请说明理由.4、如图,在ABC △中,90BAC ∠=,AD 是BC 边上的高,点E 在线段DC 上,EF AB ⊥,EG AC ⊥,垂足分别为F G ，．求证：1EG CG AD CD =； 2FD ⊥DG ．GFE D C B A5、如图,四边形ABCD 中,AC 与BD 交于点E,AC ⊥AB ,BD ⊥CD. S ∆EBC =16,S ∆AED =8.1求AD BC的值； 2问：∠BEC 是不是定角 如果是,把它求出来；如果不是,请说明理由.5、如图,在△ABC 中,角ACB 为直角,CD⊥AB 于点D,又△ACE 与△BCF 都是等边三角形,连结DE 、DF ；求证:DE⊥DFAB C DEE A D C FB中考热点：一线三等角型的相似三角形一、问题引入如图,ABC ∆中,90B ∠=︒,CD AC ⊥,过D 作DE AB ⊥交BC 延长线与E;求证：ABC CED ∆∆B E ADC三等角型相似三角形是以等腰三角形等腰梯形或者等边三角形为背景,一个与等腰三角形的底角相等的顶点在底边所在的直线上,角的两边分别与等腰三角形的两边相交如图所示：其他常见的一线三等角图形等腰三角形中底边上一线三等角等腰梯形中底边上一线三等角A BDC EF直角坐标系中一线三等角矩形中一线三等角等角的顶点在底边上的位置不同得到的相似三角形的结论也不同,当顶点移动到底边的延长线时,形成变式图形,图形虽然变化但是求证的方法不变;此规律需通过认真做题,细细体会;1等腰三角形中一线三等角例1、如图,已知在△ABC中,AB=AC=6,BC=5,D是AB上一点,BD=2,E是BC上一动点,联结DE,并作DEF B ∠=∠,射线EF 交线段AC 于F ．1求证：△DBE ∽△ECF ； 2当F 是线段AC 中点时,求线段BE 的长；3联结DF ,如果△DEF 与△DBE 相似,求FC 的长． F B AC DE 讲解：1、本题中,第一问的结论是这类题共同的特性,只要等腰三角形底边上有三等角,必有三角形相似；2、第二问中根据相似求线段的长,也很常见；有时候会反过来问,线段的长是多少是,三角线相似;变式练习1就是这类题型；3、第三问中间的三角形与左右两个形似时有两种情况,一种是DF 与底边平行,一种是E 为中点；4、在等腰三角形,将腰延长会交于一点,也构成等腰三角形,故而以上三点,在等腰梯形中也适用; 变式练习1 浦东新区22题如图,已知等边△ABC 的边长为8,点D 、F 、E 分别在边AB 、BC 、AC 上,3BD =,E 为AC 中 点,当△BPD 与△PCE 相似时,求BP 的值.变式练习2宝山22题如图6,已知ΔABC 中,AB AC =,点E 、F 在边BC 上,满足∠EAF =∠C .求证：2BF CE AB ⋅=； F E C BA变式练习3 A D如图,在三角形ABC 中,AB=4,AC=2,∠A =900,点D 为腰AC 中点,点E 在底边BC 上,且DE ⊥BD,求△CED 的面积;变式练习4已知∠ABC=90°,AD ∥BC,P 为线段BD 上的动点,点Q 在射线AB 上,且满足PQ AD PC AB = ,当AD AB ,且点Q 在线段AB 的延长线上时,求QPC ∠的大小．2等腰梯形中一线三等角例1、长宁区18题如图,等腰梯形ABCD 中,AD ∥BC ,2AD =,42BC =,∠45B =˚,直角三角板含45度角的顶点E 在边BC 上移动,一直角边始终经过点A ,斜边与CD 交于点F .若△ABE 为等腰三角形,则CF 的长等于 .第18题E FDCB A例2、如图,梯形ABCD 中,AB ∥DC , ∠B =90°,E 为BC 上一点,且△ABE ∽△ECD ;1若BC =8,AB=3,DC =4,求BE 的长 2若BC = 43 ,AB=3,DC =4,求BE 的长.3若BC =6,AB=3,DC =4,求BE 的长.例3、如图,梯形ABCD 中,AB ∥CD,∠ABC=900,AB=8,CD=6,在AB 上取动点P,连结DP,作PQ ⊥DP,使得PQ 交射线BC 与点E,设AP=x,BE=y;1当BC=4时,试求y 关于x 的函数关系式；2当BC 在什么范围时,存在点P,使得PQ 经过点C 直接写出结果;例4、徐汇区25．如图,在梯形ABCD 中,AD ∥BC ,6AB CD BC ===,3AD =．点M 为边BC 的中点,以M 为顶点作EMF B ∠=∠,射线ME 交腰AB 于点E ,射线MF 交腰CD 于点F ,联结EF ．1求证：△MEF ∽△BEM ；2若△BEM 是以BM 为腰的等腰三角形,求EF 的长；3若EF CD ⊥,求BE 的长．例4、杨浦区基础考四边形ABCD 中,AD ∥BC ,()090ABC αα∠=<<,3AB DC ==,5BC =．点P 为射线BC 上动点不与点B 、C 重合,点E 在直线DC 上,且APE α∠=．记1PAB ∠=∠,2EPC ∠=∠,BP x =,CE y =．1当点P 在线段BC 上时,写出并证明1∠与2∠的数量关系；2随着点P 的运动,1中得到的关于1∠与2∠的数量关系,是否改变 若认为不改变,请证明；若认为会改变,请求出不同于1的数量关系,并指出相应的x 的取值范围；3若cos α=13,试用x 的代数式表示y ．3坐标系中一线三等角例1、金山区24如图,住平面直角系中,直线AB ：()440y x a a=+≠分别交x 轴、y 轴于B 、A 两点,直线AE 分别交x 轴、y 轴于E 、A 两点,D 是x 轴上的一点,OA OD =,过D 作CD ⊥x 轴交AE 于C ,连接B C ,当动点B 在线段OD 上运动不与点O 点D 重合且AB BC ⊥时1求证：ABO ∆∽BCD ∆；2求线段CD 的长用a 的代数式表示；3若直线AE 的方程是1316y x b =-+,求tan BAC ∠的值．例２、如图,在直角坐标系中,直线122y x =+与ｘ轴,ｙ轴分别交于Ａ,Ｂ两点,以ＡＢ为边在第二象限内作矩形ＡＢＣＤ,使5AD = ,求点Ｄ的坐标．变式练习1在平面直角坐标系XOY 中,AOB ∆的位置如图所示,已知0060,90=∠=∠A AOB ,点A 的坐标为()1,3- （1） 求点B 的坐标；（2） 若抛物线c bx ax y ++=2经过A 、O 、B 三点,求函数解析式;变式练习2如图所示：RT △AOB 中∠AO B =90°,OA=4,OB=2,点B 在反比例函数2y x=图像上,求过点A 的双曲线解析式;变式练习3如图,在平面直角坐标系中,OB ⊥OA,且OB ＝2OA,点A 的坐标是－1,2．求过点A 、O 、B 的抛物线的表达式；4矩形中一线三等角如图,四边形ＯＡＢＣ是一张放在平面直角坐标系中的矩形纸片,点Ａ在ｘ轴上,点Ｃ在ｙ轴上,将边ＢＣ折叠,使点Ｂ落在边ＯＡ的点D 处．已知折叠线CE 且55CE =, 3tan 4EDA ∠=,求直线ＣＥ与ｘ轴交点的坐标；例6、长宁区24题．如图,在矩形ABCD 中,4AB =,6AD =,点P 是射线DA 上的一个动点,将三角板的直角顶点重合于点P ,三角板两直角中的一边始终经过点C ,另一直角边交射线BA 于点E ．1判断△EAP 与△PDC 一定相似吗 请证明你的结论；2设PD x =,AE y =,求y 与x 的函数关系式,并写出它的定义域；3是否存在这样的点P ,是△EAP 周长等于△PDC 周长的2倍 若存在,请求出PD 的长度；若不存在, 请简要说明理由．EPDCB A“一线三等角”专题练习一、知识梳理：1、如图1,AB ＝AC,∠ B ＝∠ADE,那么一定存在的相似三角形有 ；2、如图2,AB ＝AC,∠ B ＝∠EDF,那么一定存在的相似三角形有 ；B 图1 图2 3、在等腰△ABC 中,腰长10厘米,底边长16厘米,点P 在底边上以0.5厘米/秒的速度从点B 向点C 移动．当点P运动到PA 与腰垂直的位置时,点P 的运动时间为 秒．二、经典例题解析1、如图,在ΔABC 中, AB ＝AC=4,BC ＝6,∠ B ＝∠ADE ,点D 、E 分别在BC 、AC 上点D 与B 、C 不重合,设BD ＝x ,AE ＝y ,求y 关于x 的函数解析式及x 的取值范围;B2、如图：在直角梯形ABCD 中,AD ∥BC,∠B = 90°,DH ⊥BC 于H,AB = 6,BC = 16,DC = 10,线段BC 上有一动点E 不与点C 重合,过点E 作EF ⊥DC 交线段DC 于点F.1求CH 的长；2设BE = x,EF = y,求y 关于x 的函数解析式及x 的取值范围；3当以E 、F 、C 为顶点的三角形与△ABE 相似时,求BE 的长.B3、如图,在Rt △ABC 中,∠ACB =90º,AB =10,AC =6,点E 、F 分别是边AC 、BC 上的动点,过点E 作ED ⊥AB 于点D ,过点F 作FG ⊥AB 于点G ,DG 的长始终为2． 1当AD =3时,求DE 的长；2当点E 、F 在边AC 、BC 上移动时,设x AD =,y FG =,求y 关于x 的函数解析式,并写出函数的定义域； 3在点E 、F 移动过程中,△AED 与△CEF 能否相似,若能,求AD 的长；若不能,请说明理由．4、已知在梯形ABCD 中,AD ∥BC ,AD ＜BC ,且BC =6,AB =DC =4,点E 是AB 的中点． 1如图3,P 为BC 上的一点,且BP =2．求证：△BEP ∽△CPD ；2如果点P 在BC 边上移动点P 与点B 、C 不重合,且满足∠EPF =∠C ,PF 交直线CD 于点F ,同时交直线AD 于点M ,那么①当点F 在线段CD 的延长线上时,设BP =x ,DF =y ,求y 关于x 的函数解析式,并写出函数的定义域；②当BEP DMF S S ∆∆=49时,求BP 的长． 5、2009闸北22题本题满分10分,第1小题满分3分,第2小题满分7分ABC ED GFEDCBAP如图七,在平面直角坐标中,四边形OABC 是等腰梯形,CB∥OA, OA=7,AB=4,∠COA=60°,点P 为x 轴上的—个动点,但是点P 不 与点0、点A 重合．连结CP, D 点是线段AB 上一点,连结PD. 1求点B 的坐标； 2当∠C PD=∠OAB,且AB BD =85,求这时点P 的坐标.6、如图,已知在△ABC 中,AB=AC=8,cosB=58,D 是边BC 的中点,点E 、F 分在边AB 、AC 上,且∠EDF=∠B,连接EF ．1如果BE=4,求CF 的长； 2如果EF ∥BC,求EF 的长．7、徐汇2009年 25题如图,ABC ∆中,10==AC AB ,12=BC ,点D 在边BC 上,且4=BD ,以点D 为顶点作B EDF ∠=∠,分别交边AB 于点E ,交射线CA 于点F ．1当6=AE 时,求AF 的长；2当以点C 为圆心CF 长为半径的⊙C 和以点A 为圆心AE 长为半径的⊙A 相切时,求BE 的长； 3当以边AC 为直径的⊙O 与线段DE 相切时,求BE 的长．知识总结：补 充：关于“一线三等角”图形的提炼及变式：A BCDEFABCD当α为锐角时：BBB当α为直角时：当α为钝角时：E总结：在教学中要突出重点、深化学生对于“一线三等角”模型的理解；把握难点：“一线三等角”模型变式； 通过问题建构,关注课堂再生资源的挖掘,引导学生对于几何综合习题的有效分解具体的1．在教学中通过“回忆旧知”环节的师生互动过程让95%学生掌握解函数型综合题需要的必备知识储备． 2．在教学中通过一个“一线三等角”模型综合题的有效分析引导过程,让95%的学生树立几何型综合题的解决的信心,让75%的学生能够顺利解决前两小题,培养更多的学生具备解决最后压轴点一小题的能力．3．在教学中通过有效分解策略的实施,打破他们对综合题的畏惧心理,让同学们加深对于题目条件的使用：条件用完,即使题目没有求解完毕,也得到相应的分数,提高问题解决的能力,在这个师生共同探讨的过程中鼓励学生尝试着加强解后反思与培养他们欣赏试题的能力．课后作业1、如图,已知正方形ABCD 的边长为4,P 是射线CD 上一动点. 将一把三角尺的直角顶点与P 重合,一条直角边始终经过点B,另一条直角边所在直线与射线AD 相交于点E. 设CP=x,DE=y. 1当点P 在线段CD 上时,求证：△BPC ∽△PED ；2当点P 在线段CD 的延长线上时,求y 与x 的函数解析式及自变量x 的取值范围； 3当DE=1时,求CP 的长.2、如图,在矩形ABCD 中,E 为AD 的中点,EF EC ⊥交AB 于点F ,联结()FC AB AE >． 1AEF △与EFC △是否相似 若相似,证明你的结论；若不相似,请说明理由； 2设ABk BC=,是否存在这样的k 值,使得AEF BFC △∽△ 若存在,证明你的结论并求出k 的值；若不存在,请说明理由．（第12题）FBCA ED3、等腰△ABC,AB=AC=８,∠BAC=120°,P 为BC 的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P,三角板绕P 点旋转．1如图a,当三角板的两边分别交AB 、AC 于点E 、F 时．求证：△BPE ～△CFP ；2操作：将三角板绕点P 旋转到图b 情形时,三角板的两边分别交BA 的延长线、边AC 于点E 、F ． ① 探究１：△BPE 与△CFP 还相似吗 只需写出结论 ② 探究２：连结EF,△BPE 与△PFE 是否相似 请说明理由； ③ 设EF=m,△EPF 的面积为S,试用m 的代数式表示S ．4、如图,在边长为1的正方形ABCD 中,点E 在边BC 上与端点不重合,点F 在射线DC 上． 1若AF =AE ,并设CE =x ,△AEF 的面积为y ,求y 关于x 的函数解析式,并写出函数的定义域； 2当CE 的长度为何值时,△AEF 和△ECF 相似 3若41=CE ,延长FE 与直线AB 交于点G ,当CF 的长度为何值时,△EAG 是等腰三角形 BCB5、如图,在△ABC 中,AC =BC =2,∠C =900,点D 为腰BC 中点,点E 在底边AB 上,且DE ⊥AD ,则BE 的长为 .6、如图,∆ABC 中,∠ACB=90°,∠A=60°,AC=2,CD ⊥AB,垂足为D.任意作∠EDF=60°,点E 、F 分别在AC 、BC 上.设AE=x,BF=y.1求y 关于x 的函数关系式,并指出它的定义域； 2当x 为何值时,∆BDF 是等腰三角形.7、如图：AB 是等腰直角三角形ABC 的斜边,点M 在边AC 上,点N 在边BC 上,沿直线MN 将△MCN 翻折,使点C 落在AB 上,设其落点为P.1当P 是边AB 中点时,求证：PA CMPB CN =； 2当P 不是边AB 中点时,PA CMPB CN=是否仍然成立 请证明你的结论.8、如图第13题图-1,在Rt △ABC 中,∠C =90°,AC =BC ,D 是AB 边上一点,E 是在AC 边上的一个动点与点A 、C 不重合,DF ⊥DE ,DF 与射线BC 相交于点F ;1如图第13题图-2,如果点D 是边AB 的中点,求证：DE =DF ；EB2如果AD ∶DB =m ,求DE ∶DF 的值；3如果AC =BC =6,AD ∶DB =1∶2,设AE =x ,BF =y ,求y 关于x 的函数关系式,并写出定义域.9、已知9023ABC AB BC AD BC P ∠===°，，，∥，为线段BD 上的动点,点Q 在射线AB 上,且满足PQ ADPC AB=如图14-1． 1当2AD =,且点Q 与点B 重合时如图14-2所示,求线段PC 的长；2在图8中,联结AP ．当32AD =,且点Q 在线段AB 上时,设点B Q 、之间的距离为x ,APQ PBCS y S =△△,其中APQ S △表示APQ △的面积,PBC S △表示PBC △的面积,求y 关于x 的函数解析式,并写出函数定义域； 3当AD AB <,且点Q 在线段AB 的延长线上时如图14-3所示,求QPC ∠的大小．第13题图-1第13题图-2AD PQDAPCCADP BC B14-1 B Q14-2 14-3Q。
相似三角形中的 “一线三等角”模型-2023年新九年级数学核心知识点与常见题型(沪教版)(解析版)
重难点专项突破：相似三角形中的“一线三等角”模型【知识梳理】一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。
或叫“K字模型”。
三直角相似可以看着是“一线三等角”中当角为直角时的特例，三直角型相似通常是以矩形或者正方形形为背景，或者在一条直线上有一个顶点在该直线上移动或者旋转的直角，几种常见的基本图形如下：当题目的条件中只有一个或者两个直角时，就要考虑通过添加辅助线构造完整的三直角型相似，这往往是很多压轴题的突破口，进而将三角型的条件进行转化。
一般类型：基本类型：同侧“一线三等角”异侧“一线三等角”【考点剖析】例1.如图，直角梯形ABCD 中，AB // CD ，90ABC ∠=︒，点E 在边BC 上，且34AB BE EC CD ==， AD = 10，求AED ∆的面积．【答案】24．【解析】90ABC ∠=，//AB CD ， ∴90DCB ABC ∠=∠=．又34AB BE EC CD ==， ABE ECD ∴∆∆∽．∴AEB EDC ∠=∠． ∴34AE AB ED EC ==．90EDC DEC ∠+∠=，∴90AEB DEC ∠+∠=． ∴90AED ∠=．在Rt AED ∆中，10AD =，68AE ED ∴==，． 24AED S ∆∴=．【总结】本题考查一线三等角模型的相似问题，还有外角知识、平行的判定等．例2.已知：如图，△ABC 是等边三角形，点D 、E 分别在边BC 、AC 上，∠ADE ＝60°．（1）求证：△ABD ∽△DCE ；（2）如果AB ＝3，EC ＝，求DC 的长．【分析】（1）△ABC 是等边三角形，得到∠B ＝∠C ＝60°，AB ＝AC ，推出∠BAD ＝∠CDE ，得到△ABD∽△A B C DEDCE ；（2）由△ABD ∽△DCE ，得到＝，然后代入数值求得结果．【解答】（1）证明：∵△ABC 是等边三角形，∴∠B ＝∠C ＝60°，AB ＝AC ，∵∠B+∠BAD ＝∠ADE+∠CDE ，∠B ＝∠ADE ＝60°，∴∠BAD ＝∠CDE∴△ABD ∽△DCE ；（2）解：由（1）证得△ABD ∽△DCE ，∴＝，设CD ＝x ，则BD ＝3﹣x ，∴＝，∴x ＝1或x ＝2，∴DC ＝1或DC ＝2．【点评】本题考查了等边三角形的性质，相似三角形的判定和性质，注意数形结合和方程思想的应用． 例3.已知，在等腰ABC ∆中，AB = AC = 10，以BC 的中点D 为顶点作EDF B ∠=∠， 分别交AB 、AC 于点E 、F ，AE = 6，AF = 4，求底边BC 的长．【答案】46．【解析】EDC B BED ∠=∠+∠，而EDC EDF FDC ∠=∠+∠，∴B BED EDF FDC ∠+∠=∠+∠． 又EDF B ∠=∠，∴BED FDC ∠=∠．AB C D EFAB AC=，∴B C∠=∠．EDB DCF∴∆∆∽．BE BDDC CF∴=．106104BDDC−∴=−，24DC BD∴=．又12CD DB BC==，BC∴=【总结】本题是对“一线三等角”模型的考查．例4.已知：如图，AB⊥BC，AD // BC， AB = 3，AD = 2．点P在线段AB上，联结PD，过点D作PD的垂线，与BC相交于点C．设线段AP的长为x．（1）当AP = AD时，求线段PC的长；（2）设△PDC的面积为y，求y关于x的函数解析式，并写出函数的定义域；（3）当△APD∽△DPC时，求线段BC的长．满分解答：（1）过点C作CE⊥AD，交AD的延长线于点E．∵AB⊥BC，CE⊥AD，PD⊥CD，AD // BC，∴∠ABC =∠AEC =∠PDC = 90°，CE = AB = 3．∵AD // BC，∴∠A +∠ABC = 180°．即得∠A = 90°．又∵∠ADC =∠DCE +∠DEC，∠ADC =∠ADP +∠PDC，∴∠ADP =∠DCE．又由∠A =∠DEC = 90°，得△APD∽△DCE．∴AD APCE DE=．于是，由AP = AD = 2，得DE = CE = 3．…………………………（2分）在Rt△APD和Rt△DCE中，得PD=，CD=1分）AB CDPAB CD（备用图）于是，在Rt △PDC 中，得 PC = （1分）（2）在Rt △APD 中，由 AD = 2，AP = x ，得 PD 1分）∵ △APD ∽△DCE ，∴AD PD CE CD =．∴ 32CD PD ==1分）在Rt △PCD 中，22113332224PCD S PD CD x ∆=⋅⋅=⨯=+．∴ 所求函数解析式为2334y x =+．…………………………………（2分） 函数的定义域为 0 < x ≤ 3．…………………………………………（1分）（3）当△APD ∽△DPC 时，即得 △APD ∽△DPC ∽△DCE ．…………（1分）根据题意，当△APD ∽△DPC 时，有下列两种情况：（ⅰ）当点P 与点B 不重合时，可知 ∠APD =∠DPC ．由 △APD ∽△DCE ，得 AP PD DE DC =．即得AP DE PD CD =． 由 △APD ∽△DPC ，得AP AD PD DC =． ∴AD DE CD CD =．即得 DE = AD = 2． ∴ AE = 4．易证得四边形ABCE 是矩形，∴ BC = AE = 4．…………………（2分）（ⅱ）当点P 与点B 重合时，可知 ∠ABD =∠DBC ．在Rt △ABD 中，由 AD = 2，AB = 3，得 BD =．由 △ABD ∽△DBC ，得AD BD BD BC =．即得 =． 解得 132BC =．………………………………………………………（2分）∴ △APD ∽△DPC 时，线段BC 的长分别为4或132．方法总结本题重点在于：过点C 作CE ⊥AD ，交AD 的延长线于点E ．(构造一线三角，出现相似三角形，进行求解) 例5.在梯形ABCD 中,AD ∥BC ，︒=∠===90,2,1A BC AB AD .（如图1）(1)试求C ∠的度数；(2)若E 、F 分别为边AD 、CD 上的两个动点(不与端点A 、D 、C 重合),且始终保持︒=∠45EBF ,BD 与EF交于点P .（如图2）①求证:BDE ∆∽BCF ∆；②试判断BEF ∆的形状（从边、角两个方面考虑），并加以说明；③设y DP x AE ==,,试求y 关于x 的函数解析式,并写出定义域.答案：（1）作BC DH ⊥，垂足为H ，在四边形ABHD 中，AD ∥BC ，︒=∠==90,1A AB AD ，则四边形ABHD 为正方形又在CDH ∆中，1,1,90=−====∠︒BH BC CH AB DH DHC ， ∴︒︒=∠−=∠452180DHC C .（2）①∵四边形ABHD 为正方形，∴︒=∠45CBD ,︒=∠45ADB ，又∵︒=∠45EBF ，∴CBF DBE ∠=∠又∵︒=∠=∠45C BDE ,∴BDE ∆∽BCF ∆.②BEF ∆是等腰直角三角形，∵BDE ∆∽BCF ∆， ∴CB FB BD BE =,又∵︒=∠=∠45DBC EBF ,∴EBF ∆∽DBC ∆，又在DBC ∆中，︒=∠=∠45C DBC ,为等腰直角三角形，∴BEF ∆是等腰直角三角形. ③x x x x x x y +−=+−⨯=1221222，（0<x <1）.方法总结 第三问方法提示：过点P 作AD 的垂线于点H ，构造一线三直角相似，进行求解，很简单。
(完整版)几何模型：一线三等角模型
一线三等角模型一。
一线三等角概念“一线三等角”是一个常见的相似模型，指的是有三个等角的顶点在同一条直线上构成的相似图形，这个角可以是直角，也可以是锐角或钝角。
不同地区对此有不同的称呼,“K形图",“三垂直”，“弦图”等，以下称为“一线三等角”。
二. 一线三等角的分类全等篇三、“一线三等角”的性质1。
一般情况下，如图3—1,由N 仁Z2=Z3，易得△AECs^BDEo2. 当等角所对的边相等时，则两个三角形全等.如图3.中点型“一线三等角 如图3—2,当Z1=Z2=Z3,且D 是BC 中点时，△BDEs^CFDs^DFE 。
4。
“中点型一线三等角“的1如图3—4“中点型一线三等角”通常与三角形的内心或旁心相关，ZBOC 二90。
+A BAC 这是内心的^2 性质，反之未必是内心.在图3-4（右图）中，如果延长BE 与CF ，交于点P,则点D 是APEF 的旁心.图3—5其实这个第4图，延长DC 反而好理解•相当于两侧型的，不延长理解，以为是一种新型的，同 侧穿越型？不管怎么变，都是由三等角确定相似三角形来进行解题四、“一线三等角”的应用1•“一线三等角”应用的三种情况.图3-1图3-3图3-4+Ja。
图形中已经存在“一线三等角”，直接应用模型解题；b。
图形中存在“一线二等角”，不上“一等角”构造模型解题；c・图形中只有直线上一个角，不上“二等角”构造模型解题。
体会:感觉最后一种情况出现比较多，尤其是压轴题中，经常会有一个特殊角或指导该角的三角函数值时，我经常构造“一线三等角”来解题.2。
在定边对定角问题中，构造一线三等角是基本手段，尤其是直角坐标系中的张角问题，在x轴或y轴（也可以是平行于x轴或y轴的直线）上构造一线三等角解决问题更是重要的手段。
在DC的延檢銭上截眼匚E二J3•构造一线三等角的步骤：找角、定线、构相似1IJttnZAEP=aaZPFB=啦-工上则以’唾二ZPFB=a二ZAPE』所I^APAEwABPF.在CP±WCE=则曲厶斗EOunZBFD=⑶“则ZAEC-ZBFD=ZAPB•所I^APAE«ABPF・坐标系中，要讲究“线"的特殊性如图3—6,线上有一特殊角，就考虑构造同侧型一线三等角（完整版）几何模型：一线三等角模型当然只加这两条线通常是不够的，为了利用这个特殊角导线段的关系，过C、D两点作直线I的垂线是必不可少的。
一线三等角模型的定义
一线三等角模型的定义1. 什么是一线三等角模型一线三等角模型，听起来是不是有点高大上？其实它的原理挺简单的，就像我们平时聊天时，想要把一件事说得明明白白，搞得清清楚楚。
简单来说，这个模型主要用来描述事物之间的关系。
它的核心思想是把复杂的问题拆分成三个部分，就像我们吃西瓜，一刀切开，既能看见里面的红瓤，又能轻松分享。
通过这种方式，我们能更好地理解事物的本质，避免那种“说了半天，还是不明白”的窘境。
2. 三等角的构成2.1 第一等角：要素这个第一等角就像是一个基础，让我们理解整个模型。
想象一下，你在做一道菜，首先得有食材。
这里的“要素”就是构成事物的基本成分。
比如说，一个团队要成功，首先得有人才，有资源，有目标。
如果没有这些基本要素，那就跟没米下锅一样，做不出美味的饭菜。
2.2 第二等角：关系接下来，第二等角就是这些要素之间的关系了。
就像是朋友之间的交情，有的人深交，有的人泛泛之交。
在模型里，这个关系决定了要素之间的互动。
比如，一个团队里，有的成员擅长沟通，有的则技术过硬。
他们之间的合作关系，就像是一支乐队，各司其职，才能演奏出和谐的乐曲。
如果每个人都只顾自己，那就成了“众星捧月”，乱得不成样子。
2.3 第三等角：环境最后，我们得提提第三等角，就是环境。
环境就像是天气，晴天的时候大家心情都不错，工作效率高；而下雨天可能就会有点阴沉，士气也跟着低落。
这一角强调的是外部因素对要素和关系的影响。
比如，在经济不景气的时候，一个好团队可能也会受到影响，资源变得紧张，目标实现的难度就加大了。
3. 应用场景3.1 工作场所那么，这一线三等角模型在现实生活中有什么用呢？首先，在工作场所，领导可以用这个模型来分析团队的表现。
比如，发现团队里有人才流失，领导就可以先看看团队的基本要素是不是齐全，再分析成员之间的关系是否良好，最后再看外部环境对团队的影响。
这样一来，问题就能迎刃而解，领导也能做出更加精准的决策。
3.2 教育领域在教育领域，这个模型同样大显身手。
初中数学“一线三等角”模型的解析
初中数学“一线三等角”模型的解析一线三等角是初中数学中一个重要的几何模型，它涉及到线段、角度和等边三角形的关系。
本文将对一线三等角模型的定义、性质以及应用进行深入解析。
一、一线三等角模型的定义一线三等角模型是由一个线段和两个相等的角组成的几何模型。
在该模型中，线段是一条直线段，两个角分别位于线段的两侧，且两个角的度数相等。
这两个角与线段构成了一个等边三角形，同时这个等边三角形的边长等于线段的长度。
二、一线三等角模型的性质1. 线段与等边三角形的关系：线段的长度等于等边三角形的边长。
2. 角的性质：线段两侧的两个角度数相等。
由于等边三角形的三个内角都是60°，所以两个角的度数都是60°。
3. 等边三角形的性质：等边三角形的三条边相等，三个内角都是60°。
4. 线段的性质：线段可以作为等边三角形的一条边，也可以作为两个相等角的边。
三、一线三等角模型的应用1. 解题方法：在解决与一线三等角模型相关的问题时，我们可以利用线段的长度、角的性质和等边三角形的性质来分析和推导。
通过观察图像，找出线段、角和三角形之间的关系，从而找到解题的突破口。
2. 题型一：求线段的长度在一线三等角模型中，当已知一个等边三角形的边长时，可以通过等边三角形的性质求出线段的长度。
根据等边三角形的定义，三条边相等，因此线段的长度等于等边三角形的边长。
3. 题型二：求角的度数在一线三等角模型中，当已知线段的长度时，可以通过角的性质求出角的度数。
由于线段两侧的两个角度数相等，且等于60°。
因此可以根据线段的长度推导出角的度数。
4. 题型三：求等边三角形边长在一线三等角模型中，当已知一个角的度数时，可以通过等边三角形的性质求出等边三角形的边长。
由于角度数相等且等于60°，可以求出等边三角形的边长。
5. 题型四：利用一线三等角模型解决实际问题一线三等角模型可以应用于解决实际问题，如建筑设计中的视角问题、航空导航中的方向问题等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
相似三角形的基本模型一、相似三角形判定的基本模型认识（一）A字型、反A字型（斜A字型）（平行）（不平行）（二）8字型、反8字型BCBC（蝴蝶型）（平行）（不平行）（三）母子型B（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：一线三等角的变形：一线三直角的变形：（六）双垂型：二、相似三角形判定的变化模型旋转型：由A字型旋转得到8字型拓展专题练习：1.（2011）如图，等边三角形ABC 的边长为3，点P 为BC 边上一点，且BP =1，点D 为AC 边上一点，若∠APD =60°，则CD 的长为 .2.（2011）如图，四边形ABCD ，M 为BC 边的中点．若∠B =∠AMD =∠C =45°，AB =8，CD =9，则AD 的长为（ ） A ．3 B ．4 C ．5 D ．63.（2011荆州）如图，P 为线段AB 上一点，AD 与BC 交干E ，∠CPD =∠A =∠B ，BC 交PD 于F ，AD 交PC 于G ，则图中相似三角形有（ ）A ．1对B ．2对C ．3对D ．4对4. 在△ABC 中，AC =BC ，∠ACB=90°，点M 是AC 上的一点，点N 是BC 上的一点，沿着直线MN 折叠，使得点C 恰好落在边AB 上的P 点，求证：MC ：NC =AP ：PB ．5.如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ． 求证：OE OA OC ⋅=2．6.已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：DA DE DB ⋅=2；7.如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：FC FB FD ⋅=2．8.已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。
求证：(1)△AME ∽△NMD; (2)ND 2=NC ·NB9.如图，等边△ABC 中，边长为6，D 是BC 上动点，∠EDF =60° （1）求证：△BDE ∽△CFD（2）当BD =1，FC =3时，求BE10.已知ABC ∆中,120,6︒=∠==BAC AC AB ，D 是BC 的中点，AB 边上有一点AC E ,延长线上有一点F ，使.C EDF ∠=∠ 已知4=BE ，则=CFD EB11.如图，等边ABC ∆中，D 是边BC 上的一点，且3:1:=DC BD ，把ABC ∆折叠，使点A 落在BC 边上的点D 处．那么ANAM的值为 ．AB12.在矩形ABCD 中，6=AB ，8=AD ，把矩形ABCD 沿直线MN 翻折，点B 落在边AD 上的E 点处，若AM AE 2=，那么EN 的长等于FE13.在矩形ABCD 中，15=AD ，点E 在边DC 上，联结AE ，△ADE 沿直线AE 翻折后点D 落到点F ，过点F 作AD FG ⊥，垂足为点G ,如果3:1:=AD DG ，那么=DE ．NM GGAABEBE14.已知△ABC ，BC AC =，︒=∠120C ，边长9=AC ，点D 在AC 上，且6=AD ，点E 是AB 上一动点，联结DE ，将线段DE 绕点D 逆时针旋转︒30得到线段DF ，要使点F 恰好落在BC 上，则AE 的长是 。
15.如图，已知AM ∥BN ，︒=∠=∠90B A ，4=AB ，点D 是射线AM 上的一个动点（点D 与点A 不重合），点E 是线段AB 上的一个动点（点E 与点A 、B 不重合），联结DE ，过点E 作DE 的垂线，交射线BN 于点C ，联结DC ．设x AE =，y BC =． （1）当1=AD 时，求y 关于x 的函数关系式，并写出它的定义域；（2）在（1）的条件下，取线段DC 的中点F ，联结EF ，若5.2=EF ，求AE 的长；（3）如果动点D 、E 在运动时，始终满足条件AB DE AD =+，那么请探究：BCE △的周长是否随着动点D 、E 的运动而发生变化？请说明理由．EE16.如图，已知ABC ∆中，︒=∠90C ,2==BC AC ,O 是AB 的中点，将︒45角的顶点置于点O ， 并绕点O 旋转，使角的两边分别交边AC 、BC 于点D 、E ，连接DE .(1) 求证AOD ∆∽OED ∆；(2)设xAD =，试用关于x 的式子表示DE 。
C C ABBA17.如图，等边△ABC 中，边长为6，D 是BC 上动点，∠EDF =60° （1）求证：△BDE ∽△CFD（2）当BD =1，FC =3时，求BE18.如图，等腰△ABC 中，AB =AC ，D 是BC 中点，∠EDF =∠B ，求证：△BDE ∽△DFE19.如图，在△ABC 中，AB =AC =5cm ，BC =8，点P 为BC 边上一动点（不与点B 、C 重合），过点P 作射线PM 交AC 于点M ，使∠APM =∠B ； （1）求证：△ABP ∽△PCM ；（2）设BP =x ，CM =y ．求 y 与x 的函数解析式，并写出函数的定义域．（3）当△APM 为等腰三角形时， 求PB 的长．20.在∆ABC 中，AB=AC ，高AD 与BE 交于H ，EF BC ⊥，垂足为F ，延长AD 到G ，使DG=EF ，M 是AH 的中点。
求证：∠=︒GBM 9021.如图，等边△ABC 中，边长为6，D 是BC 上动点，∠EDF=60° （1）求证：△BDE ∽△CFD（2）当BD =1，FC =3时，求BE22.已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AD ＝5，AB ＝DC ＝2．（1）如图8，P 为AD 上的一点，满足∠BPC ＝∠A ． ①求证；△ABP ∽△DPC ②求AP 的长．（2）如果点P 在AD 边上移动（点P 与点A 、D 不重合），且满足∠BPE ＝∠A ，PE 交直线BC 于点E ，同时交直线DC 于点Q ，那么当点Q 在线段DC 的延长线上时，设AP ＝x ，CQ ＝y ，求y 关于x 的函数解析式，并写出函数的定义域；23.如图，已知在△ABC 中， AB =AC =6，BC =5，D 是AB 上一点，BD =2，E 是BC 上一动点，联结DE ，并作DEF B ∠=∠，射线EF 交线段AC 于F ．（1）求证：△DBE ∽△ECF ； （2）当F 是线段AC 中点时，求线段BE 的长； （3）联结DF ，如果△DEF 与△DBE 相似，求FC 的长．24.已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且BC =6，AB =DC =4，点E 是AB 的中点． （1）如图，P 为BC 上的一点，且BP =2．求证：△BEP ∽△CPD ；（2）如果点P 在BC 边上移动（点P 与点B 、C 不重合），且满足∠EPF =∠C ，PF 交直线CD 于点F ，同时交直线AD 于点M ，那么当点F 在线段CD 的延长线上时，设BP =x ，DF =y ，求y 关于x 的函数解析式，并写出函数的定义域；25.已知矩形ABCD 中，CD=2，AD=3，点P 是AD 上的一个动点，且和点A,D 不重合，过点P 作CP PE ⊥，交边AB 于点E,设y AE x PD ==,，求y 关于x 的函数关系式26.在直角ABC ∆中，43tan ,5,90===∠B AB C o，点D 是BC 的中点，点E 是AB 边上的动点，DE DF ⊥交射线AC 于点F （1）、求AC 和BC 的长（2）、当BC EF //时，求BE 的长。
（3）、连结EF,当DEF ∆和ABC ∆相似时，求BE 的长。
E DCB A P 图）EDCBA（备用图）EF C27.如图，在△ABC 中，∠A=60°，BD 、CE 分别是AC 、AB 上的高求证：（1）△ABD ∽△ACE ；（2）△ADE ∽△ABC ；28.如图，已知锐角△ABC ，AD 、CE 分别是BC 、AB 边上的高，△ABC 和△BDE 的面积分别是27和3，DE=62，求：点B 到直线AC 的距离。
C29.△ABC 是等边三角形,D 、B 、C 、E 在一条直线上,∠DAE=︒120，已知BD=1，CE=3，,求等边三角形的边长.30.已知：如图，在Rt △ABC 中，AB =AC ，∠DAE =45°．求证：（1）△ABE ∽△ACD ； （2）CD BE BC ⋅=22．C31.（1）在ABC ∆中，5==AC AB ，8=BC ，点P 、Q 分别在射线CB 、AC 上（点P 不与点C 、点B 重合），且保持ABC APQ ∠=∠.①若点P 在线段CB 上（如图10），且6=BP ，求线段CQ 的长； ②若x BP =，y CQ =，求y 与x 之间的函数关系式，并写出函数的 定义域；（2）正方形ABCD 的边长为5（如图12），点P 、Q 分别在直线．．CB 、DC 上ABC备用图 ABCD图12（点P 不与点C 、点B 重合），且保持︒=∠90APQ .当1=CQ 时，写出线段BP 的长（不需要计算过程，请直接写出结果）.32.如图，在△ABC 中，8==AC AB ，10=BC ，D 是BC 边上的一个动点，点E 在AC 边上，且C ADE ∠=∠． (1) 求证：△ABD ∽△DCE ；(2) 如果x BD =，y AE =，求y 与x 的函数解析式，并写出自变量x 的定义域； (3) 当点D 是BC 的中点时，试说明△ADE 是什么三角形，并说明理由．33.已知：如图，在△ABC 中，5==AC AB ，6=BC ，点D 在边AB 上，AB DE ⊥，点E 在边BC 上．又点F 在边AC 上，且B DEF ∠=∠． (1) 求证：△FCE ∽△EBD ；(2) 当点D 在线段AB 上运动时，是否有可能使EBD FCE S S ∆∆=4． 如果有可能，那么求出BD 的长．如果不可能请说明理由．34.如图，在△ABC 中，AB =AC =5，BC =6，P 是BC 上一点，且BP =2，将一个大小与∠B 相等的角的顶点放在P 点，然后将这个角绕P 点转动，使角的两边始终分别与AB 、AC 相交，交点为D 、E 。
（1）求证△BPD ∽△CEP（2）是否存在这样的位置，△PDE 为直角三角形？ 若存在，求出BD 的长；若不存在，说明理由。
35.如图，在△ABC 中，AB =AC =5，BC =6，P 是BC 上的一个动点(与B 、C 不重合)，PE ⊥AB 与E ，PF ⊥BC 交AC 与F ，设PC =x ，记PE =1y ，PF =2y（1）分别求1y 、2y 关于x 的函数关系式（2）△PEF 能为直角三角形吗?若能，求出CP 的长，若不能，请说明理由。