相似三角形判定拓展——K型相似
中考数学知识点复习 难题突破专题二 “K”字型相似研究

中考数学知识点复习难题突破专题二“K”字型相似研究相似基本图形中除了常见的“A”字型、“X”字型相似外,还有一个“K”字型相似,也常用于各种相似图形中.“K”字型相似由特殊到一般,题型往往丰富多彩,也是近几年浙江省中考题中常见的一种基本图形.了解一个基本图形,有助于我们在复杂图形中渗透其中的奥秘,从而找到解决问题的突破口.类型1 “K”字型相似基本图形1图Z2-1条件:如图Z2-1,B,C,E三点共线,∠B=∠ACD=∠E=90°.结论:△ABC∽△CED.证明:例题分层分析(1)证明两个三角形相似有哪些方法?(2)除了∠B=∠E=∠ACD之外,图中还可以找出哪些角相等?【应用】如图Z2-2,已知点A(0,4),B(4,1),BC⊥x轴于点C,点P为线段OC上一点,且PA⊥PB,则点P的坐标为________.图Z2-2例题分层分析(1)根据“K”字型相似,图中可以找到哪两个三角形相似?根据相似三角形又可以得到怎样的比例式?(2)设P(x,0),则根据比例式列出方程即可求得x的值,从而得到点P的坐标.解题方法点析“K”字型相似基本图形1,在于寻找三个直角相等,熟记基本图形有利于快速找到相似三角形,从而通过建立方程解决问题.类型2 “K”字型相似基本图形2条件:如图Z2-3,B,D,C三点共线,∠B=∠EDF=∠C=∠α.图Z2-3结论:△BDE∽△CFD.证明:例题分层分析(1)“K”字型相似基本图形2与基本图形1有何联系?(2)如何证明∠E=∠CDF?【应用】1.如图Z2-4,在平面直角坐标系中,四边形OABC是梯形,CB∥OA,OC=BA,OA=7,BC=1,AB=5,点P为x轴上的一个动点,点P不与点O,A重合.连结CP,过点P作PD交AB于点D.图Z2-4(1)直接写出点B的坐标:________;(2)当点P在线段OA上运动时,使得∠CPD=∠OAB,且BD∶AD=3∶2,求点P的坐标.例题分层分析(1)过点B作BQ⊥x轴于点Q,依题意可得OQ=4,AQ=3,已知AB=5,根据勾股定理求出QB即可解答.(2)根据“K”字型相似,图中可以找到哪两个三角形相似?根据相似三角形又可以得到怎样的比例式?2.如图Z 2-5,已知直线y =kx 与抛物线y =-427x 2+223交于点A (3,6).图Z 2-5(1)求直线y =kx 的函数表达式和线段OA 的长度.(2)若点B 为抛物线上对称轴右侧的点,点E 在线段OA 上(与点O ,A 不重合),点D (m ,0)是x 轴正半轴上的动点,且满足∠BAE =∠BED =∠AOD .探究:m 在什么范围内时,符合条件的点E 分别有1个、2个?例题分层分析(1)利用待定系数法求出直线y =kx 的函数表达式,根据A 点坐标用勾股定理求出线段OA 的长度.(2)①延长AB 交x 轴于点F ,由∠BAE =∠AOD 可求出点F 的坐标为________,进而再求得点B 的坐标为________,然后由两点间距离公式可求得线段AB 的长为________;②由已知条件∠BAE =∠BED =∠AOD ,可得到“K ”字型相似的基本图形2,故可得到△________∽△________,设OE =a ,则由对应边的比例关系可以得到________.从而得到关于a 的一元二次方程为____________,然后根据根的判别式可以分别得到a 的值分别为1个、2个时m 的取值范围.解题方法点析“K ”字型相似基本图形2,根据三个角相等,联想到“K ”字型基本图形1,便于快速找到相似三角形,从而利用相似的有关性质解决问题.专 题 训 练1.[2017·常州] 如图Z 2-6,已知矩形ABCD 的顶点A ,D 分别落在x 轴、y 轴上,OD =2OA =6,AD ∶AB =3∶1,则点C 的坐标是( )A .(2,7)B .(3,7)C .(3,8)D .(4,8)图Z 2-62.如图Z 2-7,在矩形ABCD 中,把DA 沿AF 对折,使得点D 与CB 边上的点E 重合,若AD =10,AB =8,则EF =________.图Z 2-73.[2017·攀枝花] 如图Z 2-8,D 是等边△ABC 边AB 上的点,AD =2,BD =4.现将△ABC 折叠,使得点C 与点D 重合,折痕为EF ,且点E ,F 分别在边AC 和BC 上,则CFCE =________.图Z 2-84.如图Z2-9,在直角梯形ABCF中,CB=14,CF=4,AB=6,CF∥AB,在边CB 上找一点E,使以E,A,B为顶点的三角形和以E,C,F为顶点的三角形相似,则CE=________.图Z2-95.如图Z2-10,在直角梯形ABCD中,∠A=90°,∠B=120°,AD=3,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.(1)当点E是AB的中点时,线段DF的长度是________;(2)若射线EF经过点C,则AE的长是________.图Z2-106.[2017·绵阳]将形状、大小完全相同的两个等腰三角形如图Z2-11所示放置,点D 在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点.若CA=5,AB=6,AD∶AB=1∶3,则MD+12MA·DN的最小值为________.图Z2-117.如图Z2-12,在四边形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连结DE,作EF⊥DE,交直线AB于点F.(1)若点F与B重合,求CE的长;(2)若点F在线段AB上,且AF=CE,求CE的长.图Z2-128.如图Z2-13,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD =∠B.(1)求证:AC·CD=CP·BP;(2)若AB=10,BC=12,当PD∥AB时,求BP的长.图Z2-139.[2017·天水] △ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.(1)如图Z2-14①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE.(2)如图Z2-14②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.图Z2-1410.在△ABC中,AB=AC,∠BAC=120°,P为BC的中点,小明拿着含有30°角的透明直角三角板,使30°角的顶点落在点P上,三角板绕点P旋转.(1)如图Z 2-15①,当三角板的一直角边和斜边分别与AB ,AC 交于点E ,F 时,连结EF ,请说明△BPE ∽△CFP .(2)操作:将三角板绕点P 旋转到图②的情形时,三角板的两边分别交BA 的延长线、边AC 于点E ,F ,连结EF .①探究1:△BPE 与△CFP 相似吗?请说明理由; ②探究2:△BPE 与△PFE 相似吗?请说明理由.图Z 2-15 参考答案类型1 “K ”字型相似基本图形1 例1 【例题分层分析】(1)证明两个三角形相似常用的判定方法有:两角对应相等的两个三角形相似;两边对应成比例且夹角相等的两个三角形相似;三边对应成比例的两个三角形相似等.(2)根据余角的性质还可以得到∠A =∠DCE ,∠ACB =∠D ,从而可证得△ABC ∽△CED . 证明:证明过程略. 应用【例题分层分析】(1)根据“K ”字型相似,可得到△AOP ∽△PCB ,所以AO PC =OPCB.(2)设P (x ,0),因为AO =OC =4,BC =1,所以OP =x ,PC =4-x ,所以44-x =x1,解得x =2,从而得到点P 的坐标为(2,0).[答案] (2,0) [解析] ∵PA ⊥PB , ∴∠APO +∠BPC =90°.∵AO ⊥x 轴, ∴∠APO +∠PAO =90°,∴∠PAO =∠BPC . 又∵BC ⊥x 轴,AO ⊥x 轴, ∴∠BCP =∠POA =90°, ∴△BCP ∽△POA ,∴AO PC =OPCB.∵点A (0,4),B (4,1),∴AO =4,BC =1,OC =4. 设P (x ,0),则OP =x ,PC =4-x ,∴44-x =x1,解得x =2,∴点P 的坐标为(2,0). 类型2 “K ”字型相似基本图形2 例2 【例题分层分析】(1)两个图形都有三个角相等,基本图形1是三个直角相等,而基本图形2是基本图形1的一般情况,更具普遍性,两个图形的形状均类似于字母“K ”,因此称之为“K ”字型相似图形.(2)∵∠B =∠EDF =∠C =∠α,由外角性质可知∠EDC =∠B +∠E =∠α+∠E . 又∵∠EDC =∠EDF +∠FDC =∠α+∠CDF , ∴∠E =∠CDF .证明:∵∠B =∠EDF =∠C =∠α,由外角性质可知∠EDC =∠B +∠E =∠α+∠E . 又∵∠EDC =∠EDF +∠FDC =∠α+∠FDC ,∴∠E =∠FDC .又∵∠B =∠C ,∴△BDE ∽△CFD .应用1【例题分层分析】(1)过点B 作BQ ⊥x 轴于点Q ,易求得BQ =4,故得到点B 的坐标为(4,4).(2)由“K ”字型相似可得到△POC ∽△DAP ,所以OC AP =OP AD, 设OP =x ,OC =AB =5,AD =25AB =2,AP =7-x , 所以57-x =x 2,解得x =2或x =5, 所以点P 的坐标为(2,0)或(5,0).解:(1)过点B 作BQ ⊥x 轴于点Q .∵AB =OC ,∴AQ =(7-1)÷2=3,在Rt △BQA 中,BA =5,由勾股定理,得BQ =AB 2-AQ 2=4, ∴点B 的坐标为(4,4).(2)∵∠CPA =∠OCP +∠COP ,即∠CPD +∠DPA =∠COP +∠OCP ,而∠CPD =∠OAB =∠COP ,∴∠OCP =∠APD ,∴△OCP ∽△APD ,∴OC AP =OP AD. ∵BD AD =32,∴AD =2. 设OP =x ,OC =AB =5,AP =7-x ,∴57-x =x 2, 解得x =2或x =5,∴点P 的坐标为(2,0)或(5,0).应用2【例题分层分析】(1)直线y =kx 的函数表达式为y =2x ,OA =32+62=3 5. (2)①点F 的坐标为(152,0),点B 的坐标为(6,2), AB =5.②根据“K ”字型相似的基本图形2,可得到△ABE ∽△OED ,设OE =a ,则AE =3 5-a (0<a <3 5), 由△ABE ∽△OED 得AE AB =OD OE, ∴3 5-a 5=m a ,∴a 2-3 5a +5m =0,依题意知m >0,∴当Δ=0,即(-3 5)2-20m =0,m =94时,符合条件的点E 有1个;当Δ>0,即(-3 5)2-20m >0,0<m <94时,符合条件的点E 有2个. 解:(1)把点A (3,6)的坐标代入y =kx ,得6=3k ,∴k =2,∴y =2x ,OA =32+62=3 5.(2)如图,延长AB 交x 轴于点F ,过点F 作FC ⊥OA 于点C ,过点A 作AR ⊥x 轴于点R.∵∠AOD =∠BAE ,∴AF =OF ,∴OC =AC =12OA =32 5.∵∠ARO =∠FCO =90°,∠AOR =∠FOC ,∴△AOR ∽△FOC ,∴OF OC =AO OR =3 53=5,∴OF =32 5×5=152, ∴点F 的坐标为⎝ ⎛⎭⎪⎫152,0. 设直线AF 的函数表达式为y =ax +b (a ≠0),把点A (3,6),F ⎝ ⎛⎭⎪⎫152,0的坐标代入,解得a =-43,b =10,∴y =-43x +10, 由⎩⎪⎨⎪⎧y =-43x +10,y =-427x 2+223,解得⎩⎪⎨⎪⎧x 1=3,y 1=6(舍去),⎩⎪⎨⎪⎧x 2=6,y 2=2,∴B (6,2),∴AB =5.∵∠BAE =∠BED ,∠ABE +∠BAE =∠DEO +∠BED ,∴∠ABE =∠DEO .∵∠BAE =∠EOD ,∴△ABE ∽△OED .设OE =a ,则AE =3 5-a (0<a <3 5),由△ABE ∽△OED 得AE AB =OD OE, 即3 5-a 5=m a ,∴a 2-3 5a +5m =0.依题意得m >0,∴当Δ=0,即(-3 5)2-20m =0,m =94时,符合条件的点E 有1个; 当Δ>0,即(-35)2-20m >0,0<m <94时,符合条件的点E 有2个. 专题训练1.A 2.5 3.54 4.2或12或285[解析] 两个三角形相似,可能是△EFC ∽△EAB ,也可能是△EFC ∽△AEB ,所以应分两种情况讨论,进而求CE 的值即可.5.(1)6 (2)2或5 [解析] (1)过点E 作EG ⊥DF ,由E 是AB 的中点,得出DG =3,从而得出∠DEG =60°,由∠DEF =120°,得∠FEG =60°,由tan ∠FEG =FG GE,即可求出GF 的长,进而得出DF 的长.(2)过点B 作BH ⊥DC ,延长AB ,过点C 作CM ⊥AB 于点M ,则BH =AD =3,再由锐角三角函数的定义求出CH 及BC 的长,设AE =x ,则BE =6-x ,利用勾股定理用x 表示出DE 及EC 的长,再判断出△EDC ∽△BCE ,由相似三角形的对应边成比例即可得出关于x 的方程,求出x 的值即可.6.2 3 [解析] 先求出AD =2,BD =4,由“K ”字型相似可得△AMD 和△BDN 相似,根据相似三角形对应边成比例可得MA BD =MD DN,求出MA ·DN =4MD ,再将所求代数式整理得出完全平方的形式,然后根据非负数的性质求出最小值即可.7.解:(1)当点F 和B 重合时,∵EF ⊥DE ,∴DE ⊥BC .∵∠B =90°,∴AB ⊥BC ,∴AB ∥DE .∵AD ∥BC ,∴四边形ABED 是平行四边形,∴AD =EF =9,∴CE =BC -EF =12-9=3.(2)过点D 作DM ⊥BC 于点M ,∵∠B =90°,∴AB ⊥BC ,∴DM ∥AB .∵AD ∥BC ,∴四边形ABMD 是矩形,∴AD =BM =9,AB =DM =7,CM =12-9=3.设AF =CE =a ,则BF =7-a ,EM =a -3,BE =12-a , 可证△FBE ∽△EMD ,∴BF EM =BE DM ,即7-a a -3=12-a 7, 解得a =5或a =17.∵点F 在线段AB 上,∴AF =CE <AB =7,∴CE =5.8.解:(1)证明:∵∠APC =∠PAB +∠B ,∠APD =∠B ,∴∠DPC =∠PAB ,又AB =AC ,∴∠ABP =∠PCD ,∴△ABP ∽△PCD ,∴AB CP =BP CD, ∴AC CP =BP CD,∴AC ·CD =CP ·BP . (2)∵PD ∥AB ,∴∠DPC =∠B ,∴∠PAB =∠B ,又∠B =∠C ,∴∠PAB =∠C .又∠PBA =∠ABC ,∴△PBA ∽△ABC ,∴BP AB =AB BC, ∴BP =AB 2BC =10212=253.9.解:(1)证明:∵△ABC 是等腰直角三角形,∴∠B =∠C =45°,AB =AC ,∵AP =AQ ,∴BP =CQ ,∵E 是BC 的中点,∴BE =CE ,在△BPE 和△CQE 中,∵⎩⎪⎨⎪⎧BE =CE ,∠B =∠C ,BP =CQ ,∴△BPE ≌△CQE (SAS );(2)∵△ABC 和△DEF 是两个全等的等腰直角三角形,∴∠B =∠C =∠DEF =45°,∵∠BEQ =∠EQC +∠C ,即∠BEP +∠DEF =∠EQC +∠C ,∴∠BEP +45°=∠EQC +45°,∴∠BEP =∠EQC ,∴△BPE ∽△CEQ ,∴BP CE =BE CQ, ∵BP =2,CQ =9,BE =CE ,∴BE 2=18,∴BE =CE =3 2,∴BC =6 2.10.解:(1)∵在△ABC 中,∠BAC =120°,AB =AC , ∴∠B =∠C =30°.∵∠B +∠BPE +∠BEP =180°,∴∠BPE +∠BEP =150°.又∵∠BPE +∠EPF +∠CPF =180°,∠EPF =30°,∴∠BPE +∠CPF =150°,∴∠BEP=∠CPF,∴△BPE∽△CFP(两角对应相等的两个三角形相似).(2)①△BPE∽△CFP,理由同(1).②△BPE与△PFE相似.理由:由①△BPE∽△CFP,得CP∶BE=PF∶PE,而CP=BP,因此BP∶BE=PF∶PE.又∵∠EBP=∠EPF,∴△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).。
相似三角形复习2—K字型
G
B
F
CD
K字型的延伸形式: A
B A
B
∟
G FC
∟
E
D E
G
F
CD
1、如图,等边△ABC的边长为3,点D是BC上一点,
且BD=1,在AC上取点E,使∠ADE=60度,AE长为
()
A. 3 B.2
2
3
C.
7 3
D.
3 4
2、四边形ABCD中,AD∥BC,AB=DC=AD=6, ∠ABC=∠C=70°,点E,F分别在线段AD,DC上, 且∠BEF=110°,若E为AD中点时,DF长为 ________.
在线段AD上是否存在一点E,使得F为CD的中点, 若存在求出AE的长,若不存在,说明理由。
3.如图,直线 l1∥l2∥l3,一等腰直角三角形 ABC 的三个顶 点 A,B,C 分别在 l1,l2,l3 上,∠ACB =90°,AC 交 l2 于点 D.已 知 l1 与 l2 的距离为 1,l2 与 l3 的距离为 3.则AB 的值为( )
1.先明确不变量及不变关系,对于变量,在 静止时刻进行代数化表示。
2.要使△APR∽△PRQ.,已有的相等条件是 什么?根据对应原则,还可以是哪两个角 对应相等?
3.若改为“当t为何值时,△APR与△PRQ相似”,应该如何解答?
4.如图,正△ABC边长为6cm,P,Q同时从 A,B两点出发,分别沿AB,BC匀速运动, 其中点P的速度为1cm/s,点Q的速度为 2cm/s,当Q点到达C点时,两点都停止运 动,设运动时间为t(s),作QR//BA交 AC于点R,连接PR,当t为何值时, △APR∽△PRQ.
1.先明确不变量及不变关系,对于变量,在 静止时刻进行代数化表示。
相似三角形中的K型图解读

西蒙诺夫 以他精准的文字 , 精巧的结构 , 真诚而炽热的情感 为我们谱写 了一首赞美诗 , 一 曲颂歌。 他赞美 的不仅是反法西斯
同盟各 国战斗 的友谊 , 南斯拉夫人 民对苏联红军的深厚感情 , 更
次, 竟给震倒 了。” 但是老妇人只是“ 取 出火柴来 , 很耐 心地再把 加讴歌 了人 性中最为动人的真善 美。让那一束战争硝烟 中 燃 起
字母 “ , 成为j i : 型图的条件 即为一线三等角 。 下面 , 我们 进一步地 来探究 K型 图 , 思考 问题 : 如图, 已知 LA= B = / _ . . MO N = 9 0  ̄ , 当点 0是 A B的中点时 , 连结 MN, 图中 最后 , 文 中两次写到 了方场上的树木。 第一次 出现是在文章 的第二段 。“ 只有一棵树还没有倒下 , 好像有一双魔手把它的上
/ _MO N = 9 0 。 ( 已知 )
・
.
相似三角形 中有一些基本 图形 , 如果 能掌握这些基本 图形 , 并把 它们从复杂 的图形 中挖掘 出来 , 构成几何 问题 中的核心结构 , 问
题 的解决也就水到渠成 。本文我们来研究 一下相似 三角形 中的
K型图。
一 .
肼
/ - - MO A +/ -N O B = 1 8 0  ̄ 一 ( 平
标。
AM A 0和 AMO N ̄ . , AO B N,显然 只要其 中一对 三角形相 似 , 根
NOB。 又 ‘ . ’ A: B . △^ 0一 △ 0 BⅣ。
如 果 把条 件 “ 厶4 = B=Z _ MO N = 9 0 。 ’ ’改为 “ 厶4 = B =
- / . _ MO N = o z ” , 那么结论仍然成立 。理由如下 : 炸 的当儿 , 蜡烛的火焰 不过 抖一下 ” 。“ 蜡烛被爆炸 的风吹灭 了, 有一次 , 竞给震倒 了” , 到后来 的“ 老妇人就取 出火柴来 , 很耐心
K型相似

K型相似【三角形中的K型相似】例:如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5,则BD的长为.变式一:如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=.变式二:如图,AB⊥DB于点B,CD⊥DB于点D,AB=6,CD=4,BD=14,点P在DB上移动.若以点C,D,P为顶点的三角形与点A,B,P为顶点的三角形相似,则DP=.变式三:如图,直线l1∥l2∥l3,l1与l2的距离为2,l2与l3的距离为3.把一块含有45°角的直角三角板如图所示放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为.【反比例函数与K型相似】例:如图,已知直线y=﹣2x+5与x轴交于点A,与y轴交于点B,将△AOB沿直线AB翻折后,设点O的对应点为点C,双曲线y=(x>0)经过点C,则k的值为.变式一:如图,已知点A是双曲线在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C 始终在双曲线上运动,则k的值是.变式二:如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=(x>0)经过点C、G,则k= .变式三:如图,点A是双曲线y=﹣在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=上运动,则k的值为.【K型相似综合题】例:如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.(1)求证:AC=AD+CE;(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q;(i)当点P与A、B两点不重合时,求的值;(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)变式一:在△ABC中,∠ABC=90°.(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠P AC=,求tan C的值;(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC=,,直接写出tan ∠CEB的值.变式二:(9分)已知顶点为A抛物线经过点,点.(1)求抛物线的解析式;(2)如图1,直线AB与x轴相交于点M,y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;(3)如图2,点Q是折线A﹣B﹣C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN1,若点N1落在x轴上,请直接写出Q点的坐标.。
中考数学复习难题突破专题二:K字型相似研究

难题突破专题二“K”字型相似研究相似基本图形中除了常见的“A”字型、“X”字型相似外,还有一个“K”字型相似,也常用于各种相似图形中.“K”字型相似由特殊到一般,题型往往丰富多彩,也是近几年浙江省中考题中常见的一种基本图形.了解一个基本图形,有助于我们在复杂图形中渗透其中的奥秘,从而找到解决问题的突破口.类型1 “K”字型相似基本图形1图Z2-11 条件:如图Z2-1,B,C,E三点共线,∠B=∠ACD=∠E=90°.结论:△ABC∽△CED.证明:例题分层分析(1)证明两个三角形相似有哪些方法?(2)除了∠B=∠E=∠ACD之外,图中还可以找出哪些角相等?【应用】如图Z2-2,已知点A(0,4),B(4,1),BC⊥x轴于点C,点P为线段OC上一点,且PA⊥PB,则点P 的坐标为________.图Z2-2例题分层分析(1)根据“K”字型相似,图中可以找到哪两个三角形相似?根据相似三角形又可以得到怎样的比例式?(2)设P(x,0),则根据比例式列出方程即可求得x的值,从而得到点P的坐标.解题方法点析“K”字型相似基本图形1,在于寻找三个直角相等,熟记基本图形有利于快速找到相似三角形,从而通过建立方程解决问题.类型2 “K”字型相似基本图形22 条件:如图Z2-3,B,D,C三点共线,∠B=∠EDF=∠C=∠α.图Z2-3结论:△BDE∽△CFD.证明:例题分层分析(1)“K”字型相似基本图形2与基本图形1有何联系?(2)如何证明∠E=∠CDF?【应用】1.如图Z2-4,在平面直角坐标系中,四边形OABC是梯形,CB∥OA,OC=BA,OA=7,BC=1,AB=5,点P为x轴上的一个动点,点P不与点O,A重合.连结CP,过点P作PD交AB于点D.图Z2-4(1)直接写出点B的坐标:________;(2)当点P在线段OA上运动时,使得∠CPD=∠OAB,且BD∶AD=3∶2,求点P的坐标.例题分层分析(1)过点B作BQ⊥x轴于点Q,依题意可得OQ=4,AQ=3,已知AB=5,根据勾股定理求出QB即可解答.(2)根据“K”字型相似,图中可以找到哪两个三角形相似?根据相似三角形又可以得到怎样的比例式?2.如图Z2-5,已知直线y=kx与抛物线y=-427x2+223交于点A(3,6).图Z2-5(1)求直线y=kx的函数表达式和线段OA的长度.(2)若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O,A不重合),点D(m,0)是x轴正半轴上的动点,且满足∠BAE=∠BED=∠AOD.探究:m在什么范围内时,符合条件的点E分别有1个、2个?例题分层分析(1)利用待定系数法求出直线y=kx的函数表达式,根据A点坐标用勾股定理求出线段OA的长度.(2)①延长AB交x轴于点F,由∠BAE=∠AOD可求出点F的坐标为________,进而再求得点B的坐标为________,然后由两点间距离公式可求得线段AB的长为________;②由已知条件∠BAE=∠BED=∠AOD,可得到“K”字型相似的基本图形2,故可得到△________∽△________,设OE=a,则由对应边的比例关系可以得到________.从而得到关于a的一元二次方程为____________,然后根据根的判别式可以分别得到a的值分别为1个、2个时m的取值范围.解题方法点析“K”字型相似基本图形2,根据三个角相等,联想到“K”字型基本图形1,便于快速找到相似三角形,从而利用相似的有关性质解决问题.专题训练1.[2019·常州] 如图Z2-6,已知矩形ABCD的顶点A,D分别落在x轴、y轴上,OD=2OA=6,AD∶AB=3∶1,则点C的坐标是( )A.(2,7) B.(3,7) C.(3,8) D.(4,8)图Z2-62.如图Z2-7,在矩形ABCD中,把DA沿AF对折,使得点D与CB边上的点E重合,若AD=10,AB =8,则EF=________.图Z2-73.[2019·攀枝花] 如图Z2-8,D 是等边△ABC 边AB 上的点,AD =2,BD =4.现将△ABC 折叠,使得点C 与点D 重合,折痕为EF ,且点E ,F 分别在边AC 和BC 上,则CFCE=________.图Z2-84.如图Z2-9,在直角梯形ABCF 中,CB =14,CF =4,AB =6,CF ∥AB ,在边CB 上找一点E ,使以E ,A ,B 为顶点的三角形和以E ,C ,F 为顶点的三角形相似,则CE =________.图Z2-95.如图Z2-10,在直角梯形ABCD 中,∠A =90°,∠B =120°,AD =3,AB =6.在底边AB 上取点E ,在射线DC 上取点F ,使得∠DEF=120°.(1)当点E 是AB 的中点时,线段DF 的长度是________; (2)若射线EF 经过点C ,则AE 的长是________.图Z2-106.[2019·绵阳]将形状、大小完全相同的两个等腰三角形如图Z2-11所示放置,点D 在AB 边上,△DEF 绕点D 旋转,腰DF 和底边DE 分别交△CAB 的两腰CA ,CB 于M ,N 两点.若CA =5,AB =6,AD ∶AB =1∶3,则MD +12MA·DN的最小值为________.图Z2-117.如图Z2-12,在四边形ABCD 中,已知AD∥BC,∠B =90°,AB =7,AD =9,BC =12,在线段BC 上任取一点E ,连结DE ,作EF⊥DE,交直线AB 于点F.(1)若点F与B重合,求CE的长;(2)若点F在线段AB上,且AF=CE,求CE的长.图Z2-128.如图Z2-13,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.(1)求证:AC·CD=CP·BP;(2)若AB=10,BC=12,当PD∥AB时,求BP的长.图Z2-139.[2019·天水] △ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.(1)如图Z2-14①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE.(2)如图Z2-14②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.图Z2-1410.在△ABC中,AB=AC,∠BAC=120°,P为BC的中点,小明拿着含有30°角的透明直角三角板,使30°角的顶点落在点P上,三角板绕点P旋转.(1)如图Z2-15①,当三角板的一直角边和斜边分别与AB,AC交于点E,F时,连结EF,请说明△BPE∽△CFP.(2)操作:将三角板绕点P旋转到图②的情形时,三角板的两边分别交BA的延长线、边AC于点E,F,连结EF.①探究1:△BPE与△CFP相似吗?请说明理由;②探究2:△BPE与△PFE相似吗?请说明理由.图Z2-15参考答案类型1 “K”字型相似基本图形1例1 【例题分层分析】(1)证明两个三角形相似常用的判定方法有:两角对应相等的两个三角形相似;两边对应成比例且夹角相等的两个三角形相似;三边对应成比例的两个三角形相似等.(2)根据余角的性质还可以得到∠A=∠DCE,∠ACB=∠D,从而可证得△ABC∽△CED.证明:证明过程略.应用【例题分层分析】(1)根据“K”字型相似,可得到△AOP∽△PCB,所以AOPC=OPCB.(2)设P(x,0),因为AO=OC=4,BC=1,所以OP=x,PC=4-x,所以44-x=x1,解得x=2,从而得到点P的坐标为(2,0).[答案] (2,0) [解析] ∵PA⊥PB,∴∠APO+∠BPC=90°.∵AO⊥x轴,∴∠APO+∠PAO=90°,∴∠PAO=∠BPC.又∵BC⊥x轴,AO⊥x轴,∴∠BCP=∠POA=90°,∴△BCP∽△POA,∴AOPC =OP CB.∵点A(0,4),B(4,1),∴AO=4,BC=1,OC=4. 设P(x,0),则OP=x,PC=4-x,∴44-x=x1,解得x=2,∴点P的坐标为(2,0).类型2 “K”字型相似基本图形2例2 【例题分层分析】(1)两个图形都有三个角相等,基本图形1是三个直角相等,而基本图形2是基本图形1的一般情况,更具普遍性,两个图形的形状均类似于字母“K”,因此称之为“K”字型相似图形.(2)∵∠B=∠EDF=∠C=∠α,由外角性质可知∠EDC=∠B+∠E=∠α+∠E.又∵∠EDC=∠EDF+∠FDC=∠α+∠CDF,∴∠E=∠CDF.证明:∵∠B=∠EDF=∠C=∠α,由外角性质可知∠EDC=∠B+∠E=∠α+∠E.又∵∠EDC=∠EDF+∠FDC=∠α+∠FDC,∴∠E=∠FDC.又∵∠B=∠C,∴△BDE∽△CFD.应用1【例题分层分析】(1)过点B作BQ⊥x轴于点Q,易求得BQ=4,故得到点B的坐标为(4,4).(2)由“K”字型相似可得到△POC∽△DAP,所以OCAP=OPAD,设OP=x,OC=AB=5,AD=25AB=2,AP=7-x,所以57-x =x2,解得x =2或x =5, 所以点P 的坐标为(2,0)或(5,0). 解:(1)过点B 作BQ⊥x 轴于点Q. ∵AB =OC ,∴AQ =(7-1)÷2=3, 在Rt △BQA 中,BA =5,由勾股定理,得BQ =AB 2-AQ 2=4, ∴点B 的坐标为(4,4). (2)∵∠CPA=∠OCP+∠COP, 即∠CPD+∠DPA=∠COP+∠OCP, 而∠CPD=∠OAB=∠COP, ∴∠OCP =∠APD, ∴△OCP ∽△APD , ∴OC AP =OP AD. ∵BD AD =32,∴AD =2. 设OP =x ,OC =AB =5,AP =7-x , ∴57-x =x 2, 解得x =2或x =5,∴点P 的坐标为(2,0)或(5,0). 应用2【例题分层分析】(1)直线y =kx 的函数表达式为y =2x ,OA =32+62=3 5. (2)①点F 的坐标为(152,0),点B 的坐标为(6,2),AB =5.②根据“K ”字型相似的基本图形2,可得到△ABE∽△OED ,设OE =a ,则AE =3 5-a(0<a <3 5), 由△ABE∽△OED 得AE AB =ODOE, ∴3 5-a 5=m a,∴a 2-3 5a +5m =0, 依题意知m>0,∴当Δ=0,即(-3 5)2-20m =0,m =94时,符合条件的点E 有1个;当Δ>0,即(-3 5)2-20m >0,0<m <94时,符合条件的点E 有2个.解:(1)把点A(3,6)的坐标代入y =kx ,得6=3k , ∴k =2,∴y =2x ,OA =32+62=3 5.(2)如图,延长AB 交x 轴于点F ,过点F 作FC⊥OA 于点C ,过点A 作AR⊥x 轴于点R.∵∠AOD =∠BAE, ∴AF =OF ,∴OC =AC =12OA =325.∵∠ARO =∠FCO=90°,∠AOR =∠FOC, ∴△AOR ∽△FOC , ∴OF OC =AO OR =3 53=5,∴OF =32 5×5=152, ∴点F 的坐标为⎝ ⎛⎭⎪⎫152,0.设直线AF 的函数表达式为y =ax +b(a≠0),把点A(3,6),F ⎝ ⎛⎭⎪⎫152,0的坐标代入,解得a =-43,b=10,∴y =-43x +10,由⎩⎪⎨⎪⎧y =-43x +10,y =-427x 2+223,解得⎩⎪⎨⎪⎧x 1=3,y 1=6(舍去),⎩⎪⎨⎪⎧x 2=6,y 2=2, ∴B(6,2),∴AB =5. ∵∠BAE =∠BED,∠ABE +∠BAE=∠DEO+∠BED, ∴∠ABE =∠DEO.∵∠BAE =∠EOD,∴△ABE ∽△OED. 设OE =a ,则AE =3 5-a(0<a <3 5), 由△ABE∽△OED 得AE AB =ODOE, 即3 5-a 5=m a,∴a 2-3 5a +5m =0. 依题意得m>0,∴当Δ=0,即(-3 5)2-20m =0,m =94时,符合条件的点E 有1个;当Δ>0,即(-3 5)2-20m >0,0<m <94时,符合条件的点E 有2个.专题训练1.A 2.5 3.544.2或12或285 [解析] 两个三角形相似,可能是△EFC∽△EAB,也可能是△EFC∽△AEB,所以应分两种情况讨论,进而求CE 的值即可.5.(1)6 (2)2或5 [解析] (1)过点E 作EG⊥DF,由E 是AB 的中点,得出DG =3,从而得出∠DEG =60°,由∠DEF =120°,得∠FEG=60°,由tan ∠FEG =FGGE,即可求出GF 的长,进而得出DF 的长. (2)过点B 作BH⊥DC,延长AB ,过点C 作CM⊥AB 于点M ,则BH =AD =3,再由锐角三角函数的定义求出CH 及BC 的长,设AE =x ,则BE =6-x ,利用勾股定理用x 表示出DE 及EC 的长,再判断出△EDC∽△BCE,由相似三角形的对应边成比例即可得出关于x 的方程,求出x 的值即可.6.2 3 [解析] 先求出AD =2,BD =4,由“K ”字型相似可得△AMD 和△BDN 相似,根据相似三角形对应边成比例可得MA BD =MDDN ,求出MA·DN=4MD ,再将所求代数式整理得出完全平方的形式,然后根据非负数的性质求出最小值即可.7.解:(1)当点F 和B 重合时,∵EF ⊥DE ,∴DE ⊥BC. ∵∠B =90°,∴AB⊥BC, ∴AB ∥DE.∵AD ∥BC , ∴四边形ABED 是平行四边形, ∴AD =EF =9,∴CE =BC -EF =12-9=3.(2)过点D 作DM⊥BC 于点M , ∵∠B =90°,∴AB ⊥BC , ∴DM ∥AB. ∵AD ∥BC ,∴四边形ABMD 是矩形,∴AD =BM =9,AB =DM =7,CM =12-9=3.设AF =CE =a ,则BF =7-a ,EM =a -3,BE =12-a , 可证△FBE∽△EMD,∴BF EM =BE DM ,即7-a a -3=12-a 7, 解得a =5或a =17.∵点F 在线段AB 上,∴AF =CE <AB =7,∴CE =5.8.解:(1)证明:∵∠APC=∠PAB+∠B,∠APD =∠B,∴∠DPC =∠PAB,又AB =AC ,∴∠ABP =∠PCD,∴△ABP ∽△PCD ,∴AB CP =BP CD, ∴AC CP =BP CD,∴AC ·CD =CP·BP. (2)∵PD∥AB,∴∠DPC =∠B,∴∠PAB =∠B,又∠B=∠C,∴∠PAB =∠C.又∠PBA=∠ABC,∴△PBA ∽△ABC ,∴BP AB =AB BC, ∴BP =AB 2BC =10212=253. 9.解:(1)证明:∵△ABC 是等腰直角三角形,∴∠B =∠C=45°,AB =AC ,∵AP =AQ ,∴BP =CQ ,∵E 是BC 的中点,∴BE =CE ,在△BPE 和△CQE 中,∵⎩⎪⎨⎪⎧BE =CE ,∠B =∠C,BP =CQ ,∴△BPE ≌△CQE(SAS);(2)∵△ABC 和△DEF 是两个全等的等腰直角三角形,∴∠B =∠C=∠DEF=45°,∵∠BEQ =∠EQC+∠C,即∠BEP+∠DEF=∠EQC+∠C,∴∠BEP +45°=∠EQC+45°,∴∠BEP =∠EQC,∴△BPE∽△CEQ,∴BPCE =BE CQ,∵BP=2,CQ=9,BE=CE,∴BE2=18,∴BE=CE=3 2,∴BC=6 2.10.解:(1)∵在△ABC中,∠BAC=120°,AB=AC,∴∠B=∠C=30°.∵∠B+∠BPE+∠BEP=180°,∴∠BPE+∠BEP=150°.又∵∠BPE+∠EPF+∠CPF=180°,∠EPF=30°,∴∠BPE+∠CPF=150°,∴∠BEP=∠CPF,∴△BPE∽△CFP(两角对应相等的两个三角形相似).(2)①△BPE∽△CFP,理由同(1).②△BPE与△PFE相似.理由:由①△BPE∽△CFP,得CP∶BE=PF∶PE,而CP=BP,因此BP∶BE=PF∶PE.又∵∠EBP=∠EPF,∴△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).2019-2020学年数学中考模拟试卷一、选择题1.加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系p=at2+bt+c(a,b,c是常数),如图记录了三次实验的数据.根据上述函数模型和实验数据,可得到最佳加工时间为()A.4.25分钟B.4.00分钟C.3.75分钟D.3.50分钟2.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是()A.CB=CDB.∠BAC=∠DACC.∠BCA=∠DCAD.∠B=∠D=90°3.我国古代《易经》一书中记载:远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )A.515B.346C.1314D.844.已知△ABC∽△DEF,其中AB=6,BC=8,AC=12,DE=3,那么△DEF的周长为()A.394B.263C.13D.265.如图,向正六边形的飞镖游戏盘内随机投掷一枚飞镖则该飞镖落在阴影部分的概率( ).A. B. C. D.6.计算a 2+4a 2的结果是( )A .4a 2B .5a 2C .4a 4D .5a 47.如图,一次函数y=kx+b 的图象经过点(-1,0)与(0,2),则关于x 的不等式kx+b >0的解集是( )A .x 1>-B .x 1<-C .x 2>D .x 2< 8.如图,P 的半径为5,A B 、是圆上任意两点,且6AB =,以AB 为边作正方形ABCD (点、D P 在直线AB 两侧).若AB 边绕点P 旋转一周,则CD 边扫过的面积为( )A .5πB .6πC .8πD .9π 9.已知抛物线2(0)y ax bx c a =++≠的对称轴为1x =-,与x 轴的一个交点在(3,0)-和(2,0)-之间,其部分图像如图所示,则下列结论:①点17(,)2y -,23(,)2y -,35(,)4y 是该抛物线上的点,则123y y y <<;②320b c +<;③()t at b a b +≤-(t 为任意实数).其中正确结论的个数是( )A .0B .1C .2D .310.袋中装有大小相同的6个黑球和n 个白球,经过若干次试验,发现“从袋中任意摸出一个球,恰是黑球的概率为34”则袋中白球大约有( ) A.2个 B.3个 C.4个 D.5个11.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )A .25B .13C .415D .1512.对于反比例函数6y x =-,当10x -<…时,y 的取值范围是( ) A .6y …B .60y -≤<C .06y <…D .6y <-二、填空题 13.甲、乙两个搬运工搬运某种货物.已知乙比甲每小时多搬运600kg ,甲搬运5000kg 所用的时间与乙搬运8000kg 所用的时间相等.设甲每小时搬运xkg 货物,则可列方程为_____.14.已知抛物线2=2(1)3y x -+-与直线2y kx m =+相交于A (-2,3)、B (3,-1)两点,则12y y ≥时x 的取值范围是___________.15.已知扇形的圆心角为60º,半径为6cm ,则扇形的弧长为 cm.16.已知 x =﹣1 是一元二次方程 ax 2﹣bx+6=0 的一个根,则 a+b 的值为_____17.计算)33的结果等于______________. 18.为了说明命题“等腰三角形腰上的高小于腰”是假命题,可以找的反例是_____.三、解答题19.已知2222x 4x 4x 11T x 2xx x x ⎛⎫-+-=+÷ ⎪-+⎝⎭ (1)化简T ;(2)若x 为△ABC 的面积,其中∠C =90°,∠A =30°,BC =2,求T 的值.20.已知二次函数y=ax 2+bx+8,经过点(1,9)和(6,−16).(1)求该二次函数的解析式;(2)设该二次函数的图象与x 轴的交点为A .B ,与y 轴的交点为C ,求△ABC 的面积。
中考数学专题之“一线三角”(K型图)证相似
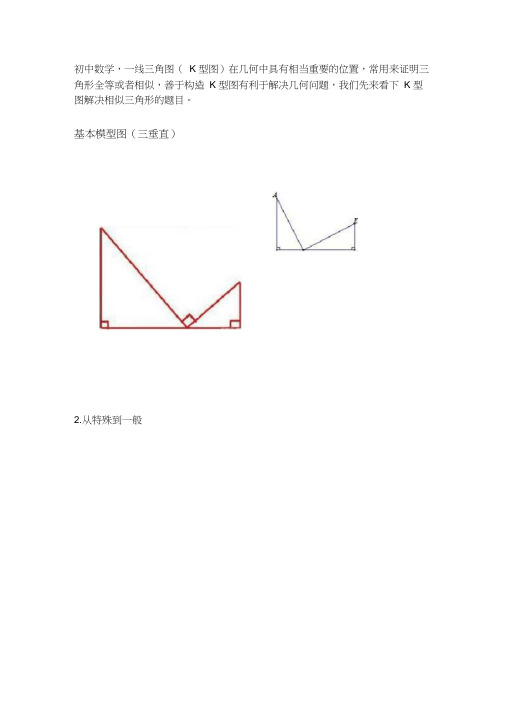
初中数学,一线三角图( K 型图)在几何中具有相当重要的位置,常用来证明三 角形全等或者相似,善于构造 K 型图有利于解决几何问题,我们先来看下 K 型 图解决相似三角形的题目。
基本模型图(三垂直)2.从特殊到一般3.相似中K 型图常见形态(A字型、8 字型)例题1:已知△ABC 中AB=AC、BC=8,D是BC 边上任意一点,AB 边上有一点E,AC 边上有一点F,使∠ EDF= ∠ C. 已知BD=6 、BE=4,求CF的长。
分析:这是一道典型的K 型图,已知∠ EDF= ∠C=∠B,从而可以得到△BDE∽△CFD例题2:如图,已知点A(0,4)、B(4,1),BC⊥x轴于点C,点P 为线段OC 上一点,且PA⊥ PB.求点P 的坐标。
分析:这是三垂直模型图(∠ AOP= ∠AOB= ∠BCP=9°0 ),我们很快可以得到△AOC 与△BCP 相似例题 3:已知矩形 ABCD 中, CD=2 ,AD=3 ,点 P 是 AD 上的一个动点,且和 点 A ,D 不重合,过点 P 作 PE ⊥CP ,交边 AB 于点 E ,设 PD=x ,AE=y ,求 y y 的最大值。
解析:由图可知:∠ A=∠EPC= ∠D=90°,是三垂直模型,可以得到 △EAP ∽△ PDC ,通过比例式得到 x 与 y 的函数关系式,进而求出 y的最大值Zi-1•等∣∣fΔJkBC l AB=AC= 8 , ZDAC=I20°F P为BC的中点,小9>⅜含30:角的透明三角板,便抄角的顶点落在点P,三角板级P点旋無•(L)如图L当三角板的两边分別交AB ∙ AC于点EP时.束证?ABPE^∆CFPJC2)揉仕箝三角板境点PfiH刚囹b惜形叭三超板的两边分别交BA的延长线、边Ae于点E、F.G)搽究Iz ABPE与ZXFP还相似吧?(只需写比结论)©持究2:连结EF, ∆BPE ⅛∆PFE g否相似?请说明環由d® IS EF=ιt, ∆EPF的面枳为S,试用氏的代数式未示S∙rSbS□①求证:ZkOCPSAPDA;②若AOCP与ZXPDA的面枳比为U 4,求边AB州Q(2)若圄1中的点P恰好罡CD边的中点丿求/OAB的度数;<3>如凰2,在⑴条件下,揀去折痕込线段申连结叭动点Jl在纟網AP上〈点M与点P. A 不重合》,动点“在线段AB的延冷虹,且盼PIv送结加交PB于点巧作KElBP于点匚试问当点讥H在移动过程中,线段EF的*度是否发主超匕?若鸡匕说明理由丿若不氐求出线段EF的≡.Zl-4阅渎理解:如團Ii 在四边形ABCD 的边AB 上任取一点E {点E 不与A 、B 重合),分别连接ED 、EC, 可以把四边形APCD 分成三个三角形,如果Rd 有两个三角形相似啟们我把E 叫做四边形ABCP 的边AB 上的“相攸点” > 如杲这三个三角形訓目饥 我们蒯巴E 叫傲四边形ABCD 的边AB 上 的“强«似点"・〈】〉扣图b ZA=ZB=ZPEC=45d ,试判浙点E 罡否定囚边形ΛK D 的边AE 上的相似駄 并说 明理由,(2) 如因2,在矩形ABS P A∙ B. C 、D 四点均在正万形网榕(网格中毎个小正万形的边长为 1>的林点〈卬厨个小正方形的顶点)上,试衽图2中画出矩形ABCD 的边AB 上泪相似点; (3) 如图3,砌返形ABCD 沿CM 折崑 使点D 落在AB 边上的点E 处,若点E 恰好定四边形 Δ≡的边AB 上的T 、窗出忙包・试抹究AB 与DC 的刘蚩关系3己知正方形ABcD 的边长为码 T 以点A 为顶点前笳。
相似三角形判定定理

探讨相似三角形判定定理的逆命题
9字
两三角形如果对应边成比例, 那么这两个三角形是否一定 相似?
9字
两三角形如果面积比等于相 似比的平方,那么这两个三 角形是否一定相似?
9字
回答是肯定的。如果两个三 角形的对应边成比例,那么 它们的对应角必然相等,因 此这两个三角形一定相似。
9字
回答也是肯定的。如果两个 三角形的面积比等于相似比 的平方,那么它们的对应边 必然成比例,因此这两个三 角形一定相似。
该定理是相似三角形判定的基础,也是 应用最广泛的判定方法之一。
判定定理二:两边对应成比例且夹角相等
如果一个三角形的两条边与另一个三角形的两条边对应成比例, 并且夹角相等,则这两个三角形相似。
该定理是相似三角形判定的另一种方法,适用于已知两边和夹 角的情况。
判定定理三:三边对应成比例
如果一个三角形的三条边与另一个三角形的三条边对应成比例,则这两个三角形相 似。
该定理是相似三角形判定的另一种方法,适用于已知三边长度的情况。
以上三个判定定理是相似三角形判定的主要方法,它们在实际应用中具有广泛的适 用性和实用性。同时,这些定理也是学习相似三角形知识的基础和关键。
03
相似三角形证明方法
综合法证明
综合运用相似三角形的性质
01
通过已知条件,结合相似三角形的对应角相等、对应边成比例
飞机的位置。
建筑设计中的应用
比例缩放
在建筑设计中,相似三角形可以帮助 设计师按比例缩放模型,使得不同大 小的建筑保持相同的比例和美感。
透视绘图
在绘制建筑透视图时,相似三角形原 理可以帮助准确表现物体的远近关系 和立体感。
结构分析
在建筑结构分析中,相似三角形可以 帮助工程师理解和计算结构的稳定性 和承重能力。
相似三角形——“K字型”相似模型

相似三角形——“K 字型”相似模型教学目标:1、理解“K 型图”的特征与其中两个三角形相似的条件,2、利用“K 型图”中两个三角形的相似性解决一些计算、证明等问题;教学重点难点:1、在已知图形中观察关键特征——“K 型”;2、在非“K 型”图形中画辅助线,得到“K 型”图形;3、在“K 型”图的两个三角形中,探索其相似条件。
教学过程:一、前测练习1.如图,在矩形ABCD 中,E 在AD 上,EF ⊥BE ,交CD 于F ,连结BF ,则∆ ∽∆2.在等边△ABC 中,D 为BC 边上一点,E 为AC 边上一点,且∠ADE=60°, 则∆ ∽∆二、模型探究课前完成填空,上课请学生回答答案,根据答案回答以下问题:问题1判定这两个三角形相似的依据是什么?学生答:两个角对应相等的两个三角形相似。
问题2图中已知角有什么共同特征?学生答:图1中顶点共线三角都是直角,图2中顶点共线三角都是60°。
问题3若顶点共线三等角的度数不是90°也不是60°,对应两个三角形还相似吗?图形演示,提问:此时这两个三角形相似吗?请同学们自己画图并证明。
请学生叙此时述证明过程:已知: n C ADE B =∠=∠=∠求证:ABD ∆∽DEC ∆证明: n B =∠n ADB BAD -=∠+∠∴180 AB D En ADE =∠n ADB CDE -=∠+∠∴180CDE BAD ∠=∠∴C B ∠=∠ABD ∆∴∽DEC ∆(或者依据外角等于不相邻的两内角之和)展示学生书写,教师分析,该同学找出的两三角形相似的第一个条件是(C B ∠=∠)第二个条件是(CDE BAD ∠=∠),他是怎么证明这两个角相等呢?方法1、外角等于不相邻的两内角之和;方法2、三角形的内角和等于平角求解,都可行。
问题4若保持共线三等角的度数不变,改变边的长度,对应两个三角形还相似吗?学生答:相似。
因为我们是依据两个角对应相等判定两个三角形相似的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目标:
能从复杂的图中抽出k型图,熟练证明 两相似三角形,提高解题速度。
练习:
1、如图,在矩形ABCD中,E在 AD上,EF⊥BE ,交CD于F,连 结BF,则图中与△ABE 一定相 似的三角形是(B) A.△EFB B.△DEF C.△CFB D.△EFB 和△DEF
学会从复杂图形中分解基本图形
3
4、如图,在直角梯形
ABCD中,
5
AD∥BC, ∠B=900,
AD=3,BC=6,DP⊥PC且
AP=5,求PB的长。
?
6
5、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC 边上的一个动点(不与B、C重合),在AC上取一点E,使 ∠ADE=45°
(1)求证:△ABD∽△DCE (2)设BD=x,AE=y,求y关于x的函数关系式
练习:
2、如图,在矩形ABCD中,E在AD上, EF⊥BE ,交CD于F,连结BF,已知AE=4, ED=2,AB=3
则DF=___8_______ 3
4
2
? 3
3、已知:D为BC上一点∠B=∠C=∠EDF=60°, BE=6 , CD=3 , CF=4 ,则BD=_______
A
E
6
B
?
F
4
D 3C
3
2
一、探究基本图形3的性质:
已知:如图∠C=∠D=∠1=n°时, 则△APC与△BPD上述结论还成立吗?为什么?
3
⌒
2
探究:
当﹤c ,﹤1 ,﹤ D在同一直线上,且满足 条件﹤__c _=﹤__1 _=_﹤_D_时,△APC与△BPD 相似 。
归纳巧记:一线三等角,相似两三角(形)
K型
相似三角形中 基本图形(之一)
解: ∵△ABD∽△DCE
A
y
∴ AB BD CD CE
即 1 x 2 x 1 y
1
B xD
E 1 y ∴ 1 y x 2 x
C ∴ y x2 2x 1
2x
21
3
21
3
注意: 复杂图形可分解基本图形
基本图形的应用:
再 见
如图,已知点A(1,2)是函数 y 2 (x>0)的图象
若AB=4,BC=6,求DG的长.
A
HD
E
G
B
F
C
A
变:点E为BC上任意一点, 若 ∠B= ∠C= ∠AEF= α, 结 论还成立吗?
△ABE∽ △ECF
F
B
E
C
A
α
α
B
E
F
α C
学习目标:
1)能从复杂的图中抽出k型图,熟练证明 两相似三角形,提高解题速度。
2)能从解题中挖掘出从特殊到一般的归 纳思想,养成良好的数学思维能力。
B
相似三角形基本图形的回顾:
A E
E A
D X型
C
B
C
A
D E
ቤተ መጻሕፍቲ ባይዱ
B
C
A
D B
E D
A
B
∠ACB=Rt∠
CD⊥AB
母子相似型
B
C A D
C
一、探究基本图形1的性质:
已知:如图∠C=∠D=∠1=90°时, 则:△APC与△BPD有什么关系?为什么?
3
2
一、探究基本图形2的性质:
已知:如图∠C=∠D=∠1=60°时, 则:△APC与△BPD还相似吗?为什么?
x
的点,连接OA,作OA⊥OB,与图象 y - 6 (x>0)
交于点B.
x
(1)求点yB的坐标; (2)求OA︰OB的值;
(3)若点A在双曲线上移
A C
动, 保持OA⊥OB 不变, OA︰OB的值变吗?
o
x
D
B
如图,由8个大小相等的小正方形构成的图案, 它的四个顶点E、F、G、H分别在矩形ABCD的 边AB、BC、CD、DA上。
A4
如图,在矩形ABCD中, E在AD上,连结BE、EF、3 BF已知AE=4,ED=2, AB=3,若以A、B、E为 B 顶点的三角形和△DEF 相似,则DF= 8或 3
32
E2D ? F
C
∵∠ADC是△ABD的外角
∴∠ADC=∠ADE+∠2=∠B+∠1
∴∠1=∠2
E
∴ △ABD∽△DCE
C
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上 的一个动点(不与B、C重合),在AC上取一点E,使 ∠ADE=45°
(1)求证:△ABD∽△DCE (2)设BD=x,AE=y,求y关于x的函数关系式
知识回顾
判定三角形相似的方法
(1)∵DE∥BC ∴△ADE∽△ABC
(2)∵ AB AC BC DE DF EF
∴△ABC∽△DEF
(3) ∵ AB AC ∠A=∠D DE DF
∴△ABC∽△DEF (4)∵∠A=∠D, ∠B= ∠E
∴△ABC∽△DEF
A
D
E
B
C
A
D
B
CE
F
A型 D
A
1
Bx D
y
E
C
如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上 的一个动点(不与B、C重合),在AC上取一点E,使 ∠ADE=45°
(1)求证:△ABD∽△DCE
A
1
B
)2 D
证明:∵AB=AC,∠BAC=90°
∴∠B=∠C=45° 又∵∠ADE=45°
∴∠ADE=∠B
