黄河小浪底调水调沙问题
每日一题483黄河冲沙清淤(简)

一题
二中地理 伴你成长
2020届山东济南高三三模 阅读材料,完成下列要求。(16分) 黄河是世界罕有的多沙河流。黄河调水调沙是根据 水库蓄水情况,充分利用自然的力量,通过精确调 度小浪底水库的水量进行冲沙减淤,辅以人工扰动 措施,调整其河道淤积形态,加大排沙量,即利用 进入下游河道水流的挟沙能力,在悬河主槽淤积最 为严重的河段实施河床泥沙扰动,扩大主槽过洪能 力。下图为黄河流域局部图及某次调水扰沙工程景 观图。据此完成1-3题。
(1)小浪底放水排沙为每年的6月下旬或7月上旬 ,但每年时间并不固定,请分析原因。(6分)
(2)说明人工扰沙工程选取图示河段的原因。(6 分)
(3)河流泥沙有害有利,请提ห้องสมุดไป่ตู้将黄河泥沙化害 为利的具体措施。(4分)
参考答案:
1.我国北方七、八月份雨季来临之前,水库需要腾 出一定的库容做好防洪准备(2分);清淤河道, 增大洪水通过能力(2分)。夏季风的强弱影响我 国雨带由南至北移动的快慢,雨带至黄河流域有 早有晚,调水调沙的时间相应调整(2分)。
2.河道弯曲,水流不畅(2分); 地势低平,流速减缓(2分); 距离小浪底水库远,沿途下渗、蒸发、取用水, 导致该河段流量小泥沙易沉积(2分)。
3.
黄河泥沙可以固堤防汛;做建筑材料;进行土地
的修复改良,即矿坑回填、盐碱地淤沙改造;河 口造陆和湿地生态系统维护。(答对其中两点即可 得4分)
小浪底调水调沙原理

小浪底调水调沙原理小浪底是位于黄河上游的一个重要水利工程,它不仅起到了水利调节的作用,还在黄河上游的泥沙调控中发挥着重要作用。
小浪底的调水调沙原理是怎样的呢?接下来我们就来详细了解一下。
首先,小浪底调水调沙的原理是基于黄河上游水沙特点的分析。
黄河上游水沙特点主要表现为年内水沙变化大、年际水沙变化大、时空分布不均等特点。
这就要求小浪底在调水调沙时要根据不同的水沙特点进行相应的调控。
其次,小浪底调水调沙的原理是基于水沙运动规律的研究。
水沙运动规律是指水流对河道床面的冲刷、沉积作用,以及泥沙在河道中的输移、淤积、冲刷等规律。
小浪底通过科学地研究水沙运动规律,可以更好地进行水沙调控,保障黄河上游地区的水资源利用和泥沙调控。
再次,小浪底调水调沙的原理是基于水利工程的实际情况进行的。
小浪底是一座大型水利工程,它的调水调沙原理需要结合实际工程情况进行研究和实践。
只有在实际工程中不断总结经验,不断改进调水调沙的方法,才能更好地发挥小浪底的作用。
最后,小浪底调水调沙的原理是基于科学技术的支撑进行的。
随着科学技术的不断发展,小浪底调水调沙的原理也在不断地进行改进和创新。
利用先进的科学技术手段,可以更好地进行水沙调控,保障黄河上游地区的生态环境和社会经济发展。
综上所述,小浪底调水调沙的原理是多方面因素综合作用的结果,它需要根据水沙特点进行调控,遵循水沙运动规律,结合实际工程情况,借助科学技术手段,不断进行改进和创新,才能更好地发挥其在水利调节和泥沙调控中的作用。
希望通过我们的努力,可以更好地保护黄河上游的生态环境,促进当地社会经济的可持续发展。
黄河小浪底调水调沙问题数学建模

黄河小浪底调水调沙问题数学建模
黄河小浪底调水调沙问题是指通过调整黄河水流的水量和输沙量来解决黄河小浪底河道的淤积问题。
数学建模可以帮助我们分析和预测黄河小浪底的水流和沙传输规律,从而提出合理的调水和调沙方案。
以下是数学建模中可能涉及的一些步骤和方法:
1. 数据收集和处理:收集黄河小浪底相关的水文数据、地质资料和历史数据,对数据进行整理和处理,建立合适的数据模型。
2. 建立水流模型:通过流体力学理论和水流实验数据,建立黄河小浪底水流的数学模型,包括水流速度、水动力和水力调控方面的参数。
3. 建立沙传输模型:根据黄河小浪底河道的地质特征和沙传输规律,建立沙传输的数学模型,包括输沙通道的沙动力和沙质输运规律方面的参数。
4. 模型验证和参数拟合:利用已有的观测数据和实验数据验证建立的水流和沙传输模型,并通过参数拟合来优化模型的准确性和适用性。
5. 模拟预测和优化调控:利用建立的数学模型,进行水流和沙传输的模拟预测,通过调整输水和输沙量来优化黄河小浪底的调水和调沙方案,以达到降低淤积和维护航道的目的。
数学建模可以辅助相关专业的研究人员和决策者做出科学的决策,使调水和调沙方案更加合理和有效,减少淤积和保护黄河流域的生态环境。
小浪底调水调沙
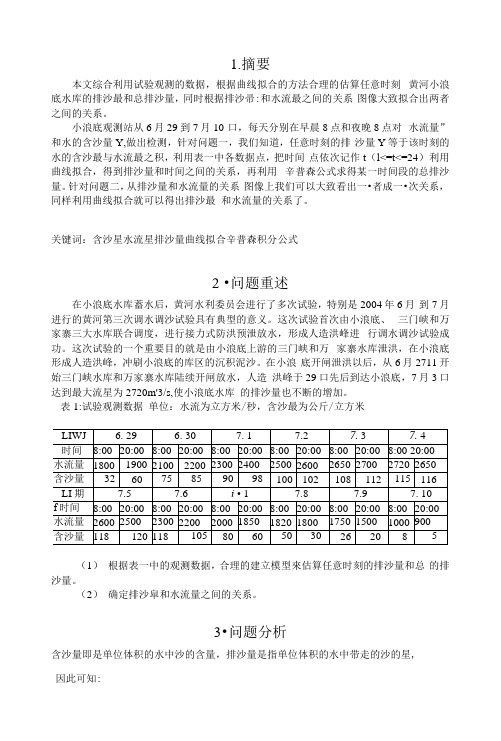
1.摘要本文综合利用试验观测的数据,根据曲线拟合的方法合理的估算任意时刻黄河小浪底水库的排沙最和总排沙量,同时根据排沙帚:和水流最之间的关系图像大致拟合出两者之间的关系。
小浪底观测站从6月29到7月10 口,每天分别在早晨8点和夜晚8点对水流量”和水的含沙量Y,做出检测,针对问题一,我们知道,任意时刻的排沙量Y等于该时刻的水的含沙最与水流最之积,利用表一中各数据点,把时间点依次记作t(l<=t<=24)利用曲线拟合,得到排沙量和时间之间的关系,再利用辛普森公式求得某一时间段的总排沙量。
针对问题二,从排沙量和水流量的关系图像上我们可以大致看出一•者成一•次关系,同样利用曲线拟合就可以得出排沙最和水流量的关系了。
关键词:含沙星水流星排沙量曲线拟合辛普森积分公式2 •问题重述在小浪底水库蓄水后,黄河水利委员会进行了多次试验,特别是2004年6月到7月进行的黄河第三次调水调沙试验具有典型的意义。
这次试验首次由小浪底、三门峡和万家寨三大水库联合调度,进行接力式防洪预泄放水,形成人造洪峰进行调水调沙试验成功。
这次试验的一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底的库区的沉积泥沙。
在小浪底开闸泄洪以后,从6月2711开始三门峡水库和万家寨水库陆续开闸放水,人造洪峰于29口先后到达小浪底,7月3口达到最大流星为2720m'3/s,使小浪底水库的排沙量也不断的增加。
表1:试验观测数据单位:水流为立方米/秒,含沙最为公斤/立方米(1)根据表一中的观测数据,合理的建立模型來估算任意时刻的排沙量和总的排沙量。
(2)确定排沙皐和水流量之间的关系。
3•问题分析含沙量即是单位体积的水中沙的含量,排沙量是指单位体积的水中带走的沙的星,因此可知:排沙量二水的存沙量X水流量静水时,水的含沙量是很少的,由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底的库底的沉积泥沙,使得水屮的含沙量增多,随着人造洪峰的逐渐平息,使水流量的减少,也使得含沙星也呈逐渐减少的趋势,所以排沙量也是减少的,由丁•洪峰在正常情况下是随着时间逐渐平息的,所以, 水的含沙量和排沙最都和时间存在着一定的关系,根据表一,水的含沙量和水流量的积求出该时刻水的排沙量,将时间按记录次库依次记作1 2 3 ........................................................... 24,然后按二次函数拟合即可得到排沙暈和时间的关系式,然后插值得到任意时刻的排沙量,对排沙最和时间的关系式在任意时间段上积分求得值就是这段时间总的排沙量。
黄河小浪底调水调沙问题的sas回归模型

《黄河小浪底调水调沙问题的SAS回归模型》1. 概述黄河,我国第二大河流,自古以来就是我国文明的摇篮。
然而,由于河道泥沙淤积、水资源短缺等问题,黄河的生态环境一直备受关注。
其中,小浪底水利枢纽工程是黄河上的重要水利工程,其调水调沙问题一直备受关注。
本文将以SAS回归模型为工具,探讨黄河小浪底调水调沙问题。
2. 调水调沙问题的背景在黄河流域,水资源的有效利用和泥沙的合理调控是极为重要的。
而小浪底水利枢纽工程作为黄河上最重要的水工枢纽之一,其调水调沙问题牵动着整个黄河流域的生态、经济发展。
据统计,黄河年均泥沙输移量高达15亿吨,泥沙淤积成灾。
如何科学、合理地调控水沙,成为了摆在工程师们面前的难题。
3. SAS回归模型在调水调沙问题中的应用SAS(Statistical Analysis System)是一种统计分析系统,也是一种数据挖掘和数据分析的软件。
在水利工程中,SAS回归模型可以很好地应用在调水调沙问题上。
通过收集大量的水文、气象、地质等数据,建立SAS回归模型,可以对小浪底水利枢纽工程的调水调沙进行精确的预测和优化。
4. 在文章中多次提及“SAS回归模型”SAS回归模型在调水调沙问题中的应用不可小觑。
它可以帮助工程师们分析水情、泥沙运移规律,优化调度方案,提高水资源的利用率和泥沙的通量。
通过SAS回归模型,可以更好地掌握黄河流域水沙情势,为实现水资源的可持续开发和利用提供有力的技术支持。
5. 个人观点和理解就我个人而言,SAS回归模型的应用给小浪底调水调沙问题带来了新的契机。
通过对大数据的分析和建模,可以更准确地把握黄河的水情、沙情,有助于实现“节水、减排、增效”的目标。
但我们也应看到,SAS回归模型在工程实践中仍面临诸多挑战,例如数据质量、模型建立等方面的问题,需要继续努力和探索。
6. 总结与展望在面对黄河小浪底调水调沙问题时,SAS回归模型的应用为我们提供了一种全新的思路。
通过深入研究和实践,可以不断完善模型,在更广泛的领域得到应用。
最新-2019小浪底调水调沙原理 精品

2019小浪底调水调沙原理篇一:黄河小浪底调水调沙黄河小浪底调水调沙问题2019年6月至7月黄河进行了第三次调水调沙试验,特别是首次由小浪底、三门峡和万家寨三大水库联合调度,采用接力式防洪预泄放水,形成人造洪峰进行调沙试验获得成功.整个试验期为20多天,小浪底从6月19日开始预泄放水,直到7月13日恢复正常供水结束.小浪底水利工程按设计拦沙量为755亿立方米,在这之前,小浪底共积泥沙达1415亿吨.这次调水调试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底库区沉积的泥沙.在小浪底水库开闸泄洪以后,从6月27日开始三门峡水库和万家寨水库陆续开闸放水,人造洪峰于29日先后到达小浪底,7月3日达到最大流量2700立方米每秒,使小浪底水库的排沙量也不断地增加.下面是由小浪底观测站从6月29日到7月10日检测到的试验数据:表1试验观测数据单位:水流为立方米秒,含沙量为公斤立方米(1)给出估算任意时刻的排沙量及总排沙量的方法;(2)确定排沙量与水流量的变化关系。
篇二:黄河小浪底调水调沙工程数学实验实验报告《数学实验》实验报告题目:黄河小浪底调水调沙工程姓名:胡迪学号:201914622专业:信息与计算科学黄河小浪底调水调沙问题2019年6月至7月黄河进行了第三次调水调沙试验,特别是首次由小浪底、三门峡和万家寨三大水库联合调度,采用接力式防洪预泄放水,形成人造洪峰进行调沙试验获得成功。
整个试验期为20多天,小浪底从6月19日开始预泄放水,至到7月13日恢复正常供水结束。
小浪底水利工程按设计拦沙量为755亿3,在这之前,小浪底共积泥沙达1415亿。
这次调水调沙试验一个重要的目的就是由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底库区沉积的泥沙,在小浪底水库开闸泄洪以后,从6月27日开始三门峡水库和万家寨水库陆续开闸放水,人造洪峰于29日先后到达小浪底,7月3日达到最大流量2700,使小浪底水库的排沙量也不断地增加。
黄河调水调沙分析与思考
黄河调水调沙分析与思考黄河是多沙河流,每年从中游携带大量泥沙,一部分淤积在下游沿途平原河道,造成河床抬升,过洪能力变小,洪水威胁两岸。
在干流河道修建水库,虽然拦蓄大量泥沙,但同时也造成水库淤积而报废,三门峡水库即是例子,水库建成后,虽然使黄河水变清,但也带来严重问题,三门峡水库因大量泥沙淤积库容逐渐减少,最后不得不进行工程改造,进行调水调沙尝试。
小浪底水库建成后进行大规模调水调沙,目的就是通过三门峡水库和小浪底水库联合调度,达到利用少量的泄水,携带淤积在水库的泥沙,排入大海,而不造成沿途淤积,一方面使水库冲淤平衡,另一方面又不造成沿途河道淤积,同时制造人工洪峰过程,改变河道河势,缩小断面宽度,增加深度。
调水调沙,就是在充分考虑黄河下游河道输沙能力的前提下,利用水库的调节库容,对水沙进行有效的控制和调节,适时蓄存或泄放,调整天然水沙过程,使不适应的水沙过程尽可能协调,以便于输送泥沙,从而减轻下游河道淤积,甚至达到冲刷或不淤的效果,实现下游河床不抬高的目的。
黄河特点是“水少沙多、水沙不平衡”,首任黄河水利委员会主任、著名水利专家王化云和他的同事们,在“上拦下排”的治黄方针的基础上比较系统地提出了“调水调沙”的治黄思想。
三门峡工程的运用实践中,三门峡水库的建设使“调水调沙”得以实施,2001年小浪底水库正式建成使用,使规模性调水调沙的水库条件具备,而且为调水调沙由理论到实践的飞跃提供了先决条件。
黄河水利委员会主任李国英说:“多年来,治黄人一直在探索通过人工手段,塑造一种人工的理想的水沙关系,利用自然规律改变当前天然不平衡的水沙关系,但这要有两个前提,一是要有大型调节水库,二是运用现代化的科技手段。
”2002年7月,利用小浪底水库开展了首次调水调沙试验,至2009年8月,调水调沙历经8年9次。
1.黄河调水调沙2002年7月,利用小浪底水库开展了首次调水调沙试验:7月4日上午9时,小浪底水库开始按调水调沙方案泄流,7月15日9时出库流量恢复正常,历时共11天。
黄河小浪底调水调沙问题
黄河小浪底调水调沙问题一、问题的提出2004年6月至7月黄河进行了第三次调水调沙实验,特别是首次由小浪底、三门峡和万家寨三大水库联合调度,采用接力式防洪预泄放水,形成人造洪峰进行调沙实验获得成功,整个试验期为20多天,小浪底从6月19日开始预泄放水,直到7月13日结束并恢复正常供水。
小浪底水利工程按设计拦沙量为亿m3,在这之前,小浪底共积泥沙达亿t。
这次调水调沙试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底库区沉积的泥沙,在小浪底水库开闸泄洪以后,从6月27日开始三门峡水库和万家寨水库陆续开闸放水,人造洪峰于6月29日先后到达小浪底,7月3日达到最大流量2700m3/s,使小浪底水库的排沙量也不断增加。
表1是由小浪底观测站从6月29日到7月10日检测到的试验数据。
现在,根据试验数据建立数学模型研究下面的问题:(1)给出估计任意时刻的排沙量及总排沙量的方法;(2)确定排沙量与水流量的关系。
二、模型的建立与求解问题一的模型1、观测时间(时刻)的确定以6月29日0时开始计时,各观测时刻(离开始计时的时间)分别为:24214123600,,,),( =-=i i t i ,其中,计时单位s 。
2、排沙量的确定记第),,,(2421 =i i 次观测时水流量为i v ,含沙量为i c ,则第i 次观测时的排沙量i i i v c y =。
其数据如下表2。
表2 i t 时刻对应的排沙量 排沙量单位:102kg3、模型建立在上述已经知道24对数据的基础上,建立任意时刻的排沙量的函数,可以通过插值或拟合的方法来实现。
考虑到实际中的排沙量应该是时间的连续函数,顾采用三次样条函数进行插值。
在求出三次样条函数)(t y y =的基础上,通过积分可以得到总的排沙量为:⎰=241t t dt t y z )(。
4、程序wv=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700 2720 2650 ... 2600 2500 2300 2200 2000 1850 1820 1800 1750 1500 1000 900]; sth=[32 60 75 85 90 98 100 102 108 112 115 116 118 120 118 105 ... 80 60 50 30 26 20 8 5];i=1:24;t=(12*i-4)*3600;y=wv.*sth;t1=t(1);t2=t(end);pp=csape(t,y'); %或采用三次B样条插值:pp=spapi(4,t,y');两种结果一样xsh= %求得插值多项式的系数矩阵,每一行是一个区间上的多项式系数TL=quadl(@(tt)ppval(pp,tt),t1,t2)5、结果:xsh =[+000 +004+000 +005+005+005+005+005+005+005+005+005+005+005+005+005+005+000 +005+000 +005+005 +004 +004 +004 +004 +003]TL =+011即:当),(11t t x ∈时,其插值多项式为:4-6-12105.76 )(1.446)(103.145-)(10-2.648⨯+-⨯+-⨯⨯-⨯⨯=12131t t t t t t y ;当),(32t t x ∈时,其插值多项式为:5-6-12101.14 )(1.160)(103.488-)(10-1.152⨯+-⨯+-⨯⨯-⨯⨯=22232t t t t t t y ;……当),(2423t t x ∈时,其插值多项式为:3-6-1108.0 )(395.)(105.114)(104.986⨯+-⨯--⨯⨯+-⨯⨯=232233230t t t t t t y ;总排沙量为11108441⨯=.TL kg 。
黄河小浪底调沙调水分析.ppt
100 0
8
900
5
• 对于第一阶段,由表5-3用Matlab作图可以看出其变化 趋势,我们用多项式作最小拟合。 • 程序如下: • x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700 2720]; • y=[32 60 75 85 90 98 100 102 108 112 115]; • plot(x,y,'r') • 如图所示:
112
115
第二阶段实验观测数据
单位:水流量为m^3/s,含沙量为kg/m^3
序 号
1
2
3
4
5
6
7
8
9
10
11
12
13
水 流 量
含 沙 量
265 0
116
260 0
118
250 0
120
230 0
118
220 0
105
200 185 0 0
80 60
182 0
50
180 0
40
175 0
32
150 0
第二阶段三次多项式拟合效果图
• 四次多项式拟合效果图: • >> x=[2650 2600 2500 2300 2200 2000 1850 1820 1800 1750 1500 1000 900]; • >> y=[116 118 120 118 105 80 60 50 40 32 20 8 5]; • >> A=polyfit(x,y,4) • A= • -0.0000 0.0000 -0.0013 1.1219 -354.5952
2017小浪底调水调沙原理
2017小浪底调水调沙原理篇一:黄河小浪底调水调沙黄河小浪底调水调沙问题2004年6月至7月黄河进行了第三次调水调沙试验,特别是首次由小浪底、三门峡和万家寨三大水库联合调度,采用接力式防洪预泄放水,形成人造洪峰进行调沙试验获得成功.整个试验期为20多天,小浪底从6月19日开始预泄放水,直到7月13日恢复正常供水结束.小浪底水利工程按设计拦沙量为亿立方米,在这之前,小浪底共积泥沙达亿吨.这次调水调试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底库区沉积的泥沙.在小浪底水库开闸泄洪以后,从6月27日开始三门峡水库和万家寨水库陆续开闸放水,人造洪峰于29日先后到达小浪底,7月3日达到最大流量2700立方米/每秒,使小浪底水库的排沙量也不断地增加.下面是由小浪底观测站从6月29日到7月10日检测到的试验数据:表1: 试验观测数据单位:水流为立方米 / 秒,含沙量为公斤/ 立方米(1) 给出估算任意时刻的排沙量及总排沙量的方法; (2) 确定排沙量与水流量的变化关系。
篇二:黄河小浪底调水调沙工程数学实验实验报告实验报告题目:黄河小浪底调水调沙工程姓名:胡迪学号:201014622 专业:信息与计算科学黄河小浪底调水调沙问题2004年6月至7月黄河进行了第三次调水调沙试验,特别是首次由小浪底、三门峡和万家寨三大水库联合调度,采用接力式防洪预泄放水,形成人造洪峰进行调沙试验获得成功。
整个试验期为20多天,小浪底从6月19日开始预泄放水,至到7月13日恢复正常供水结束。
小浪底水利工程按设计拦沙量为亿m3,在这之前,小浪底共积泥沙达亿t。
这次调水调沙试验一个重要的目的就是由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底库区沉积的泥沙,在小浪底水库开闸泄洪以后,从6月27日开始三门峡水库和万家寨水库陆续开闸放水,人造洪峰于29日先后到达小浪底,7月3日达到最大流量2700 ,使小浪底水库的排沙量也不断地增加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黄河小浪底调水调沙问题
摘要:本文利用插值拟合的方法通过Matlab工具模拟出了排沙量与时间、排沙量与水
流量的函数关系,并且求出了总排沙量为亿吨。
整个模型简单且方便计算,其中排沙量与水流量的函数关系为分段函数。
关键词:调水调沙Matlab 插值拟合
一、问题重述
2004年6月至7月黄河进行了第三次调水调沙试验,特别是首次由小浪底、三门峡和万家寨三大水库联合调度,采用接力式防洪预泄放水,形成人造洪峰进行调沙试验获得成功.整个试验期为20多天,小浪底从6月19日开始预泄放水,直到7月13日恢复正常供水结束.小浪底水利工程按设计拦沙量为亿立方米,在这之前,小浪底共积泥沙达亿吨.这次调水调试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪,在小浪底形成人造洪峰,冲刷小浪底库区沉积的泥沙.在小浪底水库开闸泄洪以后,从6月27日开始三门峡水库和万家寨水库陆续开闸放水,人造洪峰于29日先后到达小浪底,7月3日达到最大流量2700立方米/每秒,使小浪底水库的排沙量也不断地增加.下面是由小浪底观测站从6月29日到7月10日检测到的试验数据:
表1: 试验观测数据单位:水流为立方米/ 秒,含沙量为公斤/ 立方米
(1) 给出估算任意时刻的排沙量及总排沙量的方法;
(2) 确定排沙量与水流量的变化关系。
二、模型假设
1.假设所给数据客观准确的反应了现实情况
2.假设所给数据遵循一定规律变化,即是连续的
3.假设模型中不需要考虑一些外在因素
4.假设可将时间化为等分的时间点进行计算
三、符号说明
t: 时间或时间点
v: 水流量
S: 含沙量
V: 排沙量
四、问题分析
假设水流量和含沙量都是连续的,那么某一时刻的排沙量V=v(t)S(t),其中v(t)为t 时刻的水流量,而S(t)为t时刻的含沙量。
通过观察数据,这些数据是每个12小时采集一次,所以我们可以将时间设为时间点t,依次为1,2,3,……,24,单位时间为12h。
为了找到排沙量与时间的关系,我们就要先找到水流量和含沙量与时间的关系,一但找到水流量和含沙量与时间的关系,那么所要求的问题也就不难解决了。
五、模型的建立与求解
通过分析,我们假设水流量和含沙量都是连续的,那么我们开始对问题“(1) 给出估算任意时刻的排沙量及总排沙量的方法”进行求解。
我们通过Matlab工具将所知道的数据显示为直观的图像,如下所示,具体程序见附录的%。
通过观察图像,我们可以看出其变化并不光滑,而且也没有特定的表现出服从某种分布的趋势。
但是为了得到具体的计算函数,我们就必须对数据进行拟合,所以通过Matlab先利用spline方法对数据进行插值,从而提高精确度,使图像变得光滑,然后利用多项式进行拟合,当多项式次数越高拟合也越准确,但是由于数据受到的影响较多,所以这里的数据也不是准确值,因此我们可以只取三次进行拟合,也方便了后续的计算。
于是我们分别对含沙量和水流量进行插值拟合,便可以得到下面图像和结果,具体程序见附录%和%。
所得到的拟合函数为:y = *x^{3} - *x^{2} + 21*x + 16
即含沙量与时间的关系式为:S=*t^*t^2+21*t+16
所得到的拟合函数为:y = *x^{3} - 14*x^{2} + +002*x + +003
即水流量与时间的关系式为:v=*t^3-14*t^2++002*t++003
因为某一时刻的排沙量V=v(t)S(t),所以我们可以将所拟合出来的多项式带入上式,通过Matlab进行计算可以得到下面答案,程序见附录%。
ans=91/50000*t^6-73/200*t^5+2429/100*t^4-14573/25*t^3+2866*t^2+35340*t+24000即排沙量与时间的关系为:
V=*t^*t^5+*t^*t^3+2866*t^2+35340*t+24000
由于这里的多项式次数过高,不便于计算和传播,所以我们可以对其再进行一次拟合,有下面结果,程序见附录%。
所以拟合后的函数为V=95*t^+003*t^2++004*+004,通过图像可以看出排沙量与时间服从正态分布,所以也可以化成的形式e的指数形式进行拟合,这里就不再重复计算。
我们得到了拟合函数,下面就可以计算出这几天的总排沙量
,通过Matlab
编程可以计算出定积分,结果如下,程序详见附录%。
ans =
即总含沙量为亿吨。
下面我们对问题“(2) 确定排沙量与水流量的变化关系。
”进行分析计算。
以下所有相关程序见附录%,下面就不重复说明。
我们先利用Matlab将排沙量和水流量的相关数据反映到图像中。
通过观察可以看出,其关系是分段的,所以我们按时间进行分段拟合,拟合原理同问题(1)相同,于是可以得到分段前后的拟合多项式。
y = - *x^{3} + *x^{2} - +002*x + +004
y = *x^{3} - *x^{2} + +002*x - +005
综上,我们可以得到排沙量与水流量的关系式为
- *v^3+*v^+2*v++4 0<=t<9
V=
*v^*v^2++2*+5 9<=t<=24
六、模型评估
本模型的优点是:建模简单,方便计算,适用度广。
但也有最大的缺点为:精确度较低。
为了减少误差,我们可以通过增大模型中拟合多项式的次数。
当然在日后的模型改进中可以加入误差评估系统,来对模型进行完善。
附录
%
T=1:24;
S=[32 60 75 85 90 98 100 102 108 112 115 116 118 120 118 105 80 60 50 30 26 20 8 5 ];
W=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700 2720 2650 2600 2500 2300 2200 2000 1850 1820 1800
1750 1500 1000 900];
subplot(2,1,1);
plot(T,S);
hold on;
plot(T,S,'.');
title('时间与含沙量关系');
xlabel('时间t/12h');ylabel('含沙量/公斤每立方米');
subplot(2,1,2);
plot(T,W);
hold on;
plot(T,W,'.');
title('时间与水流量关系');
xlabel('时间t/12h');ylabel('水流量/立方米每秒');
%
T=1:24;
S=[32 60 75 85 90 98 100 102 108 112 115 116 118 120 118 105 80 60 50 30 26 20 8 5 ];
x=1::24;
y=interp1(T,S,x,'spline');
plot(T,S,'.',x,y);
title('时间与含沙量关系拟合图');
xlabel('时间t/12h');ylabel('含沙量/公斤每立方米');
%
T=1:24;
W=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700 2720 2650 2600 2500 2300 2200 2000 1850 1820 1800 1750 1500 1000 900];
x=1::24;
y=interp1(T,W,x,'spline');
plot(T,W,'.',x,y);
title('时间与水流量关系拟合图');
xlabel('时间t/12h');ylabel('水流量/立方米每秒');
%
syms t;
S=*t^*t^2+21*t+16;
v=*t^3-14*t^2++002*t++003;
V=v*S;
simple(V);
syms t;
V=95*t^+003*t^2++004*+004;
int(12*60*60*V,t,0,24)
%
t=1:24;
V=*t.^*t.^5+*t.^*t.^3+2866*t.^2+35340*t+24000; plot(t,V);
title('时间与排沙量关系图')
%
t=1:24;
v=*t.^3-14*t.^2++002*t++003;
V= 95*t.^+003*t.^2++004*+004;
plot(v,V,'.');
title('整理图')
figure;
t=1:9;
v=*t.^3-14*t.^2++002*t++003;
V= 95*t.^+003*t.^2++004*+004;
plot(v,V,'.');
title('前半段图')
figure;
t=10:24;
v=*t.^3-14*t.^2++002*t++003;
V= 95*t.^+003*t.^2++004*+004;
plot(v,V,'.');
title('后半段图')。
