2017小浪底调水调沙原理

合集下载

小浪底排沙原理

小浪底排沙原理小浪底排沙工程是一项重要的水利工程，其排砂原理对于河流的治理和保护具有重要的意义。

小浪底排沙原理是指利用水力学原理，通过设计合理的工程结构和施工工艺，实现对河道中的泥沙进行有效排除，从而保持河道的通畅和水质的清洁。

下面将详细介绍小浪底排沙原理的相关内容。

首先，小浪底排沙工程的设计需要充分考虑河道的水流特性和泥沙的输移规律。

在河道中，水流会携带大量的泥沙，如果泥沙过多，就会导致河道淤积，影响水流通畅，甚至引发洪灾。

因此，设计小浪底排沙工程时，需要根据当地的水文地质条件，确定合理的泥沙拦截和排除方案，以确保排沙效果和工程的稳定性。

其次，小浪底排沙工程通常采用的泥沙排除方式主要有机械排砂和水力冲沙两种方法。

机械排砂是通过设置拦砂坝和沉砂池等设施，利用机械设备将河道中的泥沙进行拦截和清除；水力冲沙则是利用水流的冲击力，通过设置合理的水流引导设施，将泥沙冲刷至河道外侧，实现排沙的效果。

这两种方法各有优劣，需要根据具体情况综合考虑，选择合适的泥沙排除方式。

另外，小浪底排沙工程的施工工艺也至关重要。

在进行排沙工程施工时，需要严格按照设计要求进行，确保工程质量和效果。

同时，还需要充分考虑工程对周边环境的影响，采取相应的环境保护措施，避免对生态环境造成不良影响。

最后，小浪底排沙工程的效果评估和监测也是不可忽视的一环。

在工程竣工后，需要对排沙效果进行定期监测和评估，及时发现问题并采取相应的处理措施，确保工程的长效运行和效果的持续性。

总的来说，小浪底排沙原理是一项涉及水文地质、水力学、土木工程等多学科知识的综合性工程，其设计、施工和运行都需要科学严谨的态度和专业技术支持。

只有充分理解和运用小浪底排沙原理，才能更好地实现河道的治理和保护，确保水资源的可持续利用和生态环境的健康发展。

小浪底调水调沙

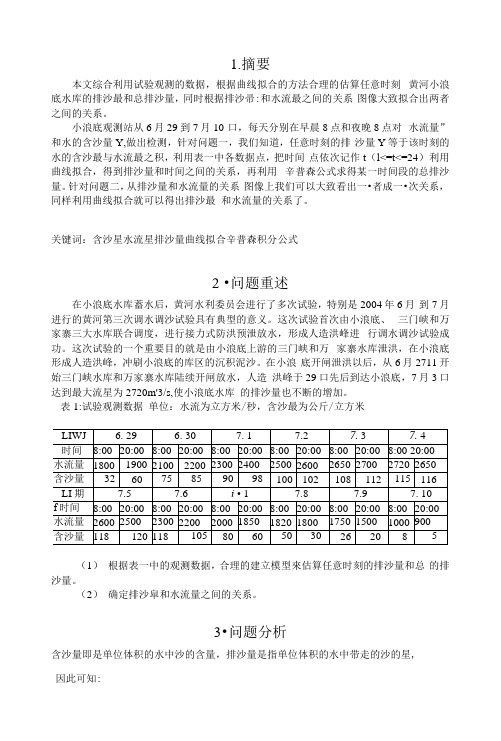
1.摘要本文综合利用试验观测的数据，根据曲线拟合的方法合理的估算任意时刻黄河小浪底水库的排沙最和总排沙量，同时根据排沙帚:和水流最之间的关系图像大致拟合出两者之间的关系。

小浪底观测站从6月29到7月10 口，每天分别在早晨8点和夜晚8点对水流量”和水的含沙量Y,做出检测，针对问题一，我们知道，任意时刻的排沙量Y等于该时刻的水的含沙最与水流最之积，利用表一中各数据点，把时间点依次记作t（l<=t<=24）利用曲线拟合，得到排沙量和时间之间的关系，再利用辛普森公式求得某一时间段的总排沙量。

针对问题二，从排沙量和水流量的关系图像上我们可以大致看出一•者成一•次关系，同样利用曲线拟合就可以得出排沙最和水流量的关系了。

关键词：含沙星水流星排沙量曲线拟合辛普森积分公式2 •问题重述在小浪底水库蓄水后，黄河水利委员会进行了多次试验，特别是2004年6月到7月进行的黄河第三次调水调沙试验具有典型的意义。

这次试验首次由小浪底、三门峡和万家寨三大水库联合调度，进行接力式防洪预泄放水，形成人造洪峰进行调水调沙试验成功。

这次试验的一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪，在小浪底形成人造洪峰，冲刷小浪底的库区的沉积泥沙。

在小浪底开闸泄洪以后，从6月2711开始三门峡水库和万家寨水库陆续开闸放水，人造洪峰于29口先后到达小浪底，7月3口达到最大流星为2720m'3/s,使小浪底水库的排沙量也不断的增加。

表1:试验观测数据单位：水流为立方米/秒，含沙最为公斤/立方米（1）根据表一中的观测数据，合理的建立模型來估算任意时刻的排沙量和总的排沙量。

（2）确定排沙皐和水流量之间的关系。

3•问题分析含沙量即是单位体积的水中沙的含量，排沙量是指单位体积的水中带走的沙的星,因此可知:排沙量二水的存沙量X水流量静水时，水的含沙量是很少的，由小浪底上游的三门峡和万家寨水库泄洪，在小浪底形成人造洪峰，冲刷小浪底的库底的沉积泥沙，使得水屮的含沙量增多，随着人造洪峰的逐渐平息，使水流量的减少，也使得含沙星也呈逐渐减少的趋势，所以排沙量也是减少的，由丁•洪峰在正常情况下是随着时间逐渐平息的，所以, 水的含沙量和排沙最都和时间存在着一定的关系，根据表一，水的含沙量和水流量的积求出该时刻水的排沙量，将时间按记录次库依次记作1 2 3 ........................................................... 24,然后按二次函数拟合即可得到排沙暈和时间的关系式，然后插值得到任意时刻的排沙量，对排沙最和时间的关系式在任意时间段上积分求得值就是这段时间总的排沙量。

小浪底排沙原理

小浪底排沙原理
小浪底排沙原理是指利用液体的旋转运动将悬浮在流体中的颗粒物聚
集到底部而形成一层沙层。

这个原理在水处理、污水处理和沙漏等领
域都得到了广泛应用。

小浪底排沙原理的工作过程是流体经过流体池时会产生旋转，沙子因
密度大而沉到底部形成沙层，而水则流向中央产生压力，并因此形成
一个低压区域。

这种低压区域可以吸引沙子，沙子又因密度大而自动
沉底，因此形成了排沙的效果。

小浪底排沙原理的优点在于：简单易行，成本低廉，可以适用于各种
流体以及不同颗粒大小和密度的固体颗粒。

但同时，它也存在一些局
限性，如在处理超过一定浓度的颗粒物时效果不佳，并且沙漏颗粒相
对较大，无法处理微观颗粒。

总之，小浪底排沙原理是一种经济、简单且广泛应用的现代工业技术，可以在许多工业领域中被用来处理废水、消除浊度，清理污水，净化
水质等不同的应用环境中。

小浪底水库调水调沙解读

小浪底水库调水调沙对黄河下游渔业资源影响及对策介子林朱文锦（河南省水产科学研究院450044）摘要：调查了调水调沙前、后黄河下游河道水域水质、水生生物、渔业资源的变化情况，调水调沙对黄河下游水环境、水生态、渔业资源产生了不利影响，这种不利影响具有叠加性和持续性，提出相应的政策和技术措施。

关键词：调水调沙；黄河下游；渔业资源；生态环境2008年农业部下达了《黄河下游生态环境监测评价—-小浪底水库调水调沙试验对黄河下游渔业资源影响评价及对策研究》项目。

在黄河流域渔业资源委员会组织协调下，河南省水产科学研究院牵头实施了该项目，2008年小浪底水库“调水调沙”期间，较全面的对黄河下游水环境和水生态的变化情况进行了检测，重点调查了“调水调沙”后期黄河“流鱼”情况，较全面的掌握了“调水调沙”对黄河下游生态环境影响，为保护黄河水生生物的物种多样性，为修复、维持黄河水生生态系统的完整性及可持续性提供了科学依据。

1．调查范围从黄河小浪底水库坝下至黄河入海口。

2008年6月19日至7月3日实施的黄河第八次调水调沙。

本次调查的时间选择在调水调沙前14天至调水调沙后14天。

根据生态学理论，不同生境条件决定不同的生态环境状况。

为全面反映黄河下游的生态环境状况，以黄河下游水文站位置为本项目监测点，监测点共7个，分别为孟津、花园口、夹河滩、艾山、洛口、高村、利津。

调查的影响因子包括河道水质、河滩地、黄河口水质、浮游植物、浮游动物、底栖动物、水生维管束植物、鱼类、渔业资源等。

定点比较调查调水调沙前、后渔业资源变化情况。

2．对渔业资源影响2.1 对河道水质的影响比较分析调水调沙过程前、后河道的水质变化，最主要的特征为：一是在较短时间内加大小浪底水库下泄水量，并通过水量一定的波动在下游形成洪峰；二是采取技术措施产生异重流，促使沉积泥沙的泛起和随水转运。

调水调沙过程中，一些水质指标如温度、溶解氧、浊度等在短期内剧烈改变；一些指标如总磷、氨氮等在短期内急剧增加。

黄河小浪底调水调沙

•
图4
所以拟合后的函数为V= 95*t^3-5.5e+003*t^2+7.7e+004*t3.2e+004，通过图像可以看出排沙量与时间近似服从正态分布，进行拟合。
计算总含沙量
通过Matlab编程可以计算出定积分，结果如下
%jisuan.m syms t; S=0.014*t^3-1.3*t^2+21*t+16; v=0.13*t^3-14*t^2+2.4e+002*t+1.5e+003; V=v*S; simple(V); syms t; V=95*t^3-5.5e+003*t^2+7.7e+004*t-3.2e+004; int(12*60*60*V,t,0,24) ans =170366976000 即总含沙量为1.704亿吨
表1: 试验观测数据
日期时间水流量 8:00 1800
单位：水流为立方米 / 秒，含沙量为公斤 / 立方米
6.29 20:00 1900 8:00
6.30 20:00 2200 8:00 2300
7.1 20:00 2400 8:00 2500
7.2 20:00 2600 8:00 2650
7.3 20:00 2700 8:00 2720
因为某一时刻的排沙量V=v(t)S(t)，所以将所拟合出来的多项式带入上式，通过Matlab进行计算可以得到下面答案即排沙量与时间的关系为： V=0.0018*t^6-0.365*t^5+24.29*t^4-582.92*t^3 +2866*t^2+35340*t+24000
由于这里的多项式次数过高，对其再进行一次拟合，有下面结果：

黄河小浪底调沙调水分析.ppt

20
100 0
8
900
5
• 对于第一阶段，由表5-3用Matlab作图可以看出其变化趋势，我们用多项式作最小拟合。 • 程序如下： • x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700 2720]; • y=[32 60 75 85 90 98 100 102 108 112 115]; • plot(x,y,'r') • 如图所示：
112
115
第二阶段实验观测数据
单位：水流量为m^3/s,含沙量为kg/m^3
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
水流量
含沙量
265 0
116
260 0
118
250 0
120
230 0
118
220 0
105
200 185 0 0
80 60
182 0
50
180 0
40
175 0
32
150 0
第二阶段三次多项式拟合效果图
• 四次多项式拟合效果图： • >> x=[2650 2600 2500 2300 2200 2000 1850 1820 1800 1750 1500 1000 900]; • >> y=[116 118 120 118 105 80 60 50 40 32 20 8 5]; • >> A=polyfit(x,y,4) • A= • -0.0000 0.0000 -0.0013 1.1219 -354.5952

2017小浪底调水调沙原理

2017小浪底调水调沙原理篇一：黄河小浪底调水调沙黄河小浪底调水调沙问题2004年6月至7月黄河进行了第三次调水调沙试验，特别是首次由小浪底、三门峡和万家寨三大水库联合调度，采用接力式防洪预泄放水，形成人造洪峰进行调沙试验获得成功．整个试验期为20多天，小浪底从6月19日开始预泄放水，直到7月13日恢复正常供水结束．小浪底水利工程按设计拦沙量为75.5亿立方米，在这之前，小浪底共积泥沙达14.15亿吨．这次调水调试验一个重要目的就是由小浪底上游的三门峡和万家寨水库泄洪，在小浪底形成人造洪峰，冲刷小浪底库区沉积的泥沙．在小浪底水库开闸泄洪以后，从6月27日开始三门峡水库和万家寨水库陆续开闸放水，人造洪峰于29日先后到达小浪底，7月3日达到最大流量2700立方米/每秒，使小浪底水库的排沙量也不断地增加．下面是由小浪底观测站从6月29日到7月10日检测到的试验数据：表1: 试验观测数据单位：水流为立方米/ 秒，含沙量为公斤/ 立方米(1) 给出估算任意时刻的排沙量及总排沙量的方法；(2) 确定排沙量与水流量的变化关系。

篇二：黄河小浪底调水调沙工程数学实验实验报告《数学实验》实验报告题目：黄河小浪底调水调沙工程姓名：胡迪学号：201014622 专业：信息与计算科学黄河小浪底调水调沙问题2004年6月至7月黄河进行了第三次调水调沙试验，特别是首次由小浪底、三门峡和万家寨三大水库联合调度，采用接力式防洪预泄放水，形成人造洪峰进行调沙试验获得成功。

整个试验期为20多天，小浪底从6月19日开始预泄放水，至到7月13日恢复正常供水结束。

小浪底水利工程按设计拦沙量为75.5亿m3,在这之前，小浪底共积泥沙达14.15亿t。

这次调水调沙试验一个重要的目的就是由小浪底上游的三门峡和万家寨水库泄洪，在小浪底形成人造洪峰，冲刷小浪底库区沉积的泥沙，在小浪底水库开闸泄洪以后，从6月27日开始三门峡水库和万家寨水库陆续开闸放水，人造洪峰于29日先后到达小浪底，7月3日达到最大流量2700 ，使小浪底水库的排沙量也不断地增加。

小浪底水库拦沙初期泥沙淤积规律及运行方式探讨

小浪底水库拦沙初期泥沙淤积规律及运行方式探讨本文论述了小浪底水库采用了“调控水位、异重流排沙、相机降低水位排沙、调水调沙、拦粗排细”等综合调度运行方式，减少了水库和下游河道的泥沙淤积，在初期运行中取得了较好的效果、发挥了显著效益。

标签：淤积；调水调沙；异重流；拦粗排细；小浪底水库小浪底水库位于黄河中游最后一个峡谷的出口处，是三门峡以下唯一能取得较大库容的控制性工程，控制黄河流域面积的92.3%和近100%的含沙量，開发目标以防洪、防凌、减淤为主，兼顾供水、灌溉和发电，水库总库容126.5亿m3，其中防洪库容41亿m3、调水调沙库容10亿m3、淤积库容75.5亿m3。

为合理利用淤积库容，尽量延长淤积库容的使用年限、取得最大的减淤效益，合理的调度运用方式成为小浪底水库减淤运用的关键。

1、小浪底水库水沙条件小浪底库区为峡谷形态，原河床比降大，河床由粗沙、砾石、大孤石和基岩组成，河床阻力比较大。

淤积以后河床组成变细，阻力相应减小，在采用“蓄清排浑”运用方式时，对排沙和保持可用库容非常有利。

当上游洪峰平均流量大于500 m3/s时，小浪底水库可能发生高含沙异重流，此时将会有大量泥沙排出库外。

根据水库泥沙研究结果得知，高含沙异重流的排沙比可达到90%以上。

高含沙异重流携带很多粗颗粒泥沙，如果小浪底排沙期下泄流量小于2600m3/s，对下游河道非常不利。

为此，在研究水库淤积形态和排沙时要考虑水库的特殊条件及其对下游河道的影响。

2 、小浪底工程初期运行的泥沙问题小浪底水库为不完全年调节水库，为充分发挥水库长期运行效益，保持长期有效库容将是水库运用的关键。

在初期运行阶段，通过合理调度运行，尽量延长淤积库容使用年限，成为运行调度的重要课题。

2.1 尽量减少水库泥沙淤积，充分发挥淤积效率小浪底水库运行初期，存在较大的拦沙库容，一是要尽量减少泥沙淤积，延长淤积库容使用年限；二是要拦粗排细，提高淤积库容的使用效率，并尽可能利用下游河道的输沙能力排沙入海，三是要合理淤积，避免在库尾及支流门口形成淤积，从而影响兴利库容。

黄河调水调沙

黄河调水调沙一、黄河调水调沙的由来黄河是世界上最复杂、最难治理的一条河流，其主要症结在于泥沙，水少沙多，水沙不平衡。

黄土高原严重的水土流失，造成大量泥沙在黄河下游强烈堆积，使黄河下游近800公里的河床还以年平均0.1米的速度淤积抬高，成为地上悬河，一般下游河床高出地面3~5米，个别地段达到10米。

在历史上，黄河下游决口频繁，造成严重灾害，与逐年抬高的"地上悬河"有很大关系。

在今后相当长的时期内，黄河依然是一条多泥沙河流，同时由于上游水库汛期蓄水，上、中游工农业用水日益增长，黄河下游汛期水少沙多的矛盾更趋严重，黄河下游河床将继续淤积抬高，防洪形势更加严峻。

因此，解决黄河下游泥沙淤积问题成为迫在眉睫的要害问题。

多年来，黄河科技工作者一直在努力探索通过人工手段改变天然水沙不平衡关系的减淤方式，力图控制位于关键地位的水库运用，塑造一种理想的水沙配比，这种水流下泄后，可使黄河下游河道不淤积，甚至对下游河道造成冲刷，从而达到“河床不抬高”的目的。

我们把这样的过程称之为调水调沙。

调水调沙治黄思想的形成经历了一个较长的过程。

这一设想的提出，最早可追溯到20世纪40年代，美国学者萨凡奇.葛罗同在1946年治理黄河的初步报告中提出，利用八里胡同水库控制洪水并发电，坝底设排沙设施，每年放空排沙一次，以减缓下游淤积。

20世纪60年代三门峡水库泥沙问题暴露以后，有人提出利用小浪底水库进行泥沙反调节的设想。

70年代后期，随着“上拦下排”治黄方针局限性的显露以及三门峡水库的运用实践，人们更深刻地认识到黄河水少沙多、水沙不平衡对黄河下游河道淤积所起的重要作用，再一次提出了调水调沙的治黄指导思想，设想在黄河上修建一系列大型水库，实行统一调度，对水沙进行有效的控制和调节，变水沙不平衡为水沙相适应，更好地排洪、排沙入海，从而减轻下游河道的淤积甚至达到不淤。

由于小浪底水库在黄河上所处的关键位置，经过专家学者反复的论证和黄委及有关部门领导的大量工作，决定先建设小浪底水库，进行调水调沙的实践。

小浪底水库调水调沙原理

小浪底水库调水调沙原理
嘿，朋友们！今天咱们就来好好唠唠小浪底水库调水调沙的原理。

你知道吗，这就好像是一场大自然的魔法秀！
想象一下，小浪底水库就像是一个巨大的水魔法盒子。

调水呢，就像是有一双神奇的手在操控着水流的走向。

比如说，当其他地方缺水了，小浪底就把水输送过去，这是不是很神奇啊？就像家里妈妈给我们分食物一样，按需分配呀！
那调沙又是咋回事呢？这就好比是给河流来一次大清扫！河水带着泥沙一路流淌，时间长了，泥沙要是堆积太多，那可不妙。

于是呢，小浪底就发挥作用啦！它通过巧妙的运作，把泥沙“赶”出去。

你看，这像不像我们定期打扫房间，把垃圾清理出去呀？
“哎呀，那这到底是怎么做到的呀？”有人可能会这么问。

别急呀，这当中涉及到好多复杂又精妙的设计和操作呢！水库有它专门的出水口和设施，能够精确地控制水流和泥沙的排放。

这可不是随便就能做到的，得靠无数专家和工作人员的智慧和努力呢！
“哇，那这也太厉害了吧！”可不是嘛！小浪底水库的调水调沙对于我们的生活影响可大啦！它能让河流更健康，能保障我们用水的安全，还能保护周边的生态环境呢。

这么重要又神奇的事情，我们能不了解一下吗？能不惊叹一下吗？
总的来说，小浪底水库调水调沙原理真的超级有趣，也超级重要！它就像一个默默守护我们的超级英雄，在我们看不到的地方发挥着巨大的作用！我们真应该好好感谢它呀！。

小浪底水库渔业发展的问题与对策

１．网箱养鱼初具规模
量，至２００５年底，浪底库区有１５００吨银鱼资源，总产值达
小浪底水库建成后，在济源市库区沿线形成了众多１．５亿元，至２０１１年，浪底库区约有２９００吨银鱼资源，总的库湾、库岔，蓄水后的小浪底水库深度大，水面宽，水产值达３亿元。流缓，水色清，库区的原有植被和建筑物被水淹没后，营养元素在水中逐步释放，水中肥力逐渐上升，便于浮游生物的生长繁殖，为鱼类的生长提供了良好的环境，同时由
导，为网箱养鱼的推广提供了有力技术支撑。四是政策驱了很多水生生物的栖息场所，也阻断了大量洄游鱼类的通
动。济源市政府不仅组织协调银信部门为渔农发放贷款，道，导致洄游性鱼类无法洄游生长，数量明显下降，甚至２００４年还出台了财政贴息贷款扶持政策，进一步推动网箱绝迹。据调查，与上世纪８０年代相比，淡水洄游鱼类减少养鱼的产业化发展，同时在政府的鼓励支持下，库区乡镇了４９％，最为典型的洄游鱼类如北方鱼，曾作为贡品名闻修通了道路，修建了码头和冷库。目前，库区网箱养鱼已于世，是我国传统的名优鱼类，自２００２年最后一次人们见发展到６０００箱，其中不投饵网箱４５００箱，投饵网箱１５００到，已近１０年不见其踪迹，被专家列入灭绝物种目录。
＝．小浪底渔业发展存在的问题
（一）水利工程建设导致部分鱼类种群灭绝
大坝的建设破坏了黄河原有水生生物的产卵、索饵和于济源市地处北岸，背风向阳，发展网箱养鱼自然条件更部分鱼类的洄游通道，破坏了水生生物的生态环境，造成为优越。但由于受传统观念影响和地理、资金、技术等条生物物种多样性严重丧失，以北方鱼为代表的珍稀鱼类已件的制约，群众一开始对发展网箱养鱼认识不足，思想上经灭绝或处于濒临灭绝的状态。为此，尽快建立黄河小浪有顾虑，济源市从四个环节人手，调动农民发展网箱养鱼底鱼类资源保护和补偿机制，迅速遏制水生生物资源严重的积极性。一是宣传发动。济源市充分发挥报纸、广播、衰退、水域生态环境持续恶化的危险局面，维系黄河流域电视等新闻媒体的作用，通过开设专题栏目，举办技术讲脆弱的生态平衡和生物多样性，实现小浪底生物资源保护座，推广生产典型等形式进行大力宣传，努力营造发展网与社会可持续发展，是我们共同面临和承担的社会责任。箱养鱼的浓厚氛围。二是示范带动。济源市水产局通过创近十几年来，有关部门对黄河小浪底库区鱼类资源办示范服务基地和扶持专业村、专业户。不投饵花白链网进行跟踪调查，在１９８６年黄河水系渔业自然资源调查中，箱单箱纯利润在１５００元以上，鲤鱼网箱单箱纯利润在３０００河南省黄河鱼类共记录有１５目、３２科、１９１种（亚种）。元以上，名特优品种黑鱼、鲟鳇鱼利润则更高。可观的经随着黄河生态环境的不断恶化，２００８年，中国科学院水生济效益，让群众实实在在看到了网箱养鱼的实惠，从根生物研究所调查，现有黄河鱼类７目、１３科、５４种，种类

黄河小浪底调沙调水分析

Φ
3
( x ) = − 2492
. 9 + 3 . 1784
* x − ( 1 . 317
* e − 3 ) *
x
2
+ ( 1 . 842
* e − 7 ) *
x
3
• 利用已知数据对其作三次多项式拟合，编写MATLAB命令如下：
• • • • • • • • • • • x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700 2720]; y=[32 60 75 85 90 98 100 102 108 112 115]; A=polyfit(x,y,3) A= 1.842*e-7 -1.317*e-3 3.1784 -2.492.9 >> z=polyval(A,x); >> plot(x,y,'*',x,y,'r',x,z,'b') 可得：a0=-2.492.9 a1=3.1784 a2=-1.317*e-3 a3=1.842*e-7 于是可得拟合多项式为：
• 假设1：水流量和排沙量都是连续的，不考虑上游泄洪所带来的含沙量和外界带来的含沙量。 • 假设2、时间是连续变化的，所取时间点依次为1,2,3， …,24,单位时间为12h
模型建立与求解
• 对于问题一，因为排沙量与时间的散点图基本符合正态曲线，如图一所示。所以，排沙量的对数与时间的函数关系就应该符合二次函数关系（曲线见图二），因而排沙量取对数后，再与时间t进行二次回归. • 假设排沙量与时间函数关系为y=e^(at^2+bt+c),两边取对数后为 Lny=at^2+bt+c先由表二做出排沙量的自然对数lny与时间t的散点图见图一，并利用SAS软件进行拟合，得到排沙量的自然对数与时间的回 SAS 归方程为： • Lny=-0.0209t^2+0.4298t+10.6321 • 由回归拟合参数表可知回归方程是显著的，因为相关系数人 R^2=0.9629,误差均方S^2=0.0543，说明回归曲线拟合效果很好。 • 所以排沙量与时间之间的函数关系式为y=e^(=0.0209t^2+0.4298t+10.6321)

小浪底调沙最简单方法

小浪底调沙最简单方法
《小浪底调沙那点事儿》
要说小浪底调沙这件事儿啊，还真挺有意思的。

什么是调沙呢？简单来说，就是让黄河里的泥沙能够更合理地被处理。

有人可能会说了，小浪底调沙能有多简单？不就是开闸放水嘛。

嘿，你还别说，这开闸放水可大有讲究呢！这可不是随随便便一拧水龙头那么简单。

想象一下，那巨大的水闸就像是一个超级大的水龙头，一打开，汹涌澎湃的江水就奔腾而出，那场面，老壮观了！但要让这水流得恰到好处，泥沙冲得刚刚好，可不容易嘞！
工作人员们就像是一群超级厉害的指挥家，他们要精准地把握每一个环节。

啥时候开闸，开多大，开多久，这都得算计得明明白白的。

他们每天都在和这些水流、泥沙打交道，那认真劲儿，就跟咱老百姓精心照顾自家的小菜园子似的。

我就琢磨啊，这调沙的过程就跟咱过日子一样。

咱过日子得算计着柴米油盐，他们得算计着水流泥沙；咱过日子得让家里井井有条，他们得让黄河乖乖听话。

你说这是不是有异曲同工之妙呀！
每次看到小浪底调沙的新闻，我就忍不住笑出声来。

那奔腾的江水和滚滚的泥沙，感觉就像是一场大自然的狂欢派对。

而那些工作人员呢，就是这场派对的组织者，让一切都热闹而有序。

有人说，小浪底调沙是一项伟大的工程，这我当然知道啦。

可我觉得，它也有可爱、有趣的一面。

它让我们感受到了人类的智慧和大自然的力量相互碰撞出来的奇妙火花。

要说这最简单的方法嘛，估计就是让专业的人干专业的事咯！那些工作人员们就是最懂小浪底调沙的人，他们的经验和技术就是最简单有效的方法呀！咱普通人呢，就好好地欣赏这场大自然和人类共同演绎的大戏，给他们点个大大的赞就好啦！嘿嘿，你说我这话说得在理不？。

小浪底水库减少泥沙淤积的调度运行方式探讨

口处，是三门峡以下唯一能取得较大库容的控制
性工程，制黄河流域面积的９．％和近１０控２３０％的
库沙量全部淤积在库内而清水下泄，到入汛前期，
为了预泄防洪库容，降低水库水位敝泄排沙，大有
ＴＵ：ｓｕｓｎｏｈｉａｃｉｇｐｒｔｎｏｄｃｎｎｃｒｔｎｉａｌｎｄｓｒｏｒ／ｂ，ｉｇ／ＹｅｌｗＲｉｅｉｅＤｉｓｉｎｔｅｄｓｔｈｎｅａｉｎｒｕｉｇｓｄａｃｅｉｎＸｉｏａｇｉｅｅｖｉｃｏｐｏｏｅａｏｒ／ｙＬ－ｒｍｇ／ｌｖｒｏＷａｅｎｄｏｏｅｅｅｏｍｅｔｏｐｒｔｎｔｒｄＨｙｒｐｗｒＤｖｌｐｎｒｏａｉａＣｏＡｂｔａｔＴｅｅｉ７．ｘｌｄｂｉｓｏａｅｃｐｃｔｏｌａｅａｌｎｄｅｅｖｉＩｒｅｓｅｓｎｂｙｉｒｖｔｓｒｃ：ｈｒ５５ＯｍｅｒｔｒｇａａｉｂｉｔｄｉＸｉｅａｇｉｓｒｏｒｎｏｄｒｏｕｅｉｒａｏａｌ，ｍｐｏｅｉｓｓｙｇｎｒ．ｔｔｓｐｏｉｕａｅｐｏｏｇｉｓｇｇ，ｔｓｐｒｔｄｉａｉｕｉｐｔｈｎｄｓｓｃｓｒｇｌｔｇａｄｃｎｒｌｎａｅｖｌｓｎｒｆｓｇ，ｒｌｎｓａｅａｅｉｉｏｅａｅｖｒｓｓａｃｉｇｍｏｅｕｈａｅｕａｉｎｏｔｌｇｗｔｒｅｅ，ａｄｔｔｕｎｏｄｎｏｉｌｄｓｈｒｉｇｉｒｆｅｓｔｏｌｗｅｖｌｔｈｕｔｂｅｌ，ｉｐｔｈｎａｅｎａｄｔｅ‘ ａｓａｄｉｎｎａｄｉｃａｇｎｔｍｓｎｉｆｗ，ｏｒｅｅｅｓｉｌｍｅｄｓａｃｉｇｗｔｒｄｓｎ，ｈ￣ｒｅｓｎｎａｄｆｅｓｎｎｅｏｄｙｌｌａｔａｉａｏｉ

小浪底水库对水沙的调控及下游河道响应

小浪底水库对水沙的调控及下游河道响应苏运启尚红霞李勇郑艳爽（黄河水利科学研究院水利部黄河泥沙重点实验室，河南郑州450003）摘要：冲积性河流上修建水库后，由于对水沙的调节，下游河道将发生相应调整，直至和新的水沙条件相适应。

小浪底水库位于控制黄河水沙的关键部位，1999年10月25日下闸蓄水，目前水库仍处于拦沙初期的运用阶段，五年来以水库异重流排沙为主，期间进行了三次调水调沙试验，绝大多数中粗泥沙拦在库内，进入下游的水沙量和过程均发生了显著变化，主要表现为：下泄水流含沙量低、泥沙颗粒较细、洪峰调平、汛期（7～10月）水量减少、非汛期水量增大。

在这种水沙条件下，黄河下游河道持续冲刷，平滩流量增大，河槽趋于窄深、河床粗化，河势发生调整。

关键词小浪底水库；水沙；调控；河道；响应中图分类号: 文献标识码：A 文章编号：1 前言多沙河流上修建水库后改变了下游河道的来水来沙过程，河床会发生一系列变化，河床的调整程度与水库运用及其对水沙的调节能力等有关[1] [2]。

小浪底水库位于控制黄河水沙的关键部位，1999年10月25日下闸蓄水，目前水库仍处于拦沙初期的运用阶段，五年来以水库异重流排沙为主，下泄水流含沙量低、泥沙颗粒较细、洪峰调平、汛期水量减少、非汛期水量增大，显著改变了出库水沙过程。

下游河道发生相应调整，主要表现为河道持续冲刷，平滩流量增大，河槽趋于窄深、河床粗化。

小浪底水库1999年10月25日下闸蓄水至2004年10月31日，水库累计蓄水37.77亿m3，其中汛期增加蓄水量99.21亿m3，非汛期泄水量61.44亿m3，蓄水量增加最多的是2003年汛期，达70.71亿m3，水库泄水最多的是2004年非汛期，泄水达53.71亿m3。

水库最高运用水位为265.58m，最大蓄水量94.9亿m3（2003年10月15日）。

2小浪底水库对水沙的调控2.1 改变了水量的年内分配由五年来进出库水量情况（表1），可以看出五年入库平均水量171.17亿m3，其中汛期占年水量的45％，而经过水库调节后，出库平均水量182.67亿m3，其中汛期占年水量为36％，即进出库水量不仅总量发生变化，而且年内分配也发生了较大变化，汛期占年水量平均减少了9％。

小浪底调水调沙原理

小浪底调水调沙原理
小浪底调水调沙原理是一种水利工程施工方法，它主要应用于河道底部有淤积堆积物的清理工作。

该原理的基本思想是通过调节水流的力量，控制河床底部的水流速度和方向，从而使淤积的沙土被悬浮并带走，实现清淤的目的。

具体而言，小浪底调水调沙的施工过程中首先需对河道内的水流进行分析和测量，确定水流的输沙能力和流速。

然后，根据实际情况进行水沙分离，将沙土与水分开，以便后续的处理。

接下来，在施工时，可以采用分段调控的方式，逐段进行调水调沙。

通常会在河道的上游设立临时堰坝，通过控制临时堰坝的开启度和泄流量，调节水流的流速和水位。

这样，河道上游的水流经过临时堰坝时会受到阻挡和加速，形成较大的水头和流速。

随着水头和流速的增大，底部的淤积物会被冲刷起来，悬浮在水中，然后被带到下游。

这样，通过连续的调水调沙操作，河道内的淤泥和沙土可以被有效地清理和疏浚。

小浪底调水调沙原理的关键是合理控制水流的力量，在不引起河岸冲击和侵蚀的情况下，提高水流的速度和冲击力，使河床底部的淤泥和沙土被有效地悬浮和带走。

总之，小浪底调水调沙原理通过调节水流的力量，将河底的淤积物悬浮并带走，从而实现了河道的清淤和疏浚。

这一原理在
水利工程建设中具有重要的应用价值，可以提高水流的通畅度，防止河道淤积和堵塞，维护了水环境的稳定和健康。

小浪底治沙原理

小浪底治沙原理
嘿，朋友们！今天咱来聊聊小浪底治沙原理。

你想想啊，那黄河水带着大量泥沙奔腾而下，就像一群调皮捣蛋的孩子在撒欢儿！那怎么才能管住这些“熊孩子”呢？
小浪底工程就像是一个超级厉害的“大管家”。

它是怎么工作的呢？比如说，它有巨大的大坝，就像一堵坚固的墙，把黄河水拦住，让水流慢下来，泥沙就能沉淀一部分，这不就跟咱跑步累了要停下来喘口气一个道理嘛！还有啊，它通过巧妙的设计和调度，让水按照特定的路线流，就好像给黄河水画了一条专属通道！
“哎呀，那这么厉害的工程是怎么建成的呀？”有人可能会问。

嘿嘿，这可是无数人努力的成果呀！建设者们就像勇敢的战士，不怕困难，一点一点地把这个伟大的工程建起来。

他们面对各种挑战，却从不退缩，简直太了不起了！
而且啊，小浪底工程带来的好处那可太多啦！它让黄河下游的河床不再快速抬高，减少了洪水的威胁，这就好比给咱的家安上了一道坚固的防盗门，是不是特别安心？
很多人可能不知道，要是没有小浪底这样的工程，咱的生活可能会受到很大的影响呢！难道不是吗？它就像一把保护伞，为我们遮风挡雨。

想想以前那些因为黄河泛滥而遭受苦难的人们，再看看现在，我们真应该好好珍惜这来之不易的成果呀！
所以说啊，小浪底治沙原理真的太重要啦！它让我们的黄河变得更加驯服，让我们的生活更加美好！咱可得好好感谢那些为小浪底工程付出努力的人们呐！。

小浪底水库工作原理

小浪底水库工作原理
哇塞，朋友们，今天咱们来聊聊小浪底水库的工作原理，这可太神奇有趣啦！
想象一下，小浪底水库就像是一个超级大“水碗”。

每年到了洪水季节，河里的水就像脱缰的野马奔腾而来。

这时候，小浪底水库这个大“水碗”就开始发挥作用啦！它把这些汹涌的洪水给接住，就像你拿碗去接倒出来的水一样。

比如说，黄河发大水了，小浪底就说：“来吧，到我这儿来！” 然
后大量的水就涌进了水库里。

那它怎么做到控制水流的呢？嘿，这里面可有大学问呢！水库有各种各样的设施和结构，就像是一个精心设计的大机关。

大坝就像是一个强壮的卫士，稳稳地站在那里，拦住水流。

还有泄洪口，就像是水龙头一样，可以根据需要调节水的流出量。

好比你在家里要控制水流大小，拧开水龙头就行啦，小浪底的泄洪口也是这个道理啊！
在枯水季节呢，小浪底又变成了慷慨的“水施主”。

它把之前储存的水慢慢放出来，让河流不至于干涸。

这就像你肚子饿的时候，有人给你送来好吃的一样，是不是很棒？
而且啊，小浪底水库的作用可不止这些呢！它还能发电呢，那电可是能点亮千家万户的灯啊！它就像一个不知疲倦的大力士，一直为我们提供着能量。

总之，小浪底水库就像是我们的保护神和好朋友，默默地为我们付出着。

它的工作原理虽然复杂，但却非常重要。

没有它，我们的生活可能会变得很不一样呢！大家说是不是呀？。

调水调沙原理

调水调沙原理
调水调沙原理是指通过调节水流的流速和流量，以及沙子的密度和颗粒大小，来实现水中沙子的分离和过滤。

这种原理在水利工程、环保工程、建筑工程等领域都有广泛的应用。

在水利工程中，调水调沙原理被用于河道治理、水库清淤、水闸调节等方面。

例如，在河道治理中，通过调节水流的流速和流量，可以使河道中的沙子被冲刷到河床的低洼处，从而达到清淤的目的。

在水库清淤中，可以利用调水调沙原理，将水库中的沙子分离出来，从而保证水库的正常运行。

在水闸调节中，可以通过调节水流的流速和流量，来控制水位的高低，从而保证水闸的正常运行。

在环保工程中，调水调沙原理被用于污水处理、海水淡化等方面。

例如，在污水处理中，可以利用调水调沙原理，将污水中的沙子和其他杂质分离出来，从而达到净化水质的目的。

在海水淡化中，可以利用调水调沙原理，将海水中的盐分和沙子分离出来，从而得到淡水。

在建筑工程中，调水调沙原理被用于混凝土搅拌、砂浆制备等方面。

例如，在混凝土搅拌中，可以利用调水调沙原理，将混凝土中的沙子和水分离出来，从而得到均匀的混凝土。

在砂浆制备中，可以利用调水调沙原理，将砂子和水分离出来，从而得到均匀的砂浆。

调水调沙原理是一种非常重要的原理，它在各个领域都有广泛的应
用。

通过调节水流的流速和流量，以及沙子的密度和颗粒大小，可以实现水中沙子的分离和过滤，从而达到各种不同的目的。