MATLAB求解总体刚度矩阵
matlab有限元常用函数

matlab有限元常用函数Matlab是一种功能强大的数值计算软件,广泛应用于工程、科学和数学领域。
它提供了丰富的数学函数和工具箱,使得有限元分析成为可能。
在本文中,我们将介绍一些常用于有限元分析的Matlab函数,并逐步解释它们的用法和作用。
有限元分析(Finite Element Analysis,简称FEA)是一种工程设计和分析方法,通过对实际结构的离散化,将其划分为许多小的单元,然后利用数值方法求解它们的行为。
下面是一些常用的有限元分析函数和工具箱。
1. finemesh函数finemesh函数是Matlab的一个内置函数,用于生成网格。
它可以根据给定的节点坐标和连接关系生成一个三角或四边形网格。
finemesh函数的语法如下:mesh = finemesh(node, elem);其中,node是一个N×2的矩阵,表示节点的坐标;elem是一个M×3或M×4的矩阵,表示节点之间的连接关系。
2. assempde函数assempde函数是Matlab Partial Differential Equation Toolbox的一部分,用于组装有限元方程。
它将已知的系数和边界条件应用于有限元方程,并返回一个描述矩阵和向量的数据结构。
assempde函数的语法如下:[stiff,force] = assempde(pde,geometry,temperature,flux);其中,pde是一个描述方程系数的结构体;geometry是一个描述几何形状的结构体;temperature和flux是分别描述温度和通量边界条件的结构体。
3. assemble函数assemble函数是一个用于组装有限元方程的通用函数。
它可以使用用户提供的形状函数和积分点来计算单元刚度矩阵和力矢量。
assemble函数的语法如下:[K,F] = assemble(p,t,c,b,v);其中,p是一个N×2的矩阵,表示节点坐标;t是一个M×3的矩阵,表示节点之间的连接关系;c是一个描述系数的函数句柄;b是描述边界条件的函数句柄;v是描述体积力的函数句柄。
matlab组装刚度矩阵代码

一、介绍MATLAB是一种被广泛应用于工程和科学领域的计算软件,它提供了强大的矩阵操作功能。
在结构力学中,组装刚度矩阵是一项基本的任务,它用于描述结构的刚度特性。
本文将介绍如何使用MATLAB编写组装刚度矩阵的代码。
二、理论基础在结构力学中,刚度矩阵描述了结构的刚度特性,它是一个对称正定的矩阵。
对于一个有限元模型来说,刚度矩阵的组装分为两个步骤:1. 定义总体刚度矩阵:需要定义一个总体的刚度矩阵,它包含了所有节点的刚度信息。
这个总体刚度矩阵的大小取决于结构的自由度数量。
2. 组装节点刚度矩阵:接下来,需要按照节点之间的连接关系,将每个节点的刚度矩阵组装到总体刚度矩阵中。
这个过程涉及到根据节点的自由度编号,将节点的刚度矩阵的子块放置到总体刚度矩阵的对应位置上。
三、MATLAB代码实现在MATLAB中,可以使用矩阵操作来实现刚度矩阵的组装。
下面是一个简单的例子,假设有一个简单的二维结构,其中包含4个节点和8个自由度。
我们将演示如何编写MATLAB代码来组装这个结构的刚度矩阵。
我们需要定义每个节点的刚度矩阵。
假设每个节点的刚度矩阵为3x3的矩阵,我们将使用一个3维的cell数组来存储这些矩阵。
代码如下:```matlab定义节点刚度矩阵k1 = [k11 k12 k13;k21 k22 k23;k31 k32 k33];k2 = [k11 k12 k13;k21 k22 k23;k31 k32 k33];k3 = [k11 k12 k13;k21 k22 k23;k31 k32 k33];k4 = [k11 k12 k13;k21 k22 k23;k31 k32 k33];nodeMatrices = {k1, k2, k3, k4};```接下来,我们需要定义总体刚度矩阵。
假设总体刚度矩阵为8x8的矩阵,我们可以使用一个8x8的零矩阵来表示。
我们按照节点的自由度编号,将每个节点的刚度矩阵组装到总体刚度矩阵的对应位置上。
《有限元基础教程》_【MATLAB算例】4.8.1(1) 基于4节点四面体单元的空间块体分析(Tetrahedron3D4Node)

【MATLAB 算例】4.8.1(1) 基于4节点四面体单元的空间块体分析(Tetrahedron3D4Node)如图4-22所示的一个块体,在右端面上端点受集中力F 作用。
基于MATLAB 平台,计算各个节点位移、支反力以及单元的应力。
取相关参数为:10110Pa,=0.25E μ=⨯,5=110N F ⨯。
图4-22 一个空间块体的分析解答:对该问题进行有限元分析的过程如下。
(1)结构的离散化与编号将结构离散为5个4节点四面体单元,单元编号及节点编号和坐标如图4-22所示,连接关系见表4-8,节点的坐标见表4-9。
表4-8 单元连接关系单元号 节点号 1 2 3 4 51 42 6 1 43 7 6 7 5 1 6 7 84 1 4 6 7表4-9 节点的坐标节点节点坐标/mxyz 1 2 3 4 5 6 7 80 0 0 0.2 0 0 0 0.8 0 0.2 0.8 0 0 0 0.6 0.2 0 0.6 0 0.8 0.6 0.20.80.6节点位移列阵[]111222888 Tu v w u v w u v w =q (4-190)节点外载列阵34780 0 0 0 TT T T T⎡⎤=⎣⎦F F F F F(4-191)其中34785000 00110N ⎡⎤⎡⎤⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥-⨯⎣⎦⎣⎦F F F F约束的支反力列阵12560000TTT T T ⎡⎤=⎣⎦R R R R R(4-192其中1256112255661256 x x x x y y y y z z z z R R R R R R R R R R R R ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥====⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦R R R R总的节点载荷列阵12345678 TT T T T T T T T⎡⎤=+==⎣⎦P F R R R R F F R R F F (4-193)(2)计算各单元的刚度矩阵(以国际标准单位)首先在MA TLAB 环境下,输入弹性模量E 、泊松比NU ,然后针对单元1和单元2,分别5次调用函数Tetrahedron3D4Node_Stiffness ,就可以得到单元的刚度矩阵k1(6×6) ~ k5(6×6)。
刚架矩阵位移法matlab计算程序

clc;%输入基本信息jd=input('请输入节点数量');free=input('请输入自由度');gj=input('请输入杆件数量');P=zeros(free,1);P=input('请输入外荷载矩阵([x;y;z])');d=zeros(free,1);member=zeros(1,6,gj);K=zeros(6,6,gj);k=zeros(6,6,gj)for i=1:1:gjangle(i)=input(sprintf('请输入第%d杆件角度(角度制)',i));E(i)=input(sprintf('请输入第%d杆件弹性模量(N/mm2)',i));A(i)=input(sprintf('请输入第%d杆件截面面积(mm2)',i));L(i)=input(sprintf('请输入第%d杆件长度(mm)',i));member(:,:,i)=input(sprintf('请输入第%d杆件定位向量([1 2 3 4 5 6])',i)); end%计算局部坐标系下单元刚度矩阵kfor i=1:1:gjk=(:,:,i)=E(i)*I(i)/L(i)^3*[A(i)*L(i)^2/I(i) 0 0 -A(i)*L(i)^2/I(i) 0 0;0 12 6*L(i) 0 -12 6*L(i);0 6*L(i) 4*L(i)^2 0 -6*L(i) 2*L(i)^2;-A(i)*L(i)^2/I(i) 0 0 A(i)*L(i)^2/I(i) 0 0;0 -12 -6*L(i) 0 12 -6*L(i);0 6*L(i) 2*L(i)^2 0 -6*L(i) 4*L(i)^2 ];end%计算各杆件转换矩阵TT=zeros(6,6,gj);for i=1:1:gjT=(:,:,i)=[cosd(angle(i)) sind(angle(i)) 0 0 0 0;-sind(angle(i)) cosd(angle(i)) 0 0 0 0;0 0 1 0 0 0;0 0 0 cosd(angle(i)) sind(angle(i)) 0;0 0 0 -sind(angle(i)) cosd(angle(i)) 0;0 0 0 0 0 1];end%计算整体坐标系下单元刚度矩阵KK(:,:,i)=T(:,:,i)'*k(:,:,i)*T(:,:,i);end%形成SSs=zeros(free);S=zeros(free);for i=1:1:gjfor n=1:1:6for j=1:1:6if (member(1,n,i)<=free && member(1,j,i)<=free)Ss(member(1,n,i),member(1,j,i))=K(n,j,i);endendendS=S+Ss ;Ss=zeros(free);end%计算杆间荷载作用PfFf=[FAbcosd-FSbsind;FAbsind+FSbcosd;FMb;FAecosd-FSbsind;FAesind+FSecosd;FMe]for i=1:1:gjgjl=input('请输入杆间力数量');ppp=zeros(1,4,gjl);for j=1:1:gjlppp(:,:,i)=input(sprintf('请输入第%d杆件l1,l2,W,a ([1 2 3 4])',i));l1=ppp(1,1,i);l2=ppp(1,2,i);W=ppp(1,3,i);a=ppp(1,3,i);if a==0,l1+l2==L(i)pd=1else if a==0,l1+l2<L(i)pd=2else if a>0,l1+l2==L(i)pd=3elsepf=4endendendswitch pdcase 1Qf(:,:,gjl)=[0;W*l2^2*(3*l1+l2);W*l1*l2^2;0;W*l1^2*(l1+3*l2);-W*l1^2*l2/L(i)^2]case 2Qf(:,:,gjl)=[W*cosd(a);W*sind(a)*l2^2*(3*l1+l2);W*sind(a)*l1*l2^2;W*cosd(a);W*sin(a)*l1^2*(l1+3*l2);-W*l1^2*l2/L(i)^2]case 3Qf(:,:,gjl)=[0;W*L(i)/2*(1-l1/L(i)^4*(2*L(i)^3-2*l1^2*L(i)+l1^3)-l2^3/L(i)^4*(2*L(i)-l2));W*L(i)^2/12*(1-l1^2/L(i)^4*(6*L(i)^2-8*l1*L(i)+3*l1^2)-l2^3/L(i)^4*(4*L(i)-3*l2));W*L(i)/2*(1-l1^3/L(i)^4*(2*L(i)-l1)-l2/L(i)^4*(2*L(i)^3-2*l2^2+l2^3));0;-W*L(i)^2/12*(1-l1^3/L(i)^4*(4*L(i)-3*l1)-l2^2/L(i)^4*(6*L(i)^2-8*l2*L(i)+3*l2^2))]case 4Qf(:,:,gjl)=[W*cosd(a)*(L(i)-l1-l2);W*sind(a)*L(i)/2*(1-l1/L(i)^4*(2*L(i)^3-2*l1^2*L(i)+l1^3)-l2^3/L(i)^4*(2*L(i)-l2));W*sind(a)*L(i)^2/12*(1-l1^2/L(i)^4*(6*L(i)^2-8*l1*L(i)+3*l1^2)-l2^3/L(i)^4*(4*L(i)-3*l2));W*sind(a)*L(i)/2*(1-l1^3/L(i)^4*(2*L(i)-l1)-l2/L(i)^4*(2*L(i)^3-2*l2^2+l2^3));W*sind(a)*cosd(a)*(L(i)-l1-l2);-W*sind(a)*L(i)^2/12*(1-l1^3/L(i)^4*(4*L(i)-3*l1)-l2^2/L(i)^4*(6*L(i)^2-8*l2*L(i)+3*l2^2)) ]endendFf(:,:,i)=T(:,:,i)'*Qf(:,:,i);endPf=zeros(free,1);for i=1:1:gjpfp=zeros(free,1);for j=1:1:6if member(1,j,i)<=freePfp(member(1,j,i),1)=Pf(j,1,i);endendPf=Pf+Pfp;end%P-Pf=S*dd=S\(P-Pf);%计算位移和内力v=zeros(6,1,gj);u=zeros(6,1,gj)Q=zeros(6,1,gj);F=zeros(6,1,gj);for i=1:1:gjc=1;for j=1:1:6if(member(1,j,i)<free+1)v(j,1,i)=d(c,1);c=c+1;endendendfor i=1:1:gju(:,:,i)=T(:,:,i)*v(:,:,i);endfor i=1:1:gjQ(:,:,i)=k(:,:,i)*u(:,:,i)endfor i=1:1:gjF(:,:,i)=T(:,:,i)'*Q(:,:,i);endzfl=jd*2;r=zeros(zfl,1);for i=1:1:gjfor j=1:1:4r(member(1,j,i),1)=F(j,1,i);endend%计算支座反力zfl=zfl-free;R=r(free+1:end)。
matlab矩阵位移法求解钢架
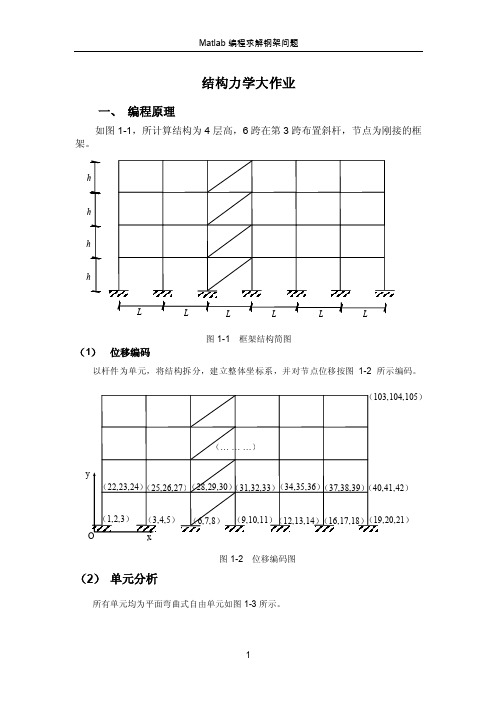
结构力学大作业一、 编程原理如图1-1,所计算结构为4层高,6跨在第3跨布置斜杆,节点为刚接的框架。
图1-1 框架结构简图(1) 位移编码以杆件为单元,将结构拆分,建立整体坐标系,并对节点位移按图1-2所示编码。
图1-2 位移编码图(2) 单元分析所有单元均为平面弯曲式自由单元如图1-3所示。
LLLLLLhhhhLLLLL图1-3 自由式单元干段位移和杆端力杆件的单元刚度矩阵322222223222000012612600646200000012612600626400EAEAllEI EI EI EI l l l l EI EI EI EI l ll l K EA EAl lEI EI EI EI l l l l EI EI EI EI l l l l ⎡⎤-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦其中32112001260640EAlEIEIl l K EI EI l l⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ 22122001260620EAl EI EI l l K EI EI l l ⎡⎤-⎢⎥⎢⎥⎢⎥-⎢⎥=⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦21222001260620EA lEI EI K l l EI EI l l⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦ 22322001260640EAl EI EI K l l EI EI l l ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦(3) 建立局部坐标系分别建立如图1-4所示的竖向分体系局部坐标系,水平分体系局部坐标系和斜杆分体系坐标系。
图1-4 分体系局部坐标系的建立(4) 建立分体系刚度分别建立三个分体系的105×105的刚度矩阵,引入循环变量,依次对相应位移刚度赋值。
(5) 坐标转换对竖向坐标系和斜杆体系进行转置,其坐标转换阵为1010100001T ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦3000001L hd d hT d ⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦其中d =。
有限元分析

网格划分结果
函数为:mesh()
ll=1; % 求节点坐标 for y=0:ysize for x=0:xsize Node(ll,1)=ll; Node(ll,2)=x*Width/xsize; Node(ll,3)=y*Height/ysize; ll=ll+1; end end ll=1; %%%%求单元所包含节点 for y=1:ysize for x=1:xsize if Etype==1 %三节点单元 Elem(ll,1)=ll; Elem(ll,2)=(xsize+1)*(y-1)+x; Elem(ll,3)=(xsize+1)*(y-1)+x+1; Elem(ll,4)=(xsize+1)*y+x; ll=ll+1; Elem(ll,1)=ll; Elem(ll,2)=(xsize+1)*(y-1)+x+1; Elem(ll,3)=(xsize+1)*y+x+1; Elem(ll,4)=(xsize+1)*y+x; ll=ll+1; else %矩形单元 Elem(ll,1)=ll; Elem(ll,2)=(xsize+1)*(y-1)+x; Elem(ll,3)=(xsize+1)*(y-1)+x+1; Elem(ll,4)=(xsize+1)*y+x+1; Elem(ll,5)=(xsize+1)*y+x; ll=ll+1; end end end ploE(Node,Etype,1);
应变计算结果
矩形单元: 9.9657e-006 0 9.9657e-006 - 1.873e-006 -1.2467e-006 0 -1.2467e-006 -1.873e-006 -2.603e-006 -1.873e-006 -2.603e-006 8.2201e-006 8.6093e-006 -1.873e-006 8.6093e-006 8.2201e-006 1.6767e-005 1.1161e-005 1.3021e-005 7.4149e-006 -8.0525e-007 4.8009e-006 1.9381e-005 2.4987e-005
MATLAB有限元编程03梁单元

MATLAB有限元编程03梁单元引言平面纯弯梁单元描述有限元基本格式描述节点位移、节点力位移场:其中,为梁单元内任一点位移,为单元形函数,注意到这里已经用到了“归一化”思想,为以后讲解等参单元做基础。
应变场:其中,为单元的几何矩阵,为所测点以中性层为起点的y方向的坐标。
应力场:其中,为弹性模量,为单元的应力矩阵。
单元刚度矩阵:单元刚度方程:模型描述Matlab编程:% 公众号:易木木响叮当,回复梁单元,即可自动获取。
function k =Beam1D2Node_Stiffness(E,I,L)% 直接组装梁单元刚度k = E*I/(L*L*L)*[12 6*L -12 6*L6*L 4*L*L -6*L 2*L*L-12 -6*L 12 -6*L6*L 2*L*L -6*L 4*L*L];function z = Beam1D2Node_Assembly(KK,k,i,j)% 该函数进行整体刚度矩阵的组装% 输入单元刚度矩阵k,单元的节点编号i、j% 输出整体刚度矩阵KKDOF(1)=2*i-1;DOF(2)=2*i;DOF(3)=2*j-1;DOF(4)=2*j;for n1=1:4for n2=1:4KK(DOF(n1),DOF(n2))= KK(DOF(n1),DOF(n2))+k(n1,n2); endendz=KK;function v = Beam1D2Node_Deflection(x,L,u)% 该函数计算单元内某点的挠度% 输入所测点距梁单元左节点的水平距离x% 输入梁单元的长度L,节点位移列阵ue=x/L;N1=1-3*e*e+2*e*e*e;N2=L(e-2*e*e+e*e*e);N3=3*e*e-2*e*e*e;N4=L(e*e*e-e*e);N=[N1,N2,N3,N4];v=N*u% -----------主程序----------------format compactE = 200*10^9;I = 118.6*10^-6;L1 = 5;L2 = 2.5;% cal element stiffnessk1 = Beam1D2Node_Stiffness(E,I,L1);k2 = Beam1D2Node_Stiffness(E,I,L2);% stiffness assemblyKK = zeros(6,6);KK = Beam1D2Node_Assembly(KK,k1,1,2);KK = Beam1D2Node_Assembly(KK,k2,2,3)% cal displacementk = KK(4:6,4:6);p = [39062;-31250;13021];u = k\p% cal node forceU = [0;0;0;u];P = KK*U% cal RFF = [-62500;-52083;-93750;39062;-31250;13021];RF = P-F最终计算得到的支反力、节点位移值与书中解析解一致,可自行验证。
matlab矩阵位移法

matlab矩阵位移法
其中,`k11, k12, k13`等表示刚度矩阵的元素,`f1, f2, f3`表示外部载荷矩阵的元素,`b1, b2, b3`表示位移边界矩阵的元素。`U`即为求解得到的节点位移。
需要根据具体的结构和问题进行相应的刚度矩阵、外部载荷矩阵和位移边界矩阵的定义和 计算。
2. 外部载荷矩阵:将外部施加在结构上的载荷按照节点自由度的顺序组合起来,得到外部 载荷矩阵。
matlab矩阵位移法
3. 位移边界条件:根据结构的边界条件,将位移边界条件转化为位移边界矩阵。
4. 静力平衡方程:根据静力平衡方程,可以得到结构的位移方程。将结构刚度矩阵、外部 载荷矩阵和位移边界矩阵代入位移方程,得到一个线性方程组。
5. 解线性方程组:通过求解线性方程组,可以得到结构的节点位移。
在MATLAB中,可以使用矩阵运算和线性方程组求解函数来实现矩阵位移法。以下是一个 简单的示例:
matlab矩阵位移法
假设有一个简单的梁结构,其刚度矩阵为K,外部载荷矩阵为F,位移边界矩阵为B。可以 通过以下代码求解结构的节点位移:
```matlab % 定义刚度矩阵K、外部载荷矩阵F和位移边界矩阵B K = [k11, k12, k13; k21, k22, k23; k31, k32, k33]; % 刚度矩阵 F = [f1; f2; f3]; % 外部载荷矩阵 B = [b1; b2; b3]; % 位移边界矩阵 % 解线性方程组,得到节点位移 U = K \ (F - B); ```
matlab矩阵位移法
在MATLAB中,矩阵位移法(Matrix Displacement Method)是一种用于求解结构静力 平衡的方法,常用于结构力学和有限元分析中。矩阵位移法基于以下原理:
