应用数理统计第二章参数估计(3)区间估计

10
得所求的标准差的置信区间为 (4.58, 9.60)
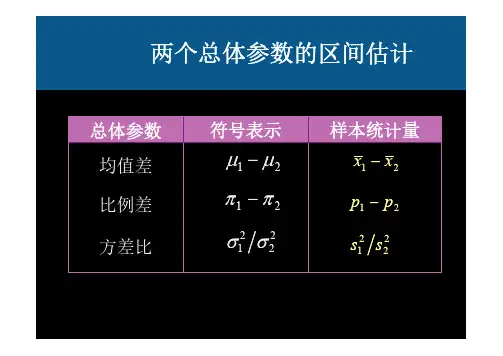
2.4.3 两个正态总体参数的区间估计
在实际中常遇到下面的问题：已知产品的某一质量指标 服从正态分布，但于原料、设备条件、操作人员不同，或 工艺过程的改变等因素，引起总体均值、总体方差有所改变, 我们需要知道这些变化有多大，这就需要考虑两个正态总体 均值差或方差比的估计问题。
1
2.4.1 区间估计的一般步骤
定义1 设总体X的分布函数F(x;)含有一个未知参数,, 对于给定值 (0<<1),若由样本X1, X2, …,Xn确定的两个统 计量 ( X 1 , X 2 ,, X n ) 和 ( X 1 , X 2 ,, X n满足 )
ˆ a ˆ b} {g(a) T ( X , X ,..., X ; ) g(b)} { 1 2 n
其中g ( x )为可逆的已知函数， T ( X 1 , X 2 ,..., X n ; } 的分布已知且与θ无关。
4
2.4.2 单个正态总体的情况
设总体X~N(,2),X1, X2, …,Xn是总体X的样本，求,2 /2 /2 的置信水平为(1)的置信区间.
求得 的置信度水平为(1)的置信区间: (2为已知)
X u u1 / 2 , X u1 / 2 或 1 2 X n n n
5
(b) 2为未知时,因为S 2是 2的点估计量,所以用S替换 ,
X
S n1
~ t ( n 1)
由此可得 1 2 的一个置信水平为 1 的置信区间为：
2 12 2 X Y z1 2 n n 1 2
12
2 2 2 2,但 2为未知. (b) 1
由定理1.15, 12 22 2 时，
M ( 1 2 ) ( X Y ) n1 S1 n2 S2
13
[例2.28] 在例2.27中,随机选取A种灯泡5只,B种灯泡7只, 做灯泡寿命实验,算得两种牌号的平均寿命分别 为1000和980小时,样本方差分别为784和1024小 时2.取置信度0.99,希望进行区间估计.
考察：
(ⅰ)两种灯泡的寿命是否有明显差异；
(ⅱ)两种灯泡的质量稳定性是否有明显差异.
(4.71,5.69)的可信程度为95%. 3)置信水平为(1)的置信区间不唯一.如上例=0.05,可证 X X ÷ P z0.96 z0.99 0.95 z , X z 0 . 0 . 96 99 ÷ / n n n 置信区间长度越短表示估计的精度越高. 7
例1 有一大批月饼，现从中随机地取16袋，称得重量（以克 计）如下：506 508 499 503 504 510 497 512 514 505 493 496 506 502 509 496 ，设袋装月饼的重量近似地服从正态 分布，试求总体均值的置信度为0.95的置信区间。 解： 2未知, 1-=0.95, /2=0.025,n-1=15, t0.975 (15) 2.1315 由已知的数据算得 x 503.75, S* 6.2022
, n 1 15 解：现在 2 0.025,1 2 0.975
2 2 (15) 27.488, 查表得 0.975 0.025 (15) 6.262
又 S* =6.2022 ，
由(4)式
n 1 S * n 1 S * , 2 ( n 1) 2 ( n 1) 1 2 2
§2 ·4
区间估计
为了估计总体X 的未知参数 ，前面已经介绍了矩估计
ˆ 法和极大似然估计法．由于总体X的未知参数 的估计量
是随机变量，无论这个估计量的性质多么好，它只能是未知 参数的近似值，而不是 的真值．并且样本不同，所得到的 估计值也不同．那么 的真值在什么范围内呢？是否能通 过样本，寻求一个区间，并且给出此区间包含参数 真值的 可信程度．这就是总体未知参数的区间估计问题．
n1 (n2 1) S12 12 n1 (n2 1) S12 P F (n 1, n1 1) 2 F (n 1, n1 1) 1 2 /2 2 2 1 / 2 2 2 n2 (n1 1) S2 n2 (n1 1) S2
P{1 2 } 1
则称随机区间 ( 1 , 2 ) 是 的置信度为 (1 ) 的置信区间,
1 和 2 分别称为置信度为 (1 ) 的双侧置信区间的置信下
限与置信上限， (1 ) 称为置信水平(置信度)． 这种估计 的方法叫做区间估计. 1）精度： 1 评价一置信区间 好坏的两个标准：
nS 2 nS 2 2 P 2 2 1 2 ( n 1) 1 2 ( n 1)
2 nS 2 2 P 2 (n 1) 2 1 2 (n 1) 1
nS 2 nS 2 , 2 ( n 1) 2 ( n 1) 2 1 2
2 越小越好； P{ 1 2 } 越大越好2 2）置信度： .
［注］
１）当Ｘ是连续型随机变量时，对于给定的，我 们总是按要求：
P{ 1 2 } 1
求出置信区间． ２）当Ｘ是离散型随机变量时，对于给定的 ， 常常找不到区间 ( 1 , 2 ) 使得 P{ 1 2 } 恰好 为 (1 )．此时我们去找 ( 1 , 2 ) 使得 P{ 1 2 } 尽可能地接近 (1 ) ．
⑴ 均值 的置信区间
u1 / 2
u1 /2
(a) 2为已知时,因为 X是,的无偏估计,且 X ~ N (0,1) / n 对于给定的(0<<1),令
X P u 1 P X u1 / 2 X u1 / 2 1 1 n n / n 2
n 1 S n 1 S , 2 ( n 1) 2 ( n 1) 1 2 2
标准差 的一个置信度为1- 的置信区间9
例2 有一大批糖果,现从中随机地取16袋,称得重量（以克计） 如下：506 508 499 503 504 510 497 512 514 505 493 496 506 502 509 496 ,设袋装糖果的重量近似地服从正态分布， 试求总体标准差 的置信度为0.95的置信区间。
又若 =1,n=16, 查表得 z 0.975 1.96
X 1 1.96 , X 1 1.96 16 16
于是得到 的置信水平为0.95 的置信区间:
即
X 0.49
2)若样本值为 x 5.20 ,则得到一个置信区间 (5.20 0.49) 即(4.71,5.69)这时已不是随机区间,说明 的真值含在
求得 的置信水平为(1)的置信区间: ( 2未知)
S S* t1 2 (n 1) or X t1 2 (n 1) X n1 n
6
1) 例如当=0.05 时,即1-=0.95, X z0.975 , X z0.975 n n
2 2 Y1,Y2,…,Yn2是Y的样本.这两个样本相互独立， X , Y , S1 , S2
分别为第一、二个总体的样本均值与方差.
1．两个总体均值差 1 2 的置信区间 (a)
12
2 和 2 已知,求 1 2 的置信区间
X Y ( 1 2 ) 2 2 2 2 ~ N ( 0 , 1 ) 相互独立 1 2 X , Y 1 2 X Y ~ N ( , ) 2 2 2 ~n1N ( n2 , X ~ N ( ), Y 1 1 , 21 2 n2 ) n 1 n1 n2
(2)方差 2 的置信区间 (只介绍 未知的情况) /2 2的无偏估计量为S*2 ， 当1- 给定后,因为
( n 1) S *
2
/2

2
~ ( n 1)
2
2 / 2 (n 1)
21 / 2 (n 1)
即
得到方差 2 的一个置信度为1- 的置信区间:
由公式(2)得均值的置信度为0.95的置信区间为
6.2022 2.1315 503.75 即（500.4, 507.1） 16 这就是说估计袋装月饼重量的均值在500.4与507.1之间，
这个估计的可信程度为95%。若以此区间内任一值作为 的 6.2022 2.1315 2 6.61 （克），这个 近似值，其误差不大于 16 误差估计的可信程度为95%。 8
2 2 / 于是得 1 2 的一个置信度为 1 的置信区间为 2 2 S*1 S*1 2 F / 2 ( n2 1, n1 1), 2 F1 / 2 ( n2 1, n1 1) S*2 S*2
3
区间估计的一般步骤：
• 1.给出“好”的点估计（按前面的标准），并 知道它的分布（只依赖待估的未知参数）；
ˆ a, ˆ b] 2.求一个区间（参数的一个邻域） [ ˆc, ˆd ]，使得对于给定的置信水平， 或 [
•
ˆ a ˆ b} 1 P{
且一般要求区间长尽可能小。 将不等式变形得到等价的形式
14
(2) 两个总体方差比 1 / 2 的置信区间 仅讨论总体均值1 ,2 为未知的情况。
2 2
由于
n1 (n2 1) S / ~ F (n1 1, n2 1) n2 (n1 1) S /
2 1 2 2 2 1 2 2
n1 (n2 1) S12 / 12 P F / 2 (n1 1, n2 1) F1 / 2 (n1 1, n2 1) 1 2 2 n2 (n1 1) S2 / 2