框架设计内力计算与组合
土木工程毕业设计 第六章 竖向荷载(恒载 活载)作用下框架内力计算讲解
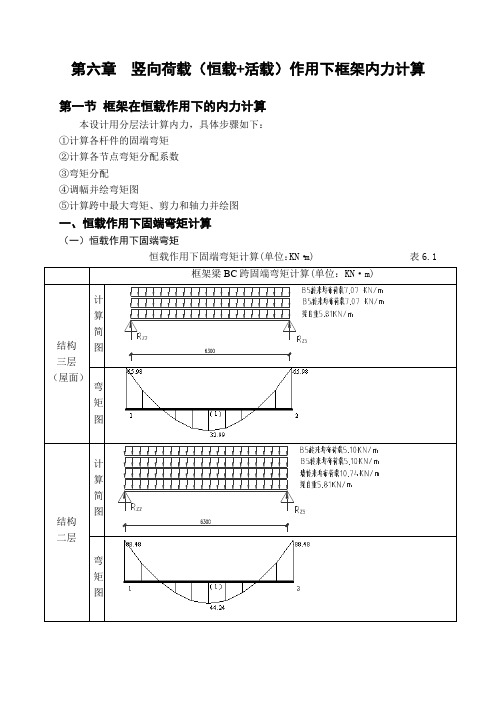
第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表6.1弯矩图恒载作用下梁固端弯矩计算统计表6.2(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以0.9修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=1.5Ir两边有楼板:I=2.0Ir④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图6.1 修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=5.37÷(5.37+1.18)=0.820①梁μB3C3μ=5.37÷(5.37+3.52+1.18)=0.533C3B3=3.52÷(5.37+3.52+1.18)=0.350μC3D3=3.52÷(3.52+1.18)=0.749μD3C3=1.18÷(5.37+1.18)=0.180②柱μB3B2=1.18÷(5.37+3.52+1.18)=0.117μC3C2=1.18÷(3.52+1.18)=0.251μD3D2结构二层①梁μ=5.37÷(1.18+1.18+5.37)=0.695B2C2=5.37÷(1.18+1.18+5.37+3.52)=0.477μC2B2μ=3.52÷(1.18+1.18+5.37+3.52)=0.313 C2D2=3.52÷(1.18+1.18+3.52)=0.5986 μD2C2=1.18÷(1.18+1.18+5.37)=0.1525②柱μB2B3μ=1.18÷(1.18+1.18+5.37)=0.1525B2B1=1.18÷(1.18+1.18+5.37+3.52)=0.105 μC2C3μ=1.18÷(1.18+1.18+5.37+3.52)=0.105 C2C1=1.18÷(1.18+1.18+3.52)=0.2007 μD2D3μ=1.18÷(1.18+1.18+3.52)=0.2007D2D1结构一层=5.37÷(1.18+1+5.37)=0.711①梁μB1C1=5.37÷(1.18+1+5.37+3.52)=0.485 μC1B1=3.52÷(1.18+1+5.37+3.52)=0.318 μC1D1=3.52÷(1.18+1+3.52)=0.618μD1C1=1.18÷(1.18+1+5.37)=0.156②柱μB1B2=1÷(1.18+1+5.37)=0.133μB1B0=1.18÷(1.18+1+5.37+3.52)=0.107μC1C2=1÷(1.18+1+5.37+3.52)=0.090μC1C0μ=1.18÷(1.18+1+3.52)=0.207D1D2μ=1÷(1.18+1+3.52)=0.175D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表6.3B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配14.650 -13.883 226.915 20.861 -251.346 84.509 -112.810 二次分配14.512 -14.512 228.818 21.278 -250.096 105.707 -105.707恒载作用下结构二层弯矩分配表6.40.768 12.717 -28.301↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配 6.931 4.431 -4.607 308.811 46.295 47.232 -385.113 169.804 -113.072 -92.837二次分配 5.901 3.401 -9.302 300.595 44.486 45.423 -390.504 191.416 -105.826 -85.591恒载作用下结构一层弯矩分配表6.52.127 9.081 -7.935↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次7.030 5.338 -12.368 267.469 35.352 22.097 -324.919 357.349 -46.247 -15.172 -295.930图6.2 弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
框架结构课程设计(1)
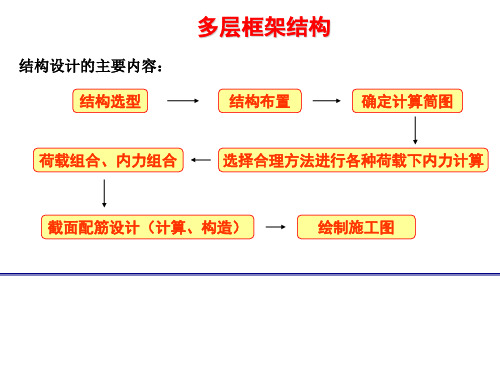
M bl
r Mb
Mu c
l ib M bl l r ( M cu M cl ) ib ib r ib r M b l r ( M cu M cl ) ib ib
水平荷载作用下的D值法 六、梁剪力、柱轴力等 同用分层法进行竖向荷载下内力计算,即:
取各梁为隔离体,由平衡关系 求得梁端剪力。
15.81kN 27.39kN 31.77kN 22.33kN
A2
15.81kN
B2
59.16kN
C2
22.33kN
29.01kN 20.89kN
72.36kN 33.11kN 38.67kN
35.53kN 28.83kN
A1
49.9kN
B1
144.14kN
C1
64.36kN
竖向荷载作用下的分层法
框架在竖向荷载作用下的计算简图:
双 向 板
双向板
单
向
板
用分层法进行竖向荷载作用下框架的内力计算。
框架在水平荷载(风载)作用下的计算简图:
视为均匀分布,风压高度变 化系数按框架顶部标高确定。
进一步将均布荷载简化为作 用在梁柱节点上的水平集中力。
框架在水平荷载(风载)作用下的计算简图:
用反弯点法或D值法进行水平荷载作用下框架的内力计算。
梁端截面: M max、 M max、Vmax
跨中截面: M max
M max 及相应的N和V
Nmax及相应的M和V
N min及相应的M和V
六、框架结构的结构构件设计
1、排架柱的计算长度l0(见教材表13-2) 2、框架节点的构造要求
A2 15.81
B2 59.16
C2 22.33
框架结构内力计算与框架梁截面设计论文

关于框架结构内力计算与框架梁截面设计的探讨摘要:框架结构内力计算与设计是建筑框架结构设计的重要组成部分,这一部分处于框架设计的核心地位,对框架结构的稳定性具有不可忽视的影响。
文章将就框架结构内力计算与设计的方法和原则进行相关的探讨。
关键词:建筑结构;框架结构;内力计算与设计abstract: the structural internal force calculation and design framework is construction frame structure design is an important part of, this part of the core position in the framework design, the stability of the frame structure can not be ignored influence. the article on internal force calculation and design frame structure of the method and principle of the relevant discussion.keywords: building structure; frame structure; internal force calculation and design中图分类号:s611文献标识码:a 文章编号:在框架内力计算中,钢筋混凝土框架结构在竖向荷栽,以及水平荷栽作用下的内力计算的简化方法是主要的内容。
框架内力组合的基本原理,以及梁、柱的内力组合目标、组合方法、框架截面设计的基本构造要求和基本规定,以及框架抗震承栽力验算的表达式和方法等也是决定设计的主要因素。
文章主要是就结构布置与计算简图、竖向荷载作用下的内力计算、框架梁截面设计与构造要求进行探讨。
一、结构布置与计算简图(一)结构布置1、柱网布置(1)框架结构柱网布置的原则。
框架在竖向荷载作用下内力计算

Mik MiFk 2Mi'k Mk' i
…3.6.4
或
Mik MiFk Mi'k (Mi'k Mk' i ) …3.6.5
➢ 根据算得的各杆端弯矩值,作最后的弯矩图并求得 相应的剪力图和轴力图。
例题:
0.463
A2
结点B2与结点A2分配系数相同
(2)计算固端弯矩:
mA2B2
1 12
q2l 2
1 12
10
82
53.333kN
gm
mB2 A2
1 12
q2l 2
1 12
10 82
53.333kN gm
(3)循环过程B2
A2
4、还原-叠加、结点不平衡弯矩再分配一次
6、计算框架梁其他截面的弯矩 计算框架梁截面的剪力 计算框架柱的轴力
结点A1:
S A1A2 4(0.9ic2 ) S A1A0 4ic1
S A1B1 4ib
S 4(ic1 0.9ic2 ib ) 4 2.478
A1
A1A2
S A1A2 S
4 0.9 1 0.363 4 2.478
A1
A1A0
S A1A0 S
4 0.801 4 2.478
1 0.0133E 12
ic 2
EIc H2
1 1 0.0666E 4 12
1 0.0166E 12
ib
EIb L
1 1 0.1029E 8Βιβλιοθήκη 121 0.0129E 12
相对线刚度: 设:ic2 1
则 ic1 0.801
ib 0.777
2、把框架以按层拆为两个开口框架
H2=4000
框架结构的内力和位移计算

H
(4.21)
(10.53)
E
(4.84)
(括号内数字为线刚度相对值)
A
(i=EI/l)
B
8.00m
2021/4/10
(8.21)
I
(2.00) q=2.4kN/m
(10.77)
F
(5.00)
C
6.00m
19
4.40m
3.80m
水平荷载作用下的近似计算——反弯点法
框架所受水平荷载主要是风力和地震作用。将在每个楼层上 的总风力和总地震作用分配给各个框架,将结构分析简化为平面 框架分析。 • 受力和变形特点 • 假定条件 • 计算方法 • 需注意的问题
3
2
2i12z1
4i12z1 1/2
1
0 3 i13 z1
4i15z1
i14 z1 -1
4
i14 z1
1/2
5
2i15z1
11
2021/4/10
弯矩分配法注意事项
12
2021/4/10
例题
G
(4.21)
D
(7.11)
q=2.8kN/m
(7.63) q=3.8kN/m
H
(4.21)
(9.53)
E
基本假定
①假定同层各节点转角相同; 承认节点转角的存在,但是为了计算的方便,假定同层各节点转角相同。 ②假定同层各节点的侧移相同。这一假定,实际上忽略了框架梁的轴向变形。这与实际结构差别不大。
优点: 1、计算步骤与反弯点法相同,计算简便实用。 2、计算精度比反弯点法高。 缺点: 1、忽略柱的轴向变形,随结构高度增大,误差增大。 2、非规则框架中使用效果不好。
点角位移 ,0 各节点只有侧移,同层各节点 水平位移相等; • 底层柱反弯点在距底端2/3h处,上层各柱反 弯点在柱高1/2处。
框架结构的内力和位移计算(精)

假定: (1)平面结构假定; (2)忽略柱的轴向变形; (3)D值法考虑了结点转角, 假定同层结点转角相等
2019/3/19
27
D 值法
计算方法 1、D值——修正抗侧刚度的计算 水平荷载作用下,框架不仅有侧移, 且各结点有转角,设杆端有相对位 移 ,转角 、 ,转角 1 2 位移方程为:
2019/3/19
22
反弯点法
2、剪力的计算 根据假定1:
V1 j d1 j j
Vij d ij j
Vij , d ij
——第j层第I根柱的剪力及其抗侧刚度
第j层总剪力
V pj
Vpj V1 j V2 j Vmj
2019/3/19 23
反弯点法
V1 j
第j层各柱剪力为
M ( z) N B
M(z)——上部水平荷载对坐标Z力矩总和 B——两边柱轴线间的距离
N
2019/3/19 44
柱轴向变形产生的侧移
N j
任意水平荷载下柱轴向变形产生的第j层处侧移 把框架连续化,根据单位荷载法:
2 ( NN / EA)dz
N j 0
Hj
N ( H j z) / B
框架结构的内力和位移计算荷载和设计要求51计算简图计算简图计算简图计算简图计算简图52竖向荷载作用下的近似计算方法分层法分层法分层法分层法力学知识回顾分层法计算过程构件弯矩图53水平荷载作用下内力近似计算方法反弯点法反弯点法弯点法反弯点法反弯点法反弯点法反弯点法反弯点法54水平荷载作用下内力近似计算方法d55水平荷载作用下侧移的近似计算梁柱刚度比k中柱
2019/3/19
9
计算简图
二、结构构件的截面抗弯刚度 考虑楼板的影响,框架梁的截面抗弯刚度应适当提高 现浇钢筋混凝土楼盖: 中框架:I=2I0 边框架:I=1.5I0 装配整体式钢筋混凝土楼盖: 截面形式选取: 框架梁跨中截面: 中框架:I=1.5 I0 T型截面 边框架:I=1.2 I0 框架梁支座截面: 装配式钢筋混凝土楼盖: 矩形截面 中框架:I=I0 边框架:I=I0 注:I0为矩形截面框架梁的截面惯性矩
内力组合及内力调整

7 内力组合及内力调整7.1内力组合各种荷载情况下的框架内力求得后,根据最不利又是可能的原则进行内力组合。
当考虑结构塑性内力重分布的有利影响时,应在内力组合之前对竖向荷载作用下的内力进行增幅。
分别考虑恒荷载和活荷载由可变荷载效应控制的组合和由永久荷载效应控制的组合,并比较两种组合的内力,取最不利者。
由于构件控制截面的内力值应取自支座边缘处,为此,进行组合前,应先计算各控制截面处的(支座边缘处的)内力值。
1)、在恒载和活载作用下,跨间max M 可以近似取跨中的M 代替,在重力荷载代表值和水平地震作用下,跨内最大弯矩max M 采用解析法计算:先确定跨内最大弯矩max M 的位置,再计算该位置处的max M 。
当传到梁上的荷载为均布线荷载或可近似等效为均布线荷载时,按公式7-1计算。
计算方式见图7-1、7-2括号内数值,字母C 、D 仅代表公式推导,不代表本设计实际节点标号字母。
2max182M M M ql +≈-右左 且满足2max 116M ql = (7-1) 式中:q ——作用在梁上的恒荷载或活荷载的均布线荷载标准值;M 左、M 右——恒载和活载作用下梁左、右端弯矩标准值;l ——梁的计算跨度。
2)、在重力荷载代表值和地震作用组合时,左震时取梁的隔离体受力图,见图7-1所示, 调幅前后剪力值变化,见图7-2。
图7-1 框架梁内力组合图图7-2 调幅前后剪力值变化图中:GC M 、GD M ——重力荷载作用下梁端的弯矩; EC M 、CD M ——水平地震作用下梁端的弯矩C R 、D R ——竖向荷载与地震荷载共同作用下梁端支座反力。
左端梁支座反力:()C 1=2GD GC EC ED ql R M M M M l--++;由0M ddx=,可求得跨间max M 的位置为:1C /X R q = ; 将1X 代入任一截面x 处的弯矩表达式,可得跨间最大弯矩为: 弯矩最大点位置距左端的距离为1X ,1=/E X R q ;()101X ≤≤; 最大组合弯矩值:2max 1/2GE EF M qX M M =-+;当10X <或11X >时,表示最大弯矩发生在支座处,取1=0X 或1=X l ,最大弯矩组合设计值的计算式为:2max C 11/2GE EF M R X qX M M =--+; 右震作用时,上式中的GE M 、EF M 应该反号。
框架结构竖向荷载作用下的内力计算

框架结构竖向荷载作用下的内力计算框架结构是由梁柱等构件组成的,在受到竖向荷载作用下,会引起构件内力的产生。
了解框架结构竖向荷载作用下的内力计算对于结构的设计和分析非常重要。
下面将详细介绍框架结构竖向荷载作用下的内力计算方法。
首先,通过建立结构模型来描述框架结构。
结构模型中包括构件、节点和连接关系。
构件可以是梁或柱,节点是构件之间的连接点,连接关系表示构件之间的刚性约束。
在竖向荷载作用下,框架结构的内力主要有两种情况:梁内力和柱内力。
1.梁内力计算:在竖向荷载作用下,梁会产生弯矩和剪力。
根据梁的基本理论,可以得出计算弯矩和剪力的公式。
-弯矩计算:弯矩是由竖向荷载作用在梁上引起的。
根据弯矩的定义,弯矩M等于施加在梁上的力乘以力臂。
当梁需要承受重力荷载时,弯矩的计算公式为M=w*l^2/8,其中w为荷载大小,l为梁的跨度。
-剪力计算:剪力是由竖向荷载作用在梁上引起的。
根据剪力的定义,剪力V等于施加在梁上的力。
当梁需要承受重力荷载时,剪力的计算公式为V=w*l/2,其中w为荷载大小,l为梁的跨度。
2.柱内力计算:在竖向荷载作用下,柱会产生压力和拉力。
根据柱的基本理论,可以得出计算压力和拉力的公式。
-压力计算:压力是由竖向荷载作用在柱上引起的。
根据力学平衡原理,压力P等于施加在柱上的荷载之和。
当柱需要承受多个重力荷载时,压力的计算公式为P=∑w,其中w为荷载大小。
-拉力计算:拉力是由竖向荷载作用在柱上引起的。
和压力类似,拉力T等于施加在柱上的荷载之和。
在实际计算过程中,需要考虑梁和柱的截面形状和材料性质,以及节点和连接部位的刚性约束等因素。
同时,还需要考虑结构的整体平衡条件和节点处的力的平衡条件。
在计算过程中,可以使用静力平衡原理和弹性力学理论来进行分析。
通过平衡方程和应变-位移关系等基本原理,可以建立结构方程组,并通过求解方程组得到内力的值。
总结起来,框架结构竖向荷载作用下的内力计算是一个复杂的过程,需要考虑多个因素和使用多种方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
四 框架内力组合 3 梁柱内力调整
强剪弱弯
强剪弱弯、强柱弱梁、强结点弱构件
组合后的调整(有地震组合) 梁剪力调整(有地震组合)
l (M b M br ) V RE b VGb ln
强剪弱弯 强柱弱梁
柱弯矩调整(有地震组合) 柱剪力调整
M
C
C M b
t b V C ( M C MC ) / Hn
强剪弱弯——梁剪力调整
受弯 0.75
受剪 0.85
l (M b M br ) V RE b VGb l n
262 .76 350 .347 0.75
29.703kN/m
292 .59 390 .12 0.75
262 .76 350 .347 0.75
B 5.4m
29.703kN/m
195 .56 260 .747 0.75
A
1.2 260 .747
A B 5.4m
29.703kN/m
1.2 350 .347
左震
135 .799
135 .799
A
B 5.4m
80 .198
80 .198
梁柱
1.2SGk 0.91.4SQK 1.4SWK 1.35SGk 1.4 0.7SQK
1.2SGk 1.4SQk
四 框架内力组合
2 梁柱内力组合
有地震作用效应的组合 rRES≤R
受弯:0.75
受剪: 0.85
SGK
SQK
SEK
屋面荷载取雪荷载 对多层结构,风荷载不参与组合
A
B
M
C
C M b
t b V C ( M C MC ) / Hn
柱端剪力增大系数,一、二、三、 四级框架分别为1.5、1.3、1.2和1.1
C
有地震作用效应的组合
风荷载组合值系数ψw 一般结构——0.0 风荷载起控制作用——0.2
SGK
基本组合
SQK
SEK
S rG SGE rEhSEhk rEvSEvk wrwSwk
梁柱
1.2SGK 0.5SQK SGE 1.3SEk
受弯 0.75
受剪 0.85
四 框架内力组合
l (M b M br ) V RE b VGb 0.85(135.799 80.198) 183.598 ln
强剪弱弯、强柱弱梁——柱剪力、弯矩调整
除顶层和轴压比小于0.15的柱,柱端 弯矩增大系数,一、二、三、四级框 架分别为1.7、1.5、1.3和1.2
29.703kN/m
195 .56 260 .747 0.75
A
5.4m
B
A 5.4m
B
161 .09 214 .787 0.75
左震
右震
l (M b M br ) V RE b VGb ln
梁端剪力增大系数,一、二、三级框架分别为1.3、1.2、1.1
i 1
n
SQK
SWK
n i 2
由可变荷载效 应控制的组合 由永久荷载效 应控制的组合
组合值系数ψc 0.7 0.7 0.6 0.7
S rG SGk rQ1SQ1k rQi Ci SQik
S rG SGk rQi Ci SQik
i 1
n
类 别 民用建筑楼面 活 荷 载 屋面活荷载 风荷载 雪荷载
3 梁柱内力调整
组合前的调整
①当活荷载与恒载之比不大于1时,可 按活荷载满布计算,但梁跨中弯矩偏低, 应将跨中弯矩乘以1.1~1.2系数予以调整
SQK
②为便于施工及提高框架延性,对竖 向荷载作用下梁端负弯矩进行调幅, 现浇框架调幅系数可取0.8~0.9,跨中 弯矩也应相应调整(调大)
SGK
SQK
A
B
2 梁柱内力组合
A
B
C
SGK
SQK
SWK
SEK
四 框架内力组合
2 梁柱内力组合
无地震作用效应的组合 r0S≤R SGK SQK SWK
屋面荷载 取屋面活荷载与雪荷载中较大值
A
B
C
一般框架简化规则
S rG SGk rQ1SQ1k
无地震作用效应的组合 SGK
基本组合
S rG SGk 0.9 rQi SQik
三 框架内力计算和变形验算 1 永久荷载作用
2 可变荷载作用
迭代法或弯矩二次分配法
注意集中力产生的偏心力矩 求柱顶轴力要加纵梁传集中力 求柱底轴力要加柱自重
3 风荷载作用 4 水平地震作用
D值法
A
B
C
四 框架内力组合
1 梁柱内力正负约定
弯矩
— —
+
—
+
剪力
轴力
拉 力
—
+
—
压 力
+
四 框架内力组合
