运算定律除法的性质例8
运算律和简便运算
运算律和简便运算（一）加减法运算定律1、加法交换律定义：两个加数交换位置，和不变 字母表示：a b b a +=+例如：16+23=23+16 546+78=78+5462、加法结合律定义：先把前两个数相加，或者先把后两个数相加，和不变。
字母表示：)()(c b a c b a ++=++ 注意：加法结合律有着广泛的应用，如果其中有两个加数的和刚好是整十、整百、整千的话，那么就可以利用加法交换律将原式中的加数进行调换位置，再将这两个加数结合起来先运算。
3、减法的性质 注意：这些都是由加法交换律和结合律衍生出来的。
减法性质①：如果一个数连续减去两个数，那么后面两个减数的位置可以互换。
字母表示：b c a c b a --=--减法性质②：如果一个数连续减去两个数，那么相当于从这个数中减去后面两个数的和。
字母表示：)(c b a c b a +-=--4、拆分、凑整法简便计算拆分法：当一个数比整百、整千稍微大一些的时候，我们可以把这个数拆分成整百、整千与一个较小数的和，然后利用加减法的交换、结合律进行简便计算。
例如：103=100+3，1006=1000+6，…凑整法：当一个数比整百、整千稍微小一些的时候，我们可以把这个数写成一个整百、整千的数减去一个较小的数的形式，然后利用加减法的运算定律进行简便计算。
例如：97=100-3，998=1000-2，…注意：拆分凑整法在加、减法中的简便不是很明显，但和乘除法的运算定律结合起来就具有很大的简便了。
（二）乘除法运算定律1.乘法交换律定义：交换两个因数的位置，积不变。
字母表示：a b b a ⨯=⨯例如：85×18=18×85 23×88=88×232、乘法结合律定义：先乘前两个数，或者先乘后两个数，积不变。
字母表示：)()(c b a c b a ⨯⨯=⨯⨯ 乘法结合律的应用基于要熟练掌握一些相乘后积为整十、整百、整千的数。
(完整版)加减乘除运算定律
加法
1.加法交换律：a+b = b+a
两个数相加，交换加数的位置，和不变。
2.加法结合律：a+b+c = (a+b)+c = a+(b+c)
三个数相加，先把前两个数相加，再和第三个数相加，或者先把后两个数相加，再和第一个数相加，和不变。
3.加法运算中综合运用交换律和结合律: a+b+c = (a+c)+b
减法
1.减法的性质：a–b–c = a–(b+c)
一个数连续减去两个数，可以用第一个数减去后面两个数的和，差不变。
乘法
1.乘法交换律：a×b = b×a
两个数相乘，交换乘数的位置，积不变。
2.乘法结合律：a×b×c = (a×b)×c = a×(b×c)
三个数相乘，先把前两个数相乘，再和第三个数相乘，或者先把后两个数相乘，再和第一个数相乘，积不变。
3.乘法运算中综合运用交换律和结合律: a×b×c = ( a×c)×b
4.乘法分配律：(a+b)×c = a×c+b×c
两个数的和与第三个数相乘，等于把这两个数分别与这个数相乘，再把它们的积加起来，结果不变。
5.乘法分配律的逆运用：a×c+b×c =(a+b)×c
除法
1.除法的性质：a÷b÷c = a÷（b×c)
一个数连续除以两个数，等于被除数除以两个除数的积，商不变。
运算定律和性质整理
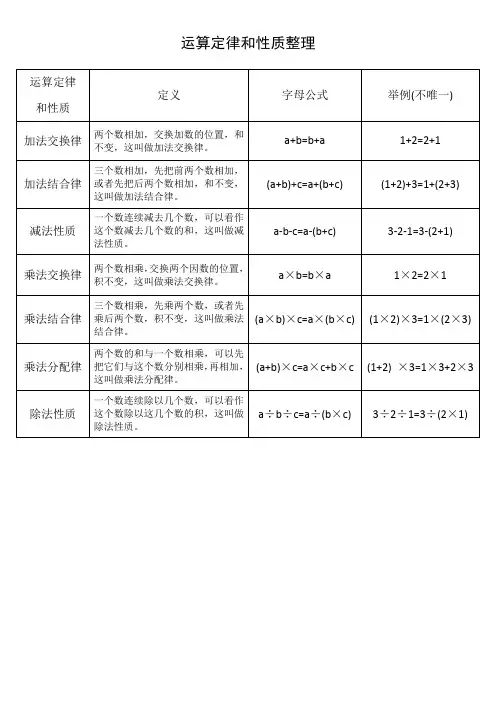
运算定律
和性质
定义
字母公式
举例(不唯一)
加法交换律
两个数相加，交换加数的位置，和不变，这叫做加法交换律。
aபைடு நூலகம்b=b+a
1+2=2+1
加法结合律
三个数相加，先把前两个数相加，或者先把后两个数相加，和不变，这叫做加法结合律。
(a+b)+c=a+(b+c)
(1+2)+3=1+(2+3)
减法性质
一个数连续减去几个数，可以看作这个数减去几个数的和，这叫做减法性质。
a-b-c=a-(b+c)
3-2-1=3-(2+1)
乘法交换律
两个数相乘，交换两个因数的位置，积不变，这叫做乘法交换律。
a×b=b×a
1×2=2×1
乘法结合律
三个数相乘，先乘两个数，或者先乘后两个数，积不变，这叫做乘法结合律。
(a×b)×c=a×(b×c)
(1×2)×3=1×(2×3)
乘法分配律
两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加，这叫做乘法分配律。
(a+b)×c=a×c+b×c
(1+2)×3=1×3+2×3
除法性质
一个数连续除以几个数，可以看作这个数除以这几个数的积，这叫做除法性质。
a÷b÷c=a÷(b×c)
3÷2÷1=3÷(2×1)
小学数学简便运算和巧算
小学数学简便运算和巧算一、数的加减乘除有时可以运用运算定律、性质、或数量间的特殊关系进性较快的运算这就是简便运算。
（一）其方法有：一：利用运算定律、性质或法则。
(1) 加法：交换律，a+b=b+a, 结合律，(a+b)+c=a+(b+c).(2) 减法运算性质：a-(b+c)=a-b-c, a-(b-c)=a-b+c, a-b-c=a-c-b,(a+b)-c=a-c+b=b-c+a.(3):乘法：利用运算定律、性质或法则。
交换律，a×b=b×a, 结合律，（a×b）×c=a×(b×c),分配率，（a+b）×c=a×c+b×c, (a-b)×c=a×c-b×c.(4)除法运算性质：a÷(b×c)=a÷b÷c, a÷（b÷c)=a÷b×c, a÷b÷c=a÷c÷b,(a+b)÷c=a÷c+b÷c, (a-b)÷c=a÷c-b÷c.前边的运算定律、性质公式很多是由于去掉或加上括号而发生变化的。
其规律是同级运算中，加号或乘号后面加上或去掉括号，。
后面数值的运算符号不变。
例1:283+52+117+148=（283+117）+（52+48）=400+200=600（运用加法交换律和结合律）。
减号或除号后面加上或去掉括号，后面数值的运算符号要改变。
例2：657-263-257=657-257-263=400-263=147.（运用减法性质，相当加法交换律。
）例3：195-（95+24）=195-95-24=100-24=76 （运用减法性质）例4; 150-(100-42)=150-100+42=50+42=92. (同上)例5：（0.75+125）×8=0.75×8+125×8=6+1000=1006. (运用乘法分配律))例6：（ 125-0.25）×8=125×8-0.25×8=1000-2=998. (同上)例7：（1.125-0.75）÷0.25=1.125÷0.25-0.75÷0.25=4.5-3=1.5。
四年级数学运算题规律
四年级数学运算题规律运算定律有什么第一类是加法运算定律：加法交换律加法结合律减法的性质第二类是乘法运算定律：乘法交换律乘法结合律乘法分配律除法的性质一、加法运算定律1.加法交换律：定义：两个数相加，交换加数的位置，和不变。
叫作加法交换律。
用字母表示为：a+b=b+a那如何判定算式是运用了加法交换律呢？你只需要确定数的位置变了，就是运用的加法交换律例如3+4=4+33和4的位置交换了，和没变，运用了加法交换律还有什么地方可以用到加法交换律呢？例如加法竖式计算验算时，你可以通过交换两个加数的位置来达到验算的目的2.加法结合律定义：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变，叫作加法结合律。
用字母表示为:(a+b)+c=a+(b+c)简单来说，加法结合律是改变了运算顺序例如：3+4+7=3+（4+7）等号左边要先算3+4，之后再加7；等号右边先算的是4+7，之后再与3相加。
那有没有既使用了加法交换律，又运用了加法结合律呢？有的，那就是数既改变了位置，又改变了运算顺序。
例如：3+8+2=8+2+3这个算式中，数的位置变了，原来是3、8、2，现在是8、2、3。
运算顺序也变了，等式左边先算的3+8，等式右边先算的8+2.3.减法的性质定义：一个数连续减去两个数，可以用这个数减去这两个减数的和，差不变。
用字母表示：a-b-c= a-(b+c)例如：120-30-60=120-（30+60）还有一个补充就是一个数连续减去两个数，任意交换减数的位置，差不变。
用字母表示：a-b-c= a-c-b例如：120-30-60=120-60-30那在这里给大家出几道简便计算的题二、乘法运算定律1.乘法交换律定义：两个数相乘，交换两个因数的位置，积不变，这叫作乘法交换律。
用字母表示为：a×b=b×a例如：5×4=4×5同样在乘法算式中，乘法交换律判定方法：改变了数的位置2. 乘法结合律定义：三个数相乘，先乘前两个数或者先乘后两个数，积不变，这就是乘法结合律。
人教版数学四年级下册【运算定律与简便计算】知识篇
加、减法的速算与巧算( 基础篇)原创不容易，为有更多动力，请【关注、关注、关注】，谢谢！落红不是无情物，化作春泥更护花。
出自龚自珍的《己亥杂诗·其五》1、加法运算定律（2个）：☆加法交换律：两个数相加，交换加数的位置，和不变。
即：a + b = b + a☆加法结合律：三个数相加，可以先把前两个数相加，再加上第三个数；或者先把后两个数相加，再加上第一个数，和不变。
即：(a + b) + c = a + (b + c)（提醒：运用加法结合律时，要注意把结合的两个数用括号括起来。
）连加的简便计算方法：①使用加法交换律、结合律凑整（把和是整十、整百、整千的数先交换再结合在一起。
）②个位：1与9，2与8，3与7，4与6，5与5，结合。
③十位：0与9，1与8，2与7，3与6，4与5，结合。
连加的简便计算例题：50+98+50 488+40+60 １６５+９３+３５ 65+28+35+72＝50+50+98 ＝488+（40+60）＝９３+１６５+３５＝（65+35）+（28+72）＝100+98 ＝488+100 ＝９３+（１６５+３５）＝ 100+100＝198 ＝588 ＝293 ＝ 2002、连减的性质：☆一个数连续减去几个数等于这个数减去这几个数的和。
即：a – b – c = a – (b + c)注：连减的性质逆用：a – (b + c) = a – b – c = a – c – b☆一个数连续减去两个数，可以用这个数先减去后一个数再减去前一个数。
即：a－b－c＝a—c－b连减的简便计算方法：①连续减去几个数就等于减去这几个数的和。
如：106-26-74 = 106-(26+74)②连续减去两个数可以先减去后一个数再减去前一个数。
如：226-58-26=226-26-58③减去几个数的和就等于连续减去这几个数。
如：106-(26+74) = 106-26-74连减的简便计算例题：528—65—35 28—89—128 528—（150+128）=528—（65+35） =528—128—89 =528—128—150=528—100 =400—89 =400—150=428 =311 =2503、加、减法混合运算的性质：在计算没有括号的加、减混合运算时，计算时可以带着运算符号“搬家”。
数学简便计算
数学简便计算：运算定律和性质1、加法交换律：两个加数交换位置，和不变。
这叫做加法交换律。
用字母表示：a+b=b+a2、加法结合律：三个数相加，先把前两个数相加，或者先把后两个数相加，和不变。
这叫做加法结合律。
用字母表示：（a+b）+c= a +( b+c)3、乘法交换律：两个因数交换位置，积不变。
这叫做乘法交换律。
用字母表示：a×b=b×a4、乘法结合律：三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积不变。
这叫做乘法结合律。
用字母表示：（a×b）×c= a ×( b×c)5、乘法分配律：两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加。
这叫做乘法分配律。
用字母表示：（a+b）×c= a×c+b×ca ×( b+c) =a×b+a×c拓展：（a-b）×c= a×c-b×ca ×( b-c) =a×b-a×c6、减法的性质1：一个数连续减去两个数，可以减去这两个减数的和。
用字母表示：a-b-c= a -( b+c)a -( b+c) = a-b-c7、减法的性质2：一个数连续减去两个数，可以先减去第二个减数，再减去第一个减数。
用字母表示：a-b-c= a-c-b8、除法的性质1：一个数连续除以两个数，可以除以这两个除数的积。
用字母表示：a÷b÷c= a ÷( b×c)a ÷( b×c) = a÷b÷c9、除法的性质2：一个数连续除以两个数，可以先除以第二个除数，再除以第一个除数。
用字母表示：a÷b÷c= a÷ c ÷ b级数学简便计算：加减法篇一、加法：1.利用加法交换律例如：254+158+246我们首先观察发现254与246相加可以凑成整百，于是交换158和246两个加数的位置，变成254+246+158。
人教四下数学【运算定律与简便计算】知识篇
人教版四年级下册数学加、减法的速算与巧算( 基础篇 )1、加法运算定律（2个）：☆加法交换律：两个数相加，交换加数的位置，和不变。
即：a + b = b + a☆加法结合律：三个数相加，可以先把前两个数相加，再加上第三个数；或者先把后两个数相加，再加上第一个数，和不变。
即：(a + b) + c = a + (b + c)（提醒：运用加法结合律时，要注意把结合的两个数用括号括起来。
）连加的简便计算方法：①使用加法交换律、结合律凑整（把和是整十、整百、整千的数先交换再结合在一起。
）②个位：1与9，2与8，3与7，4与6，5与5，结合。
③十位：0与9，1与8，2与7，3与6，4与5，结合。
连加的简便计算例题：50+98+50 488+40+60 １６５+９３+３５ 65+28+35+72＝50+50+98 ＝488+（40+60）＝９３+１６５+３５＝（65+35）+（28+72）＝100+98 ＝488+100 ＝９３+（１６５+３５）＝ 100+100＝198 ＝588 ＝293 ＝ 2002、连减的性质：☆一个数连续减去几个数等于这个数减去这几个数的和。
即：a – b – c = a – (b + c)注：连减的性质逆用：a – (b + c) = a – b – c = a – c – b☆一个数连续减去两个数，可以用这个数先减去后一个数再减去前一个数。
即：a－b－c＝a—c－b连减的简便计算方法：①连续减去几个数就等于减去这几个数的和。
如：106-26-74 = 106-(26+74)②连续减去两个数可以先减去后一个数再减去前一个数。
如：226-58-26=226-26-58③减去几个数的和就等于连续减去这几个数。
如：106-(26+74) = 106-26-74连减的简便计算例题：528—65—35 528—89—128 528—（150+128）=528—（65+35） =528—128—89 =528—128—150=528—100 =400—89 =400—150=428 =311 =2503、加、减法混合运算的性质：在计算没有括号的加、减混合运算时，计算时可以带着运算符号“搬家”。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
＝（10＋2）×25 ＝10×25＋2×25 ＝250＋50 ＝300
问题：在解决实际问题时，我们要注意什么？ （关注数据的特点，灵活运用运算定律，使计算变得简便。）
绿色圃中小学教育网
三、自主探索，发现新知
（一）独立尝试，解决问题
每支羽毛球拍多少钱？ 问题：解决这个问题，需要哪些信息？你能根据所选的信息， 解决这个问题吗？（学生独立解决问题。）
简便方法计算： 12000÷（12×40） =12000÷12÷40 =1000÷40
=25
简便方法计算： 6300÷（63×20） =6300÷63÷20 =100÷20
=5
四、巩固练习，提升认识
1.
问题： （1）你知道了什么？ （2）观察数据，有什么特点？ （3）怎样计算比较简便？
350÷14 ＝350÷（7×2） ＝350÷7÷2 ＝50÷2 ＝25（册） 答：平均每个班可以分到25册。
三、自主探索，发现新知
（二）比较观察，发现规律
方法①： 330÷5÷2
＝66÷2 ＝33
问题：1. 330÷5后，为什么还要÷2？ （要求每支羽毛球拍多少钱，330÷5求的是 一副羽毛球拍的价格。）
2. 还有不同的计算方法吗？
绿色圃中小学教育网
三、自主探索，发现新知
绿色圃中小学教育网
四、巩固练习，提升认识
2.
这学期一共有多少天？ 问题：（1）你知道了什么？ （2）你能解决这个问题吗？写出你的思考过程。 （3）谁读懂了他的意思？说一说。 （4）谁的想法和他的不一样？能再说说吗？
（5）你做的正确吗？
绿色圃中小学教育网
（二）比较观察，发现规律
方法①： 330÷5÷2 ＝66÷2 ＝33 方法②： 330÷5÷2
具有这样特点的式子 你还能写一写吗？它 们是否也相等呢？
＝330÷（5×2） ＝330÷10 ＝33 问题：1. 你能理解这位同学的想法吗？ （先求一共有10支羽毛球拍，再求每支羽毛球拍的价格。） 2. 为什么330÷5÷2和330÷（5×2）之间可以用等号连接？ （①它们的结果相等。②都是求一支羽毛球拍的价格。） 3. 观察算式的特点，看看你能发现什么规律。
四、巩固练习，提升认识
3. 李大爷家有一块菜地（如右图）， 这块菜地的面积有多少平方米？
9×21＋9×19 ＝9×（21＋19） ＝9×40 ＝360（m2 ） 答：这块菜地的面积有360 m2。
绿色圃中小学教育网
五、布置作业
作业：第30页练习八，第3题；
二、创设情境，灵活运用
（一）收集信息，明确条件问题
王老师一共买了多少个羽毛球？ 问题：你知道了什么？
（5副羽毛球拍，共330元。25筒羽毛球，每筒32元。注意引导学生观察羽 毛球的包装上的信息，“一打”是12个。）
绿色圃中小学教育网
二、创设情境，灵活运用
（二）独立思考，尝试解决问题
除法的运算性质 解决问题例8
一、复习导入
说一说我们已经学过哪些运算定b＋a
减法性质：a-b-c＝a-(b+c) 乘法交换律：a×b＝b×a 乘法结合律：（a×b）×c＝a×（b×c）
加法结合律：（a＋b）＋c＝a＋（b＋c）
乘法分配律：a×（b＋c）＝a×b＋a×c 在解决问题时，灵活地运用这些运算定律，可以使计算变得简便。
王老师一共买了多少个羽毛球？ 问题：解决这个问题，需要哪些信息？你能根据所选的信息， 解决这个问题吗？ （买了25筒羽毛球、“一打”装、“一打”是12个。）
二、创设情境，灵活运用
（三）读懂过程，感悟不同方法
方法①： 12×25＝300 1 2 ×2 5 6 0 2 4 3 0 0 方法②： 12×25 ＝（3×4）×25 ＝3×（4×25） ＝3×100 ＝300 方法③： 12×25 ＝（10＋2）×25 ＝10×25＋2×25 ＝250＋50 ＝300
（一个数连续除以两个数，可以除以后两个数的乘积。）
绿色圃中小学教育网
330÷5÷2
= 330÷（5×2）
一个数连续除以两个数，可以用这个 数除以它们的积。这叫做除法的性质。
a÷b÷c = a÷(b×c)
在横线上填入适当的数，在○里填入合适的运算符号．
1300÷25÷4＝1 300÷（ 8000÷125÷8＝____○（ a÷b÷c＝a÷（ ○ ）
700 ÷ 28 = 700 ÷（ 7 × 4 ） = 700÷ 7 ÷ 4
= 100 ÷ 4
= 25
a÷(b×c)= a÷b÷c
简便方法计算： 10800÷（108×25） =10800÷108÷25 =100÷25
=4
简便方法计算： 350÷（25×7） =350÷7÷25 =50÷25
=2
问题：比较3种不同的解法，你喜欢哪种？说一说你的理由。
（后两种方法都关注到了数字的特点，利用运算定律使计算变得简便。）
二、创设情境，灵活运用
（四）回顾反思，沟通不同方法
方法①： 12×25＝300 1 2 ×2 5 6 0 2 4 3 0 0 方法 ②： 12×25 方法③： 12×25
＝（3×4）×25 ＝3×（4×25） ＝3×100 ＝300
○ ○
）
）
简便方法计算： 4800÷25÷4 =4800÷（25×4） =4800÷100
=48
简便方法计算： 8000÷125÷8 =8000÷（125×8） =8000÷1000
=8
420 ÷ 35 = 420 ÷（ 7 × 5 ） = 420 ÷ 7 ÷ 5
= 60 ÷ 5
= 12
a÷(b×c)= a÷b÷c
第31页练习八，第7题。
绿色圃中小学教育网