上册4.4 第1课时 两个三角形相似的判定(一)
4.用角的关系判定两三角形相似课件

符号语言: 如图,在△ABC 与 △A'B'C'中
∵∠A =∠A',∠B =∠B',
C
∴△ABC ∽ △A'B'C'.
α A
β
α
B
A'
C'
β
B'
4.4.1 用角的关系判定两三角形类似
例1 如图,D,E 分别是△ABC 的边 AB,AC 上的点,DE∥BC,AB = 7,AD = 5,DE = 10,求 BC 的长. 解:∵ DE∥BC,∴∠ADE =∠B,∠AED =∠C. ∴△ADE∽△ABC ( 两角分别相等的两个三角形类似 ).
似于△A′B′C′.
C′ C
A
B
A′
B′
注意:在写两个三角 形类似时,应把表示 对应顶点的字母写在 对应的位置上.
4.4.1 用角的关系判定两三角形类似
用数学符号表示:
C′ C
A
B
A'
B'
由图 2 可知,
∵ ∠A= ∠A′ , ∠B= ∠B′,∠C=∠C′, AB BC CA A'B' B'C' C'A'
∴
.
A
∴
.
D
E
B
C
4.4.1 用角的关系判定两三角形类似
例2 如图 D、E 分别是△ABC 边 AB、AC 上的点,∠AED =∠C, △ABC 与△ADE 类似吗?如果类似请写出证明过程.
结论:△ABC 与△ADE 类似. 证明:∵∠AED = ∠C, 又∵∠A = ∠A, 所以△ABC =△ADE ( 两角分别相等的两个三角形类似 ).
北师大新版九年级数学上册-4.4 第1课时 利用两角判定三角形相似1教案带教学反思

4.4探索三角形相似的条件第1课时利用两角判定三角形相似1.理解相似三角形的定义,掌握定义中的两个条件;2.掌握相似三角形的判定定理1;(重点)3.能熟练运用相似三角形的判定定理1.(难点)一、情景导入如图,从放大镜里看到的三角尺和原来的三角尺相似吗?二、合作探究探究点一:两角分别相等的两个三角形相似在△ABC和△A′B′C′中,∠A=∠A′=80°,∠B=70°,∠C′=30°,这两个三角形相似吗?请说明理由.解:△ABC∽△A′B′C′.理由:由三角形的内角和是180°,得∠C=180°-∠A-∠B=180°-80°-70°=30°,所以∠A=∠A′,∠C=∠C′.故△ABC∽△A′B′C′(两角分别相等的两个三角形相似).方法总结:两个三角形已有一对角相等,故只要看是否还有一对角相等即可.一般地,在解题过程中要特别注意“公共角”“对顶角”“同角(或等角)的余角”等隐含条件.探究点二:相似三角形的判定定理1的应用已知:如图,△ABC的高AD、BE相交于点F,求证:AFBF=EFDF.解析:要证明AFBF=EFFD,可以考虑比例式中四条线段所在的三角形是否相似,即考虑△AFE与△BFD是否相似,利用两个角对应相等的三角形相似可以证明这个结论.证明:∵BE⊥AC,AD⊥BC,∴∠AEF=∠BDF=90°.又∵∠AFE=∠BFD,∴△AFE∽△BFD,∴AFBF=EFDF.方法总结:证明比例式,可构造相似三角形,只要证明这两个三角形相似,就可根据相似三角形的对应边成比例得到相关比例式.如图所示,已知DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,求线段BF 的长.解:方法一:因为DE ∥BC ,所以∠ADE =∠B ,∠AED =∠C ,所以△ADE ∽△ABC ,所以AD AB =DE BC ,即44+8=5BC ,所以BC =15cm.又因为DF ∥AC , 所以四边形DFCE 是平行四边形, 所以FC =DE =5cm ,所以BF =BC -FC =15-5=10(cm ). 方法二:因为DE ∥BC ,所以∠ADE =∠B .又因为DF ∥AC ,所以∠A =∠BDF , 所以△ADE ∽△DBF ,所以AD DB =DE BF ,即48=5BF ,所以BF =10cm.方法总结:求线段的长,常通过找三角形相似得到成比例线段而求得,因此选择哪两个三角形就成了解题的关键,这就需要通过已知的线段和所求的线段分析得到. 三、板书设计(1)相似三角形的定义:三角分别相等、三边成比例的两个三角形叫做相似三角形;(2)相似三角形的判定定理1:两角分别相等的两个三角形相似.感受相似三角形与相似多边形、相似三角形与全等三角形的区别与联系,体验事物间特殊与一般的关系.让学生经历从实验探究到归纳证明的过程,发展学生的合情推理能力,培养学生的观察、动手探究、归纳总结的能力.。
浙教版九年级数学上册教案《4.4两个三角形相似的判定》

《4.4两个三角形相似的判定》本节课是浙教版初中数学九年级上册《相似三角形》的内容,在这之前,学生学习了全等三角形的相关知识,相似三角形是全等三角形的拓广和发展,而相似三角形的判定是相似三角形的主要内容之一,相似三角形的判定是进一步对相似三角形的本质和定义的全面研究,也是相似三角形性质的研究基础,同时还是研究圆中比例线段和三角函数的重要工具,可见一相似三角形的判定占据着重要的地位。
【知识与能力目标】使学生掌握三角形相似的判定定理1,2,3,和它们的应用.【过程与方法目标】通过找形状相同的图形,培养学生的观察能力;同学间还要互相合作交流,锻炼了大家的合作交流能力.【情感态度价值观目标】通过认识和动手画形状相同的图形,使学生掌握基本的识图、作图技能.丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维【教学重点】判定的应用【教学难点】判定的引入教师准备课件、多媒体;学生准备课本、练习本、三角板;一、导入新课提问:1.什么是相似三角形?2.什么是全等三角形?3.全等三角形的判定方法有哪些?4.你认为三角形相似至少需要那几个条件?二、新课学习合探1 同学们观察我们的直角三角尺,直观上看它们是什么关系?到底需要满足几个条件两个三角形能够相相似?合探 2 与同伴合作,两个人分别画△ABC 和△A ′B ′C ′,使得∠A 和∠A ′都等于∠α,∠B 和∠B ′都等于∠β,此时,∠C 与∠C ′相等吗?三边的比C B BC C A AC B A AB '''''',,相等吗?这样的两个三角形相似吗?改变∠α,∠β的大小,再试一试.判定定理1:两角分别相等的两个三角形相似.这个定理的出现为判定两三角形相似增加了一条新的途径.例:如图,D ,E 分别是△ABC 的边AB ,AC 上的点,DE ∥BC ,AB =7,AD =5,DE =10,求B C 的长。
解:∵DE ∥BC ,∴∠ADE=∠B ,∠AED=∠C.∴△ADE ∽△ABC (两角分别相等的两个三角形相似). ∴AD AB =DE BC . ∴BC =AB×DE AD = 7×105=14. 合探31.(1)画△ABC 与△A ′B ′C ′,使∠A =∠A ′,B A AB ''和C A AC ''都等于给定的值k .设法比较∠B 与∠B ′的大小(或∠C 与∠C ′的大小)、△ABC 与△A ′B ′C ′相似吗?(2)改变k 值的大小,再试一试.定理2:两边成比例且夹角相等的两个三角形相似.2. 画△ABC 与△A ′B ′C ′,使B A AB ''、C B BC ''和A C CA ''都等于给定的值k . (1)设法比较∠A 与∠A ′的大小;(2)△ABC 与△A ′B ′C ′相似吗?说说你的理由.改变k 值的大小,再试一试.定理3:三边:成比例的两个三角形相似.例题学习例1:如图,D ,E 分别是△ABC 的边AC ,AB 上的点,AE =1.5,AC =2,BC =3,且AD AB =34,求DE 的长.解:∵AE =1.5,AC =2,∴AE AC =34, ∵AD AB =34, ∴AD AB =AE AC. 又∵∠EA D=∠CAB ,∴△ADE ∽△ABC (两边成比例且夹角相等的两个三角形相似).∴DE BC =AD AB =34. ∵BC =3,∴DE =34 BC =34×3=94. 例2:如图,在△ABC 和△ADE 中,AB AD =BC DE =AC AE,∠BAD=20°,求∠CAE 的度数.解:∵AB AD =BC DE =AC AE, ∴△ABC ∽△ADE (三边成比例的两个三角形相似).∴∠BAC=∠DAE ,∴∠BAC -∠DAC =∠D AE -∠DAC ,即∠BAD=∠CAE .∵∠BAD=20°,∴∠CAE=20°.结论总结本节学习了相似三角形两个判定定理,一定用时要注意它们使用的条件.四、课堂练习1.如图,在△ABC 和△A′B′C′中,已知∠A =50°,∠B =∠B′=60°,∠C′=70°,△ABC 与△A′B′C′相似吗?为什么?2.如图,D 、E 分别是三角形ABC 边AB ,AC 上的点,DE ∥BC ,AB=7,AD=5,DE=10,求BC的长。
九年级数学上册-北师大版九年级上册数学 4.4 第1课时 利用两角判定三角形相似

4.4 探索三角形相似的条件第1课时 利用两角判定三角形相似学习目标:1、掌握并会推导相似三角形的判定定理1.2、会用相似三角形的判定定理1进行一些简单的判断、证明和计算.学习重点:灵活运用相似三角形的判定定理1证明和解决有关问题.预设难点:相似三角形的判定定理1的推导和应用.【预习案】1.对应角相等,对应边也相等的两个三角形全等,你还记得三角形全等的其他判别条件吗?2.相似三角形的定义是什么?你认为判别两个三角形相似至少需要哪些条件?【探究案】合探1 同学们观察我们的直角三角尺,直观上看它们是什么关系?到底需要满足几个条件两个三角形能够相相似?合探2 与同伴合作,两个人分别画△ABC 和△A ′B ′C ′,使得∠A =∠A ′都等于∠α, ∠B 和∠B ′都等于∠β,此时,∠C 与∠C ′相等吗?对应边的比C B BC C A AC B A AB '''''',,相等吗?这样的两个三角形相似吗?改变∠α,∠β的大小,再试一试.思考:在实际画图过程中,同学们画了几个角相等?为什么?由此得到相似三角形的判定方法1:例:如图,D 、E 分别是△ABC 边AB 、AC 上的点,DE ∥B C ,AB =7,AD =5,DE =10,求BC 的长。
【训练案】1、如图D 、E 分别是△ABC 边AB 、AC 上的点,∠AED=∠C ,△ABC 与△ADE 相似吗?如果相似请写出证明过程 AB C ED2、已知:如图,∠1=∠2=∠3,求证:△ABC ∽△ADE .3.在R t ⊿ABC 中,CD 是斜边上的高,则⊿ABC ∽⊿CBD ∽⊿ACD 。
4.如图,点A 、O 、D 与点B 、O 、C 分别在一条直线上,如果AB ∥CD 那么△AOB 与△DOC 相似吗?为什么? D C B AA BOC D。
浙教版数学九年级上册4.4 两个三角形相似的判定(一).docx

4.4 两个三角形相似的判定(一)1.如图,在△ABC 中,DE ∥B C.若AD AB =13,DE =4,则BC =(D )(第1题)A. 9B. 10C. 11D. 122.有一个角相等的两个等腰三角形(C ) A. 一定相似 B. 一定不相似 C. 不一定相似 D. 一定全等3.如图,在▱ABCD 中,E 是BC 边上一点,AE 交BD 于点F .如果EC BE =23,那么BFFD 的值为(B )A. 25B. 35 C. 23 D. 53(第3题)(第4题)4.如图,在△ABC中,若∠AED=∠B,DE=6,AB=10,AE=8,则BC的长为(C)A. 154 B. 7C. 152 D.2455.如图,在▱ABCD中,F是BC上一点,直线DF与AB的延长线交于点E,作BP∥DF,与AD 交于点P,请从图中找出一组相似的三角形:△ABP∽△AED(答案不唯一).(第5题)6.如图,在△ABC中,D为AB边上一点,且∠BCD=∠A.已知BC=2 2,AB=3,则BD=__83__.(第6题)7.如图,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为4__2.(第7题)8.如图,在△ABC中,AB=AC,BE⊥AC于点E,D是BC的中点,连结AD与BE交于点F.求证:△AFE∽△BCE.(第8题)【解】∵AB=AC,D是BC的中点,∴AD⊥BC,∴∠ADC=90°,∴∠FAE+∠C=90°.∵BE⊥AC,∴∠BEC=90°,∴∠CBE+∠C=90°.∴∠FAE=∠CBE.又∵∠AEF=∠BEC=90°,∴△AFE∽△BCE.9.如图,四边形ABCD内接于⊙O,AB=AC,AD,BC的延长线交于点E,显然△EAB∽△ECD,在不添辅助线的情况下,请你再找出一对相似三角形,并加以证明.(第9题) 【解】结论:△AEC∽△AC D.证明:∵四边形ABCD是圆内接四边形,∴∠ADC+∠B=180°.∵AB=AC,∴∠B=∠AC B.∴∠ADC+∠ACB=180°.又∵∠ACE+∠ACB=180°,∴∠ACE=∠AD C.又∵∠EAC=∠CAD,∴△AEC∽△AC D.10.如图,在▱ABCD 中,E ,F 分别是AD ,AB 的中点,EF 交AC 于点G ,则AG ∶GC 的值为(B ) A. 1∶2 B. 1∶3 C. 1∶4 D. 2∶3(第10题)【解】 如解图,连结BD ,交AC 于点O .(第10题解)∵E ,F 分别是AD ,AB 的中点, ∴EF 是△ABD 的中位线, ∴EF ∥DB ,且EF =12DB ,∴△AEF ∽△ADB ,△AEG ∽△ADO , ∴AG AO =AE AD =EF DB =12. ∴G 为AO 的中点. ∴AG =GO . 又∵OA =OC , ∴AG ∶GC =1∶3.11.已知在▱ABCD 中,点E 在直线AD 上,AE =13AD ,连结CE 交BD 于点F ,则EF ∶CF 的值是23或43.【解】 当点E 在线段AD 上时,如解图①. ∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AD =BC , ∴△EFD ∽△CFB ,∴EF ∶CF =DE ∶B C. ∵AE =13AD ,∴DE =2AE =23AD =23BC , ∴DE ∶BC =2∶3, ∴EF ∶CF =2∶3.(第11题解)当点E 在线段DA 的延长线上时,如解图②. 同上可得△EFD ∽△CFB , ∴EF ∶CF =DE ∶B C. ∵AE =13AD ,∴DE =4AE =43AD =43BC ,∴DE ∶BC =4∶3,∴EF ∶CF =4∶3. 综上所述,EF ∶CF 的值是23或43.12.如图,在Rt △ABC 中,∠ACB =90°,AC =5 cm ,∠BAC =60°,动点M 从点B 出发,在BA 边上以2 cm/s 的速度向点A 匀速运动,同时动点N 从点C 出发,在CB 边上以 3 cm/s 的速度向点B 匀速运动,设运动时间为t (s)(0≤t ≤5),连结MN .(1)若BM =BN ,求t 的值.(2)若以M ,B ,N 为顶点的三角形与△ABC 相似,求t 的值. (3)当t 为何值时,四边形ACNM 的面积最小?并求出最小值.(第12题)【解】 (1)∵在Rt △ABC 中,∠ACB =90°,AC =5,∠BAC =60°,∴∠B =30°,∴AB =2AC =10,BC =5 3. 由题意,得BM =2t ,CN =3t , ∴BN =5 3-3t .当BM =BN 时,2t =5 3-3t ,解得t =10 3-15. (2)分两种情况:①当△MBN ∽△ABC 时,MB AB =BN BC ,即2t 10=5 3-3t 5 3,解得t =52. ②当△NBM ∽△ABC 时,NB AB =BM BC ,即5 3-3t 10=2t 5 3,解得t =157. 综上所述,当t =52或t =157时,△MBN 与△ABC 相似.(3)如解图,过点M 作MD ⊥BC 于点D ,则MD ∥AC ,∴△BMD ∽△BAC ,(第12题解)∴MD AC =BM BA ,即MD 5=2t 10,解得MD =t .设四边形ACNM 的面积为y ,则y =12×5×5 3-12(5 3-3t )×t =32t 2-5 32t +25 32=32⎝⎛⎭⎫t -522+75 38.∴当t =52时,y 取得最小值,为75 38,即当t =52时,四边形ACNM 的面积最小,为75 38 cm 2.13.如图,在△ABC中,∠C=90°,∠A=30°.在△A′B′C′中,∠C′=90°,A′C′=B′C′.能否分别将这两个三角形各自分割成两个三角形,使△ABC所分成的两个三角形与△A′B′C′所分成的两个三角形分别对应相似?若能,请设计一种分割方案;若不能,请说明理由.(第13题)【解】能分割,如解图所示(答案不唯一).(第13题解)初中数学试卷鼎尚图文**整理制作。
九年级数学上册4.4探索三角形相似的条件第1课时两角分别相等的判定方法课件(新版)北师大版

40° 80° ? 80° 60°
B
C
E
F
练习2 有一个锐角相等的两直角三 角 形是否为相似 三角形?
相似三角形的复习 相似三角形的判定定理1
B'
C'
用数学符号表示:
A A'
咦?是 这么表示 的?
B
Cห้องสมุดไป่ตู้
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
练习:
ΔABC和ΔDEF中, ∠A=40°, ∠B=80°,∠E=80°, ∠F=60°。 ΔABC与ΔDEF 相似 (“相似”或 “不相似”)。 D
A
动 动 手 啊
B
A
AB BC CA A' B' B' C' C' A'
∴ △ABC∽△A'B'C'
C'
相似三 角形的定义 可以作为三 角形相似的 一种判定方 法。
A'
B'
A
问题:
在△ABC 和△ A'B'C'中,
∠A=∠A',∠B= ∠B'
B A' C △ABC与△ A'B'C'是否相似?
判定定理1:如 果一个三角形的两 个角与另一个三角 形的两个角对应相 等,那么这两个三 角形相似。可以简 单说成: 两角对应 相等,两三角形相 似。
4.4
探索三角形相似的条件
第1课时 两角分别相等的判定方法
观察一下:这些图片有什么特点?
不错!这些图片都是相似的。 形状相同、大小不同!
4.4相似三角形的定义及判定(第1课时)同步练习(含答案)
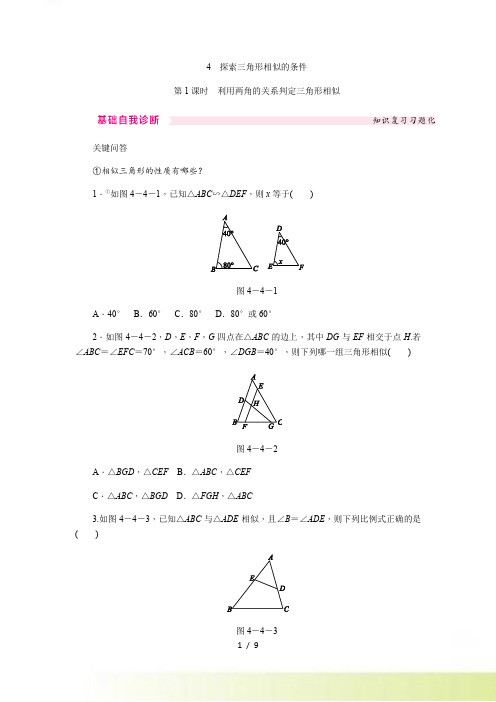
4探索三角形相似的条件第1课时利用两角的关系判定三角形相似关键问答①相似三角形的性质有哪些?1.①如图4-4-1,已知△ABC∽△DEF,则x等于()图4-4-1A.40°B.60°C.80°D.80°或60°2.如图4-4-2,D,E,F,G四点在△ABC的边上,其中DG与EF相交于点H.若∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=40°,则下列哪一组三角形相似()图4-4-2A.△BGD,△CEF B.△ABC,△CEFC.△ABC,△BGD D.△FGH,△ABC3.如图4-4-3,已知△ABC与△ADE相似,且∠B=∠ADE,则下列比例式正确的是()图4-4-3A.AD∶AC=DE∶BC B.AE∶BE=AD∶DCC.AE∶AB=AD∶AC D.AE∶AC=AD∶AB命题点1利用两角分别相等判定两三角形相似[热度:93%]4.②如图4-4-4,P为线段AB上一点,AD分别交BC,PC于点E,G,BC交PD于点F,∠CPD=∠A=∠B,则图中相似三角形有()图4-4-4A.1对B.2对C.3对D.4对方法点拨②根据相似三角形的定义可知:若△ABC∽△A′B′C′,△A′B′C′∽△A″B″C″,则△ABC∽△A″B″C″,即三角形相似具有传递性.5.③·株洲如图4-4-5所示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.(1)求证:△DAE≌△DCF;(2)求证:△ABG∽△CFG.图4-4-5解题突破③由正方形和等腰直角三角形我们可以得到哪些线段相等,哪些角相等?命题点2根据两三角形相似进行计算[热度:90%]6.④[·毕节]如图4-4-6,在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC =2 2,AB=3,则BD=________.图4-4-6方法点拨④在写相似表达式时要像写全等表达式那样,对应顶点的字母写在对应的位置上,这样也有利于正确写出边的比例式,保证结果正确.7.⑤将三角形纸片ABC按如图4-4-7所示的方式折叠,使点C落在AB边上的点D 处,折痕为EF.已知AB=AC=3,BC=4,若以点B,D,F为顶点的三角形与△ABC相似,则CF的长是________.图4-4-7易错警示⑤注意根据对应顶点分类讨论.8.⑥·六盘水如图4-4-8,在▱ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF=________.图4-4-8解题突破⑥作平行线构造“A”字形图的相似三角形.命题点3有关相似三角形的存在性问题[热度:80%]9.⑦如图4-4-9,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过点P作PF⊥AE于点F.(1)求证:△PF A∽△ABE.图4-4-9(2)当点P在射线AD上运动时,设P A=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由.易错警示⑦注意x的值可能不止一个.10.⑧如图4-4-10①,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,O是AC边上一点,连接BO交AD于点F,OE⊥OB交BC于点E.(1)求证:△ABF∽△COE;(2)当O 为AC 边的中点,AC AB =2时,如图②,求OFOE 的值;(3)当O 为AC 边的中点,AC AB =n 时,请直接写出OFOE的值.图4-4-10方法点拨⑧求线段的比时常借助相似三角形的性质,当比例式中的线段不能构成相似形时,可考虑利用等量代换的方法求解.详解详析【关键问答】①相似三角形的性质:对应角相等、对应边成比例.1.C[解析] ∵△ABC∽△DEF,∴∠B=∠E.∵∠B=80°,∴∠E=x=80°.故选C.2.B[解析] ∵∠ABC=∠EFC=70°,∴EF∥AB,∴△ABC∽△EFC,故B正确;在△BDG中,∠B=70°,∠DGB=40°,则∠GDB=70°;在△ABC中,∠B=70°,∠ACB=60°,则∠A=50°,∴△ABC,△CEF与△BGD不相似,故A,C错误;∵EF∥AB,∴△FGH∽△BGD;∵△BGD与△ABC不相似,∴△FGH与△ABC不相似,故D错误.故选B.3.D[解析] 由∠B=∠ADE可知△ABC∽△ADE,∴AE∶AC=AD∶AB.故选D.4.C[解析] 在△PCF和△BCP中,∵∠CPF=∠B,∠C为公共角,∴△PCF∽△BCP;在△APD和△PGD中,∵∠GPD=∠A,∠D为公共角,∴△APD∽△PGD;∵△APD∽△PGD,∴∠APD=∠PGD,∴∠BPF=∠AGP.又∵∠A=∠B,∴△AGP∽△BPF.共有3对相似三角形.故选C.5.证明:(1)由正方形ABCD及等腰直角三角形DEF,可知∠ADC=∠EDF=90°,AD =CD,DE=DF,∴∠ADE+∠ADF=∠ADF+∠CDF,∴∠ADE=∠CDF.在△DAE和△DCF中,DE=DF,∠ADE=∠CDF,AD=CD,∴△DAE≌△DCF.(2)延长BA交ED于点M,如图所示.∵△DAE≌△DCF,∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF.∵∠MAD=∠BCD=90°,∴∠EAM=∠BCF.∵∠EAM=∠BAG,∴∠BAG=∠BCF.又∵∠AGB=∠CGF,∴△ABG∽△CFG.6.83[解析] ∵∠BCD=∠A,∠ABC=∠CBD,∴△ABC∽△CBD,∴BCBD=ABBC,即2 2BD=32 2,∴3BD=8,∴BD=83.7.127或2[解析] 因为△ABC沿EF折叠后点C和点D重合,所以FD=CF.设CF=x,则BF=4-x,若以点B,D,F为顶点的三角形与△ABC相似,分两种情况:①若∠BFD=∠C,则FDBF=ACBC,即x4-x=34,解得x=127;①若∠BFD=∠A,则FDBF=ACAB,即x4-x=1,解得x=2.综上所述,CF的长为127或2.8.169[解析] 如图,过点O作OM∥AD交AB于点M.∵四边形ABCD是平行四边形,∴OB=OD,∴MO是△ABD的中位线,∴AM=BM=12AB=52,MO=12BC=4.∵AF∥OM,∴△AEF∽△MEO,∴AEME=AFMO,即22+52=AF4,∴AF=169.9.[解析] (1)在△PF A与△ABE中,易得∠P AF=∠AEB及∠PF A=∠ABE=90°,故可得△PF A∽△ABE;(2)分两种情况列出关系式.解:(1)证明:∵四边形ABCD 是正方形, ∴AD ∥BC ,∴∠P AF =∠AEB . 又∵∠PF A =∠ABE =90°, ∴△PF A ∽△ABE .(2)若△EFP ∽△ABE ,,如图① 则∠PEF =∠EAB ,∴PE ∥AB , ∴四边形ABEP 为矩形, ∴P A =BE =2,即x =2;若△PFE ∽△ABE ,如图②, 则∠PEF =∠AEB .∵∠P AF =∠AEB ,∴∠PEF =∠P AF , ∴PE =P A .∵PF ⊥AE ,∴F 为AE 的中点. ∵AE =AB 2+BE 2=2 5, ∴EF =12AE = 5.∵PE AE =EF EB ,即PE 2 5=52, ∴PE =P A =5,即x =5. ∴满足条件的x 的值为2或5.10.[解析] (1)要求证△ABF ∽△COE ,只要证明∠BAF =∠C ,∠ABF =∠COE 即可. (2)作OH ⊥AC ,交BC 于点H ,易证△OF A 和△OEH 相似,根据相似三角形的对应边的比相等,即可得出所求的值.(3)同(2)可得,OFOE=n .解:(1)证明:∵AD ⊥BC ,∴∠DAC +∠C =90°. ∵∠BAC =90°,∴∠BAD +∠DAC =90°, ∴∠BAD =∠C .∵OE ⊥OB ,∴∠BOA +∠COE =90°. 又∵∠BOA +∠ABF =90°, ∴∠ABF =∠COE . ∴△ABF ∽△COE .(2)如图,过点O 作AC 的垂线交BC 于点H ,则OH ∥AB .由(1)得∠ABF =∠COE ,∠BAF =∠C , ∴∠AFB =∠OEC , ∴∠AFO =∠HEO .又∵∠BAF =∠C ,∠BAF +∠F AO =∠C +∠EHO =90°, ∴∠F AO =∠EHO ,∴△OF A ∽△OEH ,∴OF OE =OAOH .又∵O 为AC 的中点,OH ∥AB , ∴OH 为△ABC 的中位线, ∴OH =12AB ,OA =OC =12AC .而AC AB =2,∴OA OH =2,∴OF OE=2. (3)OF OE=n .。
4.4 两个三角形相似的判定第1课时 两个三角形相似的判定(1)浙教版数学九年级上册课件

2.如图,点D,E,F分别在△ABC的各条边上,且 DE∥BC,DF∥AC. 请尽可能多地找出图中的相似三角 形,并说明理由. (3)△ADE∽△DBF. 理由如下: ∵DE∥BC, ∴∠ADE=∠DBF,∠EDF=∠DFB. 又∵DF∥AC, ∴∠EDF=∠AED.∴∠DFB=∠AED. ∴△ADE∽△DBF.
4.4 两个三角形相似的判定
第1课时 两个三角形相似的判定(1)
✓ 掌握判定三角形相似的预备定理,并了解它的证 明过程.
✓ 掌握利用两角判定三角形相似的定理,了解证明 过程,并会根据相似三角形的判定定理判定两个 三角形相似.
✓ 能利用三角形的相似解决简单的实际问题.
怎样运用三角形的相似测量河的宽度?
∠B=∠ B′. 求证:△ABC∽△A′B′C′.
证明:如图,在A′B′上截取A′D=AB,
作DE∥B′C′,交A′C′于点E,
则△A′DE∽△A′B′C′.
A′
又∵∠A=∠A′, ∠B=∠B′=∠A′DE,
A
D
E
∴△ABC≌△A′DE,
B
C B′
C′
∴△ABC∽△A′B′C′.
由两角对应相等判定三角形相似是所有判定方法中最常 用的方法之一,其关键是找准对应角,解题时应注意挖 掘公共角、对顶角、同角的余角(或补角)等相等关系. 常见的基本图形如下:
在解决这个问题之前,我们先思考: 判定两个三角形相似需要多少条件?
回顾判定两个三角形全等的条件,相应的,猜想判定两 个三角形相似有哪些条件? 两个三角形全等的条件:
AAS,ASA, SAS, SSS,
两角对应相等 两边对应成比例,且夹角相等 三边对应成比例
HL.
如图,在△ABC中,D,E分别是AB,AC上的点,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.4 两个三角形相似的判定
第1课时两个三角形相似的判定(一)
1.如图4-4-9,∠1=∠2=∠3,则以下结论不正确的是(C) A.△DEC∽△ABC B.△ADE∽△BEA
C.△ACE∽△BEA D.△ACE∽△BCA
图4-4-9
【解析】由∠1=∠2=∠3,∠C=∠C,根据有两组角对应相等的两个三角形相似,即可证得△DEC∽△ABC及△ACE∽△BCA,由∠2=∠3,可判定DE∥AB,继而可得∠DEA=∠BAE,又∠1=∠3,即可证得△ADE∽△BEA.
2. 如图4-4-10所示,已知DE∥BC,AD=5,DB=3,BC=10,∠B=50°,
则∠ADE=__50°__,DE=__6.25__.
图4-4-10
【解析】∵DE∥BC,∴∠ADE=∠B=50°.
∵AB=AD+DB=5+3=8,
又∵DE ∥BC ,
∴△ADE ∽△ABC ,
∴AD AB =DE BC ,即58=DE 10,
∴DE =6.25.
3.如图4-4-11所示,已知AB 是⊙O 的直径,弦CD ⊥AB ,垂足为H .
(1)求证:AH ·AB =AC 2;
(2)若过A 的直线与弦CD (不含端点)相交于点E ,与⊙O 相交于点F .求证:AE ·AF =AC 2.
图4-4-11 第3题答图
证明:(1)连结CB .∵AB 是⊙O 的直径,
∴∠ACB =90°.∵CD ⊥AB ,
∴∠AHC =∠ACB =90°.
又∵∠CAH =∠BAC ,
∴△CAH ∽△BAC ,
∴AH AC =AC AB ,
即AH ·AB =AC 2.
(2)连结BF .
∵AB 是⊙O 的直径,
∴∠AFB =90°.∴∠AHE =∠AFB =90°.
又∵∠HAE =∠F AB , ∴△AHE ∽△AFB , ∴AE AB =AH AF ,
即AE ·AF =AH ·AB . 又∵AH ·AB =AC 2, ∴AE ·AF =AC 2.。
