4.2 微积分基本定理 课件(北师大选修2-2)
合集下载
4.2.1 微积分基本定理 课件(北师大版选修2-2)

0 ������ ( ������������������������ ������ )������������ -������
=
0 -������
0 -������
������������������ ������������������-
������ ������ ������������ = ������ -1.
3
B.F(x)=x
1
3
C.F(x)=3 x +1
3 2
3
D.F(x)=3 x +c(c 为常数)
3
3
【解析】因为(x )'=3x ,所以 F(x)=x 不正确.
2
1 -1
������|������������等于( C ).
1
A. B. C. D.
-1 1 -1 0 -1 0
������ ������������ ������������������ ������������������ +
【解析】
������ ( 2������-1)������������=6,则 0
2
t=
������
2
3
.
������ ( 2������-1)������������ 0
= (������ -������) =t -t=6,解得
0
t=3(t=-2 舍去).
4
计算定积分:
1 3
1 2 ( ������ -1
微积分基本定理
导.学. 固. 思
1.直观了解并掌握微积分基本定理的含义.
2.会利用微积分基本定理求函数的积分.
导.学. 固. 思
1664年秋,牛顿开始研究微积分问题,他反复阅读笛卡儿《几何学》,对
推荐高中数学第四章定积分4.2微积分基本定理课件北师大版选修2_2

k=0(舍去).故 k=1.
答案:1
1 2 3 4 56
5.求下列定积分:
(1)
4 0
|2x-6|dx;
π
(2)
2
0
cos
4xdx.
分析利用微积分基本定理解决,其中计算定积分
������ ������
f (x)dx
的关键是
找到满足 F'(x)=f(x)的函数 F(x).
解(1)∵y=|2x-6|=
1 0
(������ + 2������)d������
=
1 2
������2
+
2������������
|10
=
1 2
+
2������,
则
a=
1 2
+
2������,
������
=
−
12.
所以 f(x)=x-1.
= π -π sin xdx+ π -π cos xdx
| | π
π
=(-cos x) + sin ������
-π
-π
=0+0=0.
答案:A
题型一 题型二 题型三
题型一 由微积分基本定理求定积分
【例 1】 计算下列定积分:
(1)
2 1
������
+
1 ������
dx;
(2)
3 1
(1+x+x2)dx.
������ ������
������(������)d������
=
������(������)
− ������(������). 定理中的式子称为牛顿
4.2 微积分基本定理 课件(北师大版选修2-2)

复习回顾
* 定积分: f ( x )dx A
a b
* 定积分的性质: 性质1 性质2
性质3 性质4
1dx b a kf ( x )dx k f ( x)dx f ( x) g ( x)dx f ( x)dx g ( x)dx b c b a f ( x)dx a f ( x)dx c f ( x)dx
0
cos xdx 的值就是区间 [0, ]
其中 x 轴上方的面积为正值,x 轴下方面积为负值。 y
o
x
y cosx
返回
分析: 被积函数是由两个函数的和构成的,由定积分
的性质可知,和的定积分等于定积分的和:
f ( x) g ( x)dx
b a
b
ห้องสมุดไป่ตู้
a
f ( x )dx g ( x )dx
a b
b a b a
b
b
b
a
a
a
引入
通过学习发现,虽然被积函数 y x 2 很简单,但 直接用定积分定义计算 对于定积分
1
2
1
么有没有更加简便、有效的方法求定积分呢?
0 1 dx ,直接用定义计算几乎不可能。那 x
x dx 的值却比较麻烦,而
2
前面我们学习了微积分学中的最基本、最重要的
概念:导数和定积分,那么二者之间有没有内在的联
a
b
解:
2
1
2
(e x 3 x )dx
x 2 x 2 1
3 22 e dx 3 xdx e x 1 1 1 2 3 9 2 2 ( e e) (4 1) e e 2 2
* 定积分: f ( x )dx A
a b
* 定积分的性质: 性质1 性质2
性质3 性质4
1dx b a kf ( x )dx k f ( x)dx f ( x) g ( x)dx f ( x)dx g ( x)dx b c b a f ( x)dx a f ( x)dx c f ( x)dx
0
cos xdx 的值就是区间 [0, ]
其中 x 轴上方的面积为正值,x 轴下方面积为负值。 y
o
x
y cosx
返回
分析: 被积函数是由两个函数的和构成的,由定积分
的性质可知,和的定积分等于定积分的和:
f ( x) g ( x)dx
b a
b
ห้องสมุดไป่ตู้
a
f ( x )dx g ( x )dx
a b
b a b a
b
b
b
a
a
a
引入
通过学习发现,虽然被积函数 y x 2 很简单,但 直接用定积分定义计算 对于定积分
1
2
1
么有没有更加简便、有效的方法求定积分呢?
0 1 dx ,直接用定义计算几乎不可能。那 x
x dx 的值却比较麻烦,而
2
前面我们学习了微积分学中的最基本、最重要的
概念:导数和定积分,那么二者之间有没有内在的联
a
b
解:
2
1
2
(e x 3 x )dx
x 2 x 2 1
3 22 e dx 3 xdx e x 1 1 1 2 3 9 2 2 ( e e) (4 1) e e 2 2
4.2 微积分基本定理 课件(北师大选修2-2)63571
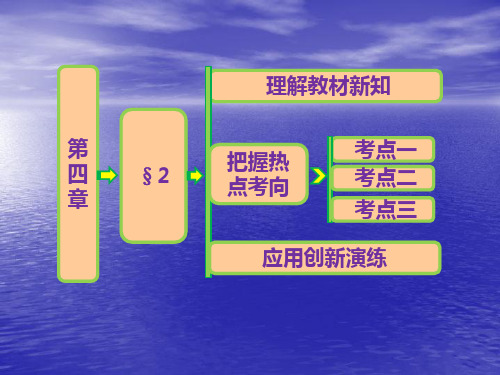
[精解详析] (1)∵(x2+3x)′=2x+3, ∴∫10(2x+3)dx=(x2+3x)| 01=1+3=4. (2)∵(sin x+ex)′=cos x+ex, ∴∫0-π(cos x+ex)dx =(sin x+ex)| -0 π=1-e-π. (3)∵x2+1x′=2x-x12, ∴∫312x-x12dx=x2+1x| 31=7+13=232.
1dx+
=(-cos x)
2
+x
2
+12x2-x|42
0
2
=1+2-π2+(4-0)=7-π2.
[一点通] (1)分段函数在区间[a,b]上的定积分 可分成n段定积分和的形式,分段的标准可按照函数的 分段标准进行.
(2)带绝对值号的解析式,可先化为分段函数,然 后求解.
[例 3] 已知函数 f(x)=∫x0(at2+bt+1)dt 为奇函数,且 f(1)-f(-1)=13,试求 a,b 的值.
[精解详析] f(x)=∫x0(at2+bt+1)dt =a3t3+b2t2+t |x0=a3x3+b2x2+x. ∵f(x)为奇函数,∴b2=0,即 b=0. 又∵f(1)-f(-1)=13,∴a3+1+a3+1=13.∴a=-52.
3.求下列定积分:
(1)
2 0
sin2x2dx;(2)23(2-x2)·(3-x)dx.
解:(1)sin2x2=1-c2os x,
而12x-12sin x′=12-12cos x,
∴2 0
sin2x2dx=
2 0
12-12cos
xdx
=12x-12sin
∫abf(x)dx=F(x)| ba= F(b)-F(a) .
优课系列高中数学北师大版选修22 4.2微积分基本定理 课件(共17张)

• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
(三)活学活用: 利用微积分基本定理解决前面的问题
21
1
dx x
1 x 3 dx 0
找出f(x)的原 函数是关健
解(1)∵
( l n x ) = 1 x
定积分的几何意义:
b f(x) dx
在几何上表示由yf
(x)、xa、xb
与
a
x 轴所围成的曲边图形面积的代数和(即x轴上
方的面积减去x轴下方的面积).
牛顿
• 牛顿,是英国伟大的数学家、物理学家、天文学家 和自然哲学家。1642年12月25日生于英格兰林肯郡格 兰瑟姆附近的沃尔索普村,1727年3月20日在伦敦病逝。
• 牛顿在科学上最卓越的贡献是微积分和经典力学的 创建。
莱布尼茨
• 莱布尼茨,德国数学家、哲学家,和牛顿同为微积分的创始人; 1646年7月1日生于莱比锡,1716年11月14日卒于德国的汉诺威。
• 他父亲是莱比锡大学伦理学教授,家庭丰富的藏书引起他广 泛的兴趣。1661年入莱比锡大学学习法律,又曾到耶拿大学学习 几何,1666年在纽伦堡阿尔特多夫取得法学博士学位。他当时写 的论文《论组合的技巧》已含有数理逻辑的早期思想,后来的工 作使他成为数理逻辑的创始人。
• 牛顿1661年入英国剑桥大学三一学院,1665年获文 学士学位。随后两年在家乡躲避瘟疫。这两年里,他制 定了一生大多数重要科学创造的蓝图。1667年回剑桥后 当选为三一学院院委,次年获硕士学位。1669年任卢卡 斯教授直到1701年。1696年任皇家造币厂监督,并移 居伦敦。1703年任英国皇家学会会长。1706年受女王 安娜封爵。他晚年潜心于自然哲学与神学。
•
(三)活学活用: 利用微积分基本定理解决前面的问题
21
1
dx x
1 x 3 dx 0
找出f(x)的原 函数是关健
解(1)∵
( l n x ) = 1 x
定积分的几何意义:
b f(x) dx
在几何上表示由yf
(x)、xa、xb
与
a
x 轴所围成的曲边图形面积的代数和(即x轴上
方的面积减去x轴下方的面积).
牛顿
• 牛顿,是英国伟大的数学家、物理学家、天文学家 和自然哲学家。1642年12月25日生于英格兰林肯郡格 兰瑟姆附近的沃尔索普村,1727年3月20日在伦敦病逝。
• 牛顿在科学上最卓越的贡献是微积分和经典力学的 创建。
莱布尼茨
• 莱布尼茨,德国数学家、哲学家,和牛顿同为微积分的创始人; 1646年7月1日生于莱比锡,1716年11月14日卒于德国的汉诺威。
• 他父亲是莱比锡大学伦理学教授,家庭丰富的藏书引起他广 泛的兴趣。1661年入莱比锡大学学习法律,又曾到耶拿大学学习 几何,1666年在纽伦堡阿尔特多夫取得法学博士学位。他当时写 的论文《论组合的技巧》已含有数理逻辑的早期思想,后来的工 作使他成为数理逻辑的创始人。
• 牛顿1661年入英国剑桥大学三一学院,1665年获文 学士学位。随后两年在家乡躲避瘟疫。这两年里,他制 定了一生大多数重要科学创造的蓝图。1667年回剑桥后 当选为三一学院院委,次年获硕士学位。1669年任卢卡 斯教授直到1701年。1696年任皇家造币厂监督,并移 居伦敦。1703年任英国皇家学会会长。1706年受女王 安娜封爵。他晚年潜心于自然哲学与神学。
4.2 微积分基本定理课件 北师大版选修2-2课件

1
0
1
1 1 3 = [ x+3x]dx+ [(2-x)+3x]dx
1 0
1
2 3 1 2 1 1 2 1 2 3 2 =(3x +6x )|0+(2x-2x +6x )|1 2 1 1 2 3 =3+6+(2x-3x )|1 5 1 1 13 =6+6-3× 9-2+3= 6 .
a b a (3)① f ( x )d x = F ( a ) - F ( a ) = 0 ;② f ( x )d x =- f(x)dx;
a a b
a ③若 f(x)在[-a,a]上连续,则当 f(x)是偶函数时, a 2 f(x)dx;当 f(x)是奇函数时, a-a f(x)dx=0.
第四章 §2
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-2
[ 分析 ]
从图形可以看出,所求图形的面积可以转化为
一个梯形与一个曲边梯形面积的差,进而可以用定积分求出
面积.为了确定出被积函数和积分的上、下限,我们需要求
出两条曲线的交点的横坐标.
第四章 §2
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-2
1 求由曲线y= x,y=2-x,y=-3x围成的图形面积.
[分析]
本题考查定积分在几何中的应用,可以先画出
草图,求得其交点后,确定出积分的上限及下限,从而转化 为定积分问题求解.
第四章 §2
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-2
[解析] 图形如图所示,
y= x, 由 y=2-x
y= x, 与 1 y=-3x y=2-x, 及 得交点分别为(1,1),(0,0),(3,-1). 1 y=-3x,
0
1
1 1 3 = [ x+3x]dx+ [(2-x)+3x]dx
1 0
1
2 3 1 2 1 1 2 1 2 3 2 =(3x +6x )|0+(2x-2x +6x )|1 2 1 1 2 3 =3+6+(2x-3x )|1 5 1 1 13 =6+6-3× 9-2+3= 6 .
a b a (3)① f ( x )d x = F ( a ) - F ( a ) = 0 ;② f ( x )d x =- f(x)dx;
a a b
a ③若 f(x)在[-a,a]上连续,则当 f(x)是偶函数时, a 2 f(x)dx;当 f(x)是奇函数时, a-a f(x)dx=0.
第四章 §2
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-2
[ 分析 ]
从图形可以看出,所求图形的面积可以转化为
一个梯形与一个曲边梯形面积的差,进而可以用定积分求出
面积.为了确定出被积函数和积分的上、下限,我们需要求
出两条曲线的交点的横坐标.
第四章 §2
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-2
1 求由曲线y= x,y=2-x,y=-3x围成的图形面积.
[分析]
本题考查定积分在几何中的应用,可以先画出
草图,求得其交点后,确定出积分的上限及下限,从而转化 为定积分问题求解.
第四章 §2
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-2
[解析] 图形如图所示,
y= x, 由 y=2-x
y= x, 与 1 y=-3x y=2-x, 及 得交点分别为(1,1),(0,0),(3,-1). 1 y=-3x,
高中数学北师大版选修2-2 4.2微积分基本定理 课件(17张)

x)
0
2
②
1 1 x2 dx 0
4
③设
f
(
x)
x 1
2, x 0,(1为自然对数的底数),
x , x 1,e
则
e f xdx 0
1
f (x)dx
e
f (x)dx
x2
1 ln | x |
e
4
0
1
30
13
13
2、①求曲线 y x2与 y x所围成图形的面积,
其中正确的是( B)
b
f
(
2
x) dx
.
a
若非匀速运动物体的速度为v(t),则此物体从t=a到t=b时刻所
走过的路程S=
b v(t)dt. a
7
题型一、定积分的计算
例1、①
( 1(ex 2x)dx 0
A、1 B、e-1
) C、e
解:
D、e+1
1(ex 2x)dx 0
(ex x2 ) |10
(e1 12 ) (e0 02 )
定积分与微积分基本定理
1
高考要求
• (1)了解定积分的实际背景,了解定积分 的基本思想,了解定积分的概念;
• (2)了解微积分基本定理的含义。
2
常见题型预览
题一:下列积分值等于1的是( )C
A.
1
0
题二:曲线
1
xdBx. 0 (x 1)Cdx.
y 与1直线
x
x
011dDx.
11
0 2 dx
1, x及 4 轴x所围成的区域
(4, 2)
y x 2
由草图知所求面积
y=x-2
【数学】4.2 微积分基本定理 课件(北师大版选修2-2)

第四章 定积分 §2 微积分基本定理
复习回顾
定积分的概念:
b
a
f ( x )dx lim f i △xi
n i 1
b
n
定义求定积分:
分割→近似代替→求和→取极限(得定积分 f ( x )dx )
即①分割: n 等分区间 a , b ;
ba f ( i ) ; ③求和: n i 1
ba Si t s (ti 1 ) v(ti 1 ) n
'
由定积分的定义得
S v(t )dt s(b) s(a)
a b
牛顿—莱布尼茨公式
定理 (微积分基本定理)
如果f(x)是区间[a,b]上的连续函数,
并且F’(x)=f(x),则
b a
或 f ( x )dx F ( x ) |b F (b) F (a ) a
2 2 ( 2 x |1 2(ln x) |1 2 1) (ln2 ln1) 1 2 ln 2
公式1: 公式二:
b
a
1 b dx = lnx|a x
例3 计算下列定积分
(1)
2 0
cos xdx
(2)
2 0
sin xdx
(3) 2
0
cos 2 xdx
' 解(1) sin x) cos x (
ba S s1 s2 si sn Si v(t ) n i 1 i 1
n n
b b ba S lim Si lim v(t ) v(t )dt s ' (t )dt s(b) s(a) a a n n n i 1 i 1 n n
复习回顾
定积分的概念:
b
a
f ( x )dx lim f i △xi
n i 1
b
n
定义求定积分:
分割→近似代替→求和→取极限(得定积分 f ( x )dx )
即①分割: n 等分区间 a , b ;
ba f ( i ) ; ③求和: n i 1
ba Si t s (ti 1 ) v(ti 1 ) n
'
由定积分的定义得
S v(t )dt s(b) s(a)
a b
牛顿—莱布尼茨公式
定理 (微积分基本定理)
如果f(x)是区间[a,b]上的连续函数,
并且F’(x)=f(x),则
b a
或 f ( x )dx F ( x ) |b F (b) F (a ) a
2 2 ( 2 x |1 2(ln x) |1 2 1) (ln2 ln1) 1 2 ln 2
公式1: 公式二:
b
a
1 b dx = lnx|a x
例3 计算下列定积分
(1)
2 0
cos xdx
(2)
2 0
sin xdx
(3) 2
0
cos 2 xdx
' 解(1) sin x) cos x (
ba S s1 s2 si sn Si v(t ) n i 1 i 1
n n
b b ba S lim Si lim v(t ) v(t )dt s ' (t )dt s(b) s(a) a a n n n i 1 i 1 n n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
π ∴f2 =1.
答案:1
8.已知 f(x)是一次函数,其图像过点(3,4),且 f(x)dx=1,
0
1
求 f(x)的解析式.
解:设 f(x)=ax+b(a≠0), 则 4=3a+b, 又 f(x)dx=
0
1 1
1 a 2 ax +bx |1= +b=1, (ax+b)dx= 2 0 2 0
b ∵f(x)为奇函数,∴ =0,即 b=0. 2 1 a a 1 5 又∵f(1)-f(-1)= ,∴ +1+ +1= .∴a=- . 3 3 3 3 2
[一点通] (1)当被积函数中含有参数时,必须分清参数和自变 量,再进行计算,以免求错原函数.另外,需注意积分
下限不大于积分上限.
(2)当积分的上(下)限含变量x时,定积分为x的函数, 可以通过定积分构造新的函数,进而可研究这一函数的 性质,解题过程中注意体会转化思想的应用.
x
x
1 22 1 1 2 2 = x |1+ln x |1= ×2 - ×12+ln 2-ln 1 2 2 2 3 = +ln 2. 2
3.求下列定积分: (1) sin dx;(2) (2-x2)· (3-x)dx. 2 1-cos x 2x 解:(1)sin = , 2 2
1 1 x- sin 而2 2 1 1 ′= - cos x 2 2
x
x
3
3
[一点通]
应用微积分基本定理求定积分时,首先
要求出被积函数的一个原函数,在求原函数时,通常先
估计原函数的类型,然后求导数进行验证,在验证过程 中要特别注意符号和系数的调整,直到原函数F(x)的导 函数F′(x)=f(x)为止(一般情况下忽略常数),然后再利用 微积分基本定理求出结果.
问题3:求F(2)-F(1)的值.
1 1 3 2 2 提示:F(2)-F(1)= ×2 - ×1 = . 2 2 2
问题4:你得出什么结论?
提示: f(x)dx=F(2)-F(1),且 F′(x)=f(x).
问题 5:由 f(x)dx 与 F(2)-F(1)之间的关系,你认为导
1
2
2 1
(2)∵(sin x+ex)′=cos x+ex, ∴∫0 π(cos x+ex)dx -
0 =(sin x+ex)| -π=1-e-π.
1 1 2 x + ′=2x- 2, (3)∵ x x
1 1 1 22 ∫32x- 2dx=x2+ | 3=7+ = . ∴ 1 1
2 =∫2x2dx+∫22xdx+∫13dx 1 1
x3 2 25 2 2 2 = |1+x |1+3x |1= . 3 3
(2)∫π(sin x-cos x)dx 0 =∫πsin xdx-∫πcos xdx 0 0
π =(-cos x) |π-sin x |0 =2. 0
1 21 ∫2x+ dx=∫2xdx+∫1 dx (3) 1 1
理解教材新知
第 四 章
§2
把握热 点考向
考点一 考点二 考点三
应用创新演练
1 2 已知函数f(x)=x,F(x)= x . 2 问题1:f(x) 和F(x)有何关系?
提示:F′(x)=f(x).
问题2:利用定积分的几何意义求 xdx的值. 3 2 ∫1xdx= . 提示: 2
2 1
2 0
2 0
2x
3 2
x,
xdx
∴
2 0
sin dx= 2
2x
1 1 - cos 2 2
1 1 x- sin =2 2
x
2 0
π 1 π-2 = - = . 4 2 4
(2)原式= (6-2x-3x2+x3)dx
1 4 3 2 3 =6x-x -x +4x |2 1 1 2 3 4 2 3 4 =6×3-3 -3 +4×3 -6×2-2 -2 +4×2
[2,4]三段积分求和.
[精解详析]
图像如图.
4 0 4
f(x)dx=
2 0
sin xdx+
2 2
1dx+
2
(x-1)dx
2 0
=(-cos x)
+x
2 2
1 4 2 +2x -x|2
π π 2- +(4-0)=7- . =1+ 2 2
4
2
2
0 |-2=8+2=10.
答案:10
5.已知
sin x-1,x≤0, F(x)= 2 x ,x>0,
求定积分∫1 1F(x)dx. -
0 解:∫1 1F(x)dx=∫-1(sin x-1)dx+∫1x2dx - 0
=(-cos
0 x-x) |-1+
1 31 x |0 3
6.若∫1(k-2x)dx=2 012,则 k=________. 0
1 1 解析:∫0(k-2x)dx=(kx-x2) 0=k-1=2 012,
∴k=2 013.
答案: 2 013
π ∫asin xdx,则 f( )=________. 7.已知函数 f(a)= 0 2
a 解析:f(a)=∫asin xdx=-cos x |0=-cos a+1, 0
1 1. xdx=________.
e 1
1 解析: xdx=ln e-ln 1=1.
e 1
答案: 1
2.求下列函数的定积分: (1)∫2(x2+2x+3)dx; 1 (2)∫π(sin x-cos x)dx; 0 1 ∫2x+ dx. (3) 1
x
解:(1)∫2(x2+2x+3)dx 1
数与定积分之间有什么联系?
提示: f(x)dx=F(b)-F(a), 其中 F′(x)=f(x).
b a
微积分基本定理 如果连续函数f(x)是函数F(x)的导函数,即f(x)=F′(x), 则有
∫bfxdx= F(b)-F(a) a
定理中的式子称为 牛顿—莱布尼茨公式 ,通常称
F(x)是f(x)的一个 原函数 .
[一点通]
(1)分段函数在区间[a,b]上的定积分
可分成n段定积分和的形式,分段的标准可按照函数的
分段标准进行.
(2)带绝对值号的解析式,可先化为分段函数,然 Байду номын сангаас求解.
4 4.∫-2|x|dx=________.
1 2 1 24 4 0 解析:∫-2|x|dx=∫0xdx+∫-2(-x)dx= x |0+- x
在计算定积分时,常常用记号F(x) | F(a),于是牛顿—莱布尼茨公式也可写作
b ∫af(x)dx=F(x)| b= F(b)-F(a) . a b a
来表示F(b)-
微积分基本定理揭示了导数与定积分之间的关系, 即求定积分与求导互为逆运算,求定积分时只需找到导
函数的一个原函数,就可以代入公式求出定积分.
3 2
7 =- . 4
[例 2]
π sin x,0≤x≤2 , 已知函数 f(x)= π 1,2<x<2, x-1,2≤x≤4,
先画
出函数图像,再求这个函数在[0,4]上的定积分.
[思路点拨] 按
π π f(x)的分段标准,分成0,2 ,2,2,
6 2 所以 a= ,b= , 5 5 6 2 即 f(x)= x+ . 5 5
求定积分的一些常用技巧:
(1)对被积函数,要先化简,再求积分. (2)求被积函数是分段函数的定积分,依据定积分的 性质,分段积分再求和. (3)对于含有绝对值符号的被积函数,要去掉绝对值 符号后才能积分.
5 =cos 1- . 3
[例 3]
已知函数 f(x)=∫x(at2+bt+1)dt 为奇函数, 且 0
1 f(1)-f(-1)= ,试求 a,b 的值. 3
[精解详析]
f(x)=∫x(at2+bt+1)dt 0
a b2 x a 3 b 2 3 =3t +2t +t |0= x + x +x. 3 2
[例1]
计算下列各定积分:
(1)∫1(2x+3)dx; 0 (2)∫0 π(cos x+ex)dx; - 1 ∫3(2x- 2)dx. (3) 1 x
[思路点拨]
先求被积函数的原函数,然后利用微积
分基本定理求解.
[精解详析]
(1)∵(x2+3x)′=2x+3,
1 ∴∫1(2x+3)dx=(x2+3x)| 0=1+3=4. 0
