缓和曲线计算程序
缓和曲线)计算公式
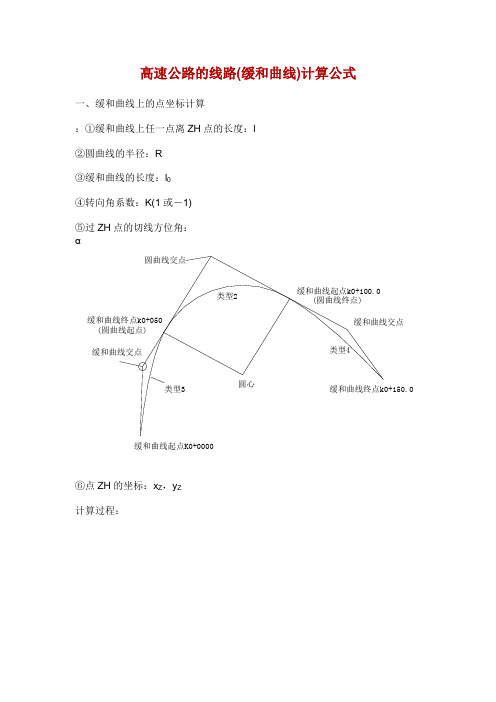
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,那么:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,那么:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度〔或缓曲上任意点到缓曲起点的长度〕l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算:①第一坡度:i1(上坡为“+〞,下坡为“-〞)②第二坡度:i2(上坡为“+〞,下坡为“-〞)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点〔过渡段终点〕的间隔:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-〞,右转为“+〞)⑦曲线终点处曲率:P1(左转为“-〞,右转为“+〞)求:①线路匝道上点的坐标:x,y ②待求点的切线方位角:αT计算过程:。
缓和曲线的计算方法三种课件

b0
20
ls 3R
此外还有极坐标法、弦线支距法、长弦偏角 法。
缓和曲线的计算方法三种
要注意:点是位于缓和曲线上,还是位于圆曲线上。
位于缓和曲线
位于圆曲线
缓和曲线的计算方法三种
(1)当点位于缓和曲线上,有:
x y
l l5
40
R
2
l
2 s
l3 l7 6 Rl s 336 R
3l
3 s
(2)当点位于圆曲线上,有:
xRsinq yR(1c os)p
缓和曲线的计算方法三种
2、偏角法(整桩距、短弦偏角法) 要注意:点是位于缓和曲线,还是位于圆曲线。
位于圆曲线 位于缓和曲线
缓和曲线的计算方法三种
2、偏角法(整桩距、短弦偏角法)
(1)当点位于缓和曲线上,有:
总偏(常 角量 )0 6lR s
偏角
l2 ls2
0
距离:用曲线长l来代替弦长。放样出第1点后, 放样第2点时,用偏角和距离l交会得到。
缓和曲线的计算方法三种
(2)当点位于圆曲线上
方法:架仪HY (或YH),后视ZH(或HZ),拨角b0,即找 到了切线方向,再按单圆曲线偏角法进行。
缓和曲线的计算方法三种
(2)测设方法。(见例题)
例题:如图,设某公路的交点桩号为K0+518.66,右 转角αy=180018'36",圆曲线半径R=100m,缓和曲 线长ls=10m,试测设主点桩。(作为实习课内容)
解:(一)计算测设元素
p=0.04m;q=5.00m;
02lR s 1800205153
缓和曲线的计算方法三种
2、回旋缓和曲线(spiral curve)基本公式
缓和曲线计算公式

一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
铁路缓和曲线坐标计算方法
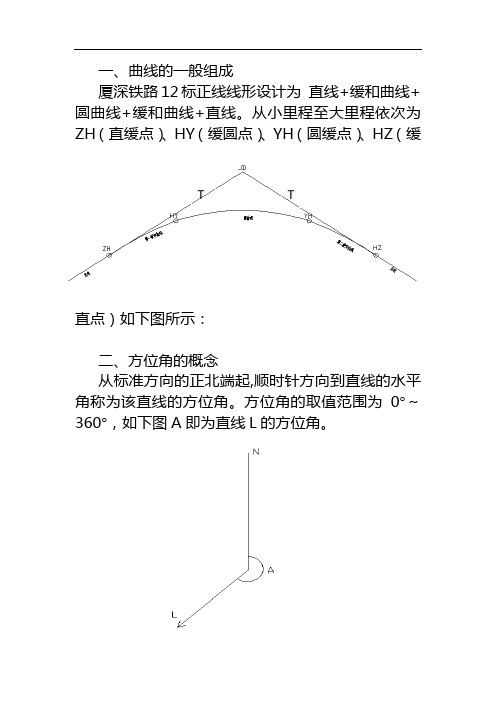
一、曲线的一般组成厦深铁路12标正线线形设计为 直线+缓和曲线+圆曲线+缓和曲线+直线。
从小里程至大里程依次为ZH (直缓点)、HY (缓圆点)、YH (圆缓点)、HZ (缓直点)如下图所示:二、方位角的概念从标准方向的正北端起,顺时针方向到直线的水平角称为该直线的方位角。
方位角的取值范围为0°~360°,如下图A 即为直线L 的方位角。
TT三、某点坐标的计算已知A 点坐标为(491548,2505452),B 点距离A 点L=125m ,直线AB 的方位角为235°,计算B 点坐标。
计算方法:Y=491548+125×SIN235=491445.606X=2505452+125×COS235=2505380.303四、曲线上任一点的坐标及切线方位角计算1 直线段上任一点的坐标及方位角直线上的坐标计算比较简单,只需要求出该点所在直线的方位角以及线路中的里程即可求得例1,求DK495+520处左中线的坐标及方位角由设计院所给的曲线要素表可知该点位于JD57 JD58的直线上,查曲线要素表JD57,JD58的坐标分别为(488809.902,2504127.029),(485660.627,2504491.226)。
通过坐标反算直线JD57 JD58TT的方位角:A=atg((485660.627-488809.902)/( 2504491.226-25 04127.029))=276.59665°注意:A的取值可根据下述条件确定ΔY>0,ΔX>0,第一象限0-90°ΔY>0,ΔX<0,第二象限90°-180°ΔY<0,ΔX<0,第三象限180°-270°ΔY<0,ΔX>0,第四象限270°-360°查曲线表,JD58切线长T= 690.303m,JD58坐标(Y58,X58)=(485660.627,2504491.226),ZH点里程为DK496+093.885。
缓和曲线计算

缓和曲线计算方法如下:
1.确定两个直线或两条曲线的交点。
2.确定圆曲线的半径。
圆曲线的半径应该足够大,使车辆或列车
可以在转弯时平稳地行驶,同时也不能太大,以免影响道路或
铁路的设计。
3.确定过渡曲线的长度。
过渡曲线是圆曲线和直线之间的曲线,
用于将两者之间的变化平滑地连接起来。
过渡曲线的长度应该
足够长,以确保车辆或列车可以逐渐进入或离开圆曲线,从而
减少冲击和颠簸。
4.根据圆曲线和过渡曲线的参数,计算出缓和曲线的形状和尺寸。
需要注意的是,计算缓和曲线需要考虑多种因素,包括车辆或列车的速度、载重、惯性等因素,以及道路或铁路的设计标准和要求。
因此,在进行缓和曲线计算时,需要综合考虑各种因素,以确保计算结果的准确性和可行性。
圆曲线、缓和曲线计算方法

● 圆曲线方法一:sin (1cos )180i i i i i i x R y R l R ϕϕϕπ⎧⎪=⎪=-⎨⎪︒⎪=⋅⎩——i l 为待定点i P 至起点间的弧长i ϕ为i l 所对的圆心角R 为曲线半径方法二:11802l A R π︒=⋅⋅ 2sin l R A =⋅00cos(/)sin(/)x x l A y y l A =+⋅+-⎧⎨=+⋅+-⎩起点方位角左减右加起点方位角左减右加——00(,)x y 为圆曲线起点坐标方法三:180l A R π︒=⋅ 00cos(/)sin(/)x x R B A y y R B A =+⋅+-⎧⎨=+⋅+-⎩——l 为圆曲线上任意一点距起点距离00(,)x y 为圆曲线圆心坐标B 为圆心到圆曲线起点的方位角,A 为任意点对应的圆心角● 缓和曲线522030406l x l R l ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩——l 为曲线上任一点至起点的曲线长R 曲线半径0l 为缓和曲线全长圆曲线、缓和曲线计算方法1、直线段:先由JD1以及JD2的坐标算出JD1到JD2的方位角,即直线段方位角A ,故可算出HZ 、ZH 坐标及其直线段各点坐标。
2、缓和曲线:以HZ 、ZH 为起点,缓和曲线上任意一点离HZ 、ZH 距离为l ,利用公式522003040()6l x l R l l R ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩为缓和曲线全长,为圆曲线半径算出该点的相对起点坐标,利用arctan y x算出该点相对起点的方位角B ,再根据线路走向及直线段方位角可算出该点的方位角C (顺时针加,逆时针减),用可求出该点相对起点的距离D ,最后用00cos sin x x D C y y D C =+⎧⎨=+⎩可求出该点的坐标。
(00(,)x y 为缓和曲线起点的坐标)3、圆曲线:用上述方法求出圆曲线两端点HY 、YH 坐标,算出HY 到YH 的方位角F ,以及两点间的距离E ,用12arccos ER可算出两端点连线与起点到圆心连线的夹角G ,根据线路走向求出起点到圆心的方位角H (H=F+/-G ),00(,)x y 圆曲线为起点坐标,根据00cos sin x x R H y y R H=+⎧⎨=+⎩,求出圆心坐标。
公路缓和曲线原理及缓和曲线计算公式

一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
发布日期:2012-01-31 作者:李秋生浏览次数:1494)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
圆曲线、缓和曲线、竖曲线、非完整缓和曲线计算程序

圆曲线、缓和曲线、竖曲线、非完整缓和曲线计算培训1、圆曲线计算程序:“X0”?P 曲线起点X坐标“Y0”?Q 曲线起点Y坐标“X1”?X 曲线交点X坐标“Y1”?Y 曲线交点Y坐标“QDLC”?Z 曲线起点桩号“R”?R 曲线半径“L1R2”?O 曲线前进方向:左为1、右为2Lbl 0“1N-X,2X-N”?S 1为大转小、2为小转大Pol(P-X,Q-Y):ClsJ+180→K 曲线切线方位角计算If S=1:Then Goto 1:Else Goto 2:IfEndLbl 1“N”?U:“E”?V 测量的大坐标(U-P)cos(K)+(V-Q)sin(K)+Z→Z[1]:(V-Q)cos(K)-(U-P)sin(K)→Z[2] If O=1:Then -R→D:Else R→D:IfEndtan-1((Z[1]-Z)/Abs(D-Z[2]))→Z[3]Abs(D)sin(Z[3])+Z →Z[4]:Abs(D)(1-cos(Z[3])) →Z[5]If O=1:Then –Z[5]→Z[5]:Else Z[5]→Z[5]:IfEndPol(Z[4]-Z,Z[5]-D):ClsJ+180 →Z[6]Z+Z[3](Abs(D)π)/180→Z[7](Z[1]-Z[4])cos(Z[6])+(Z[2]-Z[5])sin(Z[6]) →Z[8]If O=1:Then –Z[8]→Z[8]:Else Z[8]→Z[8]:IfEnd“X=”:Z[7]◢计算后的X小坐标“Y=”:Z[8]◢计算后的X小坐标Goto 0Lbl 2“X”?U:“Y”?V 测量的小坐标180(U-Z)/(Rπ)→Z[1]:Rsin(Z[1])+Z→Z[2]:R(1-cos(Z[1]))→Z[3]If O=1:Then –Z[3]→Z[3]:–V→C:–R→D:Else Z[3]→Z[3]:V→C:R→D:IfEnd Pol(Z[2]-Z,Z[3]-D):ClsJ+180→Z[4]Z[2]+Ccos(Z[4])→Z[5]:Z[3]+Csin(Z[4])→Z[6]P+(Z[5]-Z)cos(K)-Z[6]sin(K)→Z[7]Q+(Z[5]-Z)sin(K)+Z[6]coc(K)→Z[8]“N=”:Z[7] ◢计算后的X大坐标“E=”:Z[8]◢计算后的Y大坐标Goto 02、缓和曲线计算程序:“X0”?P 曲线起点X坐标“Y0”?Q 曲线起点Y坐标“X1”?X 曲线交点X坐标“Y1”?Y 曲线交点Y坐标“ZHZH”?Z 曲线起点桩号“R”?R 圆曲线段半径“L”?L 缓和曲线单边曲线长度“L1R2”?O 曲线前进方向左为1右为2Lbl 0“LCZH”?F 测量里程Abs(F-Z)→BIf B<L:Then Goto 1:Else Goto 4:IfEnd 缓和段及圆曲线段计算转换Lbl 1180B2/(2RLπ)→A:RL/B→E:B-B5/(40R2L2)+B9/(3456R4L4)- B13/(599040R6L6)+ B17/(175472640R8L8)- B21/(7.80337152*1010R10L10)→C (红色的为计算小半径增加精度)B3/(6RL)-B7/(336R3L3)+B11/(42240R5L5)- B15/(9676800R7L7)+ B19/(3535596640R9L9)- B23/(1.8802409472*1012R11L11)→D:C-Esin(A) →G(红色的为计算小半径增加精度)If O=1:Then Goto 2:Else Goto3:IfEndLbl 2-D→D:D-Ecos(A) →HGoto 7D→D:D+Ecos(A) →HGoto 7Lbl 4180(B-L/2)/(Rπ)→A:L/2-L3/(240R2)→E:L2/(24R)-L4/(2688R3)→M E+Rsin(A) →C:C-Rsin(A) →GIf O=1:Then Goto 5:Else Goto 6:IfEndLbl 5-(M+R(1-cos(A)) →D:D-Rcos(A) →HGoto 7Lbl 6M+R(1-cos(A)) →D:D+Rcos(A) →HGoto 7Lbl 7Pol(P-X,Q-Y):ClsJ+180→KP+Ccos(K)-Dsin(K) →Z[2]:Q+Csin(K)+Dcos(K) →Z[3]P+Gcos(K)-Hsin(K) →Z[4]:Q+Gsin(K)+Hcos(K) →Z[5]Pol(Z[2]-Z[4],Z[3]-Z[5]):ClsJ+180→Z[1]“U”?U:“V”?V 测量所得大地坐标(U-Z[2])cos(Z[1])+(V-Z[3])sin(Z[1]) →Z[6](V-Z[3])cos(Z[1])-(U-Z[2])sin(Z[1]) →Z[7]If F>Z:Then Goto 9:Else Goto A:IfEndLbl 9If O=1:Then Z[7]→Z[7]:-Z[6]→Z[6]:Else –Z[7]→Z[7]:Z[6]→Z[6] IfEndGoto BLbl AIf O=1:Then –Z[7] →Z[7]:Z[6] →Z[6]:Else Z[7] →Z[7]:-Z[6] →Z[6] IfEndGoto BLbl B“X=”:Z[7] ◢计算后轴线X坐标“Y=”:Z[6] ◢计算后轴线X坐标“0→Goto 0,1→BZZB”?S 0为还回计算过程、1为进行轴线坐标计算大坐标If S=0:Then Goto 0Else Goto 8:IfEndLbl 8“X”?T:“Y”?WIf F>Z:Then Goto C:Else Goto D:IfEndLbl CIf O=1:Then T→Z[8]:-W→Z[11]:Else -T→Z[8]:W→Z[11]:IfEndGoto ELbl DIf O=1:Then -T→Z[8]:W→Z[11]:Else T→Z[8]:-W→Z[11]:IfEndGoto ELbl EZ[2]+Z[11]cos(Z[1])-Z[8]sin(Z[1]) →Z[9]Z[3]+Z[11]sin(Z[1])+Z[8]cos(Z[1]) →Z[10]“N=”:Z[9] ◢计算后X大坐标“E=”:Z[10] ◢计算后Y大坐标Goto 03、竖曲线计算程序:“ZH1”?A 交点1桩号“H1”?B 交点1高程“ZH2”?C 交点2桩号“H2”?D 交点2高程“ZH3”?E 交点3桩号“H3”?F 交点3高程“R”?R 曲线半径(D-B)/(C-A) →Z[1]:(F-D)/( E-C) →Z[2]:Z[2]-Z[1] →W:Abs(RW/2)→T Lbl 0“ZHC”?G:“HC”?H 测量桩号及高程If G≤(C-T):Then Goto 1:Else Goto 2:IfEndLbl 1H-(G-A) Z[1]-B →Z[3]“H+-”:Z[3] ◢计算值+为向下、-为向上Goto 0Lbl 2If G≥(C+T):Then Goto 3:Else Goto 4:IfEnd Lbl 3H-(G-C) Z[2]-D→Z[3]“H+-”:Z[3] ◢计算值+为向下、-为向上Goto 0Lbl 4(G-(C-T))2/(2R) →Z[4](G-A) Z[1]+B →Z[5]If W>0:Then Goto 5:Else Goto 6:IfEndLbl 5H-(Z[5]+Z[4]) →Z[3]“H+-”:Z[3] ◢计算值+为向下、-为向上Goto 0Lbl 6H-(Z[5]-Z[4]) →Z[3]“H+-”:Z[3] ◢计算值+为向下、-为向上Goto 0非完整缓和曲线计算起点和交点方向大坐标Lbl 0“X1”?A 非完整缓和曲线起点X坐标“Y1”?B 非完整缓和曲线起点Y坐标“X2”?C 非完整缓和曲线终点X坐标“Y2”?D 非完整缓和曲线终点Y坐标“A”?E 缓和曲线A值“R”?F 缓和曲线半径“L1”?G 图纸标注缓和曲线长度“L1R2”?R 方向左1右2E2÷F→H 缓和曲线完整计算长度H-G→K 缓和曲线打断长度K-K5÷(40×E4)+K9÷(3456×E8) -K13÷(599040×E12)+K17÷(175472640×E16)-K21÷(78033715200×E20) →LK3÷(6×E2)-K7÷(336×E6)+K11÷(42240×E10)-K15÷(9676800×E14)+K19÷(3530096640×E18)-K23÷(1880240947200×E22) →MH-H5÷(40×E4)+H9÷(3456×E8) -H13÷(599040×E12)+H17÷(175472640×E16)-H21÷(78033715200×E20) →NH3÷(6×E2)-H7÷(336×E6)+H11÷(42240×E10)-H15÷(9676800×E14)+H19÷(3530096640×E18)-H23÷(1880240947200×E22) →OTan-1((O-M)÷(N-L))→PPol(A-C,B-D)J+180→QIf R=1Then Q+P→SElse Q-P→SIfEndAbs(Lcos(S)-Msin(S)-A) →TAbs(Lsin(S)-Mcos(S)-B) →UT+100cos(S) →VU+100sin(S) →W“A0”:T◢完整缓和曲线原点X坐标计算值“B0”:U◢完整缓和曲线原点Y坐标计算值“A1”:V◢完整缓和曲线交点方向X坐标计算值“B1”:W◢完整缓和曲线交点方向Y坐标计算值Goto 0。
