非轴对称移动载荷下有限长圆柱厚壳的动力响应

合集下载

有限元分析基础知识

2000，4
ANSYS单元分类
1. 杆单元，包括二维杆单元和三维杆单元，线性调节元，主要包括： LINK1，LINK8，LINK10，LINK11，LINK180等。 2. 弹簧阻尼单元，包括COMBIN系列： COMBIN7,COMBIN14,COMBIN37,COMBIN40等。 3. 质量元，MASS21。
ANSYS/Structural求解功能
ANSYS/Structural求解功能
Static -- 结构静力问题（包括线性和非线性问题） Modal -- 模态振动特性计算分析（结构固有频率和振型） Harmonic -- 谐波分析 Transient -- 瞬态分析 Spectrum -- 谱分析 Eigen Buckling -- 特征值屈曲分析（线性） Substructural -- 子结构分析。。。。。。
2000，4
有限元分析步骤（续）
• 集合所有单元的平衡方程，集合依据的是所有相邻单元在公共节点处的位移相等；建立总体的有限元方程组。 • 引入边界条件 • 求解有限元方程组，得到未知节点位移 • 计算单元应力，对不同的单元，对应力的处理还有不同的方法
2000，4
ANSYS文件结构
二进制文件 Jobname.db （数据库文件） Jobname.dbb （备份文件） Jobname.rst （结构分析结果文件） Jobname.rth （热分析结果文件） Jobname.rmg （电磁场分析结果文件） Jobname.rfl （流体分析结果文件） Jobname.tri （三角化刚度矩阵文件） Jobname.emat （单元矩阵文件） Jobname.esav （单元保存文件）
2000，4
简例（续）

【国家自然科学基金】_圆柱分布函数_基金支持热词逐年推荐_【万方软件创新助手】_20140801

2009年序号 1 2 3 4 5 6 7 8 9 10
科研热词距离多普勒贝塞尔函数目标识别电磁热弹耦合旋转效应拉普拉斯变换广义热弹性理论圆柱体双向反射分布函数光散射
推荐指数 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
2011年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2011年科研热词边界元法灵敏度有限元法声辐射功率优化非淹没赫兹接触盾构机相对比磁导淹没植物标量磁位有限元明渠流速分布径向充磁圆筒永磁直线同步电机回转支承刚度分离变量法倾覆弯矩推荐指数 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
科研热词饱和土预旋调节轴对称轴向压缩试验空间导叶离心泵流体力学正交各向异性横观各向同性格子boltzmann方法柱面载荷应变率应力分布 navier-stokes方程 green函数 biot波动方程
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年序号 1 2 3 4 5
2014年科研热词轴对称圆柱精化理论横观各向同性压电热弹性材料 bessel函数推荐指数 1 1 1 1 1
ቤተ መጻሕፍቲ ባይዱ
2013年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

非对称循环载荷下Q235钢力学响应特性分析

第42卷第4期2021年4月哈㊀尔㊀滨㊀工㊀程㊀大㊀学㊀学㊀报Journal of Harbin Engineering UniversityVol.42ɴ.4Apr.2021非对称循环载荷下Q235钢力学响应特性分析张庆玲1,2,金淼1,2,李群1,2,郭宝峰1,2(1.燕山大学先进锻压成形技术与科学教育部重点实验室,河北秦皇岛066004;2.燕山大学机械工程学院,河北秦皇岛066004)摘㊀要:为了准确判断Q235钢在非对称应力循环载荷作用下产生的棘轮效应㊁包申格效应及循环软/硬化特性对材料性能的影响,本文进行了多种非对称应力条件下的循环加载试验㊂采用数据分析的方法,研究了Q235钢力学变形行为与加载工况之间的关系㊂试验表明:Q235钢棘轮应变和棘轮应变率的正负与平均应力符号相同;平均应力为负值时,表现为循环硬化特性,压缩屈服应力大于拉伸屈服应力;平均应力为正值时,表现为循环软化特性,拉伸屈服应力大于压缩屈服应力;在平均应力符号相同条件下,第1周的屈服应力也基本相同㊂研究结果为结构设计和建立精确的循环本构模型提供了理论依据㊂关键词:非对称循环载荷;包申格效应;循环软硬化;棘轮效应;屈服应力;Q235钢;平均应力;应力幅值DOI :10.11990/jheu.201905041网络出版地址:http :// /kcms /detail /23.1390.u.20210302.1345.014.html 中图分类号:TB31㊀文献标志码:A㊀文章编号:1006-7043(2021)04-0581-07Analysis of the mechanical response characteristics of Q 235steel under asymmetrical cyclic loadingZHANG Qingling 1,2,JIN Miao 1,2,LI Qun 1,2,GUO Baofeng 1,2(1.Key Laboratory of Advanced Forging &Stamping Technology and Science (Yanshan University),Ministry of Education of China,Qinhuangdao 066004,China;2.School of Mechanical Engineering,Yanshan University,Qinhuangdao 066004,China)Abstract :To accurately determine the effects of the ratcheting effect,Bauschinger effect,and cyclic softening and hardening characteristics of Q235steel on the material properties under asymmetric cyclic stress loading,we con-duct various cyclic loading tests under asymmetric stress conditions.The relationships between the mechanical de-formation behaviors of Q235steel and loading conditions are discussed by means of data analysis.The test shows that the positive and negative signs of ratcheting strain and ratcheting strain rate of Q235steel are the same as those of the mean stress.When the mean stress is negative,it shows a cyclic hardening characteristic,and the compres-sive yield stress is greater than the tensile yield stress.When the mean stress is positive,it shows a cyclic softening characteristic,and the tensile yield stress is greater than the compression yield stress.Under the condition of the same mean stress sign,the yield stress of the first cycle is basically the same.Results provide theoretical data for the structural design and the establishment of an accurate cyclic constitutive model.Keywords :asymmetric cyclic loading;Bauschinger effect;cyclic softening and hardening;ratcheting;yield stress;Q235steel;mean stress;stress amplitude收稿日期:2019-05-13.网络出版日期:2021-03-02.基金项目:国家自然科学基金项目(52075474);河北省自然科学基金项目(E2019203560);河北省高校创新团队领军人才培育计划(LJRC012).作者简介:张庆玲,女,高级实验师,博士研究生;金淼,男,教授,博士生导师.通信作者:金淼,E-mail:jmiao@.㊀㊀工程中的承载结构在工作中常由于载荷或几何形状不连续而产生应力集中,甚至会在局部出现塑性变形㊂此时,对于受循环载荷作用的结构件则可能出现棘轮效应㊁包申格效应㊁循环软/硬化等变形行为,从而影响结构性能㊂因此,深入了解材料在循环载荷作用下的力学相应特性对于结构设计及安全评定具有十分重要的意义㊂棘轮应变会随着循环次数的增加而增加,会严重恶化部件的性能[1]㊂棘轮应变的累积取决于载荷中平均应力和应力幅值的组合[2-3]㊂在恒平均应力时,无论应力速率如何变化,随应力幅值的增加,棘轮寿命都会下降,棘轮应变累积率增加[4-6]㊂这些研究使人们对金属材料棘轮效应的基本特性有了较为深入的了解㊂哈㊀尔㊀滨㊀工㊀程㊀大㊀学㊀学㊀报第42卷包申格效应是指金属材料在经历了一定量的单向拉伸或压缩塑性变形之后再反向加载,其屈服应力会低于连续正向变形的屈服应力,这是造成金属材料力学方向性的重要原因之一[7-9]㊂盛光敏等[10]通过对AZ31进行拉压和压拉循环试验,得出其包申格效应比反包申格效应明显;文献[11-12]分析了不同应变历史㊁预应变量㊁应变速率和循环周次对铝合金7A04和高强钢10CrNi5MoV 包申格效应的影响;文献[13-14]对Q345㊁Q460和Q235进行循环加载试验,指出3种钢材均存在包申格效应㊂当外加循环载荷使得材料进入塑性变形后,反复变形会令金属的塑性流动特性发生变化,造成材料抵抗变形的能力增强或减弱,这种现象称为循环硬化或循环软化㊂文献[15]探讨了不同加载条件下不锈钢316L 的循环软硬化行为;文献[16-18]指出低碳钢S355循环硬/化行为随塑性应变范围的增大而增大,循环软化行为随塑性应变范围的减小而减小;文献[19-21]研究发现Q235钢在不同应变幅值和平均应变组合下表现为循环硬化,循环硬化指数随平均应变水平的增加而增大㊂学者们对不同材料在不同条件下的循环变形特性进行了深入探讨,但对于焊接结构件最为常用的Q235钢在非对称应力控制下产生棘轮效应㊁包申格效应及循环软硬化特性的系统研究却鲜见报道㊂本文以Q235钢为研究对象,进行了多种条件下的循环加载试验,运用数据分析的方法,并结合唯象理论,对试验结果进行系统分析,深入研究了此材料的力学响应特性㊂1㊀应力循环加载试验方案试验所用原材料为20mm 厚Q235钢板,测得其弹性模量为210GPa,上㊁下屈服极限分别为310MPa 和243MPa㊂沿轧制方向取样,按照GB /T 3075-2008‘金属材料疲劳试验轴向力控制方法“加工成圆形截面循环加载试样,其平行段直径9mm,平行段长度27mm,过渡圆弧半径25mm㊂在精度为0.2kN 的Instron8801型电液伺服疲劳试验机上进行循环加载试验,并通过精度为0.1μm,标距为25mm 的接触式引伸计采集轴向应变㊂试验加载波形如图1所示,加载应力率为40MPa /s,循环周次为30周,具体试验方案如表1所示㊂图1㊀应力循环加载曲线Fig.1㊀Single stage stress cyclic loading curves表1㊀应力循环试验加载工况Table 1㊀Loading conditions of stress cycle test试样编号平均应力/MPa应力幅值/MPaFYL-01-20300FYL-02-20320FYL-03-20340FYL-04-40300FYL-05-60300ZYL-0920300ZYL-1020320ZYL-1120340ZYL-1240300ZYL-13603002㊀棘轮效应分析本文材料在非对称应力循环载荷作用下产生的棘轮应变εr 为:εr =(εT max +εT min )/2(1)式中εT max ㊁εTmin 分别表示某一个循环周次的最大真应变和最小真应变㊂如无特殊说明,本文所涉及应变均为真应变㊂由于Q235钢存在屈服平台,使得第1周的应变值较大,棘轮应变的计算均从第2周开始㊂将相邻2个循环周次内棘轮应变的变化量定义为棘轮应变率Δεr ,其反映了循环加载过程中棘轮应变累积的快慢程度㊂应力幅值为300MPa,平均应力分别为-20MPa 和20MPa 时,循环加载过程中Q235钢的应力应变曲线如图2所示㊂可以看出,正㊁负平均应力时均产生了棘轮效应㊂当平均应力为负值时,随循环周次的增加,滞回曲线向负应变方向移动;当平均应力为正值时,滞回曲线则向正应变方向移动㊂应力幅值为300MPa,不同平均应力条件下棘轮应变随循环周次的变化如图3所示㊂由图可知,平均应力为正值时棘轮应变为正值,平均应力为负值时棘轮应变为负值,棘轮应变的绝对值均随循环周次增加而增大㊂不同正负平均应力条件下棘轮应变的变化趋势不同,且棘轮应变率也不相同,但棘轮应变率均在第20周后趋于稳定㊂平均应力为正值时,棘轮应变率为正值,平均应力越大,棘轮应变率越高;平均应力为负值时,棘轮应变率为负值,平均应力绝对值越大,棘轮应变率也越高㊂应力幅值为300MPa 时,棘轮应变率稳定值㊃285㊃第4期张庆玲,等:非对称循环载荷下Q235钢力学响应特性分析与平均应力之间的关系曲线如图4所示,两者之间呈指数函数关系㊂图2㊀循环应力应变曲线Fig.2㊀Cyclic stress-straincurve图3㊀应力幅值为300MPa 时的棘轮应变Fig.3㊀Ratcheting strain at stress amplitude 300MPa图4㊀应力幅值为300MPa 时不同平均应力下的棘轮应变率Fig.4㊀Ratcheting strain rate under different mean stressat stress amplitude 300MPa㊀㊀图5所示为不同应力幅值下Q235钢的棘轮应变曲线㊂无论平均应力为正值还是负值,棘轮应变及棘轮应变速率均随应力幅值的增加而增大㊂由上述分析可知,Q235钢在循环过程中产生的棘轮应变与平均应力㊁应力幅值和循环周次有关,根据唯象理论得出棘轮应变的预测模型:εr =10-4λησm σᶄs0-σs0exp(η)N +εᶄη,σm >010-4λσm(σᶄs0-σs0)ηexp(η)N -εᶄη,σm <0ìîíïïïïïï(2)式中:λ为材料参数,可通过试验数据获取,此处取λ=3.5;N 为循环周次;σm 为平均应力;σa 为应力幅值;σᶄs0㊁σs0分别为单向拉伸时的上㊁下屈服极限;η=σa /σs ;εᶄ为循环加载试验时应力峰值在单向拉伸试验曲线中所对应的应变值㊂图5㊀不同应力幅值条件下的棘轮应变Fig.5㊀Ratcheting strain at different stress amplitude如图6所示,将计算得到的棘轮应变与试验数据进行对比,两者吻合良好,说明该公式可以在非对称应力控制的循环加载试验中,较好的表征Q235钢的棘轮效应㊂图6㊀棘轮应变试验值与拟合值比较Fig.6㊀Comparison of test and fitting data of ratchetingstress㊃385㊃哈㊀尔㊀滨㊀工㊀程㊀大㊀学㊀学㊀报第42卷3㊀包申格效应分析包申格效应在金属材料构件中一般扮演着负面的角色,会影响到材料的抗疲劳性能,造成工件不能满足正常的服役条件㊂试验发现,Q235钢在循环加载过程中产生了明显的包申格效应㊂为使计算结果更有可比性,在循环第1周取屈服平台的值作为屈服应力,其他不产生屈服平台且无明显屈服点的循环周次,取相应周次发生0.2%相对塑性变形时对应的应力值,即取该周应力应变曲线起始部分的斜率,然后偏移0.2%应变量对应得到的应力值㊂图7给出了应力幅值为300MPa,不同平均应力条件下的屈服应力随循环周次的变化曲线㊂图中显示,当平均应力为负值时,压缩屈服应力大于拉伸屈服应力,平均应力绝对值越大,拉伸屈服应力越小,压缩屈服应力越大;而当平均应力为正值时,拉伸屈服应力大于压缩屈服应力,平均应力越大,拉伸屈服应力越大,压缩屈服应力越小㊂且随循环周次的增加无论平均应力为正值还是负值,拉伸和压缩方向的屈服应力均呈现下降趋势㊂图7㊀不同平均应力条件下屈服应力随循环周次变化曲线Fig.7㊀Changing curves of yield stress with cycle numbers at different mean stresses㊀㊀图8为相同平均应力不同幅值条件下各循环周次的屈服应力㊂结合图7的结论,可以得出,在应力载荷控制下,在拉伸和压缩2个方向哪个方向载荷大,对应方向的屈服应力相对较高㊂平均应力一定时,随应力幅值的增大,拉伸屈服应力和压缩屈服应力均略有增大,在循环到第30周时相邻载荷条件下的屈服应力相对变化量不超过2%㊂对比图7和图8,可以看出,平均应力和应力幅值分别增大所得到的屈服应力变化规律并不一致,相同峰值条件下,平均应力比应力幅值对屈服应力的影响更为明显㊂这是因为,平均应力为负值时,平均应力增大,应力峰值减小,应力谷值绝对值增大;平均应力为正值时,平均应力增大,应力峰值增大,应力谷值绝对值减小;而应力幅值增大,正负平均应力下的应力峰值和应力谷值的绝对值均增大㊂图8㊀不同应力幅值下的屈服应力变化曲线Fig.8㊀Changing curve of yield stress at different stress amplitude and same mean stresses㊀㊀从上述对屈服应力的数据分析可以得出,屈服应力是关于循环周次㊁平均应力和应力幅值的函数㊂当外加载荷大于上屈服极限时,屈服应力σs 随循环周次的演化规律为:σs =σi ,N =1(μ+λi )σi ηMiN,N >1{(3)式中:i =1,2分别代表拉伸和压缩;σi 为第1周屈服应力值,平均应力为正值时,拉伸屈服应力为289MPa,㊃485㊃第4期张庆玲,等:非对称循环载荷下Q235钢力学响应特性分析压缩屈服应力为189MPa;平均应力为负值时,拉伸屈服应力为191MPa,压缩屈服应力为320MPa;λi 为材料参数,通过试验获取,平均应力为正值时,λ1取0.78,λ2取1.10;平均应力为负值时,λ1取0.87,λ2取1.15;μ=σmσᶄs0;M i 为指数指标,M 1=10σm ησP,M 2=10σmσP,σp 为应力峰值㊂将计算得到的屈服应力与试验值进行比较,如图9所示㊂不同正负平均应力条件下,两者在初始几个循环周次相差较多,最大相对误差为5%,但在10周之后最大相对误差仅为2%,说明拟合效果良好㊂图9㊀屈服应力试验值与拟合值比较Fig.9㊀Comparison of test data and fitting data about yield stress㊀㊀包申格系数B 与循环载荷作用下预拉伸/压缩变形后屈服应力的变化直接相关,可对包申格效应进行定量表征和描述,其表达式为:B =σ-0.2-σ+0.2σ-0.2,σm <0σ+0.2-σ-0.2σ+0.2,σm >0ìîíïïïïïï(4)式中:σ+0.2㊁σ-0.2分别为材料的拉伸和压缩屈服应力㊂屈服应力下降越大,包申格系数越高,包申格效应越明显㊂Q235钢在幅值为300MPa,不同平均应力下包申格系数的变化如图10所示㊂图10㊀应力幅值为300MPa 时包申格系数随循环周次的变化Fig.10㊀The variation of Bauschinger coefficient with cyclenumbers at stress amplitude 300MPa可以看出,不同应力状态第1周时的包申格系㊀㊀数基本相同,约为0.346,说明Q235在经历一定的预拉伸/压缩变形后再反向压缩/拉伸时均表现出明显的包申格效应㊂从第2周开始,包申格系数随平均应力的变化表现出较大差异,但相同应力条件下则变化很小㊂因此,可以用第2周的包申格系数来描述材料的包申格效应㊂平均应力绝对值越大,包申格效应越显著㊂平均应力绝对值相同时,Q235钢在正平均应力条件下表现出的包申格效应更明显㊂4㊀循环软/硬化特性分析Q235钢在不同应力组合条件下表现出不同的循环软/硬化行为㊂不同平均应力和应力幅值条件下的响应应变幅值随着循环周次的变化曲线如图11所示㊂可以看出,当平均应力为负值时,表现出轻微的硬化特性;当平均应力为正值时,则表现出明显的软化特性,但2种工况下,应力幅值越大应变幅值越大,而平均应力绝对值越大应变幅值却越小㊂随循环周次的增加,Q235钢循环软/硬化速率在第20周之后趋于稳定㊂将不同应力条件下的循环软/硬化速率稳定值列于表2,负值表示循环硬化,正值表示循环软化㊂比较发现,负平均应力时,循环硬化速率随平均应力绝对值的增大逐渐减小,即硬化程度减弱;正平均应力时,循环软化速率随平均应力的增大呈增长趋势,即软化程度增强;应力幅值增大使循环软硬化速率均增加,软硬化程度更显著㊂㊃585㊃哈㊀尔㊀滨㊀工㊀程㊀大㊀学㊀学㊀报第42卷图11㊀不同条件下的应变幅值变化曲线Fig.11㊀Changing curve of strain amplitude at different conditions表2㊀不同条件下的循环软/硬化速率Table 2㊀Cyclic softening /hardening rate at different condi-tions应力/MPa幅值均值速率/10-6300-60-1.46010.4-40-3.2408.5-20-3.420 6.0320-20-4.420 6.3340-20-14.32010.95㊀结论1)在非对称应力循环载荷作用下,负平均应力产生负棘轮应变,正平均应力产生正棘轮应变㊂2)外加载荷平均应力相同,应力幅值增大,或外加载荷应力幅值相同,平均应力绝对值增大,均会造成棘轮应变绝对值增大,棘轮应变率升高㊂3)在非对称应力循环载荷作用下,Q235钢表现出明显的包申格效应㊂当平均应力为负值时,压缩屈服应力大于拉伸屈服应力;当平均应力为正值时,拉伸屈服应力大于压缩屈服应力㊂在循环的第1周屈服应力值基本相同,可以用第2周的包申格系数来表征材料的包申格效应㊂4)当外加载荷平均应力为负值时,Q235钢表现出循环硬化特性,平均应力绝对值越小或应力幅值越大,循环硬化现象越明显;当外加载荷平均应力为正值时,Q235钢表现出循环软化特性,平均应力或应力幅值越大,循环软化现象越明显㊂参考文献:[1]陈旭,焦荣,田涛.棘轮效应预测及其循环本构模型研究进展[J].力学进展,2003,33(4):461-470.CHEN Xu,JIAO Rong,TIAN Tao.Research advances of ratcheting effects and cyclic constitutive models [J].Ad-vances in mechanics,2003,33(4):461-470.[2]LIN Y C,LIU Zhenghua,CHEN Xiaomin,et al.Uniaxialratcheting and fatigue failure behaviors of hot-rolled AZ31B magnesium alloy under asymmetrical cyclic stress-controlled loadings[J].Materials science and engineering:A,2013,573:234-244.[3]赵路远,黄俊,陈涛,等.7075铝合金的单轴棘轮行为[J].机械工程材料,2018,42(9):21-25.ZHAO Luyuan,HUANG Jun,CHEN Tao,et al.Uniaxial ratcheting behavior of 7075aluminum alloy[J].Materials for mechanical engineering,2018,42(9):21-25.[4]PAUL S K,SIVAPRASAD S,DHAR S,et al.Key issuesin cyclic plastic deformation:experimentation[J].Mechan-ics of materials,2011,43(11):705-720.[5]PAUL S K,SIVAPRASAD S,DHAR S,et al.Cyclic plas-tic deformation behavior in SA333Gr.6C-Mn steel [J].Materials science and engineering:A,2011,528(24):7341-7349.[6]PAUL S K,SIVAPRASAD S,DHAR S,et al.Cyclic plas-tic deformation and damage in 304LN stainless steel [J].Materials science and engineering:A,2011,528(15):4873-4882.[7]XIANG Yang,VLASSAK J J.Bauschinger effect in thin metalfilms[J].Scripta materialia,2005,53(2):177-182.[8]CHAWLA N,JESTER B,VONK D T.Bauschinger effectin porous sintered steels[J].Materials science and engi-neering:A,2003,346(1/2):266-272.[9]张功庭,盛光敏,黄利.金属包申格效应的表征㊁影响因素与机理研究进展[J].材料导报,2008,22(S3):135-138.[10]盛光敏,张功庭,阎春.AZ31镁合金包辛格效应研究[J].稀有金属材料与工程,2011,40(4):615-619.SHENG Guangmin,ZHANG Gongting,YAN Chu.Re-search of bauschinger effect of AZ31magnesium alloy[J].Rare metal materials and engineering,2011,40(4):615-619.[11]BAIRSTOW L.The elastic limits of iron and steel undercyclical variations of stress[J].Proceedings of the royal society A:mathematical,physical and engineering sci-㊃685㊃第4期张庆玲,等:非对称循环载荷下Q235钢力学响应特性分析ences,1909,82(557):483-485.[12]LIN Y C,LIU Zhenghua,CHEN Xiaomin,et al.Uniaxialratcheting and fatigue failure behaviors of hot-rolled AZ31B magnesium alloy under asymmetrical cyclic stress-controlled loadings[J].Materials science and engineer-ing:A,2013,573:234-244.[13]DUTTA K,SIVAPRASAD S,TARAFDER S,et al.In-fluence of Asymmetric cyclic loading on substructure for-mation and ratcheting fatigue behaviour of AISI304LN stainless steel[J].Materials science and engineering:A, 2010,527(29/30):7571-7579.[14]DUTTA K,RAY K K.Ratcheting strain in interstitial freesteel[J].Materials science and engineering:A,2013, 575:127-135.[15]XIE Xuefang,JIANG Wenchun,CHEN Jingkai,et al.Cyclic hardening/softening behavior of316L stainless steel at elevated temperature including strain-rate and strain-range dependence:experimental and damage-coupled con-stitutive modeling[J].International journal of plasticity, 2019,114:196-214.[16]WANG Chen,FAN Jiansheng,XU Liyan,et al.Cyclichardening and softening behavior of the low yield point steel:implementation and validation[J].Engineeringstructures,2020,210:110220.[17]GUO Yibin,HO H C,CHUNG K F,et al.Cyclic de-formation characteristics of S355and S690steels under different loading protocols[J].Engineering structures, 2020,221:111093.[18]KROLO P,GRANDIC'D,SMOLC㊅IC'Ž.Experimental andnumerical study of mild steel behaviour under cyclic load-ing with variable strain ranges[J].Advances in materials science and engineering,2016,2016:7863010. [19]GUO Yi,LUO Yunrong,WANG Qingyuan.Mean straineffect on the cyclic stress-strain behavior of steel structure materials Q235[J].Advanced materials research,2012, 602-604:430-434.[20]WANG J G,JIA Weiping,JU Dongying.Cyclic deforma-tion behavior and fatigue crack propagation of low carbon steel prestrained in tension[J].Advances in materials sci-ence and engineering,2009,2009:657284. [21]高柳.不同拉压循环下Q235钢单轴拉伸力学性质研究[D].南宁:广西大学,2016:32-50.GAO Liu.Effect of fatigue damage on the dynamic tensile behavior of Q235abstract[D].Nanning:Guangxi Univer-sity,2016:32-50.本文引用格式:张庆玲,金淼,李群,等.非对称循环载荷下Q235钢力学响应特性分析[J].哈尔滨工程大学学报,2021,42(4):581-587. ZHANG Qingling,JIN Miao,LI Qun,et al.Analysis of the mechanical response characteristics of Q235steel under asymmetrical cyclic loading[J].Jour-nal of Harbin Engineering University,2021,42(4):581-587.㊃785㊃。

壳体中的轴对称模态和非轴对称模态

壳体中的轴对称模态和非轴对称模态董奇１郑津洋２胡八一１１．中国工程物理研究院流体物理研究所　绵阳６２１９００２．浙江大学化工机械研究所　杭州３１００２７摘要　壳体在承受各种载荷情况下，呼吸模态之外的其他模态也可能被激发出来。

因此，准确理解圆柱形壳体和球形壳体的振动模态至关重要。

本文研究了圆柱壳和球壳中的轴对称模态和非轴对称模态，为分析容器在各种载荷条件下的响应提供了研究基础。

关键词　柱壳；球壳　；　轴对称模态；非轴对称模态Ａｘｉｓｙｍｍｅｔｒｉｃ　ａｎｄ　ｎｏｎａｘｉｓｙｍｍｅｔｒｉｃ　ｖｉｂｒａｔｉｏｎ　ｍｏｄｅｓ　ｉｎ　ｓｈｅｌｌｓＤｏｎｇ　Ｑｉ１Ｚｈｅｎｇ　Ｊｉｎｙａｎｇ２Ｈｕ　Ｂａｌｉ１　１．　Ｉｎｓｔｉｔｕｔｅ　ｏｆ　Ｆｌｕｉｄ　Ｐｈｙｓｉｃｓ，　Ｃｈｉｎａ　Ａｃａｄｅｍｙ　ｏｆ　Ｅｎｇｉｎｅｅｒｉｎｇ　ＰｈｙｓｉｃｓＭｉａｎｙａｎｇ６２１９００Ｐ．Ｒ．　Ｃｈｉｎａ２．　Ｉｎｓｔｉｔｕｔｅ　ｏｆ　Ｐｒｏｃｅｓｓ　Ｅｑｕｉｐｍｅｎｔ，　Ｚｈｅｊｉａｎｇ　ＵｎｉｖｅｒｓｉｔｙＨａｎｇｚｈｏｕ　３１００２７Ｐ．　Ｒ．　ＣｈｉｎａＡｂｓｔｒａｃｔＷｈｅｎ　ｓｈｅｌｌｓ　ａｒｅ　ｓｕｂｊｅｃｔｅｄ　ｔｏ　ｖａｒｉｏｕｓ　ｌｏａｄｉｎｇ　ｃｏｎｄｉｔｉｏｎｓ，　ｎｏｔ　ｏｎｌｙ　ｔｈｅ　ｂｒｅａｔｈｉｎｇ　ｍｏｄｅ，　ｂｕｔ　ａｌｓｏ　ｔｈｅ　ｏｔｈｅｒ　ｖｉｂｒａｔｉｏｎ　ｍｏｄｅｓ　ｍａｙ　ｂｅ　ｅｘｃｉｔｅｄ．　Ｔｈｅｒｅｆｏｒｅ，　ｉｔ　ｉｓ　ｖｅｒｙ　ｉｍｐｏｒｔａｎｔ　ｔｏ　ｕｎｄｅｒｓｔａｎｄ　ｔｈｅ　ｖｉｂｒａｔｉｏｎ　ｍｏｄｅｓ　ｉｎｃｙｌｉｎｄｒｉｃａｌ　ａｎｄ　ｓｐｈｅｒｉｃａｌ　ｓｈｅｌｌｓ．　Ｉｎ　ｔｈｉｓ　ｐａｐｅｒ，　ｗｅ　ｓｕｍｍａｒｉｚｅ　ｔｈｅ　ｆｕｎｄａｍｅｎｔａｌ　ｆｅａｔｕｒｅｓ　ｏｆ　ａｘｉｓｙｍｍｅｔｒｉｃ　ａｎｄ　ｎｏｎａｘｉｓｙｍｍｅｔｒｉｃ　ｍｏｄｅｓ　ｉｎ　ｓｈｅｌｌｓ，　ａｓ　ｗｅｌｌ　ａｓ　ｔｈｅ　ａｐｐｌｉｃａｔｉｏｎ　ｅｘａｍｐｌｅｓ，　ｗｈｉｃｈ　ｍａｙ　ｐｒｏｖｉｄｅ　ｂｅｔｔｅｒ　ｕｎｄｅｒｓｔａｎｄｉｎｇ　ｏｎ　ｒｅｓｐｏｎｓｅｓ　ｏｆ　ｐｒｅｓｓｕｒｅ　ｖｅｓｓｅｌｓ．Ｋｅｙｗｏｒｄｓｃｙｌｉｎｄｒｉｃａｌ　ｓｈｅｌｌ；　ｓｐｈｅｒｉｃａｌ　ｓｈｅｌｌ；　ａｘｉｓｙｍｍｅｔｒｉｃ　ｍｏｄｅ；　ｎｏｎａｘｉｓｙｍｍｅｔｒｉｃ　ｍｏｄｅ、蕾矿（ｃ）Ｈ－３、，炉３阶非轴对称模态振型图１圆柱壳的模态振型ｏｕｔｘｅｙ　ＩＡ，　ｔｅｌＶｉｂｒａｔｉｏｎｓ　ｏｆＶｉｂｒａｔｉｏｎ　ｅｎｄ　，￣ＷｉｌｋｉｎｓｏｎＪＥ　］Ａｃ，　ｏｕｓｔ．　Ｓｏｃ．　Ａ￣壳体中的轴对称模态和非轴对称模态作者：董奇，郑津洋，胡八一作者单位：董奇,胡八一(中国工程物理研究院流体物理研究所绵阳621900)，郑津洋(浙江大学化工机械研究所杭州310027)本文链接：/Conference_7785360.aspx。

【国家自然科学基金】_heaviside函数_基金支持热词逐年推荐_【万方软件创新助手】_20140730

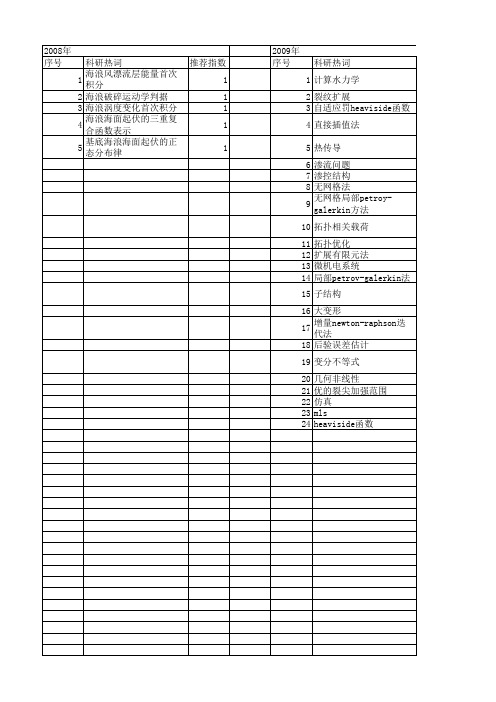
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
科研热词推荐指数裂隙网络 2 自由面 2 渗流 2 应力强度因子 2 变分不等式 2 非轴对称移动载荷 1 解析解 1 裂纹扩展 1 裂纹体 1 裂纹 1 罚函数 1 纤维铺角 1 离散材料优化 1 水平集法 1 无网格局部petrov-galerkin法 1 无网格伽辽金法 1 断裂力学 1 数值模拟 1 收敛率 1 拓扑优化 1 扩展有限元 1 扩展无网格方法 1 惩罚模型 1 弹性力学 1 应力 1 奇异权函数 1 天线辐射梁 1 复合材料 1 基结构法 1 圆柱壳 1 单位分解 1 动力响应 1 刚架结构 1 位移 1 交叉过滤 1 不连续近似 1 ssph近似 1 signorini型条件 1 heaviside函数 1
2014年序号 1 2 3 4 5 6 7 8 9 10 11 12
2014年科研热词推荐指数黏弹性流体 1 非线性热传导问 1 结构动力问题 1 相变 1 焓方法 1 滑动kriging插值 1 滑动 kriging 插值 1 无网格法 1 无网格局部petrov-galerkin 1 无网格局部 petrov-galerkin 法 1 充模过程 1 heaviside函数 1
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
科研热词非连续零膨胀结构线性互补法接触条件扩展有限单元法扩展有限元形函数应力强度因子富集多目标优化均匀化拓扑优化单位分解位移外推法三维裂纹三相材料

轴向冲击下环向加筋复合材料圆柱壳的非线性动力响应

船舶工程结构中。加筋复合材料圆柱壳是一种十分常见的结构形式。因此研究加筋复合材料圆柱壳的力学行为，尤其是加筋结构在动载荷作用下的非线性响应就具有更重要的工程意义。关于加筋复合材料结构，．Ｗ．ｉ】ＹＫｍ－利用能量法计算了环向加筋复合材料圆柱壳的振动频率以及在阶跃冲击作用下层合壳的动态响应。并讨论了加筋结构的离心率，目，数尺寸以及位置分布对层合壳的影响，所得到的结果与有限元结果相比相符。Ｇｉａ２利．Ｓｈ－ｎ用有限元方法计算了有肋骨加强的复合材料板壳结构的动态响应。使用高精度任意形状的三角形单元作为壳体单元。万志敏等应用Ｌｖｏｅ的壳体理论得到非轴对称变形的复合材料圆柱壳的控制方程，并在对层合壳在轴向冲击载荷下的动态稳定性研究考虑了几何非线性。唐文勇等基于修正的一阶剪切变形理论，利用Ｈｍｌｎ原理导出包含横向剪切变形和转动惯量ａｉｏｔ的复合材料场圆柱曲板的非线性动力方程，用Ｒ并．Ｋｔ方法数值求解，ｕａｔ讨论了载荷形式、几何非线性、横向剪切变形以及铺层方式等因素对动力响应的影响。张振华，锡等利用有限元数值模拟了爆炸冲击波朱作用下自由环肋圆柱壳的非线性动态响应，虑了几考何非线性以及结构的初始缺陷的影响，并和实验结果吻合较好。Ｎｓｒ ’ ｏｉ ‘ 修正了Ｒｄｙ型一阶及三阶理论ｅ。ｅｄ中的非线性动力方程，用修正后的理论，述了层合板描的内部及边界区域问题，高了分析结果精度，论了提讨非线性、剪切变形、转动惯量影响。本文将环向加筋复合材料圆柱壳离散成圆柱壳和加筋肋骨组成，两者在接触处刚性连接的壳体一肋骨系统，考虑了壳体剪切变形、转动惯量以及加筋肋骨的

ANSYS-STRUCTURAL基础培训-

实体几何模型载荷
培训手册
CFD Analysis with ANSYS/FLOTRAN
优点改变网格不影响载荷涉及到的加载实体少缺点生成的单元在当前激活的单元座标下，节点为总体直角座标，因此实体与有限元模型可能有不同座标系统和载荷方向实体载荷在凝集分析中不方便，因载荷加在主自由度上施加关键点约束较繁锁
简例〔续〕
培训手册
CFD Analysis with ANSYS/FLOTRAN
下面以小变形弹性静力问题为例，加以具体介绍。几何方程：eij=1/2(ui,j+uj,i) 物理方程：sij=aijklekl 平衡方程：sij,j+fi=0 边界条件：
位移已知边界条件 ui=ui 〔在边界Гu上位移已知〕外力已知边界条件 sij,j+pi=0〔在边界Гp上外力已知〕
2. 弹簧阻尼单元，包括COMBIN系列： COMBIN7,COMBIN14,COMBIN37,COMBIN40等。
3. 质量元，MASS21。
CFD Analysis with ANSYS/FLOTRAN
ANSYS单元分类
初级培训
4 . 梁单元，分为二维和三维单元，弹性和塑性；可定义各种截面。主要包括： BEAM3，BEAM4，BEAM23，BEAM24，BEAM44， BEAM188，BEAM189。
〔1-1〕
简例〔续〕
培训手册
CFD Analysis with ANSYS/FLOTRAN
即 {F} 1=[K] 1{δ}1 在〔1-1〕中令U11=1，V11=U21=V21=0 则F1x1=K11 ，F1y1=K21 ，F1x2=K31 ，F1y2=K41
上式说明，当节点1沿X方向产生一单位位移，而单元1的其余节点位移为零时，各节点施于单元1 上的力将组成一平衡力系，表示单元1抵抗位移 U11的刚度。

圆柱壳体动力响应中的模态参与问题研究

第 37 卷第 1 期2024 年1 月振动工程学报Journal of Vibration EngineeringVol. 37 No. 1Jan. 2024圆柱壳体动力响应中的模态参与问题研究徐港辉，祝长生（浙江大学电气工程学院，浙江杭州 310027）摘要: 以两端简支圆柱壳体为例，研究了考虑正、余弦模态成分影响的圆柱壳体动力响应中的模态参与问题，提出了根据模态参与因子的分布特征判定模态截断阶次的方法，采用正、余弦模态叠加得到了圆柱壳体在冲击激励及旋转行波激励作用下的动力响应，基于响应的收敛性验证了判定方法的可靠性。

理论计算与有限元仿真结果表明，与圆柱壳体模态特性分析不同，在求解圆柱壳体动力响应时必须同时考虑正、余弦模态成分的影响；冲击激励作用下，圆柱壳体各阶正、余弦模态在响应中的参与程度与激振点和观测点的位置相关；旋转行波激励作用下，圆柱壳体各阶正、余弦模态在响应中的参与程度与激励的阶次和频率密切相关。

关键词: 圆柱壳体；正余弦模态；模态参与；模态叠加；模态截断；动力响应中图分类号: O326； TB53； TH113.1 文献标志码: A 文章编号: 1004-4523（2024）01-0083-12DOI：10.16385/ki.issn.1004-4523.2024.01.009引言圆柱壳体作为常见的结构，广泛应用于机电、航空航天和航海等领域，如电机定子、航空发动机机匣、潜艇船体等。

在复杂激励条件下，圆柱壳体容易产生振动噪声、疲劳损伤甚至故障失效。

因此，开展圆柱壳体在不同激励作用下的动力响应分析具有重要的理论价值和工程意义。

作为圆柱壳体动力响应分析的基础，圆柱壳体自由振动分析是相关研究的一个热点。

由于壳体振动的复杂性，在不同的假设下形成了诸多壳体理论［1］。

然而圆柱壳体自由振动的解析解仅在少数边界条件（如两端简支）下可以相对容易地求得，而在其他边界条件下，由于圆柱壳体轴向振型函数较为复杂，其自由振动的解析解难以求得。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

摘要：在介绍圆柱厚壳应力与位移理论分析发展的前提下，建立了有限长圆柱厚壳在非轴对称移动载荷作用下
的三维力学模型，假设沿厚度方向径向剪切应变二次分布、径向正应变线性分布，且建立了为满足边界条件待定的位移表达式，采用Ｈｅａｖｉｓｉｄｅ函数和Ｄｉｒａｃ函数表达移动和作用变化着的移动载荷的基础上，用最小势能原理建立了该圆柱厚壳
解进行了对比，从而相互印证了解的可靠性。
关键词：圆柱厚壳；非轴对称移动载荷；最小势能原理；动力响应；位移；应力
中图分类号：０３４７．１文献标识码：Ａ
Ｄｙｎａｍｉｃｒｅｓｐｏｎｓｅｏｆａｌｅｎｇｔｈ－ｌｉｍｉｔｅｄｃｙｌｉｎｄｒｉｃａｌｔｈｉｃｋｓｈｅｌｌｕｎｄｅｒｎｏｎ－ａｘｉｓｙｍｍｅｔｒｉｃｍｏｖｉｎｇｌｏａｄｓ
ｏｆｔｈｅｓｈｅｌｌｗｅｒｅｄｅｉｒｖｅｄｕｓｉｎｇｔｈｅｍｉｎｉｍｕｍｐｏｔｅｎｔｉａｌｅｎｅｒｇｙｐｒｉｎｃｉｐｌｅ．ＵｓｉｎｇＧｌｅａｒｋｉｎｍｅｔｈｏｄａｎｄｔｈｅｍｏｄｉｉｆｅｄＲｕｎｇｅ —
Ａｂｓｔｒａｃｔ：Ｔｈｅｔｈｅｏｒｅｔｉｃａｌｓｔｕｄｙｈｉｓｔｏｒｙｏｆｃｙｌｉｎｄｒｉｃａｌｔｈｉｃｋｓｈｅｌｌｓ ’ｓｔｒｅｓｓａｎｄｄｉｓｐｌａｃｅｍｅｎｔｗａｓｉｒｆｓｔｌｙｒｅｖｉｅｗｅｄ，ａｎｄａ３Ｄｍｅｃｈａｎｉｃａｌｍｏｄｅｌｏｆａｌｅｎｇｔｈ— ｌｉｍｉｔｅｄｃｙｌｉｎｄｉｃｒａｌｔｈｉｃｋｓｈｅｌｌｕｎｄｅｒｎｏｎ — ａｘｉｓｙｍｍｅｔｉｃｒｍｏｖｉｎｇｌｏａｄｓｗａｓｅｓｔａｂｌｉｓｈｅｄ．Ｔｈｅｎ，ｂａｓｅｄｏｎｔｈｅａｓｓｕｍｐｔｉｏｎｏｆｒａｄｉａｌｓｈｅａｒｓｔｒａｉｎｓｗｉｔｈｑｕａｄｒａｔｉｃｄｉｓｔｒｉｂｕｔｉｏｎａｎｄｒａｄｉａｌｎｏｒｍａｌｓｔｒａｉｎｓｗｉｔｈｌｉｎｅａｒｄｉｓｔｒｉｂｕｔｉｏｎａｌｏｎｇｔｈｅｒａｄｉａｌｃｏｏｒｄｉｎａｔｅ，ｉｔｓｄｉｓｐｌａｃｅｍｅｎｔｅｘｐｒｅｓｓｉｏｎｓｓａｔｉｓｆｙｉｎｇｂｏｕｎｄａｙｒｃｏｎｄｉｔｉｏｎｓｗｅｒｅｅｓｔａｂｌｉｓｈｅｄ．Ｔｈｅｎｏｎ－ａｘｉｓｙｍｍｅｔｒｉｃｌｏａｄｓｗｅｒｅｅｘｐｒｅｓｓｅｄｗｉｔｈＨｅａｖｉｓｉｄｅｆｕｎｃｔｉｏｎａｎｄＤｉｒａｃｆｕｎｃｔｉｏｎ，ａｎｄｔｈｅｄｙｎａｍｉｃｄｉｆｆｅｒｅｎｔｉａｌｅｑｕａｔｉｏｎｓ
ＺＨＡＯＪｉａｎ — ｂｏ，ＳＩＸｉｕ — ｙｏｎｇ，ＢＡＩＸｉａｎｇ — ｚｈｏｎｇ
（ＣｏｌｌｅｇｅｏｆＣｉｖｉｌＥｎｇｉｎｅｅｒｉｎｇ＆Ｍｅｃｈａｎｉｃｓ，ＹａｎｓｈａｎＵｎｉｖｅｒｓｉｔｙ，Ｑｉｎｈｕａｎｇｄａｏ０６６００４，Ｃｈｉｎａ）
的动力学微分方程组，应用Ｇａｌｅｒｋｉｎ法和修正的Ｒｕｎｇｅ－Ｋｕｔｔａ — Ｆｅｈｌｂｅｒｇ法，求得了非轴对称移动载荷作用下的圆柱厚壳的
动力响应。通过具体算例，对有限长圆柱厚壳的位移响应和应力状态进行了分析，并将动态响应的理论解与ＡＮＳＹＳ数值
振第３２卷第１４期
动
与
冲
击
பைடு நூலகம்
ＪＯＵＲＮＡＬＯＦＶＩＢＲＡＴＩＯＮＡＮＤＳＨＯＣＫ
非轴对称移动载荷下有限长圆柱厚壳的动力响应
赵建波，司秀勇，白象忠
（燕山大学建筑工程与力学学院，河北秦皇岛０６６００４）
Ｋｕｔｔａ — Ｆｅｈｌｂｅｒｇｍｅｔｈｏｄ，ｔｈｅｄｙｎａｍｉｃｒｅｓｐｏｎｓｅｓｏｆｔｈｅｃｙｌｉｎｄｉｃｒａｌｔｈｉｃｋｓｈｅｌｌｕｎｄｅｒｎｏｎ－ａｘｉｓｙｍｍｅｔｒｉｃｍｏｖｉｎｇｌｏａｄｓｗｅｒｅｏｂｔａｉｎｅｄ．ＴｈｉｓｍｅｔｈｏｄｗａｓｖｅｉｆｒｉｅｄｗｉｔｈａｃｏｍｐａｒａｔｉｖｅａｎａｌｙｓｉｓｏｆｔｈｅｔｈｅｏｒｅｔｉｃａｌｓｏｌｕｔｉｏｎｓａｎｄＡＮＳＹＳｎｕｍｅｒｉｃａｌｒｅｓｕｌｔｓｏｆ