重庆市重庆一中2016-2017学年高一上学期期中考试试题_数学_Word版含答案
重庆市第一中学2016-2017学年高一上学期期中考试化学试题 Word版含答案
秘密★启用前2016年重庆一中高2019级高一上期半期考试化学试题卷2016.12化学试题共7页。
满分150分。
时间120分钟。
注意事项：1.答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号。
3.答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答，在试题卷上答题无效。
可能用到的相对原子质量：H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 S 32 Fe 56 Ba 137Ⅰ卷（选择题，共69分）选择题(本题包括23个小题，每小题只有一个选项符合题意，每小题3分，共69分)1.下列仪器可用于加热且不必垫石棉网的是①试管②烧杯③坩埚④蒸发皿⑤锥形瓶⑥蒸馏烧瓶A. ②④⑤B. ①③④C.①②③D. ②⑤⑥2.如果家里炒菜的食用油混了大量水，采用的简单分离方法为A.过滤B.萃取C.分液D.蒸馏3.下列各项中，符合实验安全操作要求的是A.金属钠着火，立即用水浇灭B.将使用剩余的金属钠放回原瓶C.给试管中的液体加热过程中加入碎瓷片D.皮肤上不慎沾上NaOH溶液，立即用盐酸冲洗4.歌乐山森林公园是重庆主城的肺叶之一，素有“天然氧吧”之称，其原因是森林空气中富含被称为“空气维生素”的负氧离子，O2－就是其中一种，其摩尔质量为A.33B.32C.33 g·molˉ1D.32 g·molˉ15.分类法在化学学科发展中起到了非常重要的作用，下列分类标准合理的是A.根据是否含氧元素，将物质分为氧化剂和还原剂B.根据是否具有丁达尔效应，将分散系分为溶液、浊液和胶体C.根据水溶液是否能够导电，将物质分为电解质和非电解质D.根据反应中是否有电子转移，将化学反应分为氧化还原反应和非氧化还原反应6.下列分散系中，分散质微粒半径最小的是A.霾B.KCl溶液C.蛋白质胶体D.新制Cu(OH)2悬浊液7.下列叙述正确的是A.将植物油倒入水中用力搅拌形成油水混合物属于胶体B.向氢氧化钠溶液中逐滴加入FeCl3饱和溶液制备氢氧化铁胶体C.一束平行光线射入稀豆浆里，可以看到一条光亮的通路D.可用过滤方法除去氢氧化铁胶体中的NaCl杂质8.下列有关实验操作正确的是A.图①：配制0.2 mol·L-1的NaOH 溶液B.图②：除去NaCl溶液中的KNO3杂质C.图③：用CCl4萃取碘水中的碘后的分液操作D.图④：蒸馏工业酒精获取无水酒精9.下列有关物质的类别正确的是A.盐：碳酸氢钠氯化铵纯碱B.电解质：H2SO4 Ba(OH)2CO2C.氧化物：H2O CO HNO3D.混合物：空气玻璃水银10.若N A表示阿伏加德罗常数的值，下列说法正确的是A.16g O2和O3的混合气体中含N A个氧原子B.0.5 mol·L-1硫酸钠溶液中含有N A个Na+C.在0 ℃、101 kPa时，22.4 L CCl4中含有N A个碳原子D.在H2O2 + Cl2 =2HCl + O2反应中，每生成32g氧气，则转移4N A个电子11.己知在标准状况下4.48L 某气体质量为8.8g，则该气体可能为A.CH4B.NOC.NH3D.CO212.铁、铝两种金属分别和等体积、等浓度的稀硫酸反应，消耗两种金属的物质的量相等，则下列叙述一定正确的是A.生成氢气的体积相等B.消耗的硫酸的物质的量相等C.两反应转移电子的数目之比为2:3D.加入的两种金属质量相等13.同温同压下，相同体积的SO2和O3气体，下列叙述中错误的是A.质量比4∶3B.电子数比1∶1C.密度比4∶3D.氧原子数比2∶314.下列有关钠的叙述中，错误的是A.少量金属钠可保存在煤油中B.金属钠的密度比水小，比煤油大C.金属钠可以置换出硫酸铜溶液中的铜D.钠元素在自然界中只能以化合态存在15.下列叙述正确的是A.溶于水后能电离出H+的化合物都是酸B.NaCl溶液在电流作用下电离成Na+与Cl-C.硫酸溶液的导电性一定比醋酸溶液导电性强D.氯化氢溶于水能导电，但液态氯化氢不能导电16.下列反应的离子方程式错误的是A.氢氧化钡溶液中加入硫酸镁溶液Mg2+ + 2OH- = Mg(OH)2↓B.稀硫酸溶液中加入氧化铜CuO＋2H＋= Cu2+＋H2OC.碳酸钙与稀盐酸制二氧化碳CaCO3＋2H＋=Ca2+＋CO2↑＋H2OD.碳酸氢钙溶液中加入少量氢氧化钾溶液Ca2+＋HCO3-＋OH-=CaCO3↓＋H2O17.某无色透明的强酸性溶液中能大量共存的离子组是A.Mg2+、K+、SO42-、OH-B.Ca2+、K+、CO32-、C1-C.K+、Na+ 、Cl-、NO3-D.Cu2+、K+、NO3-、Cl-18.已知某溶液中Na+、Cl－、K+、SO42－物质的量之比为1:1:2:1，则其溶质可能是A.KCl、Na2SO4B.KCl、Na2SO4、NaClC.NaCl、Na2SO4、K2SO4D.KCl、K2SO4、Na2SO419.下列反应不属于四种基本反应类型，但属于氧化还原反应的是A.CaO+H2O=Ca(OH)2B.Fe＋CuSO4=FeSO4＋CuC.6FeBr2＋3Cl2=2FeCl3＋4FeBr3D.AgNO3＋KCl=AgCl↓＋KNO320.下图是某燃煤发电厂处理废气的装置示意图。
重庆一中高一数学上学期期中试题
重庆一中2014-2015学年高一数学上学期期中试题一、选择题（每题5分，共50分。
每题只有一个正确答案）1. 以下表示正确的是（ ）A. 0∅=B. {0}∅=C. {0}∅∈D. {0}∅⊆2.函数()ln(2)f x x =-的定义域为（ ）A. [1,2)-B. (1,)-+∞C. (1,2)-D. (2,)+∞3.函数41()2x x f x +=的图像（ ） A. 关于原点对称 B.关于x 轴对称 C. 关于y 轴对称 D. 关于直线y x =轴对称4. 已知a =132-，b =21log 3，c =121log 3，则（ ） A. a b c >> B. a c b >> C. c a b >> D. c b a >>5. 已知幂函数()f x 的图像经过点（4,2），则()f x 的增区间为（ ）A. (,)-∞+∞B. (,0)-∞C. (0,)+∞D. (1,)+∞6. （原创）1x >的充分不必要条件是（ ）A. 0x >B. 1x ≥C. 0x =D. 2x =7.已知1)()3,f x f a =+=且则实数a 的值是（ ）A. 2±B. 2C. 2-D. 48.（原创） 函数241,(0)()2,(0)x x x f x x x ⎧-+≥=⎨+<⎩，若互不相等的实数123,,x x x 满足123()()()f x f x f x ==，则123x x x ++的取值范围为（ ）A. (]5,4-B. (5,3)-C. (1,4)-D. (]1,3-9. 已知函数()22lg 12(1)3y a x a x ⎡⎤=---+⎣⎦的值域为R ，则实数a 的取值范围是（ ） A. [2,1]- B. [2,1]-- C. (2,1)- D. (,2)[1,)-∞-+∞U10.已知定义在R 上的函数()f x 满足[()]()1f f x xf x =+，则方程()0f x =的实根个数为（ ）A. 0B. 1C. 2D. 4二、填空题（每小题5分，共25分）11. 函数21,[1,2]y x x =+∈-的值域为 ；12. 已知函数1()31x f x a =++为奇函数，则常数a = ； 13. 函数22log (4)y x x =-的增区间为 ；14. 已知不等式20ax bx c ++>的解集为1(,2)2-，对于系数,,a b c 有如下结论：①0a >；②0b >；③0c >；④0a b c ++>；⑤0a b c -+>。
重庆市2016—2017学年高一上学期期末数学 试卷 Word版含解析
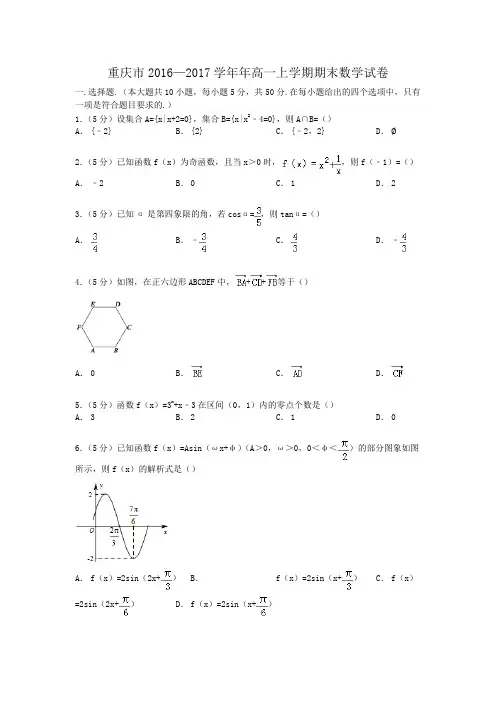
重庆市2016—2017学年年高一上学期期末数学试卷一.选择题.（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．（5分）设集合A={x|x+2=0}，集合B={x|x2﹣4=0}，则A∩B=（）A．{﹣2} B．{2} C．{﹣2，2} D．∅2．（5分）已知函数f（x）为奇函数，且当x＞0时，，则f（﹣1）=（）A．﹣2 B．0 C．1 D．2 3．（5分）已知α是第四象限的角，若cosα=，则tanα=（）A．B．﹣C．D．﹣4．（5分）如图，在正六边形ABCDEF中，++等于（）A．0 B．C．D．5．（5分）函数f（x）=3x+x﹣3在区间（0，1）内的零点个数是（）A．3 B．2 C．1 D．0 6．（5分）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜）的部分图象如图所示，则f（x）的解析式是（）A．f（x）=2sin（2x+）B．f（x）=2sin（x+）C．f（x）=2sin（2x+）D．f（x）=2sin（x+）7．（5分）下列函数中，既是偶函数，又在区间（1，2）内是增函数的为（）A．y=cosx B．y=ln|x| C．y=D．y=tan2x8．（5分）设a=tan35°，b=cos55°，c=sin23°，则（）A．a＞b＞c B．b＞c＞a C．c＞b＞a D．c＞a＞b9．（5分）定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈B．C．D．二.填空题.（本大题共5小题，每小题5分，共25分.）11．（5分）tan=．12．（5分）如图所示，平行四边形ABCD的对角线AC与BD相交于点O，点M是线段OD的中点，设=，=，则=．（结果用，表示）13．（5分）（lg25﹣lg）÷100=．14．（5分）求值：=．15．（5分）设g（x）=x﹣1，已知f（x）=，若关于x的方程f（x）=m恰有三个互不相等的实根x1，x2，x3，则x12+x22+x32的取值范围是．三.解答题.（本大题共6小题，共75分.解答须写出文字说明、证明过程和演算步骤.）16．（13分）已知＜α＜π，tanα﹣=﹣．（Ⅰ）求tana的值；（Ⅱ）求的值．17．（13分）平面内给定三个向量=（3，2），=（﹣1，2），=（4，1）．（Ⅰ）设向量=+，且||=，求向量的坐标；（Ⅱ）若（+k）∥（2﹣），求实数k的值．18．（13分）已知函数f（x）=a x（a＞0，a≠1）在区间上的最大值是最小值的8倍．（Ⅰ）求a的值；（Ⅱ）当a＞1时，解不等式log a（2a+2x）＜log a（x2+1）．19．（12分）已知函数g（x）=4sin（ωx+），h（x）=cos（ωx+π）（ω＞0）．（Ⅰ）当ω=2时，把y=g（x）的图象向右平移个单位得到函数y=p（x）的图象，求函数y=p（x）的图象的对称中心坐标；（Ⅱ）设f（x）=g（x）h（x），若f（x）的图象与直线y=2﹣的相邻两个交点之间的距离为π，求ω的值，并求函数f（x）的单调递增区间．20．（12分）已知函数f（x）=log2（4x+1）+mx．（Ⅰ）若f（x）是偶函数，求实数m的值；（Ⅱ）当m＞0时，关于x的方程f（8（log4x）2+2log2+﹣4）=1在区间上恰有两个不同的实数解，求m的范围．21．（12分）已知定义在（﹣∞，﹣1）∪（1，+∞）函数满足：①f（4）=1；②对任意x ＞2均有f（x）＞0；③对任意x＞1，y＞1，均有f（x）+f（y）=f（xy﹣x﹣y+2）．（Ⅰ）求f（2）的值；（Ⅱ）证明：f（x）在（1，+∞）上为增函数；（Ⅲ）是否存在实数k，使得f（sin2θ﹣（k﹣4）（sinθ+cosθ）+k）＜2对任意的θ∈恒成立？若存在，求出k的范围；若不存在说明理由．重庆市2016—2017学年年高一上学期期末数学试卷参考答案与试题解析一.选择题.（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1．（5分）设集合A={x|x+2=0}，集合B={x|x2﹣4=0}，则A∩B=（）A．{﹣2} B．{2} C．{﹣2，2} D．∅考点：交集及其运算．专题：计算题．分析：分别求出两集合中方程的解，确定出A与B，找出A与B的公共元素即可求出交集．解答：解：由A中的方程x+2=0，解得x=﹣2，即A={﹣2}；由B中的方程x2﹣4=0，解得x=2或﹣2，即B={﹣2，2}，则A∩B={﹣2}．故选A点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．（5分）已知函数f（x）为奇函数，且当x＞0时，，则f（﹣1）=（）A．﹣2 B．0 C．1 D．2考点：函数的值．专题：函数的性质及应用．分析：利用奇函数的性质，f（﹣1）=﹣f（1），即可求得答案．解答：解：∵函数f（x）为奇函数，x＞0时，f（x）=x2+，∴f（﹣1）=﹣f（1）=﹣2，故选A．点评：本题考查奇函数的性质，考查函数的求值，属于基础题．3．（5分）已知α是第四象限的角，若cosα=，则tanα=（）A．B．﹣C．D．﹣考点：同角三角函数基本关系的运用．专题：三角函数的求值．分析：由α为第四象限角，以及cosα的值，利用同角三角函数间的基本关系求出s inα的值，即可确定出tanα的值．解答：解：∵α是第四象限的角，若cosα=，∴sinα=﹣=﹣，则tanα==﹣，故选：D．点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．4．（5分）如图，在正六边形ABCDEF中，++等于（）A．0 B．C．D．考点：向量的加法及其几何意义．专题：平面向量及应用．分析：利用正六边形ABCDEF的性质，对边平行且相等得到向量相等或者相反，得到所求为0向量．解答：解：因为正六边形ABCDEF中，CD∥AF，CD=AF，所以++=++=；故选A．点评：本题考查了向量相等以及向量加法的三角形法则，属于基础题．5．（5分）函数f（x）=3x+x﹣3在区间（0，1）内的零点个数是（）A．3 B．2 C．1 D．0考点：函数零点的判定定理．专题：计算题；函数的性质及应用．分析：函数f（x）=3x+x﹣3在区间（0，1）上连续且单调递增，利用函数零点的判定定理求解即可．解答：解：函数f（x）=3x+x﹣3在区间（0，1）上连续且单调递增，又∵f（0）=1+0﹣3=﹣2＜0，f（1）=3+1﹣3=1＞0；∴f（0）•f（1）＜0；故函数f（x）=3x+x﹣3在区间（0，1）内有一个零点，故选C．点评：本题考查了函数零点的判定定理的应用及函数的单调性的应用，属于基础题．6．（5分）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜）的部分图象如图所示，则f（x）的解析式是（）A．f（x）=2sin（2x+）B．f（x）=2sin（x+）C．f（x）=2sin（2x+）D．f（x）=2sin（x+）考点：正弦函数的图象．专题：三角函数的图像与性质．分析：根据图象确定A，ω和φ的值即可求函数的解析式解答：解：由图象知函数的最大值为2，即A=2，函数的周期T=4（）=2，解得ω=1，即f（x）=2sin（x+φ），由五点对应法知+φ=π，解得φ=，故f（x）=2sin（x+），故选：B点评：本题主要考查函数解析式的求解，根据条件确定A，ω和φ的值是解决本题的关键．要要求熟练掌握五点对应法．7．（5分）下列函数中，既是偶函数，又在区间（1，2）内是增函数的为（）A．y=cosx B．y=ln|x| C．y=D．y=tan2x考点：函数单调性的判断与证明；函数奇偶性的判断．专题：函数的性质及应用．分析：根据余弦函数的单调性，对数函数的单调性，偶函数、奇函数的定义即可判断每个选项的正误．解答：解：A．y=cosx在（1，2）是减函数，所以A错误；B．显然y=ln|x|是偶函数，且在（1，2）内是增函数，所以B正确；C．显然函数是奇函数，所以该选项错误；D．tan﹣2x=﹣tan2x，所以该函数是奇函数，所以该选项错误．故选B．点评：考查余弦函数的单调性，对数函数的单调性，以及奇函数、偶函数的定义．8．（5分）设a=tan35°，b=cos55°，c=sin23°，则（）A．a＞b＞c B．b＞c＞a C．c＞b＞a D．c＞a＞b考点：正弦函数的图象．专题：三角函数的求值．分析：利用三角函数的诱导公式结合三角函数的单调性即可得到结论．解答：解：由诱导公式可得b=cos55°=cos（90°﹣35°）=sin35°，由正弦函数的单调性可知sin35°＞sin23°，即b＞c，而a=tan35°=＞sin35°=b，∴a＞b＞c，故选：A点评：本题考查三角函数值大小的比较，涉及诱导公式和三角函数的单调性，属基础题．9．（5分）定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈B． C．D．考点：函数的值域．专题：函数的性质及应用．分析：化简得出令=m，则1+sinx=2m﹣mcosx，sinx+mcosx=2m﹣1，φ）=2m﹣1得sin（x+φ）=，由≤1，解得0，利用函数性质求解f（m）=单增，解答：解：f（x）==﹣==﹣=令=m，则1+sinx=2m﹣mcosx，sinx+mcosx=2m﹣1，φ）=2m﹣1得sin（x+φ）=，由≤1，解得0，f（m）=单增，值域为点评：本题考察了函数的性质，换元法求解问题，属于难题，计算量较大．二.填空题.（本大题共5小题，每小题5分，共25分.）11．（5分）tan=﹣．考点：运用诱导公式化简求值．专题：三角函数的求值．分析：原式中的角度变形后，利用诱导公式及特殊角的三角函数值计算即可得到结果．解答：解：tan=tan（π﹣）=﹣tan=﹣．故答案为：﹣点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．12．（5分）如图所示，平行四边形ABCD的对角线AC与BD相交于点O，点M是线段OD的中点，设=，=，则=．（结果用，表示）考点：向量的三角形法则．专题：平面向量及应用．分析：利用向量的三角形法则、向量共线定理可得+==，即可得出．解答：解：+===．故答案为：．点评：本题考查了向量的三角形法则、向量共线定理，属于基础题．13．（5分）（lg25﹣lg）÷100=20．考点：有理数指数幂的化简求值．专题：函数的性质及应用．分析：根据对数的运算法则和有理数的公式进行化简即可．解答：解：（lg25﹣lg）÷100=（lg100）×=2×10=20，故答案为：20．点评：本题主要考查有理数的化简，比较基础．14．（5分）求值：=1．考点：三角函数的恒等变换及化简求值．专题：计算题．分析：先把原式中切转化成弦，利用两角和公式和整理后，运用诱导公式和二倍角公式化简整理求得答案．解答：解：原式=sin50°•=cos40°===1故答案为：1点评：本题主要考查了三角函数的恒等变换及其化简求值，以及两角和公式，诱导公式和二倍角公式的化简求值．考查了学生对三角函数基础知识的综合运用．15．（5分）设g（x）=x﹣1，已知f（x）=，若关于x的方程f（x）=m恰有三个互不相等的实根x1，x2，x3，则x12+x22+x32的取值范围是（，1）．考点：根的存在性及根的个数判断；分段函数的应用．专题：计算题；作图题；函数的性质及应用．分析：化简f（x）=，从而作出其图象，结合图象可得0＜m＜，从而分别讨论x1，x2，x3，再令y=x12+x22+x32=+1﹣2m，化简并利用换元法求取值范围即可．解答：解：∵g（x）=x﹣1，f（x）=，f（x）=；即f（x）=；作出其图象如下，若方程f（x）=m有三个根，则0＜m＜，且当x＞0时，方程可化为﹣x2+x﹣m=0，易知，x2+x3=1，x2x3=m；当x≤0时，方程可化为x2﹣x﹣m=0，可解得x1=；记y=x12+x22+x32=+1﹣2m=﹣m﹣+；令t=∈（1，），则y=﹣t2﹣t+，解得，y∈（，1）．故答案为：（，1）．点评：本题考查了分段函数的应用及数形结合的思想应用，同时考查了换元法的应用及方程的根与函数的图象的交点的关系应用，属于中档题．三.解答题.（本大题共6小题，共75分.解答须写出文字说明、证明过程和演算步骤.）16．（13分）已知＜α＜π，tanα﹣=﹣．（Ⅰ）求tana的值；（Ⅱ）求的值．考点：同角三角函数基本关系的运用；运用诱导公式化简求值．专题：三角函数的求值．分析：（Ⅰ）设tanα=x，已知等式变形后求出方程的解确定出x的值，即可求出tana 的值；（Ⅱ）原式利用诱导公式化简，再利用同角三角函数间基本关系变形，将tanα的值代入计算即可求出值．解答：解：（Ⅰ）令tanα=x，则x﹣=﹣，即2x2+3x﹣2=0，解得：x=或x=﹣2，∵＜α＜π，∴tanα＜0，则tanα=﹣2；（Ⅱ）原式==tanα+1=﹣2+1=﹣1．点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．17．（13分）平面内给定三个向量=（3，2），=（﹣1，2），=（4，1）．（Ⅰ）设向量=+，且||=，求向量的坐标；（Ⅱ）若（+k）∥（2﹣），求实数k的值．考点：平面向量共线（平行）的坐标表示；平面向量的坐标运算．专题：平面向量及应用．分析：（Ⅰ）根据向量的坐标运算以及模长公式，求出λ的值即可；（Ⅱ）根据向量平行的坐标表示，列出方程，即可求出k的值．解答：解：（Ⅰ）∵向量=（3，2），=（﹣1，2），∴=+=（，）+（﹣，）=（λ，3λ）；又||=，∴=，解得λ=±1，∴=（1，3）或=（﹣1，﹣3）；（Ⅱ）∵+k=（3，2）+k（4，1）=（3+4k，2+k），2﹣=2（﹣1，2）﹣（3，2）=（﹣5，2）；且（+k）∥（2﹣），∴2×（3+4k）﹣（﹣5）×（2+k）=0，解得k=﹣．点评：本题考查了平面向量的坐标运算问题，也考查了向量平行与求向量模长的问题，是基础题目．18．（13分）已知函数f（x）=a x（a＞0，a≠1）在区间上的最大值是最小值的8倍．（Ⅰ）求a的值；（Ⅱ）当a＞1时，解不等式log a（2a+2x）＜log a（x2+1）．考点：指数函数的图像与性质．专题：函数的性质及应用．分析：（Ⅰ）分类讨论当a＞1时，当0＜a＜1时，求出最大值，最小值，即可求解答案．（Ⅱ）转化log2（4+2x）＜log2（x2+1）得出得出不等式组，求解即可解答：解：f（x）max=a2，f（x）min=a﹣1，则=a2=8，解得a=2；当0＜a＜1时，f（x）=max=a﹣1，f（x）min=a2，则=a﹣3=8，解得a=；故a=2或a=（Ⅱ）当a＞1时，由前知a=2，不等式log a（2a+2x）＜log a（x2+1）即得解集为（﹣2，﹣1）∪（3，+∞）．点评：本题考察了指数函数的性质，分类讨论的思想，属于中档题，关键是分类得出方程，不等式组．19．（12分）已知函数g（x）=4sin（ωx+），h（x）=cos（ωx+π）（ω＞0）．（Ⅰ）当ω=2时，把y=g（x）的图象向右平移个单位得到函数y=p（x）的图象，求函数y=p（x）的图象的对称中心坐标；（Ⅱ）设f（x）=g（x）h（x），若f（x）的图象与直线y=2﹣的相邻两个交点之间的距离为π，求ω的值，并求函数f（x）的单调递增区间．考点：函数y=Asin（ωx+φ）的图象变换；正弦函数的图象；余弦函数的图象．专题：三角函数的求值；三角函数的图像与性质．分析：（Ⅰ）由题意，先求得：p（x）=4sin（2x+），令2x+=kπ，即可求得函数y=p（x）的图象的对称中心坐标；（Ⅱ）先求得解析式f（x）=2sin（2ωx﹣）﹣，由题意T=π，可解得ω的值，令t=2x﹣是x的增函数，则需y=2sint﹣是t的增函数，由2k≤2x﹣≤2k，可解得函数f（x）的单增区间．解答：解：（Ⅰ）当ω=2时，g（x）=4sin（2x+），g（x﹣）=4sin（2x﹣+）=4sin（2x+），p（x）=4sin（2x+），令2x+=kπ，得x=﹣+，中心为（﹣+，0）（k∈Z）；（Ⅱ）f（x）=4sin（ωx+）（﹣cosωx）=﹣4cosωx=2sinωxcosωx﹣2cos2ωx=sin2ωx﹣（1+cos2ωx）=2sin（2ωx﹣）﹣由题意，T=π，∴=π，ω=1令t=2x﹣是x的增函数，则需y=2sint﹣是t的增函数故2k≤2x﹣≤2k，2k≤2x≤2kπ+，k≤x≤kπ+函数f（x）的单增区间是（k∈Z）．点评：本题主要考查了函数y=Asin（ωx+φ）的图象变换，三角函数的图象和性质，属于基础题．20．（12分）已知函数f（x）=log2（4x+1）+mx．（Ⅰ）若f（x）是偶函数，求实数m的值；（Ⅱ）当m＞0时，关于x的方程f（8（log4x）2+2log2+﹣4）=1在区间上恰有两个不同的实数解，求m的范围．考点：对数函数的图像与性质；指数函数综合题．专题：函数的性质及应用．分析：（Ⅰ）根据f（x）是偶函数，建立方程关系即可求实数m的值；（Ⅱ）利用对数函数的性质，利用换元法，转化为两个函数的交点问题即可得到结论．解答：解：（Ⅰ）若f（x）是偶函数，则有f（﹣x）=f（x）恒成立，即：log2（4﹣x+1）﹣mx=log2（4x+1）+mx．于是2mx=log2（4﹣x+1）﹣log2（4x+1）=log2（）﹣log2（4x+1）=﹣2x，即是2mx=﹣2x对x∈R恒成立，故m=﹣1．（Ⅱ）当m＞0时，y=log2（4x+1），在R上单增，y=mx在R上也单增所以f（x）=log2（4x+1）+mx在R上单增，且f（0）=1，则f（8（log4x）2+2log2+﹣4）=1可化为f（8（log4x）2+2log2+﹣4）=f（0），又f（x）单增，得8（log4x）2+2log2+﹣4=0，换底得8（）2﹣2log2x+﹣4=0，即2（log2x）2﹣2log2x+﹣4=0，令t=log2x，则t∈，问题转换化为2t2﹣2t+﹣4=0在t∈，有两解，即=﹣2t2+2t+4，令y=﹣2t2+2t+4，则y=﹣2t2+2t+4=﹣2（t﹣）2+，∴当t=时，函数取得最大值，当t=0时，函数y=4，当t=时，函数取得最小值，若方程f（8（log4x）2+2log2+﹣4）=1在区间上恰有两个不同的实数解，则等价为4≤＜，解得＜m≤1，故求m的范围为＜m≤1．点评：本题主要考查函数奇偶性的应用，以及对数函数的应用，利用方程和函数之间的关系，转化为两个函数的交点问题是解决本题的关键．21．（12分）已知定义在（﹣∞，﹣1）∪（1，+∞）函数满足：①f（4）=1；②对任意x ＞2均有f（x）＞0；③对任意x＞1，y＞1，均有f（x）+f（y）=f（xy﹣x﹣y+2）．（Ⅰ）求f（2）的值；（Ⅱ）证明：f（x）在（1，+∞）上为增函数；（Ⅲ）是否存在实数k，使得f（sin2θ﹣（k﹣4）（sinθ+cosθ）+k）＜2对任意的θ∈恒成立？若存在，求出k的范围；若不存在说明理由．考点：函数恒成立问题；抽象函数及其应用．专题：函数的性质及应用；三角函数的图像与性质．分析：（Ⅰ）将条件③变形得到f（m+1）+f（n+1）=f（mn+1）对任意m，n＞0均成立，其中m=x﹣1，n=y﹣1，令m=n=1，即可解得f（2）=0；（Ⅱ）由（Ⅰ），将f（m+1）+f（n+1）=f（mn+1）变形得f（mn+1）﹣f（n+1）=f（m+1），则要证明f（x）在（1，+∞）上为增函数，只需m＞1即可．显然当m＞1即m+1＞2时f（m+1）＞0；（Ⅲ）利用条件①②将问题转化为是否存在实数k使得sin2θ﹣（k﹣4）（sinθ+cosθ）+k＜或1＜sin2θ﹣（k﹣4）（sinθ+cosθ）+k＜10对任意的θ∈恒成立．再令t=sinθ+cosθ，，则问题等价于t2﹣（k﹣4）t+k﹣1＜或1＜t2﹣（k﹣4）t+k﹣1＜10对恒成立．分情况讨论，利用二次函数的性质即可解题．解答：解：（Ⅰ）由条件③可知f（x）+f（y）=f（xy﹣x﹣y+2）=f=f，令m=x﹣1，n=y﹣1，则由x＞1，y＞1知m，n＞0，并且f（m+1）+f（n+1）=f（mn+1）对任意m，n＞0均成立．令m=n=1，即有f（2）+f（2）=f（2），故得f（2）=0．（Ⅱ）由（Ⅰ），将f（m+1）+f（n+1）=f（mn+1）变形得：f（mn+1）﹣f（n+1）=f（m+1），要证明f（x）在（1，+∞）上为增函数，只需m＞1即可．设x2=mn+1，x1=n+1，其中m，n＞0，m＞1，则x2﹣x1=n（m﹣1）＞0，故x2＞x1，则f（x2）﹣f（x1）=f（mn+1）﹣f（n+1）=f（m+1），m＞1，m+1＞2，所以f（m+1）＞0，即f（x2）﹣f（x1）＞0，所以f（x2）＞f（x1），即f（x）在（1，+∞）上为增函数；（Ⅲ）∵由f（m+1）+f（n+1）=f（mn+1）对任意m，n＞0均成立，及f（4）=1∴令m=n=3，有f（4）+f（4）=f（10），即f（10）=2．令m=9，n=，则f（9+1）+f（+1）=f（9×+1）=f（2），故f（）=f（2）﹣f（10）=﹣2，由奇偶性得f（﹣）=﹣2，则f（x）＜2的解集是．于是问题等价于是否存在实数k使得sin2θ﹣（k﹣4）（sinθ+cosθ）+k＜或1＜sin2θ﹣（k﹣4）（sinθ+cosθ）+k＜10对任意的θ∈恒成立．令t=sinθ+cosθ，，问题等价于t2﹣（k﹣4）t+k﹣1＜或1＜t2﹣（k﹣4）t+k﹣1＜10对恒成立．令g（t）=t2﹣（k﹣4）t+k﹣1，则g（t）对恒成立的必要条件是，即解得，此时无解；同理1＜g（t）＜10恒成立的必要条件是，即解得，即；当时，g（t）=t2﹣（k﹣4）t+k﹣1的对称轴．下面分两种情况讨论：（1）当时，对称轴在区间的右侧，此时g（t）=t2﹣（k﹣4）t+k﹣1在区间上单调递减，1＜g（t）＜10恒成立等价于恒成立，故当时，1＜g（t）＜10恒成立；（2）当时，对称轴在区间内，此时g（t）=t2﹣（k﹣4）t+k﹣1在区间上先单调递减后单调递增，1＜g（t）＜10恒成立还需，即，化简为k2﹣12k+24＜0，解得，从而，解得；综上所述，存在，使得f（sin2θ﹣（k﹣4）（sinθ+cosθ）+k）＜2对任意的θ∈恒成立．点评：本题考查了抽象函数的运算，单调性，以及函数恒成立问题，需要较强的分析、计算能力，属于难题．。
重庆一中2017届高三上学期期中数学试卷(文科) 含解析
2016—2017学年重庆一中高三(上）期中数学试卷(文科）一、选择题:本大题共12个小题,每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知=2+i，则复数z=()A．﹣1+3i B．1﹣3i C．3+i D．3﹣i2．设全集I是实数集R，M=｛x｜x≥3｝与N=｛x|≤0}都是I的子集（如图所示）,则阴影部分所表示的集合为（）A．{x｜1＜x＜3} B．{x|1≤x＜3｝ C．｛x｜1＜x≤3｝D．｛x｜1≤x≤3｝3．已知直线方程为cos300°x+sin300°y=3，则直线的倾斜角为（)A．60°B．60°或300°C．30°D．30°或330°4．函数f（x)=x2+xsinx的图象关于（)A．坐标原点对称 B．直线y=﹣x对称C．y轴对称D．直线y=x对称5．点(﹣1，﹣2)关于直线x+y=1对称的点坐标是（)A．(3，2）B．（﹣3,﹣2) C．(﹣1,﹣2）D．（2，3)6．已知某棱锥的三视图如图所示，则该棱锥的表面积为（）A．2+B．3+C．2+D．3+7．已知函数f（x）=3x+x，g(x）=log3x+x，h（x)=log3x﹣3的零点依次为a，b,c，则（）A．c＜b＜a B．a＜b＜c C．c＜a＜b D．b＜a＜c8．重庆市乘坐出租车的收费办法如下:(1）不超过3千米的里程收费10元（2）超过3千米的里程2元收费（对于其中不足千米的部分,若其小于0.5千米则不收费，若其大于或等于0.5千米则按1千米收费），当车程超过3千米时，另收燃油附加费1元．相应系统收费的程序框图如图所示,其中x(单位：千米）为行驶里程，用[x]表示不大于x的最大整数，则图中①处应填（）A．y=2［x+］+4 B．y=2[x+］+5 C．y=2[x﹣]+4 D．y=2[x﹣］+59．若不等式组表示的平面区域经过所有四个象限，则实数λ的取值范围是(）A．（﹣∞，4）B．［1，2]C．[2，4］D．（2,+∞)10．已知在△ABC中，∠ACB=90°，BC=6，AC=8，P是线段AB上的点，则P到AC,BC 的距离的乘积的最大值为(）A．12 B．8 C． D．3611．当曲线y=与直线kx﹣y﹣2k+4=0有两个相异的交点时，实数k的取值范围是（）A．（0，) B．（，］C．（，1]D．（，+∞]12．已知函数f（x)=ax2+bx﹣2lnx（a＞0，b∈R），若对任意x＞0都有f(x)≥f（2）成立,则（)A．lna＞﹣b﹣1 B．lna≥﹣b﹣1 C．lna＜﹣b﹣1 D．lna≤﹣b﹣1二、填空题(每题5分，满分20分,将答案填在答题纸上）13．已知某长方体的长宽高分别为2，1，2，则该长方体外接球的体积为．14．若函数y=（)x在R上是减函数，则实数a取值集合是．15．若圆锥的侧面积与过轴的截面面积之比为2π，则其母线与轴的夹角的大小为．16．已知函数f(x）=如果对任意的n∈N＊，定义f n(x）=，例如:f2(x）=f(f（x）），那么f2016(2)的值为．三、解答题（本大题共5小题，共70分。
重庆市第一中学高一数学上学期期中试题
2018年重庆一中高2021级高一上期期中考试数学测试试题卷注意事项：1. 答卷前，考生务必将自己的姓名、准考证号码填写在答卷上。
2. 作答时，务必将答案写在答题卡上，写在本试卷及草稿纸上无效。
3. 考试结束后，将答题卡交回.一、 选择题:本题共12小题，每题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知幂函数()y f x =的图像经过点(2,4)，则f 的值为（ ）A ． 1B ．2C ．3D ． 4 2．函数()1log (2)a f x x =+-的图像经过定点（ )A ．(3， 1)B ．（2, 0）C ． (2， 2)D ．（3， 0） 3．已知集合{}|2,1xA y y x ==<,则集合R C A =（ )A ．(0,2)B ． [2,)+∞C ．(,0]-∞D ．(,0][2,)-∞+∞ 4．已知函数2()48f x x kx =--在(,5]-∞上具有单调性,则实数k 的取值范围是( ）A ．(24,40)-B ．[24,40]-C ．(,24]-∞-D ．[40,)+∞5．命题“0x ∃<，使2310x x -+≥"的否定是( ）A ．0x ∃<，使2310x x -+<B ．0x ∃≥,使2310x x -+<C ．0x ∀<，使2310x x -+<D ．0x ∀≥，使2310x x -+<6．在数学史上，一般认为对数的发明者是苏格兰数学家—-纳皮尔（Napier ，1550-1617年)。
在纳皮尔所处的年代，哥白尼的“太阳中心说”刚刚开始流行，这导致天文学成为当时的热门学科.可是由于当时常量数学的局限性，天文学家们不得不花费很大的精力去计算那些繁杂的“天文数字”，因此浪费了若干年甚至毕生的宝贵时间.纳皮尔也是当时的一位天文爱好者，为了简化计算，他多年潜心研究大数字的计算技术，终于独立发明了对数。
重庆市第一中学2016-2017学年高一10月月考数学试题 含解析
一、选择题（本大题共12个小题,每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1。
设全集{0,1,2,3,4}U =，集合{0,1,2,3}A =，{2,3,4}B =,则()()u U C A C B 等于（ ）A ．{0}B ．{0,1}C ．{0,1,4}D ．{0,1,2,3,4} 【答案】C 【解析】试题分析：{}{}4,0,1U U C A C B ==，所以{}()()0,1,4U U C A C B =。
考点：集合交集，并集，补集．2.下列有关集合的写法正确的是( ）A ．{0}{0,1,2}∈B ．{0}∅=C ．0∈∅D ．{}∅∈∅ 【答案】D 【解析】试题分析:元素和集合是属于或不属于的关系，空集是没有元素的集合，所以D 选项正确. 考点:元素和集合的关系．3。
满足{1,2}{1,2,3,4,5}A ⊂⊆≠的集合A 的个数是( ）A ．3个B ．5个C ．7个D ．8个【解析】试题分析：列举得{}{}{}{}{}{}{}1,2,1,2,3,1,2,4,1,2,5,1,2,3,4,1,2,3,5,1,2,4,5共7种. 考点：子集与真子集．4.下列函数中，在区间(1,1)-上是单调减函数的函数为（ ）A ．23y x =-B ．1y x= C 。
y =D ．23y x x =- 【答案】D 【解析】试题分析：A 是增函数，B 定义域没有零，C 的定义域是12x ⎧⎫≤⎨⎬⎩⎭，都不符合题意。
所以只有D 正确.考点:函数的单调性．5.以下从M 到N 的对应关系表示函数的是（ ） A ．{|0}:||M R N y y f x y x ==>→=，，B ．*{|2,}M x x x N =≥∈，*{|0,}N y y y N =≥∈,2:22f x y x x →=-+C 。
{|0}M x x =>,N R =，:f x y →=D ．M R =，N R =，1:f x y x→= 【答案】B 【解析】试题分析：A ，D 选项0没有对应，所以不是函数;C 选项不是一一对应，不是函数；故选B ． 考点:函数的定义．6。
【全国百强校】重庆市第一中学2015-2016学年高一上学期期中考试数学试题(原卷版)
重庆市第一中学2015-2016学年高一上学期期中考试数学试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项 是符合题目要求的.1、已知集合{}15,M x x x N =<<∈，{}1,2,3S =，那么M S =（ ） A 、{}1,2,3,4 B 、{}1,2,3,4,5 C 、{}2,3 D 、{}2,3,42、式子32log 2log 27的值为（ ）A 、2B 、3C 、13D 、-3 3、下列函数为奇函数的是（ ） AB 、31x - CD 、21x -4、已知():lg 30p x -<，2:04x q x -<-，那么p 是q 的（）条件 A 、充分不必要 B 、充要 C 、必要不充分 D 、既不充分也不必要5、已知幂函数()222a y a a x =--在实数集R 上单调，那么实数a =（ ）A 、一切实数B 、3或-1C 、-1D 、36、（原创）定义在实数集R 上的函数()y f x =满足121212()()0()f x f x x x x x ->≠-，若(5)1f =-，(7)0f =，那么(3)f -的值可以为（ ）A 、5B 、-5C 、0D 、-17、对于任意的1,1a b >>，以下不等式一定不成立的是（ ）A 、log 0a b >B 、1b a >C 、111ba ⎛⎫> ⎪⎝⎭ D 、log log 2ab b a +≥ 8、以下关于函数21()(3)3x f x x x -=≠-的叙述正确的是（ ） A 、函数()f x 在定义域内有最值B 、函数()f x 在定义域内单调递增C 、函数()f x 的图象关于点()3,1对称D 、函数5y x=的图象朝右平移3个单位再朝上平移2个单位即得函数()f x 9、（原创）函数()f x 满足()(2),f x f x x R =-∈，且当1x ≤时，32()44f x x x x =--+，则方程()0f x =的所有实数根之和为（ ）A 、2B 、3C 、4D 、110、已知关于x 的方程2222320x ax a a -+-+=有两个不等的实数根12,x x ，那么()212x x -的取值范围是（ ）A 、()0,+∞B 、[]0,1C 、(]0,1D 、()0,1 11、（原创）已知函数2()log 32a f x x x ⎛⎫=+- ⎪⎝⎭在区间[)1,+∞上单调递增，那么实数a 的取值范围是（ ） A 、()1,3- B 、(]1,3- C 、[]0,3 D 、[)0,3 12、对于任意x R ∈，函数2()2124f x x x x a x =------+的值非负，则实数a 的最小值为（）A 、118-B 、-5C 、-3D 、-2第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13、将函数()2()log 321f x x =+-的图象向上平移1个单位，再向右平移2个单位后得到函数()g x ，那么()g x 的表达式为__________.14、（原创）已知[]{}21,562x R x x a ⊆∈-≤+，那么实数a 的最小值为_________. 15、函数32()f x ax bx cx d =+++是实数集R 上的偶函数，并且()0f x <的解为()2,2-，则d b 的值为__________.16、（原创）函数()2x f x =，25()22g x x kx =-+，若对于任意的[]1,2s ∈-，都存在[],21t k k ∈+，使得()()f s g t =成立，则实数k 的取值范围是__________.三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17、（12分）（原创）集合()1302A x x x ⎧⎫⎛⎫=--=⎨⎬ ⎪⎝⎭⎩⎭，29ln 04B x x ax a ⎧⎫⎛⎫=+++=⎨⎬ ⎪⎝⎭⎩⎭. （1）若集合B 只有一个元素，求实数a 的值；（2）若B 是A 的真子集，求实数a 的取值范围.18、（12分）函数22()()22x xx x f x x R ---=∈+. （1）判断并证明函数()f x 的奇偶性；（2）求不等式315()517f x ≤≤的解集. 19、（12分）如图，定义在[]1,2-上的函数()f x 的图象为折线段ACB .（1）求函数()f x 的解析式；（2）请用数形结合的方法求不等式()2()log 1f x x ≥+的解集，不需要证明.20、（12分）集合{}930,x x A x p q x R =+⋅+=∈，{}9310,x x B x q p x R =⋅+⋅+=∈，且实数0pq ≠.（1）证明：若0x A ∈，则0x B -∈；（2）是否存在实数p ，q 满足A B ≠∅且{}1R A B =ð？若存在，求出p ，q 的值，不存在说明理由.21、（12分）（原创）函数()()233()log 1log 32(0,)f x x a x a x a R =+-+->∈.（1）若函数()f x 的值域是[)2,+∞，求a 的值；（2）若3(3)log (9)0f x x +≤对于任意[]3,9x ∈恒成立，求a 的取值范围.22、（10分）已知函数(0)a y x a x =+>在区间(上单调递减，在区间)+∞上单调递增；函数3322111(),22h x x x x x x ⎛⎫⎛⎫⎛⎫⎡⎤=+++∈ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎝⎭. （1）请写出函数22()(0)a f x x a x =+>与函数()(0,,3)n n a g x x a n N n x=+>∈≥在()0,+∞的单调区间（只写结论，不证明）；（2）求函数()h x 的最值；（3）讨论方程22()3()20(030)h x mh x m m -+=<≤实根的个数.：。
重庆市重庆一中高一数学上学期期中试题湘教版
秘密★启用前2013年重庆一中高2016级高一上期半期考试数 学 试 题 卷 2013.11一、选择题.( 本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.)1. 已知映射()():,3,3f x y x y x y →-+，在映射f 下()3,1-的原象是 （ ） (A) ()3,1- (B) ()5,7- (C) ()1,5 (D) 1,23⎛⎫- ⎪⎝⎭2．设集合{|,101},{|,||5}A x x Z x B x x Z x =∈-≤≤-=∈≤且且，则A B U 中的元素个数是 （ ） （A ） 15 （B ） 16 （C ） 10 （D ） 113.“12x -<成立”是“(3)0x x -<成立”的 ( ) (A)必要不充分条件 (B)充分不必要条件(C)充分必要条件 (D)既不充分也不必要条件4.下列函数中是奇函数的是 （ ） (A)2()f x x = (B)3()-f x x = (C)()=f x x (D)()+1f x x = 5．已知1,(1)()3,(1)x x f x x x +≤⎧=⎨-+>⎩，那么5[()]2f f 的值是（ ）（A ）32 （B ） 52 （C ） 92 （D ） 12- 6. 函数()()ln 11f x x x =+-+在下列区间内一定有零点的是 ( )(A)[0,1] (B)[2,3] (C)[1,2] (D)[3,4]7．已知不等式|3||4|x x m -+-≥的解集为R ，则实数m 的取值范围（ ） （A ） 1m < （B ） 1m ≤ （C ） 110m ≤（D ） 110m < 8.已知定义在R 上的函数()f x 的图象关于y 轴对称，且满足3()()2f x f x =-+，(1)1,(0)2f f -==-，则(1)(2)...(2015)f f f +++的值为 （ ）（A ）1 （B ）2 （C ） 1- （D ）2-9(原创).已知函数lg ,010y ()16,102x x f x x x ⎧<≤⎪==⎨-+>⎪⎩若a,b,c 互不相等，且)()()(c f b f a f ==，则abc 的取值范围是 （ ） （A ）（1,10） （B ）（5,6） （C ）（10,12） （D ）（20,24） 10. (原创)若关于x 的方程24xkx x =+有四个不同的实数解，则k 的取值范围为 （A ）（0，1） （B ）(14,1) （C ）(14,+∞) （D ）(1, +∞)二.填空题(每小题5分,共25分)11．已知{1,2,3,4,5,6},{1,3,4}I A ==,则I C A = . 12.函数22()2x x f x -+=的单调递增区间为 .13.函数()f x =R ，那么a 的取值范围是________ 14．已知53()8f x ax bx cx =++-，且(2)20f -=，则(2)f =15.(原创)设定义在[],(4)a b a ≥-上的单调函数()f x，若函数())g x f m =与()f x 的定义域与值域都相同，则实数m 的取值范围为_________三.解答题.( 本大题共6小题,共75分.) 16.(13分) 计算： （1）3log 5333322log 2log log 839-+- （2）()04130.7533642162---⎛⎡⎤--+-+ ⎣⎦⎝⎭17.(13分)已知集合222{|560},{|180},{|280}A x x x B x x ax C x x x =-+==-+==+-=，若A B ≠∅I ，B C =∅I ，（1）用列举法表示集合A 和集合C （2）试求a 的值。
重庆市第一中学2016-2017学年高一上学期数学期中试题及答案
重庆市第一中学2016-2017学年高一数学上学期期中试题共4页，满分150分，考试时间120分钟。
注意事项：1.答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号。
3.答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答，在试题卷上答题无效。
第I 卷（选择题，共60分） 一、选择题：(本大题共12个小题，每小题5分，共60分)在每小题给出的四个选项中，只有一项是符合题目要求的；各题答案必须答在答题卡上相应的位置.1. 设全集{}4,3,2,1=U ，集合{}{}4,2,4,3,1==B A ，则()U C A B ⋂=（ ） A ．{}2B ．{}4,2C ．{}4,2,1 D ．φ2. 函数()()1011≠>-=-a a a x f x 且的图象必经过定点（ ）A ．()1,0-B ．()1,1-C ．()0,1-D ．()0,13. 在0到π2范围内，与角34π-终边相同的角是（ ） A ．6π B ．3π C ．32π D ．34π4. 函数()()2lg 231++-=x xx f 的定义域是（ ）A ．⎪⎭⎫ ⎝⎛-232， B ．⎥⎦⎤ ⎝⎛-232， C ．()∞+-，2 D ．⎪⎭⎫ ⎝⎛∞+，23 5. 已知3.0log 24.053.01.2===c b a ，，，则（ ） A ．b a c << B ．c b a << C ．a b c << D ．bc a <<6. 函数()xx x f 1ln -=的零点所在的大致区间是（ ） A ．⎪⎭⎫ ⎝⎛1,1eB ．()e ,1C ．()2,e e D ．()32,e e7. 已知函数()(),03)0(log 2⎩⎨⎧≤>=x x x x f x则⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛81f f 的值是（ ） A ．27-B ．271-C ．27D ．2718. 函数xx y xe ⋅=的图像的大致形状是（ ）A B C D9. 已知函数()()53log 221+-=ax x x f 在[)∞+-，1上是减函数，则实数a 的取值范围是（ ） A ．(]6,-∞- B ．[)68，- C ．(]68--，D ．[)+∞-,8 10. （原创）已知关于x 的方程12=-m x 有两个不等实根，则实数m 的取值范围是（ ）A ． (]1,-∞-B ．()1,-∞-C ．[)∞+，1 D ．()∞+，1 11.（原创）已知函数()()()1011ln2≠>-+++=a a a a x x x f xx且，若()()313log lg 2=f ，则()()=2log lg 3f （ ）A ．0B ．31C ．32D ． 1 12. 设函数()a x e x f x-+=2（e R a ,∈为自然对数的底数），若存在实数[]1,0∈b 使()()b b f f =成立，则实数a 的取值范围是（ ）A ．[]e ，0B ．[]e 1,1+C ． []e +2,1D ．[]1,0第II 卷（非选择题，共90分）二、填空题：(本大题共4个小题，每小题5分，共20分)各题答案必须填写在答题卡相应的位置上. 13. 幂函数()()3221-+--=m mx m m x f 在()∞+，0上为增函数，则实数m =______. 14. 扇形的周长为8cm ，圆心角为2弧度，则该扇形的面积为____2cm .15. 已知函数()x f 是定义在R 上的奇函数，且当0≥x 时，()x x x f 22+=，则当0<x 时，()x f =__________.16. 已知函数()3||log )(31+-=x x f 的定义域是[]b a ,()Z b a ∈,，值域是[]0,1-，则满足条件的整数对()b a ,有________对．三、解答题：解答应写出文字说明、证明过程或演算步骤. 17.（10分）（原创）化简：（1）()7112log 4231123log 743π⎛⎫--++ ⎪⎝⎭；（2）()5262512lg 20lg 5lg 2--+++⋅.18.（12分）(原创）已知集合A 为函数()[]2,1,122∈-+=x x x x f 的值域，集合⎭⎬⎫⎩⎨⎧≤--=014x x xB ，则（1）求A B I ；（2）若集合{}1+<<=a x a x C ，C C A =⋂，求实数a 的取值范围.19. （12分）（原创）已知函数()x f y =为二次函数，()40=f ，且关于x 的不等式()02<-x f 解集为{}21<<x x ，（1）求函数()x f 的解析式；（2）若关于x 的方程()0=-a x f 有一实根大于1，一实根小于1，求实数a 的取值范围.20. （12分）（原创）已知函数()xx xx a x f --+⋅-=2222是定义在R 上的奇函数.（1）求实数a 的值，并求函数()x f 的值域；（2）判断函数()x f y =的单调性（不需要说明理由），并解关于x 的不等式()03125≥-+x f .21. （12分）（原创）已知函数()⎪⎪⎩⎪⎪⎨⎧>+-≤⎪⎭⎫⎝⎛-=0,1210,2122x x x x x f x，（1）画出函数()x f 的草图并由图像写出该函数的单调区间；（2）若()a x g xx -=-23，对于任意的[]1,11-∈x ，存在[]1,12-∈x ，使得()()21x g x f ≤成立，求实数a的取值范围.22. （12分）对于在区间],[n m 上有意义的函数)(x f ，若满足对任意的21,x x ],[n m ∈，有|)()(|21x f x f -1≤恒成立，则称)(x f 在],[n m 上是“友好”的，否则就称)(x f 在],[n m 上是“不友好”的．现有函数()xaxx f +=1log 3， （1）若函数)(x f 在区间]1,[+m m ()21≤≤m 上是 “友好”的，求实数a 的取值范围； （2）若关于x 的方程()[]1423log )(3=-+-a x a x f 的解集中有且只有一个元素，求实数a 的取值范围．2016年重庆一中高2019级高一上期半期考试数 学 答 案2016.12一、选择题：(本大题共12个小题，每小题5分，共60分) ADCAA BDBCD CB二、填空题：(本大题共4个小题，每小题5分，共20分) 13. 2 14.4 15. x x 22+- 16.5三、解答题：解答应写出文字说明、证明过程或演算步骤。
重庆市第一中学2016-2017学年高一上学期期中考试数学试题Word版含解析
数学试题
一、选择题（本大题共 12 个小题，每小题 5 分，共 60 分. 在每小题给出的四个选 项中，只有一项是符合题目要求的 . ）
1. 设全集 U 1,2,3,4 ，集合 A 1,3,4 ， B 2,4 ，则 CU A B （ ）
A． 2
【答案】 B
．
2
e
，e3
考点：函数的零点的判定 .
7. 已知函数 f x
log 2 x x
x
3x0
0 ，则 f
1 f
8
的值是（
）
A． 27
B
．1
C.27
D
27
【答案】 D
1 ．
27
【解析】
试题分析：因 f (1) 8
log
2
1 8
3 , 故 f ( 3) 3 3
1
, 应选 D.
27
考点：对数函数指数函数的求值计算 .
【答案】 (1) 1 ，1 ； (2) 单调递增， [0 ， ) .
【解析】
试题分析： (1) 借助题设条件运用奇函数的性质求解； (2) 借助题设运用函数的单调性探求 .
试题解析：
（ 1）由题意易知 f 0
0
20 20
a 20 20
，故 a
1.
所以 f x
x
x
22
x
x
22
2x
21
2
2x
1 2x
x R，
|x| 3
. 求解时
0 |x| 2
运用分析检验的方法进行分析推证 , 不难求出符合条件的数对为
a2a2
或
数学---重庆市沙坪坝区重庆一中2016-2017学年高一上学期期中考试试题
2016年重庆一中高2019级高一上期半期考试 数 学 试 题 卷第I 卷（选择题 共60分）一、选择题：(本大题共12个小题，每小题5分，共60分)在每小题给出的四个选项中，只有一项是符合题目要求的；各题答案必须答在答题卡上相应的位置.）1. 设全集{}4,3,2,1=U ，集合{}{}4,2,4,3,1==B A ，则()U C A B ⋂=（ ） A ．{}2B ．{}4,2C ．{}4,2,1 D ．φ2. 函数()()1011≠>-=-a a a x f x 且的图象必经过定点（ ）A ．()1,0-B ．()1,1-C ．()0,1-D ．()0,13. 在0到π2范围内，与角34π-终边相同的角是（ ） A ．6π B ．3π C ．32π D ．34π4. 函数()()2lg 231++-=x xx f 的定义域是（ ）A ．⎪⎭⎫ ⎝⎛-232， B ．⎥⎦⎤ ⎝⎛-232， C ．()∞+-，2 D ．⎪⎭⎫ ⎝⎛∞+，235. 已知3.0log 24.053.01.2===c b a ，，，则（ ）A ．b a c <<B ．c b a <<C ．a b c <<D ．b c a <<6. 函数()xx x f 1ln -=的零点所在的大致区间是（ ） A ．⎪⎭⎫ ⎝⎛1,1eB ．()e ,1C ．()2,e e D ．()32,e e7. 已知函数()(),03)0(log 2⎩⎨⎧≤>=x x x x f x则⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛81f f 的值是（ ）A ．27-B ．271-C ．27D ．271 8. 函数xx y xe ⋅=的图像的大致形状是（ ）A B C D9. 已知函数()()53log 221+-=ax x x f 在[)∞+-，1上是减函数，则实数a 的取值范围是（ ）A ．(]6,-∞-B ．[)68，- C ．(]68--，D ．[)+∞-,810.已知关于x 的方程12=-m x有两个不等实根，则实数m 的取值范围是（ ）A ． (]1,-∞-B ．()1,-∞-C ．[)∞+，1D ．()∞+，1 11.（原创）已知函数()()()1011ln 2≠>-+++=a a a a x x x f xx且，若()()313l o g lg 2=f ，则()()=2log lg 3f （ ） A ．0B ．31 C ．32D ． 1 12. 设函数()a x e x f x-+=2（e R a ,∈为自然对数的底数），若存在实数[]1,0∈b 使()()b b f f =成立，则实数a 的取值范围是（ ）A ．[]e ，0B ．[]e 1,1+C ． []e +2,1D ．[]1,0第II 卷（非选择题，共90分）二、填空题：(本大题共4个小题，每小题5分，共20分)各题答案必须填写在答题卡相应的位置上.13. 幂函数()()3221-+--=m m xm m x f 在()∞+，0上为增函数，则实数m =______. 14. 扇形的周长为8cm ，圆心角为2弧度，则该扇形的面积为____cm 2.15. 已知函数()x f 是定义在R 上的奇函数，且当0≥x 时，()x x x f 22+=，则当0<x 时，()x f =__________.16. 已知函数()3||log )(31+-=x x f 的定义域是[]b a ,()Z b a ∈,，值域是[]0,1-，则满足条件的整数对()b a ,有________对．三、解答题：解答应写出文字说明、证明过程或演算步骤.17.（10分）（原创）化简：（1）()71102log 4231123log 743π⎛⎫--++ ⎪⎝⎭；（2）()5262512lg 20lg 5lg 2--+++⋅.18.（12分）(已知集合A 为函数()[]2,1,122∈-+=x x x x f 的值域，集合⎭⎬⎫⎩⎨⎧≤--=014x x xB ，则（1）求A B ；（2）若集合{}1+<<=a x a x C ，C C A =⋂，求实数a 的取值范围.19. （12分）（原创）已知函数()x f y =为二次函数，()40=f ，且关于x 的不等式()02<-x f 解集为{}21<<x x ，（1）求函数()x f 的解析式；（2）若关于x 的方程()0=-a x f 有一实根大于1，一实根小于1，求实数a 的取值范围.20.（12分）已知函数()xx xx a x f --+⋅-=2222是定义在R 上的奇函数.（1）求实数a 的值，并求函数()x f 的值域；（2）判断函数()x f y =的单调性（不需要说明理由），并解关于x 的不等式()03125≥-+x f .21. （12分）（原创）已知函数()⎪⎪⎩⎪⎪⎨⎧>+-≤⎪⎭⎫⎝⎛-=0,1210,2122x x x x x f x，（1）画出函数()x f 的草图并由图像写出该函数的单调区间； （2）若()a x g xx-=-23，对于任意的[]1,11-∈x ，存在[]1,12-∈x ，使得()()21x g x f ≤成立，求实数a 的取值范围.22. （12分）对于在区间],[n m 上有意义的函数)(x f ，若满足对任意的21,x x ],[n m ∈，有|)()(|21x f x f -1≤恒成立，则称)(x f 在],[n m 上是“友好”的，否则就称)(x f 在],[n m 上是“不友好”的．现有函数()xaxx f +=1log 3， （1）若函数)(x f 在区间]1,[+m m ()21≤≤m 上是 “友好”的，求实数a 的取值范围； （2）若关于x 的方程()[]1423log )(3=-+-a x a x f 的解集中有且只有一个元素，求实数a 的取值范围．2016年重庆一中高2019级高一上期半期考试 数 学 答 案一、选择题ADCAA BDBCD CB二、填空题13. 2 14. 4 15. x x 22+- 16.5三、解答题17.解：（1）原式=2321123=+--. （2）原式= ()()()2215252lg 5lg 2lg 10lg ---+++()012lg 5lg 2lg 5lg =-+⋅+=.18[](]41721:，，，）（解==B A ,A B []4,2=. (2)由题意可知 A C ⊆,则⎩⎨⎧≤+≥712a a 解得62≤≤a . 综上，a 的取值范围为[]6,2.19. （12分）解：（Ⅰ）∵设函数()()02≠++=a c bx ax x f ，则()40==c f ,()0222<++<bx ax x f 即, 故aa b 221,21=⨯-=+,3,1-==b a ,∴()432+-=x x x f .（2）()a x x x g -+-=432,则()024311<-=-+-=a a g , 故2>a .20.解：（1）由题意易知()0000222-200+⋅==a f , 故1=a ,所以()122112122222222+-=+-=+-=--x x x x xx x x f ()R x ∈. 0122211210112022222<+-<-∴<+<∴>+∴>x x x x112211-2<+-<∴x, 故函数()x f 的值域为()1,1-. （2）由（1）知()12212+-=x x f ,易知()x f 在R 上单调递增,且()5314211=+-=f . 故112≥+x ,0≥∴x .所以不等式()03125≥-+x f 的解集为[)∞+，0.21.解：（1）如下图所示，易知函数()x f 的单调递减区间为()1,0，单调递增区间为()()∞+∞，，，10-.（2）由题意可得()[]()[]max 2max 1x g x f ≤,其中()()10max ==f x f ()()a g x -=-=91g max ，， 即a -≤91,故8≤a .综上所述：(]8，∞-∈a . 22.解：（1）由题意可得()⎪⎭⎫⎝⎛+=+=a x x ax x f 1log 1log 33在]1,[+m m 上单调递减， 故()(),1log 3max ⎪⎭⎫⎝⎛+==a m m f x f ()(),11log 13in ⎪⎭⎫⎝⎛++=+=a m m f x f m ∴()()111log 1log 33min max ≤⎪⎭⎫⎝⎛++-⎪⎭⎫ ⎝⎛+=-a m a m x f x f ,即3111⋅⎪⎭⎫⎝⎛++≤+a m a m ,∴()max11221⎪⎪⎭⎫ ⎝⎛+-⋅-≥m m m a . 令)31(12≤≤-=t m t ，则21+=t m ，则()1434134423211122++=++=+⋅+=+-=tt t t t t t t m m m y , 当31或=t 时，21min =y ,41-≥∴a .又对于任意的]1,[+∈m m x ，011>+=+a x x ax ，故31111max-≥+-=⎪⎭⎫⎝⎛->m x a . 综上，a 的取值范围是⎭⎬⎫⎩⎨⎧-≥41a a .（2）()[]1423log )(3=-+-a x a x f ，即()04231>-+-=+a x a a x ，且()1423≠-+-a x a ,（1）()()01432=--+-∴x a x a ，即()[]()0113=+--x x a , （2）当3=a 时，方程(2)的解为1-=x ,代入（1），成立. 当2=a 时，方程(2)的解为1-=x ,代入（1），不成立. 当32≠≠a a 且时，方程(2)的解为1-=x 或31-=a x . 将1-=x 代入（1），则()01423>-=-+-a a x a ,且11≠-a . 所以21≠>a a 且.将31-=a x 代入（1），则()032423>-=-+-a a x a ,且132≠-a , 所以223≠>a a 且,则要使方程有且仅有一个解，则231≤<a .综上，若方程()[]1423log )(3=-+-a x a x f 的解集中有且仅有一个元素，则a 的取值范围为⎭⎬⎫⎩⎨⎧=≤<3231a a a 或.。
重庆市第一中学2017届高三上学期期中考试数学(理)试题 Word版含答案
数学试题卷（理科）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项 是符合题目要求的.1.函数()sin cos f x x x =的最小正周期等于（ ） A ．4πB ．2πC ．πD ．2π2.已知向量(1,2)a = ，(,2)b x =- ，且a b ⊥ ，则||a b +=（ ）A ．5B C ．D 3.已知x ，y 均为非负实数，且满足1,42,x y x y +≤⎧⎨+≤⎩则2z x y =+的最大值为（ ）A ．1B ．12C ．53D ．24.《张丘建算经》是我国南北朝时期的一部重要数学著作，书中系统的介绍了等差数列，同类结果在三百多年后的印度才首次出现．书中有这样一个问题，大意为：某女子善于织布，后一天比前一天织的快，而且每天增加的数量相同，已知第一天织布5尺，一个月（按30天计算）总共织布390尺，问每天增加的数量为多少尺?该问题的答案为（ ） A ．829尺 B ．1629尺 C ．3229尺 D ．12尺 5.设函数()2sin(2)6f x x π=+，将()f x 图象上每个点的横坐标缩短为原来的一半之后成为函数()y g x =，则()g x 图象的一条对称轴方程为（ ） A ．24x π=B ．512x π=C ．2x π=D ．12x π=6.已知函数()xxf x e ae -=+为偶函数，若曲线()y f x =的一条切线的斜率为32，则切点的横坐标等于（ ）A ．ln 2B ．2ln 2C ．2 D7.若“1,22x ⎡⎤∃∈⎢⎥⎣⎦，使得2210x x λ-+<成立”是假命题，则实数λ的取值范围为（ ）A ．(,-∞B ．⎡⎤⎣⎦C ．⎡⎤-⎣⎦D ．=3λ8.若函数()f x x λ=-+在[]1,1-上有两个不同的零点，则λ的取值范围为（ ）A ．B ．(C ．(1]-D ．[1,1]-9.设椭圆2211612x y +=的左右焦点分别为1F ，2F ，点P 在椭圆上，且满足129PF PF ⋅= ，则12||||PF PF ⋅的值为（ ） A ．8B ．10C ．12D ．1510.已知函数21()1214x xf x =+++满足条件(log 1))1a f =，其中1a >，则(log 1))a f -=（ ）A ．1B ．2C ．3D ．411.已知(0,)2x π∈，则函数()sin tan cos cot f x x x x x =+的值域为（ ）A ．[1,2)B ．)+∞C ．D ．[1,)+∞12.设A ，B 在圆221x y +=上运动，且||AB =P 在直线34120x y +-=上运动，则||PA PB +的最小值为（ ）A ．3B ．4C ．175D ．195第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.点(1,3)P 关于直线220x y +-=的对称点为Q ，则点Q 的坐标为 ．14.已知(,)2παπ∈，且sin α=，则tan(2)4πα+= ．15.设正实数1x y +=，则22x y +的取值范围为 ．16.在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且满足条件2221b c a bc +-==，1cos cos 8B C =-，则△ABC 的周长为 ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.已知等比数列{}n a 单调递增，记数列{}n a 的前n 项之和为n S ，且满足条件26a =，326S =．（1）求数列{}n a 的通项公式；（2）设2n n b a n =-，求数列{}n b 的前n 项之和n T ．18.根据某电子商务平台的调查统计显示，参与调查的1000位上网购物者的年龄情况如图． （1）已知[30,40)、[40,50)，[50,60)三个年龄段的上网购物者人数成等差数列，求a ，b 的值；（2）该电子商务平台将年龄在[30,50)之间的人群定义为高消费人群，其他的年龄段定义为潜在消费人群，为了鼓励潜在消费人群的消费，该平台决定发放代金券，高消费人群每人发放50元的代金券，潜在消费人群每人发放80元的代金券．已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人，现在要在这10人中随机抽取3人进行回访，求此三人获得代金券总和X 的分布列与数学期望．19.已知四棱柱1111ABCD A B C D -的底面是边长为2的菱形，且3BAD π∠=，1AA ⊥平面ABCD ，11AA =，设E 为CD 的中点．（1）求证：1D E ⊥平面1BEC ；（2）点F 在线段11A B 上，且//AF 平面1BEC ，求平面ADF 和平面1BEC 所成锐角的余弦值．20.已知椭圆C ：22221(0)x y a b a b +=>>，椭圆C 和抛物线2y x =交于M ，N 两点，且直线MN 恰好通过椭圆C 的右焦点。
(完整版)重庆市第一中学2016_2017学年高一数学上学期期末考试试题
2017 年重庆一中高2019 级高一上期期末考试数学试题卷一. 选择题 .( 每题5分,共 60 分)1. 已知扇形的半径为 2 ，弧长为 4 ，则该扇形的圆心角为（）A ． 2B ． 4C ． 8D ． 162. 设全集 U {1,2,3,4,5} ，会合 M {1,4} ， N {1,3,5} ，则 N C U M 等于 ( ) A．{1,3} B ．{1,5} C ．{3,5} D ． {4,5}3.14（）sin3A. 3B. 1C. 1D. 32 2 224. 幂函数 y x( p 1)(4 p) ( p N ) 为偶函数，且在0, 上单一递加，则实数p （）A ． 1B ． 2C ． 4D ． 55. 已知( , )，且 sin 5 ，则 tan 2 （）52A ．2B ．1C ．4D ． 42 3 36. 函数 y a sin x b cos x 知足 f ( 2 x) f (x) ，那么a＝（）3 bA ．3B ． 1C ．－ 3D ．－ 17. 已知函数 f ( x) log 1 sin 2 x ，则以下说法正确的选项是（）2A ．函数f (x)为奇函数B ．函数 f ( x) 有最大值0C ．函数f (x)在区间( k ,2 k )(k Z) 上单一递加4D ．函数f (x)在区间(0, ) 上单一递加48. 函数 f ( x) Asin( x )( A 0, 0, ) 的图象如下图，为2了获得 g( x) Asin 2x的图象，则只要将 f (x) 的图象（）A ．向左平移个长度单位12B ．向右平移 个长度单位12C ．向左平移 个长度单位6D ．向右平移 个长度单位69. 已知函数 f ( x)2 xx 2 ，则不等式 f (2sin x) 3,x[2 , ] 的解集为（）2A ．(, )B ．．D ．6 6(, 3 ) C [,)(, ][ ,)( , ]3266 22 3 3 210. 若 关 于 x 的 函 数 f ( x) t x22 x t2x 2si n x(t 0)的最大值为M ，最小值为 N ，且x 2 tM N 4 ，则实数 t 的值为（ ）A ． 1D ． 411. （原创）已知对于 x 方程 log x1 1.4 x 1 ，则该方程的全部根的和为（）12. （原创）已知f (x) 是定义在 R 上的奇函数，对随意 x R 知足 f (2 x 8) f (2 x )，且当x (0,4) 时， f (x)x 2x cosx 1 ，则函数 f ( x) 在区间 [ 4,12] 上的零点个数是（）A ．7B． 9C． 11D．13二. 填空题 .( 每题 5 分, 共 20 分)13. 已知角的始边落在 x 轴的非负半轴上，且终边过点 P( 3,1) ，且 [0,2 )，则.14. 求值： 2log 2 (lg5)lg 2ln e 2 ________ ___. （此中 e 为自然对数的底）15.求值： 2cos10 (1 sin10 ) . cos 2016. 已知二次函数 f ( x) ax2 bx c 知足条件：① 4a b 2a ；② x[ 1,1]时， f (x)1 ，若对随意的 x [ 2, 2] ，都有 f ( x) m 恒建立，则实数 m 的取值范围为 .三.解答题 .( 共 6小题,共 70分) 17.（本小题满分 10 分）已知（ 1）求sin的值；(0, ), tan3，2 4（2）求 2sin( ) cos( )的值.sin( ) cos( )2 218. （本小题满分12 分）已知函数f (x) 2 log 2 x 的定义域为 A ，关于x的不等式x2 (a2 a) x a3 0 的解集为B，此中a 0 ，（1）求A；2ABB，务实数 a 的取值范围.（）若19. （本小题满分12 分）在ABC 中，A, B为锐角，角A, B, C 所对应的边分别为a,b, c ，且cos 2A 3 , sinB 10 .5 10（1）求A B 的值；（ 2）求函数 f (x) cos 2x 2 5 sin Asin x 的最大值.20. （本小题满分 12 分）已知函数 f ( x) (sin x cos x)2 2cos 2 x 2(0) ．（ 1）若f ( x)的最小正周期为，求 f (x) 在区间[ , ] 上的值域；4 4（ 2）若函数 f ( x) 在 ( , ) 上单一递减.求的取值范围.221. （原创）（本小题满分 12 分）已知 f (x) 2x2 x , 定义在 (0,) 上的连续不停的函数 g( x) 知足 g( xy) g( x)g( y) ，当 x 1时， g( x)0 且 g(2)2 ．（ 1）解对于 x 不等式：f (2x) 5 f ( x)2 0 ；2（ 2）若对随意的 x 1 (1, ) ，存在 x 2 R ，使得 g 2 ( x 1 )(1a) g( x 12) g (4) a f (2 x 2 ) 4 f ( x 2 ) 7 建立，务实数 a 的范围 .222. （原创）（本小题满分 12 分）已知函数f ( x) 2 x 1 ， g( x)x 211 x3 ，333 2 32（ 1） a R ，若对于 x 的方程log 4 [ f ( x 1) ] log 2 ( a x) log 2 ( 4 x ) 有两个不一样解，2 4务实数 a 的范围；（ 2 ）若对于 x 的方程： x[ f ( x) g ( x)] mx 0 有三个不一样解 0, x 1, x 2 (x 1 x 2 ) ，且对随意的x [ x 1 , x 2 ] ， x[ f ( x) g( x)] m( x 1) 恒建立，务实数 m 的范围 .2 017 年重庆一中高 2019 级高一上期期末考试数 学 答 案一、选择题 ACDBDCCDCBDB二、填空题13.514.3 15.3 16. ( , 5]64三、解答题17. 解：（ 1） sin3 ；（ 2） 2sin( ) cos( ) 2sin cos 2tan 1 2 .5sin() cos() cos sin1 tan72218. 解：（ 1） 2 log 2 x 0,log 2 x 2 log 2 4, A (0, 4] ；（ 2）因为 AB B 因此BA ，x 2(a 2 a) x a 3 0(x a)( x a 2 ) 0 ，若 a 1 ， B，切合题意；若 a 1 ， B (a,a 2 ) (0, 4] ，则 a 2 4 1 a 2 ；若 0a 1， B (a 2 , a)(0, 4] ，则 0 a 1，综上， 0 a 2 .19. 解：（Ⅰ）A 、B 为锐角， sin B10 ， cos B1 sin2 b3 101010又 cos2A1 2sin2 A3 ， sin A5 ， cos A1 sin2 A 2 5 ，5 55 cos( AB) cos A cos B25 3 10 5 10 2 0 A Bsin Asin B5105102A B；4（ 2） f ( x) cos 2x 2 5 sin Asin x cos 2x 2sin x2sin 2 x 2sin x12(sin x 1)2 3 ，因此函数的最大值为 3 .2 2 220. 解：（Ⅰ）f ( x) (sin x cos x)22cos2x 2 sin 2x cos2x sin 2 x 1 2cos 2 x 2sin 2 x cos2 x 2 sin(2 x ) ， f (x) 的最小正周期为， T 2 ，所以241, f (x ) 2 s i nx( 2 ， x) [ , ] 时， 2x4 [4,3] ， sin(2 x ) [2,1]，4 4 4 4 4 2 因此函数值域为 [ 1, 2]；（ 2）0 时，令2k 2 x 3, k Z ，f ( x)的单减区间为2 42k2k[ k , 5 k] ，由题意 ( , ) [ k 5, k ，] 可得8k2，解得8 8 2 8 8 581 2k 5 k, k Z，只有当 k 0 时，15 .4 80 4 821. 解：（ 1）f (2x) 5f ( x) 0 (22 x 2 2 2 x ) 5 (2x 2 x) 05 2 1)(2 x2(2 x 2 x ) 0 (2x 2) 0，解得 1 x 1 ；2 2（ 2）y f (2 x) 4 f ( x) 7 (2 2 x 2 2 2 x) 4(2 x 2 x ) 5(2 x 2 x 2) 2 1 ，问题转变为对随意的x (0, ) ，有g2(x1) (1 a)g ( x12 ) g(4) a 1 恒2建立，即 g 2 ( x) (2 a) g( x) 4 a 1 恒建立，下证函数g ( x) 在(0, ) 上单增：取任意的 x1 x2 (0, ) ，g ( x1 ) g( x2 ) g( x1 ) g( x1 x2 ) g(x2 ) 0 ，因此函数 g( x) 在 (0, ) 上单增，x1 x1因为 g(1) 0 ， g(2) 2 ，因此 x1 (1, ) 时函数可取到 (0, 2] 之间的全部值，g2 (x) 2g( x) 3( g( x) 1) 2恒建立，因此 a 2 2 ，当 g( x) 2 1时取等.ag( x) 1 g( x) 1log 4 (x 1) log a xx a1) ( ax )2，即22. 解：（ 1 ）原方程可化为，且，即 (x4 x 1 x 44 x x 1a x，且方程要有解， a 1 ，4 x①若 1 a 4，则此时 1x a 4 ，方程为 x 26 x a 4 0 ，20 4a 0 ，方程的解为x 35 a ，仅有 x35 a 切合 1x a 4 ；②若 a4，此时 1 x 4 ，20 4a 0 ，即 4 a 5 ，方程的解为x 3 5 a (1,4) 均切合题意，综上4 a5 ；（ 2）原方程等价于x( x 2 3x2 m) 0 ，则 x 1 , x 2 为 x 2 3x 2m 0 的两个不一样根，因此9 4(2m) 0 ，解得 m1 ，而且令 h( x) x( x2 3x 2 m) ，4又对随意的x [ x 1, x 2 ] ， x[ f (x) g(x)]m(x 1) 恒建立，即 x[ f ( x)g ( x)] mxm ，取x x 1 ，有 m 0 ，即 m 0，综上 1m 0,4由 维 达 定 理 x 1 x 2 2m 0 , x 1x 23 ，0 所 以 0 x 1 x 2 ， 则 对 任 意 x ( x 1 , x 2 ) ，h( x) x(x 23x2 m) x( x x 1)( x x 2 ) 0 ，且 h max ( x) h(x 1) 0 ，因此当1 m 0 时，14原不等式恒建立，综上m 0 .4。
重庆一中高一(上)期中数学试卷含答案
本题考查复合函数的单调性，解题的关键是确定内函数的单调性，属于中档题．
10.【答案】D
【 +当解 푚1析=】2푥解−1：>2−푥−1푚时=，1有或一2个푥−解푚， = −1，即푚 = 2푥−1，或者푚， = 2푥
当푚 = 2푥 +1 > 1时，有一个解， 所以푚 > 1时，方程|2푥−푚| = 1有两个不等实根， 故选：D． 分离参数，再根据指数函数性质求出． 考查方程根的个数问题，利用了分类讨论法，分离参数法，中档题．
第 6 页，共 15 页
4.【答案】A
【解析】解：由{3푥−+2푥2
> >
00，解得−2
<
푥
< 32．
∴ 函数푓(푥) =
1 3−2푥
+
lg(푥
+ 2)的定义域是(−2,32).
故选：A．
由分母中根式内部的代数式大于 0，对数式的真数大于 0 联立不等式组求解．
本题考查函数的定义域及其求法，是基础题．
5.【答案】A
【解析】解： ∵ 0 < 푎 = 0.42.1 < 0.40 = 1 ， 푏 = 20.3 > 20 = 1， 푐 = log50.3 < log51 = 0． ∴ 푐 < 푎 < 푏． 故选：A． 利用有理指数幂与对数的运算性质分别比较 a，b，c 与 0 和 1 的大小得答案． 本题考查对数值的大小比较，考查有理指数幂与对数的运算性质，是基础题．
A. (1e,1)
B. (1,푒)
C. (푒,푒2)
{ 7.
已知函数푓(푥)
=
푙표푔2푥(푥 > 3푥(푥 ≤ 0)
重庆市一中高一数学上学期期中试题(含解析)
2017年重庆一中高2010级高一上半学期考试数学试题卷第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 实数不是下面哪一个集合的元素（）A. 整数集B.C.D.【答案】C【解析】由题意，C选项集合为，不包含1，故选C。
2. 不等式的解集是（）A. B. C. D.【答案】D【解析】，，所以，故选D。
3. 已知幂函数的图象过点，则（）A. B. C. D.【答案】D【解析】，则，，所以，故选D。
4. 已知，则（）A. B. C. D.【答案】A【解析】，所以，故选A。
5. 函数的单调递减区间是（）A. B. C. D.【答案】C【解析】令，由复合函数“同增异减”性质，的单调递减区间即单调递减区间，所以单调递减区间为，故选C。
6. 将函数的图象经过下列哪一种变换可以得到函数的图象（）A. 向左平移1个单位长度B. 向右平移1个单位长度C. 向左平移2个单位长度D. 向右平移2个单位长度【答案】B【解析】，所以是由右移1个单位得到，故选B。
7. 已知定义在上的减函数满足条件：对任意，总有，则关于的不等式的解集是（）A. B. C. D.【答案】C【解析】令，则，得，所以，又在单调递减，所以，得，故选C。
8. 函数的值域是（）A. B. C. D.【答案】B【解析】令，，则或，故选B。
9. 若，则（）A. B. C. D.【答案】A【解析】，所以，故选A。
10. 已知函数与的定义如下表：则方程的解集是（）A. B. C. D.【答案】A【解析】时，，是方程的解；时，，不是方程的解；时，，不是方程的解；所以方程的解集为，故选A。
..................11. 已知函数的值域是，则（）A. B. C. D.【答案】D【解析】，所以在是奇函数，则，所以，故选D。
点睛：观察题目，题目函数较复杂，定义域为对称性区间，则函数很有可能具有对称性，经验证得到函数为奇函数，则值域的最大最小值互为相反数，得，所以。
重庆市第一中学2016届高三数学上学期期中试题理
重庆一中高2016级2015—2016学年度上学期半期考试数 学 试 题 卷（理科）2015.11数学试题共4页，满分150分，考试时间120分钟。
注意事项：1、答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2、答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号。
3、答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。
4、所有题目必须在答题卡上作答，在试题卷上答题无效。
第I 卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1、已知集合()()(){}2,12,,log 23A B x x =-∞-+∞=+≤，则A B =（ ）A 、()2,6B 、()(],12,6-∞-C 、()(]2,12,6--D 、(]3,62、已知复数1z i =-（i 是虚数单位），则22z z-的共轭．．复数是（ ） A 、13i -B 、13i +C 、13i -+D 、13i --3、已知双曲线()222210,0x y a b a b-=>>的一条渐近线与直线25y x =+平行，则双曲线的离心率等于（ ）A 、2BC 、5D4、已知倾斜角为θ的直线l ，与直线:310m x y -+=垂直，则22sin23sin cos θθθ=-（ ） A 、133B 、1013-C 、313-D 、10135、已知向量()()()3,1,1,3,,2a b c k ===-，若()//a c b -，则向量a 与向量c 的夹角的余弦是（ ）A 、5B 、15C 、5-D 、15-6、要得到函数()sin 26f x x π⎛⎫=+ ⎪⎝⎭的导函数()'f x 的图象，只需将()f x 的图象（ ）A 、向右平移4π个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变） B 、向右平移2π个单位，再把各点的纵坐标缩短到原来的2倍（横坐标不变）C 、向左平移2π个单位，再把各点的纵坐标缩短到原来的2倍（横坐标不变）D 、向左平移4π个单位，再把各点的纵坐标伸长到原来的2倍（横坐标不变）7、对于函数()tan 2f x x =，下列选项中正确的是（ ） A 、()f x 在,24ππ⎛⎫-⎪⎝⎭上是递增的B 、()f x 在定义域上单调递增C 、()f x 的最小正周期为πD 、()f x 的所有对称中心为,04k π⎛⎫⎪⎝⎭8、已知0,0a b >>满足1a b +=，则19a b+的最小值为（ ） A 、12B 、16C 、20D 、259、已知1cos ,0,632ππαα⎛⎫⎡⎤+=∈ ⎪⎢⎥⎝⎭⎣⎦，那么cos α等于（ ）A B C D 10、已知某个几何体的三视图如下，根据图中标出的尺寸，那么可得这个几何体最长的棱长是（ ）A 、2BC 、D 、11、定义在0,2π⎛⎫⎪⎝⎭上的函数()f x ，()'f x 是它的导函数，且恒有()()sin 'cos x f x x f x ⋅>⋅成立，则（ ）A 64f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭B 63f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭C 264f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭D 63f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭12、O 是坐标原点，点()1,1A -；点(),P x y 为平面区域0201x x y y kx ≥⎧⎪-≤⎨⎪≤+⎩上的一个动点，函数()()f OP OA R λλλ=-∈的最小值为M ，若M ≤则k 的取值范围是 ） A 、1k ≤B 、11k -≤≤C 、03k ≤≤D 、13k k ≤≥或第II 卷（非选择题，共90分）本卷包括必考题和选考题两部分。
重庆市一中高三数学上学期期中试卷 文(含解析)
2015-2016学年重庆一中高三（上）期中数学试卷（文科）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合 A={1，2，4}，B={a，3，5}，若A∩B={4}，则A∪B=( )A．{4} B．{1，2，4，5} C．{1，2，3，4，5} D．{a，1，2，3，4，5}2．命题“对任意x∈R，都有x2﹣2x+4≤0”的否定为( )A．对任意x∈R，都有x2﹣2x+4≥0B．对任意x∈R，都有x2﹣2x+4≤0C．存在x0∈R，使得x02﹣2x0+4＞0 D．存在x0∈R，使x02﹣2x0+4≤03．已知复数和复数z2=cos30°+isin30°，则z1•z2为( )A．1 B．﹣1 C．D．4．已知k＜0，则曲线和有相同的( )A．顶点 B．焦点 C．离心率D．长轴长5．已知a，b是两条不同的直线，α是一个平面，则下列说法正确的是( )A．若a∥b，b⊂α，则a∥αB．若a∥α，b⊂α，则a∥bC．若a⊥α，b⊥α，则a∥b D．若a⊥b，b⊥α，则a∥α6．要得到函数y=sin（2x﹣）的图象，只需将函数y=sin2x的图象( )A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位7．对于函数f（x）=tan2x，下列选项中正确的是( )A．f（x）在（﹣，）上是递增的B．f（x）在定义域上单调递增C．f（x）的最小正周期为πD．f（x）的所有对称中心为（，0）8．已知a＞0，b＞0满足a+b=1，则的最小值为( )A．12 B．16 C．20 D．259．已知，，那么cosα等于( )A．B．C．D．10．已知某个几何体的三视图如下，根据图中标出的尺寸，那么可得这个几何体最长的棱长是( )A．2 B．C．2 D．211．定义在（0，）上的函数f（x），f′（x），是它的导函数，且恒有sinx•f′（x）＞cosx•f （x）成立，则( )A．f（）＞f（） B．f（）＞f（） C．f（）＞2f（）D．f（）＜f（）12．O是坐标原点，点A（﹣1，1），点P（x，y）为平面区域的一个动点，函数f（λ）=|﹣λ|（λ∈R）的最小值为M，若M≤恒成立，则k的取值范围是( ) A．k≤1 B．﹣1≤k≤1C．0≤k≤3D．k≤1或≥3二、填空题：本大题共4小题，每小题5分．13．已知直线l1：ax+y+3=0，l2：x+（2a﹣3）y=4，l1⊥l2，则a=__________．14．已知等差数列{a n}，若a1+a2+a3=﹣24，a18+a19+a20=78，则S20=__________．15．已知球O的体积为36π，则球的内接正方体的棱长是__________．16．椭圆（a＞b＞0）的右顶点为A，上、下顶点分别为 B2、B1，左、右焦点分别是F1、F2，若直线 B1F2与直线 AB2交于点 P，且∠B1PA为锐角，则离心率的范围是__________．三、解答题：解答应写出文字说明、证明过程或演算步骤．17．已知等差数列{a n}满足a2=4，a6+a8=18．（I）求数列{a n}的通项公式；（II）求数列{}的前n项和．18．已知函数f（x）=2sin cos+2cos2．（I）求f（x）的最小正周期和单调递减区间；（II）若f（B）=3，在△ABC中，角 A，B，C的对边分别是a，b，c，若b=3，sinC=2sin A，求a，c的值．19．如图，在四棱柱 ABCD﹣A1 B1C1D1中，CC1⊥底面 ABCD，底面 ABCD为菱形，点 E，F分别是 AB，B1C1的中点，且∠DAB=60°，AA1=AB=2．（I）求证：EF∥平面 AB1D1；（II）求三棱锥 A﹣CB1D1的体积．20．在平面直角坐标系xOy中，已知圆C1：（x+3）2+（y﹣1）2=4和圆C2：（x﹣4）2+（y﹣5）2=1．（I）若直线l过点 A（4，0），且被圆C1截得的弦长为2，求直线l的方程；（II）若从圆C1的圆心发出一束光线经直线x﹣y﹣3=0反射后，反射线与圆C2有公共点，试求反射线所在直线的斜率的范围．21．已知函数f（x）=xe ax+lnx﹣e（a∈R）．（I）当a=1时，求函数y=f（x）在点（1，f（1））处的切线方程；（II）设g（x）=lnx+﹣e，若函数h（x）=x•在定义域内存在两个零点，求实数a的取值范围．选修4-1：几何证明选讲22．如图，在Rt△ABC中，∠C=90°，B E平分∠A BC交 AC于点E，点D在AB上，DE⊥EB，且，AE=6．（I）判断直线 AC与△BDE的外接圆的位置关系并说明理由；（II）求EC的长．选修4-4：坐标系与参数方程23．已知曲线C1的参数方程是（θ为参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，曲线C2的极坐标方程是ρ=﹣4cosθ．（1）求曲线C1与C2交点的极坐标；（2）A、B两点分别在曲线C1与C2上，当|AB|最大时，求△OAB的面积（O为坐标原点）．选修4-5：不等式选讲24．（I）求|2x﹣1|+|2x+3|＜5的解集；（II）设a，b，c均为正实数，试证明不等式，并说明等号成立的条件．2015-2016学年重庆一中高三（上）期中数学试卷（文科）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合 A={1，2，4}，B={a，3，5}，若A∩B={4}，则A∪B=( )A．{4} B．{1，2，4，5} C．{1，2，3，4，5} D．{a，1，2，3，4，5}【考点】交集及其运算；并集及其运算．【专题】计算题；集合．【分析】由A，B，以及两集合的交集确定出a的值，进而确定出B，找出两集合的并集即可．【解答】解：∵A={1，2，4}，B={a，3，5}，且A∩B={4}，∴a=4，即B={3，4，5}，则A∪B={1，2，3，4，5}，故选：C．【点评】此题考查了交集及其运算，并集及其运算，熟练掌握各自的定义是解本题的关键．2．命题“对任意x∈R，都有x2﹣2x+4≤0”的否定为( )A．对任意x∈R，都有x2﹣2x+4≥0B．对任意x∈R，都有x2﹣2x+4≤0C．存在x0∈R，使得x02﹣2x0+4＞0 D．存在x0∈R，使x02﹣2x0+4≤0【考点】命题的否定．【专题】简易逻辑．【分析】根据全称命题的否定是特称命题即可得到结论．【解答】解：根据全称命题的否定是特称命题得：存在x0∈R，使得x02﹣2x0+4＞0，故选：C【点评】本题主要考查含有量词的命题的否定，比较基础．3．已知复数和复数z2=cos30°+isin30°，则z1•z2为( )A．1 B．﹣1 C．D．【考点】复数代数形式的乘除运算．【专题】计算题；函数思想；数系的扩充和复数．【分析】化简复数z2为代数形式，利用复数的乘法求解即可．【解答】解：复数和复数z2=cos30°+isin30°=，z1•z2===．故选：D．【点评】本题考查复数的代数形式的混合运算，考查计算能力．4．已知k＜0，则曲线和有相同的( )A．顶点 B．焦点 C．离心率D．长轴长【考点】椭圆的简单性质．【专题】计算题；规律型；函数思想；圆锥曲线的定义、性质与方程．【分析】求出两个椭圆的焦距，判断选项即可．【解答】解：曲线的焦距为：2；k＜0，的焦距为：2=2．焦点坐标都在x轴上，焦点坐标相同．故选：B．【点评】本题考查椭圆的简单性质的应用，考查计算能力．5．已知a，b是两条不同的直线，α是一个平面，则下列说法正确的是( )A．若a∥b，b⊂α，则a∥αB．若a∥α，b⊂α，则a∥bC．若a⊥α，b⊥α，则a∥b D．若a⊥b，b⊥α，则a∥α【考点】空间中直线与平面之间的位置关系．【专题】探究型；空间位置关系与距离．【分析】根据有关定理中的诸多条件，对每一个命题进行逐一进行是否符合定理条件去判定即可．【解答】解：若a∥b、b⊂α，则a∥α或a⊂α，故A错误；若a∥α、b⊂α，则a∥b或a，b异面，故B错误；若a⊥α，b⊥α，则a∥b，满足线面垂直的性质定理，故正确若b⊥α，a⊥b，则a∥α或a⊂α，故D错误；故选：C【点评】本题考查空间中直线与直线、直线与平面、平面与平面的位置关系，是基础题．解题时要认真审题，仔细解答，注意空间想象能力的培养．6．要得到函数y=sin（2x﹣）的图象，只需将函数y=sin2x的图象( )A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位【考点】函数y=Asin（ωx+φ）的图象变换．【专题】计算题．【分析】根据“左加右减”的平移法则将y=sin2x向右平移单位即可，从而可得答案．【解答】解：将函数y=sin2x的图象y=sin，即为y=sin（2x﹣）的图象．故选D．【点评】本题考查函数y=Asin（ωx+φ）的图象变换，掌握平移方向与平移单位是关键．7．对于函数f（x）=tan2x，下列选项中正确的是( )A．f（x）在（﹣，）上是递增的B．f（x）在定义域上单调递增C．f（x）的最小正周期为πD．f（x）的所有对称中心为（，0）【考点】正切函数的周期性；正切函数的奇偶性与对称性．【专题】计算题；数形结合；三角函数的图像与性质．【分析】求出函数的周期，判断A、C的正误；正切函数的单调性判断B的正误；求出对称中心判断D的正误；【解答】解：x=﹣时，函数没有意义，A不正确；正切函数在定义域上不是单调函数，B不正确；函数f（x）=tan2x的周期为：，所以C不正确；（，0）是函数的对称中心，所以D正确．故选：D．【点评】本题考查正弦函数的简单性质的应用，考查计算能力．8．已知a＞0，b＞0满足a+b=1，则的最小值为( )A．12 B．16 C．20 D．25【考点】基本不等式．【专题】计算题；转化思想；不等式的解法及应用．【分析】通过“1”的代换，化简所求表达式，利用基本不等式求出它的最小值．【解答】解：∵a＞0，b＞0，且满足a+b=1，则==10+≥10+2=16，当且仅当，即a=，时，等号成立．故的最小值为16，故选：B．【点评】本题主要考查基本不等式的应用，注意基本不等式的使用条件，并注意检验等号成立的条件，式子的变形是解题的关键，属于基础题．9．已知，，那么cosα等于( )A．B．C．D．【考点】两角和与差的余弦函数．【专题】计算题；函数思想；转化思想；三角函数的求值．【分析】利用同角三角函数的基本关系式以及两角和与差的余弦函数化简求解即可．【解答】解：，，可得=．cosα=cos（α+﹣）=+==．故选：B【点评】本题考查两角和与差的三角函数，同角三角函数的基本关系式的应用，考查转化思想的应用．10．已知某个几何体的三视图如下，根据图中标出的尺寸，那么可得这个几何体最长的棱长是( )A．2 B．C．2 D．2【考点】由三视图求面积、体积．【专题】对应思想；数形结合法；空间位置关系与距离．【分析】根据几何体的三视图，得出该几何体是底面是等腰三角形，且侧面垂直于底面的三棱锥，画出图形，结合图形即可求出该三棱锥中最长棱是多少．【解答】解：根据几何体的三视图，得；该几何体为底面是等腰三角形，且侧面垂直于底面的三棱锥，如图所示；且三棱锥的高为SD=2，底面三角形边长BC=2，高AD=2；∴该三棱锥的最长棱是SA===2．故选：C．【点评】本题考查了空间几何体三视图的应用问题，解题的关键是根据三视图得出几何体的结构特征，是基础题目．11．定义在（0，）上的函数f（x），f′（x），是它的导函数，且恒有sinx•f′（x）＞cosx•f （x）成立，则( )A．f（）＞f（） B．f（）＞f（） C．f（）＞2f（）D．f（）＜f（）【考点】函数的单调性与导数的关系．【专题】转化思想；综合法；导数的综合应用．【分析】构造函数g（x）=，求出g（x）的导数，得到函数g（x）的单调性，从而判断出函数值的大小即可．【解答】解：由f′（x）sinx＞f（x）cosx，则f′（x）sinx﹣f（x）cosx＞0，构造函数g（x）=，则g′（x）=，当x∈（0，）时，g′（x）＞0，即函数g（x）在（0，）上单调递增，∴g（）＜g（），∴f（）＜f（），故选：D．【点评】本题考查了导数的应用，考查函数的单调性问题，构造函数g（x）=是解题的关键，本题是一道中档题．12．O是坐标原点，点A（﹣1，1），点P（x，y）为平面区域的一个动点，函数f（λ）=|﹣λ|（λ∈R）的最小值为M，若M≤恒成立，则k的取值范围是( ) A．k≤1 B．﹣1≤k≤1C．0≤k≤3D．k≤1或≥3【考点】简单线性规划．【专题】数形结合；分类讨论；转化思想；数形结合法；分类法；函数的性质及应用；不等式的解法及应用；直线与圆．【分析】画出满足条件的可行域，分析出函数f（λ）的最小值为M≤恒成立表示可行域内的点到直线OA：x+y=0的最大距离不大于，结合可行域的图象，分类讨论，可得答案．【解答】解：满足约束条件的可行域如下图所示：函数f（λ）=|﹣λ|（λ∈R）表示P点到直线OA上一点的距离，若函数f（λ）的最小值为M≤恒成立，则仅需可行域内的点到直线OA：x+y=0的最大距离不大于即可，若k≥2，则不存在满足条件的点，若k＜2，则存在B点（，）到直线OA：x+y=0的距离最远，此时d=≤，解得：k≤1，故选：A【点评】本题考查了简单的线性规划，考查了数形结合的解题思想方法及分类讨论的数学思想方法，关键是对题意的理解，是难题．二、填空题：本大题共4小题，每小题5分．13．已知直线l1：ax+y+3=0，l2：x+（2a﹣3）y=4，l1⊥l2，则a=1．【考点】直线的一般式方程与直线的垂直关系．【专题】计算题；转化思想；综合法；直线与圆．【分析】利用两直线垂直，x，y系数积的和为0的性质求解．【解答】解：∵直线l1：ax+y+3=0，l2：x+（2a﹣3）y=4，l1⊥l2，∴a+（2a﹣3）=0，解得a=1．故答案为：1．【点评】本题考查直线方程中参数值的求法，是基础题，解题时要认真审题，注意直线垂直的性质的合理运用．14．已知等差数列{a n}，若a1+a2+a3=﹣24，a18+a19+a20=78，则S20=180．【考点】等差数列的性质．【专题】计算题；转化思想；综合法；等差数列与等比数列．【分析】由条件a1+a2+a3=﹣24，a18+a19+a20=78可得到a1+a20=18，再由等差数列的前20项和的式子可得到答案．【解答】解：∵a1+a2+a3=﹣24，a18+a19+a20=78∴a1+a20+a2+a19+a3+a18=54=3（a1+a20）∴a1+a20=18∴S20=（a1+a20）=180故答案为：180【点评】本题主要考查等差数列的前n项和公式的应用．考查等差数列的性质．比较基础．15．已知球O的体积为36π，则球的内接正方体的棱长是．【考点】球内接多面体．【专题】计算题；转化思想；综合法；空间位置关系与距离．【分析】先确定球的半径，利用球的内接正方体的对角线为球的直径，即可求得结论．【解答】解：∵球的体积为36π∴球的半径为3∵球的内接正方体的对角线为球的直径∴球的内接正方体的对角线长为6设球的内接正方体的棱长为a，则a=6∴a=2故答案为：2．【点评】本题考查球的内接正方体，解题的关键是利用球的内接正方体的对角线为球的直径，属于基础题．16．椭圆（a＞b＞0）的右顶点为A，上、下顶点分别为 B2、B1，左、右焦点分别是F1、F2，若直线 B1F2与直线 AB2交于点 P，且∠B1PA为锐角，则离心率的范围是．【考点】椭圆的简单性质．【专题】转化思想；向量法；圆锥曲线的定义、性质与方程．【分析】由题意，∠B1PA就是与的夹角，设椭圆的长半轴、短半轴、半焦距分别为a，b，c，则=（a，﹣b）、=（﹣c，﹣b），由向量的夹角为锐角可得﹣ac+b2＞0，把b2=a2﹣c2代入不等式，从而可求椭圆离心率的取值范围．【解答】解：由题意，∠B1PA就是与的夹角，设椭圆的长半轴、短半轴、半焦距分别为a，b，c，则=（a，﹣b）、=（﹣c，﹣b），由向量的夹角为锐角，知道与的数量积大于0，所以有：﹣ac+b2＞0，把b2=a2﹣c2代入不等式得：a2﹣ac﹣c2＞0，除以a2得1﹣e﹣e2＞0，即e2+e﹣1＜0，解得＜e＜，又0＜e＜1，所以0＜e＜，故答案为：0＜e＜．【点评】本题考查椭圆的几何性质，解题的关键是利用与的数量积大于0，建立不等式，属于中档题．三、解答题：解答应写出文字说明、证明过程或演算步骤．17．已知等差数列{a n}满足a2=4，a6+a8=18．（I）求数列{a n}的通项公式；（II）求数列{}的前n项和．【考点】数列的求和；等差数列的通项公式．【专题】计算题；方程思想；数学模型法；等差数列与等比数列．【分析】（I）利用等差数列的通项公式即可得出；（II）利用“裂项求和”即可得出．【解答】解：（I）设等差数列{a n}的公差为d，∵a2=4，a6+a8=18．∴，解得：a1=3，d=1，故数列{a n}的通项公式为a n=3+（n﹣1）=2+n．（II）设数列的前n项和为S n，，∴，∴，化为．【点评】本题考查了等差数列的通项公式、“裂项求和”，考查了推理能力与计算能力，属于中档题．18．已知函数f（x）=2sin cos+2cos2．（I）求f（x）的最小正周期和单调递减区间；（II）若f（B）=3，在△ABC中，角 A，B，C的对边分别是a，b，c，若b=3，sinC=2sin A，求a，c的值．【考点】正弦函数的图象；三角函数中的恒等变换应用；正弦定理．【专题】计算题；转化思想；综合法；三角函数的图像与性质；解三角形．【分析】（I）由条件利用三角恒等变换化简函数的解析式，再根据正弦函数的周期性和单调性得出结论．（II）在△ABC中，由f（ B）=3，求得B的值，由由sinC=2sinA及正弦定理求得c=2a；再根据b=3及余弦定理求得a的值，可得c的值．【解答】解：（I）由已知可得：，所以f（x）的最小正周期为2π．由，k∈Z，得，k∈Z．因此函数f（x）的单调递减区间为，k∈Z．（II）在△ABC中，若f（ B）=3，求得sin（B+）=1，故．由sinC=2sinA及，得c=2a．由b=3及余弦定理b2=a2+c2﹣2accos B，得9=a2+c2﹣ac，将c=2a代入得，求得，故．【点评】本题主要考查三角恒等变换，正弦函数的周期性和单调性，正弦定理和余弦定理的应用，属于基础题．19．如图，在四棱柱 ABCD﹣A1 B1C1D1中，CC1⊥底面 ABCD，底面 ABCD为菱形，点 E，F分别是 AB，B1C1的中点，且∠DAB=60°，AA1=AB=2．（I）求证：EF∥平面 AB1D1；（II）求三棱锥 A﹣CB1D1的体积．【考点】棱柱、棱锥、棱台的体积；直线与平面平行的判定．【专题】转化思想；分割补形法；空间位置关系与距离．【分析】（I）如图，连接A1C1交B1D1于O点，连接OF，OA．利用三角形的中位线定理、平行四边形的判定可得AOFE是平行四边形，再利用线面平行的判定定理即可证明．（II）连接AC交BD于点M，连接D1M，B1M．可得=，=+，由于四边形BACD是菱形，BB1⊥平面ABCD，可得平面BDD1B1⊥平面ABCD，AM⊥平面BDD1B1，即可得出=．【解答】证明：（I）如图，连接A1C1交B1D1于O点，连接OF，OA．∵，，∴．∴AOFE是平行四边形，∴EF∥OA，而EF⊄平面 AB1D1，OA⊂平面 AB1D1；∴EF∥平面 AB1D1．（II）连接AC交BD于点M，连接D1M，B1M．则=，=+=2，∵四边形BACD是菱形，∴AC⊥BD．∵BB1⊥平面ABCD，∴平面BDD1B1⊥平面ABCD，∴AM⊥平面BDD1B1，∴==×2×2=，∴=．【点评】本题考查了空间线面位置关系及其判定、三棱锥的体积计算公式，考查了推理能力与计算能力，属于中档题．20．在平面直角坐标系xOy中，已知圆C1：（x+3）2+（y﹣1）2=4和圆C2：（x﹣4）2+（y﹣5）2=1．（I）若直线l过点 A（4，0），且被圆C1截得的弦长为2，求直线l的方程；（II）若从圆C1的圆心发出一束光线经直线x﹣y﹣3=0反射后，反射线与圆C2有公共点，试求反射线所在直线的斜率的范围．【考点】直线与圆的位置关系．【专题】综合题；转化思想；综合法；直线与圆．【分析】（I）因为直线l过点A（4，0），故可以设出直线l的点斜式方程，又由直线被圆C1截得的弦长为2，根据半弦长、半径、弦心距满足勾股定理，我们可以求出弦心距，即圆心到直线的距离，得到一个关于直线斜率k的方程，解方程求出k值，代入即得直线l的方程．（II）圆C1的圆心（﹣3，1）经直线x﹣y﹣3=0对称后的点记为 A（4，﹣6），直线与圆C2有公共点即直线与圆相交或相切，故利用点到直线的距离公式列出关于k的不等式，即可求反射线所在直线的斜率的范围．【解答】解：（I）由于直线x=4与圆C1不相交；∴直线l的斜率存在，设l方程为：y=k（x﹣4）圆C1的圆心到直线l的距离为d，∵l被⊙C1截得的弦长为2∴d=1∴d==1，从而k（24k+7）=0即k=0或k=﹣∴直线l的方程为：y=0或，即y=0或7x+24y﹣28=0．（II）圆C1的圆心（﹣3，1）经直线x﹣y﹣3=0对称后的点记为 A（4，﹣6），设反射光线所在的直线的斜率为k，则反射光线所在的直线方程为y+6=k（x﹣4）⇒kx﹣y﹣4k﹣6=0．圆C2的圆心（4，5）．直线与圆C2有公共点即直线与圆相交或相切，则⇒⇒k2≥120⇒或．【点评】此题考查了直线与圆的位置关系，涉及的知识有：点到直线的距离公式，圆的标准方程，两直线垂直时斜率满足的关系，关于坐标轴对称的点的特点，切线的性质．解决与圆相关的弦长问题时，我们有三种方法：一是直接求出直线与圆的交点坐标，再利用两点间的距离公式得出；二是不求交点坐标，用一元二次方程根与系数的关系得出，即设直线的斜率为k，直线与圆联立消去y后得到一个关于x的一元二次方程再利用弦长公式求解，三是利用圆中半弦长、弦心距及半径构成的直角三角形来求．对于圆中的弦长问题，一般利用第三种方法比较简捷．21．已知函数f（x）=xe ax+lnx﹣e（a∈R）．（I）当a=1时，求函数y=f（x）在点（1，f（1））处的切线方程；（II）设g（x）=lnx+﹣e，若函数h（x）=x•在定义域内存在两个零点，求实数a的取值范围．【考点】利用导数研究曲线上某点切线方程；函数的零点与方程根的关系．【专题】转化思想；分类法；导数的概念及应用；导数的综合应用．【分析】（I）求得函数的导数，求得切线的斜率和切点，由点斜式方程即可得到所求切线的方程；（II）化简函数h（x），由题意可得x2e ax﹣1=0在（0，+∞）有两个零点．对a讨论，注意运用单调性和极值判断，即可得到a的范围．【解答】解：（I）y=f（x）的定义域为（0，+∞），∵a=1，∴f（x）=xe x+lnx﹣e，f（1）=0，∴，∴f'（1）=2e+1，所以函数y=f（x）在点（1，f（1））处的切线方程为y=（2e+1）（x﹣1）；（II）=x2e ax﹣1在定义域内存在两个零点，即x2e ax﹣1=0在（0，+∞）有两个零点．令φ（x）=x2e ax﹣1，φ'（x）=ax2e ax+2xe ax=xe ax（ax+2），i、当a≥0时，φ'（x）=xe ax（ax+2）＞0，∴y=φ（x）在（0，+∞）上单调递增，由零点存在定理，y=φ（x）在（0，+∞）至多一个零点，与题设发生矛盾．ii、当a＜0时，xe ax（ax+2）=0，则，xφ'（x）+ 0 ﹣φ（x）单调递增极大值单调递减因为φ（0）=﹣1，当x→+∞，φ（x）→﹣1，所以要使φ（x）=x2e ax﹣1在（0，+∞）内有两个零点，则即可，得，又因为a＜0，所以．综上，实数a的取值范围为．【点评】本题考查导数的运用：求切线的方程和单调区间、极值，考查函数方程的转化思想的运用，考查运算能力，属于中档题．选修4-1：几何证明选讲22．如图，在Rt△ABC中，∠C=90°，B E平分∠A BC交 AC于点E，点D在AB上，DE⊥EB，且，AE=6．（I）判断直线 AC与△BDE的外接圆的位置关系并说明理由；（II）求EC的长．【考点】直线与圆的位置关系．【专题】综合题；转化思想；综合法；直线与圆．【分析】（I）取BD的中点0，连结OE，如图，由∠BED=90°，根据圆周角定理可得BD为△BDE 的外接圆的直径，点O为△BDE的外接圆的圆心，再证明OE∥BC，得到∠AEO=∠C=90°，于是可根据切线的判定定理判断AC是△BDE的外接圆的切线；（II）设⊙O的半径为r，根据勾股定理得，解得r=2，根据平行线分线段成比例定理，由OE∥BC得=，然后根据比例性质可计算出EC．【解答】解：（I）取BD的中点0，连结OE，如图，∵DE⊥EB，∴∠BED=90°，∴BD为△BDE的外接圆的直径，点O为△BDE的外接圆的圆心，∵B E平分∠ABC，∴∠CBE=∠OBE，∵OB=OE，∴∠OBE=∠OEB，∴∠OEB=∠CBE，∴OE∥BC，∴∠AEO=∠C=90°，∴OE⊥AE，∴AC是△BDE的外接圆的切线．（II）设△BDE的外接圆的半径为r．在△AOE中，OA2=OE2+AE2，即，解得，∴=，即=，∴CE=3．【点评】本题考查了切线的判定：经过半径的外端且垂直于这条半径的直线是圆的切线．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．也考查了勾股定理和平行线分线段成比例定理．选修4-4：坐标系与参数方程23．已知曲线C1的参数方程是（θ为参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，曲线C2的极坐标方程是ρ=﹣4cosθ．（1）求曲线C1与C2交点的极坐标；（2）A、B两点分别在曲线C1与C2上，当|AB|最大时，求△OAB的面积（O为坐标原点）．【考点】简单曲线的极坐标方程．【专题】坐标系和参数方程．【分析】（1）把消去θ化为普通方程，由极坐标方程ρ=﹣4cosθ化为直角坐标方程得x2+y2=﹣4x，联立求出交点的直角坐标，化为极坐标得答案；（2）画出两圆，数形结合得到A，C1，C2，B依次排列且共线时|AB|最大，求出|AB|及O到AB 的距离代入三角形的面积公式得答案．【解答】解：（1）由，得，两式平方作和得：x2+（y﹣2）2=4，即x2+y2﹣4y=0；由ρ=﹣4cosθ，得ρ2=﹣4ρcosθ，即x2+y2=﹣4x．两式作差得：x+y=0，代入C1得交点为（0，0），（﹣2，2）．其极坐标为（0，0），（）；由平面几何知识可知，A，C1，C2，B依次排列且共线时|AB|最大．此时|AB|=，O到AB的距离为．∴△OAB的面积为S=．【点评】本题考查了参数方程化普通方程，极坐标与直角坐标的互化，考查了数形结合的解题思想方法，是基础的计算题．选修4-5：不等式选讲24．（I）求|2x﹣1|+|2x+3|＜5的解集；（II）设a，b，c均为正实数，试证明不等式，并说明等号成立的条件．【考点】不等式的证明；绝对值不等式的解法．【专题】证明题；转化思想；转化法；不等式的解法及应用．【分析】（Ⅰ）把要解的不等式等价转化为与之等价的三个不等式组，求出每个不等式组的解集，再取并集，即得所求．（Ⅰ）根据（+）≥≥，当且仅当a=b时等号成立，同理得到其它，相加即可得以证明．【解答】解：（Ⅰ）由|2x﹣1|+|2x+3|＜5，可得①，②，，③，解①求得x∈∅，解②求得﹣≤x＜，解③求得≤x＜，综上可得，不等式|2x﹣1|+|2x+3|＜5的解集为{x|﹣≤x＜}；（Ⅱ）证明：∵a，b，c均为正实数，∴（+）≥≥，当且仅当a=b时等号成立；（+）≥≥，当且仅当b=c时等号成立；（+）≥≥，当且仅当a=c时等号成立；三个不等式相加，得，当且仅当a=b=c时等号成立．【点评】本题考查了绝对值值不等式的解法和基本不等式的应用，关键是掌握其性质，并注意等号成立的条件，属于中档题．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
秘密★启用前2016年重庆一中高2019级高一上期半期考试数 学 试 题 卷2016.12数学试题共4页，满分150分，考试时间120分钟。
注意事项：1.答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号。
3.答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答，在试题卷上答题无效。
第I 卷（选择题，共60分）一、选择题：(本大题共12个小题，每小题5分，共60分)在每小题给出的四个选项中，只有一项是符合题目要求的；各题答案必须答在答题卡上相应的位置.1. 设全集{}4,3,2,1=U ，集合{}{}4,2,4,3,1==B A ，则()U C A B ⋂=（ ） A ．{}2B ．{}4,2C ．{}4,2,1 D ．φ2. 函数()()1011≠>-=-a a a x f x 且的图象必经过定点（ ）A ．()1,0-B ．()1,1-C ．()0,1-D ．()0,13. 在0到π2范围内，与角34π-终边相同的角是（ ） A ．6π B ．3π C ．32π D ．34π4. 函数()()2lg 231++-=x xx f 的定义域是（ ）A ．⎪⎭⎫ ⎝⎛-232， B ．⎥⎦⎤ ⎝⎛-232， C ．()∞+-，2 D ．⎪⎭⎫ ⎝⎛∞+，23 5. 已知3.0log 24.053.01.2===c b a ，，，则（ ） A ．b a c << B ．c b a << C ．a b c << D ．bc a <<6. 函数()xx x f 1ln -=的零点所在的大致区间是（ ） A ．⎪⎭⎫ ⎝⎛1,1eB ．()e ,1C ．()2,e e D ．()32,e e7. 已知函数()(),03)0(log 2⎩⎨⎧≤>=x x x x f x则⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛81f f 的值是（ ） A ．27-B ．271-C ．27D ．2718. 函数xx y xe ⋅=的图像的大致形状是（ ）A B C D9. 已知函数()()53log 221+-=ax x x f 在[)∞+-，1上是减函数，则实数a 的取值范围是（ ）A ．(]6,-∞-B ．[)68，- C ．(]68--，D ．[)+∞-,8 10. （原创）已知关于x 的方程12=-m x 有两个不等实根，则实数m 的取值范围是（ ）A ． (]1,-∞-B ．()1,-∞-C ．[)∞+，1 D ．()∞+，1 11.（原创）已知函数()()()1011ln 2≠>-+++=a a a a x x x f xx且，若()()313log lg 2=f ，则()()=2log lg 3f （ ） A ．0B ．31C ．32D ． 1 12. 设函数()a x e x f x-+=2（e R a ,∈为自然对数的底数），若存在实数[]1,0∈b 使()()b b f f =成立，则实数a 的取值范围是（ ）A ．[]e ，0B ．[]e 1,1+C ． []e +2,1D ．[]1,0第II 卷（非选择题，共90分）二、填空题：(本大题共4个小题，每小题5分，共20分)各题答案必须填写在答题卡相应的位置上.13. 幂函数()()3221-+--=m mx m m x f 在()∞+，0上为增函数，则实数m =______. 14. 扇形的周长为8cm ，圆心角为2弧度，则该扇形的面积为____2cm .15. 已知函数()x f 是定义在R 上的奇函数，且当0≥x 时，()x x x f 22+=，则当0<x 时，()x f =__________.16. 已知函数()3||log )(31+-=x x f 的定义域是[]b a ,()Z b a ∈,，值域是[]0,1-，则满足条件的整数对()b a ,有________对．三、解答题：解答应写出文字说明、证明过程或演算步骤.17.（10分）（原创）化简：（1）)7112log 423112log 743π⎛⎫-++ ⎪⎝⎭；（2）()5262512lg 20lg 5lg 2--+++⋅.18.（12分）(原创）已知集合A 为函数()[]2,1,122∈-+=x x x x f 的值域，集合⎭⎬⎫⎩⎨⎧≤--=014x x x B ，则（1）求AB ；（2）若集合{}1+<<=a x a x C ，C C A =⋂，求实数a 的取值范围.19. （12分）（原创）已知函数()x f y =为二次函数，()40=f ，且关于x 的不等式()02<-x f 解集为{}21<<x x ， （1）求函数()x f 的解析式；（2）若关于x 的方程()0=-a x f 有一实根大于1，一实根小于1，求实数a 的取值范围.20. （12分）（原创）已知函数()xx xx a x f --+⋅-=2222是定义在R 上的奇函数. （1）求实数a 的值，并求函数()x f 的值域；（2）判断函数()x f y =的单调性（不需要说明理由），并解关于x 的不等式()03125≥-+x f .21. （12分）（原创）已知函数()⎪⎪⎩⎪⎪⎨⎧>+-≤⎪⎭⎫⎝⎛-=0,1210,2122x x x x x f x，（1）画出函数()x f 的草图并由图像写出该函数的单调区间； （2）若()a x g xx-=-23，对于任意的[]1,11-∈x ，存在[]1,12-∈x ，使得()()21x g x f ≤成立，求实数a 的取值范围.22. （12分）对于在区间],[n m 上有意义的函数)(x f ，若满足对任意的21,x x ],[n m ∈，有|)()(|21x f x f -1≤恒成立，则称)(x f 在],[n m 上是“友好”的，否则就称)(x f 在],[n m 上是“不友好”的．现有函数()xaxx f +=1log 3， （1）若函数)(x f 在区间]1,[+m m ()21≤≤m 上是 “友好”的，求实数a 的取值范围； （2）若关于x 的方程()[]1423log )(3=-+-a x a x f 的解集中有且只有一个元素，求实数a 的取值范围．命题人：苏华丽审题人：黄勇庆2016年重庆一中高2019级高一上期半期考试数 学 答 案2016.12一、选择题：(本大题共12个小题，每小题5分，共60分)ADCAA BDBCD CB二、填空题：(本大题共4个小题，每小题5分，共20分)13. 2 14. 4 15. x x 22+- 16.5 三、解答题：解答应写出文字说明、证明过程或演算步骤。
17. （10分）解：（1）原式=2321123=+--（2）原式= ()()()2215252lg 5lg 2lg 10lg ---+++()012lg 5lg 2lg 5lg =-+⋅+=18. （12分）[](]41721:，，，）（解==B A ,A B []4,2= (2)由题意可知 A C ⊆,则⎩⎨⎧≤+≥712a a 解得62≤≤a综上，a 的取值范围为[]6,219. （12分）解：（Ⅰ）∵设函数()()02≠++=a c bx ax x f ，则()40==c f()0222<++<bx ax x f 即 故aa b 221,21=⨯-=+3,1-==b a∴()432+-=x x x f（2）()a x x x g -+-=432 则()024311<-=-+-=a a g 故2>a20. （12分）解：（1）由题意易知 ()0000222-200+⋅==a f 故1=a 所以()122112122222222+-=+-=+-=--x x x x xx x x f ()R x ∈ 0122211210112022222<+-<-∴<+<∴>+∴>x x x x 112211-2<+-<∴x 故函数()x f 的值域为()1,1- （2）由（1）知()12212+-=xx f易知()x f 在R 上单调递增 且()5314211=+-=f故112≥+x 0≥∴x所以不等式()03125≥-+x f 的解集为[)∞+，0 21. （12分）解：（1）如下图所示，易知函数()x f 的单调递减区间为()1,0，单调递增区间为()()∞+∞，，，10-（2）由题意可得()[]()[]max 2max 1x g x f ≤ 其中()()10max ==f x f ()()a g x -=-=91g max ，即a -≤91 故8≤a综上所述：(]8，∞-∈a 22. （12分）解：（1）由题意可得()⎪⎭⎫⎝⎛+=+=a x x ax x f 1log 1log 33在]1,[+m m 上单调递减，故()(),1log 3max ⎪⎭⎫ ⎝⎛+==a m m f x f ()(),11log 13in ⎪⎭⎫⎝⎛++=+=a m m f x f m ∴()()111log 1log 33min max ≤⎪⎭⎫⎝⎛++-⎪⎭⎫ ⎝⎛+=-a m a m x f x f即3111⋅⎪⎭⎫⎝⎛++≤+a m a m ∴()max11221⎪⎪⎭⎫ ⎝⎛+-⋅-≥m m m a 令)31(12≤≤-=t m t ，则21+=t m ，则()1434134423211122++=++=+⋅+=+-=tt t t t t t t m m m y 当31或=t 时，21min =y 41-≥∴a又对于任意的]1,[+∈m m x ，011>+=+a x x ax ，故31111max-≥+-=⎪⎭⎫⎝⎛->m x a 综上，a 的取值范围是⎭⎬⎫⎩⎨⎧-≥41a a（2）()[]1423log )(3=-+-a x a x f ，即()04231>-+-=+a x a a x，且()1423≠-+-a x a （1）()()01432=--+-∴x a x a ，即()[]()0113=+--x x a （2）当3=a 时，方程(2)的解为1-=x ,代入（1），成立 当2=a 时，方程(2)的解为1-=x ,代入（1），不成立当32≠≠a a 且时，方程(2)的解为1-=x 或31-=a x将1-=x 代入（1），则()01423>-=-+-a a x a ,且11≠-a 所以21≠>a a 且将31-=a x 代入（1），则()032423>-=-+-a a x a ,且132≠-a所以223≠>a a 且则要使方程有且仅有一个解，则231≤<a 综上，若方程()[]1423log )(3=-+-a x a x f 的解集中有且仅有一个元素，则a 的取值范围为⎭⎬⎫⎩⎨⎧=≤<3231a a a 或。