点、直线与圆的位置关系
直线与圆的位置关系

直线与圆的位置关系:直线与圆的位置关系有三种:直线与圆相交,直线与圆相切,直线与圆相离。
(1)相交:直线和圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线,公共点叫做交点AB与⊙O相交,d<r;(2)相切:直线和圆有唯一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,这个唯一的公共点叫做切点。
AB与⊙O相切,d=r。
(3)相离:直线和圆没有公共点时,叫做直线和圆相离,AB与圆O相离,d>r。
(d为圆心到直线的距离)直线与圆的三种位置关系的判定与性质:(1)数量法:通过比较圆心O到直线距离d与圆半径的大小关系来判定,如果⊙O的半径为r,圆心O到直线l的距离为d,则有:直线l与⊙O相交d<r;直线l与⊙O相切d=r;直线l与⊙O相离d>r;(2)公共点法:通过确定直线与圆的公共点个数来判定。
直线l与⊙O相交d<r2个公共点;直线l与⊙O相切d=r有唯一公共点;直线l与⊙O相离d>r无公共点。
圆的切线的判定和性质(1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
(2)切线的性质定理:圆的切线垂直于经过切点的半径。
切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长叫做这点到圆的切线长。
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
直线与圆的位置关系判定方法:平面内,直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0的位置关系判断一般方法是:1.由Ax+By+C=0,可得y=(-C-Ax)/B,(其中B不等于0),代入x2+y2+Dx+Ey+F=0,即成为一个关于x的方程如果b2-4ac>0,则圆与直线有2交点,即圆与直线相交。
如果b2-4ac=0,则圆与直线有1交点,即圆与直线相切。
如果b2-4ac<0,则圆与直线有0交点,即圆与直线相离。
2.如果B=0即直线为Ax+C=0,即x=-C/A,它平行于y轴(或垂直于x轴),将x2+y2+Dx+Ey+F=0化为(x-a)2+(y-b)2=r2。
直线和圆的位置关系

直线和圆的位置关系【基础知识】1.直线和圆的位置关系(1)相交:直线与圆有两个公共点时,叫做直线和圆相交,这时直线叫做圆的割线。
(2)相切:直线和圆有惟一公共点时,叫做直线和圆相切,这时直线叫做圆的切线,惟一的公共点做切点。
(3)相离:直线和圆没有公共点时,叫做直线和圆相离。
(4)直线与圆的位置关系的确定:设⊙O的半径为r ,圆心O 到直线的距离为d ,则 ①d<r<===>直线L 和⊙O相交。
②d=r<===>直线L 和⊙O相切。
③d>r<===>直线L 和⊙O相离。
2.切线的判定:经过直径的一端,并且垂直于这条直径的直线是圆的切线。
切线的性质:圆的切线垂直于过切点的直径。
【课堂练习】1.已知⊙O 的半径为10cm ,如果一条直线和圆心O 的距离为10cm ,那么这条直线和这个圆的位置关系为( )A. 相离B. 相切C. 相交D. 相交或相离 2.如右图,A 、B 是⊙O 上的两点,AC 是⊙O 的切线, ∠B=70°,则∠BAC 等于( ) A. 70° B. 35° C. 20° D. 10°3.如图,已知⊙O 的直径AB 与弦AC 的夹角为30°,过C 点的切线PC 与AB 的延长线交于P ,PC=5,则⊙O 的半径为( ) A. 335 B.635 C. 10 D. 54.如图,PA 切⊙O 于A,PB 切⊙O 于B ,OP 交⊙O 于C , 下列结论中,错误的是( )A. ∠1=∠2B. PA=PBC. AB ⊥OPD. 2PA PC ·PO5.如图5,已知AB 是⊙O 的直径,弦AD 、BC 相交于点P ,那么CD ︰AB 等于∠BPD 的( )A. 正弦B. 余弦C. 正切D. 余切(第3题图)(第4题图)6.如图6,在Rt △ABC 中,∠C=90°,∠A=60°,BC =4cm ,以点C 为圆心,以3cm 长为半 径作圆,则⊙C 与AB 的位置关系是 .图5 图67. AB 是⊙O 的直径,PA 切⊙O 于A ,OP 交⊙O 于C ,连BC .若30P ∠= ,求B ∠的度数.8. 如图,AB 为⊙O 的直径,C 为⊙O 上一点,AD 和过点C 的切线垂直于D ,BE 和过点C 的切线垂直于E 求证:(1)AC 平分∠DAO(2)BC 平分∠EBO (3)DC = CE9. 如图,已知△ABC 內接于⊙O ,AB 为直径,∠CAE = ∠B 。
点和圆、线和圆的位置关系

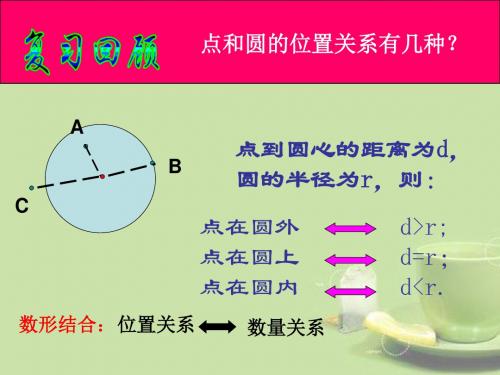
点和圆、线和圆的位置关系考点一1.点与圆的位置关系有三种:点在圆内、点在圆上、点在圆外.如果圆的半径是r,点到圆心的距离为d,那么:(1)点在圆上⇔d=r;(2)点在圆内⇔d<r;(3)点在圆外⇔d>r.2.过三点的圆(1)经过三点作圆:①经过在同一直线上的三点不能作圆;②经过不在同一直线上的三点,有且只有一个圆.(2)三角形的外接圆:经过三角形各顶点的圆叫做三角形的外接圆;外接圆的圆心叫做三角形的外心;这个三角形叫做这个圆的内接三角形.(3)三角形外接圆的作法:①确定外心:作任意两边的中垂线,交点即为外心;②确定半径:两边中垂线的交点到三角形任一个顶点的距离作为半径.例1 (2009·江西)在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2,下列说法中不.正确..的是()A.当a<5时,点B在⊙A内B.当1<a<5时,点B在⊙A内C.当a<1时,点B在⊙A外D.当a>5时,点B在⊙A外例2考点二1.直线与圆的位置关系的有关概念(1)直线和圆有两个公共点时,叫做直线和圆相交,这时的直线叫做圆的割线;(2)直线和圆有唯一公共点时,叫做直线和圆相切,唯一的公共点叫做切点,这时的直线叫圆的切线;(3)直线和圆没有公共点时,叫做直线和圆相离.2.直线和圆的位置关系的性质与判定如果⊙O的半径为r,圆心O到直线l的距离为d,那么:(1)直线l和⊙O相交⇔d<r;(2)直线l和⊙O相切⇔d=r;(3)直线l和⊙O相离⇔d>r.例3 如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是()A.相离B.相切C.相交D.相切或相交例4如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是()A.-1≤x≤1 B.-2≤x≤ 2C.0≤x≤ 2 D.x> 2考点三1.切线的判定方法(1)和圆只有一个公共点的直线是圆的切线;(2)到圆心的距离等于半径的直线是圆的切线;(3)过半径外端点且和这条半径垂直的直线是圆的切线.2.切线的性质(1)切线的性质定理:圆的切线垂直于经过切点的半径;(2)推论1:经过切点且垂直于切线的直线必经过圆心;(3)推论2:经过圆心且垂直于切线的直线必经过切点.例5 如图,已知Rt△ABC,∠ABC=90°,以直角边AB为直径作⊙O,交斜边AC于点D,连结BD.(1)若AD=3,BD=4,求边BC的长;(2)取BC的中点E,连结ED,试证明ED与⊙O相切.例6 如图,在Rt△ABC中,∠ABC=90°,斜边AC的垂直平分线交BC于点D,交AC于点E,连结BE.(1)若BE是△DEC外接圆的切线,求∠C的大小;(2)若AB=1,BC=2时,求△DEC外接圆的半径.考点四1.切线长:在经过圆外一点的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.2.切线长定理.....:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分这两条切线的夹角.例7 如图,从⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,若PA=8 cm,C是AB上的一个动点(点C与A、B两点不重合),过点C作⊙O的切线,分别交PA、PB于点D、E,则△PED的周长是________.例8变式练习1.如图,P 为⊙O 外一点,PA 切⊙O 于点A ,且OP =5,PA =4,则sin ∠APO 等于( B ) A.45 B.35 C.43 D.342.如图,从⊙O 外一点P 引⊙O 的两条切线PA 、PB ,切点分别为A 、B ,如果∠APB =60°,PA =8,那么弦AB 的长是( B )A .4B .8C .4 3D .833.⊙O 的半径为5,圆心O 到直线l 的距离为3,则直线l 与⊙O 的位置关系是( A )A .相交B .相切C .相离D .无法确定4.如图,CD 切⊙O 于点B ,CO 的延长线交⊙O 于点A.若∠C =36°,则∠ABD 的度数是( B )A .72°B .63°C .54°D .36°5.如图,⊙O 的半径OA =10 cm ,弦AB =16 cm ,P 为AB 上一动点,则点P 到圆心O 的最短距离为6cm.6.△ABC 中,AB =10 cm ,AC =8 cm ,BC =6 cm ,以点B 为圆心、6 cm 为半径作⊙B ,则边AC 所在的直线与⊙B 的位置关系是相切.一、选择题1.(2011中考预测题)如图,AB 是⊙O 的直径,点D 在AB 的延长线上,DC 切⊙O 于点C ,若∠A =25°,则∠D 等于( )A .40°B .50°C .60°D .70°2.(2009中考变式题)如图,EB 为半圆O 的直径,点A 在EB 的延长线上,AD 切半圆O 于点D ,BC ⊥AD 于点C ,AB =2,半圆O 的半径为2,则BC 的长为( )A .2B .1.5C .1D .0.53.(2009中考变式题)如图,在平面直角坐标系中,⊙P 与x 轴相切于原点O ,平行于y 轴的直线交⊙P 于M 、N 两点.若点M 的坐标是(2,-1),则点N 的坐标是( )A .(2,-4)B .(2,-4.5)C .(2,-5)D .(2,-5.5)4.(2011中考预测题)如图,已知⊙O 的半径为R ,AB 是⊙O 的直径,D 是AB 延长线上一点,DC 是⊙O 的切线,C 是切点,连结AC ,若∠CAB =30°,则BD 的长为( )A .2R B.3RC .R D.32R④ ⑤5.(2009中考变式题)如图,AB 是⊙O 的直径,AC 是⊙O 的切线,A 为切点,连结BC 交⊙O 于点D ,连结AD ,若∠ABC =45°,则下列结论正确的是( ) A .AD =12BC B .AD =12AC C .AC>AB D .AD>DC6.(2011中考预测题)在Rt △ABC 中,∠C =90°,AC =3 cm ,BC =4 cm ,以C 为圆心、3 cm 长为半径的圆与AB 的关系为( )A .相切B .相离C .相交D .无法判断7.(2010·眉山)下列命题中,真命题是( )A .对角线互相垂直且相等的四边形是正方形B .等腰梯形既是轴对称图形又是中心对称图形C .圆的切线垂直于经过切点的半径D .垂直于同一直线的两条直线互相垂直8.(2009中考变式题)如图,PA 、PB 分别是⊙O 的切线,A 、B 为切点,AC 是⊙O 的直径,已知∠BAC =35°,则∠P 的度数为( )A .35°B .45°C .60°D .70°9.(2009中考变式题)下列四个命题:①与圆有公共点的直线是该圆的切线;②到圆心的距离等于该圆半径的直线是该圆的切线;③垂直于圆的半径的直线是该圆的切线;④过圆直径的端点,垂直于此直径的直线是该圆的切线,其中正确的是()A.①②B.①④C.②④D.③④10.(2011中考预测题)如图,已知⊙O的直径AB与弦AC的夹角为35°,过C点的切线与AB的延长线交于点P,则∠P等于()A.15°B.20°C.25°D.30°11.(2009中考变式题)如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为2,则等边三角形ABC的边长为()A. 3B. 5 C.2 3 D.2512.(2010·武汉)如图,⊙O的直径AB的长为10,弦AC长为6,∠ACB的平分线交⊙O于D,则CD的长为() A.7 B.7 2 C.8 2 D.9二、填空题13.(2009·河北)如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC.若∠A=36°,则∠C=________.14.(2010·河南)如图,AB切⊙O于点A,BO交⊙O于点C,点D是OMA上异于点C、A的一点.若∠ABO=32°,则∠ADC的度数是________.15.(2011中考预测题)如图,从⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,若PA=8 cm,C是AB上的一个动点(点C与A、B两点不重合),过点C作⊙O的切线,分别交PA、PB于点D、E,则△PED的周长是________.16.(2010·杭州)如图,已知△ABC,AC=BC=6,∠C=90°.O是AB的中点,⊙O与AC、BC分别相切于点D 与点E.点F是⊙O与AB的一个交点,连结DF并延长交CB的延长线于点G,则CG=________.三、解答题17.(12分)(2010·广东)如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点.已知OA =2,OP=4.(1)求∠POA的度数;(2)计算弦AB的长.18.(12分)(2010·北京)已知:如图,在△ABC中,D是AB边上的一点,⊙O过D、B、C三点,∠DOC=2∠ACD =90°.(1)求证:直线AC是⊙O的切线;(2)如果∠ACB=75°,⊙O的半径为2,求BD的长.19.(12分)(2010·襄樊)如图,已知:AC是⊙O的直径,PA⊥AC,连结OP,弦CB∥OP,直线PB交直线AC于D,BD=2PA.(1)证明:直线PB是⊙O的切线;(2)探究线段PO与线段BC之间的数量关系,并予以证明;(3)求sin∠OPA的值.。
直线和圆的位置关系

例2
△ABC的内切圆⊙O与BC,CA,AB分别相 切于点D.E.F,AB=9,BC=14,CA=13,求AF、
BD、CE的长.
B
练习
在△ABC中, ∠ABC=50°,∠ACB=75°,点O 是△ABC的内心,求∠BOC的度数。
练习
△ABC的内切圆半径为R ,△ABC的周长为L求 △ABC的面积。
小结
判断直线与圆的位置关系有两种方法:
1、从直线与圆的公共点的个数来断定; 2、用d与r的大小关系来断定.
判断直线与圆的位置关系
1、从公共点的个数来判断: • 直线与圆有两个公共点时,直线与圆相交; • 直线与圆有唯一公共点时,直线与圆相切; • 直线与圆没有公共点时,直线与圆相离. 2、从点到直线的距离d与半径r的大小关系来判断: • d<r时,直线与圆相交; • d=r时,直线与圆相切; • d>r时,直线与圆相离.
复习巩固
6、如图所示,PA、PB是⊙O的切线,A,B为切 点,AC是⊙O的直径, ∠BAC=25°求∠P的度数.
C
综合运用
7、已知AB=6cm,画半径为4cm的圆,使它经过AB 两点,这样的圆能画多少个?如果半径为3cm,2cm 呢?
综合运用 8、分别做出锐角三角形、直角三角形和钝角三角形 的外接圆,它们外心的位置有什么特点?
从一块三角形材料中,能否剪下一个圆使其与各边都相切?
分析:假设符合条件的圆已作出,则它的圆心到三角形三边的 距离相等.因此,圆心在这个三角形三个角的平分线上,半径 为圆心到三边的距离。 解: (1)作∠B、∠C的平分线BE和CF,交点为I。 (2)过I作ID⊥BC,垂足为D。 (3)以I为圆心,以ID为半径作⊙I。 ⊙I就是所求的圆。
分析:因为台风影响的范围可以看成以台风中心为圆心,半径为200千米的圆,A城 能否受到影响,即比较A到直线BF的距离d与半径200千米的大小.若d>200,则无 影响,若d≤200,则有影响.
初三数学直线和圆的位置关系

初三数学直线和圆的位置关系一.直线和圆的位置关系:①相交:直线和圆有两个公共点,这时说这条直线和圆相交;这条直线叫做圆的割线;②相切:直线和圆有唯一公共点,这时说这条直线和圆相切;这条直线叫做圆的切线,这个点叫做切点.③相离:直线和圆没有公共点,这时说这条直线和圆相离.二.直线和圆的位置关系的判定:(1)定理:若⊙O的半径为R,圆心到直线l 的距离为d. 则直线l与⊙O相交d﹤R;直线l与⊙O相切 d =R;直线l与⊙O相离d﹥R;(2)“圆心到直线的距离d和半径R的数量关系”与“直线和圆的位置关系”之间的对应与等价关系列表如下:例1、1.在Rt△ABC中,∠C=,AC=3cm,AB=6cm,以点C为圆心,与AB边相切的圆的半径为_________cm.2.如图,⊙O的半径OD为5cm,直线l⊥OD,垂足为O,则直线l沿射线OD方向平移_________cm时与⊙O相切.3.已知⊙O的直径为6cm,如果直线l上的一点C到圆心的距离为3cm,则直线l与⊙O的位置关系是_________.4.⊙O的半径为R,圆心O到直线l的距离d与R是方程x2-6x+9=0的两个实数根,则直线l和⊙O的位置关系是_________.三.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线;2.切线的性质:①切线垂直于过切点的半径;②切线和圆心的距离等于半径;③经过圆心且垂直于切线的直线必过切点;④经过切点垂直于切线的直线必过圆心.综上所述,在解决有关圆的切线的问题,连接圆心和切点的线段是最常见的辅助线.四、切线长的定义及切线长定理过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长,如图所示,PA,PB 是⊙O的两条切线,A,B为切点,线段PA,PB的长即为点P到⊙O的切线长.切线长定理:过圆外一点所画的圆的两条切线长相等.例2、如图,AB是⊙O的直径,BC切⊙O于点B,AD∥CO.求证:CD是⊙O的切线.1、⊙O的半径为R,直线l和⊙O有公共点,若圆心到直线l的距离是d,则d与R的大小关系是()A.d>RB.d<RC.d≤RD.d≥R2、点A为直线l上任一点,过A点与直线l相切的圆有()个.A.1 B.2C.不存在 D.无数个3、在Rt△ABC中,∠A=,BA=12,CA=5,若以A为圆心,5为半径作圆,则斜边BC与⊙A的位置关系是()A.相交 B.相离C.相切 D.不确定4、等边△ABC的边长为6,点O为△ABC的外心,以O为圆心,为半径的圆与△ABC的三边()A.都相交B.都相离C.都相切D.不确定5、两个同心圆的半径分别为3cm和5cm,作大圆的弦MN=8cm,则MN与小圆的位置关系是()A.相交 B.相切C.相离D.无法判断6、如图,在直角坐标系中,⊙O的半径为1,则直线与⊙O的位置关系是()A.相离 B.相交C.相切 D.以上三种情形都有可能7、下列说法正确的是()A.垂直于切线的直线必过切点B.垂直于半径的直线是圆的切线C.圆的切线垂直于经过切点的半径D.垂直于切线的直线必经过圆心8、已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm的长为半径作圆,则这个圆与斜边所在的直线的位置关系是()A.相交 B.相切C.相离 D.不能确定9、如右上图,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,则AD的长为()10、如下图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,∠D=__________.11、如图,⊙O的半径为1,圆心O在正三角形的边AB上沿图示方向移动,当⊙O移动到与AC相切时,OA=__________.12、设⊙O的半径为R,⊙O的圆心到直线的距离为d,若d、R是方程x2-6x+m=0的两根,则直线l 与⊙O相切时,m的值为__________.13、已知∠ABC=60°,点O在∠ABC的平分线上,OB=5cm,以O为圆心,2cm为半径作⊙O,则⊙O与BC的位置关系是__________.14、如图,Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,DB的长为半径作⊙D.求证:(1)AC是⊙D的切线;(2)AB+EB=AC.15、如图,以边长为4的正△ABC的BC边为直径作⊙O与AB相交于点D,⊙O的切线DE交AC于E,EF⊥BC,点F是垂足,求EF的长.16、如图,PA是⊙O的切线,切点是A,过点A作AH⊥OP于点H,交⊙O于点B.求证:PB是⊙O的切线.17、如图,已知AB是⊙O的直径,AB=2,∠BAC=30°,点C在⊙O上,过点C与⊙O相切的直线交AB 的延长线于点D,求线段BD的长.1.弧长公式:n°的圆心角所对的弧长l公式不要死记硬背,可依比例关系很快地随手推得:2.扇形面积公式:(1)和含n°圆心角的扇形的面积公式同样不要死记硬背,可依比例关系很快地随手推得:.(2)将弧长公式代入扇形面积公式中,立即得到用弧长和半径表示的扇形面积公式:。
直线与圆、圆与圆的位置关系

直线与圆、圆与圆的位置关系一、直线与圆的位置关系:1、直线与圆的位置关系有三种:如图所示. (1)直线与圆相交:有两个公共点; (2)直线与圆相切:有一个公共点; (3)直线与圆相离:没有公共点.2、直线与圆的位置关系的判定的两种方法:直线l 和圆C 的方程分别为:Ax+By+C=0,x 2+y 2+Dx+Ey+F=0. 1)代数法判断直线与圆的位置关系:由l 和C 的方程联立方程组220Ax By C x y Dx Ey F ++=⎧⎨++++=⎩, ①若方程有两个不相等的实数根(△>0),则直线与圆相交; ②若方程有两个相等的实数根(△=0),则直线与圆相切; ③若方程无实数根(△<0),则直线与圆相离.2)几何法判断直线与圆的位置关系:圆心C(a ,b)到直线的距离d=22||Aa Bb C A B+++与半径r 作比较①若d<r 时,直线l 和圆C 相交;②若d=r 时,直线l 和圆C 相切;③若d>r 时,直线l 和圆C 相离. 3、圆的切线的求法:(1)当点(x 0,y 0)在圆x 2+y 2=r 2上时,切线方程为x 0x+y 0y=r 2;(2)若点(x 0,y 0)在圆(x -a)2+(y -b)2=r 2上时,切线方程为(x 0-a)(x -a)+(y 0-b)(y -b)=r 2; (3)斜率为k 且与圆x 2+y 2=r 2相切的切线方程为21y kx k =±+;斜率为k 且与圆(x -a)2+(y -b)2=r 2相切的切线方程的求法:先设切线方程为y=kx+m ,然后变成一般 式kx -y+m=0,利用圆心到切线的距离等于半径来列出方程求m ;(4)点(x 0,y 0)在圆外面,则切线方程为y -y 0=k(x -x 0),再变成一般式,因为与圆相切,利用圆心到直线距离 等于半径,解出k ,注意若此方程只有一个实根,则还有一条斜率不存在的直线,务必要补上. 4、直线与圆相交的弦长公式1)平面几何法求弦长公式:如图所示,直线l 与圆相交于两点A 、B ,线段AB 的长 即为直线l 与圆相交的弦长.设弦心距为d ,圆的半径为r ,弦长为AB ,则有 222()2AB d r +=,即AB=222r d - . 2)解析法求弦长公式:如图所示,直线l 与圆相交于两点A(x 1,y 1),B(x 2,y 2),当直线AB 的倾斜角存在时,联 立方程组,消元得到一个关于x 的一元二次方程,求得x 1+x 2和x 1x 2.于是2121212||()4x x x x x x -=+-,这样就求得2121221||1||1||AB k x x y y k=+-=+-。
直线和圆的位置关系(1)
在实际应用中,常采用第二种方法判定。
3、切线的性质:圆的切线垂直于过切点的直 径
拓展 已知⊙A的直径为6,点A的坐标为 (-3,-4),则x轴与⊙A的位置关系是 _相__离__, y轴与⊙A的位置关系是_相__切__。
出它们的对称轴吗?
相
离
B
2、右图,直线CD与⊙O相切于
点A,直径AB与直线CD有怎样的
●
O
位置关系?说说你的理由.
CA D
3、你看得懂小颖和小亮的做法吗?
点拨
B
小颖的理由是:
●O
∵右图是轴对称图形,
AB是对称轴,
C
A
D
∴沿直线AB对折图形时,AC与AD 重合,
∴ ∠BAC=∠BAD=90°.
利用圆的轴对称性
B
∴当∠r=A2=c6m0时°,.d>r,AB与⊙C相离
;因C当此Dr,=当4Ac半Cm径时si长n,dA为<r2,43AsBicn与m6时⊙0,0CAB相与2交⊙3.Cc相m切. .
B
C
1、如图,在Rt△ABC中,∠C=90°,AB=5cm,
A相C切=,3则cm这,个以圆C的为半圆径心是的圆与152AcmB 。
A
2、直线L 和⊙O有公共点,则直线L与⊙O( D ). A、相离;B、相切;C、相交;D、相切或相交。
3.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( A):
A.d >3 B.d<3 C.d ≤3 D.d =3
4.判断:若直线和圆相切,则该直线和圆一定有一个公共
点和圆、直线和圆的位置关系

§24.2 点和圆、直线和圆的位置关系一、知识点过关知识点1 点和圆的位置关系(重点;掌握)点和圆的位置关系有三种,设点P 到圆心O 的距离d OP =,⊙O 的半径为r ,则有: 点P r >;点P 在圆上 r =;点P 在圆内 r <; 【命题点1 根据d 与r 的数量关系判定点与圆的位置关系】例1 已知⊙O 的面积是16π,若5.4=OP ,则点P 在⊙O ;若4=OP ,则点P 在⊙O ;若OP ,则点P 在⊙O 内.针对性训练1、若点)0(,a B 在以点)01(,A 为圆心,2为半径的圆内,则a 的取值范围为 ( ) 31.<<-a A 3.<aB 1.->aC 13.-<>ora a D知识点2 圆的确定(重点;理解)不在同一条直线上的三个点确定一个圆。
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心. 【命题点2 求三角形外接圆的半径】例2 △ABC 中,10==AC AB ,12=BC ,求△ABC 的外接圆半径.针对性训练1. 如图,点A ,B ,C 在同一条直线上,点D 在直线AB 外,过这4个点中的任意3个点,能画圆的个数是( )A.1B.2C.3D.4知识点3 直线和圆的位置关系(重点;掌握)1.相交、相切与相离的概念[画图板书](1)直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.(2)直线和圆有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.(3)直线和圆没有公共点,这时我们说这条直线和圆相离.2.直线与圆的位置关系如果设⊙O 的半径为r ,圆心到直线l 的距离为d ,可归纳出下列结论: (1)直线l 和⊙O 相离 r d >; (2)直线l 和⊙O 相切 r d =; (3)直线l 和⊙O 相交 r d <;【命题点3 根据直线与圆的位置关系求半径R 的取值范围】例3 已知︒=∠30MON ,在ON 边上有一点P ,cm OP 5=,若以点P 为圆心,以R 为半径作圆,求满足下列条件的⊙P 的半径R 的取值范围. (1)射线OM 与⊙P 只有一个公共点; (2)射线OM 与⊙P 有两个公共点.针对性训练1、在Rt △ABC 中,cm AC 3=,cm BC 4=,︒=∠90ACB .若以点C 为圆心,r 为半径的圆与直线AB 不相离,求r 的取值范围.知识点4 圆的切线的判定与性质(重点、难点;理解)1.切线的判定(1)和圆只有一个公共点的直线是圆的切线.(2)如果圆心到直线的距离等于半径,那么直线是圆的切线.经过半径的外端并且垂直于这条半斤的直线是圆的切线(切线的判定定理) 2.切线的性质定理圆的切线垂直于过切点的半径. 【命题点4 切线的性质定理的应用】例4 如图所示,AB 为⊙O 的直径,PD 切⊙O 于点C ,交AB 的延长线于点D ,且CAD D ∠=∠2.连接OC. (1)求D ∠的度数;(2)若2=CD ,求BD 的长.针对性训练1、已知⊙O 中,AC 为直径,MA ,MB 分别切⊙O 于点A ,B. (1)如图①,若︒=∠25BAC ,求AMB ∠的大小;(2)如图②,过点B 作AC BD ⊥于点E ,交⊙O 于点D ,若MA BD =,求AMB ∠的大小.知识点5 切线长的定义及定理(重点、难点;掌握)1.定义经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这点到圆的切线长. 2.切线长定理从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 【命题点5 利用切线长定理求角的度数】例5 如图所示,PA ,PB 是⊙O 的切线,A 、B 为切点,BC 是⊙O 的直径,连接AB ,AC ,OP.︒=∠20BAC ,则P ∠的度数为 ( )A.50°B.70°C.110°D.40°针对性训练1、如图所示,PA ,PB 是⊙O 的切线,切点分别为A 、B ,已知BC 是⊙O 的直径,连接AB ,AC ,OP. 求证:(1)ABC APB ∠=∠2;(2)AC ∥OP.【命题点6 利用切线长定理求线段的长】例5 如图所示,PA ,PB 是⊙O 的切线,切点分别是A 、B ,Q 为︵AB上一点,过Q 点作⊙O 的切线,交PA ,PB 与E ,F 两点,已知cm PA 10=,求△PEF 的周长.针对性训练1、如图,P 是⊙O 外一点,PA ,PB 分别和⊙O 相切于点A ,B ,C 是劣弧︵AB上任意一点,过C 作⊙O 的切线DE ,分别交PA ,PB 于点D ,E. 已知△PDE 的周长为8,︒=∠70DOE ,点M ,N 分别在PB ,PA 的延长线上,MN 与⊙O 相切于点F ,且DN ,EM 的长是方程0102=+-k x x 的两根. (1)求P ∠的度数;(2)求PA 的长;(3)求四边形DEMN 的周长.知识点6 三角形的内切圆(重点、难点;掌握)(1)与三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.(内切圆与外接圆对比)(2)三角形的内心到三角形三边的距离都相等.(3)三角形的内切圆的作法:先作出三角形的两条角平分线,以两条角平分线的交点为圆心,交点到一边的距离为半径作圆,即而已得到三角形的内切圆.推论:同弧或等弧所对的圆周角相等.半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径. 【命题点6 利用三角形内心求角的度数】例6 如图所示,⊙O 是△ABC 的内切圆,与边BC 、CA 、AB 的切点分别为D ,E ,F ,若上︒=∠70A ,则EDF ∠= 度.针对性训练1、⊙O 是Rt △ABC 的内切圆,切点分别为D 、E 、F ,︒=∠90C ,4=AC ,3=AB ,求⊙O 的半径r .知识点7 圆内接多边形的概念及圆内接四边形的性质(重点;理解)1.概念:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.2.性质:圆内接多边形的对角互补.【命题点7 圆内接四边形与垂径定理的综合应用】例7 如图所示,四边形ABCD 的四个顶点都在⊙O 上,BD AC ⊥于E ,AB OF ⊥于F ,求证:CD OF =2.针对性训练1、如图所示,在圆内接四边形ABCD 中,︒=∠30B ,则=∠D .二、全方位技巧类型题1 根据点与圆的位置关系求r 的取值范围例1 已知△ABC ,︒=∠90C ,2=AC ,3=BC ,AB 的中点为M. (1)以C 为圆心,2为半径作⊙C ,则点A ,B ,M 与⊙C 的位置关系如何?(2)若以C 为圆心作⊙C ,使A ,B ,M 三点至少有一点在⊙C 的内部,且至少有一点在⊙C 的外部,求⊙C 的半径r 的取值范围.类型题2 有关圆与一元二次方程的综合题例2 设⊙O 的半径为2,点P 到圆心的距离m OP =,且m 使关于x 的方程012222=-+-m x x 有实数根,试确认点P 与⊙O 的位置关系.类型题3 切线的判定和性质的综合应用例3 如图所示,已知AB 是⊙O 的直径,BC 是⊙O 的切线,OC 与⊙O 相交于点D ,连接AD 并延长,与BC 相交于点E. (1)若3=BC ,1=CD ,求⊙O 的半径;(2)取BE 的中点F ,连接DF ,求证DF 是⊙O 的切线.类型题4 圆的切线与四边形的综合应用例4 如图所示,AB 是半圆O 的直径,点C 为半径OB 上一点,过点C 作CD ⊥AB 交半圆O 于点D ,将△ACD 沿AD 折叠得到△AED ,AE 交半圆于点F ,连接DF. (1)求证DE 是半圆的切线;(2)当BC OC =时,判断四边形ODFA 的形状,并证明你的结论.类型题5 圆周角定理的推论与垂径定理的综合应用例5 如图所示,点C ,D 在以AB 为直径的⊙O 上,且CD 平分ACB ∠,若2=AB ,︒=∠15CBA ,则CD 的长为 .类型题6 巧引辅助线,构造特殊三角形解题例6 如图所示,在⊙O 中,︒=∠=∠60BDC ACB ,cm AC 32=. (1)求BAC ∠的度数. (2)求⊙O 的周长.三、分层实战训练【基础巩固】1.已知点P 与圆周上的点的最小距离为6cm ,最大距离为16cm ,求该圆的半径.2.⊙O 的圆心到直线l 的距离为d ,⊙O 的半径为R ,若R d ,是方程02092=+-x x 的两个实数根,则直线和圆的位置关系是 .3.如图,△ABC 内接于半径为5的⊙O ,圆心O 到弦BC 的距离等于3, 则A ∠的正切值等于 ( ) 53.A 54.B 43.C 34.D4.已知AB 是⊙O 的直径,点D 在AB 的延长线上,OB BD =,点C 在圆上,︒=∠30CAB .求证:DC 是⊙O 的切线.5.AB 是⊙O 的直径,点C 在⊙O 上,连接BC ,AC ,作OD ∥BC 与过点A 的切线交于点D ,连接DC 并延长交AB 的延长线于点E.求证:DE 是⊙O 的切线.6.AB 是⊙O 的直径,点F ,C 是⊙O 上两点,且︵AF =︵FC =︵CB ,连接AC ,AF ,过点C 作AF CD ⊥,交AF 的延长线于点D ,垂足为D.求证:CD 是⊙O 的切线.7.已知⊙O 的直径为AB ,AB AC ⊥于点A ,BC 与⊙O 相交于点D ,在AC 上取一点E ,使得EA ED =. (1)求证:ED 是⊙O 的切线;(2)当3=OA ,4=AE 时,求BC 的长度.8.如图所示,在△ABC 中,BC AC =,α=∠CAB (定值),⊙O 的圆心O 在AB 上,并分别与AC ,BC 相切于点P ,Q. (1)求POQ ∠的大小;(2)设D 是CA 延长线上的一个动点,DE 与⊙O 相切于点M ,E 在CB 的延长线上,试判断DOE ∠的大小是否随着D 点位置的变化而变化,并说明理由. (3)在(2)的条件下,如果m AB =(m 为已知数),53cos =α,设y DE x AD ==,,求y 关于x 的函数解析式.9.如图所示,在平面直角坐标系中,以点O 为圆心,半径为2的圆与y 轴交于点A ,点)24(,P 是⊙O 外一点,连接AP ,直线PB 与⊙O 相切于点B ,交x 轴于点C. (1)求证PA 是⊙O 的切线;(2)求点B 的坐标.10.如图,AB 是⊙O 的直线,弦CD 与AB 交于点E ,过点A 作⊙O 的切线与CD 的延长线交与点F ,如果CE DE 43=,58=AF ,D 为EF 的中点. (1)求证:ACF AFC ∠=∠;(2)求AB 的长.11.(2014*江苏扬州)如图,⊙O 与Rt △ABC 的斜边AB 相切与点D ,与直角边AC 相交于E 、F 两点,连接DE.已知︒=∠30B ,⊙O 的半径为12,弧DE 的长度为4π. (1)求证:DE ∥BC ;(2)若CE AF =,求线段BC 的长度.12.(2014*黑龙江哈尔滨)如图,⊙O 是△ABC 的外接圆,弦BD 交AC 于点E ,连接CD ,且DE AE =,CE BC =.(1)求ACB ∠的度数;(2)过点O 作AC OF ⊥于点F ,延长FO 交BE 与点G ,3=DE ,2=EG ,求AB 的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学教案A.点P在⊙
例题二在
交BC于点E
考法3点和圆的位置关系的综合应用
例题二如图,
的半径为2,
A.0
考法2画三角形的外接圆
考法3与三角形外接圆有关的计算
例题一某中学在校内安放了几个圆柱形饮水桶的木制支架(如图①)例题二如图,⊙O是△ABC的外接圆,∠
考法4与三角形外接圆有关的证明
例题一
例题二
例题三=,点
考法5与三角形外接圆有关的综合问题
例题一已知:⊙
例题二如图,等腰
求证:AE=BD+DE
知识点三
1:判断直线和圆的位置关系
为圆心、A.相切
例题四如图,
BA交半圆于点为圆心,考法2由直线和圆的位置关系确定字母的取值范围。
