曲线的齿化与虚化
齿轮齿廓中最常用的曲线形式

齿轮齿廓中最常用的曲线形式齿轮是机械传动中常用的零件之一,广泛应用于各种机械设备中。
齿轮的齿廓形状对于传动效果和工作性能有着至关重要的影响。
在齿轮制造中,最常用的曲线形式是圆弧形和渐开线形。
圆弧形齿廓是最早应用于齿轮设计中的曲线形式。
它的特点是曲线简单、容易加工,但是在高速传动中会产生较大的动载荷和噪声。
由于不适合用于高速齿轮传动,因此在现代机械设计中用得相对较少。
与圆弧形齿廓相比,渐开线形齿廓更加常见也更加重要。
渐开线是一条特殊的曲线,它既要满足齿轮的传动功能,又要尽量减小传动中的冲突和噪声。
与其他曲线相比,渐开线形齿廓的独特之处在于,在齿轮接触和分离时会产生渐变的速度和压力分布,从而减小了传动中的冲突。
渐开线形齿廓的优点不仅仅体现在传动效果上,还有助于提高齿轮的使用寿命和传动效率。
首先,渐开线形齿廓减小了齿轮在接触过程中的压力和应力集中,避免了齿轮齿面的过早磨损和断裂。
其次,渐开线形齿廓减小了齿面接触的冲击和滑动,减少了能量损失,提高了传动效率。
为了生成渐开线形齿廓,需要选择适当的齿廓参数,如渐开线系数和压力角。
渐开线系数是描述渐开线形状的重要参数,它决定了渐开线齿廓的弧度变化率。
渐开线系数越大,齿轮的齿廓形状越渐进,接触过程中的冲击和噪声越小。
压力角是描述齿轮传动时齿面受力的角度,它对齿轮的强度和传动效果有着重要影响。
常用的压力角有20度和14.5度两种,其中20度压力角的齿轮传动更常见。
在实际齿轮制造中,为了保证齿轮的精度和稳定性,通常采用渐开线形齿轮副。
这种齿轮副不仅能够实现稳定的传动效果,还能够减小齿轮的噪声和振动。
与此同时,渐开线形齿廓也可以通过工艺优化和制造精度的提高来进一步改善齿轮的传动性能。
综上所述,齿轮齿廓中最常用的曲线形式是渐开线形和圆弧形。
其中,渐开线形对于齿轮传动的效果和性能有着重要影响,能够减小冲突和噪声,提高使用寿命和传动效率。
在齿轮制造中,选择适当的齿廓参数和制造工艺,可以进一步优化渐开线形齿轮副的传动性能。
photoshop操作中常见的锯齿问题

有感于一些朋友的作品(尤其是页面\软件界面设计这种对精度要求很高的地方)在细节方面总是受到锯齿的困扰,而拉低了整体档次。
特根据自己的经验讲一讲常见的毛刺问题。
随笔写写,有些可能不是很完善很对~俺记性一向不好。
另外像素风格图片、gif边缘锯齿不再这次讨论范围之内。
(本教程以cs3为例,快捷键的不同不再另行说明。
另,cs4中新增的蒙版控制功能可以结合使用)1、ctrl+t 类变形导致的锯齿问题1-1 原因:常规选项设置不当(很少有的情况)解决:打开菜单[编辑]-[首选项]-[常规]。
请确保你的[图像插值]设置为“两次立方(适用于平滑渐变)”。
当然你有特殊需要且明确这里选项的含义则另当别论(比如说像素风格的缩放一般用“邻近”来确保不模糊)。
1-2 原因:旋转与缩小等产生的锯齿与走形解决:1-2-1 先旋转后缩小,分两步走(把一次ctrl+t 拆分为两次,最后一次再缩小可以减少变形/旋转产生的毛刺)。
1-2-2 采用矢量对象(比如常见的文字透视变形,不要选择[栅格化],而采用[转换为形状])。
矢量对象在一般情况下变形更保真,另一个显著优点是经得起反复ctrl+t 而不会产生问题。
1-2-3 有多大画多大,最好别ctrl+t (特别适用于简单形状)。
同理,能少ctrl+t,就不要反复ctrl+t 。
特别忌讳拉大又拉小,转来又转去~~ 结合第一条:如果存在缩小,最好是两次变形,一次形状到位,第二次缩小。
1-3 原因:旋转90度/180度时,如果用中点定位则会发生重新运算。
导致模糊or锯齿产生。
解决:要想最大程度保持原样,最好在90度(180度)旋转时用角点定位(随便哪个角点)。
这样可以避免重新运算像素导致的质量损失。
2、多次填充选区产生的锯齿问题原因:反复的填充(包括涂画、拉渐变等等)导致原本用于平滑的边缘半透明像素叠加,越来越不透明产生实体锯齿。
解决:(首先,将可能需要反复填充的区域弄在独立的层)2-1 填充一次后,立即锁定图层的透明区域。
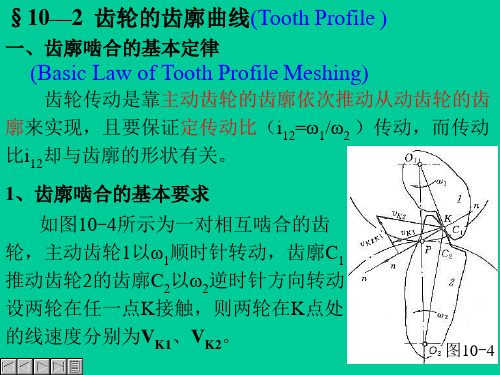
§10—2齿轮的齿廓曲线
圆盘1上的已知曲线C1就会走出一 1 C 系列的轨迹,作这些轨迹的包络 线,则得到所求的齿廓曲线C2。
三、齿廓曲线的选择 理论上,只要给出一齿廓C1 ,就可以求出另一条满足 定传动比的共轭齿廓C2。但生产实际上,选择齿廓曲线时, 不仅要满足传动比要求,还必须从设计、制造、安装和使 用等方面予以考虑。 目前对定传动比传动的齿轮来说,最常用的齿廓是渐 开线(Involute) ,其次是摆线(Cycloid) 和变态摆线,近年 来出现了圆弧(Arc) 、抛物线(Parabola) 等。 由于渐开线齿廓具有良好的传动性能,便于制造、安 装、测量和互换性好等优点,所有目前绝大部分齿轮都采 用渐开线齿廓。 本章只讨论渐开线齿轮。
一、齿廓啮合的基本定律
(Basic Law of Tooth Profile Meshing)
齿轮传动是靠主动齿轮的齿廓依次推动从动齿轮的齿 廓来实现,且要保证定传动比(i12=ω1/ω2 )传动,而传动 比i12却与齿廓的形状有关。 1、齿廓啮合的基本要求 、 如图10-4所示为一对相互啮合的齿 轮,主动齿轮1以ω1顺时针转动,齿廓C1 推动齿轮2的齿廓C2以ω2逆时针方向转动。 设两轮在任一点K接触,则两轮在K点处 的线速度分别为VK1、VK2。
目前对定传动比传动的齿轮来说最常用的齿廓是渐开线involute其次是摆线cycloid和变态摆线近年来出现了圆弧arc抛物线parabola由于渐开线齿廓具有良好的传动性能便于制造安装测量和互换性好等优点所有目前绝大部分齿轮都采用渐开线齿廓
齿轮的齿廓曲线(Tooth Profile ) §10—2 齿轮的齿廓曲线
4、节点(pitch point) 和节圆(pitch circle) 、 1)节点 节点P——过齿廓啮合点的公法线与连心线的交点。 节点 2)节圆 节圆 如要求定比传动即i12=C,则应 使O2P/ O1P= C。由于O1、O2为定点, 所以欲使 O2P/ O1P= C,则节点P在 O1O2上必须是定点。 ∴ 定比传动齿轮的齿廓啮合基本定律 可以表述为:要使两齿轮作定传动 比传动,则不论两齿廓在何处接触, 过接触点所作的公法线必须与连心 线交于一定点。
目前广泛应用的齿轮齿廓曲线是摆线【“曲线”形态的在现代设计中广泛应用的原因】

目前广泛应用的齿轮齿廓曲线是摆线【“曲线”形态的在现代设计中广泛应用的原因】一、生理需求人作为建筑使用的主要对象,人性化的创作应该作为建筑设计思考当中的首要因素。
这类创作力图改变建筑与人类之间的冰冷关系,实现人与建筑相互沟通交流的理想状态。
这是相互沟通的感受是建立在人与建筑之间最直接的接触当中,包括建筑给予的关怀,都可以激发人类对其的情感。
这种知觉上的情感可以转化为精神和心理的安慰。
所以建筑作为人类的使用对象是否可以让人觉得舒适,则是建筑好坏的基本评价标准。
1、人体的曲线表现《圣经》为人类的诞生描绘出美丽的图画:上帝耶和华创造天地海洋和万物后,第六日造人,用尘土造出男人亚当,用肋骨造出女人夏娃。
他们在吞下善恶果之前,裸露袒程,无忧无虑地生活在嘉林丰茂,硕果累累的伊甸园里。
人类在漫长的生命进化历程中,人最初确实是以赤裸的躯体拥抱大自然的。
人类在不断完善自身的同时,也以各种不同的方式达到人与自然的和谐。
人类创造财富,也创造了自身。
人体艺术美是人对自身构造之完美的认识和礼赞。
人体艺术美的发现是人的觉醒的一个重要组成部分,是人脱离自然状态,获得自我意识的重要标志,是人的实践和思维能力的本质的飞跃。
人体从骨骼到细胞组织甚至是头发都呈现出优雅的曲线,我们可以观察自己的身体除了男性的短胡须以外,基本找不出任何一条直线。
人的整个身体基本都由柔和优雅的曲线构成。
人体的曲线就像一本展示去曲线美的教科书。
古希腊艺术家也称人体是世界上最完美的形体。
2、人体工程学当设计中结合了人体工程学使很多方面得到了更好的协调,人和使用对象之间就产生了配合默契,很显然可以达到和使用对象之间整合的目的――高效。
人在工作时是有一定的活动空间,设计是否合理直接关系到工作效率。
举了简单的例子,众所周知同等面积的四边形周长要比圆形长,那么在工作的时候需要从一边走道另一边,按照人体工程学人的行走路线是曲线形的,将直角换成圆弧线是不是就可以提高效率。
齿轮的齿廓曲线 ppt课件

pn
α
α
α
p
ppt课件
B 26
三、内齿轮(internal gears)
结构特点:轮齿分布在空心圆柱体内表面上。
不同点:
1)轮齿与齿槽正好与外齿轮相反。
2) df>d>da,da=d-2ha,df=d+2hf
3) 为保证齿廓全部为渐开线,
要求da>db。
se p
B
hhfha
N
pn
rb
能搭配起来正确传动,比如说 一个齿轮的齿距很小,另一个
定律,K在N1N2上,K’在N1N2上,KK’为相 两齿同侧齿廓间的法向齿距
在齿轮1上: kk’=pb1
邻
齿轮的齿距很大,显然两个齿
轮是无法搭配传动的。
pb1
O1
rb1
ω1
在齿轮2上: kk’= pb2
r1
∴ pb1= pb2
N1
K’
将pb=πmcosα代入得: m1cosα1=m2cosα2
ppt课件
31
§10-5 渐开线直齿圆柱齿轮的啮合传动
0、一对渐开线轮齿的啮合过程
ppt课件
32
B1B2——实际啮合线
由于基圆内无渐开线,故B1、B2两点不能超出N1、N2 两点,因此N1、N2两点称为啮合极限点。
N1N2: 理论上可能的最长啮合线段—— 理论啮合线段
一般情况下,实际啮合线段长度小于理论啮合线段长 度。
啮 合 线 又 是 接 触 点 的 法 线 ,N2
O1 ω1
N1 α’ K K’ P C2 C1
正压力总是沿法线方向,故其传
力方向不变。这对于传动的平稳 rb2
性是有利的。
过度曲线

3.4.5齿根过渡曲线对于展成加工的齿轮,过渡曲线是加工中自动形成的。
由于塑料齿轮、粉末冶金齿轮应用的扩展,这类齿轮是由模具形成的,齿根过渡曲线如果处理得不好,会影响啮合性能。
3.4.5.1 过渡曲线的类型用齿条型刀具加工的时候,齿根过渡曲线,随变位系数、刀具齿顶圆弧的变化而变化。
图14-1-4E 是在刀具齿顶圆弧固定时,不同变位系数的情况。
刀具齿顶圆弧中心轨迹。
①当x <(hfp -ρfp) ,图中的<F2/F3>延伸渐开线②当x =(hfp -ρfp) ,<F4>渐开线③当x >(hfp -ρfp) ,<F5>缩短渐开线齿根过渡曲线则是它们的等距线。
将齿条刀具变成齿轮型刀具,延伸渐开线变成延伸外摆线。
对齿轮型刀具随着变位系数的增加,也是图形所示的长幅外摆线、外摆线、短幅外摆线。
<F4> 实际上的过渡曲线,在理论上是一个与刀具齿顶圆弧一样的圆弧,但是由于刀具是有限齿槽,不可能正好在那个位置有刀刃切削,可能由1—2 个刀刃切出来。
GB/T3374-1992 《齿轮基本术语》2.3.2 摆线类trochoids2.3.2.1 外摆线epicyeloid2.3.2.2 长幅外摆线prolate epicyeloid2.3.2.3 短幅外摆线curlate epicyeloid…………………..2.3.3 渐开线involute2.3.3.1 渐开线(圆的渐开线)involute to a circle, involute2.3.3.2 延伸渐开线prolate involute2.3.3.3 缩短渐开线curlate involute同样的prolate , 一个是长幅,一个是延伸;同样的curlate, 一个是短幅,一个是缩短。
标准术语尚且如此,难怪术语不能统一。
3.4.5.2 过渡曲线与啮合干涉在AGMA相关标准和DIN3960标准中,都十分注意一对齿轮啮合状况的图形。
AE曲线变形效果制作方法

AE曲线变形效果制作方法在AE软件中,曲线变形效果是一种常用的制作技巧,可以实现各种有趣的效果。
本文将介绍AE中使用曲线变形效果的具体步骤和一些使用技巧。
首先,我们需要导入一个图层,在图层上点击右键,选择“新建”>“调整层”。
在效果窗口中找到“曲线变形”效果,将其拖拽到图层上。
一旦将曲线变形效果应用到图层上,可以看到图层被分成许多控制点,它们构成了一个网格。
通过调整这些控制点的位置,图层可以被扭曲、拉伸或变形。
为了更好地控制曲线变形效果,我们可以使用另一个工具——网格变形工具。
在AE工具栏上找到网格变形工具,点击后在图层上会出现一个网格,通过拖拽网格上的控制点,可以调整图层的形状。
除了调整控制点的位置来改变形状外,我们还可以通过调整曲线形状来实现更精确的控制。
在效果窗口中,可以看到“曲线”选项,点击它可以打开一个新的窗口。
在这个窗口中,可以看到一个曲线图,通过调整曲线的形状,可以改变图层的变形效果。
曲线图中有两条曲线,一条是输入曲线,用来表示原始图层的像素位置;另一条是输出曲线,用来表示经过变形效果后的图层的像素位置。
通过调整这两条曲线的形状和位置,可以实现更多样化的效果。
在使用曲线变形效果时,还有一些技巧和注意事项需要注意。
首先,保持控制点的平滑过渡是非常重要的,这样可以避免图层变形后出现不自然的边缘。
其次,可以尝试结合其他效果,比如模糊、颜色调整等,来增强整体效果。
此外,可以使用遮罩来限制曲线变形效果的作用区域,从而实现更精确的控制。
总结起来,AE中的曲线变形效果是一种非常有用的技巧,可以用来实现各种各样的效果。
通过调整控制点的位置、调整曲线的形状以及结合其他效果和遮罩的使用,可以创造出非常出色的动画效果。
希望本文对大家了解AE曲线变形效果的制作方法有所帮助,希望大家可以通过学习和实践,掌握这个技巧,在自己的作品中创造出更多的精彩效果。
画齿轮的曲线方程

要画出齿轮的曲线方程,通常需要使用参数方程或极坐标方程。
下面是一个简单的示例,描述了一个基础的齿轮形状。
假设我们要画一个基本的齿轮形状,其齿形是一个简单的正弦波。
### 使用极坐标方程在极坐标中,我们可以使用以下方程来描述一个齿轮的形状:r(θ) = a + b * sin(n * θ)其中:* r(θ) 是从原点到齿轮上一点的距离(半径)。
* θ 是极角(从正x轴逆时针测量)。
* a 是齿轮的基础半径。
* b 是齿的振幅(即齿的高度)。
* n 是齿的数量。
例如,如果我们想要一个基础半径为5,齿高为2,有6个齿的齿轮,那么方程就是:r(θ) = 5 + 2 * sin(6 * θ)### 使用参数方程在笛卡尔坐标中,我们可以使用参数方程来描述齿轮:x(t) = (a + b * sin(n * t)) * cos(t)y(t) = (a + b * sin(n * t)) * sin(t)其中:* x(t) 和y(t) 分别是齿轮上一点的x和y坐标。
* t 是一个参数,通常从0到2π。
* a, b, 和n 的含义与上面的极坐标方程相同。
对于同样的齿轮(基础半径为5,齿高为2,有6个齿),参数方程为:x(t) = (5 + 2 * sin(6 * t)) * cos(t)y(t) = (5 + 2 * sin(6 * t)) * sin(t)要使用这些方程来绘制齿轮,你可以在你的绘图软件或编程语言中选择适当的工具或函数,并输入这些方程作为输入。
例如,在Python中,你可以使用matplotlib库来绘制这些方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有趣的曲线齿化与虚化
马跃进(江西省赣县教师进修学校,341100) (mayuejin60@ )
新课标高中数学必修4(北师大版)第一章三角函数中,有如下一道习题: 利用五点法或借助信息技术画出函数sin sin y x x =-的图像.
无论是利用五点法,还是利用几何画板来画上述函数的图像,都是一道难度不大的习题,但笔者借助几何画板,画出了更多的形如:
()()sin sin ,,0,*,y a b nx nx a b b n =+±∈≠∈R N 下同的函数图像,发现它们均呈锯齿线
形状.如图1为函数
()
20.2sin10sin10y x x =+-([]2π,2πx ∈-)
的图像.
通过进一步探究,发现方程
()sin sin y a b nx nx =+-的曲线具有下
列性质:
(1)在[]0,2π上曲线的齿数为n ;
(2)齿长(齿尖到直线y a =的距离)为2b ; (3)当0b >时齿尖向下,0b <时齿尖向上 探究没有就此结束,我们尝试把方程
()sin sin y a b nx nx =+-中的a 换为m kx +,
即变成方程
()sin sin y kx m b nx nx =++-.
不妨取取()
210.2sin10sin10y x x x =++-,通过几何画板,画出其曲线为图2所示.
显然,图2把直线12+=x y 齿线化了,即方程()
210.2sin10sin10y x x x =++-,把直线12+=x y 齿线化了.因而可知,方程()
sin sin y kx m b nx nx =++-把直线m kx y +=齿线化了.
更有趣的是,上述结论可以进一步推广. 为叙述方便,我们给出如下定义:
若曲线()x f y C =:,则曲线()()nx nx b x f y C sin sin :-+=∑(
)*
∈≠N
n b ,0①为曲线
C 的一种齿化曲线,称①为曲线C 的齿化曲线方程,()()nx nx b x g sin sin -=为齿化函数
.
图 1
图2
如图3,分别为直线,m kx y +=抛物线,2x y =双曲线1
,y x
=对数曲线x y ln =的一种齿化曲线.
可以写出它们从左到右的一个齿化曲线方程顺次为 (1)()
0.510.2sin 20sin 20y x x x =++-; (2)2x y =()
0.2sin 30sin 30x x +-; (3)()1
0.2sin 40sin 40y x x x
=
--; (4)()
ln 0.2sin 30sin 30y x x x =--.
通过进一步探究发现,曲线的齿化函数()x g 并非只有上述这一种.事实上,只要确保()x g 是一个图像具有齿线形状的周期函数即可.
如()()()nx b nx b x g cos arccos
,sin arcsin =()
*
∈≠N n b ,0均可. 如图4,分别为直线,m kx y +=抛物线,2x y =双曲线1
,y x
=对数曲线x y ln =的一种齿化曲线. 可以写出它们从左到右的一个齿化曲线方程顺次为
(1)()x x y 20cos arccos
2.015.0++=; (2)()x x y 30cos arccos 2.02
+=;
图3
图4
(3)()x x
y 40cos arccos 2.01
+=
; (4)()x x y 30cos arccos 2.0ln +=. 类比可以得到:
在极坐标系中,若曲线()θρρ=
:C ,则曲线()()θθθρρn n b C sin sin :-+=∑
()*
∈≠N n b ,0②为曲线C
的一种齿化曲线,称②为曲线C 的齿化曲线方程,
()()θθθn n b g sin sin -=为齿化函数.
利用几何画板,可以画出极坐标系中,圆2:=ρC 的一种齿化曲线
:C ∑()20.2sin 20sin 20ρθθ=±-.
如图4所示,左图为
齿化曲线:C ∑()20.2sin 20sin 20ρθθ
=+-;
右图为齿化曲线:C ∑(
)20.2sin 20sin 20ρθθ=--.
上述齿线一周有20个齿,齿长为0.4,但形状不同.
如取齿化函数()()θθ20cos arccos 2.0=g ,可得到圆2:=ρC 的一种齿化曲线
:C ∑()θρ20cos arccos 2.02±= .
如图5所示,左图为
齿化曲线:C ∑()θρ20cos arccos
2.02+=; 右图为齿化曲线:C ∑()θρ20cos arccos
2.02-=. 上述齿线一周有20个齿,齿长为0.2π,形状略有不同.
这样,我们就得到两个非常漂亮的齿线,同时也无形之中给出了一种具有实用价值的设计圆形齿轮的简洁方法.依照这个方法完全可以根据轮齿的多少,齿长的大小等要求来设计齿轮.
如图6是极坐标系中,取齿化函数
()()θθθ60sin 60sin 2.0-=g
的一些迷人的曲线的齿化曲线.
图
4
图
5
从左到右,可得出它们一个齿化曲线方程为
(1)()
0.21 1.5sin 60sin 60,[0,5π];ρθθθθ=+--∈; (2
)()0.2sin 60sin 60;ρθθ=
--
(3)()
2(1cos )0.2sin 60sin 60;ρθθθ=+--
(4)()()
2
310.85cos 2sin 40.2sin 60sin 60ρθθθθ=+++-.
如图7是极坐标系中,取齿化函数()()θθ60cos arccos 2.0=g 的上述相应迷人的曲线的齿化曲线
从左到右,可得出它们一个齿化曲线方程为 (1)()0.210.2arccos cos60ρθθ=++; (2
)()0.2arccos cos60ρθ=
+;
(3)()()21cos 0.2arccos cos60ρθθ=++;
(4)()
()θθθρ60cos arccos 2.04sin 2cos 85.0132
+++=.
另外,如若我们注意到取函数(
)(
)g x g x ==,如取函数(
)g x =,则可由几何画板画出方程:
(1
)0.51y x =++ (2
)2
y x =+ (3
)1
2
y =
+
图7
(4
)ln y x =+.
从图像上可以看出,这些曲线全被虚线化了.因此,可以认为,欲画出一曲线的虚线,只需在曲线方程()x f y =(或
()θρρ=)后,加上一个函数(
)g x x =((
)g θ=,便可通过几何画板画出其曲线的虚线. 如图9自左到右,是极坐标系中
,()0.21,21cos ρθρρθ=+=
=+;
()2310.85cos 2sin 4ρθθ=++,被虚化的曲线,其虚化函数为(
)g θ=
本文发表在《中学数学教学》2010年第5期
图
8
图9。
