齿廓啮合基本定律与齿轮的齿廓曲线
第七章齿轮传动

(4)啮合角不变
啮合线与两节圆公 切线所夹的锐角称为啮 合角,用α’表示 。 显然,齿轮传动啮合角 不变,正压力的方向也 不变。因此,传动过程 比较平稳。
C
五、直齿圆柱齿轮基本参数和几何尺寸
齿数—Z,齿槽
1、齿顶圆da 2、齿根圆df 3、在任意圆周上 ①齿槽宽ek
②齿厚SK
③齿距PK=eK+SK
根切的危害: ①切掉部分齿廓; ②削弱了齿根强度;
③严重时,切掉部分渐开
线齿廓,降低重合度。
产生根切的原因:
当刀具齿顶线与啮合线的交点超过啮合极限点N,
刀具由位置Ⅱ继续移动时,便将根部已切制出的渐开
线齿廓再切去一部分。
七、斜齿圆柱齿轮传动
1、曲面的形成
当斜齿轮发生面与基圆柱相切,发生线与轴线成βb 。 当角βb=0时,即形成直齿圆柱齿轮的齿廓曲面。
措施:提高齿面硬度,采用油性好的润滑油。
2、齿轮材料及其热处理
1)齿轮材料
45号钢 中碳合金钢 最常用,经济、货源充足 35SiMn、40MnB、40Cr等 20Cr、20CrMnTi等
金属材料
低碳合金钢
铸钢
铸铁
ZG310-570、ZG340-640等
HT350、QT600-3等
非金属材料
尼龙、夹木胶布等
v k 1 = w 1 o1 k
k2 = w 2 o2k
即 k 1 cos k 1 = k 2 cos k 2
w1 O2 N 2 O2 C = = i12 = w 2 O1 N1 O1 C
要保证传动比为定值,点C应为连心线上定点,称为节点。
O1、O2为圆心, 过节点C所作的两个相 切的圆称为节圆 。
机械原理第10章齿轮机构及其设计

2、具有标准顶隙:c = c *m
2.1.2 标准中心距
a=ra1+c+rf2 =r1+h*am+c*m+r2-( h*am+c*m)
=r1+r2=m(z1+z2) / 2
两轮的中心距a应等于两轮分度 圆半径之和,我们把这种中心距称为 标准中心距a
实际中心距a’
2.1.3 啮合角
啮合角α’——两轮传动时其节点P的圆周速度方向与啮合线 N1N2之间所夹的锐角,其值等于节圆压力角。 压力角α和啮合角α’的区别
2、对于按标准中心距安装的标准齿轮传动,当两轮的 齿数趋于无穷大时的极限重合度εαmax=1.981。
3、重合度εα还随啮合角α’的减小和齿顶高系数ha*的增 大而增大。
4、重合度是衡量齿轮传动质量的指标。 重合度承载能力传动平稳性
[例] 已知 z1=19、z2=52、=20、m =5mm、ha*=1。求 。
rb1+rb2=(r1+r2)cosα=(r1’+r2’)cos α’
齿轮的中心距与啮合角的关系为: a’cos α’=acos α
r1 =r1
O1
ω1 rb1 N1
=
r1 r1
O1
ω1 rb1 N1
N2
P
rb2 r2 =r2
P
N2 a
rb2
r2
r2
a
ω2
ω2
O2
O2
2.2 齿轮与齿条啮合传动 齿轮与齿条标准安装:齿轮的分度圆和齿条的分度线相切。
2.齿轮传动的中心距和啮合角
2.1 外啮合传动
2.1.1 齿轮正确安装的条件: 1、齿侧间隙为零:
即 s'1 e'2 及s'2 e'1
机械设计基础习题答案

绪论一、判断题(正确T,错误F)1. 构件是机械中独立制造的单元。
(F )2. 能实现确定的相对运动,又能做有用功或完成能量形式转换的机械称为机器。
(T )3. 机构是由构件组成的,构件是机构中每个作整体相对运动的单元体。
(T )4. 所有构件一定都是由两个以上零件组成的。
(F )二、单项选择题1. 如图所示,内燃机连杆中的连杆体1是( B )。
A 机构B 零件C 部件D 构件2. 一部机器一般由原动机、传动部分、工作机及控制部分组成,本课程主要研究( B )。
A 原动机B 传动部分C 工作机D 控制部分三、填空题1. 构件是机械的运动单元体,零件是机械的______单元体。
2. 机械是______和______的总称。
参考答案一、判断题(正确T,错误F)1. F2. T3. T4. F二、单项选择题1. B2. B三、填空题1. 制造2. 机构机器第一章平面机构的自由度一、判断题(正确T,错误F)1. 两构件通过点或线接触组成的运动副为低副。
( F )2. 机械运动简图是用来表示机械结构的简单图形。
(F )3.两构件用平面低副联接时相对自由度为1。
(T )4. 将构件用运动副联接成具有确定运动的机构的条件是自由度数为1。
( F )5. 运动副是两构件之间具有相对运动的联接。
(F)6. 对独立运动所加的限制称为约束。
(T )7. 由于虚约束在计算机构自由度时应将其去掉,故设计机构时应尽量避免出现虚约束( F )8. 在一个确定运动的机构中,计算自由度时主动件只能有一个。
( F )二、单项选择题1. 两构件通过( B )接触组成的运动副称为高副。
A 面B 点或线C 点或面D 面或线2. 一般情况下,门与门框之间存在两个铰链,这属于(C )。
A 复合铰链B 局部自由度C 虚约束D 机构自由度3. 平面机构具有确定运动的条件是其自由度数等于(C )数。
A 1B 从动件C 主动件D 04. 所谓机架是指( D )的构件。
齿轮啮合原理2
加工齿数范围
1
12~13
2
14~16
3
17~20
4
21~25
1、齿廓啮合基本定律
齿廓啮合基本定律及渐开线齿形
3 P13 o1 ω1 1 (P12) k1 k n i12=1/2= C
对齿轮传动的基本要求是保证 瞬时传动比:
两齿廓在任一瞬时(即任意点k接 触时)的传动比:i12=1/2 点p是两齿轮廓在点K接触时的相 对速度瞬心, 故有 Vp= o p= o p
' N2
o2 o'2 '
2
4、啮合角是随中心距而定的常数
•啮合角——— 过节 点所作的两节圆的内 公切线(t — t)与两齿 廓接触点的公法线所 夹的锐角。用'表示。
一对齿廓啮合过程 中,啮合角始终为常数。 当中心距加大时,啮合 角随中心距的变化而改 变。 啮合角在数值上 等于节圆上的压力角。
1 o1
1 O2 P i12 2 O1 P
1 1
2 2
p
n
2 P23
由此可见,两轮的瞬时传动比与瞬时接触 点的公法线把连心线分成的两段线段成反比。 o2
ω2
要使两齿轮的瞬时传动比为一 常数,则不论两齿廓在任何位置接 触,过接触点所作的两齿廓公法线 o1 都必须与连心线交于一定点p 。 节圆 1 r2
三、无侧隙啮合传动
四、连续传动的条件
(1)一对渐开线轮齿的啮合过程
一对轮齿在啮合线上啮合的起 始点—— 从动轮2的齿顶圆与 啮合线N1N2的交点B2
一对轮齿在啮合线上啮合的终 止点—— 主动轮的齿顶圆与 啮合线N1N2的交点B1。
o1 ra1
N2 B1
1 rb1
简述齿廓啮合基本定律

简述齿廓啮合基本定律
齿廓啮合基本定律是指在齿轮啮合过程中,齿轮的齿廓形状必须满足一定的规律。
具体来说,它包括以下三个定律:
1. 齿廓曲线法向量定律:齿廓曲线上的法向量必须始终指向啮合点。
2. 等倾条件定律:齿廓曲线上的压力角必须始终相等。
3. 接触线条件定律:齿廓曲线必须与接触线相切。
这些定律保证了齿轮能够正常啮合并传递动力。
在设计齿轮时,必须根据齿轮的模数、压力角、齿数等参数,合理地确定齿廓形状,以满足上述基本定律。
- 1 -。
齿轮机构的齿廓啮合基本规律特点和类型
第八节 直齿圆锥齿轮传动
圆锥齿轮传动用来传递相交 两轴的运动和动力。
分直齿圆锥齿轮和曲 齿圆锥齿轮
返回
一、传动比和几何尺寸计算
1)分度圆:d1=mz1, d2=mz2 2)齿顶高:ha=m, 齿根高:hf=1.2m
3)传动比:i12= d2/d1 = z2/z1
=ctg δ1=tg δ2
1 2 2 d1 d 2 2 注意:分度圆锥角:δ1=arcctg i12, δ2= 900-δ1 齿顶角:θa1= θa2=arctg ha/R, 齿根角: θf1= θf2=arctg hf/R 锥距: R
图5-20 背锥及当量齿数
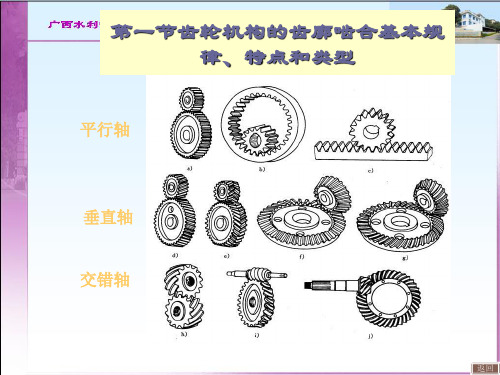
平行轴
垂直轴
交错轴
返回
一、齿轮机构的特点和类型
(一)平行轴线齿轮传动
返回
(二)空间齿轮传动
5
返回
齿轮传动的基本要求
传动准确和平稳(任意瞬时传动比恒定)------由齿
轮轮廓和制造精度决定。
传动比
1 i12 2
承载能力强(足够强度、刚度、耐磨)--------由齿
轮尺寸、材料和工艺决定。
返回
三、正确啮合条件
mn1= mn2 =m αn1= αn2=200 β1= -β2外啮合 (mt1= mt2 ) (αt1= αt2) ( β1=β2内啮合 )
返回
四、当量齿数
图5-18 斜齿圆柱齿轮的当量齿数
zmt 2 d z zv 2 3 pn pn cos pt cos cos3
5、分度圆---圆周上的 P/ π =m(模数)为标准值 GB1357-87,压力角α亦为标准值的圆。 d=m Z,α=200,标准齿轮 P=s+e,s=e= π m/2
齿轮的齿廓曲线--ppt课件(2024版)

将pb=πmcosα代入得: m1cosα1=m2cosα2
因m和α都取标准值,使上式成立 的条件为:
m1=m2,α1=α2
pb2
pb1
由前述可知,一对渐开线齿廓能保证定传动比传动,但这不等于说任意两个渐开线齿轮都能搭配起来正确传动,比如说一个齿轮的齿距很小,另一个齿轮的齿距很大,显然两个齿轮是无法搭配传动的。
§10-5 渐开线直齿圆柱齿轮的啮合传动
*
ppt课件
B1B2——实际啮合线
N1N2: 理论上可能的最长啮合线段——
由于基圆内无渐开线,故B1、B2两点不能超出N1、N2两点,因此N1、N2两点称为啮合极限点。
理论啮合线段
一对轮齿啮合传动的区间是有限的。要使齿轮能连续转动,则在前一对轮齿脱离啮合之前,后一对轮齿必须及时地进入啮合。
基节pb=法节pn
*
ppt课件
rb
O
pn
齿距 (周节)—— pk= sk +ek 同侧齿廓弧长
齿宽(face-width)—— B
ha
hf
h
B
p
ra
法向齿距(法节) —— pn
s
e
sk
ek
= pb(基节)
pb
rf
r
pk
轮齿介于分度圆与齿顶圆之间的部分称为齿顶,其径向高度称为齿顶高,
同一圆上
*
ppt课件
A
K
渐开线
B
发生线
渐开线AK 的展角
O
基圆
rb
(1)渐开线的形成
定直线
*
ppt课件
*
ppt课件
N
发生线
渐开线k0k 的展角
《机械设计原理》齿轮的齿廓曲线

§6-2 齿轮的齿廓曲线
2. 齿廓曲线的选择
共轭:按一定的规律相配的一对。
共轭齿廓:能按预
轭
定传动比规律相互啮
合传动的一对齿廓。
给定预定的传动比和 一条齿廓曲线,可根据 齿廓啮合基本定律求得 另一条齿廓曲线。
§6-2 齿轮的齿廓曲线
能满足一定传动比规律的共轭齿廓曲线有很多。
➢ 瞬时传动比为多少?
2
O2
根据速度瞬心可知,瞬时传动比:
i12 1 / 2 O2P / O1P
§6-2 齿轮的齿廓曲线
O1
1
n K
n
P C2 C1
此式表明:相互啮合传动的一对 齿轮,在任意位置时的传动比,都 与其连心线O1O2被其啮合齿廓在接 触点处的公法线所分成的两线段长 成反比。
这个规律称为齿廓啮合基本定律。
第6章 齿轮机构
§6-2 齿轮的齿廓曲线
主要内容: ➢ 齿廓啮合基本定律 ➢ 齿廓曲线的选择
平均传动比:
i12 n1 / n2 z2 / z1
§6-2 齿轮的齿廓曲线
O1
1. 齿廓啮合基本定律
1
➢ 怎样才能使一对齿廓连续接触而传
n 动?
vc1 vc2
K
n
P C2 C1
两齿廓沿接触点的公法线方向的 速度应相等;相对速度只能沿接触 点处的公切线方向。
比传动。
r2 P 点在轮1或2的运动平面上的轨迹为
一个圆,称为节圆(pitch circle)。
2
O2
传动过程中,两齿轮的节圆作纯滚 动。
§6-2 齿轮的齿廓曲线
变传动比传动:两齿廓的节点P 按其传动比
的变化规律在其连心线上移动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.2 齿廓啮合基本定律与齿轮的齿廓曲线
7.2.1 平均传动比和瞬时传动比的概念
一对齿轮的啮合传动是通过主动齿轮1的齿面依次推动从动齿轮2的齿面而实现的,在一段时间内两轮转过的周数1n 、2n 之比称为平均传动比,用i 或12i 表示,若两轮的齿数分别为1z 、2z ,则
121221
n z i n z == (7-1) 由此可见,两齿轮的平均传动比与其齿数成反比,当一对齿轮的齿数确定后,其平均传动比是一个常数。
但这并不能保证在一对齿廓的啮合过程中,其任一瞬时的传动比(即瞬时传动比)也是常数,因为,这取决于齿面的齿廓形状。
7.2.2 齿廓啮合基本定律
如图7-2所示,设主动轮1和从动轮2分别绕O 1、
O 2轴转动,角速度分别为ω1、ω2,方向相反,两齿廓在K
点接触。
为保证二齿廓既不分离又不相互嵌入地连续转动,要
求沿齿廓接触点K 的公法线n -n 方向上,齿廓间不能有相
对运动,即二齿廓接触点公法线方向上的分速度要相等,
12n n n v v v ==
显然,在切线方向上二齿廓接触点的速度不相等,即
齿廓沿切线方向存在相对滑动。
根据三心定理,两齿轮的相对速度瞬心在过接触点的公法线n -n 与连心线O 1O 2的交点C 上,其速度为:
11
22c v OC O C ωω== 由此可得齿轮机构的瞬时传动比:
1221O C i O C
ωω== (7-2) 从上面的分析可看出,相互啮合传动的一对齿轮,在任一位置时的传动比都与其连心线被齿廓接触点处公法线所分隔的两线段长度成反比。
这一规律称为齿廓啮合基本定律。
该定律表明齿轮的瞬时传动比与齿廓曲线之间的关系。
齿廓啮合基本定律既适用于定传动比齿轮机构,也适用于变传动比齿轮机构。
对于定传动比机构,齿廓啮合基本定律可表达为:两齿廓在任一位置啮合时,过啮合点所作两齿廓的公法线与两轮的连心线相交于一定点。
图7-2 齿廓啮合过程
齿廓啮合基本定律表明:
1、不同的齿廓曲线,其啮合接触点的公法线与连心线的交点不同,因此其瞬时传动比也就不同。
这个交点称为齿轮啮合节点,简称节点。
2、对于给定的一对齿廓曲线,啮合接触点不同,节点C 的位置也可能不同,各个瞬时传动比也就不同。
3、齿轮机构实现定传动比的条件是:一对齿廓曲线不论在何处接触,过接触点所作的公法线与两轮的连心线相交于同一点,即节点C 为连心线上的一个固定点。
7.2.3 共轭齿廓曲线与节圆
1、共轭齿廓曲线
齿轮机构的传动比取决于齿廓曲线的形状,能够实现预定传动比规律(即满足齿廓啮合基本定律)的一对相啮合的齿廓称为共轭齿廓。
从理论上讲,只要给出一条齿廓曲线,就可以根据齿廓啮合的基本定律求出与其共轭的另一条齿廓曲线。
但在生产实际中,结合设计、制造、安装和使用方面的诸多要求(如强度、效率、磨损、寿命、互换性、加工性),通常选用的定传动比齿廓曲线有渐开线、摆线和圆弧。
由于渐开线齿廓具有制造容易、便于安装、互换性好等多方面优点,所以目前大部分齿轮采用渐开线齿廓。
2、节圆
如图7-2所示,两齿轮啮合传动时,节点C 在两轮各自运动平面内的轨迹称为相对瞬心线,它们分别是以O 1、O 2为圆心,以O 1C 、O 2C 为半径的圆C 1和C 2,称为齿轮的节圆。
故节圆就是齿轮的相对瞬心线,齿轮的啮合传动相当于其两节圆作无滑动的纯滚动。
设两齿轮的节圆半径分别为'1r 、'2r ,则齿轮的传动比可表示为一对节圆半径的反比:
122211''
O C r i r O C ωω=== (7-3)。
