2017辽宁单招数学试题【附答案解析】
单招数学试题库及答案

的解集是(
A.
C
B.
C.
75、若指数函数
A.
)
D.
是R上的减函数,则
B.
C.
的取值范围是(
D.
76、已知圆心在点C(1,-3),半径是 2 的圆的标准方程是(
A.
B.
C.
D.
77、函数
B.偶函数
78、与直线
C.非奇非偶函数
B.
C.
79、 函数
B.-1 7
C.32
C.5
81、已知
83、
C
上,则
D.-5
B.
)
C.
56、下列说法中,正确的是( B
D.
)
A. 若
B. 若
C.若
D.
57、用区间表示集合
A.(-1,3]
58、若
正确的是 (
B. [-1,3]
不小于
A.
59、不等式
A.
);
C.(-1,3)
,那么实数
)
D. [-1,3)
的取值范围是(
B.
C.
的解集是( B
B.
D
D.
)
D
)
C.
D.
60、在定义域内下列函数既是奇函数,又是增函数的是( A
4.不等式-2<x≤3 用区间表示正确的是(
A. 〔-2,3〕
)
B.{x∣x>5}
C.{x∣x≥5}
B.f(x)=2x+1
C.f(x)=2x3
D. (-∞,2)
D.{x∣x≠5}
D.f(x)=3x2
D.{4}
12.已知函数 f(x)=x2 -4x ,则 f(-1)= (
辽宁单招真题数学答案解析

辽宁单招真题数学答案解析数学真题答案解析近年来,随着高考竞争的日益激烈,越来越多的学生和家长开始关注单独招生考试,希望通过这一途径获得更好的升学机会。
辽宁省作为单招制度的实施地区之一,单招数学考试一直备受关注。
在本篇文章中,我们将对辽宁省单招数学真题的答案进行解析,帮助考生更好地备考。
首先,我们来解析辽宁省单招数学真题的选择题部分。
选择题是考试中相对简单的一部分,但也是需要细心和技巧的。
考生要注意仔细审题,理解题意后再选择答案。
在计算过程中要注意小数和分数的转换,避免粗心错误。
同时,推荐考生做题时给出具体解题步骤,以便更好地理清思路。
接下来,我们解析辽宁省单招数学真题的解答题部分。
解答题是考生综合能力的考察,需要运用所学的知识进行推算和证明。
考生在解答题时要注意结构完整和条理清晰,给出充分的解题步骤和推理过程。
同时,要注意无论是字母变换还是数字代入,都要将代入的过程清晰地写出,并给出相应的解释。
在计算过程中,要注意步骤清晰、有条不紊,避免出现计算错误。
而对于具体的数学知识点,辽宁省单招数学真题广泛覆盖,如集合与常用逻辑、函数基本概念和性质、直线与曲线、立体图形、概率论与数理统计等。
考生在备考过程中要特别关注这些知识点,对于每个知识点都要进行系统性的学习和掌握。
此外,解析辽宁省单招数学真题还需要注意思维的灵活运用。
在解答题中,往往存在不同的解题思路和方法。
考生可以借鉴一些常用的解题方法,如分类讨论法、递归法、反证法等,以提高解题的效率和准确性。
同时,要学会灵活运用数学工具,如解题公式、计算器等,使解题过程更加顺利。
最后,我们需要提醒考生在备考过程中要注重实际的练习。
辽宁省单招数学真题解析只是一种辅助性的学习方法,真正的提高离不开大量的练习。
考生可以通过刷题软件、参加模拟考试等方式增加练习机会,提高解题速度和准确性。
同时,考生还可以参加一些辅导班和培训机构的辅导,以获得更专业的指导和建议。
总之,数学真题的答案解析是考生备考过程中不可或缺的一部分。
2017年单招数学试题(二)

单招数学试题模拟题
一、选择题(4×10=40分)
1、已知集合A={a 、b 、x},B={x ,y ,z},则A B ⋃=( )
A 、φ
B 、{x}
C 、{a,b,x,y,z}
D 、{a ,b ,y ,z }
2、已知f (x )=x 2-1,则f (-1)=( )
A 、-2
B 、-1
C 、0
D 、1
3、不等式(x-2)(x+1)≤0的解集是( )
A 、(-1,2)
B 、(-∞,-1)⋃ (2,+∞)
C 、[-1,2]
D 、(-∞ ,-1]⋃[2,+∞)
4、“a=0”是“ab=0”的( )
A 充分但不必要条件
B 、必要但不充分条件
C 、充要条件
D 、既不充分也不必要条件
二、填空题(10×3=30分)
1、函数f (x )=x -2 +lg (x-1)的定义域是 ;
2、1+2+3 +100= ;
3、cos30 cos15 -sin30 sin15 的值是 ;
三、解答题(15×2=30分)
1、冰箱里放了形状相同的3罐可乐,2罐橙汁和4罐冰茶,小明从中任意取出1罐饮用,设事件C={取出可乐或橙汁},试用概率的加法公式计算P (C ).
2、某公司推出一款新产品,其成本为500元/件,经实销得知:当销售价为650元/件时一周可卖出350件;当销售价为800元/件时一周可卖出200件。
如果销售量y 可以近似的看销售价x 的一次函数y=kx-b ,问销售价定为多少时,此产品一周能获得的利润最大,并求出最大利润。
2017年辽宁省高考数学试卷(理科)含答案
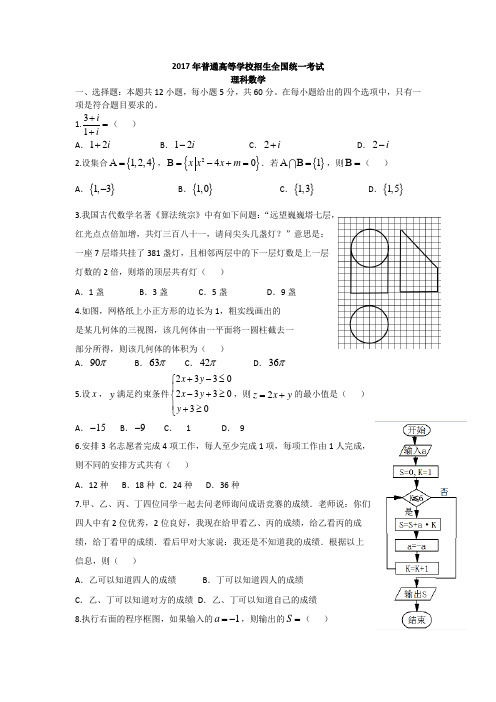
2017年普通高等学校招生全国统一考试理科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.31ii+=+( ) A .12i + B .12i - C .2i + D .2i -2.设集合{}1,2,4A =,{}240x x x m B =-+=.若{}1AB =,则B =( )A .{}1,3-B .{}1,0C .{}1,3D .{}1,5 3.我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层, 红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是: 一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层 灯数的2倍,则塔的顶层共有灯( )A .1盏B .3盏C .5盏D .9盏 4.如图,网格纸上小正方形的边长为1,粗实线画出的 是某几何体的三视图,该几何体由一平面将一圆柱截去一 部分所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π5.设x ,y 满足约束条件2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩,则2z x y =+的最小值是( )A .15-B .9-C . 1D . 96.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成, 则不同的安排方式共有( )A .12种B .18种C .24种D .36种7.甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们 四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成 绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上 信息,则( )A .乙可以知道四人的成绩B .丁可以知道四人的成绩C .乙、丁可以知道对方的成绩D .乙、丁可以知道自己的成绩 8.执行右面的程序框图,如果输入的1a =-,则输出的S =( )A .2B .3C .4D .59.若双曲线C:22221x y a b-=(0a >,0b >)的一条渐近线被圆()2224x y -+=所截得的弦长为2,则C 的离心率为( )A2 BCD.310.已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )ABCD11.若2x =-是函数21`()(1)x f x x ax e -=+-的极值点,则()f x 的极小值为( )A.1-B.32e --C.35e -D.112.已知ABC ∆是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC ⋅+的最小值是( )A.2-B.32-C. 43- D.1- 二、填空题:本题共4小题,每小题5分,共20分。
2017年辽宁省高考数学试卷(理科)含答案

2017年普通高等学校招生全国统一考试理科数学12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有2x 3y -3 < 05 .设x, y 满足约束条件〈2x —3y +3之0,则z = 2x + y 的最小值是()y 3-0A. -15B. -9C. 1D. 96 .安排3名志愿者完成4项工作,每人至少完成 1项,每项工作由1人完成, 则不同的安排方式共有()A. 12 种B. 18 种C. 24 种D. 36 种7 .甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成 绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上 信息,则()A.乙可以知道四人的成绩B. 丁可以知道四人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩8 .执行右面的程序框图,如果输入的 a = T,则输出的S=()1.3^-=( 1 iA. 1 +2iB. 1 -2iC. 2 iD. 2-i2.设集合A =,1,2,4 ) B - lxx2—4x+m=0}.若 A 「B ={1},则 B =() A, {1,-3} B.11,04C. i1,3)D.i1,5)一、选择题:本题共 项是符合题目要求S^S+a ■ Ka 二一a弦长为2,则C 的离心率为()线 g 与BG 所成角的余弦值为()B H511.若x = —2是函数f (x ) =(x 2+ax —1)e"的极值点,则f (x )的极小值为( )一 §3A. -1B. -2eC. 5eD.112.已知 MBC 是边长为2的等边三角形,P 为平面ABC 内一点,则PA (PB + PC )的最小 值是()A. -2B. —C. —D. T23二、填空题:本题共 4小题,每小题5分,共20分。
13 .一批产品的二等品率为 0.02 ,从这批产品中每次随机取一件,有放回地抽取100次,X表示抽到的二等品件数,则D (X )=.14 .函数 f (x } = sin 2x + J 3cosx-3 ( x w ]。
辽宁铁道职业技术学院单招数学模拟试题(附答案解析)

2016辽宁铁道职业技术学院单招数学模拟试题(附答案解析)一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.1.(文)已知命题甲为x>0;命题乙为,那么()A.甲是乙的充分非必要条件B.甲是乙的必要非充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件,也不是乙的必要条件(理)已知两条直线∶ax+by+c=0,直线∶mx+ny+p=0,则an=bm是直线的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.(文)下列函数中,周期为的奇函数是()A.B.C.D.(理)方程(t是参数,)表示的曲线的对称轴的方程是()A.B.C.D.3.在复平面中,已知点A(2,1),B(0,2),C(-2,1),O(0,0).给出下面的结论:①直线OC与直线BA平行;②;③;④.其中正确结论的个数是()A.1个B.2个C.3个D.4个4.(文)在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为()A.1∶B.1∶9C.1∶D.1∶(理)已知数列的通项公式是,其中a、b均为正常数,那么与的大小关系是()A.B.C.D.与n的取值相关5.(文)将4张互不相同的彩色照片与3张互不相同的黑白照片排成一排,任何两张黑白照片都不相邻的不同排法的种数是()A.B.C.D.(理)某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表:表1市场供给量表2市场需求量()A.(2.3,2.6)内B.(2.4,2.6)内C.(2.6,2.8)内D.(2.8,2.9)内6.椭圆的焦点在y轴上,长轴长是短轴长的两倍,则m的值为()A.B.C.2D.47.若曲线在点P处的切线平行于直线3x-y=0,则点P的坐标为()A.(1,3)B.(-1,3)C.(1,0)D.(-1,0)8.已知函数是R上的偶函数,且在(-∞,上是减函数,若,则实数a的取值范围是()A.a≤2B.a≤-2或a≥2C.a≥-2 D.-2≤a≤29.如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为()A.60°B.45°C.0°D.120°10.圆心在抛物线上,并且与抛物线的准线及x轴都相切的圆的方程是()A.B.C.D.11.双曲线的虚轴长为4,离心率,、分别是它的左、右焦点,若过的直线与双曲线的右支交于A、B两点,且是的等差中项,则等于()A.B.C.D.8.12.如图,在正方形ABCD中,E、F、G、H是各边中点,O是正方形中心,在A、E、B、F、C、G、D、H、O这九个点中,以其中三个点为顶点作三角形,在这些三角形中,互不全等的三角形共有()A.6个B.7个C.8个D.9个二、填空题:本题共4小题,共16分,把答案填在题中的横线上13.若是数列的前n项的和,,则________.14.若x、y满足则的最大值为________.15.有A、B、C、D、E五名学生参加网页设计竞赛,决出了第一到第五的名次,A、B两位同学去问成绩,教师对A说:“你没能得第一名”.又对B说:“你得了第三名”.从这个问题分析,这五人的名次排列共有________种可能(用数字作答).16.若对n个向量,…,存在n个不全为零的实数,,…,,使得成立,则称向量,,…,为“线性相关”.依此规定,能说明(1,2),(1,-1),(2,2)“线性相关”的实数,,依次可以取________(写出一组数值即中,不必考虑所有情况).三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤.17.(12分)已知,求的值.18.(12分)已知等比数列的公比为q,前n项的和为,且,,成等差数列.(1)求的值;(2)求证:,,成等差数列.19.(12分)一个口袋中装有大小相同的2个白球和3个黑球.(1)从中摸出两个球,求两球恰好颜色不同的概率;(2)从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率.注意:考生在(20甲)、(20乙)两题中选一题作答,如果两题都答,只以(19甲)计分.20甲.(12分)如图,正三棱柱的底面边长为a,点M在边BC上,△是以点M为直角顶点的等腰直角三角形.(1)求证点M为边BC的中点;(2)求点C到平面的距离;(3)求二面角的大小.20乙.(12分)如图,直三棱柱中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,=3a,D为的中点,E为的中点.(1)求直线BE与所成的角;(2)在线段上是否存在点F,使CF⊥平面,若存在,求出;若不存在,说明理由.21.(12分)已知双曲线C:(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足、、成等比数列,过F作双曲线C在第一、第三象限的渐近线的垂线l,垂足为P.(1)求证:;(2)若l与双曲线C的左、右两支分别相交于点D、E,求双曲线C的离心率e的取值范围.22.(14分)设函数,,且方程有实根.(1)证明:-3<c≤-1且b≥0;(2)若m是方程的一个实根,判断的正负并加以证明.参考答案1.(文)A(理)C2.(文)A(理)B3.C4.(文)D(理)B 5.(文)D(理)C6.A7.C8.B9.A10.D11.A12.C 13.3314.715.1816.只要写出-4c,2c,c(c≠0)中一组即可,如-4,2,1等17.解析:.18.解析:(1)由,,成等差数列,得,若q=1,则,,由≠0得,与题意不符,所以q≠1.由,得.整理,得,由q≠0,1,得.(2)由(1)知:,,所以,,成等差数列.19.解析:(1)记“摸出两个球,两球恰好颜色不同”为A,摸出两个球共有方法种,其中,两球一白一黑有种.∴.(2)法一:记摸出一球,放回后再摸出一个球“两球恰好颜色不同”为B,摸出一球得白球的概率为,摸出一球得黑球的概率为,∴P(B)=0.4×0.6+0.6+×0.4=0.48法二:“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”.∴∴“有放回摸两次,颜色不同”的概率为.20.解析:(甲)(1)∵△为以点M为直角顶点的等腰直角三角形,∴且.∵正三棱柱,∴底面ABC.∴在底面内的射影为CM,AM⊥CM.∵底面ABC为边长为a的正三角形,∴点M为BC边的中点.(2)过点C作CH⊥,由(1)知AM⊥且AM⊥CM,∴AM⊥平面∵CH在平面内,∴CH⊥AM,∴CH⊥平面,由(1)知,,且.∴.∴.∴点C到平面的距离为底面边长为.(3)过点C作CI⊥于I,连HI,∵CH⊥平面,∴HI为CI在平面内的射影,∴HI⊥,∠CIH是二面角的平面角.在直角三角形中,,,∴∠CIH=45°,∴二面角的大小为45°(乙)解:(1)以B为原点,建立如图所示的空间直角坐标系.∵AC=2a,∠ABC=90°,∴.∴B(0,0,0),C(0,,0),A(,0,0),(,0,3a),(0,,3a),(0,0,3a).∴,,,,,,∴,,,,,.∴,,∴,∴.故BE与所成的角为.(2)假设存在点F,要使CF⊥平面,只要且.不妨设AF=b,则F(,0,b),,,,,0,,,,,∵,∴恒成立.或,故当或2a时,平面.21.解析:(1)法一:l:,解得,.∵、、成等比数列,∴,∴,,,,,∴,.∴法二:同上得,.∴PA⊥x轴..∴.(2)∴.即,∵,∴,即,.∴,即.22.解析:(1).又c<b<1,故方程f(x)+1=0有实根,即有实根,故△=即或又c<b<1,得-3<c≤-1,由知.(2),.∴c<m<1∴.∴.∴的符号为正.。
2017辽宁高考数学真题

2017辽宁高考数学真题2017年辽宁高考数学真题2017年的辽宁高考数学真题在难度和题型上都颇具挑战性,考查了学生们对数学知识的掌握和应用能力。
以下将分别对真题中的部分题目进行解析,帮助考生更好地理解并掌握数学知识。
一、解析第一题第一题要求计算一个函数在给定区间内的极值点。
首先,我们需要对函数的导数进行计算,然后求得导函数为0的点,即为极值点。
最后结合区间端点和极值点的函数值进行比较,得出最终的结果。
二、解析第二题第二题是一道概率题,考查了考生对概率计算的掌握程度。
在解答该题时,首先要确定事件的独立性,然后根据题目给定的条件和概率公式进行计算,最后得出最终的概率值。
三、解析第三题第三题是一道几何题,需要考生运用几何知识进行解答。
在解答该题时,要根据题目中给出的条件绘制几何图形,并根据图形的特点和已知条件进行推理,最终得出所求结果。
四、解析第四题第四题是一道复合函数求导的题目,考查了考生对导数计算的理解和掌握能力。
在解答该题时,要根据链式法则和复合函数求导法则进行计算,最终得出导数的结果。
五、解析第五题第五题是一道综合题,综合考查了考生对数学知识的整体掌握能力。
在解答该题时,要综合应用所学的各种知识点,逐步分析和解决问题,最终得出正确的答案。
通过以上对部分高考数学真题的解析,相信考生们对数学知识的学习和应用有了更深入的理解。
希望考生们在备战高考的过程中,不仅要熟练掌握各种数学知识,还要注重实际应用能力的培养,才能在考试中取得优异的成绩。
祝愿所有参加高考的考生们都能取得理想的成绩,实现自己的梦想!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如图,E、F是梯形ABCD的腰AD、BC上的点,其中ABCD2,ABEF//,
若
EFCDAB
EF
,则EDAE .
【答案】
2
2
【解析】取CD的中点,连结AN交EF于点M,如图:
设,1EMmAB,
则
1
12DNNCDCAB
,
∵
EFCDAB
EF
,∴2(1)12m,∴21m,
∵ABEF//,∴
211AEENADDN
,
∴121ADDNAEEN,∴
21
AEEDAE
,
A
B
EF
C
D
M
N
A
B
EF
C
D
∴2EDAE,∴EDAE22.
2.如图,AB是半圆的直径,C是半圆O上异于A、B的点,CDAB,
垂足为D,已知2AD,43CB,则CD .
【答案】23
【解析】∵
2
CBBDBA
,∴2(43)(2)BDBD,
∴
2
6,12BDCDADBD
.
3.如图,AB是圆O的直径,直线CE与圆O相切于点C,ADCE于点D,若圆
O的面积为4
,30ABC,则AD的长为 .
【答案】1
【解析】设圆O的半径为r,则
2
4r
,∴2r,
∵AB是圆O的直径,∴4AB.
∵30ABC,∴
1
22ACAB
.
∵30ACDABC,90ADC,
O
A
B
C
D O
A
D
E
C
B
O
∴
1
12ADAC
.
4.如图,是⊙的直径,是延长线上的一点,过作⊙的
切线,切点为,23PC,若30CPA,则⊙的直径
.
【答案】4
【解析】PC是⊙的切线,连接OC,
∴90OCP,
∵30CPACPO,
tan
OC
CPOPC
,
∴tan23tan302OCPCCPO,∴4AB.
ABOPABP
O
C
32PC
O
AB
O
C
O
A
B
P
5.如图,已知圆中两条弦AB与CD相交于点F,CE与圆相切交AB延长线上于点
E
,若22DFCF,::4:2:1AFFBBE,则线段CE的长为 .
【答案】7
【解析】∵22DFCF,
∴DFCFAFFB,
∴22228AFFB,
∵::4:2:1AFFBBE,
∴428BEBE,∴1BE,
∴4AF,2FB,7AE,
∵BACBCE,EE,
∴ACE∽CBE,
∴
BECE
CEAE
,7CEBEAE.
6.如图所示,AB与CD是圆O的直径,ABCD,P是AB延长线上一点,连
PC
交O于点E,连DE交AB于点F,若42BPAB,则PF .
A
B
C
D
E
F
O
E
FDPCB
A
【答案】3
【解析】∵42BPAB,∴2OC,4OP,
∴
22
25PCOCOP
,
∵PEPCPBPA,
∴
126255PBPAPEPC
,
∵PEF∽POC,PA是圆O的切线,
∴
PEOP
PFPC
,
6
25534PEPCPFOP
.
