整式的乘除与因式分解复习学案
整式的乘除与因式分解复习导学案
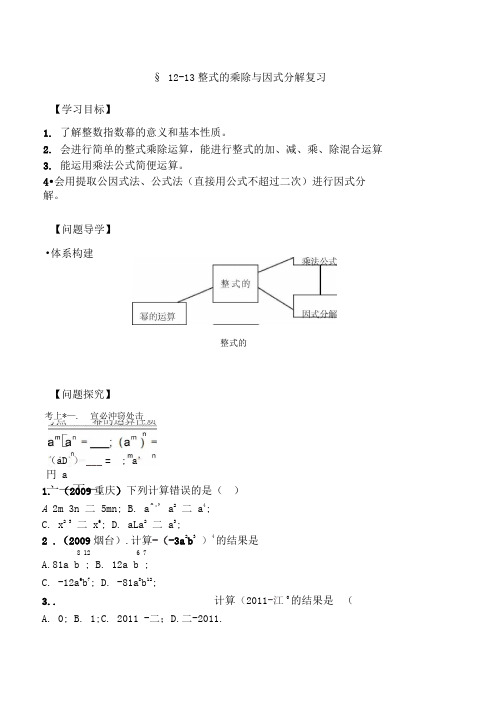
§ 12-13整式的乘除与因式分解复习【学习目标】1. 了解整数指数幕的意义和基本性质。
2. 会进行简单的整式乘除运算,能进行整式的加、减、乘、除混合运算3. 能运用乘法公式简便运算。
4•会用提取公因式法、公式法(直接用公式不超过二次)进行因式分解。
【问题探究】1. (2009重庆)下列计算错误的是( ) A 2m 3n 二 5mn; B. a^:' a 2 二 a 4;C. x 2 3 二 x 6;D. aLa 2 二 a 3;2 .(2009烟台).计算-(-3a 2b3 )4的结果是8 12 6 7 A.81a b ; B. 12a b ;C. -12a 6b 7;D. -81a 8b 12;3.. 计算(2011-江0的结果是 (A. 0;B. 1;C. 2011 -二;D.二-2011.考上*—. 宣必沖窃处击(aD ) ___ = ; a円 a亠—丁―. 【问题导学】•体系构建整式的考点二乘法公式 a+b a-b = ______ ;2 2(a+b ) =; (a-b ) =4. 下列运算结果错误的是 ()2 2 2 2 2A x y x - y = x - y ; B. a- b \ - a - b ;2 2 2C. -x-2 x 4x 4;D. x 2 x-3 = x -x-6;5. 在边长为a 的正方形中挖去一个边长为 b 的小正方形(a . b )(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可 考点三整式的运算乘法法则:;除法法则:;混合运算顺序:先乘方,再,最后,有括号的先计算的,注意乘法公式简化运算。
7. (2009泸州)化简-3x 2 2x 3的结果是( )A. -6x 5;B. -3x 5;C. 2x 6;D. 6x 5.38.. 计算(2x ) U 的结果正确的是( ).A.8x 2;B. 6x 2;C. 8x 3;D. 6x 3.9.计算:ab 2 L -a 3b 「丨 5ab ;考点四因式分解 以验证()A .B .C . 2 2 2(a b)二a 2ab b2 2 2(a -b) -a -2ab b2 2a -b = (a b)(a -b)2 2(a 2b)(a _b) =a ab -2b a2011- 20102.(用乘法公式)D . b图乙10.下列各式从左到右的变形中,是因式分解的是()2A.x 1 x 2 = x 3x 2;B.2a b c = 2ab 2ac;2 2C.m -n mn m-n;2D.x「4 2x = (x 2)(x「2) 2x11.把多项式x3-2x2• x分解因式结果正确的是()2 2A . x(x -2x)B . x (x「2)2C. x(x 1)(x -1)D. x(x -1)12.因式分解:(1)9a-a3 = ________ ;(2) 2x3 -6x2 +4x = _________ .【达标检测】—、填空题1.(2010大理)下列运算中,结果正确的是()6 3 2 2 22 4A. a ' a =a ;B. 2ab i;=2a b ;C. aLa2 a3;D. a b $ = a2 b2;2.下列计算结果正确的是. ).A. -2x2y3Ltxy =「2x3y4;B. 3x2y -5xy2=「2x2y;C.28x4y2,7x3y =4xy;D. -3a-2 3a-2 i; = 9a2-4.3.把x2 3x c分解因式得x2 3x x 1 x 2 ,则c的值为()A. 2;B. 3;C. -2;D. -3.4 . (2009 枣庄)若 m n =3,则 2m2 4mn 2n2 -6 的值为()A. 12;B. 6;C. 3;D. 0.二、选择题5.(2010 清远)计算:a* + a2=_;6.(2009贺州)计算:f-2^\-a3-^= ;\4丿7.(2009 齐齐哈尔)已知 10m =2,10n =3,则 103m '2^ _________ 三、解答题8.先化简,再计算:[】xy 2 xy-2 -2右-2八xy ,其中x =10, y =-9.(2009衢州)给出三个整式a2、b2和2ab.(1)当 a =3,b =4 时,求 a2 b2 2ab 的值;(2)在上面的三个整式中任意选择两个整式进行加法或减法运算,使所得的多项式能够因式分解,请写出你所选的式子及因式分解的过程。
第十五章 整式的乘除与因式分解 全章学案

15.1.1同底数幂的乘法自主学习重难点:1.熟记同底数幂的乘法的运算性质,了解法则的推导过程 2.能熟练地进行同底数幂的乘法运算学习过程:二.1. 同底数幂的乘法概念:探究:根据乘方的意义填空,看看计算结果有什么规律。
(1) 2×2×2×2×2=(),a·a·…·a=( )m个(2) 23×22=( )×( )=2( ),(3) 53×52=( )×( )=5( ),(4) a3a4=( )×( )=a( )。
(5) a n中a叫,n叫做,它表示。
2.同底数幂的乘法法则如果把a3×a4中指数3和4分别换成字母m和n(m、n为正整数)同底数幂的乘法法则:同底数幂相乘, 不变, 相加.(1) 公式:a m·a n=(m、n为正整数)(2) 推广:a m·a n·a p=(m、n、p为正整数)例1计算:(1) 52)()(xx•;(2) 6)()(aa•;➢熟记同底数幂的乘法的运算性质,了解法则的推导过程。
➢学习目标一.141~142(3) 34)2()2(2⨯⨯ ; (4) 13)()(+•m m x x 。
例2,计算:32)()(a a -⋅-例3:光的速度为3×510千米/秒,太阳光照射到地球上约需5×210秒,问:地球离太阳多远?若飞机时速856千米/秒,飞行这么远的距离需多长的时间?练习:① 23)()(x x -⋅- ②23)()()(a a a -⋅-⋅-③ n n t t -+-⋅-123)()( ④ y 2n ·y n+115.1.2幂的乘方自主学习重难点:1.熟记幂的乘方的运算法则2. 了解幂的乘方的运算性质学习过程:1.如果—个正方体的棱长为16厘米,即42厘米,那么它的体积是多少?2.计算:(1)a 4·a 4·a 4; (2)x 3·x 3·x 3·x 3。
《整式的乘法与因式分解复习》导学案

第14章整式的乘法与因式分解复习导学案【学习目标】1、复习整式乘除的基本运算规律和法则,因式分解的概念、方法以及两者之间的关系.2、通过练习,熟悉常规题型的运算,并能灵活运用.【重点难点】重点:整式的乘除运算与因式分解难点:灵活进行整式的乘除运算和多项式的因式分解.一、知识梳理1. 有关法则⑴幂的四个运算性质:(2)单项式乘以单项式的法则:把系数、同底数幂分别相乘后,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数一起作为积的一个因式.⑶单项式与多项式相乘的法则:单项式与多项式相乘,就是根据乘法分配律用单项式去乘多项式的每一项,再把所得的积相加.⑷多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.⑸单项式除以单项式的法则:把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.⑹多项式除以单项式法则:先把这个多项式的每一项除以这个单项式,再把所得的商相加.2. 有关公式:⑴平方差公式:两个数的和与这两个数差的积等于这两个数的平方差,用字母表示为:(a+b)(a-b)= a2- b2.⑵完全平方公式:两个数和(或差)的平方,等于它们的再加上(或减去)这两数的平方,即:(a±b)2=a2±2 a b+ b2.3. 有关概念 ⑴因式分解:把一个多项式化为几个整式的积的形式,叫做多项式的因式分解.⑵提公因式法:把多项式各项的公因式提出来,这种分解因式的方法叫做提公因式法,即am bm cm ++=m (a +b +c ).提公因式法的实质是逆用乘法分配律.⑶公式法:把乘法公式()()a b a b +-= a 2- b 2、2()a b ±= a 2±2 a b + b 2逆用,就得到分解因式的公式22a b -=(a +b )(a -b ),222a ab b ±+=(a ±b )2,这种运用公式分解因式的方法叫做公式法.(4)十字相乘法:pq x q p x +++)(2=(x +p )(x +q )。
整式乘法与因式分解复习学案

课题:整式的乘除与因式分解复习 课型:单元强化巩固课学习目标:1.掌握幂的运算法则和整式乘法;2.会对一个多次式进行因式分解。
学习环节学习重点:整式乘法和因式分解的区别与联系 学习难点:知识的综合应用一、前置作业一、知识点 1、幂的运算同底数幂相乘文字语言_________________ 符号语言____________.幂的乘方文字语言_____________________; 符号语言____________.积的乘方文字语言_______________________________; 符号语言____________.同指数幂相乘文字语言____________________________; 符号语言____________.同底数幂相除文字语言____________________________; 符号语言____________. 2、整式的乘除法单项式乘以单项式_________________________________ 单项式乘以多项式________________________________; 多项式乘以多项式________________________________; 单项式除以单项式______________________________ ;、 多项式乘以单项式________________________________。
3、乘法公式 平方差公式 :文字语言____________________________; 符号语言______________。
完全平方公:文字语言_______________________; 符号语言______________4、添括号法则____________________________________5、因式分解定义:___________________________________________ 方法:(1)________;(2)_________(___________________) 步骤:______________________________二、基础知识:1.计算:(1)32a a ⋅=_______;(2)43)(x =_______;(3)32)(ab =_______;(4)35a a ÷=___________;(5)b a ab 32552⋅-=__(6)32348923y x z y x ÷-=____(7))2)(2(y x y x +-=___________; (8)2)32(b a -=___________(9))23)(25(b a b a -+=___________;2.(1)边长为a 、b 的长方形,它的周长为14,面积为10,则22ab b a +的值为________。
《整式的乘除与因式分解全章复习》(优质视频实录+配套课件+配套教案+配套练习等素材)

新世纪教育网版权所有单位租用个人充值QQ:448966300 第15课时整式的乘除与因式分解复习
教学建议
一、教材分析
整式的乘除与因式分解是八年级上册数学中最难的一个内容,也是今后学习分式和根式运算、函数知识的基础.虽然学生在七年级上册已经初步了解了整式的概念、分类和加减运算,但本章的所学内容的难度远远超过了前面所学的.尤其是本章中出现的因式分解,更是令大多数学生深感头痛.究其原因就是相当部分学生对整式乘除运算、乘法公式掌握不好.
二、设计理念
1、本节课,以多层次的习题为主线,充分调动学生学习的主动性,注重培养学生观察、分析、对比、归纳的学习行为,突出学生在教学过程中的主体地位.
2、在复习因式分解及其运用中,重点帮助学生学会分析,要求学生从不同方法去试探,帮助学生去总结规律,不断提高运用能力,充分发挥教师的引领作用.
3、本节课教学设计环环相扣、层层推进,学生主动参与,掌握的程度较高,达到预计效果.
三、教学建议
针对教材内容和初二学生的实际情况,达到会算、会灵活运用、会选择运用本章知识来解决有关实际问题的目的.
1、在课堂上要关注学生公式的熟练选择运用,通过有效的练习来加强对知识的记忆和理解,并并对极少数学习有困难的学生要检查、落实,指导.
2、突破教学难点时不要着急,要善于分层教学和对知识的引导.
新世纪教育网版权所有单位租用个人充值QQ:448966300。
数学人教版八年级上册《整式的乘除与因式分解(复习课)》教学设计

《整式的乘除与因式分解(复习课)》教学设计玉州区城西一中黄夏静一、教学内容:整式的乘除与因式分解(复习课)二、教学目标:1、掌握整式的运算的有关公式和规律2、掌握因式分解的方法3、培养学生分析问题解决问题的能力三、教学重难点:重点:整式的乘除与因式分解的运算难点:因式分解公式的灵活运用四、教学过程:一、整式的有关概念1、代数式2、单项式3、单项式的系数及次数4、多项式5、多项式的项、次数6、整式(一)整式的加减法去括号,合并同类项(二)整式的乘法1、同底数幂的乘法2、幂的乘方3、积的乘方4、同底数的幂相除5、单项式乘以单项式6、单项式乘以多项式7、多项式乘以多项式8、平方差公式9、完全平方公式(三)整式的除法1、单项式除以单项式2、多项式除以单项式1、单项式数与字母乘积,这样的代数式叫单项式。
单独的一个数或字母也是单项式。
2、单项式的系数:单项式中的数字因数。
3、单项式的次数:单项式中所有的字母的指数和。
4、多项式:几个单项式的和叫多项式。
5、多项式的项及次数:组成多项式中的单项式叫多项式的项,多项式中次数最高的项的次数叫做这个多项式的次数。
特别注意,多项式的次数不是组成多项式的所有字母指数和!!!6、整式:单项式与多项式统称整式。
(分母含有字母的代数式不是整式)二、整式的运算(一)整式的加减法基本步骤:去括号,合并同类项。
(二)整式的乘法1、同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加。
数学符号表示:2、幂的乘方法则:幂的乘方,底数不变,指数相乘。
数学符号表示:3、积的乘方法则:积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。
符号表示:4.单项式与单项式相乘的法则:单项式与单项式相乘,把它们的系数、相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
5 .多项式与多项式相乘:(a+b)( m+n)=am+an+bm+bn法则: 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.6.乘法公式:(1)、平方差公式 mn n m a a =)(mn n m a a =)()()(),(,)(为正整数其中为正整数其中n c b a abc n b a ab n n n n n n n ==即两个数的和与这两个数的差的积,等于这两个数的平方差。
整式的乘除复习学案

七年级数学学科导学案一、 课题:《整式的乘除复习学案》 二、 复习目标:1、 整式的混合运算,提高整式的运算能力;2、 整式的综合应用,对全章知识体系的梳理和把握;3、 通过实践,培养学习数学的严谨态度。
学习重点:整式的综合应用,特别是乘法公式的灵活应用。
学习难点:乘法公式的灵活应用。
知识点: 三、 教学过程【温故知新】m n1、同底数幕的乘法,底数不变,指数相加。
即:a a都是正整数)。
C 5C 6(1) 3 3a 7 a 4 (1) — 5、整式的乘法:(1) 单项式与单项式相乘,把它们的系数、相同字母的幕分别相乘, 其余字母连同它的指数不变,作为积的因式。
2xy 2z 1 xy ____________如: 3。
(2) 单项式与多项式相乘,用这个单项式去乘以这个多项式的每一 项。
(注意符号)反思 栏1 2mb2、幕的乘方,底数不变,指数相乘。
整数)。
即:a mn a mn m,n 都是正32 .55(1) 2 = _________ (2) b—3、积的乘方等于每一个因数乘方的积。
r n J即:a bn2n 1x填空:(1)3x 2(3)1?xy4、同底数幕相除,底数不变,指数相减。
0,m, n 都是正整数,且 即:m > n ), (a0, P 是正整数)4(3) xyxy4ab 2ab 23a 2b(3)多项式与多项式相乘,用一个多项式的每一项去乘以另一个多 项式的每一项。
2x y x 2y6平方差公式:两数和与这两数差的积,等于它们的平方差。
(1) 有两项(2) 一项相同另一项互为相反数(3)变形为相同的在第一项, 互为相反数的在第二项(4)多项的要运用整体法。
2 .2a b o 即:a b a b / 八 5 8x 5 8x (1)7、完全平方公式: a b 2a 22a ----------- (2) (a-b+c) (a+b-c)=(1)和的完全平方:(2 )差的完全平方:b b 2a b 242(1) 2x同时,也可以用观察情境来推导,如图所示(2)mn2ab b 2。
第十五章整式的乘除与因式分解复习课学案

整式的乘除与因式分解复习 一、知识回顾:1、代数式的分类: 整式有关概念 (1)单项式:表示 的积的式子叫做单项式。
单项式中____________叫做这个单项式的系数;单项式中___________ _叫做这个单项式的次数;单独的数或字母也是单项式。
(2)多项式:几个 的和,叫做多项式。
在多项式里,每个单项式叫做多项式的 ,其中___________ 叫做常数项。
多项式中 的次数,就是这个多项式的次数。
例1:单项式252axy -的系数是 ,次数是 ;多项式πππ2322--r R 次数是 ,常数项是 。
2、整式的运算⑴同类项:所含 相同,并且 也相同的项,叫做同类项。
⑵整式的加减其实就是合并同类项。
例2、⑶整式的乘除法:①幂的运算:01;;();();1;(0,)m n m n m n m n m n mn n n n p p a a a a a a a a ab a b a a a p a+--⋅=÷=====≠为整数 ②整式的乘法法则 单项式与单项式相乘:把系数、____________的幂分别相乘。
对于只在一个单项式中含有字母,连同指数作为积的______。
单项式乘以多项式:()m a b += 。
多项式乘以多项式:()()m n a b ++= 。
③乘法公式:平方差: 。
完全平方公式: 。
2()()()a b x a x b x a b x ab ++=+++、型公式:④整式的除法:单项式除以单项式:把系数与 幂分别相除作为_______的因式,对于只在被除式里含有的______,则连同它的指数作为商的一个______.多项式除以单项式:先把这个多项式的_________除以这个单项式,再把所得的_____相加。
代数式 有理式无理式二、巩固练习:1、计算:⑴ )8()52()2(42232y x y x y x ÷-⋅ ⑵ )3()]92(2)32[(2y y x x y x -÷+-+⑶(a 2b -1)(1+a 2b ) ⑷(-2x -3)2 ⑸2)2(c b a +-2、⑴如图,边长为a 、b 的矩形,它的周长为14,面积为10,则22ab b a +的值为________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
整式的乘除与因式分解复习
教学目标:通过知识的梳理和题型训练,提高学生观察、分析、 推导能力,培养学生运用数学知识解决问题的意识。
重点 :根据新课标要求,整式的乘除运算法则与方法和因式分解的方法与应用 难点 : 整式的除法与因式分解的应用是本课难点。
教学过程
一.回顾知识点
(一)整式的乘法
1、同底数的幂相乘
2、幂的乘方
3、积的乘方
4、同底数的幂相除
5、单项式乘以单项式
6、单项式乘以多项式
7、多项式乘以多项式 8、平方差公式
9、完全平方公式
(二)整式的除法
1、单项式除以单项式
2、多项式除以单项式
(三)因式分解
1、因式分解的概念
2、因式分解与整式乘法的关系
3、因式分解的方法
4、因式分解的应用
二.练习巩固
(一)单项式乘单项式
(二)单项式与多项式的乘法
(三)乘法公式应用
)31()43()32)(4(),())(3()
4()3)(2(),2()5)(1(25322323223c ab c bc a b a b a b ab y x x n m ⋅-⋅--⋅--⋅--⋅)212)()(3()2)(1()3)(2)(2(),32()2)(1(y x y x y x y x c y x a --+-+-++-+⋅-
(四)整式的除法
(五)提取公因式法因式分解
(1) 3ay-3by+3y
(2) -4a3b2+6a2b-2ab
(3) 3(x-y)3-6(x-y)2
(4) 5m(a-b)4-4m2(b-a)3
(六)乘法公式因式分解
(1) 25-16x2
(2) -81x2+4(y-1)2
(3) x2-14x+49
(4) (x+y)2-6(x+y)+9
(七)因式分解的应用
1、解方程
(1)9x2+4x=0 (2) x2=(2x-5)2
2、计算
(1)(2mp-3mq+4mr)÷(2p-3q+4r)
(2)(16-x4 )÷(4+x2) ÷(x-2)
三.探究活动:
求满足31942
2=-y x 的正整数解。
)
73)(73)(3()9)(4)(2()6)(6)(1(y x y x y x y x y x y x --+-+--+-)5.0()4331)4()
6()645)(3(])(3
1[)(6)2()2(()4
1)(1(21231221223233225346y x y x y x y x x x y x y x b a b a c a c b a m m m n m -+--÷+-÷+--÷-÷-。
